다단 천음속 축류홴에서 블레이드 스윕이 공력 성능에 미치는 영향

1. 서 론

항공기 엔진으로 사용되는 가스터빈의 압축기 앞 부분에 장착되는 넓은 코드(Chord)를 갖는 축류홴(Axial fan)은 항공기의 운전 상태에 따라 입구 유동의 변화가 심하기 때문에 안정적이고 넓은 운전범위를 가져야할 뿐 아니라 고효율 설계가 이루어져야 한다. 이러한 설계 목표를 달성하기 위해 지난 수십 년 간 동익(Rotor) 형상 제어 방법들이 연구되어 왔다. 특히, 동익의 스윕(Sweep) 및 린(Lean) 등과 같은 반경방향 중첩선(Stacking line)의 변화가 축류홴의 성능에 미치는 영향에 대한 연구가 많이 진행되었으며, 중첩선의 원주방향 변화가 천음속 축류홴에 발생하는 충격파와 팁 누설 와류(Tip leakage vortex)의 구조를 변화시켜 축류홴의 작동 안정성에 영향을 미친다는 것이 밝혀졌다.^(1,2) 충격파와 팁누설 와류의 상호작용으로 인해 발생하는 실속현상은 심한 진동을 유발하게 되어 효율과 작동 안정성의 저하를 야기하는 것으로 알려져 있다.⁽³⁾

Samad 등⁽⁴⁾은 단열 효율, 전압력비 및 전온도비를 향상시키기 위해 스윕, 린 및 스큐(Skew)를 적용한 동익의 형상에 대해 다양한 대리모델을 사용하여 최적설계를 수행하였다. Wu 등⁽⁵⁾은 중첩선의 스윕과 허브 반경을 변화시켜 동익의 압력비를 향상시켰으며, Wadia 등⁽⁶⁾은 단단 축류 압축기의 동익에 대하여 회전방향으로 스윕한 전향익(Forward-curved blade)과 반대방향으로 스윕한 후향익(Backward-curved blade)을 사용하여 각 동익의 형상 변화가 축류 압축기의 공력성능에 미치는 영향을 실험을 통해 분석하였다. 전향익을 사용한 단단 축류압축기의 효율과 스톨 마진(Stall Margin)이 향상되었으나 후향익을 사용한 경우 상대적으로 효율과 스톨 마진이 감소된 것을 확인하였다.

Hah 등⁽⁷⁾은 동익이 전향익 혹은 후향익으로 구성된 축류압축기의 수치해석을 통해 내부 유동 및 공력성능을 분석하였다. 동익의 팁 부근에서 전향익의 경우 충격파가 후향익보다 상대적으로 하류에서 발생하였으며, 유동이 더 안정되는 것을 확인하였으나, 전향익을 사용할 경우 동익에 작용하는 부하가 증가하게 되어 구조적으로 불안정하게 되는 단점이 발생하였다.

이상과 같이 축류 압축기의 작동 안정성과 효율을 향상시키기 위해 내부 유동장 분석과 동익 형상 제어에 대한 많은 연구들이 수행되어 왔다. 그러나 항공기용 가스터빈의 축류 압축기 앞부분에 장착되는 넓은 코드를 갖는 다단 천음속 축류홴에 대해서는 고회전 상태에서의 천음속 유동 특성과 저회전 상태에서의 아음속 유동 특성을 모두 고려한 연구는 수행되지 않았다.

따라서 본 연구에서는 동익의 구조적 안정성을 고려하여 블레이드 스윕에 제한을 두어 조절함으로써, 서로 다른 회전속도에서 동익의 스윕 변화가 천음속 다단 축류 홴의 공력성능에 미치는 영향을 삼차원 레이놀즈평균 나비어-스톡스 방정식(Reynolds-averaged Navier-Stokes equations; RANS)을 사용하여 분석하였다.

2. 연구방법

2.1 연구대상

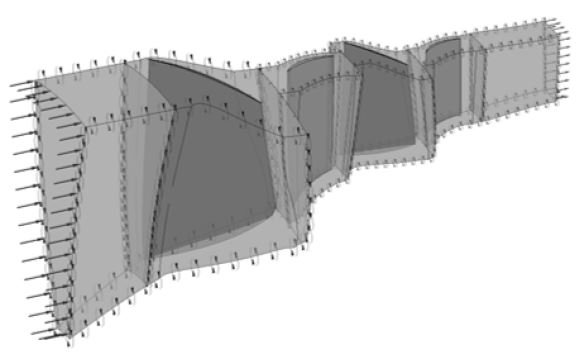
본 연구에서 사용된 천음속 축류홴의 삼차원 형상은 Fig. 1과 같이 총 2단으로 구성되어 있고, 1단은 18개의 동익과 40개의 정익으로 구성되었으며 2단은 36개의 동익과 56개의 정익으로 구성되었다. 본 천음속 축류홴은 0.301의 유량계수에서 0.984의 전압계수를 갖도록 설계되었고, 유량계수와 전압계수는 다음과 같은 식으로 표현된다.

Fig. 1

3D geometry of multi-stage transonic axial fan

$\[ \varphi =\frac{Q}{\frac{\pi }{4}{D}^{2}U} \]$

(1)

$\[ \psi =\frac{\mathrm{\Delta }{P}_t}{U^2\rho } \]$

(2)

여기서 Q, D 및 U는 각각 유량, 팁 직경 및 팁 속도를 의미하고, ΔP_t 과 ρ는 각각 전압상승과 작동유체의 밀도를 의미한다. 자세한 설계사양은 Table 1에 나타내었다.

Table 1

Design specifications for the transonic axial fan

2.2 유동해석 방법

본 연구에서는 천음속 축류홴의 공력성능과 유동장 분석을 위해 상용코드인 ANSYS CFX-15.0⁽⁸⁾을 사용하였고, 난류모델로는 SST Reattachment Modification 모델⁽⁹⁾을 사용하여 RANS 해석을 수행하였다. SST Reattachment Modification 모델은 기존의 SST 모델의 난류운동에너지 방정식에 압력항을 추가하여 유동의 박리이후 재부착 지점 예측을 향상시킨 모델이다.⁽⁹⁾ 계산영역은 Fig. 2와 같이 회전방향으로 주기조건을 적용하여 단일유로로 구성하였으며 회전영역과 정지영역의 경계면에는 상류영역의 물성치를 평균하여 하류영역으로 입력시키는 방식인 Stage기법을 적용하였다. 입구의 경계조건은 균일한 상태의 전압력과 전온도 조건으로 대기압인 101,325 Pa과 상온인 288.15 K를 각각 적용하였으며, 단일 유로에 대한 질량유량과 균일한상태의 정압을 출구의 경계조건으로 부여하였다.

Fig. 2

Computational domain

2.3 동익 스윕

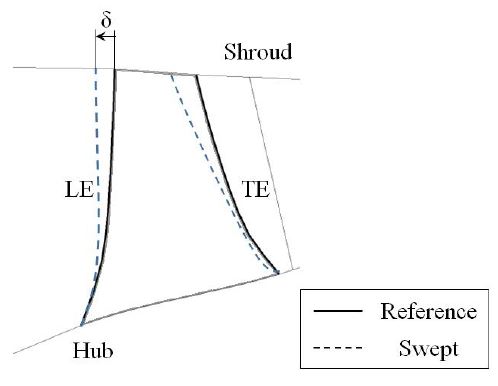
Fig. 3에서는 본 연구에서 적용한 천음속 축류홴 첫 단 동익의 스윕을 도식화 하였다. Fig. 3에서 보는 바와 같이 동익 팁에서의 스윕을 정의하고, 스윕의 기준선은 기준 모델(Reference)의 허브에서 팁까지의 반경선으로 정의하였다. 스윕의 변화량(δ)은 동익의 허브를 기준으로 팁까지 11개의 층을 구성하여 각 층에서 선형적으로 증가 시켰고, 다음과 같은 식으로 정의하였다.

Fig. 3

Schematic of blade sweep

$\[ {\delta }_N=a\frac{\left(R_N-R_{hub}\right)}{\left(R_{tip}-R_{hub}\right)}, \left(N=hub,\mathrm{1,2}, \cdots ,9,tip\right) \]$

(3)

여기서 δ_N와 R_N은 각각 각 층의 스윕 변화량과 허브로부터의 반경을 의미하고, a는 상수이다.

동익 팁에서의 스윕 변화량(δ_tip)에 대해서는 천음속 축류홴의 구조적 안정성을 고려하여 ±0.9 mm의 범위로 제한하였고, 스윕 변화량이 0인 동익 형상을 기준 모델로 정의하였다. 본 연구에서 고려된 Model 1과 Model 2의 경우 동익 팁의 스윕 변화량은 각각 0.9 mm (전향익) 와 –0.9 mm (후향익)로 설정하였다.

3. 결과 및 검토

3.1 격자의존성 테스트

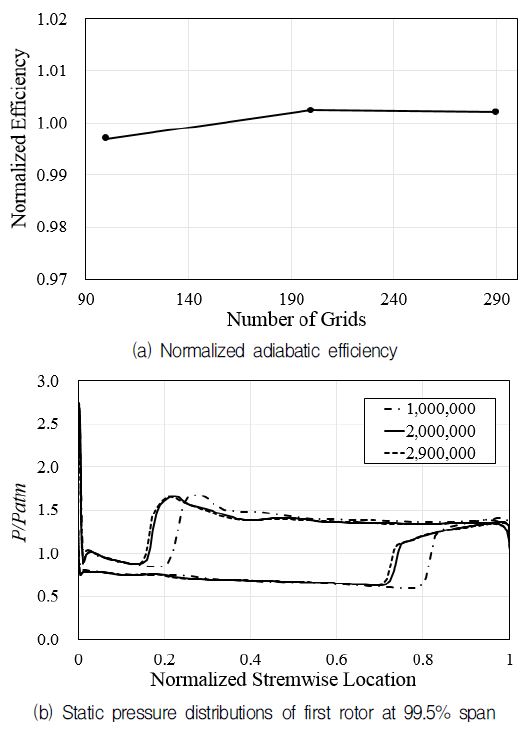
본 연구에서는 수치해의 격자의존성을 제거하기 위해 약 100만개에서 290만개 사이의 격자수를 사용한 격자의존성 시험을 수행하여 Fig. 4에 각각 나타내었다. Fig. 4(a)에서는 설계유량에서의 무차원화 된 단열효율을 비교하였으며, Fig. 4(b)에서는 설계유량에서 첫 단 동익의 99.5% 스팬에서의 정압분포를 보여주고 있다. Fig. 4에서 보는 바와 같이 약 200만개의 격자수에서 격자 의존성이 제거되었으므로 이격자수를 본 연구를 위한 최적의 격자수로 선정하였다.

Fig. 4

Grid dependency test

3.2 공력성능

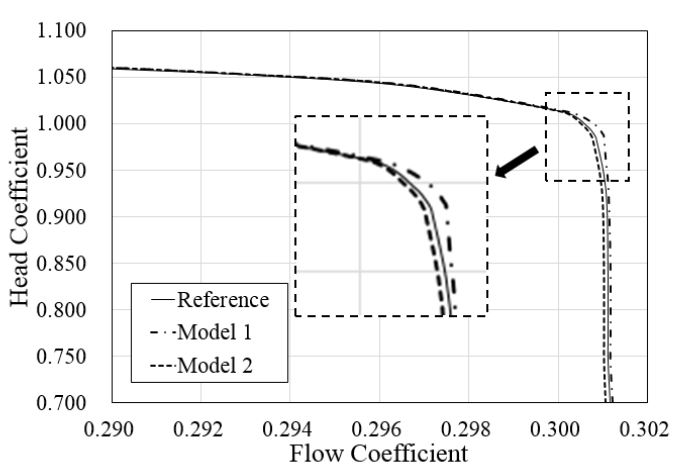
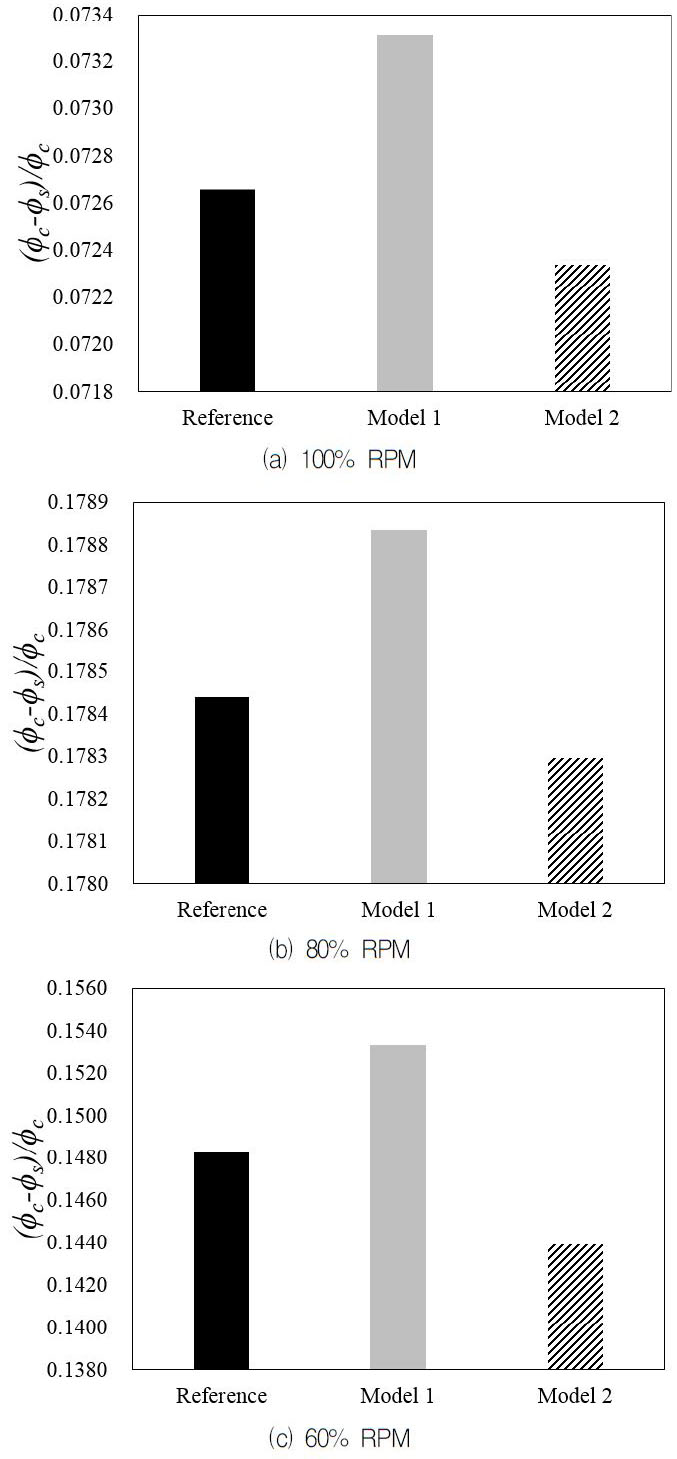
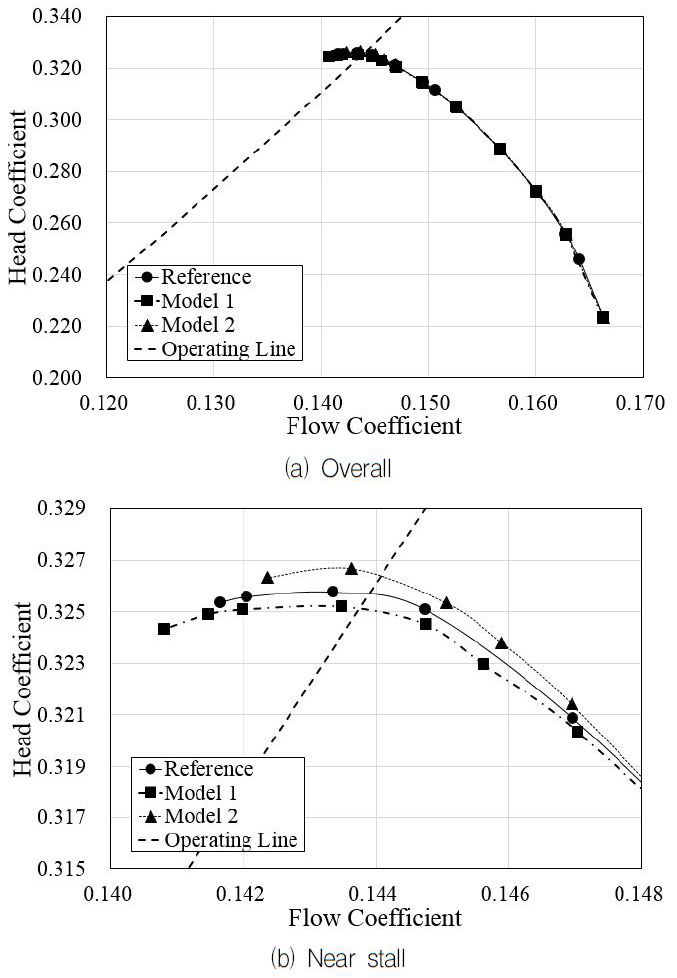
본 연구 대상인 천음속 축류홴의 기준 모델, Model 1 및 Model 2에 대해 천음속 축류홴의 설계 회전속도(100% RPM)에서의 유량계수와 전압계수의 관계에 대한 성능곡선을 Fig. 5에 나타내었다. Fig. 5에서 보는 바와 같이 100% RPM의 설계전압계수(ψ=0.989)에서 유량계수의 차이가 가장 크게 발생하는 것을 확인하였고, Table 2에 설계점에서의 유량계수와 단열효율을 각 모델별로 나타내었다. 유량계수와 단열효율은 Model 1을 사용한 천음속 축류홴의 경우 기준모델대비 각각 0.057% 및 0.12% 증가하였고, Model 2를 사용한 천음속 축류홴은 각각 0.013% 및 0.12% 감소하였다. Model 1과 2의 스윕의 차이가 작기 때문에 두 Model 사이의 유량계수와 효율의 정량적 차이는 미소하였지만, 경향이 서로 반대로 나타났다. Fig. 6은 설계 회전속도 및 탈설계 회전속도에서 작동영역(Operating range)을 나타내며, 이 작동영역은 다음과 같은 식으로 표현된다.

$\[ operating range=\frac{{\Phi }_c-{\Phi }_s}{{\Phi }_c} \]$

(4)

Fig. 5

Aerodynamic performance curves at 100% RPM

Fig. 6

Operating range at each rotational speed

Table 2

Aerodynamic performance at designed head coefficient(ψ=0.989)

여기서 Φ는 유량계수를 나타내고, 하첨자 c와 s는 각 모델에서의 초킹(Choking)과 실속 근처(Near stall)를 나타낸다. Fig. 6에 나타난 바와 같이 Model 1의 경우 기준모델 대비 100%, 80% 및 60% 회전속도에서 작동 영역이 증가하였으나 Model 2의 경우 기준모델 대비 각 회전속도에서 작동영역이 감소한 것을 확인할 수 있었다. 이러한 결과는 앞서 언급한 Wadia 등⁽⁶⁾의 연구 결과와 일치한다.

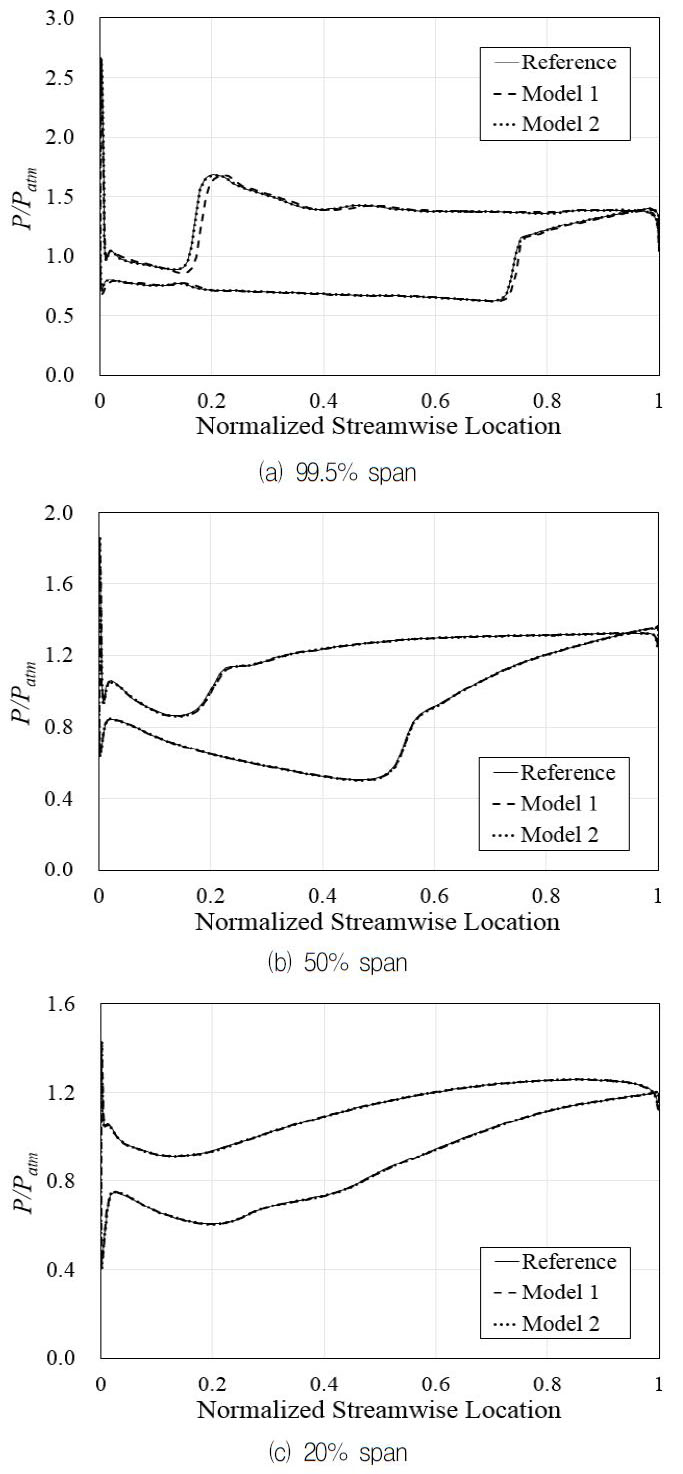
Fig. 7은 설계 전압계수에서 각 Model 첫 단 동익의 99.5%, 50% 및 20% 스팬에서 압력분포를 나타내고 있다. 이 그림에서 보이는 바와 같이 스윕의 변화량이 상대적으로 작은 허브 부분에서는 동익에 작용하는 정압분포의 차이가 발견되지 않았으나 스윕의 변화량이 가장 큰 동익의 팁 부분에서는 정압분포에 차이가 발생하는 것을 확인할 수 있고, Model 1의 경우 설계 전압계수에서 상대적으로 증가한 유량계수의 영향으로 인해 Fig. 7(a)에서와 같이 충격파의 발생으로 인한 압력상승이 하류로 이동한 것을 확인할 수 있었다.

Fig. 7

Static pressure distributions at design head coefficient (100% RPM)

Fig. 8은 60% 회전속도에서 성능곡선과 임의의 운전 곡선(Operating line)을 함께 보여주고 있다. Fig. 8(b)는 실속유량 근처에서 각 Model의 성능곡선을 나타내고 있다. Fig. 8(b)에서와 같이 Model 1은기준모델 보다 작동 영역이 증가한 반면 Model 2는 작동 영역이 감소한 결과를 보여주었다. 그러나 전압계수의 경우 이와 반대로 Model 1은 기준모델보다 감소하였고, Model 2는 증가한 것을 알 수 있었다.

Fig. 8

Aerodynamic performance curves and operating line (60% RPM)

Table 3은 각 Model의 운전점(Operating point)을 기준으로 하여 다음과 같이 정의되는 스톨 마진값을 비교해 주고 있다.

$\[ S.M.=\left(\frac{\dot{m_{op}}}{\dot{m_{stall}}}\times \frac{P{R}_{stall}}{P{R}_{op}}-1\right)\times 100\% \]$

(5)

Table 3

Normalized stall margin (60% RPM)

여기서 $$ \dot{m}$$과 PR은 각각 질량유량과 입출구 전압력비를 나타내며, 하첨자 op와 stall은 각각 운전점과 실속점을 나타낸다. 설계회전속도의 60% 회전속도에서 Model 1과 Model 2의 스톨 마진은 기준모델에 비해 각각 절대값이 0.34% 증가하고 0.30% 감소하였다.

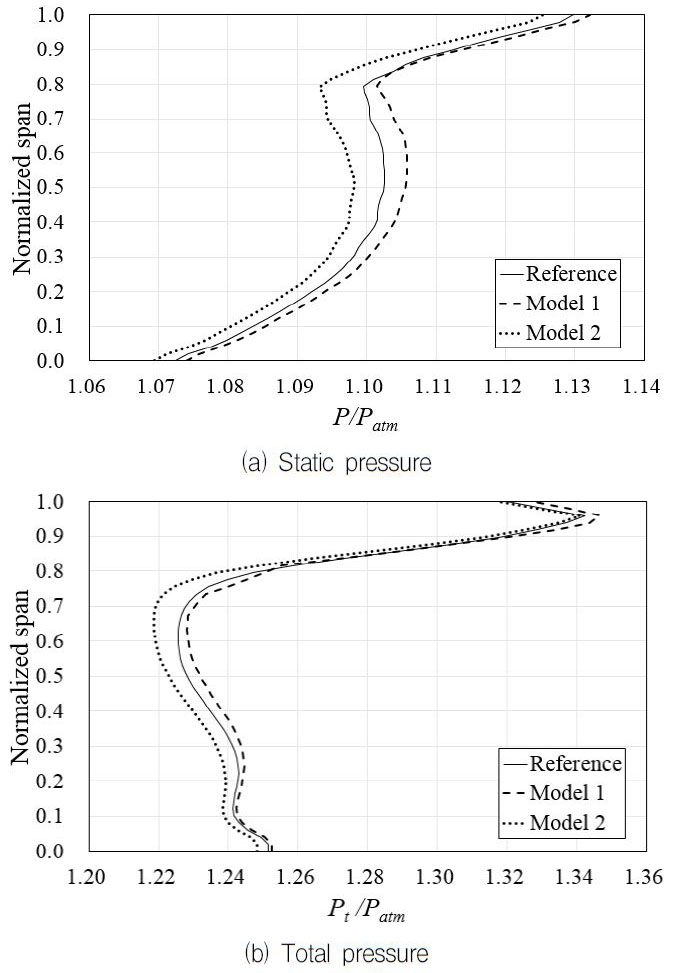
60% 회전수 실속 근처 유량에서 각 Model의 첫 단 동익출구부에서 스팬방향으로의 정압 및 전압 분포는 Fig. 9에 나타난다. 이 그림에서 보이는 바와 같이 정압과 전압 모두 Model 1을 사용한 천음속 축류홴에서 상대적으로 높은 값을 갖고, Model 2를 사용한 경우 반대 경향이 나타나는 것을 확인할 수 있다.

Fig. 9

Static and total pressure distributions at the outlet of first rotor (60% RPM, Φ=0.142)

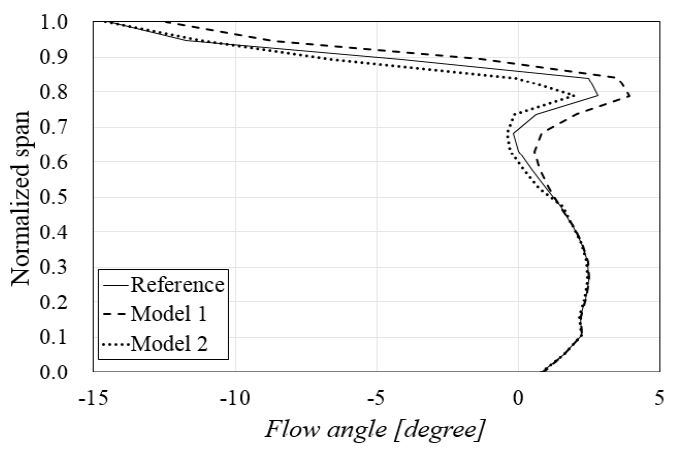
회전축과 유동방향 사이의 각도인 유동각의 분포는 60% 회전수와 실속 근처 유량에서 첫 단 출구부에서 스팬방향으로의 분포가 Fig. 10에 나타난다. 50% 스팬에서부터 100% 스팬까지 Model들 간의 유동각 분포에 차이가 발생하였으며, Model 1을 사용한 천음속 축류홴의 경우 기준모델과 Model 2에 비해 회전방향으로 유동각이 증가한 것을 확인할 수 있었다. 이에 따라 2단 동익의 입구에서 회전방향 유동각(C_ϴ,in)이 증가하게 되며 이로 인해 유동의 영각(Incidence angle)이 감소하게 된다. 유동 현상이 복잡한 동익의 팁부분에서 영각의 감소는 스톨 발생을 지연시켜 유동을 안정시킨다고 널리 알려져 있다.⁽¹⁰⁾ 이러한 결과로 인해 Model 1의 작동 안정성이 향상되고, Model 2의 작동 안정성은 감소된 것으로 사료된다.

Fig. 10

Flow angle distributions at the outlet of first stage (60% RPM, Φ=0.142)

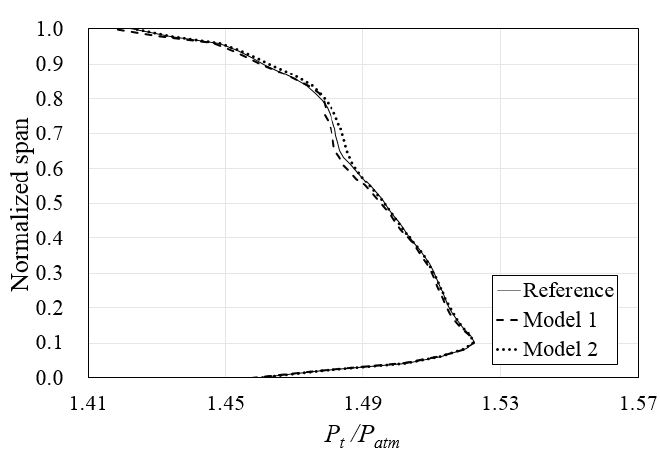
Fig. 11는 60% 회전수와 실속 근처 유량에서 두 번째 단출구부에서 스팬방향으로의 전압 분포를 나타내고 있다. Fig. 9(b)와 같이 첫 단 동익에서의 전압 상승 차이에도 불구하고 세 가지 Model의 전압 분포가 거의 동일한 것을 확인할 수 있다. Model 1의 경우 Fig. 10과 같이 첫 단 출구부에서 유동각이 회전방향으로 증가하여 두 번째 단 동익의 입구 유동각이 기준모델에 비해 감소하게 되어, 두 번째 단의 압축일이 감소하는 것으로 사료되며, 이러한 이유로 전체 단의 전압력비가 Fig. 11과 같이 동일한 수준이 되는 것으로 사료된다.

Fig. 11

Total pressure distributions at the outlet of second stage (60% RPM, Φ=0.142)

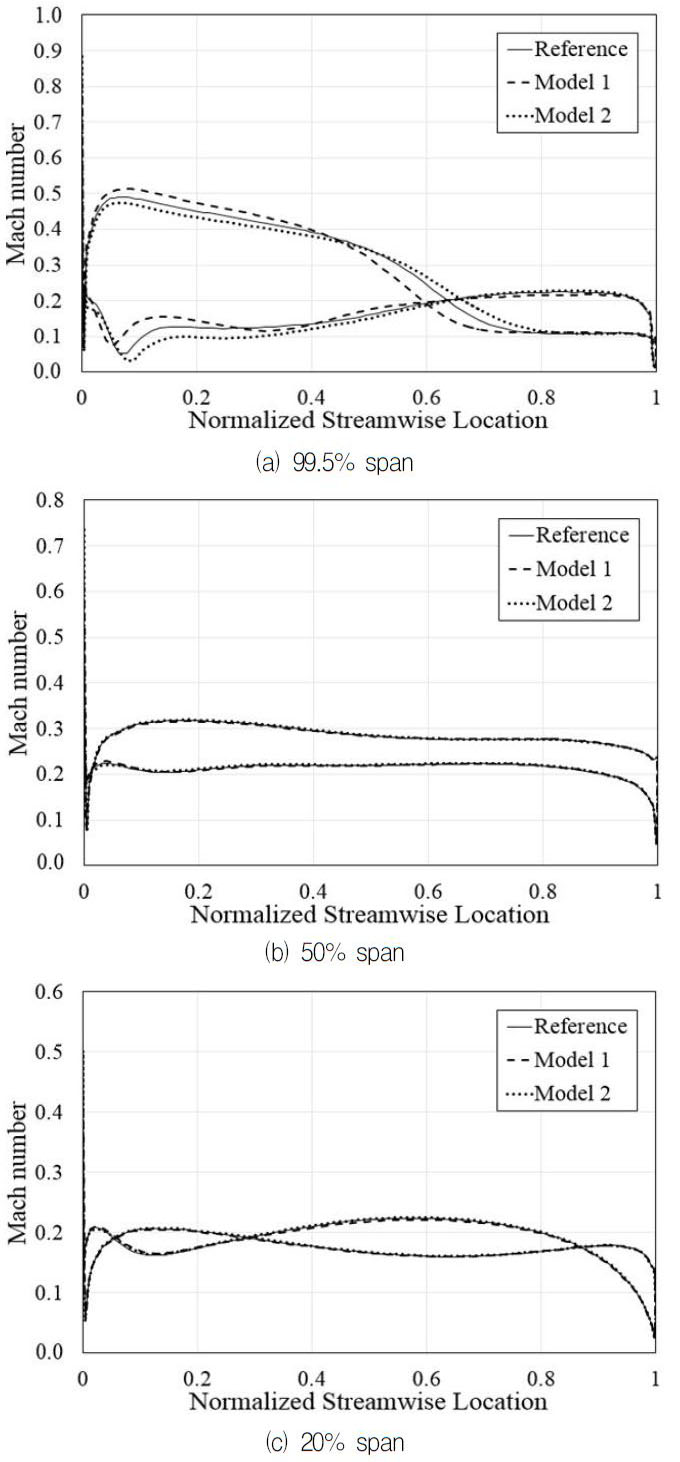
Model 2에 대해 실속 근처 유량에서 첫 단 동익의 99.5%, 50% 및 20% 스팬에서 마하수 분포가 Fig. 12에 나타난다. Fig. 12(a)에서와 같이 스윕의 변화량이 최대인 팁 부분에서 마하수 분포의 차이가 발생한 것을 관찰할 수 있었다. Model 1의 경우 영각의 증가로 인해 동익 전연부 흡입면에서 상대적으로 높은 마하수 분포를 보인 반면 Model 2의 경우 영각의 감소로 인해 동익 전연부 흡입면에서 상대적으로 낮은 마하수 분포를 확인할 수 있다.

Fig. 12

Relative mach number distributions at near stall condition (60% RPM, Φ=0.142)

4. 결 론

본 연구에서는 삼차원 RANS해석을 사용하여 천음속 다단 축류홴에서 블레이드의 스윕이 공력 성능에 미치는 영향을 분석하였다. 천음속 다단 축류홴 첫 단 동익에 스윕을 주었으며, 동익의 허브에서부터 팁까지의 스윕을 조절하였다. 팁에서의 스윕 변화량(δ_tip)이 0.9 mm (전향익)인 Model 1과 – 0.9 mm (후향익)인 Model 2의 공력성능을 스윕이 없는 기준모델과 함께 설계 회전속도와 탈설계 회전속도에서 분석을 수행하였다. 전향익인 Model 1의 경우 설계 회전속도와 탈설계 회전속도에서 운전 영역이 향상되었으며 60% 설계 회전속도에서 기준모델과 비교하여 스톨 마진이 0.34% 증가하였고, 설계 전압계수에서 단열 효율이 기준모델과 비교하여 0.12% 증가한 것을 확인하였다. 후향익인 Model 2의 경우 설계 회전속도와 탈설계 회전속도에서 운전 영역이 기준모델과 비교하여 감소하였으며, 60% 설계 회전속도에서 스톨 마진이 0.3% 감소하였고, 설계 전압계수에서 단열 효율이 0.12% 감소하였다.단단 축류 압축기를 대상으로 한 선행연구⁽⁶⁾의 결과와 비교해볼 때 본 연구의 대상인 다단 천음속 축류홴에서도 전향익을 사용했을 때 설계 회전속도에서 운전영역과 단열 효율이 증가하는 것을 확인할 수 있었다. 아울러 탈설계 회전속도에서 스윕의 영향성을 분석한 결과, 전향익을 사용한 축류홴의 운전 영역이 증가되었고, 후향익을 사용한 축류홴은 운전 영역이 감소된 결과를 얻을 수 있었다.

Acknowledgments

본 연구는 방위사업청, 국방과학연구소의 선도형 핵심기술개발 과제 중 한화테크윈이 주관하는 ‘Blisk형 Wide Chord 팬개발 과제’의 지원에 의해 수행되었으며, 이에 감사드립니다.

References

• John D. Denton, (2002), “The Effects of Lean and Sweep on Transonic Fan Performance: A Computational Study”, Task Quarterly, 6(1), p7-23.
• Denton, J. D., and Xu., L., (2002), “The Effects of Lean and Sweep on Transonic Fan Performance”, ASME Turbo Expo, Amsterdam, Netherlands, pGT2002-30327. [https://doi.org/10.1115/gt2002-30327]
• Wilke, I., Kau, H. P., and Brignole, G., (2005), “Numerically Aided Design of a High-Efficient Casing Treatment for a Transonic Compressor”, ASME Turbo Expo, Nevada, USA, pGT2005-68993. [https://doi.org/10.1115/gt2005-68993]
• Samad, A., Kim, K. Y., Goel, T., Hafka, R. T., and Shyy, W., (2008), “Multiple Surrogate Modeling for Axial Compressor Blade Shape Optimization”, AIAA Journal of Propulsion and Power, 24(2), p302-310. [https://doi.org/10.2514/1.28999]
• Wu, H., Li, Q., and Zhou, S., (2007), “Optimization of Loaded Fan rotor Based on Through Flow Model”, ASME Turbo Expo, Montreal, Canada, pGT2007-27603.
• Wadia, A. R., Szucs, P. N., and Grall, D. W., (1997), “Inner Working of Aerodynamic Sweep”, ASME Turbo Expo, Florida, USA, 97-GT-401. [https://doi.org/10.1115/97-gt-401]
• Hah, C., Puterbaugh, S. L., and Wadia, A. R., (1998), “Control of Shock Structure and Secondary Flow Field Inside Transonic Compressor Rotors Through Aerodynamic Sweep”, ASME Turbo Expo, Stockholm, Sweden, 98-GT-561. [https://doi.org/10.1115/98-gt-561]
• ANSYS CFX-15.0, (2013), Ansys Inc.
• Lechner, R., Langtry, R., and Menter, F., (2010), “SST Reattachmen Modification in ANSYS CFX”, Ansys Inc.
• Ciorciari, R., Lesser, A., Blaim, F., and Niehuis, R., (2012), “Numerical Investigation of Tip Clearance Effects in an Axial Transonic Compressor”, Journal of Thermal Science, 21(2), p109-119. [https://doi.org/10.1007/s11630-012-0525-6]