선형 터빈 익렬에서 열전달 수치해석 및 실험과 비교

1. 서 론

터빈에서 발생하는 출력은 터빈 입·출구의 압력비와 터빈 입구 온도와 비례한다. 높은 압력 비는 여러 개의 터빈 단을 구성함으로써 초킹(Choking)현상으로 인한 유량이 포화되는 것을 해결할 수 있다. 그러나 터빈 입구온도를 증가시키는 것은 금속의 용융점으로 인해 한계가 명확하다. 그래서 터빈 날개 냉각에 대한 연구가 많이 이루어지고 있는데, 이러한 연구 결과의 일환으로 최근 일본의 미쯔비시 중공업은 1600℃의 가스 터빈 입구온도를 달성하였다.⁽¹⁾ 효과적인 터빈 냉각을 위해서는 우선 터빈 주위에서 발생하는 유동현상을 규명해야 한다. 그러나 horseshoe vortex와 corner vortex 등과 같은 secondary flow로 인해 복잡한 유동 현상이 발생하는 어려움이 있다. 기존에는 이러한 복잡한 유동현상 내 열전달을 주로 실험적으로 연구하였는데, Turner A.B.⁽²⁾는 터빈 날개 주변의 국소 열전달 계수에 대한 실험을 통해 leading edge에서 높은 열전달이 일어남을 보고하였고, Hylton, L. D. 등⁽³⁾은 이론적으로 설계된 형상과 실험을 통해 film cooling을 고려하지 않은 터빈 표면의 열전달 분포를 예측하여 터빈 형상을 개선하였다. 그러나 film cooling을 고려할 경우의 터빈 날개 주위의 유동현상은 더욱 복잡해진다. 또한 터빈 날개를 이용한 열전달 실험을 수행하는 것은 많은 비용을 요구한다. 그래서 최근에는 수치해석을 통한 연구가 주로 이루어지고 있다. Ameri, A. A. 등⁽⁴⁾은 수치해석을 이용해 터빈 날개 tip의 냉각 효과 및 열전달에 대해 연구하였고, Verstraete, T 등⁽⁵⁾은 소형 가스 터빈 날개와 축의 열전달에 대한 연구를 수행하였다.

터빈 익렬 내부의 열전달 실험 중 열경계층을 직접 측정하는 경우는 경계층 두께에 따른 어려움으로 인해 제한된 수의 연구만이 수행되었다. 본 연구에서는 S. Han 등⁽⁶⁾의 선행연구에서 열경계층을 직접 측정하여 수행된 열전달 실험의 결과와 실험과 동등한 조건의 수치해석을 통해 얻은 결과를 비교하였다.

2. 본 론

2.2. 선행 실험

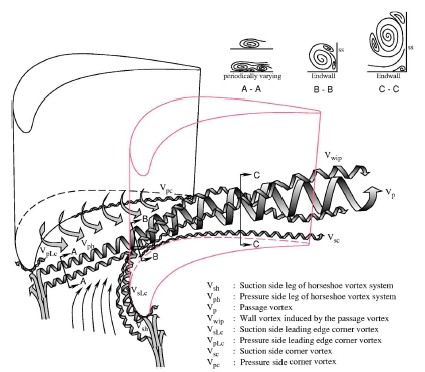
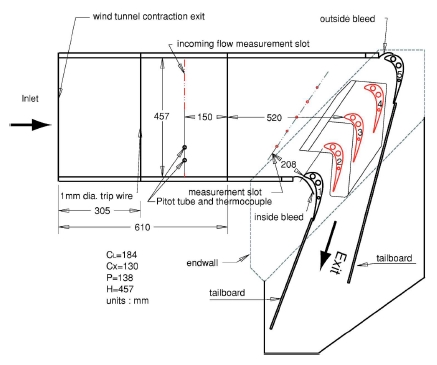
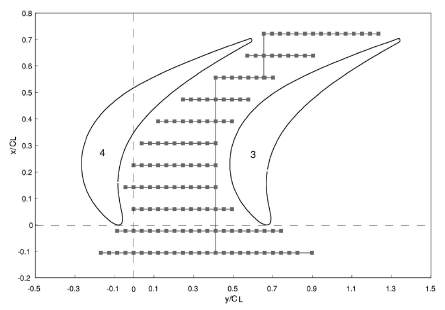
S. Han 등⁽⁶⁾은 Fig. 1에서 보는 것처럼 복잡한 secondary flow가 발생하는 선형 터빈 날개 열(cascade)에서 hub와 터빈 날개 표면의 열전달을 측정하는 실험을 수행했다. 이 실험의 결과와 본 연구의 수치해석 결과를 비교하기에 앞서 실험내용을 설명하고자 한다. S. Han 등⁽⁶⁾의 실험은 blow type의 풍동에 터빈 날개를 위치시켰고(Fig. 2), hub 면은 열전대와 히터를 PI제어를 통해 등온 상태를 유지했다. 그리고 열전대로 측정한 공기의 온도, 외삽법을 이용해 계산한 벽 온도, 온도 측정으로 계산된 온도구배를 이용해 식(3)으로 Nu를 얻었다. 실험의 현의 길이(C_l)는 0.184m이고, 온도 구배 계산을 위한 온도 측정은 Blackwell, B 등⁽⁷⁾의 연구에서 제안된 butt welded 열전대를 이용하여 endwall으로부터 10 um씩 수직방향으로 이동하면서 Fig. 3에 표시된 모든 지점에서 측정하였다.

Fig. 1

Vortex model in turbine cascades(8)

Fig. 2

Test section in the wind tunnel for the heat and mass transfer experiment(6)

Fig. 3

Endwall measurement positions of experiment(6)

2.3 수치해석 모델

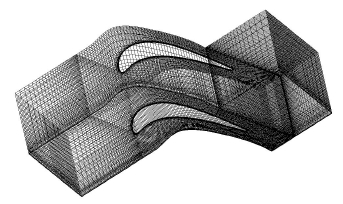
선행 실험 결과와 비교하기 위해서 Fig. 4에서 보는 것과 같이 풍동 실험의 터빈 날개와 같은 형상에 structured 격자를 생성하였다. 수치해석은 격자와 난류 모델에 따라 네 가지 경우(Table 1)에 대해 수행하였다. Case 1~3은 격자 의존성을 확인해보기 위해 모든 경계 조건은 동일하게 하고, hub 면에서의 y+(Non-dimensional wall distance)값이 다르게 격자를 생성하여 해석을 수행하였다. 그리고 난류 모델에 따른 수치해석 결과를 비교하기 위하여 Table 1의 Case 3~4와 같이 두 가지 난류 모델을 이용하였다. 난류 모델은 Boussinesq 가정을 만족하는 난류점성모델의 SST와 난류점성에 대한 가정 없이 각각의 Reynolds 응력이 다르게 발달 하는 것을 고려하여 이에 대해 수송방정식을 구성하는 Reynolds stress 모델을 채택하였다. 실제 사례들에서는 2방정식보다 좋지 못한 예를 종종 보이고 있으나, 이론적으로 Reynolds stress 모델은 특정조건에서 복잡한 유동에 더 적합하다는 점⁽⁹⁾을 고려해 Reynolds stress 모델을 사용하였다.

수치해석에 사용된 경계조건은 Table 2에서 보는 것과 같으며, S. Han 등⁽⁶⁾의 실험 Heat-Run11 경우와 동일하다. T_in과 U_in은 입구에서 입구 온도, 입구면에 수직한 방향의 유체 속도이고, P_out, Re_ex, U_ex은 각각 출구 압력, Reynolds 수, 유체의 속도이다. 여기서 U_ex는 입구와 출구면의 비율인 AR을 입구에서 유체의 속도에 곱한 값(U_ex=AR∙U_in)이다. Tu는 난류 강도로 0.2%이며, T_w는 끝벽(Endwall)의 온도이다.

Fig. 4

Generated coarse mesh for numerical analysis

Table 1

Cases for numerical analysis

Table 2

Boundary conditions for numerical analysis

2.4 수치해석 결과 및 비교

S. Han 등⁽⁶⁾의 선행 실험은 Fig. 3의 각각의 점에서 점성 저층(벽으로부터 약 300 μm 이하)에 위치하는 점에서 온도를 측정한 후에 온도 구배를 이용하여 Nu를 계산하였다. 수치해석에서는 실험에서 온도를 측정한 위치와 동일한 점들에서 온도 데이터를 추출하여 같은 방법으로 Nu를 계산하고 비교하였다.

2.4.1 경계층 비교

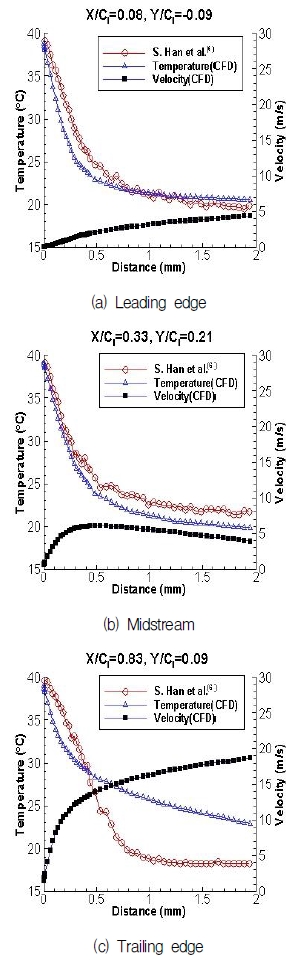
경계층의 두께 및 유동특성을 확인하기 위한 온도 및 속도 분포는 Fig. 5에서 볼 수 있으며,Case 3의 조건을 이용하였다. Nu 계산에 중요한 온도 구배는 leading edge와 midstream에서는 실험과 수치해석이 서로 매우 유사하지만, trailing edge에서는 차이를 보이고 있다. Leading edge에서 속도 경계층은 얇게 형성되고, 이 때 열경계층은 유사한 분포를 나타내는 반면에 midstream에서는 속도가 미세하게 줄어들면서 이로 인해 실험과 수치해석 결과의 온도 값 차이가 조금 늘어나는 것을 알 수 있다. 그리고 trailing edge에서는 leading edge와 midstream보다 속도 경계층이 두텁게 발달하고 있다. 이 결과로 수치해석과 실험의 속도 경계층 사이에 차이가 있을 것으로 예상되고, 그래서 실험과 수치해석의 온도경계층이 다른 양상을 띠는 것으로 보인다.

Fig. 5

Comparison of temperature profile between experiment and CFD

2.4.2 격자에 따른 수치해석 결과

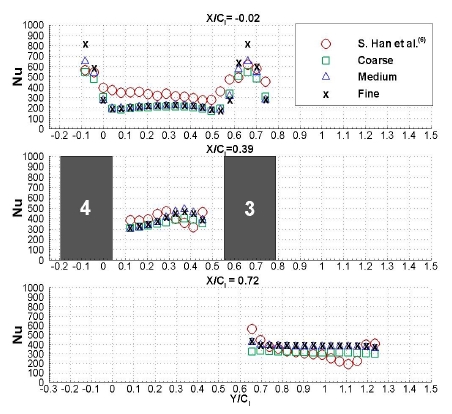
격자 변화에 따른 수치해석 결과(Case 1~3)는 Fig. 6에서 볼 수 있으며 x축은 Y/C_l, y축은 Nu 값이고, Reynolds 수는 2.56×10⁵, 난류강도(Tu)는 0.2%이다. 위에서부터 leading edge 근처(X/C_l=-0.02), midstream(X/C_l=0.39), trailing edge 근처(X/C_l=0.72)로 세 개의 위치에서 비교하였다. Fig. 7의 날개 번호 3, 4는 Fig. 3에서 확인할 수 있다.

Fig. 6

Nusselt number for various mesh at different X/Cl with Re=2.56×105

Fig. 7

Nusselt number for various turbulence model at different X/Cl with Re=2.56×105

우선 leading edge 근처에서는 세 가지 격자 모두 실험과 매우 유사한 경향성을 나타내고 있으며, coarse 격자의 경우가 조금 차이가 있는 것을 확인했다. 그리고 Nu가 최대인 Y/C_l이 약 -0.1과 0.65인 경우, 실험에서는 전도 오차(Conduction error)가 존재하기 때문에 CFD의 Nu가 더 높게 나타나야 한다. 그러나 coarse 격자는 실험보다 작은 값을 가진다. X/C_l이 0.39인 midstream의 Y/C_l이 약 0.1~0.3 일 때는 수치해석 결과가 모두 비슷하게 나타난다. 그리고 Y/C_l이 0.3보다 클 때는 secondary flow에 의한 영향으로 3가지 격자 모두 실험과 다른 경향성을 보인다. Trailing edge근처에서는 전체적으로 수치해석 결과는 실험과 경향성 차이를 나타내고, coarse 격자가 조금 더 작은 Nu를 갖는다.

2.4.3 난류모델에 따른 수치해석 결과

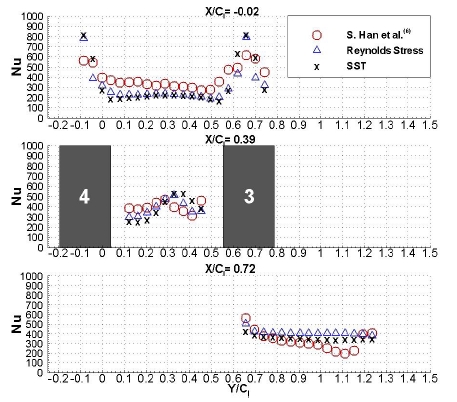
두 가지 난류모델의 수치해석 결과(Case 3~4)도 앞 절과 같이 실험과 같은위치에서 Nu 분포를 비교하였다.

Leading edge 근처(X/C_l=-0.02)에서 Nu가 최대인 Y/C_l이 약 0.65일 때, SST 모델과 Reynolds Stress (RS) 모델 모두 전도 오차를 반영하는 실험값보다 높은 Nu를 갖는다. Midstream에서는 SST모델보다 RS모델이 실험에 조금 더 근사한 값을 보인다. Trailing edge 근처에서는 Y/C_l 값이 가장 작은 두 개의 점(Y/C_l≅0.6~0.7)을 제외한 모든 점에서는 SST model이 가장 실험 결과와 비슷하다. 그러나 Y/C_l이 커짐에 따라 SST, RS 모델 모두 실험과 차이가 커지며 경향성 또한 다르게 나타난다. 각각의 난류 응력에 대해 수송방정식을 구성하는 RS모델이 더 정확한 결과를 나타낼 것으로 기대했으나, SST 모델과 유사한 결과를 보이고 있다.

2.4.4 실험 및 수치해석 결과 비교

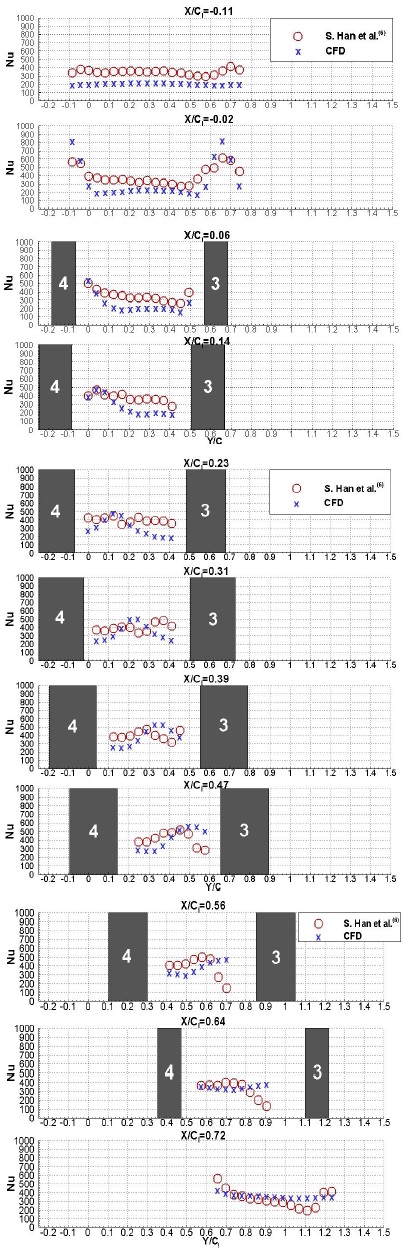
본 절에서는 실험에서 측정한 모든 데이터를 수치해석 결과와 비교하고자 한다. 수치해석 결과는 Case 3의 경계조건을 이용하였다. 우선 Fig. 8(a)의 값들로부터 미루어볼 때, 수치해석의 Nu 값이 실험값보다 전체적으로 작게 나온 것으로 보인다.

Fig. 8

Nusselt number distribution at different X/Cl with Re=2.56×105

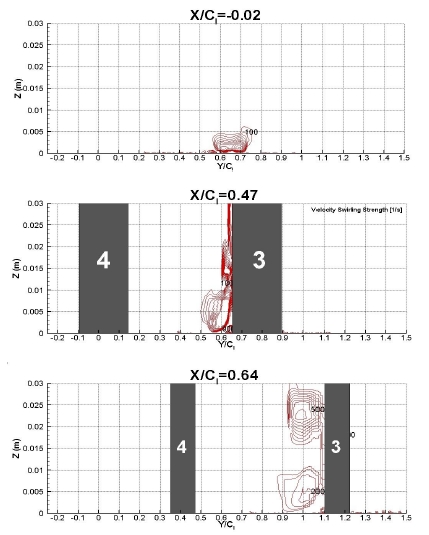
앞서 설명한 것과 같이 leading edge의 정체점인 X/C_l이 -0.02, Y/C_l이 약 -0.1과 6.5일 때, 전도 오차로 인해 실험의 Nu가 낮게 나온 것을 알 수 있으며, Fig. 9의 velocity swirling strength가 강하게 나타나고 있다.Velocity swirling strength(⋋_ci)는 속도 구배 tensor(식 4)의 고유값(Eigenvalue)을 이용하여 와류(Vortex)를 도식화하는데 사용되는 변수이다.⁽⁹⁾  식 (4)는 속도 구배 텐서를 고유값을 이용하여 분해한 식으로 하첨자 r은 실수, cr과 ci는 복소수의 실수와허수부분을 의미하며, 속도 구배 텐서는 실수 고유값 ⋋_r과 복소수 고유값 ⋋_ci±i⋋_ci를 갖는다.

Fig. 9

Contour of velocity swirling strength at different locations

$\[ \nabla u=\left[d_{ij}\right]=\left[{\upsilon }_r{\upsilon }_{cr}{\upsilon }_{ci}\right]\left[\begin{array}{ccc}{⋋}_r& 0& 0\\ 0& {⋋}_{cr}& {⋋}_{ci}\\ 0& -{⋋}_{ci}& {⋋}_{cr}\end{array}\right]{\left[{\upsilon }_r{\upsilon }_{cr}{\upsilon }_{ci}\right]}^{-1} \]$

(4)

X/C_l이 0.06이고 Y/C_l이 0과 0.3일 때, 실험과 수치해석 모두 Nu가 큰 것은 leading edge corner vortex에 의한 영향으로 보인다. X/C_l이 0.23~0.56일 때, 수치해석에 의한 Nu가 최댓값을갖는 Y/C_l 위치가 점점 증가하는 것을 볼 수 있는데, 이것은 Fig. 9의 velocity swirling strength가 강하게 나타나는 것은 passage vortex에 의한 영향임을 알 수 있다. Fig. 9와 Fig. 10(a)로 미루어 볼 때, leading edge의 정체점에서는 horseshoe vortex, midstream과 trailng edge 근처에서는 passage vortex가 강하게 나타나고 있는 것을 알 수 있다.

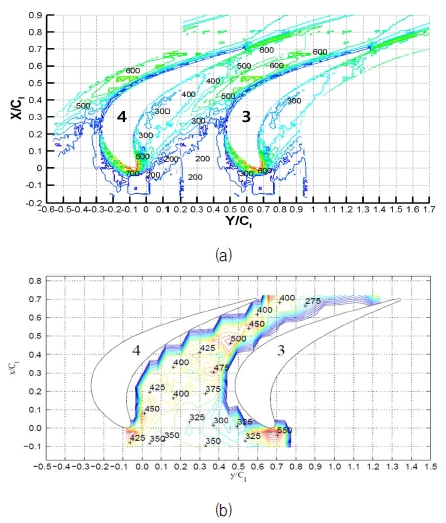
그러나 실험에 의한 결과는 조금 다른 경향을 보이고 있는데, 이것은 S. Han⁽⁶⁾의 연구에서 언급된 것과 같이 3차원 vortex가 발생하는 것을 적절하게 측정하지 못한 것으로 보인다. 그리고 Trailing edge 부분인 X/C_l이 0.72, Y/C_l이 0.65, 1.2일 때, vortex shedding 및 suction side corner vortex로 인해 실험과 수치해석의 Nu 값이 차이가 있는 것은 유동 구조가 다르게 발달한 것 때문으로 보인다. 이는 열 경계층 비교(Fig. 7)와 끝벽의 Nu 수의 등고선 비교(Fig. 10)에서도 실험과 큰 차이를 보이는 것으로 부터도 알 수 있다. Fig. 10은 정량적인 비교를 위한 끝 벽에서의 Nu 등고선그림이다. Nu 분포는 Fig. 7의 결과처럼 midstream까지는 비슷한 양상을 나타내고, 그 이후로는 차이를 보여주고 있다. 그리고 X/C_l이 약 0.6일 때 3번 날개의 흡입면근처에서 passage vortex에 의한 영향도 다르게 나타나고 있다.

Fig. 10

Nusselt number distribution by CFD (upper) and experiment(6) (lower)

3. 결 론

복잡한 유동이 발생하는 터빈 열의 endwall에서 열전달을 알아보기 위해 수치해석을 수행하고, 선행 실험의 결과와 비교하였다. 수치해석의 격자, 난류 모델의 변경에 따른 수치해석 결과를 비교하였고, 실험에서 측정을 한 데이터와도 대조하였다. 이것을 정리하면 다음과 같다.

(1) 선행 연구의 형상을 이용하여 structured mesh를 생성하였고, hub면에서 평균 y+가 2.5, 1.2, 0.9가 되도록 격자를 생성하여 수치해석을 수행하였다. 평균 y+가 1.2인 경우와 0.9일 때 Nu 값의 큰 차이가 없는 것으로 나타났다.

(2) SST, Reynolds Stress 두 가지 난류 모델에 대해 수치해석 결과를 비교하였다. Reynolds Stress 모델은 실험값과 SST모델과 비슷한 경향성을 보여주고 있고, leading edge의 정체점의 값은 두 가지 모델 모두 실험보다 큰 Nu 값을 나타낸다. 이는 수치해석에서 전도오차가 발생하지 않기 때문이다.

(3) Leading edge 근처에서의 실험과 수치해석 결과를 비교를 통해 수치해석의 Nu가 전체적으로 조금 작게 나타나는 것을 확인했다. Midstream에서의 Nu 값을 비교를 통해서, passage vortex에 의한 효과로 수치해석의 값이 크게 나오는 반면 실험의 결과는 Nu 값이 작게 나오는 것은 3차원 vortex를 제대로 반영하지 못한 이유인 것으로 보인다. 결론적으로 secondary flow가 강하게 작용하는 곳을 제외하고, 전체적으로 수치해석의 결과는 실험과 유사한 경향을 가진다.

References

• Mitsubishi Heavy Industries News, “MHI Achieves 1,600℃ Turbine Inlet Temperature in Test Operation of World’s Highest Thermal Efficiency “J-Series” Gas Turbine”, Available at http://www.mhi-global.com/news/story/1105261435.html.
• Turner, A. B., (1971), “Local Heat Transfer Measurements on a Gas Turbine Blade”, Journal of Mechanical Engineering Science, 13(1), p1-12. [https://doi.org/10.1243/jmes_jour_1971_013_003_02]
• Hylton, L. D., et al , (1983), “Analytical and Experimental Evaluation of the Heat Transfer Distribution over the Surfaces of Turbine Vanes.”.
• Ameri, A. A., and Rigby, D. L., (1999), “A Numerical Analysis of Heat Transfer and Effectiveness on Film Cooled Turbine Blade Tip Models.”.
• Verstraete, T., Alsalihi, Z., and Van den Braembussche, R. A., (2007), “Numerical Study of the Heat Transfer in Micro Gas Turbines”, Journal of Turbomachinery, 129(4), p835-841. [https://doi.org/10.1115/1.2720874]
• Han, S., and Goldstein, R. J., (2007), “Heat Transfer Study in a Linear Turbine Cascade using a Thermal Boundary Layer Measurement Technique”, Journal of Heat Transfer, 129(10), p1384-1394. [https://doi.org/10.1115/1.2754972]
• Blackwell, B. F., and Moffat, R. J., (1975), “Design and Construction of a Low Velocity Boundary Temperature Probe”, ASME J. Heat Transfer, 972, p313-315.
• Wang, H. P., Olson, S. J., Goldstein, R. J., and Eckert, E. R., (1997), “Flow Visualization in a Linear Turbine Cascade of High Performance Turbine Blades”, Transactions-American Society Of Mechanical Engineers Journal Of Turbomachinery, 119, p1-8. [https://doi.org/10.1115/1.2841006]
• ANSYS, C, (2011), 14.0. Theory Guide.