일체형 원자로의 선형출력변화에서 증기가압기에 대한 과도해석
Abstract
In this study, a series of transient analysis is conducted to evaluate thermal hydraulic performance for pressurizer (PZR) of an integral reactor. Mass and energy conservation equations are used for the transient calculation, and electrical heater and heat loss are additionally considered to solve the PZR energy equation. Linear power variations can yield in-surge and out-surge flow between the RCS and the PZR, and the amount of surge flow rates are calculated to assess the PZR performance. The PZR region is assumed to be maintained the saturation state during the transient analysis. As time passes by, the thermal hydraulic behaviors (pressure and level) of the PZR are mainly investigated whether the results exceed the operation limits or not. Moreover it is also discussed to compare the heat loss and the PZR heater power. Finally, the calculation results show that the PZR can be operated within the operation limits during the linear power variation.
Keywords:
Steam pressurizer, Integral reactor, Transient analysis, Linear power variation키워드:
증기가압기, 일체형 원자로, 과도해석, 선형출력변화1. 서 론
일체형 원자로는 가압기(Pressurizer, PZR), 핵연료(nuclear fuel),증기발생기(Steam Generator, SG) 그리고 원자로냉각재펌프(Reactor Coolant Pump, RCP)등의 1차계통기기를 단일 용기 안에 내장하고 있다. 이러한 구조는 1차계통 구성요소를 연결하는 대형배관이 존재하지 않으므로 배관파손에 의한 대형냉각재상실사고의 가능성을 원천적으로 배제할 수 있다. 일체형 원자로에서 원자로 냉각재의 온도는 핵연료에서 발생되는 열과 증기발생기에 의해 제거되는 열이 평형을 이루는 온도로 결정된다. 원자로 출력변화에 의한 원자로냉각재의 온도변화는 원자로냉각재의 부피변화로 이어져 내밀림(in-surge), 외밀림(out-surge) 유량을 유발한다. 이러한 밀림유량이 발생하더라도 일체형 원자로의 계통 압력은 가압기에 의해 설계범위 내에서 유지되어야 한다. 본 연구에서 해석한 일체형 원자로의 가압기는 증기가압기로서 원자로 상부에 위치한다. 증기가압기의 경우, 가압기 내부에는 포화상태의 액체(물)와 기체(증기)가 함께 존재한다. 내밀림 또는 외밀림 유량이 발생하더라도 내부에 비교적 큰 증기 공간을 갖는 일체형 원자로의 가압기는 살수(spray)를 작동하지 않고도 전열기에 의해 증발-응축량을 조절하여 압력변화를 수용할 수 있도록 설계되었다.
본 연구에서는 일체형 원자로의 선형출력변화에서 증기가압기 거동에 대한 과도해석을 수행하였으며, 시간에 따른 일체형 원자로의 계통 압력, 온도, 가압기 수위 및 밀림유량의 변화를 관찰하였다.
2. 해석 방법(Analysis Methods)
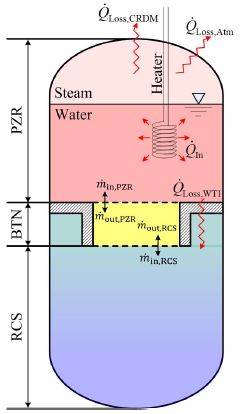
Fig. 1과 같이, 증기가압기와 원자로냉각재계통(Reactor Coolant System, RCS)은 각각 일체형 원자로의 상부와 하부에 위치하고 있다. 증기가압기의 내부는 포화상태의 증기와 물로 채워져 있으며, 원자로냉각재계통은 과냉상태의 물로만 채워져 있다. 정체구간(Bottle Neck, BTN)은 그 사이에 위치하여 완충 역할을 수행한다.
과도해석에서 일체형 원자로는 3개의 검사체적(가압기, 원자로냉각재계통, 정체구간)으로 분리되었다. 계산 프로그램은 각각의 검사체적에 대해 질량 및 에너지의 유․출입을 계산하도록 작성되었다. 일체형 원자로에서 발생되는 질량전달 및 열전달 경로는 Fig. 1에 표기하였다.
2.1 지배방정식(Governing Equation)
지배방정식은 아래의 식 (1)-(3)과 같으며, 검사체적의 질량과 내부에너지는 검사체적 경계에서 유․출입하는 질량유량, 엔탈피, 열전달량으로 결정된다. 식 (1)은 가압기, 정체구간 및 원자로냉각재계통의 질량 보존식이다. 식 (2)는 정체구간 및 원자로냉각재계통의 에너지 보존식이다. 이와 같이 보존 방정식을 이용한 과도해석방법은 기존 연구(1,2)에서 이미 소개된 바 있다.
| (1) |
| (2) |
| (3) |
위의 식 (1)-(3)에서, m과 은 검사체적의 질량과 검사체적경계를 지나는 질량유량을 나타내며, u와 i는 주어진 압력과 온도에서 비내부에너지(specific internal energy)와 비엔탈피(specific enthalpy)를 나타낸다. 는 열전달률을 의미하며, 이에 대해서는 2.4절과 2.5절에서 자세히 설명하였다.
가압기 내부에는 포화상태의 증기와 물이 공존하므로 가압기 건도(quality)는 식 (4)와 같이 도출 할 수 있다. 여기서 비체적(specific volume)은 식 (5)를 이용하여 계산할 수 있다.
| (4) |
| (5) |
여기서 x, v, 그리고 V는 각각 건도, 비체적, 그리고 체적을 의미한다. 하첨자 f와 g는 각각 포화액체와 포화기체를 의미한다. 가압기 체적은 구조물에 의한 공간이므로 시간에 따라 변하지 않는 변수이며, 가압기 질량은 식 (1)을 이용하여 계산할 수 있다.
2.2 가정 (Assumption)
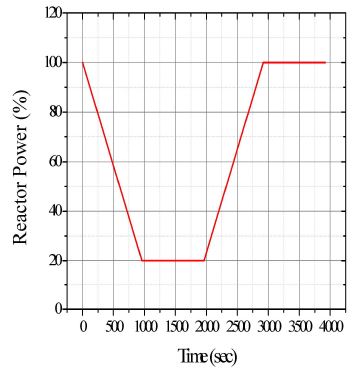
Fig. 2는 시간에 따른 원자로 출력변화를 보여준다. 원자로 출력은 선형으로 분당 5%포인트만큼 감소 및 증가하는 것으로 가정하였다. 최초의 출력은 100%에서 시작하였으며 960 초 동안 20%까지 선형으로 감소시켰다. 그리고 1,000초 동안 원자로 출력은 20%를 유지하였다. 그 이후에 출력은 960 초 동안 20%에서 100%까지 선형으로 증가시켰다. 그리고 1,000초 동안 원자로 출력은 100%를 유지하였다.
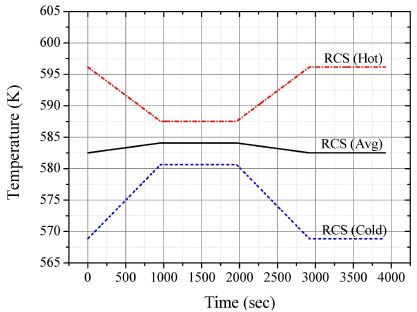
Fig. 3은 시간에 따른 원자로냉각재의 고온부, 저온부 그리고 평균온도를 보여준다. 위의 온도데이터는 원자로 출력에 대한 함수로 제시되었으며, 원자로냉각재의 평균온도는 원자로 출력과 반비례 관계이다. 반비례 관계의 주요원인은 원자로 냉각재 저온부가 고온부보다 더 큰 온도변화를 보이기 때문이다. 이와 같은 원자로냉각재의 평균온도가 과도해석의 가정으로 사용되었다.
2.3 초기조건(Initial Condition)
Table 1은 과도해석에서 사용된 가압기, 정체구간 그리고 원자로냉각재계통의 압력과 온도의 초기조건을 보여준다. 가압기 초기압력은 운전압력인 15.0 MPa으로 선정하였으며, 가압기 초기온도는 615.31 K(운전압력의 포화온도)로 선정하였다. 원자로냉각재 고온부 초기온도는 596.15 K, 저온부 초기온도는 568.85 K로 선정하였다. 정체구간 초기온도는 가압기 초기온도와 원자로냉각재의 평균온도의 평균값으로 선정하였다.
2.4 열손실(Heat Loss)
가압기 검사체적의 내부에너지가 열손실에 의해 감소되면, 가압기 압력도 동시에 감소된다. 해석에서 고려한 열손실은 고온의 가압기 검사체적에서 외부대기 및 원자로냉각재계통 검사체적 방향으로 발생한다고 가정하였다. 구체적인 열손실 경로는 단열재가 설치된 원자로 용기의 대류 열손실과 25개의 제어봉구동장치(Control Rod Drive Mechanism, CRDM)를 통한 전도 열손실로 가정하였다. 아울러 원자로냉각재계통 검사체적 방향으로는 습식단열재(Wet Thermal Insulation, WTI)의 유효열전도도를 반영하여 전도열손실이 존재한다고 가정하였다. 이와 같이 열손실에 대한 수식은 아래의 식 (6)-(8)과 같다.
| (6) |
| (7) |
| (8) |
위의 식에서, , 그리고 는 각각 외부대기, 제어봉구동장치 그리고 습식단열재의 열손실을 의미한다. hVes. 및 APZR은 각각 단열재로 둘러싸인 원자로용기의 대류열전달계수 및 가압기의 표면적을 나타낸다. keff, AWTI 그리고 dWTI는 각각 습식단열재의 유효열전도도, 면적 그리고 두께를 의미한다.
2.5 전열기 제어(Heater Control)
가압기 전열기는 원자로용기로 빠져나가는 열손실을 보상하면서, 가압기 압력을 제어하기 위해서 사용된다. 용량은 정상운전중에 가압기 열손실을 보상하고 가압기 압력을 제어하기 위해서 600 kW로 선정하였다. 출력은 정상운전범위인 14.8 MPa 와 15.2 MPa 내에서 다음의 식 (9)와 같이 선형으로 비례제어 된다.
| (9) |
여기서 은 비례전열기에서 가압기로 공급되는 전기에너지를 의미한다. 전열기에서 공급되는 전기에너지는 가압기내부로 시간지연 없이 즉시 더해지도록 가정하였다.
가압기 관점에서 열손실은 에너지유출을, 전열기출력은 에너지유입을 의미하므로 열손실과 전열기출력의 합은 순 에너지 전달율(net energy transfer rate)로 생각할 수 있다. 비록 열손실은 제어할 수 없는 변수지만, 전열기의 출력을 제어하면 순 에너지 전달율을 제어할 수 있다. 즉, 가압기 압력은 전열기를 이용하여 순 에너지 전달율을 조절함으로써 제어할 수 있다. 예를들어 원자로냉각재가 가압기로 유입(내밀림)되면 압력이 증가하게 되는데, 이때 가압된 압력을 낮추기 위해서 전열기가 열손실보다 낮은 출력으로 제어된다. 전열기 출력이 낮아짐으로써 가압기 에너지는 외부로 손실되고 결과적으로 가압기 압력이 감소하게 된다.
2.6 계산과정(Calculation Procedure)
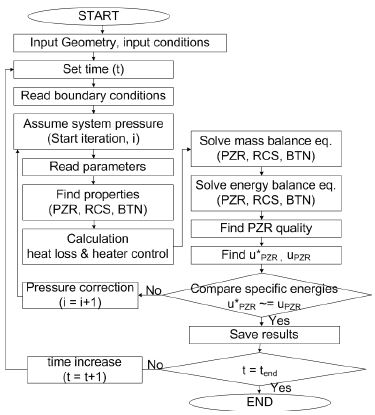
Fig. 4는 과도해석 계산과정을 보여준다. 해석이 시작되면 일체형 원자로 구조 및 초기조건이 Table 1에 제시된 값으로 입력된다. 계산과정에서 두 개의 반복문이 수행되며 첫 번째 반복문(외부반복문)에 두 번째 반복문(내부반복문)이 포함되도록 구성하였다.
외부반복문은 시간경과에 따른 일체형 원자로의 출력을 경계조건으로 입력하고 내부반복문의 계산결과를 저장한다. 내부반복문은 해당 시간에서의 질량보존식 및 에너지보존식에 대한 반복계산을 수행한다. 이때 가압기의 열손실과 원자로냉각재의 부피팽창 및 수축에 의한 밀림유량이 계산된다. 반복계산은 가압기영역의 비내부에너지가 충분히 수렴했을 때 종료되도록 설정하였다.
특히 가압기 압력은 다음과 같은 과정으로 추산할 수 있다. 임의의 압력을 가정하고 그 압력에서의 포화상태의 물성치 및 건도를 아래의 식 (10)에 대입하면 가정한 압력에서의 비내부에너지를 계산할 수 있다.
| (10) |
여기서 상첨자 *는 임의로 가정된 값임을 의미한다. 질량보존식(식 (1)) 및 에너지보존식(식 (3))에서 구한 질량과 내부에너지를 아래의 식 (11)에 대입하면 해당시간에서의 비내부에너지가 도출된다.
| (11) |
만약 식 (10)에서 계산된 값과 식 (11)에서 계산된 값이 다르다면, 계산결과의 차이가 수렴기준을 만족할 때까지 임의로 가정한 압력을 수정하면서 반복계산이 수행된다. 이때 계산이 발산하지 않도록 0~1 사이의 적절한 이완계수(relaxation factor)가 적용되었다. 수렴기준이 만족되었다면 계산결과를 저장하고 다음 시간증분에서의 과도해석이 수행된다.
3. 계산 결과(Calculation Result)
3.1 밀림유량(Surge Flow)
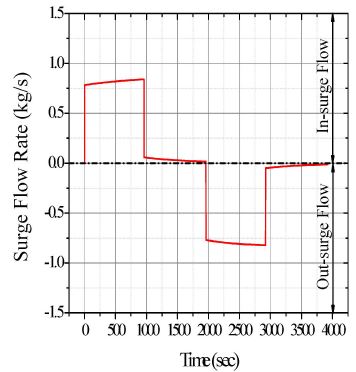
Fig. 5는 시간에 따른 밀림유량을 보여준다. 밀림유량은 원자로냉각재가 가압기 내부로 유입되면 내밀림, 외부로 유출되면 외밀림으로 정의하였다.
0-960초에서 원자로출력감소에 따라 원자로냉각재 평균온도가 상승하여 원자로냉각재의 부피는 팽창한다. 원자로냉각재 부피가 팽창함에 따라서 가압기로 밀려들어오는 내밀림 유량이 발생하는 것을 확인할 수 있다. 그와 반대로 1,961-2,920초에서 원자로출력증가에 따라 원자로냉각재 부피가 수축하여 외밀림 유량이 발생하는 것을 확인할 수 있다. 그 이외의 시간에서는 미량의 밀림유량이 발생하는 것을 확인할 수 있다. 이는 원자로냉각재 부피변화 이외에도 가압기 열손실과 전열량에 의해 발생하는 것으로 판단된다.
3.2 가압기 수위(Pressurizer Level)
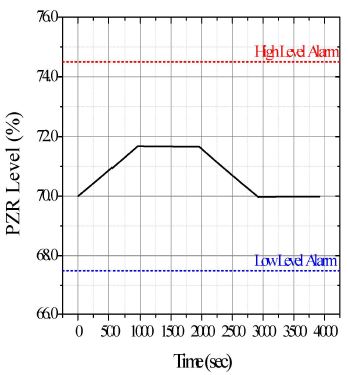
Fig. 6은 시간에 따른 가압기 수위변화를 보여준다. 0-960초에서 내밀림 유량에 의해서 가압기 수위는 점차 상승하는 것을 확인할 수 있다. 961초 이후에 가압기 수위는 약 71.7%로 유지되면서 고수위경보 기준을 초과하지 않음을 확인할 수 있다. 1,961-2,920초에서 외밀림 유량에 의해서 가압기 수위는 점차 감소하여 초기수위인 70%로 수렴하는 것을 확인할 수 있다. 961-1,960초와 2,921-3,920초에서도 각각 미량의 내밀림 유량과 외밀림 유량이 발생하지만, 밀림유량이 수위에는 큰 영향을 미치지 않는 것을 확인할 수 있다. 따라서 증기가압기는 고수위경보, 저수위경보 기준 내에서 운전되는 것을 확인할 수 있다.
3.3 가압기 압력과 전열기 제어(Pressurizer Pressure and Heater Control)
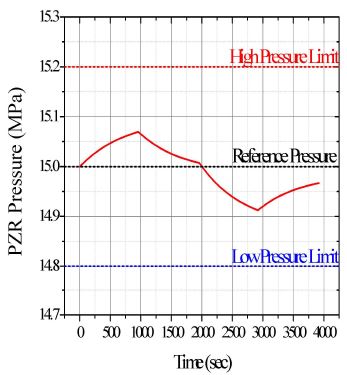
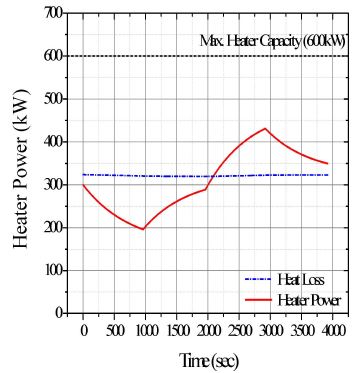
Fig. 7은 시간에 따른 가압기 압력변화를 보여주며, Fig. 8은 전열기에서 가압기로 공급되는 전열량을 보여준다. 0-960초에서 내밀림에 의해서 유입된 원자로냉각재가 가압기를 압박하여 압력이 상승하는 것을 확인할 수 있다. 그와 동시에 가압기의 열손실량은 비슷한 수준을 유지하지만 전열기출력은 점차 감소하므로 순 에너지 손실은 점차 증가하게 된다. 그 결과, 내밀림에 의해 가압기 압력이 상승하지만, 그 기울기는 점차 감소하는 것을 확인할 수 있다.
961-1,960초에서 가압기 압력이 감소하는 것은 미량의 내밀림 유량에 의한 영향보다 가압기의 순 에너지 손실에 의해 내부에너지가 감소하는 효과가 지배적인 것으로 판단된다. 아울러 이 구간에서 가압기 압력이 기준압력인 15.0 MPa로 수렴하는 것은 전열기가 열손실량을 보상하면서 제어되는 결과로 사료된다.
1,961-2,920초에서 외밀림 유량에 의해서 유출된 원자로 냉각재가 가압기를 감압하여 압력이 감소하는 것을 확인할 수 있다. 감소한 가압기 압력에 의해 전열량은 증가하게 된다. 전열량이 증가하지만 가압기의 열손실량은 유사한 수준을 유지하기 때문에 순 에너지 유입은 점차 증가하게 된다. 그 결과, 외밀림에 의해 가압기 압력이 감소하는 기울기가 감소하는 것을 확인할 수 있다.
2,921-3,920초에서 가압기 압력이 증가하는 것은 미량의 외밀림 유량에 의한 영향보다 가압기의 순 에너지 유입에 의해 내부에너지가 증가하는 효과가 지배적인 것으로 판단된다. 아울러 이 구간에서 가압기 압력이 운전압력인 15.0 MPa로 수렴하는 것은 열손실에 의한 압력감소를 전열기가 보상한 결과로 판단된다.
현재 전열기 제어 프로그램은 운전압력(15.0 MPa)에서 300 kW를 보상하도록 작성되었다. 하지만 가압기 열손실량은 운전압력에서 약 324 kW로 전열량보다 많은 것으로 평가되었다. 과도해석동안 열손실량과 전열량을 시간에 따라서 적분하면 열손실량이 더 많음을 확인할 수 있다. 그러므로 과도해석이 종료된 3,920초에서 가압기 압력은 15.0 MPa 보다 낮은 것으로 판단된다. 만약 운전압력에서 열손실량에 해당하는 전열량을 공급할 수 있도록 전열기 제어 프로그램이 상향으로 수정된다면, 과도해석이 종료된 시점에서 가압기 압력은 15.0 MPa에 더 근접할 것으로 예상된다. 가압기 열손실량과 전열기 제어 프로그램에 대한 평가는 추후 연구에서 수행할 예정이다.
4. 결 론(Conclusion)
본 연구에서는 일체형 원자로의 선형출력변화에서 증기가압기의 과도해석을 수행하였다. 일체형 원자로의 출력에 따라서 원자로냉각재의 평균온도가 가정으로 입력되었고 이는 원자로냉각재의 부피를 팽창시키거나 수축시켜 밀림유량이 형성되는 결과로 이어진다. 내밀림 유량이 형성되면 가압기 압력이 상승하게 되지만, 전열기의 전열량이 감소하도록 제어되므로 압력상승 기울기가 감소한다. 반면에 외밀림 유량이 형성되면 가압기 압력이 감소하게 되지만, 전열기의 전열량이 증가되어 압력감소 기울기가 작아진다. 이러한 내밀림, 외밀림 유량에 대해서 가압기 압력과 수위가 모두 허용범위 내에서 유지됨을 확인하였다.
본 연구에서는 가압기 내부의 액체상과 기체상이 항상 포화상태로 열평형을 이룬다고 가정하였다. 그러므로 액체상과 기체상 사이에서 발생하는 과도 상변화(일시적 과냉 또는 과열 상태)를 반영하지 못한 한계가 있다. 추후 연구에서는 가압기의 액체상과 기체상을 분리하고 상변화 기구(mechanism)를반영하여 가압기 작동성능 해석의 정확도를 높이고자 한다.
Acknowledgments
2015 한국유체기계학회 동계 학술대회 발표 논문, 2015년 12월 2일~12월 4일, 제주
이 논문은 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행되었음(2016M2C6A1930039).
References
- Cengel, Y. A., and Boles, M. A., (2007), “Thermodynamics–an Engineering Approach”, McGraw-Hill, 5th Edition.
- Todreas, N. E., and Kazimi, M. S., (1990), “Nuclear Systems I–Thermal Hydraulic Fundamentals”, Hemisphere Publishing Corporation.