가스터빈 이차 냉각 유로에 적용되는 프리스월러 노즐의 분사 방식 차이에 따른 시스템 특성 연구
Abstract
Pre-swirler is classified into the Tangential On-Board Injection (TOBI) type and the Radial On-Board Injection (ROBI). The TOBI type has a spatial margin from the duct inlet to the pre-swirler inlet, it is possible to install an additional guide system that can create the pre-swirl effect, maximize system performance. Whereas, the ROBI type has the advantage of making the pre-swirl effect even when the installation space of the secondary cooling air system is insufficient. In this study, two types of the pre-swirl system performance were compared by selecting the ROBI type with the same swirl ratio and mass flow rate as the TOBI type. When the swirl ratio of two types were the same, the temperature drop was not significantly different, but the discharge coefficient of the ROBI type was 8.1% higher than the TOBI type. When the mass flow rate of the two types were the same, the temperature drop of the TOBI type was 13.8% higher than the ROBI type and the discharge coefficient of the TOBI type was 4.1% lower than the ROBI type.
Keywords:
Computational Fluid Dynamics, Cooling System, Gas Turbine, Pre-swirler, Radial On-Board Injection, Tangential On-Board Injection키워드:
전산유체역학, 냉각 시스템, 가스 터빈, 프리스월러, 반경 방향 분사 방식, 접선 방향 분사 방식1. 서 론
가스터빈은 터빈 입구 온도를 높일수록 출력과 효율을 증가시킬 수 있으나, 소재의 내열 온도 한계로 인해 공기 등을 이용한 추가적인 냉각이 필수적으로 요구 된다.(1) 가스터빈 효율을 향상시키기 위해 지난 수십 년간 개발된 기술은 주로 터빈 입구 온도를 높이기 위한 냉각과 관련된 기술로써, 터빈 블레이드와 같은 단위 부품뿐만 아니라, 냉각 공기 공급을 위한 이차 유로 시스템 등을 포함한다. 가스터빈 이차 냉각 유로 시스템 중 프리스월러(Pre-swirler)는 압축기에서 이차 냉각 유로로 추출된 냉각 공기가 회전부로 유입되기 전, 냉각 공기를 미리 회전시켜 유동 손실을 최소화 하는 장치이다.(2) 냉각 공기의 유동 손실이 감소되면, 터빈 블레이드의 냉각 효율을 증가시킴으로써 가스터빈 전체 시스템 효율을 향상시킬 수 있다.
프리스월러는 형상에 따라 홀 형(Hole type)과 베인 형(Vane type)으로 구분된다. 베인 형은 홀 형에 비해 비교적 가공이 어렵고 제작비용이 많이 들지만, 공력 손실이 적다.
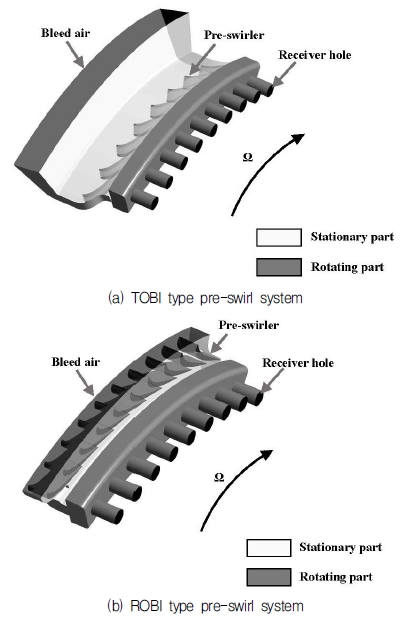
프리스월러는 회전 성분을 유발하는 방식에 따라 TOBI (Tangential On-Board Injection), ROBI (Radial On-BoardInjection) 프리스월 시스템으로 분류 된다.(3) ROBI type 프리스월 시스템에 비하여 TOBI type 프리스월 시스템은 덕트(Duct) 입구에서 프리스월러 입구까지 공간적 여유가 있기 때문에 프리스월 효과를 만들 수 있는 추가적인 가이드 시스템 설치가 가능하다. 따라서 시스템의 성능을 극대화 시킬 수 있는 장점을 가지고 있어 일반적으로 많이 사용된다. 반면, ROBI type 프리스월 시스템은 이차 냉각 유로 시스템의 설치 공간이 부족한 상황에서도 프리스월 효과를 만들 수 있다는 장점을 가지고 있다.
프리스월러 설계 시에는 터빈 블레이드에 공급되는 유량 확보와 온도강하를 동시에 달성해야 한다. 이 때문에 가스터빈 이차 냉각 유로 시스템의 효율을 높이기 위한 프리스월러에 대한 많은 연구가 이루어져 왔다.
Dittmann 등(4)은 실험을 통해 측정된 유량과 이론식을 통해 얻어진 유량의 비율인 유량 계수를 정의하였으며, 프리스월 시스템 내에서 발생되는 손실을 예측하였다. 실험을 통하여 압력 비에 따른 유량 계수를 구하였고, 압력 비와 유량 계수는 비례한다는 결과를 나타내었다.
Lee 등(5)은 프리스월 시스템의 유량 계수를 향상시키기 위한 홀 형 노즐 형상을 최적화하였다. 스월 비 1을 만족하는 조건에서 노즐의 입구부분과 출구부분의 길이를 조절하여 노즐을 설계하였으며, 일반 홀 형의 입구 부분에서 발생하는 손실을 감소시켜 유량 계수를 약 17% 향상시켰다.
Kim 등(6)은 스플리터(Splitter)를 적용한 베인 형 프리스월러의 특성을 확인하기 위해 스플리터 위치 별 유량 계수와 스월 비를 비교하였다. 프리스월 시스템 설계 시 유량 계수와 스월 비를 고려하여 스플리터 설치유무에 따른 성능을 비교하여 최적의 스플리터 위치를 도출하였다.
Geis 등(7)은 실험을 통해 측정된 전온도값과 이론값을 비교하며 프리스월 시스템의 온도 강하를 연구하였다. 노즐의 내부 손실과 캐비티(Cavity)내 혼합(Mixing)때문에 회전 속도가 증가할수록 실험값과 이론값의 온도 강하의 차이가 발생함을 확인하였다.
Javiya 등(8)은 CFD를 이용하여 일반 홀 형, 공기역학적 홀 형, 베인 형 프리스월러 형상에 관한 연구를 진행하였다. 압력 비 변화에 따른 노즐의 유량 계수와 스월 비 변화에 따른 온도 강하로 각 노즐의 성능을 비교하였는데 베인 형이 일반 홀 형 대비 약 22%, 공기역학적 홀 형 대비 약 5.5% 높은 노즐 유량 계수를 나타내었으나, 온도 강하는 베인 형과 홀 형 큰 차이가 없음을 확인하였다.
Liu 등(9)은 기존 베인의 흡입 면과 압력 면을 확장한 새로운 프리스월러(Vane Shape Hole type : VSH)를 설계하여 기존 프리스월러와 성능을 비교하였다. 동일 압력 비 조건에서 유량 계수는 베인 형이 VSH 형 대비 5% 높은 값을 나타내었지만, 베인 형 대비 확장된 VSH 형의 후연부로 인하여 2차 유동 강도를 감소시키고 끝 벽 손실을 감소시킬 수 있음을 나타내었다.
Laurello 등(10)은 ROBI type 프리스월 시스템에 관한 실험 및 CFD 연구를 진행하며 프리스월 시스템 위치 별 주요 설계 인자들의 변화를 비교하였다. 또한, 프리스월러를 통하여 회전 부에서 발생되는 일을 감소시켜 엔진의 출력과 터빈의 효율이 상승됨을 실험을 통하여 밝혔다.
참고문헌 중 Laurello 등의 연구를 제외한 대부분의 연구는 TOBI type으로 제한되어 있어 본 연구에서는 ROBI type 프리스월 시스템 장착 시 발생하는 효과를 비교해 보고자 한다. 본 연구에서는 기존에 설계된 TOBI type 프리스월러와 동일한 스월 비와 유량을 가지는 ROBI type 프리스월러를 선정하여 비교하였다. 또한, 프리스월 시스템의 성능을 평가하는 지표로 유량 계수와 온도강하를 선택하였다. ROBI type 프리스월러의 스월 비와 유량이 TOBI type 프리스월러와 각각 일치할 때 시스템 성능 변화를 확인하였으며, 결과적으로 두 프리스월 시스템의 성능을 비교분석하여 ROBI type 프리스월 시스템 설계 시 적합한 설계 가이드라인을 제시하였다.
2. 본 론
2.1 형상 정의
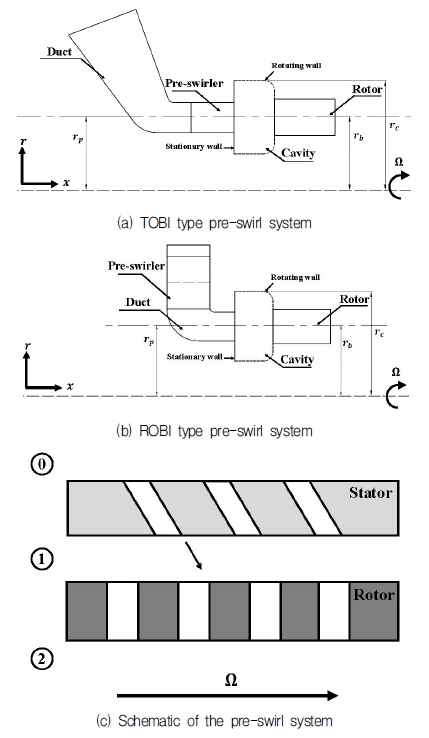
본 연구에 사용된 TOBI, ROBI type 프리스월 시스템은 덕트, 프리스월러, 캐비티, 리시버 홀(Receiver hole)로 구성되어 있으며, Fig. 1은 동일한 베인이 장착된 TOBI, ROBI type 프리스월 시스템 형상을 나타내었다.
두 프리스월 시스템을 비교하기 위하여 기존에 설계된 TOBI type과 동일한 스월 비와 출구 유량을 갖도록 ROBI type 프리스월러의 블레이드 개수(N)를 조절하였으며, 출구 목면적을 각각 다르게 설정하였다. 본 연구에서 사용된 케이스들의 프리스월러 형상 정보를 Table 1에 정리하였다. Table 1에 표시된 목면적은 각 케이스의 프리스월러 출구 목면적(At)을 TOBI type 프리스월러의 출구 목면적(Aref)로 나눈 무차원화 된 값으로 표시하였다. ROBI type 프리스월러는 스월 비와 출구 유량의 오차가 TOBI type과 약 0.1% 차이를 보이는 위치를 도출하여 연구에 적용하였다. TOBI type과 프리스월러 출구 스월 비를 일치시킨 ROBI type을 ROBI-1, 프리스월 시스템 유량을 일치시킨 ROBI type을 ROBI-2로 정의하였다. 본 연구에서 사용된 프리스월 시스템의 형상을 도식화하여 Fig. 2에 나타내었다.
2.2 프리스월 시스템 성능 평가 지표
스월 비(Swirl ratio)는 시스템의 회전 속도에 대한 유동의 원주 방향 속도 성분의 비율로 정의되며, 유동의 원주 방향 속도 측정 위치에 따라 프리스월러 출구에서의 스월 비와 리시버 홀 입구에서의 스월 비로 분류된다. 유동의 원주 방향 속도 성분과 시스템의 회전 속도가 일치할 경우 스월 비는 1이 되며, 이때 회전하는 리시버 홀에 적은 손실로 냉각 공기를 공급할 수 있다. 식 (1)에 본 연구에서 사용된 프리스월러 출구에서의 스월 비를 나타내었다.(7)
| (1) |
여기서 υΦ는 전산해석을 통해 프리스월러 출구에서 측정 된 유동의 원주 방향 속도 성분. rp은 캐비티 입구까지의 반경 거리, Ω은 터빈의 회전 속도이다.
무차원화 된 유량(Non-dimensional mass flow rate)은 실제 유량을 무차원화하기 위해 캐비티 입구에서 측정 된 점성과 캐비티의 외경을 나눈 값이며, 식 (2)으로 나타낼 수 있다.(7)
| (2) |
여기서 μ은 캐비티 입구에서 측정 된 점성, rc는 캐비티의 외경을 나타낸다.
유량 계수(Discharge coefficient)는 이상적인 유량에 대한 실제 유량의 비율로 정의되며, 프리스월러 출구 목 면적, 압력, 온도가 고려된 무차원수이다. 유량 계수가 1에 근접할수록 프리스월 시스템의 실제 유량이 이상적인 유량에 가깝다는 것을 의미하며, 터빈 블레이드로 공급되는 냉각 유량을 증가시킬 수 있다는 것을 의미한다. 식 (3)에 프리스월 시스템의 유량 계수를 나타내었다.(4)
| (3) |
여기서 은 프리스월 시스템의 실제 유량, At은 프리스월러의 출구 목면적, p0t는 프리스월 시스템 입구 전압, R은 기체 상수, T0t은 입구 전온도, γ은 비열 비, p2s은 리시버 홀 출구에서의 정압을 나타낸다.
2.3 전산해석
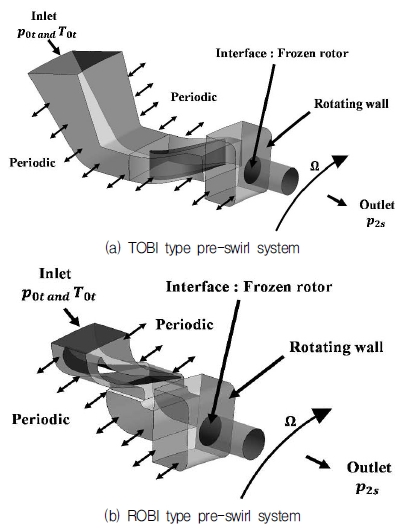
TOBI, ROBI type 프리스월 시스템의 전산해석 영역은 고정 영역과 회전 영역으로 구분되며, Fig. 3에 각 프리스월 시스템의 전산해석 영역을 나타내었다.
각 프리스월 시스템의 입구는 전압과 전온도 조건을, 출구는 정압 조건을 주었다. 회전 영역은 3,600 rpm으로 회전하며, 전산모델의 벽면 조건은 No slip condition을 적용하였다.
각 프리스월 시스템은 원주방향으로 주기적이기 때문에 해석시간을 감소시키기 위해 주기조건을 적용한 단일 경로(Passage)를 사용하여 해석을 진행하였다. 덕트와 프리스월러의 경계면에는 동일한 고정 영역이기 때문에 일반 연결 방법(General connection)인 None기법을 적용하였다. 또한 고정 영역과 회전 영역의 경계 면에는 프로즌 로터(Frozen rotor)기법을 적용하였다.(11)프로즌 로터 기법은 회전 영역의 움직임을 고정한 정상상태 해석기법으로 고정 영역과 회전 영역이 각각 절대 좌표계와 회전 좌표계에서 계산된다.(12) 프리스월 시스템 노즐의 특성 상 프리스월러 출구의 유동 속도가 원주 방향에 따라 다르기 때문에 원주 방향으로 압력, 속도 등을 평균하여 회전부로 전달되는 Stage 기법은 적합하지 않다.
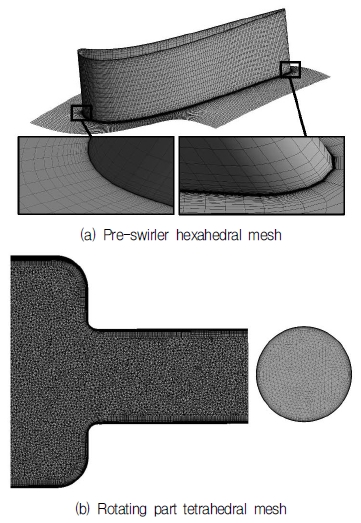
Fig. 4에 전산해석에 사용된 프리스월러 격자 및 리시버 홀 출구 격자를 나타내었다. 전산해석에 사용 된 프리스월러 격자는 육면체 격자로, 나머지 유동 영역은 사면체 격자로 구성하였다. 벽면 근처에서의 정확한 유동 모사를 위하여 벽면에는 Prism 격자를 구성하였으며, 최대 y+<1을 만족하도록 설정하였다. 격자 의존성 시험에 따라 회전 영역 격자수는 약 420만 개, 프리스월러 격자수는 약 150만 개, 덕트 영역은 약 320만 개, 프리스월러는 약 150만 개, 회전 영역 격자수는 약 420만 개 의 격자로 총 890만개의 격자가 사용되었다.
전산해석은 Ansys 社의 CFX ver. 17.2를 이용하였다. Reynolds Averaged Navier-Stokes Equation (RANS) 모델을 사용하여 정상상태 유동해석을 수행하였으며, 모든 변수들에 대하여 Root Mean Square (RMS) Residual이 1.0 × 10-5 이하를 만족하도록 하였다. 프리스월 시스템의 회전 성분이 지배적인 캐비티 영역과 베인 근처 점성 효과를 고려해야 하기 때문에 k - ω based Shear Stress Transport (SST)난류모델을 사용하였다. SST 난류모델은 벽면 근처(Near wall)유동모사에 적합한 k - ω 난류모델과 원거리 장(Far-field)의 유동을 잘 모사하는 k - ϵ 난류모델의 장점을 결합한 난류모델이다.(11)
2.4 결과 및 분석
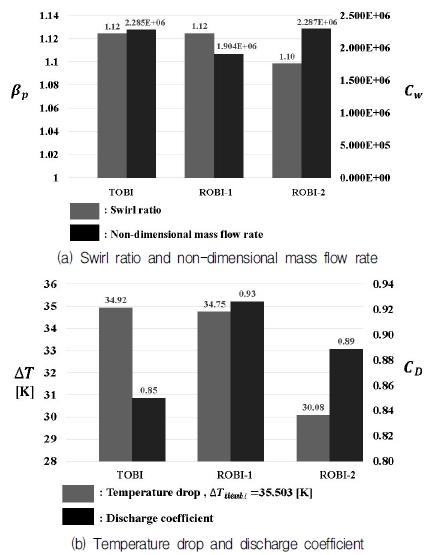
TOBI, ROBI type 프리스월 시스템의 온도 강하 성능 비교 결과를 Fig. 5에 나타내었다. 온도강하는 기존 설계된 TOBI type의 이상적인 온도강하를 기준으로 비교하였다. 이상적인 온도강하는 프리스월러 내부 손실이나 캐비티 내 혼합(Mixing)에 의한 손실을 배제한 값이기 때문에,(7) 실제 온도강하와 값의 차이를 보였다. ROBI-1과 TOBI type의 온도강하는 약 0.5% 차이를 보였는데, 이는 이상적인 온도강하보다 약 2.7% 낮은 값을 보였다. ROBI-2의 경우 TOBI type 보다 약 13.8% 낮은 온도강하를 나타내었는데, 이때 이상적인 온도강하보다 약 15.3% 낮은 값을 보였다.
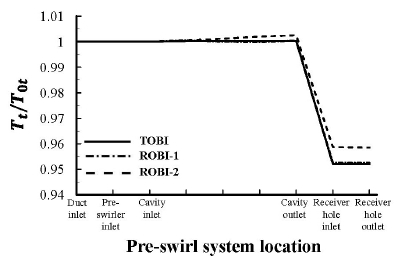
3가지 케이스의 온도강하 차이를 캐비티 전후 전온도 변화에서 확인하였다. Fig. 6는 TOBI type과 ROBI type 프리스월 시스템의 위치에 따른 전온도 변화를 나타내었다. 전온도는 프리스월 시스템 입구 전온도(T0t)를 위치별 전온도(Tt)로 나눈 무차원화 값을 사용하였다. 프리스월 시스템 위치별 전온도는 프리스월 시스템 입구, 캐비티 입구, 리시버 홀 입구, 리시버 홀 출구에서 측정 된 값을 비교하였다. 리시버 홀 입구부터 상대 좌표(Relative frame)에서 측정 된 전온도 값을 사용하였다.
3가지 케이스 공통적으로 캐비티 입구까지 비슷한 전온도 분포를 보이지만, ROBI-2의 경우 캐비티 내에서 전온도가 상승함을 확인 할 수 있었다. ROBI-2는 프리스월러 출구 원주 속도 성분이 낮기 때문에 유동이 캐비티 내에서 회전하는 리시버 홀로 유입 시 상대속도 차이로 인한 손실로 전온도가 낮게 감소한 것으로 보인다. 따라서 TOBI type과 동일한 스월 비를 가지는 ROBI type 프리스월러 설계가 온도강하 면에서 유리할 것으로 보인다. 또한 스월 비가 온도강하에 영향을 주는 지표임을 밝힌 선행연구의 결과(7,8)들과 동일함을 확인하였다. TOBI type과 ROBI type의 실제 출구 유량을 일치시킬 경우, 스월 비 차이가 발생하여 온도강하가 줄어드는 것을 확인하였다.
TOBI, ROBI type 프리스월 시스템의 유량 계수 성능 비교결과를 Fig. 5에 나타내었다. 유량 계수는 ROBI-1이 가장 높은 값을 나타내었으며, TOBI type 대비 약 8.1% 높은 값을 나타내었다. ROBI-2의 경우 TOBI type보다 약 4.1% 높은 유량 계수를 보였다. Fig. 5를 통하여 TOBI type이 ROBI type보다 많은 유량 손실을 보이고, 같은 ROBI type의 경우 스월 비가 낮을수록 유량 계수가 낮게 나타나는 것을 확인 할 수 있다.
3가지 케이스의 유량 계수 차이는 TOBI type에서 이상적인 유량 대비 손실 되는 실제 유량이 많음을 의미하는데, TOBI type의 유동 손실을 입구 덕트와 캐비티 영역에서의 유동분포에서 확인하였다.
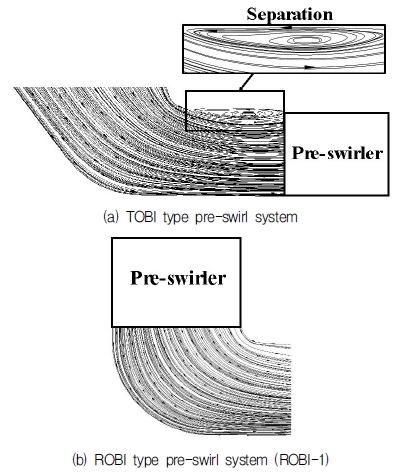
Fig. 7은 프리스월러 출구 스월 비가 동일한 ROBI-1과 TOBI type의 입구 덕트에서 유선을 나타낸다. TOBI type은 덕트 형상에 의하여 발생 된 박리(Separtion)로 인한 차폐 효과(Blockage effect)때문에 유로의 면적이 ROBI-1보다 감소된 것을 확인할 수 있다. 반면, ROBI-1은 덕트의 유로가 원주 방향에서 축 방향으로 꺾이기 전에 프리스월러를 지나기 때문에 원주 방향 속도 성분이 지배적이었다. 이에 따라 ROBI-1의 유로에서는 박리가 발생하지 않았다.
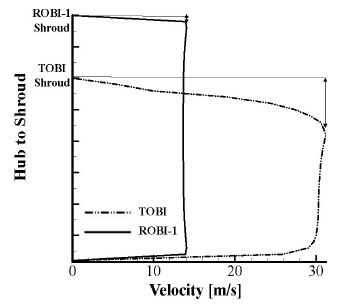
Fig. 8은 TOBI type과 ROBI-1의 Hub에서 Shroud까지 단위 길이 당 측정 된 프리스월러 입구 속도 분포를 나타내었다. Shroud 부분과 Hub 부분에서 균일한 속도 분포를 나 타내는 ROBI-1에 비하여 TOBI type의 속도 분포는 Shroud 부근의 차폐 효과로 인해 Hub 부분에 비해 낮은 속도를 나타냈다. 한편, 노즐 입구 면적 차이로 인하여 TOBI type의 속도가 더 높은 분포를 나타냄을 확인하였다.
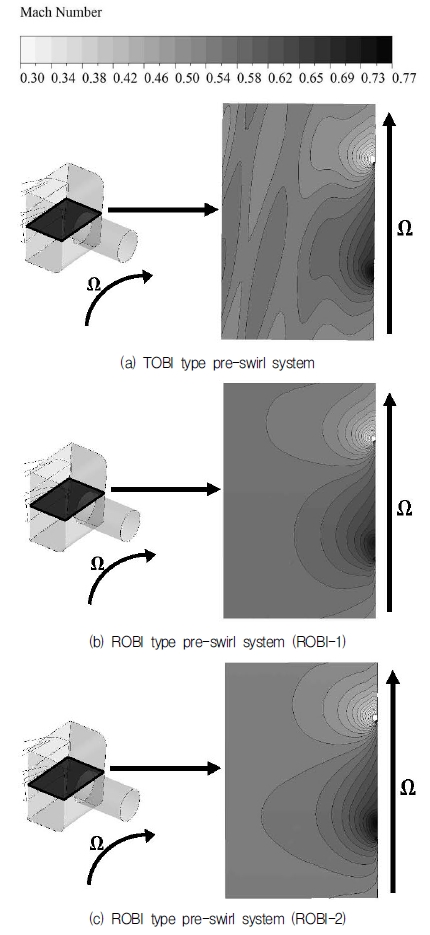
Fig. 9는 캐비티 내 Pitch radius에서 측정된 Mach number 분포를 나타내었다. TOBI type은 프리스월러의 위치가 캐비티와 근접하기 때문에 캐비티 내에서 ROBI type에 비해 불규칙적인 유동 분포를 나타내었다. 반면, 캐비티 내부로 시스템의 회전 방향에 맞게 미리 회전하여 유입되는 ROBI type은 TOBI type에 비해 안정적인 유동분포를 나타내었다. 따라서 TOBI type이 ROBI type에 비해 캐비티 내 혼합(Mixing)에 의한 유동 손실이 더 크게 발생된 것으로 보인다.
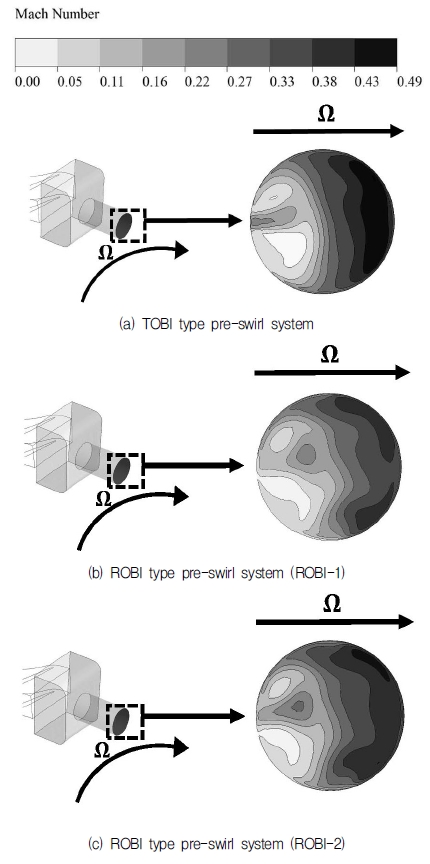
Fig. 10은 프리스월 시스템 리시버 홀 출구에서의 Mach number 분포를 나타내었다. TOBI type은 ROBI type에 비해 회전 방향과 비회전 방향의 Mach number 분포 차이가 크게 나타났다. 따라서 TOBI type에 비해 안정적인 유동분포를 보이는 ROBI type이 유동 손실이 더 적게 발생된 것으로 판단된다.
3. 결 론
본 연구에서는 ROBI type 프리스월 시스템 장착 시 발생하는 효과를 비교해 보고자 기존에 설계된 TOBI type 프리스월러와 동일한 스월 비와 유량을 가지는 ROBI type 프리스월러를 선정하여 프리스월 시스템 성능을 비교하였다. 두 프리스월 시스템 성능은 유량 계수와 온도강하로 비교하였으며, 일정 구속 조건들에 따른 프리스월 시스템 성능 결과 값들을 정리하였다.
두 프리스월 시스템의 스월 비가 일치할 경우 ROBI type은 TOBI type대비 낮은 유동 손실을 보였다. 반면, 실제 유량이 일치할 경우, 스월 비 차이가 발생하여 온도강하가 덜 발생하였다. 따라서 스월 비는 온도강하에 영향을 주는 요인임을 밝힌 선행연구의 결과들과 동일함을 확인하였다.
온도강하의 차이는 캐비티 전후 전온도 변화에서 확인하였다. 프리스월러 출구 원주 속도 성분이 가장 낮은 ROBI-2의 경우 캐비티 전후 전온도 상승이 가장 높은 값을 나타났다. 이는 유동이 캐비티 내에서 회전하는 리시버 홀로 유입 시 상대속도 차이로 인한 손실로 전온도가 낮게 감소한 것으로 보인다.
유량 계수는 TOBI type이 ROBI type 보다 낮은 값을 나타내었다. 이러한 유량 계수의 차이는 TOBI type 프리스월 시스템의 입구 덕트에서 발생한 박리로 인한 차폐 효과와 캐비티 영역 내 불규칙적인 유동분포가 원인인 것으로 보인다.
본 연구에 사용된 ROBI type 프리스월러는 TOBI type 프리스월러를 이용하였기 때문에 ROBI type에 맞는 프리스월러 설계가 필요하다. 따라서 TOBI type과 일치하는 스월 비를 나타내는 ROBI type 프리스월러로 설계를 진행한다면 가스터빈 이차 냉각 유로 공간이 부족한 상황에서도 비슷한 온도강하를 낼 수 있을 것으로 판단된다. 향후 스월 비와 실제 출구 유량을 동시에 만족하는 ROBI type 프리스월러를 설계하여 추가적인 연구를 진행할 예정이다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행하였습니다(No. 2013101010170A).
References
- Saravanamuttoo, H. I. H., Rogers, G. F. C., Cohen, H., and Straznicky, P. V., (2009), Gas Turbine Theory, 6th Edition, Prentice Hall, London, p366-376.
- Rolls-Royce, (1996), “The JET ENGINE,” Rolls-Royce plc, 5th Edition, p85-88.
- D. Glasspoole, Y. Schraenen, (2001), US Patent No. 6183193.
-
Dittmann, M., Geis, T., Schramm, V., Kim, S., and Wittig, S., (2002), “Discharge Coefficients of a Preswirl System in Secondary Air Systems”, ASME Journal of Turbomachinery, 124, p119-124.
[https://doi.org/10.1115/1.1413474]

-
Lee, H., Lee, J., Kim, D., and Cho, J., (2017), “Pre-swirl Nozzle Geometry Optimization to Increase Discharge Coefficient Using CFD Analysis”, The KSFM Journal of Fluid Machinery, 20(1), p21-28.
[https://doi.org/10.5293/kfma.2017.20.1.021]

-
Kim, D., Kim, J., Lee, H., and Cho, J., (2017), “Effect of Splitter Location on the Characteristics of a Vane-type Pre-swirl System”, Journal of Mechanical Science and Technology, 31(3), p1267-1274.
[https://doi.org/10.1007/s12206-017-0225-y]

-
Geis, T., Dittmann, M., and Dullenkopf, K., (2004), “Cooling Air Temperature Reduction in a Direct Transfer Preswirl System”, Journal of Engineering for Gas Turbines and Power, 126(4), p809-815.
[https://doi.org/10.1115/1.1765124]

-
Javiya, U., Chew, J., and Hills, N., (2011), “A Comparative Study of Cascade Vanes and Drilled Nozzle Designs for Pre-Swirl”, ASME Turbo Expo, Vancouver, British Columbia, Canada, GT-2011-4006.
[https://doi.org/10.1115/gt2011-46006]

-
Liu, Y., Liu, G., Kong, X., and Feng, Q., (2016), “Design and Numerical Analysis of a New Type of Pre-swirl Nozzle”, ASME Turbo Expo, Seoul, South Korea, GT-2016-56738.
[https://doi.org/10.1115/gt2016-56738]

-
Laurello, V., Yuri, M., Fujii, K., Ishizaka, K., Nakamura, T., and Nishimura, H., (2004), “Measurement and Analysis of an Efficient Turbine Rotor Pump Work Reduction System Incorporating Pre-Swirl Nozzles and a Free Vortex Pressure Augmentation Chamber”, ASME Turbo Expo, Vienna, Austria, GT-2004-53090.
[https://doi.org/10.1115/gt2004-53090]

- Dulac, A., (2012), “A CFD Analysis Towards Flow Characteristics of Three Pre-swirler Designs”, Master of Science Thetis, Department of Energy Technology, Division of Heat and Power Technology, KTH Industrial Engineering and Management.
- Noh, J. G., Jeong, E. H., Lee., E. S., and Kim, J., (2004), “Numerical Flow Analysis of a Partial Admission Turbine Using a Frozen Rotor Method”, The KSFM Journal of Fluid Machinery, 7(6), p15-20.