축류 팬 허브의 홀 형상 최적화를 통한 모터 열 해석 및 유동 특성에 대한 수치해석적 연구
Abstract
The motor used to drive an axial flow fan generates heat due to internal resistance, which negatively affects performance and shortens the fan’s life span. In this study, cooling of the fan motor using the passive flow control (PFC) method was employed via the hole shape optimization of the axial fan hub. Four design parameters were selected and design points were created using an optimal space-filling design method. The Kriging model was used to construct the response surface. The optimization process using the multi-objective genetic algorithm (MOGA) was performed until the error between the candidate value and the CFD value was less than 0.1%. By comparing the candidate with the initial shape, the optimized shape generated air flow from the back to the front of the axial fan hub. The maximum temperature of the motor was reduced by 17.47 K under the same rotational speed. Conversely, the temperature was further reduced by 6.21 K when compared with the initial shape and operated at the same total pressure.
Keywords:
Air-cooling, Computational fluid dynamics, Design optimization, Passive flow control, Thermal analysis키워드:
축류 팬, 전산유체해석, 최적화 설계, 피동유동제어, 열 해석1. 서 론
축류 팬은 로터를 이용하여 기계적인 에너지를 기체에 전달하여 압력과 속도에너지로 변환시켜 유동을 축에 평행한 방향으로 이동시키는 유체기계로, 가정용 및 산업용으로서 다양하게 사용된다.(1,2) 이러한 축류 팬의 구동에는 일반적으로 모터를 이용하는데, 전기에너지를 운동에너지로 바꾸는 모터의 특성 상 내부 저항으로 인해 발열이 발생하게 된다. 이것은 코일(Coil)이나 도체의 저항에 의해 모터의 통전부에 발생하는 동손, 자력선이 지나갈 때의 철심재료의 저항, 철심을 자화시키기 위하여 철손부에 발생하는 철손에 의한 전기적 손실로, 이는 모터의 성능저하 및 수명 단축의 원인이 된다.(3) 일반적으로, 모터의 수명을 결정하는 절연체는 아레니우스 식(Arrhenius Equation)에 의해 온도가 10 ˚C 높아질 때마다 수명이 절반으로 감소한다.(4) 이러한 이유로, 모터의 효율과 수명 감소를 방지하기 위해 모터 냉각을 위한 많은 연구가 이루어져 왔다.(3~7)
Yoon 등(3)은 냉각에 따른 인덕션 모터의 효율 증가 해석을 진행하여 코일의 효율과 온도 사이의 관계를 확인하였다. 실험 결과, 코일 온도를 10 ˚C 낮추었을 경우 100% 부하에서 효율이 0.25 % 증가하고, 125 % 부하에서 효율이 0.5 % 증가하는 것을 확인하였다.
Ulbrich 등(5)은 진화 알고리즘(Genetic Algorithm, GA)을 이용하여 밀폐된 공간에 있는 2차원 모터의 열 방출을 극대화하기 위한 핀의 최적화를 진행하여 그때의 매개변수 집합을 연구하고 CFD 후보군을 선정하였다.
Kang 등(6)은 3차원 난류 모델링을 이용하여, 외부 냉각 블레이드 및 냉각 구멍의 회전을 통해 강제 대류를 발생시킴으로써 기존 BLDC 모터 모델에 비해 열전달률을 8.1 % 증가시켰다.
Yang 등(7)은 485 kW급 모터를 3차원 모델링을 통해 유한체적법(Finite Volume Method, FVM) 방법으로 수치 해석하여 모터의 냉각설계 변수가 되는 요소를 도출하였다. 이를 통해 온도상승을 예측할 수 있는 해석 절차를 수립하였으며, 덕트 폭 또는 팬의 변화가 냉각 설계에 더 지배적인 인자임을 발견하였다.
그러나, 일반적인 축류 팬 형상에서 핀 또는 외부 냉각 블레이드를 이용하는 등의 추가 형상 설치 방법은 팬에서 발생하는 유동의 흐름을 방해하여 급격한 효율 저하를 야기시킬 수 있다. 본 연구에서는 축류 팬의 허브부에 홀(Hole) 형상 제작을 통한 피동유동제어(Passive Flow Control, PFC) 기법을 이용하여 모터를 냉각시키고, 부가적으로 축류 팬 전ㆍ후면부의 압력 차이와 요구 토크(Torque)를 분석하여 축류 팬 성능의 변화에 대한 공기역학적 특성을 확인하였다.
2. 본 론
2.1 전산해석 모델
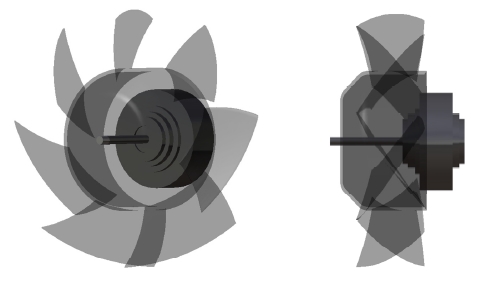
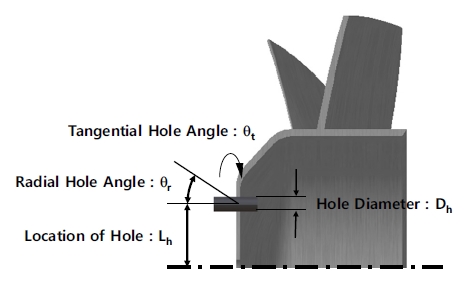
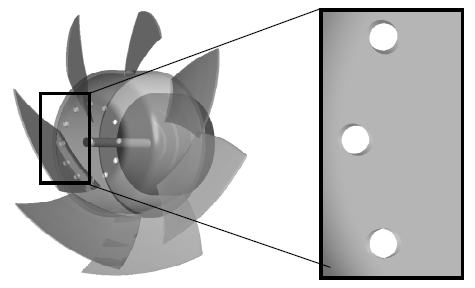
본 연구에 사용된 축류 팬 모터 냉각 시스템은 모터, 덕트, 허브 부분에 홀이 있는 축류 팬으로 구성되어 있다. 축류 팬은 7개의 날개를 가진 팁 235mm, 허브 130mm의 기 설계된 모델을 이용하였다. 축류 팬 허브에서의 홀의 개수 N, 홀의 지름 Dh, 중심으로부터의 거리 Lh 및 중심 축과의 반경방향 각도 θr, 접선방향 각도 θt가 모터의 냉각에 미치는 영향을 확인하였다. 축류 팬과 모터의 결합 형상은 Fig. 1에 등각도와 측면도로 나타냈고, 크기와 각도 등에 대한 자세한 정보는 Fig. 2 와 Table 1에 나타내었다. 엇갈림각(Stagger angle)은 블레이드가 유동 방향과 이루는 각도이며, 비틀림각(Twist angle)은 블레이드의 Span 방향에 따른 각도 차이를 나타낸다.
Base model
Design variables of hole shape
Axial fan specifications
형상 변수는 팬 허브 부와 홀 형상의 크기를 고려하여 생성 가능한 범위 내로 설정하였고, 홀의 개수는 형상 제작 과정에서의 편의성을 고려하여 6개, 8개, 12개로 설정하였다. 홀 형상은 축류 팬의 허브 부 위에 위치하며, 각각 60 ˚, 45 ˚, 30 ˚의 등간격을 이룬다. 덕트와 모터는 기 설계된 모델을 이용하였고, 이에 관한 정보는 Table 2와 Table 3에 나타내었다.
Duct specifications
Motor specifications
2.2 성능평가 지표
모터 냉각 최적화 형상의 첫 번째 성능 평가 기준으로는 모터 평균 표면온도를 설정하였다. 홀 형상 생성으로 인해 발생하는 유동이 모터의 전반적인 냉각에 미치는 영향성을 분석하기 위하여 모터의 평균 표면온도를 기준으로 비교하였다.
정상상태에서, 원통 내 발생하는 열발생률은 원통 표면에서 이동하는 유체로 대류 전달되는 열전달률과 같아야 한다. 열전도율 k가 일정할 때, 원통 내에서 온도분포는 식(1)과 같이 정의된다.
| (1) |
여기서, r은 원통의 반지름, 는 체적 당 에너지 발생률, k는 열전도율이다. 체적 내 균일한 열 발생을 가정했을 때, 속이 꽉 찬 원통에서 중심선은 온도분포의 대칭선이며 온도구배는 0이어야 한다. 표면온도 Ts와 저온유체의 온도 T∞에 대하여, 대류열전달계수 h를 이용하여 총합 에너지 평형을 사용하면 원통형 형상의 온도분포는 식 (2)와 같다.(8)
| (2) |
이 때. 식(2)에서 구한 온도는 모터의 전체 에너지 중 모터가 한 일을 제외한 일부에서 발생하기 때문에, 모터에 유입되는 전체 전력 대비 Table 3에서 구한 모터의 효율 62.4 %를 제외하고, 그 중 일반적인 동손인 80 %가 모두 모터의 발열로 전환된다고 가정하였다.
축류 팬은 유동을 입구 방면에서 출구 방면으로 이동시키는 유체기계이기 때문에, 팬의 출구 방면과 입구 방면의 압력 차이가 존재한다. 이에 허브부에 홀을 생성했을 경우와 그렇지 않은 경우에 대하여, 팬의 전/후면부 압력차가 다르게 나타나기 때문에 팬에 작용하는 토크가 변화하게 되고, 이는 팬 소모동력의 변화로 이어진다.
회전축에 작용하는 토크는 유동이 팬에 가하는 운동량의 관점에서 표현될 수 있다. 동력이 일정할 때, 아래의 관계식을 통해 팬의 소비전력을 계산하였다.(9)
| (3) |
이 때, τ는 팬의 토크, N은 팬의 회전속도이다.
식 (3)과 같이, 팬의 소비전력은 팬의 토크와 회전속도에 비례하고, 모터의 효율과 반비례한다.
팬의 회전속도가 일정하기 때문에 팬의 소비전력은 팬의 요구 토크와 비례한다. 본 연구에서는 축류 팬 허브부의 홀 형상 비교를 통해 축류 팬 가동 시 요구 토크의 변화를 확인하였다.
팬의 구동에 의한 이송공기가 갖는 압력은 공기가 흐르고 있는 관이나 장치 등에서 발생하는 유동저항을 극복하는 데 필요한 압력으로, 팬 성능평가의 기준으로 사용된다.
| (4) |
이 때, 팬의 성능을 증가시키기 위한 목적함수는 전압효율로서, 식 (4)와 같다. 여기서, ηt는 전압효율, P는 전압, Q는 유량, τ는 팬 토크이며, ω는 팬의 회전 각속도이다. 압력을 제외한 유량과 팬 토크, 각속도가 일정할 경우, 팬의 효율은 압력에 비례하기 때문에, 전압과 팬의 효율은 비례한다고 할 수 있다.
본 연구에서 사용된 형상은, 팬 허브의 홀 형상으로 인해 축류 팬 내부를 흐르는 유동이 후면부에서 전면부로 이동하며 모터를 냉각시키기 때문에, 압력의 변화는 불가피하다. 이에 홀 형상 최적화를 진행하여 축류 팬 전ㆍ후면부의 압력을 비교하고, 모터 냉각을 만족하면서 최소한의 압력 감소를 목표로 하는 홀 형상을 연구하였다. 또한 이때의 압력 차이를 비교하여, 각 결과 별 축류 팬의 성능에 미치는 영향을 파악하는 기준으로 설정하였다. 축류 팬 성능 예측에는 아래 식 (5)의 팬 법칙(Fan laws)을 이용하였다.
| (5) |
여기서, p는 팬에서 발생하는 압력, n은 팬의 회전속도, d는 팬의 지름, ρ는 작동유체의 밀도이다. 동일 조건에서 팬의 전압력 차이를 일치시키기 위한 팬 회전속도 조정이므로, 이를 적용하면 식 (6)과 같다.
| (6) |
식 (6)을 이용하여 기본 형상과 최적화 형상의 압력 차이 값을 일치시킨 후, 그 때의 전압력 비교를 통해 팬 성능의 변화 유무를 판단하였다.
2.3 전산해석 기법
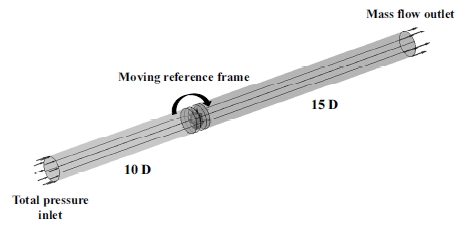
상용 전산유체역학 도구인 ANSYS CFX ver. 17.2를 이용하여 전산해석을 수행하였다. Fig. 3과 같이, 전산해석은 회전운동을 정상상태로 가정하여 좌표계를 회전시키는 MRF(Moving Reference Frame) 기법을 이용하여 축류 팬의 회전을 모사하였다. 축류 팬의 지름을 1D로 하였을 때, 해석영역의 크기는 전면부 10 D, 후면부 15 D로 설정하였다. 표준 대기상태 기준, 입구조건으로 균일 전압력 조건, 출구조건으로 균일유량 조건을 적용하였으며, 이에 관한 정보는 Table 4에 나타내었다. 전산해석에는 RANS 방정식(Reynolds Averaged Navier-Stokes Equation)을 이용하여 정상상태의 유동을 해석하였다. RANS 방정식은 시간 평균 기법을 이용한 Navier-Stokes 방정식이다. 난류 모델은 경계층이 있는 유동에서 벽면 열전달 예측에 효과적인 SST κ-ω(Shear Stress Transport κ-ω)을 이용하였다. κ-ω 기반 SST 모델은 벽면 인근에서 κ-ω를, 그 이외의 공간에서는 κ-ϵ 모델을 사용함으로써 두 모델의 장점을 결합한 모델이다.(10)
Computational domain
Boundary conditions
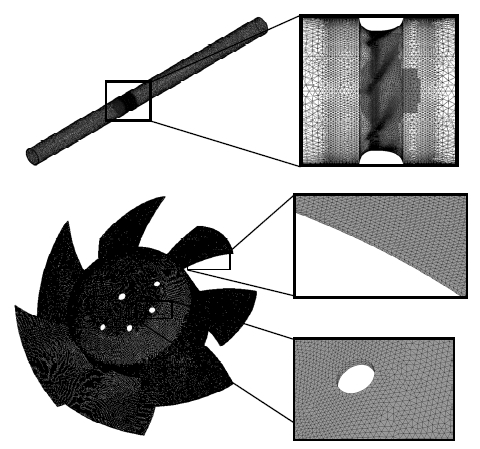
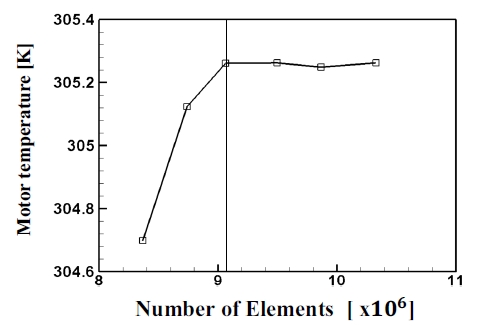
Fig. 4와 같이 블레이드의 전ㆍ후면부와 홀 주위, 회전영역의 입ㆍ출구부에서는 최대 격자간격을 2mm로 설정하였다. 고정영역과 회전영역의 경계면은 동일 격자를 이용한 Frozen rotor 조건을 설정하였다. 경계층 영역에 프리즘 격자 생성을 통해 결과의 정확도를 높였다. 모터 주위 격자는 y+<1을 만족하는 경계층 조건을 설정하였다. 블레이드의 앞전(Leading edge)과 뒷전(Trailing edge)에는 맵 메쉬(Mapped mesh)를 이용하여 곡면을 형성하였다. Fig. 5는 격자 의존성 확인 결과를 나타내었으며, 약 906만 개의 사면체 및 프리즘 격자를 형성하였다.
Grids of axial fan configuration
Grid dependency test
2.4 최적화 기법
최적화 과정 진행에 이용할 설계점 추출에는 실험계획법(Design Of Experiment, DOE)을 이용한 반응표면 최적화(Response surface optimization) 기법을 사용하였다. 실험설계법은 이론적 모델이 아닌 실험 데이터 분석에 기반한 해석 및 이를 통한 성능 향상을 위해 적용할 수 있는 모델이다. 반응 표면 최적화 기법은 결과에 영향을 미치는 여러 개의 핵심 인자가 선정된 후, 각 인자의 최적 조건을 도출하기 위하여 사용하였다. 실험설계법을 통한 설계점 선별 작업을 통해, 4개의 형상변수를 이용해 만들어진 15개 설계점을 이용하여 최초의 반응면을 구성하였다. 각 설계점은 Optimal space-filling design 방식을 이용하여 실험설계법을 진행하는 공간 내에서 균일한 분포를 만족시킨 후, Maxi-min distance type을 이용하여 두 설계점 사이의 거리를 최대화하였다. 설계점 수를 결정하는 sample type은 full quadratic model 방식을 이용하여 기존 설계점을 이용한 2차 모델을 생성하였다.
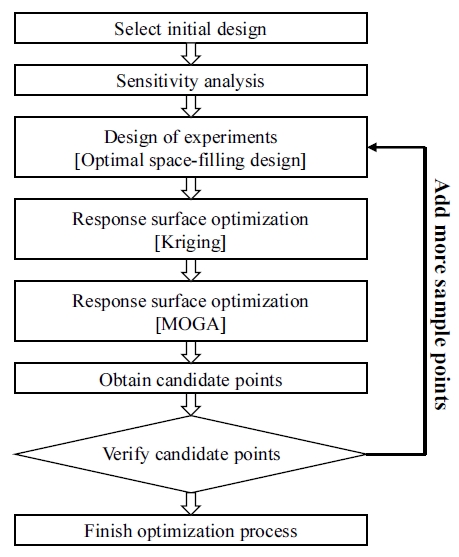
생성된 반응면을 이용하여, 모터의 온도와 팬의 토크, 정압을 만족시키는 최적의 점을 찾기 위해 크리깅(Kriging) 기법을 사용하여 반응면의 최적점을 도출하였다. 크리깅 기법은 설계영역 내 실험점들의 실험 횟수를 줄임으로써 근사 성능을 향상시키는 기법이다. 반응 표면 모델로서 크리깅 모델은 비선형성을 잘 표현해 줄 뿐만 아니라, 실험점들을 추가하여 모델의 충실도를 높일 수 있다는 장점이 있기 때문에, 위 네 설계변수에 대한 최적값을 찾을 수 있다고 판단되어 사용하였다.(11) 제작된 반응면을 바탕으로, 다목적 유전 알고리즘(Multi-Objective Genetic Algorithm, MOGA)을 사용한 최적화를 진행하였다.(12) 최적화 과정은 간략하게 Fig. 6에 도식화하였다.
Optimizing process
본 연구에서는 4개의 설계변수를 가지며, 각 설계변수 별 해석구간이 넓기 때문에, 기존의 미분을 이용한 유전 알고리즘에 비해 효과적이라고 판단되어 사용하였다. 위 과정을 통해 얻은 3개의 추천 설계점을 반응면에 추가하여 해석을 반복하였고, 예상 해석값과 전산해석 값의 오차가 0.1 % 이하를 만족한 후 최적화 과정을 종료하였다.
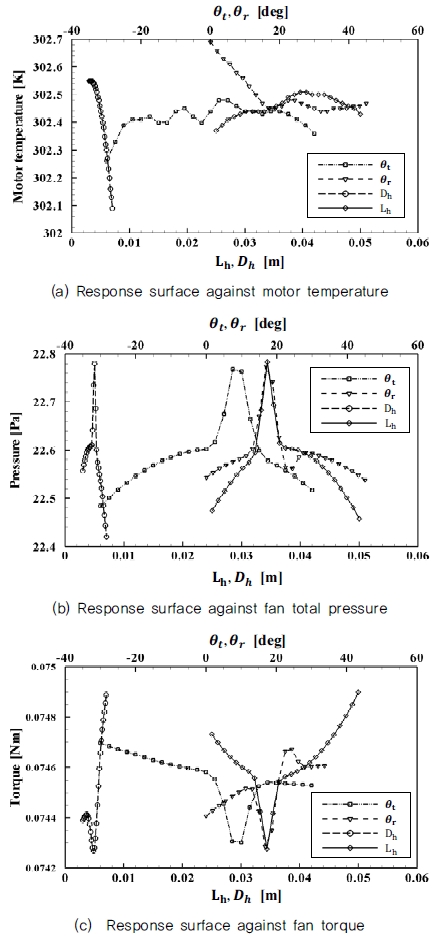
Fig. 7은 반응표면 최적화를 통해 4개 설계변수에 따른 모터 평균 표면온도와 전압력 차이, 토크에 대한 2차원 반응면을 나타내었다.
Response surface model
중심으로부터의 거리 Lh가 증가할수록, 모터의 온도는 증가하는 경향을 보였다. Lh에 따른 전압력은 볼록한 형태의 완만한 이차곡선 형상을 띄고 있으며, 약 34mm의 지점에서 최고값을 가졌고, 팬 토크의 경우 전압력과 정반대의 형상을 나타내었다. Lh의 크기가 작으면, 유동 사이의 간섭 및 원심력 등의 이유로 허브 캡 내부에서 유동 발생이 원활하지 않게 되며, 크기가 클 경우 팬의 후면부에서 전면부로 이동하는 유동이 모터의 열을 충분히 냉각할 수 없기 때문인 것으로 사료된다.
수직방향 각도 θr가 커질수록 팬의 회전으로 발생하는 원심력에 의해 허브 캡 내부에서 유출되는 유동이 증가하기 때문에 모터의 평균 온도는 낮아지는 경향을 보인다. 전압력은 볼록한 이차곡선 형태를, 팬 토크는 전압력과 반대의 형상을 나타내었다.
접선방향 각도 θt의 경우, 팬의 정면을 기준했을 때 시계방향으로 회전하기 때문에, 접선방향 각도는 0 ˚~30 ˚의 범위에서 모터 온도 감소의 효과가 발생하며, 전압력 감소, 토크 감소 경향을 확인하였다. 특히, 10 ˚ 이상의 각도에서 급격한 전압력 감소가 발생하였다.
홀의 지름 Dh의 크기가 클수록 그 면적에 비례하여 유동이 많아지기 때문에 모터의 냉각에는 긍정적인 영향을 끼치나, 팬의 정압 감소 및 팬 토크의 증가를 확인하였다.
3. 결 과
3.1 최적화 형상 선정
모터 평균 표면온도와 팬의 소모동력, 모터의 압력변위를 종합하여, 팬의 성능 감소를 방지하며 팬 모터의 냉각 역할을 만족시키는 최적의 형상을 Table 5에 나타내었다. 최적 형상의 선정 기준으로는, 성능 평가 지표에 나타낸 모터 온도, 팬의 소비전력, 이때의 전압 차이를 모두 고려하였다. 모터의 평균 온도가 낮을수록, 팬의 입/출구 전압차이가 클수록, 소비전력이 작을수록 최적 형상은 우수한 결과를 갖는다.
Optimized model specification with base model
동일 회전수 기준, 최적 형상은 기본 형상에 비해 전압력 차이가 약 1.68 Pa 더 발생하고, 열 집중 현상이 발생하는 모터 중심부의 온도는 약 17.47 K 낮게 나타났다. Fig. 8에 최적화 형상을 나타냈고, Fig. 9은 동일 회전수에서 기본형상과 최적 형상의 모터 냉각효과 차이를 나타내었다.
Optimized model
Motor wall temperature
모터의 표면온도와 팬 요구 토크, 전압력 차이 세 개의 변수를 종합적으로 비교하기 위하여 하나의 변수를 통일한 뒤 비교하는 방식으로 최적화 형상을 선정하였다. 식 (5)에 나타낸 팬 법칙을 이용하여, 최적 형상에서 팬의 회전속도 조정을 통해 팬의 전압력 차이를 일치시키고, 이 때의 모터의 온도 감소 효과와 소비전력을 비교하여 형상을 선정하였다.
최적화 과정을 완료한 형상은 Fig. 8에 나타내었다.
3.2 성능 비교
기본 형상과 최적화 형상의 명확한 비교를 위해, 위 Table 5에 나타낸 두 형상의 전압력 값을 식 (5)의 팬 법칙과 보간법을 이용하여 일치시킨 후 성능을 비교하였다. 전압력 차이가 21.10 Pa 부근일 때, 기존 형상 대비 최적화된 형상은 모터의 평균 표면온도가 감소함과 동시에, 소비전력 값 사이의 오차는 약 0.09 % 로 확인되었다. 이는 전산해석의 오차 범위를 감안하였을 때, 추가적인 동력의 소모 없이 유동제어만으로 모터의 온도 냉각 작용이 수행되었음을 의미한다.
아래 온도, 압력, 소비전력 비교에서는 최적화된 형상을 이용하되, Table 6에 나타낸 RPM 변경 후의 성능을 기준으로 하여 비교하였다.
Optimized model specification with base model (Equalize total prressure)
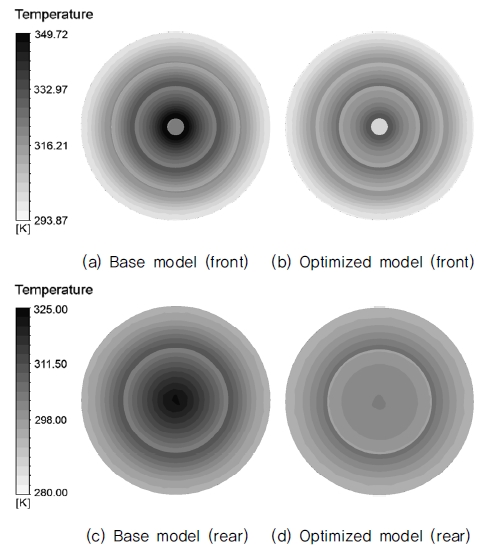
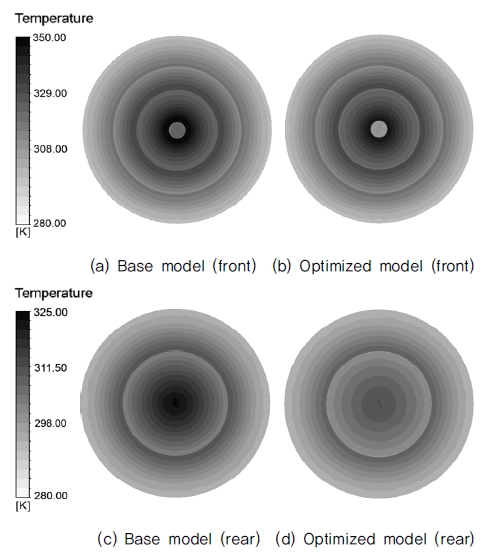
Table 6에서, 최적화 형상에서의 모터 평균 표면온도는 305.26 K에서 304.23 K로 1.03 K 감소하였다. 위와 같은 모터 평균 표면온도 분석은 유동이 모터에 미치는 영향을 알기에 직관적이나, 실제 모터 구동 시에는 모터 코일 및 중심부의 온도집중현상으로 인해 문제가 발생한다. 이에 Fig. 10에서는 기본 팬 형상과 최적화 결과를 비교하여 온도집중현상의 해소여부를 확인하였다. 확인 결과, 모터 전면 중심부의 온도 차이는 약 349.80 K에서 343.59 K로 6.21 K 차이를 보이므로, 온도 강하 측면에서 최적화 형상은 모터의 냉각에 긍정적인 영향을 주었다고 판단하였다.
Motor wall temperature
Fig. 11에서는 Fig. 10에서 나타난 온도 구배가 주변 온도에 미치는 영향을 나타내었다. 허브 부에 홀이 없는 (a)의 경우, 열 집중현상이 발생할 것으로 예상되는 모터의 전면 중심부에서 고 열원 부의 크기가 큰 반면, (b)의 경우 (a)에 비해 비교적 그 크기가 작은 것을 알 수 있다.
Temperature rendering at motor wall
3.2.2 팬 소비전력 비교
본론에서 언급한 식 (3)에 의거하여, 팬의 요구 토크는 팬이 가동하는 데 필요한 소비전력에 비례한다. 동일 성능 기준, 소비전력이 클수록 비효율적이므로 팬의 요구 토크가 작을수록 팬의 효율이 더 좋은 것이다. 기본 형상과 최적화된 형상의 팬 토크 부하를 비교하였다. 기본 형상에서의 소비전력이 16.51W일 때, 최적화 형상의 소비전력은 16.53W로 기본 형상 결과값과 약 0.02W 차이가 발생하였으나, 두 값의 차이가 약 0.09 %로 전산해석의 오차범위 내 결과값으로 판단되기 때문에 동일하다고 판단하였다.
3.2.3 전압력 유동특성 분석
기본 형상과 최적화 형상의 비교 목적으로 압력 차이를 일치시켰으나, 팬의 허브 부와 모터 사이의 허브 캡 내부 공간에서는 압력이 변화한다. 기본 형상과 최적화된 형상에서 발생하는 허브 캡 내부의 압력 분포를 확인하였다.
Fig. 12는 팬 허브와 모터 사이의 내부 압력을 나타내었다. 팬 블레이드가 있는 외부는 압력 차이가 동일하나, 허브 부의 홀 형상으로 인해 유동이 발생하고, 허브 캡 내부의 압력이 감소하는 것을 확인하였다.
Total pressure at hub cap zone
허브 캡 내부의 압력은 (a)기본 형상의 경우 13.22 Pa로 균일한 압력을 가지고 있으나, (b)최적 형상은 팬 허브의 전면부로 작용하는 압력이 감소한 것을 확인하였다. 홀 형상으로 인해 압력 차이가 발생하고, 허브 캡 내부의 유동을 발생시켜, 최종적으로 모터에서 발생하는 열응력을 해소시켰다.
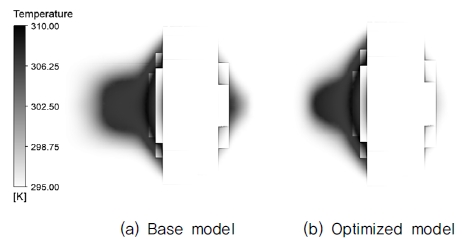
Fig. 13은 팬의 허브 캡 내부 단면을 나타낸다. (a)좌측의 기본 형상과 (b)우측의 최적 형상을 비교하였을 때, 허브 캡 내부 전면부와 모터 전면부에서 발생하는 와류가 감소한 것을 확인하였다. 이는 홀 최적화 형상이 허브 캡 내부의 높은 압력으로 인한 부하를 해소시킴으로써 와류 저감 및 이를 통한 팬 토크의 감소에 영향을 끼쳤을 것으로 사료된다.
Streamline at hub cap zone
4. 결 론
축류 팬의 허브부에 홀 형상을 제작하고, 이 때 발생하는 유동을 이용한 팬 모터의 냉각에 대한 전산해석을 수행하여 유동이 모터의 온도 강하에 미치는 영향과, 이때 팬의 공기역학적 특성을 확인하였다.
전산 해석을 통해 기본 형상에서의 모터의 평균 표면온도와 온도집중부의 온도를 확인하고, 최적화 형상과의 비교를 통한 냉각 효과를 확인하였다. 비교 결과, 동일 회전속도일 때 최적화 형상에서 모터의 평균 표면온도는 2.81 K 감소하였으며, 모터 표면의 최대 온도는 17.47 K 감소하여 모터 중심부의 열 집중현상도 해소하였다. 부가적으로 팬의 전압력 차이는 1.68 Pa 증가하였다. 팬의 소모동력 차이는 0.1 % 이하였기 때문에, 전산해석의 오차범위 이내로 판단되어 성능 개선효과가 기존 형상보다 우수하다고 판단되었다.
본 연구를 통해 축류 팬의 허브부에 홀 형상을 제작하였을 때 모터의 냉각 효과에 대한 개선 가능성을 확인하였다. 향후 허브부의 홀 형상에 대한 변경 또는 개선사항을 적용하여 모터의 냉각 뿐만 아니라 팬의 성능 개선에도 활용할 수 있을 것으로 예상되며, 본 연구결과를 바탕으로 추가적인 연구를 수행하고자 한다.
References
- Fans – Design and operation of centrifugal, axial-flow and cross-flow fans, Bruno Eck, Pergamon press.
- Axial Flow Fans and Ducts, (1993), R. Allan Wallis, Krieger Publishing Company.
-
M. K. Yoon, C. S. Jeon, and S. Ken Kauh, Efficiency Increase of an Induction Motor by Improving Cooling Performance, (2002), IEEE Transactions on Energy Conversion, 17(1).
[https://doi.org/10.1109/60.986430]
- Andreas, J. C., (1992), Energy-Efficient Electronic Motors: Selection and Application, Marcel Dekker, Inc., p243-245.
-
Stefan Ulbrich, Jeanette Kopte, and Jens Proske, Cooling Fin Optimization on a TEFC Electrical Machine Housing Using a 2-D Conjugate Heat Transfer Model, (2018), IEEE Transactions on Industrial Electronics, 65(2).
[https://doi.org/10.1109/tie.2017.2748051]
-
S. Kang, K. Lee, S. Wang, H. Shim., Thermal and Flow Analysis of Outer-Rotor Type BLDC Motor with Cooling Blades, (2007), Transactions of the Korean Society of Mechanical Engineers - B, 31(9), p772-779.
[https://doi.org/10.3795/ksme-b.2007.31.9.772]
- P. Yang, H. Lee, W. Jung, A Study on Improvement of Electric Motor Thermal Performance Using CFD, (2003), The Korean Society of Mechanical Engineers, p261-265.
- Frank P. Incropera, David P. Dewitt, Theodore L. Bergman, Adrienne S. Lavine, Foundations of Heat Transfer sixth edition, John Wiley&Sons, Inc., p139-147.
- R. Allen Wallis, Axial Flow Fans and Ducts, Krieger Publishing Company, Malabar, (1993), p262.
- J. E. Bardina, P. g. Huang, T. J. Coakley, Turbulence Modeling Validation, Testing, and Development, (1997), NASA Technical Memorandum 110446.
-
Y. Shin, Y. Lee, J. Ryu, D. Choi, Sequential Approximate Optimization Using Kriging Metamodels, (2005), Transactions of the Korean Society of Mechanical Engineers – A, 29(9), p1199-1208.
[https://doi.org/10.3795/ksme-a.2005.29.9.1199]
-
Abdullah Konak, David W. Coit, Alice E. Smith, Multi-objective optimization using genetic algorithms: A tutorial, (2006), Reliability Engineering and System Safety, 91, p992-1007.
[https://doi.org/10.1016/j.ress.2005.11.018]