캡슐트레인 CFD 해석을 위한 압축기 성능해석 모듈 개발

1. 서 론

하이퍼루프 시스템은 2013년에 스페이스엑스(SpaceX) 사의 엘론 머스크(E. Musk)가 ‘하이퍼루프 알파(Hyperloop Alpha)’에서 제안한 1/1000기압 정도의 진공튜브 내부를 총신에서의 총알과 같이 음속에 가까운 속도로 운행하는 캡슐트레인(capsule train) 개념의 차세대 초고속 운송시스템이다.⁽¹⁾ 음속에 가까운 속도로 운행하는 캡슐트레인 차량이 진공에 가까운 튜브 내부에서 고속 주행하면 차량 전방에서는 압축파가 형성된다. 압축파의 강도는 튜브 전체 면적 대비 차량이 차지하는 면적 비율인 차폐율(blockage ratio, BR)이 클수록 더욱 증가하고, 유속이 특정 한계속도인 Kantrowitz limit을 넘어설 때까지 차량의 항력계수(drag coefficient) C_D는 계속 증가한다.⁽²⁾ 이러한 문제점 극복을 위하여 캡슐트레인 차량 전두부에 압축기를 장착하여 차량 전방의 유동을 흡입하는 개념이 하이퍼루프 알파에서 제시되어 있으며, 압축기는 튜브 내 유동의 초킹(choking) 현상 방지 및 추진력을 확보하기 위한 캡슐트레인 설계의 주요 요소이다.

기존의 하이퍼루프 시스템에서는 압축기를 튜브 내 유동의 초킹 해소를 위하여 적용하면서 압축기에 의하여 생성된 고압의 공기를 차량 하부로 분사하여 에어베어링으로 활용함으로써 부상력을 확보하는 동시에 차량 후방으로도 분사하여 추진력을 확보하는 데에도 활용하였다. 반면에 국내에서 연구가 추진되고 있는 하이퍼루프 시스템의 일종인 하이퍼튜브 시스템에서는 캡슐트레인의 부상력은 자기부상을 통하여 해결하고, 차량의 추진력은 일정 간격으로 배치된 가속스테이션을 활용하는 방식으로 검토하고 있으며, 압축기는 차량 전방의 유동 초킹 해소가 주목적으로 캡슐트레인에 장착하는 것으로 연구가 추진되고 있다.⁽³⁾ 그러므로 본 연구에서는 차량 전방의 유동 초킹 해소를 주목적으로 캡슐트레인에 적용하기 위한 압축기의 개념설계를 수행하고, 이를 바탕으로 압축기 성능해석 모듈을 구축하도록 한다. 그리고 이를 활용하여 진공 튜브 내를 아음속으로 운행하는 캡슐트레인의 3차원 정상상태 유동해석을 수행하여 압축기에 의한 성능향상 결과를 압축기가 구동하지 않을 때와 비교⋅검증하였다.

2. 압축기 성능해석 모듈 구축

하이퍼튜브의 캡슐트레인의 경우 아음속의 고속으로 주행하므로 차량의 주행 저항은 대부분이 공기저항이며, 차량의 증속 또는 속도 유지를 위한 동력 최소화를 위해서는 공기 저항과 연관한 차량 주변의 유동해석이 필수적이다. 차량 주변 유동현상에 영향을 미치는 주요한 인자로는 진공 튜브 내부의 초기 압력, 차량 운행속도의 마하수(Mach number) 및 차량과 튜브 간의 차폐율, BR를 들 수 있다. 특히 튜브 내부에서 고속으로 차량이 운행하는 경우 차량 주변에서 유동의 초킹 현상이 발생할 수 있으며, 이러한 초킹 현상은 차량 전방부로 유입되는 유동의 마하수와 차량과 튜브 사이의 BR에 크게 영향을 받는다.^(3-5) 이 때, 캡슐트레인의 주요 유동조건인 압력, 마하수 및 BR 등에 따라 차량 주변 유동에서 초킹이 발생하지 않는 차량의 한계 속도가 존재하며, 이를 ‘Kantrowitz limit’이라고 한다.⁽³⁾ 이에 본 연구에서는 압축기 개념설계 결과를 적용한 압축기 입⋅출구 성능을 도출할 수 있는 성능해석 모듈을 구성하고, 이를 활용하여 압축기가 장착된 아음속 캡슐트레인 차량에 대한 3차원 정상 유동해석을 수행하여 압축기가 구동하지 않을 때와 차량의 공기 저항 변화양상 및 Kantrowitz limit을 초과하는 속도에서의 차량 주변 유동현상의 변화를 비교⋅분석하고자 하였다.

2.1. 압축기 입구조건 적용을 위한 CFD 전처리 작업

2.1.1. CFD 해석을 위한 차량 형상 및 격자

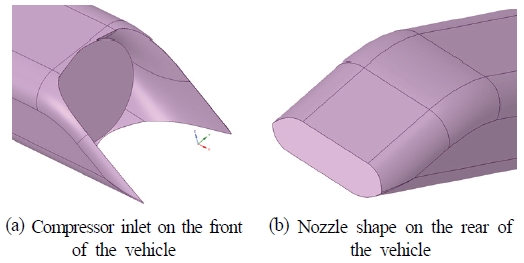
압축기가 장착되어 압력이 100 Pa(약 1/1000기압)로 유지되는 진공 튜브 내부에서 음속에 가까운 속도로 주행하는 아음속 캡슐트레인 차량의 3차원 형상은 하이퍼루프 알파 차량의 제원을 참고하여 Fig. 1과 같이 생성하였다.

Fig. 1

Overall shape of capsule train vehicle

캡슐트레인 차량의 전체 길이는 27 m이며, 차량 전면의 최대 면적은 약 1.4 m², 차량과 튜브의 BR은 0.36으로 설정하였으며, 차량 전면의 압축기 입구면적은 0.933 m², 차량 후면에서 고압 공기가 토출되는 노즐 면적은 0.362 m²로 하였으며, 형상은 Fig. 2와 같다.

Fig. 2

Shapes of Compressor inlet and nozzle

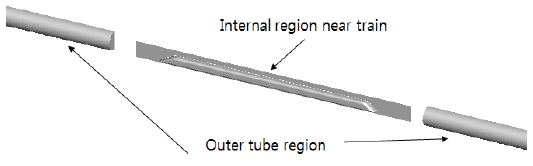
CFD 해석을 위한 격자 생성은 Fig. 3에서와 같이 전체 계산 영역을 차량 근처의 내부 영역과 차량에서 먼 외부의 튜브 영역으로 분리하고, 경계면에서는 Interface 경계 조건을 적용하여 상호 유동 정보의 교환이 가능하도록 구성하였다.

Fig. 3

Combination of inner and outer CFD computation domains

차량의 표면에서는 Fig. 4의 (a), (b)와 같이 삼각형 격자를 사용하였으며, 경계층 모사를 위해서는 차량 표면에서 첫번째 격자층까지의 거리를 0.05 mm로 하여 20개의 층을 구성하였다.

Fig. 4

Three-dimensional shape and surface grid of the vehicle with the compressor

그 후, 사면체 격자를 사용하여 내부영역에 격자를 조밀하게 분포시켰다. 바깥 쪽 영역은 경계면(interface)의 격자를 튜브 방향으로 스윕(sweep)하여 구성하였으며, 이를 통해 압력파가 전파되는 경우에 대하여 수치 점성에 의한 소산을 최대한 억제하도록 하였다. 전체 계산 영역의 전⋅후방 경계면까지의 거리는 약 300 m로 하여 열차 길이 27 m의 10배 이상이 되도록 하였고, 전체 계산 영역에 대하여 3차원 격자 생성을 수행한 결과, CFD 해석을 위한 총 격자수는 약 5,570,000개이다. 차량 표면의 y+ 값은 O(1)이 되도록 하여 FLUENT를 이용한 유동해석을 수행하였다.

2.1.2. CFD 해석을 위한 경계조건

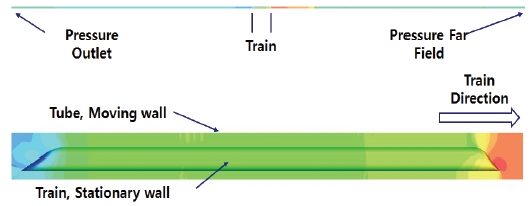
CFD 해석을 위한 경계조건(boundary condition)으로 튜브 입구에서는 압력값의 반사가 일어나지 않고 전파되도록 하는 압력원방(pressure far field) 조건을 사용하였다. 경계면에서의 자유류 유속은 310.48 m/s로, 경계면에서의 초기 압력은 튜브 내부 압력인 100 Pa을 적용하였다. 튜브 출구는 일정한 압력값이 경계면에서 토출방향으로 정의되는 압력토출(pressure outlet) 조건을 사용하여 유동이 흘러나가도록 설정하고 경계면 압력은 튜브 내부 압력과 동일한 100 Pa을 적용하였으며, 튜브 내부 온도는 293.15 K로 설정하였다. 튜브 벽면은 자유류의 속도와 동일한 유속을 부여하여 동일한 속도로 움직일 수 있도록 이동벽면(moving wall) 조건을 적용하였다. 캡슐트레인 차량은 고정벽면(stationary wall) 조건을 부여하여 차량과 튜브 간의 상대운동을 반영하여 정상상태 유동해석을 수행하도록 하였다. 또한 압축기 입구에는 압력토출 조건의 목표 질량유량(target mass flow) 옵션을 추가하여 압축기 성능해석 모듈에 의하여 계산된 압축기 입구 질량유량(mass flow rate, $$ \dot{m}$$)을 목표 질량유량 값으로 부여하여 이에 맞춰서 입구에서의 압력 및 유속, 밀도 등을 계산할 수 있도록 하였다. 노즐 부분은 질량유량유입(mass flow inlet) 조건을 사용하여 압축기 입구에서의 질량유량과 동일한 질량유량을 지정하도록 하였다. 전체 CFD 계산 영역에 대하여 적용한 경계조건을 정리하면 Fig. 5와 같다.

Fig. 5

Boundary conditions for CFD analysis

압축기 관련 경계조건의 경우, 초기 압축기가 가동하지 않는 경우에 대해서는 노즐과 압축기 입구 부분은 차량과 동일하게 고정벽면 경계 조건을 적용하여 압축기가 가동하지 않는 상태의 해석을 수행하여 압축기 작동을 위한 초기 유동 조건을 도출하였다. 다음 단계로 초기 유동 조건을 압축기 개념설계 결과를 적용한 성능해석 모듈과 연계시켜서 압축기 입구에서의 질량유량 및 전온도(total temperature)를 얻었다. 이후 압축기 입구에서 경계조건을 압력토출로 설정하고 주어진 질량유량을 만족하도록 입구에서의 압력 및 유속, 밀도 등의 해석 결과를 수렴시켜가는 목표질량유량 옵션을 추가하여 질량유량 및 전온도 등의 값을 입력하였다. 차량 후미부의 노즐 부분에는 질량유량유입 조건을 사용하여 압축기 입구에서의 질량유량 값과 동일한 질량유량 값을 지정하였다. 또한 유동이 고속으로 뿜어지기 위해서는 차량 후면 노즐 출구에서의 압력이 배압보다 커야 하므로 노즐 출구에는 튜브의 초기 내부 압력인 100 Pa을 설정하였다. 마지막으로 압축기에서 토출되는 고압의 유동은 일반적으로 후방냉각기(after cooler) 등을 거치면서 냉각수와의 열교환을 통하여 온도가 대폭 낮아지게 되며, 본 연구에서는 이를 고려하여 노즐 출구에서의 전온도를 300 K로 설정하였다.

2.2. 압축기 개념설계

2.2.1. 압축기 설계조건 및 제약조건

본 연구에서는 캡슐트레인 차량의 압축기 개념설계를 위하여 필요한 설계조건들은 하이퍼루프 알파에 제시된 데이터를 바탕으로 정의하였으며, 이는 다음의 Table 1과 같다.

Table 1

Design conditions for compressor

하이퍼루프 알파에서는 압축기 흡입구(inlet)의 입구조건을 시스템 개요도에 Table 1에서 정리한 바와 같이 압력과 온도를 99 Pa, 292 K로 제시하였으므로 이 값을 압축기 개념설계의 입구조건으로 적용하고, 이를 공기의 상태방정식에 적용하여 압축기 흡입공기의 밀도를 계산하였다. 하이퍼튜브 캡슐트레인 차량의 주행에 의하여 압축기 입구로 튜브의 공기가 유입되므로 압축기 입구 유속은 차량의 주행속도인 마하수 0.91을 m/s로 환산하여 310.48 m/s로 적용하였다.

압축기의 개념설계를 위해서는 설계 목표성능을 분석하는 것도 중요하나, 설계 과정에서 반드시 준수해야 하는 제약조건을 분석하는 것도 중요하다. 본 연구의 압축기 입구단면적은 캡슐트레인 차량의 전두부 단면 내에 들어가야 하므로 최대 반경이 제한적이다. 본 연구의 캡슐트레인 차량의 단면형상은 CFD 해석을 수행하기 위하여 만든 3D 모델링 결과를 활용하여 도출하였으며, 해당 단면에 포함될 수 있는 최대 크기의 원면적은 1.33 ㎡로 계산되었다. 그러나, 압축기의 실제 입구단면적은 차량 전체 단면에 대하여 포함할 수 있는 최대 크기의 원면적(100% 단면적)이 아니라, 실제 차량에서 설계 및 제작이 가능하도록 차량 내부에 적용 가능한 최대범위의 실질적인 원의 크기를 고려해야 한다. 그 결과, 최대 크기의 입구단면적 대비 70% 면적인 0.9328 ㎡를 압축기 입구단면적으로 적용하여 압축기 개념설계를 추진하였다.

이와 같이 캡슐트레인 차량의 경우 단면적이 제한적이므로 하나의 축에 다수의 단을 설치하여 입구단면적으로 최소로 할 수 있는 다단 축류압축기를 적용하도록 한다. 이 과정에서 다단 축류압축기의 각 단 중 가장 반경이 큰 1단 로터의 원면적을 앞서 계산한 실제 압축기 최대 입구단면적인 0.9328 ㎡로 제한하였다. 그리고 이를 만족할 수 있도록 1단 로터의 반경을 0.5449 m 이내로 설계해야 한다는 제약조건을 설정하였다. 이 경우 입구유속은 차량 주행 속도와 동일하게 유지하고, 개념설계를 위한 입구압력, 온도도 초기값인 99 Pa, 292 K을 유지하면 입구단면적의 제약으로 인하여 압축기 흡입 질량유량은 하이퍼루프 알파의 0.49 kg/s보다 감소할 것으로 예상하였다. 이에 따라 축류압축기 설계 및 해석에 많이 사용되는 상용 소프트웨어인 Concept NREC의 Axial™를 이용하여 반복적으로 개념설계를 수행하여 1단 로터의 최대반경 0.5449 m를 만족할 때의 압축기 개념설계 결과로 압축기의 입구 질량유량을 도출할 수 있도록 하였다.

2.2.2. 압축기 개념설계 결과

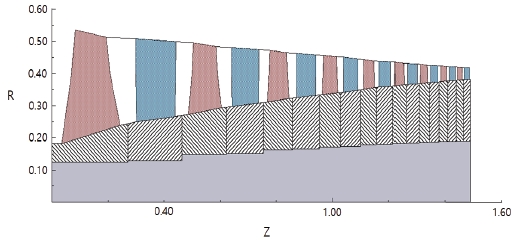
본 연구에서 Table 1에서 정리한 데이터를 활용하여 설계목표인 압축기 시스템 토출압력 2.1 kPa을 달성하면서, 동시에 70% 입구단면적인 0.9328 ㎡ 이내가 되도록 1단 로터의 반경을 0.5449 m로 제약하도록 압축기 개념설계를 수행하였다. 그 결과, 모터에 의한 압축기 회전속도가 낮은 경우 압축기 토출압력을 만족할 수 없거나 압축기의 단수가 너무 많아지는 등 비현실적인 설계 결과가 도출되었다. 이와 같이 느린 압축기의 회전속도에서는 압축능력이 부족하여 단수가 증가하게 되므로 압축기 회전축과 모터축 사이의 커플링을 직결 방식이 아닌 기어 연결로 고려하고 치수 비를 조정하여 압축기 회전속도가 9,000 rpm이 되도록 조정하면 1단 로터 반경이 제약조건을 만족하면서 토출압력 2.1 kPa 이상의 9단 축류압축기 설계 결과를 도출할 수 있었으며, Axial™을 이용한 개념설계 결과 압축기 단면형상은 Fig. 6과 같다.

Fig. 6

Sectional shapes from the conceptual design of the compressor

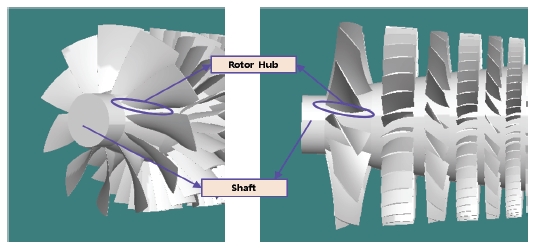
개념설계 결과 압축기 입구 질량유량은 0.17 kg/s로 하이퍼루프 알파에 비하여 감소하였다. 이는 1단 로터 최대반경이 제한되어 압축기 입구단면적 자체가 감소하였고, Fig. 7에서와 같이 실제 압축기의 회전축, 허브 등의 요소는 조립 및 안정성을 위하여 일정 크기 이상은 유지해야 하므로 유효단면적의 감소가 70% 입구단면적 비율보다 상대적으로 더 컸기 때문이라고 분석할 수 있다.

Fig. 7

Reduction of the effective cross-sectional area of the rotor shaft and hub

2.2.3. 압축기 성능해석 모듈의 구성

본 연구에서 Table 1에서 정리한 데이터를 활용하여 설계목표인 압축기 시스템 토출압력 2.1 kPa을 달성하면서, 동시에 70% 입구단일반적으로 압축기의 성능을 나타내는 지표로는 실제 유량 대비 토출압력(또는 압축비), 유량 대비 효율 곡선을 활용한다. 설계된 압축기를 정해진 조건에서만 운전하는 경우에는 입⋅출구조건 및 운용조건이 고정되어 있으므로 실제 질량유량 대비 토출압력(압축비) 및 효율 곡선을 활용하면 각 단의 토출압력과 해당 단에서의 효율 값을 쉽게 예측할 수 있어 편리하다. 그러나 진공 튜브 내를 주행하는 하이퍼튜브 차량의 경우 정상운전 상태에서의 속도는 마하수 0.9 정도로 일정하나 가속 및 감속 등에 의하여 실제로는 다양한 속도 영역에서 주행을 하게 되어 운전조건이 달라지면 동일한 압축기를 사용하더라도 질량유량, 토출압력, 소요 축파워 등의 실제 성능 지표들이 달라진다. 이러한 경우 설계된 압축기의 무차원화 성능계수를 이용하면 로터 등 공력부의 성능 특성을 고유값으로 고정할 수 있어 변경된 운전조건을 적용한 압축기의 성능을 조건별로 예측할 수 있다. 그러므로 CFD 해석의 경계조건으로 적용하기 위하여 하이퍼튜브 차량의 다양한 운전 조건에 대한 압축기의 성능을 예측할 수 있는 성능해석 모듈을 구성하기 위해서는 먼저 기존 압축기의 설계결과를 유량계수, 양정계수와 같은 무차원화 성능계수로 전환해야 한다.⁽⁶⁾

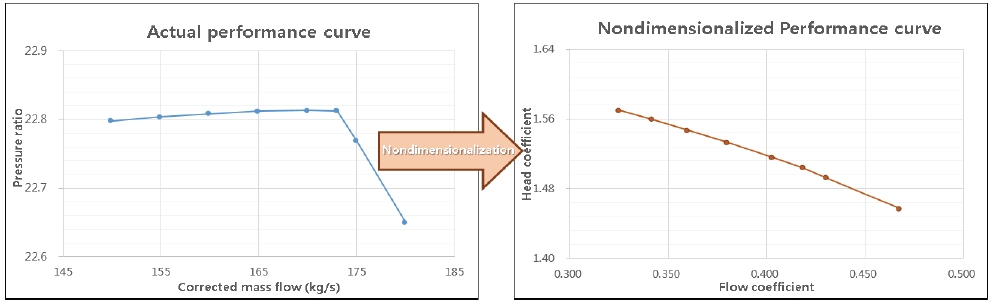
압축기의 성능예측을 위하여 압축기 설계 결과를 무차원화하려면 실제 시험으로 얻거나 설계 과정에서 도출한 질량유량(혹은 체적유량)과 토출압력(또는 압축비)을 바탕으로 압축기의 입구온도와 밀도, 로터 직경, 회전속도 등을 이용하여 무차원화 성능계수인 유량계수와 양정계수의 계산해야 한다. 이를 위하여 본 연구에서는 기존에 설계된 압축기의 입구밀도 및 온도, 로터 직경, 회전속도 등의 운전조건에 관한 데이터와 함께 기존 설계 결과의 각 단 질량유량 대비 토출압력 성능곡선을 활용하여 압축기의 무차원화 성능계수인 유량계수와 양정계수를 계산하여 각 단과 시스템의 유량계수 대비 양정계수 성능곡선을 도출한다. 본 연구에서는 최종적으로 Fig. 8과 같이 도출한 압축기 무차원화 성능곡선을 활용하여 CFD 해석을 위한 경계조건으로써 압축기의 입⋅출구조건을 제공할 수 있는 성능해석 모듈을 구축하였다.

Fig. 8

Nondimensionalized compressor performance curve

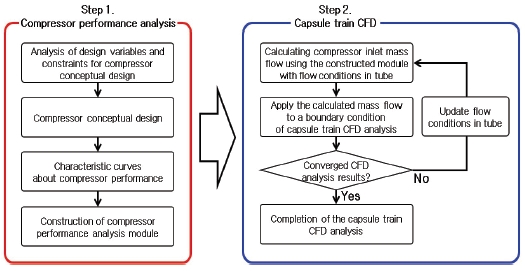
이러한 압축기 성능해석 모듈을 활용하여 CFD 해석의 경계조건으로 적용하기 위한 압축기 입구에서의 질량유량 계산은 Fig. 9와 같이 1단계로 성능해석 모듈 구성을 수행하고, 이를 2단계 프로세스인 CFD 해석에 활용하도록 진행하였다. 우선 압축기 특성곡선을 활용한 성능해석 모듈을 이용하여 튜브 내 유동조건을 적용한 압축기 입구의 실제 질량유량을 계산한다. 이렇게 계산된 값을 Target Mass Flow 조건에서의 질량유량으로 지정하고 CFD 해석을 진행하였으며, CFD 해석 결과 업데이트된 튜브 내 유동조건을 다시 압축기 성능해석 모듈에 적용하였다. 그 결과 성능해석 모듈의 무차원화된 성능계수를 이용한 계산을 수행하여 압축기 입구 질량유량을 계산하고, 업데이트된 질량유량을 적용하여 CFD 해석을 수행한다. 이와 같은 프로세스를 통하여 압축기 입구에서의 예측 질량유량을 이용하여 튜브 내 유동에 대한 CFD 해석의 경계조건으로 적용하여 유동해석 결과가 수렴할 때까지 CFD 해석을 반복한다.

Fig. 9

CFD analysis procedure of vehicle concerning the compressor performance analysis

3. 압축기 성능해석 모듈을 활용한 CFD 해석결과

압축기 및 노즐에서의 질량유량을 고려한 튜브 내 캡슐트레인의 3차원 정상 유동해석을 위하여 먼저 압축기가 작동하지 않는 상태의 3차원 정상 유동해석을 수행하였다. 튜브 내부 압력은 100 Pa, 온도는 293.15 K을 적용하였으며, 차량 속도(M_capsule)는 마하수 0.4부터 0.1씩 증속하여 캡슐트레인의 운행조건인 0.9까지 총 6개 Case에 대해 압축기가 작동하지 않은 상태에서 차량 전체의 주행저항에 관한 항력계수 C_D가 일정 값으로 수렴할 때까지 해석을 진행하였다. 압축기가 가동하지 않은 상태에 대하여 C_D가 일정하게 수렴하면, 차량 전방부와 후미부 경계면에 압축기와 노즐 경계에 각각 목표 질량유량 옵션이 추가된 압력토출 조건 및 질량유량유입 조건을 부여하여 압축기가 작동하는 차량의 C_D 값이 수렴할 때까지 해석을 진행하였다. 이러한 프로세스를 반복하여 최종적인 압축기 입·출구에서의 질량유량 및 차량의 C_D와 주행저항(Drag)을 도출하였다.

이와 같이 CFD 해석 결과인 C_D가 수렴할 때까지 해석 프로세스를 진행한 결과 Fig. 10에서와 같이 2회차에 수렴하였으며, 최종적인 압축기 입구 유동조건을 정리하면 Table 2와 같다.

Fig. 10

Results of CD analyses according to the compressor operation

Table 2

Final inlet flow conditions of the compressor

Table 2에서와 같이 차량속도가 증가함에 따라 튜브 내부의 압력 및 온도가 초기 조건 대비 증가한 것을 확인할 수 있으며, 이는 튜브 내부를 차량이 고속으로 진행함에 따라 전방으로 압축파가 전파되어 발생한 결과로 추정할 수 있다.⁽⁷⁾

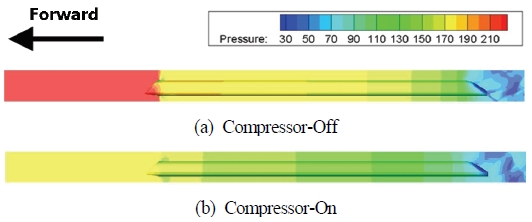
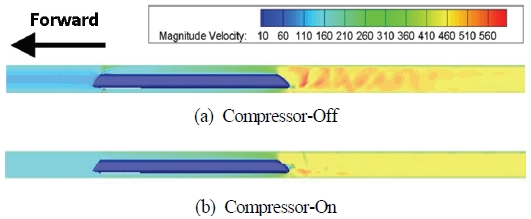
그리고 캡슐트레인의 운행속도인 마하수 0.9에서 차량 주변 유동의 압력과 속도 분포를 압축기 작동 여부에 따라 비교하면 Fig. 11 및 Fig. 12와 같다. 각 그래프에서 압축기 작동 시 차량 전후방 압력 값과 차량 후방에서의 유속이 감소하므로 압축기 작동에 따라 차량 전후방에서 발생하는 압축파 및 팽창파에 의한 영향이 감소하는 것을 확인할 수 있다.

Fig. 11

Comparison of pressure distribution of the flow around the vehicle (Mcapsule=0.9)

Fig. 12

Comparison of velocity distribution of the flow around the vehicle (Mcapsule=0.9)

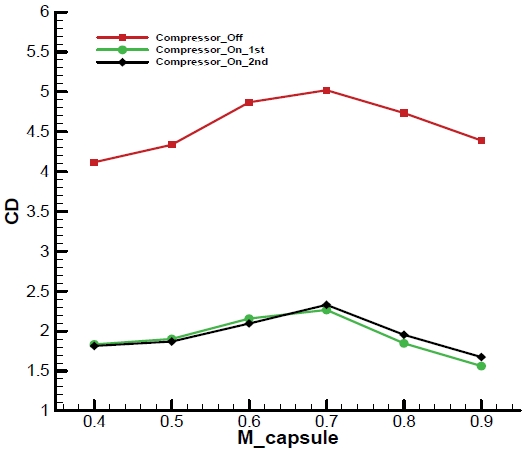
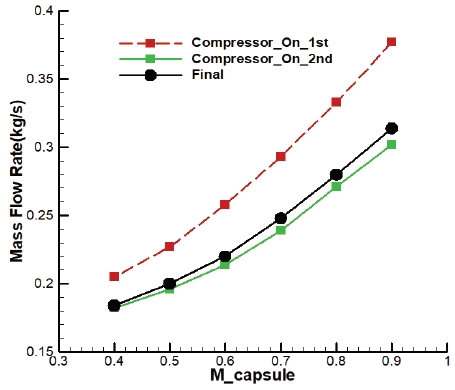
또한, 압축기 작동 조건에 대한 반복 계산을 통해서 얻게 된 차량 속도별 압축기 입구로 유입되는 유동의 질량유량($$ \dot{m}$$)을 Fig. 13에 도시하였다.

Fig. 13

Comparison of changes of mass flow at the compressor inlet

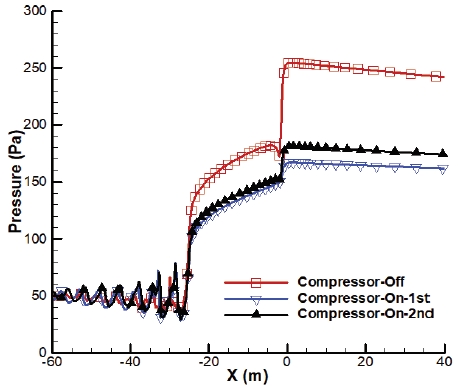
Fig. 13에서 압축기가 작동하는 경우에는 압축기가 작동하지 않은 초기 해석 결과 대비 압축기 입구 질량유량이 모든 속도 영역에서 감소하는 것을 확인할 수 있다. 이는 압축기의 작동으로 차량 주변의 압축파 및 팽창파가 감소하여 유동의 압력도 감소함에 따라 압축기 입구 유동의 밀도도 감소하여 질량유량도 줄어든 것으로 판단할 수 있다. 이와 같은 압축파와 팽창파의 영향을 분석해 보기 위하여 튜브 벽면에서의 차량 주변 압력을 압축기를 작동하지 않은 초기값과 압축기의 작동을 반영한 1회차 및 2회차 해석 결과를 비교하면 Fig. 14와 같이 도시할 수 있다. Fig. 14에서 확인할 수 있는 바와 같이 압축기 작동에 따라 1회차에는 압력값이 대폭 감소하였다가 2회차에는 일부 상승하였고, Fig. 10에서 2회차에 수렴한 것으로 확인되었으므로 2회차의 압력값이 최종 결과로 볼 수 있다. 이에 Fig. 13의 질량유량 비교 결과에서 초기 대비 최종 질량유량이 감소한 것은 Fig. 14에서와 같이 압축기 작동에 의하여 튜브 내부의 유동 압력이 감소하여 압축기에 유입되는 유동의 밀도가 감소한 결과라고 판단할 수 있다.

Fig. 14

Comparison of pressure distribution on tube wall (Mcapsule=0.9)

마지막으로 압축기를 작동하지 않았을 때와 비교한 마하수 대비 계산한 C_D와 이를 이용하여 실제 차량에 작용하는 주행저항을 계산해 보면 Table 3과 같으며, 압축기를 작동하는 경우 C_D와 주행저항이 큰 폭으로 감소하였다.

Table 3

Comparison of CD according to Mach number

4. 결 론

본 연구에서는 진공 튜브 내부에서 아음속으로 운행하는 캡슐트레인 시스템인 하이퍼튜브의 유동 주행저항을 저감하기 위한 압축기의 적용에 따른 유동해석에 관한 연구를 수행하였다. 먼저 캡슐트레인에 적합한 압축기의 개념설계를 수행하고, 그 결과 도출된 무차원화된 압축기 성능곡선을 적용하여 압축기 성능해석 모듈을 구축하였다. 그리고 이 모듈을 활용하여 압축기를 작동한 경우 압축기 입⋅출구 질량유량, 토출압력 등을 CFD 경계조건으로 적용한 3차원 정상상태 유동해석을 수행하여 최종적으로 압축기에 의한 주행저항에 대한 유동 성능향상 결과를 압축기가 구동하지 않을 때와 비교⋅검증하였다. 이 과정에서 캡슐트레인 차량 주변 유동의 C_D 변화에 대한 분석을 수행하여 유동해석의 수렴 여부를 판단하였으며, 압축기를 작동한 경우 튜브 내 압력이 감소하고, 그로 인하여 유동의 C_D와 주행저항 모두 크게 감소하는 것을 확인할 수 있었다.

본 연구의 결과를 요약하면 다음과 같다.

• 1) Axial™을 이용하여 캡슐트레인에 장착하기 위한 압축기의 개념설계를 수행하였고, 그 결과 9단 축류압축기에 대한 무차원화 성능곡선을 도출하였다. 이를 활용하여 CFD 해석을 위한 압축기 입⋅출구에서의 경계조건을 도출할 수 있도록 압축기 성능해석을 진행할 수 있는 툴(tool)인 ‘압축기 성능해석 모듈’을 개발하여 매번 상용 프로그램을 사용하지 않고도 CFD 해석의 경계조건 도출을 위한 대략적인 압축기 성능해석을 수행할 수 있도록 하였다.
• 2) 압축기 성능해석 모듈에서 도출된 CFD 해석의 경계조건을 적용하여 압축기 작동여부에 따라 진공 튜브 내부를 아음속으로 주행하는 캡슐트레인에 관한 3차원 정상 유동해석을 수행하고, 그 결과를 비교하였다. 이를 위하여 CFD 해석 과정에서 압축기 성능해석 모듈에서 도출된 압축기 입⋅출구에서의 경계조건을 적용하여 CFD 해석을 수행하여 차량의 C_D를 계산하고, 그 결과가 수렴할 때까지 CFD 해석과 압축기 성능해석 모듈 계산을 반복하였다.
• 3) 압축기가 작동하는 경우에는 압축기에 의하여 차량 전방의 유동 중 일부가 압축기로 흡입되면서 차량 전후방에서 발생하는 압축파와 팽창파가 감소하고, 이로 인하여 차량 주변 유동의 압력 및 유속이 감소하는 것을 확인할 수 있었다. 그 결과, 최종적으로 차량 주변 유동의 C_D 및 주행저항 값이 압축기를 작동하지 않았던 초기 해석 결과에 비하여 감소하는 것을 확인할 수 있었다.

Acknowledgments

본 연구는 2017년도 동양미래대학교 학술연구지원사업의 지원을 받아 수행된 연구과제입니다.

References

• Musk, E., (2013), Hyperloop Alpha, SpaceX, Retrieved August 13, from http://www.spacex.com/hyperloopalpha.
• Kantrowitz, A., (1945), Donaldson, C. D., “Preliminary investigation of supersonic diffusers”, National Advisory Committee on Aeronautics, Langley Memorial Aeronautical Laboratory, Langley Field, Virginia.
• Hong, S. W., Kang, H. M., Kim, Y. M., and Kwon, H. B., (2018), “CFD ANALYSIS FOR CAPSULE TRAIN USING THE RESULT OF COMPRESSOR PERFORMANCE ANALYSIS”, KSCFE 2018 Spring Annual meeting.
• Opgenoord, M. J., and Caplan, P. C., (2017), “On the Aerodynamic Design of the Hyperloop Concept”, In Proceedings of the 35th AIAA Applied Aerodynamic Conference. [https://doi.org/10.2514/6.2017-3740]
• Van Wie, D.M., Kwok, T., and Walsh, R. F., (1996), “Starting characteristics of supersonic inlets”, AIAA paper 96-2914. [https://doi.org/10.2514/6.1996-2914]
• Hong, S. W., (2017), “Construction of aerodynamic performance analysis framework for centrifugal compressor”, The KSFM Journal of Fluid Machinery, 20(3), p36-41. [https://doi.org/10.5293/kfma.2017.20.3.036]
• Kang, H. M., and Kwon, H. B., (2018), “Stability Assessment of the Contact Force of CX Pantograph during HEMU-430X Train’s Running in Tunnel”, Korean Society of Computational Fluid Engineering, 23(1), p94-100. [https://doi.org/10.6112/kscfe.2018.23.1.094]