소화 노즐 내부 다중격벽의 방출구 직경이 방출소음에 미치는 영향
Abstract
Fire extinguishing facilities are built differently depending on the object and purpose of protection. Gaseous extinguishing equipment is generally used to suppress the fire generated by electronic equipment. Electronic equipment is sensitive to vibrational energy. Therefore, the extinguishing ability of the fire extinguishing equipment and the flow noise are considerable factors. However, this subject has not yet been considerably investigated. In this study, the effect of multiple partitions in the fire extinguishing nozzle on the discharge noise was numerically investigated. Further, modified models with diameter ratios of 1.25, 1.0, and 0.75 and a reference model were compared, and the pressure and velocity distributions were graphically depicted using variables. Furthermore, the model with a diameter ratio of 0.75 exhibited a noise level that was approximately 17.54% lower than that exhibited by the reference model.
Keywords:
Extinguishing nozzle, Gaseous extinguishing systems, Discharge noise, CFD, CAA키워드:
소화 노즐, 가스계 소화설비, 방출소음, 전산유체역학, 공력음향해석1. 서 론
화재는 발생 원인과 특징에 따라 처리 방법이 나뉘게 된다(1). Fig. 1에서 확인할 수 있듯이 목재, 천, 종이 등을 비롯한 일반적인 가연성 물질의 경우는 Class A로 분류되며, 인화성 액체, 가연성 액체 석유 등과 같은 물질은 Class B로 분류된다. 또한 전기 장비에 대한 화재는 Class C로 분류되는데, 일반적으로 물을 사용하여 화재를 진압하기 어려운 전기실과 같은 장소에 많이 발생한다. 가스계 소화설비는 이러한 장소의 화재를 진압하는 것을 목적으로 하며(2,3), 1989년 이후부터는 몬트리올 의정서(Montreal Protocol)에 의하여 오존층 파괴물질인 할로겐(halogen)계를 제외한 다른 아르곤, 질소, 이산화탄소 등과 같은 물질이 가스계 소화설비의 소화 약제로 사용되고 있다. 일반적으로 압축 용기에 고압으로 저장되는 소화 약제는 화재가 발생하였을 경우 설치된 배관과 소화 노즐을 통하여 방호구역으로 방출되며, 이 경우 질식 및 냉각작용으로 화재를 진압하게 된다. Jeon 등(4)은 개구부 면적이 CO2 소화설비의 소화 성능에 미치는 영향을 고찰하였으며, 소화설비의 소화 성능을 CFD(computational fluid dynamics)을 사용하여 계산하였다. 소화 성능은 개구부가 없는 100 m3 공간에서, 1분 이내에 질식소화가 가능한 소화약제의 양을 기준으로 계산하였으며, 개구부의 면적에 비례하여 소화 완료 시간이 증가함을 보였다. Rosa 등(5)은 불활성 가스 혼합물의 농도에 따른 소화효과를 조사하였으며, 밀폐된 장소에서 최소 산소(O2)농도에 도달하는 시간을 측정하여 소화 성능을 테스트하였다. 상기 연구들은 소화 성능에 초점을 두고 있으나 최근 연구에 따르면 소화 성능뿐만 아니라 소화 노즐에서 발생하는 소음 또한 해결해야 할 문제로 대두되고 있다. 그 이유는 가스계 소화 노즐이 설치된 장소는 대부분 전기설비로부터 발생하는 화재인 Class C를 진압하여 전산장비를 방호하게 되는데 발생한 소음의 진동에너지에 의해 전산장비들이 손상을 입어 제 기능을 하지 못하게 되기 때문이다. Dutta와 Andrew(6)는 외부소음이 하드디스크 드라이브(hard disk drive) 기능에 끼치는 영향을 실험적으로 연구하였으며, 4~10 kHz 영역의 소음은 시판되고 있는 많은 종류의 하드디스크 드라이브에 치명적이라는 것을 밝혔다. 또한, SIMENS社에서는 이러한 가스계 소화 노즐의 문제점을 지적하여 저소음 소화 노즐을 연구 및 개발한 바 있다(7).
본 연구에서는 가스계 소화 노즐 내부 다중격벽의 방출구 직경이 방출소음에 미치는 영향을 고찰하였으며, 상용코드 ANSYS FLUENT 18.1을 사용하여 소화약제 유동과 방출소음을 수치적으로 계산하였다.
2. 수치해석
2.1 지배방정식
LES(large eddy simulation)는 난류를 계산격자로 해결할 수 있는 큰 난류와 작은 난류를 구분하여 계산하는 방법이다. 구분은 필터링을 사용하여 계산격자보다 작은 난류들을 제거하며, 큰 난류에 대해서 직접 계산하게 된다(8,9). 작은 난류에 대해서는 모델링을 통해 근사화과정을 다루게 되는데, 지배방정식으로는 연속방정식, 운동량방정식, 에너지 방정식을 사용한다. 또한, 큰 난류에 대해서는 다음과 같은 지배방정식을 이용하여 유동특성을 고찰하게 된다.
| (1) |
| (2) |
| (3) |
| (4) |
여기서 ρ는 밀도[kg/m3], μ는 점성계수[Pa·s], u, v는 속도[m/s], Cp는 등압 열용량[J/kg·K], T는 온도[K], p는 압력[Pa], τ는 응력 텐서[Pa], α는 열팽창률[1/K], k는 열전도도[J/m.K], Φ는 단위 부피당 점성소산(viscous dissipation)[W/m3], H는 단위 질량당 내부 열에너지 발생률[W/kg], t는 시간[s], 그리고 τij는 서브 그리드 응력(sub-grid stress)[MPa]을 각각 나타낸다.
전산공력음향해석(Computational Aero Acoustics, CAA)은 유동해석 정보를 기반으로 수행하게 되는데, 고차-고해상도의 수치기법을 필요로 한다. 선행된 전산공력음향연구들은 이러한 이유로 LES를 사용하여 수치해석을 수행하였는데, 이에 본 연구에서도 LES를 사용하여 소화 노즐의 유동해석을 수행하였다(10-14).
Lighthill(11)은 유체유동으로부터 발생하는 소음을 수학적으로 정의하였으며 이를 음향상사식으로 나타내었다. 이후 제트유동, 난류소음, 환경소음 등 여러 유동에 대한 소음문제를 해결하기 위한 많은 연구들이 진행되어왔다. 이 과정에서 Lighthill의 음향상사식은 점차 확장되어 왔으며, 본 연구에서는 Ffowcs Williams와 Hawkings(FW-H) 음향상사식을 이용하여 공력음향해석을 수행하였다.
| (5) |
여기서 c0는 유동장의 음속 [m/s], Pij는 압축응력텐서[Pa],Tij는 Lighthill 응력텐서[Pa], p′는 원거리 음압[Pa]이다. 또한, δ(f)은 Dirac delta 함수, H(f)는 계단함수(step function), 그리고 f는 경계함수이다.
고속 푸리에 변환(fast Fourier transform, FFT)은 임의의 도메인에서 얻이진 신호를 주파수 도메인으로 또는 그 반대로 변환하는 방법이다. 주파수 도메인으로 변환은 주기함수들의 합으로써 이루어지며, 각 성분들은 주파수와 강도로 표현이 된다.
본 연구에서는 여러 관측점에서 측정된 압력 맥동을 시간영역에서 주파수영역으로 변환하였으며, 그에 따른 방정식은 다음과 같이 나타낸다.
| (6) |
여기서, p(t)는 시간 영역 압력함수, p(f)는 주파수 영역 압력 함수이며, f는 주파수를 나타낸다.
2.2 해석모델
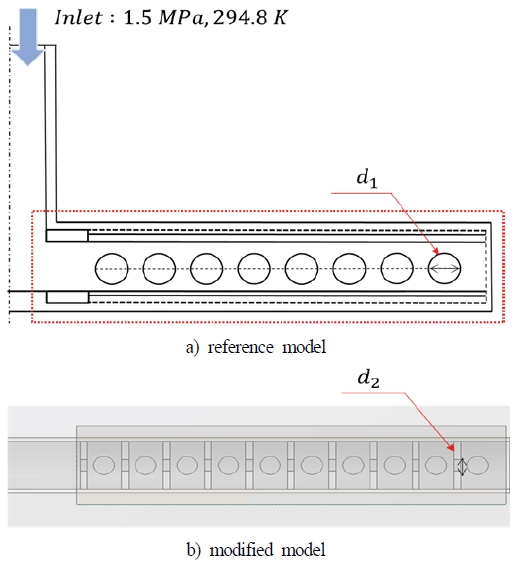
격벽은 과거부터 소음저감 대책으로 사용되었던 방법 중 하나이며, 총기 소음기와 자동차 머플러 등에서 쉽게 찾아 볼 수 있다. 이에 본 연구에서는 T형 커넥터에 달린 소화 노즐을 기본형상으로 선정하였으며, 소화 노즐 내 다중격벽에 의한 유동소음을 분석하였다. 격벽은 방출구 사이에 하나씩 삽입하였으며, 소화약제가 통과할 수 있도록 중앙에 구멍을 형성하였다. 격벽내부 구멍의 지름은 외부 방출구 지름(d1)과 동일한 것(case 2)을 기준으로 25% 작은 직경(case 3)과 큰 직경(case 1)을 선정하였다. 이는 구멍이 있는 다중격벽에 대한 영향을 개략적으로 조사하기 위한 것이며, 방출되는 소화약제의 유동소음을 계산하여 기본형상과 비교하였다. 구성된 소화 노즐은 Fig. 2에 도시하였으며, Table 1에 각 case별 직경 비(diameter ratio)를 기술하였다.
2.3 격자계 구성
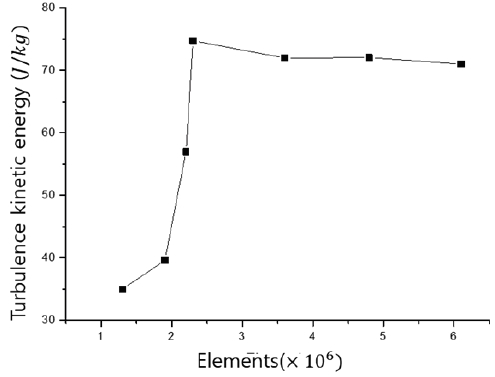
ANSYS Meshing을 사용하여 수치해석을 위한 격자계를 구성하였다. 사면체(tetrahedral), 육면체(hexahedral)형태를 주로 사용하였으며, 각뿔(pyramid)형태를 사용하여 사면체와 육면체 격자의 연결부위를 구성하였다. 곡선의 형태가 많은 소화 노즐 내부는 주로 사면체 격자를 사용하여 소화 노즐 형상을 잘 모사할 수 있도록 하였고, 방출구 인근 유동장(6d1)까지 사면체 격자를 확장하여 사용하였다. 외부 유동장(24d1)은 주로 정렬격자인 육면체 격자를 사용하여 격자계를 구성하였으며, 이를 Fig. 3에 도시하였다. 격자 의존도 평가는 노즐 중심으로 10d1 거리에 떨어진 임의 점에서의 난류운동에너지를 측정하였으며, 노즐내부의 격자크기를 중심으로 성장률(growth rate)이 1.1을 갖도록 격자수를 점차 증가시켰다. 그 결과, 전체 도메인 1/4기준으로 약 480만개의 격자수로 격자계를 구성하였으며(Fig. 4 참조), 격자품질은 직교성(orthogonal quality)이 최소값 0.11, 뒤틀림성(skewness quality)이 최대값 0.89를 갖는다.
2.4 경계조건
본 연구에서는 ANSYS FLUENT ver. 18.1을 사용하여 수치해석을 수행하였다. 경계조건으로는 질소청정소화약제인 IG-100을 작동유체로 선정하였으며, 소화 노즐입구에서 1.5 MPa의 압력으로 유입되어 1 atm의 대기로 분출되는 현상을 모사하였다. 난류모델은 LES(large eddy simulation)를 사용하였고, sub-grid scale모델은 WALE(wall-adapting local eddy-viscosity)을 사용하였다. 수치해석은 비정상상태(transient)로 10s의 유동시간을 계산하였으며, 관심주파수 영역은 0~12.5 kHz로 선정하였다. 또한, 전산공력음향해석을 위한 전파모델은 FW-H 모델을 사용하였으며 주위 대기조건 및 경계조건은 Table 2에 기술하였다.
3. 결과 및 고찰
3.1 유동해석
Courant 수는 격자 크기, 속도, 계산시간 간격(time step)에 대한 비율로 다음과 같이 정의된다(15).
| (7) |
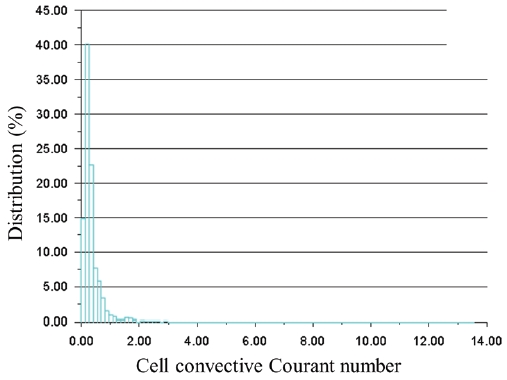
여기서 C는 Courant 수, U는 속도, ∆t는 계산시간 간격이다. 이는 비정상 유동해석 후 선택된 시간 간격과 격자 등에 대해 안정되었는지를 판단하는 기준이 되며, Courant 수는 계산도메인의 가장 민감한 영역에서 40 이내의 값을 가져야 하는 것으로 알려져 있다(16).
Fig. 5는 기본모델 계산도메인에서의 Courant 수 분포를 도시한 것이다. 대부분의 영역이 약 1이하에 분포함을 확인하였으며, 이로써 비정상유동해석에 대한 설정이 안정적임을 알 수 있다.
작동유체의 내부 에너지와 운동 에너지를 더하여 단위 질량당 엔탈피 개념으로 나타내는 것이 유동해석결과를 비교하는 데에 유용하게 되는데, 유체의 위치에너지를 무시할 경우 다음과 같이 정의된다.
| (8) |
여기서 h0는 전 엔탈피(total enthalpy)[kJ/kg], h는정(static) 엔탈피[kJ/kg], 그리고 V는 속도[m/s]이다.
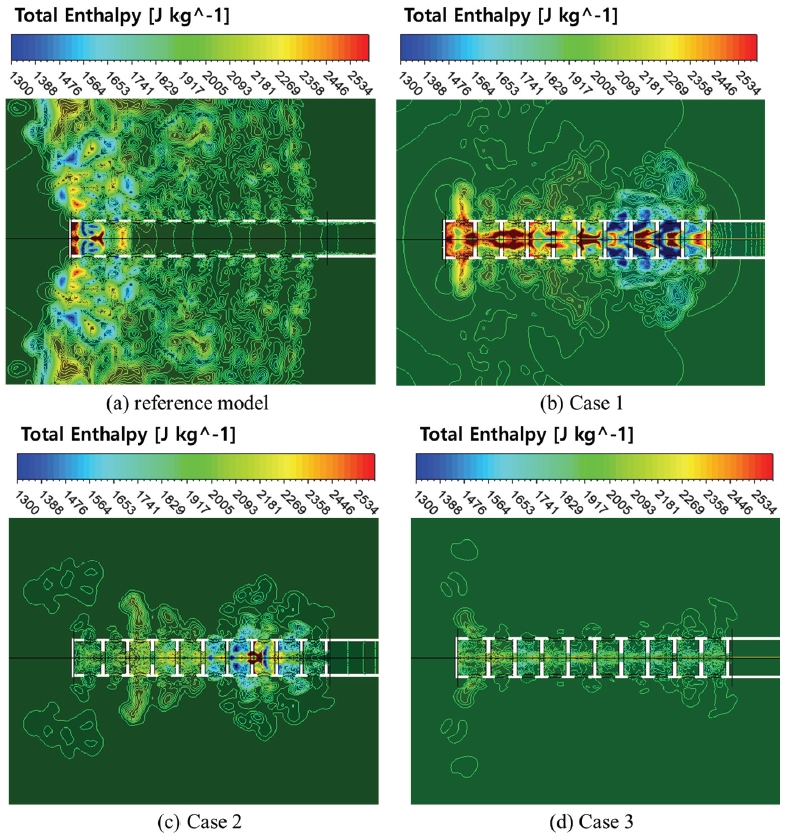
Fig. 6은 각 형상별 전 엔탈피를 도시한 것이다. 기준모델의 경우 노즐 끝단으로 갈수록 에너지가 집중되는 것을 확인할 수 있으며, case 3으로 갈수록 전체 에너지가 줄어들고, 균등하게 분포되는 것을 확인할 수 있다. 기준모델의 경우는 평균 1946.09 [J/kg]의 전 엔탈피를 갖는 것을 확인하였으며, case 1은 1983.51 [J/kg], case 2는 1929.33 [J/kg], case 3은 1922.9 [J/kg]를 갖는 것을 확인하였다.
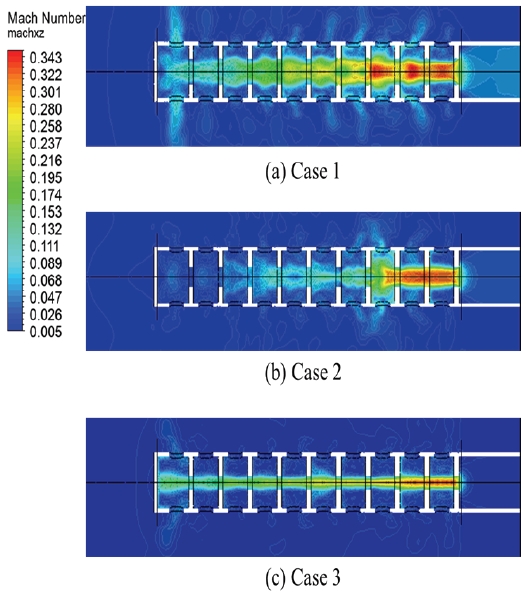
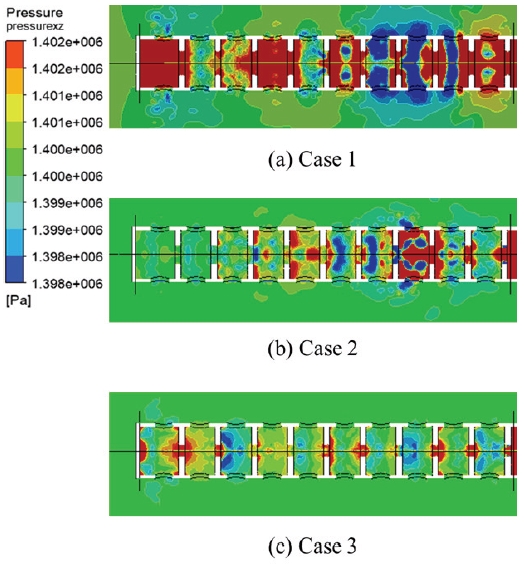
Fig. 7은 각 형상별 Mach 수 분포를 도시한 것이다. 동일 압력을 갖는 압축탱크에서 방출된 소화약제가 배플을 통과하면서 좁아지는 배플구멍 지름에 따라 속도와 유량이 결정되게 된다. 기준모델의 경우 Ma=0.290의 입구속도를 가지며, case 1은 Ma=0.055, case 2는 Ma=0.029, case 3은 Ma=0.013의 입구속도를 가지게 된다. 소화약제가 배플을 통과하면서 속도는 증가하고 압력은 감소하게 되는데, 일정량의 소화약제는 양 옆으로 분출되고 나머지 소화약제는 다음 실로 이동하게 된다. 따라서 방출되는 소화약제와 대기와의 압력차는 상대적으로 많이 감소함을 알 수 있는데, 이는 Fig. 8에 도시한 형상별 압력분포에서 확인할 수 있다. Case 1은 노즐내부 압력이 반복적으로 증감하는 경향을 볼 수 있으며, 이에 따라 방출되는 약제의 압력 또한 불규칙함을 알 수 있다. Case 2부터는 더 많은 압력감소가 발생하였고, 이에 따라 방출되는 소화약제의 압력 또한 안정되는 경향을 나타내었다.
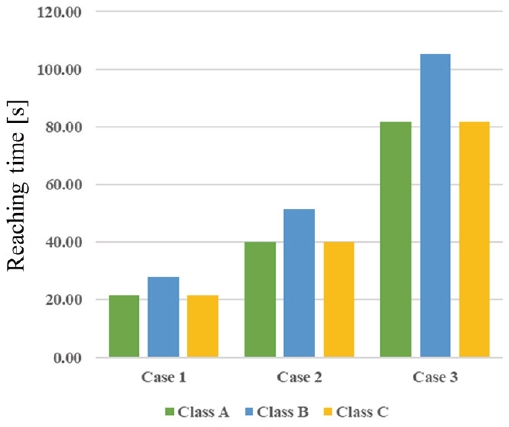
화재예방, 소방시설 설치/유지 및 안전관리에 관한 법률에 따르면, 가스계 소화설비는 2분 이내에 설계농도 30%에 도달하는 조건을 만족해야한다(17). 소화약제 설계농도는 A급, B급, 그리고 C급 화재에 대해 조사하였으며, Fig. 9에 도시하였다. 모든 case들은 120초 이내로 설계농도 30%를 만족하는 것을 확인하였지만, 다중격벽에 설치된 구멍지름이 작아짐에 따라 도달시간이 증가함을 알 수 있다.
3.2. 소음해석
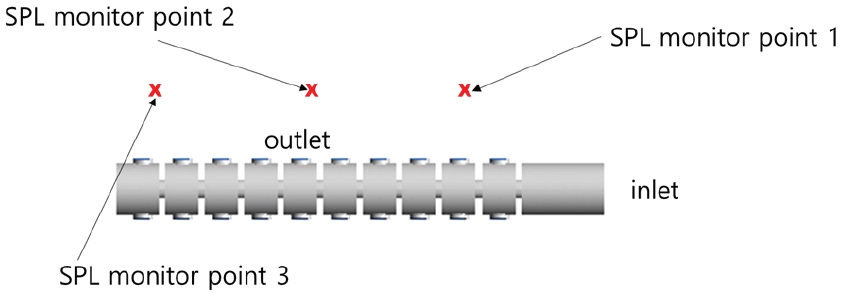
Fig. 10은 소음해석을 위한 압력 측정점을 개략적으로 도시한 것이다. 총 세 점에서 데이터를 측정하였으며, 이를 기반으로 소음해석을 진행하여 각 형상별 결과를 비교하였다. 각 지점에서 측정된 시간에 따른 압력맥동은 FFT(fast Fourier transform)을 사용하여 주파수 영역으로 변환하였으며, FW-H의 음향상사식으로 소음해석을 수행하였다. 소음도인 SPL(sound pressure level)은 다음과 같이 정의한다.
| (9) |
여기서, prms는 압력변동의 RMS(root mean square)값을 나타내며, p0는 기준 SPL값인 2×10-5 [Pa] 이다.
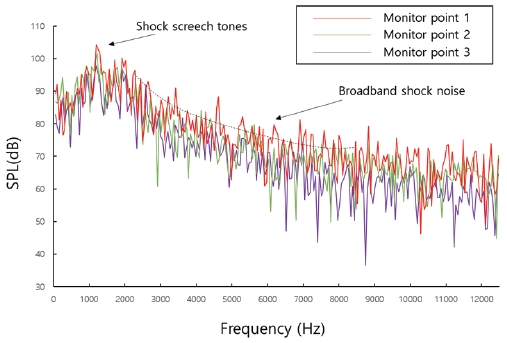
기준모델의 SPL은 Fig. 11에 도시하였으며, 관심주파수 영역인 0~12.5 kHz를 각 측정점에 따라 나타내었다. 소음도 분석결과 크게 소음은 두 가지로 나뉘는 것을 확인하였다. 노즐로부터 나오는 소화약제의 충격과 난류구조 사이에서 강력하게 발생하는 소음인 충격소음(shock screech tone)과 전단층의 난류구조와 충격층의 약한 상호관계에서 전파되는 광대역소음(broadband noise)으로 구분할 수 있다(18~20).
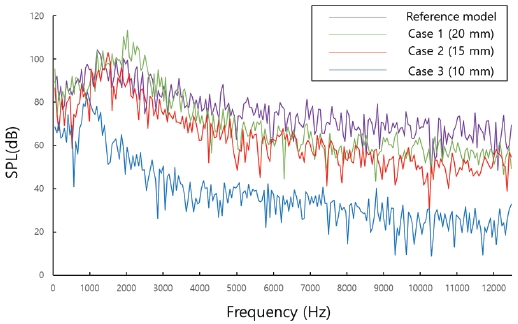
각 형상별 소음도를 주파수대역별로 Fig. 12에 도시하였다. Case 1의 경우 충격소음이 기준모델보다 큰 값을 나타냈지만, 광대역소음은 점차 낮아지는 경향을 보였다. Case 1의 최대소음(peak noise) 값은 113.188 dB으로, 기준모델의 104.319 dB보다 약 9 dB 정도 크게 계산되었다. 하지만 이후 광대역소음으로 인해 평균소음도(overall sound pressure level)는 기준모델의 129.666 dB보다 약 6 dB 높은 135.574 dB로 계산되었다. 이와 반대로 case 2와 case 3의 최대소음은 각각 102.955 dB와 84.919 dB로 계산되었으며, 평균소음도는 125.621 dB와 106.926 dB를 나타내었다. 이는 기준모델 대비 약 3.12%, 17.54% 감소한 소음도를 나타낸다.
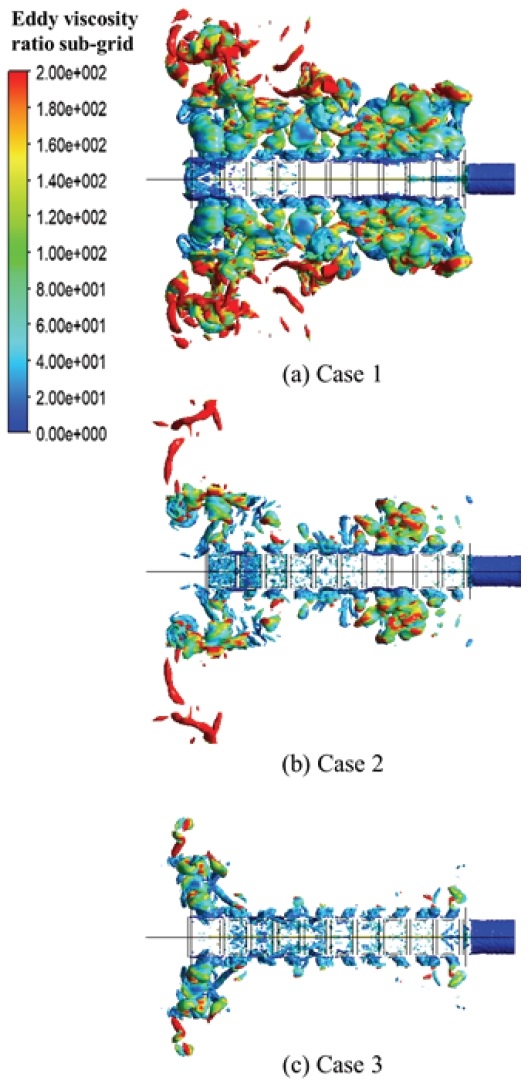
Fig. 13은 난류 점도 비율(eddy viscosity ratio) 분포를 나타내는데, 이는 난류 길이를 추정하는데 사용된다. 가장 큰 광대역 소음을 갖는 case 1의 경우 다른 case에 비하여 큰 난류 크기를 가지며, 광대역 소음의 크기는 난류 크기에 비례하는 경향을 알 수 있다.
소화 노즐내 다중격벽에 구성된 방출구 지름은 소화약제 방출시 나타나는 충격소음과 광대역소음 주파수영역에 영향을 끼치는 것을 알 수 있는데, 지름의 증가는 충격소음의 최대주파수와 비례하여 증가하는 경향을 나타내었다. 또한 일정한 입구압력 조건에서는 지름의 크기가 작아질수록 전체 소음은 감소하는 것을 확인하였다.
4. 결 론
가스계 소화설비는 화재진압능력 뿐만 아니라 방출소음도 중요하다. 이에 본 연구에서는 소화 노즐내 다중격벽을 설치하여 방출소음에 미치는 영향을 수치적으로 고찰하였다. 기본형상은 T형 커넥터의 달려있는 소화 노즐로 선정하였으며, 고해상 유동해석모델인 LES와 소음전파방정식인 FW-H 음향상사식을 사용하여 소음해석을 수행하였다. 형상변수로는 방출구 지름을 기준으로, 격벽의 구멍지름비가 1.25, 1.0, 0.75인 세 가지 형상을 기본형상과 비교하였다. 경계조건은 1.5 MPa의 일정한 압력이 분출되는 소화약제 설비가 대기압으로 분출되는 상황을 가정하여 적용하였으며, 약 10초의 과도(transient)상태 유동해석을 수행하였다. 해석결과 일정한 압력은 배플의 지름에 따라 유입속도와 유량이 변하며, 배플로 구성된 공실은 소화약제가 통과할 때마다 압력을 감소시키는 역할을 수행함을 알 수 있었다. 이는 소화약제 방출시 충격소음을 낮추는데 큰 역할을 하게 되는데, 특히 광대역소음을 저감시키는데 탁월한 효과를 유발시키는 것으로 사료된다. 본 연구에서 고려한 Case 3의 경우 평균소음도가 기준모델에 대비하여 17.54% 감소함을 확인하였으며, 추후 배플 구멍형상과 지름 등에 관한 최적설계와 실험적 연구가 수반되어야 할 것이다.
Acknowledgments
2019 한국유체기계학회 하계학술대회 발표 논문, 2019년 7월 3일~7월 5일, 휘닉스 평창
본 연구는 국토교통기술사업화지원사업의 연구비 지원(18TBIP-C127226-02)에 의해 수행되었습니다.
References
- NFPA(National Fire Protection Association), (2018), “Standard For Portable Fire Extinguishers, 2018 Edition”, NFPA 10.
- NFPA(National Fire Protection Association), (2012), “Standard on Clean Agent Fire Extinguishing Systems, 2012 Edition”, NFPA 2001.
- NEMA, (2013), “National Fire Safety Code of Clean Agent Fire Extinguishing System”, NFSC 107A.
- Jeon, H., K., Choi, Y., S., and Park, J., T., (2008), “The Effects of the Area of Openings on the Performance of a CO2 Extinguishing System”, J. of Korean Institute of Fire Sci. & Eng., 22(1), p1-9, (in Korean).
- Rosa, D., Maria, I., and Charles, D. L., (2007), “Effectiveness of Various Concentrations of an Inert Gas Mixture for Preventing and Suppressing Mining Equipment Cab Fires: Development of a Dual Cab Fire Inerting System”, Fire Technology, 43(1), p29-44.
-
Dutta, T., and Andrew, R. B., (2017), “Performance of Hard Disk Drives in High Noise Environments”, Home Noise Control Engineering Journal, 65(5), p386-395.
[https://doi.org/10.3397/1/376555]

- Siemens, (2011), “Potential Problems With Computer Hard Disks When Fire Extinguishing Systems Are Released”, A White Paper issued by Siemens.
- Smagorinsky, J., (1963), “General Circulation Experiments With the Primitive Equations: I. The Basic Experiment”, Monthly Weather Review, 91(3), p99-164.
-
Deardorff, J. W., (1970), “A Numerical Study of Three-Dimensional Turbulent Channel Flow at Large Reynolds Numbers”, Journal of Fluid Mechanics, 41(2), p453-480.
[https://doi.org/10.1017/s0022112070000691]

-
Andersson, N., Eriksson, L., E., and Davidson, L., (2005), “Large-Eddy Simulation of Subsonic Turbulent Jets and Their Radiated Sound”, AIAA Journal, 43(9), p1899-1912.
[https://doi.org/10.2514/1.13278]

- Lighthill, M., J., (1952), “On Sound Generated Aerodynamically I. General Theory”, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 211(1107), p564-587.
-
Xia, H., Tucker, P., G, and Eastwood, S., (2009), “Large-Eddy Simulations of Chevron Jet Flows with Noise Predictions”, International Journal of Heat and Fluid Flow, 30(6), p1067-1079.
[https://doi.org/10.1016/j.ijheatfluidflow.2009.05.002]

- Kaltenbacher, M., Escobar, M., Becker, S., and Ali, I., (2009), “Numerical Simulation of Flow‐induced Noise Using LES/SAS and Lighthill's Acoustic Analogy”, International Journal for Numerical Methods in Fluids, 63(9), p1103-1122.
-
Nichols, J., Lele, S., Moin, P., Ham, F., Bres, G., and Bridges, J., (2012), “Large-Eddy Simulation for Supersonic Rectangular Jet Noise Prediction: Effects of Chevrons”, 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), p2212.
[https://doi.org/10.2514/6.2012-2212]

- Ferziger, J. H., and Peric, M., (2012), “Computational Methods for Fluid Dynamics”, Springer Science & Business Media.
- ANSYS Help version 18.1, (2018), Ansys Inc.
- NEMA, (2017), “Technical Standards for Performance Certification and Product Inspection of Gas System Fire Extinguishing System Design Program”, No. 15810.
- Powell, (1953), “On the Noise Emanating from a Two-Dimensional Jet Above the Critical Pressure”, The Aeronautical Quarterly, 4(2), p103-122.
- Norum, T., D., and Seiner, J., M., (1982), “Broadband Shock Noise from Supersonic Jets”, AIAA Journal, 20(1), p68-73.
- Lassiter, L., W., and Hubbard, H., H., (1956), “The Near Noise Field of Static Jets and Some Model Studies of Devices for Noise Reduction”, NACA Technical Report 1261.