난류처리기법에 따른 소화노즐 배기소음 예측연구
Abstract
Fire-extinguishing equipment that can be used to suppress unexpected fire and that can minimize its damage is essential in all industries. Different fire-extinguishing agents and nozzle types have been introduced depending on the type of objects to protect, and various studies have been accordingly conducted. However, only a few of these studies have focused on the exhaust noise from fire-extinguishing systems. This noise can damage the electrical equipment; hence, the investigation of this noise is necessary. Computational fluid dynamics software ANSYS FLUENT ver. 18.1 was used herein. A numerical analysis was conducted to analyze the fluid flow characteristics depending on the turbulent treatment methods. Subsequently, the noise was calculated. The turbulent treatment methods considered here were Reynolds-averaged Navier–Stokes simulations and large eddy simulation. Furthermore, the Ffowcs Williams–Hawkings equation was used to calculate the noise. Consequently, the averaged velocity and pressure values are similarly described, while the frequency graphs of the noise and eddy of fluctuation are separately shown.
Keywords:
Fire extinguishing nozzle, Noise, CFD, CAA키워드:
소화노즐, 소음, 전산유체역학, 공력음향해석1. 서 론
예상치 못한 화재를 제압하고 피해를 최소화하기 위한 소화설비는 우리 생활에 필수적인 장비이다. 이러한 소화설비는 방호대상 및 목적에 따라서 소화약제와 노즐형식이 다르게 구성되는데, 이에 따른 여러 연구들이 진행되어 왔다. Wang 등(1)은 화재 진압을 위한 물방울 크기 최적화를 위한 전산유체역학 연구를 수행하였으며, 가장 짧은 소화시간과 적은 물소비로 최대 효과를 얻을 수 있는 최적의 물방울 크기를 제시하였다. Lee(2)는 원자력 발전소에 사용되는 소화시스템을 연구하였으며, 물 미스트 제트에 대한 분석으로 소화시스템 노즐의 최적화를 연구하였다.
반면, 물을 이용하여 화재를 진압하기 어려운 전자장비실, 전기실, 박물관 등과 같은 공간에는 국내외를 막론하고 가스계 소화설비를 설치하도록 되어있으며(3,4), 1989년에는 오존층 보호를 위한 몬트리올 의정서에 의해 기존의 소화약제였던 할로겐(halogen)계가 규제되었다. 이에 Saito 등(5)은 할론 1301, 아르곤, 질소, 그리고 이산화탄소의 소화효과에 대해 연구하였고, Rosa 등(6)은 불활성 가스 혼합물의 농도에 따른 화재 진압효과를 연구하였다.
최근 가스계 소화설비에서 발생되는 소음이 고집적화 되어 있는 전자장비에 피해를 끼치는 사례가 발생하면서(7-9) 소화설비 소음에 대한 연구 필요성이 커지고 있으나, 대부분의 연구는 빠른 소화효과에 대해 수행되어왔을 뿐, 소음에 대한 연구는 미미한 실정이다.
본 연구에서는 가스계 소화설비의 배기소음에 대한 분석을 하고자 난류처리기법인 RANS(Reynolds Averaged Navier-Stokes Simulations)방법과 LES(Large Eddy Simulation)방법을 비교하여 유동 및 소음특성을 고찰하였다.
2. 수치해석
3차원 압축성 유동특성을 수치적으로 계산하기 위해 두 가지 난류처리기법을 상용코드인 ANSYS FLUENT ver 18.1을 사용하여 계산을 수행하였다.
2.1 지배방정식
고체의 진동으로 발생하는 소음이 아니라, 유체의 흐름으로 발생하는 소음의 경우 1950년대 Lighthill(10)에 의해 발표된 음향상사식으로 인해 첫 수학적 정의가 내려졌으며, 제트유동으로 인해 발생하는 음원에 대한 파동방정식을 유도하였다. 이후, 많은 연구자들에 의해 유동소음 문제를 위한 음향상사식이 확장되었으며, 본 연구에서는 Lighthill과 Curle의 음향상사식을 확장한 Ffowcs Williams와 Hawkings(FW-H)의 음향상사식 (식 (4) 참조)을 사용하여 소음도를 계산하였다(11).
또한, 유동해석을 위한 지배방정식으로는 연속방정식, 운동량방정식, 에너지방정식을 이용하였다.
| (1) |
| (2) |
| (3) |
| (4) |
여기서, ρ 는 밀도[kg/m3], t 는 시간[s], v는 속도[m/s], Cp는 등압 열용량[J/kg·K], T는 온도[K], p 는 압력 [Pa], τ 는 응력 텐서[Pa], α 는 열팽창률[1/K], k는 열전도도[J/m. K], φ는 단위 부피당 점성소산(viscous dissipation)[W/m3], 그리고 H 는 단위 질량당 내부 열에너지 발생률[W/kg]을 각각 나타낸다.
또한, FW-H 음향상사식(4)에서 Pij는압축응력텐서[Pa], Tij는 Lighthill의 응력텐서[Pa], c0는 유동장의 음속 [m/s], p′는 원거리 음압 [Pa]을 각각 나타낸다. 그리고 δ(f)은 Dirac delta 함수, H(f)는 단계함수(step function), f는 경계함수로 다음과 같이 표기된다.
| (5) |
| (6) |
2.2 해석모델
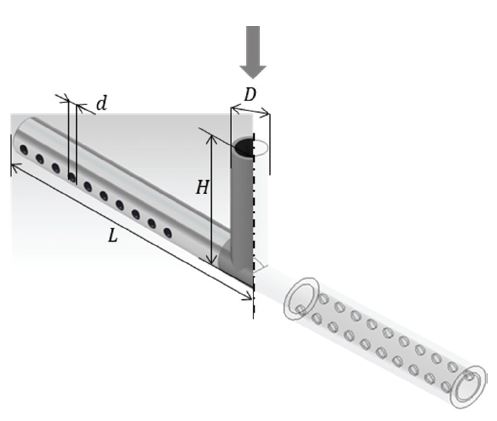
본 연구에서는 국내 J社에서 제공된 가스계 소화노즐의 소음도 및 유동특성을 전산유체역학(CFD)으로 고찰하였다. 소화노즐은 42개의 방출구를 가지며, 벽면 캐비닛에서 소화 약제를 방출하는 것을 고려하여 약 250˚의 방출각을 갖도록 구성되어있다. 형상은 ANSYS Design Modeller를 이용하여 설계하였으며 Fig. 1에 도시하였다. 노즐은 직경(d) 7.5mm의 유입구를 가지며, 길이(L) 200mm, 높이(H) 120mm, 그리고 실린더 지름(D)은 20mm이다.
2.3 경계조건 및 격자계 구성
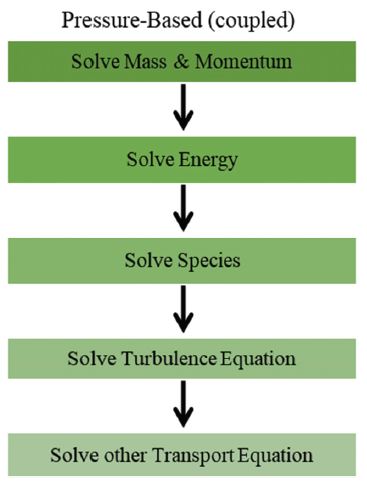
본 연구에서 사용된 소화약제는 불활성 소화약제인 질소(N2)를 이용하였다. 입구조건으로는 1.334MPa의 압력이 오리피스를 지나도록 설정하였으며, 대기압상태로 분출하도록 하였다(Table 1 참조). 또한 압축성 유동에 대한 수치해석을 위해 압력기반의 연성해석을 수행하였으며(Fig. 2 참조), 작동유체는 이상기체의 운동과 온도변화에 따른 점도변화를 고려한 Sutherland 법칙을 따르도록 설정하였다.
각 계산격자에서 압력구배를 계산하기 위한 보간법으로는 큰 스월유동(swirling flow)과 가파른 압력구배가 예상되는 흐름에 적합한 PRESTO!(the pressure staggering option) scheme을 적용하였다.
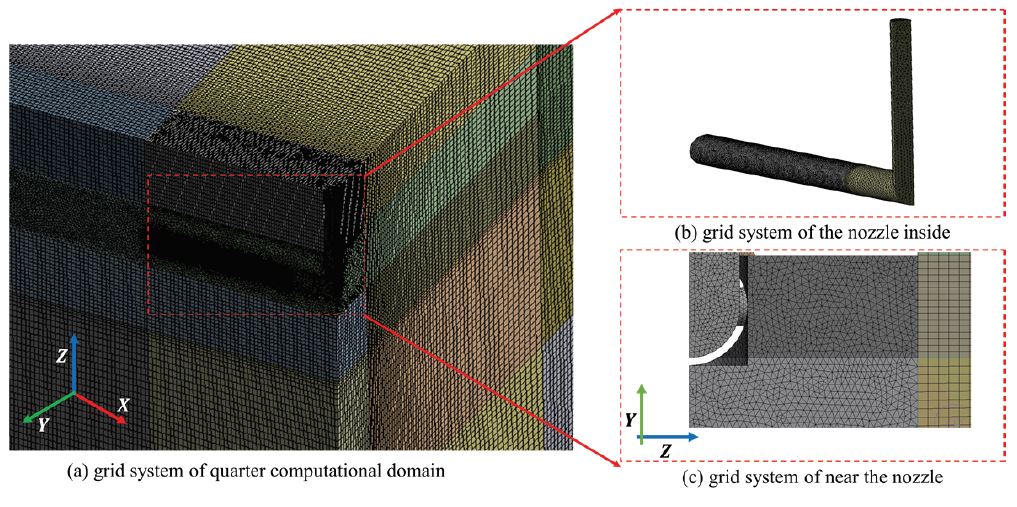
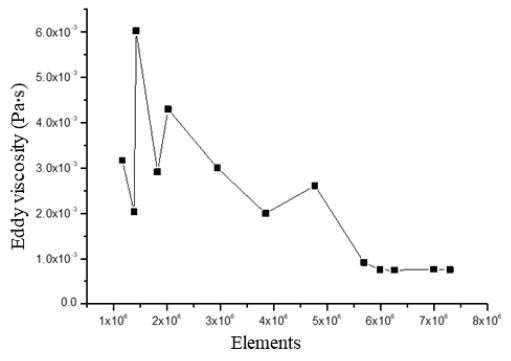
수치해석을 위한 격자는 ANSYS Meshing을 사용하여 구성하였으며 Fig. 3에 도시하였다. 비교적 속도가 빠르고 조밀한 곳에는 사면체(tetrahedral type)를 이용하여 구성하였으며, 외부 유동장은 육면체 격자(hexahedral type)를 이용하여 구성하였다. 총 격자수는 격자의존도 시험을 통해 결정되었으며 약 626만개의 격자수로 구성되었다(Fig. 4 참조). 또한, 셀 중심에서 인접 셀의 중심까지의 직교성(orthogonal quality)은 최대 0.10, 셀의 볼륨 편차를 나타내는 비대칭성은 최소 0.89의 값을 갖도록 하였다.
2.4 난류처리기법
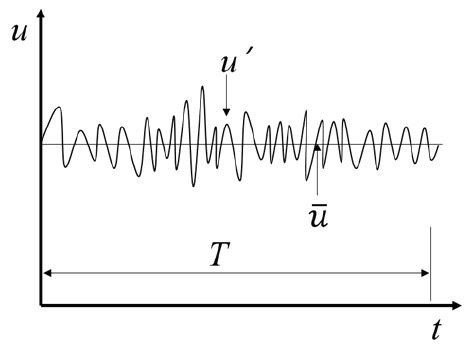
일반적으로 난류장 해석에 많이 사용되는 RANS 모델은 시간평균기법을 사용하여 모든 비정상성은 평균화시키고 공학적 근사(engineering approximations)로 해결하기 위해 모델링 하게 된다(Fig. 5 참조)(12). LES 모델은 계산격자에 의해 해결할 수 있는 큰 기본 난류구조를 직접 계산하며, 작은 난류들은 모델링하여 근사화 하는 방법을 말하며 Smagorinsky(13,14)에 의해 처음 제안되었다.
본 연구에서는 이 두 가지 난류처리기법을 이용하여 유동해석을 진행하였다. RANS 모델은 k-ε 난류 모델과 k-ω 난류 모델의 장점을 결합한 SST(shear stress transport) 모델을 사용하게 되는데, 이는 RANS 모델 중 난류 전단응력의 수송을 잘 모사하고, 역압력구배(adverse pressure gradient) 하에서 유동박리(flow separation) 시작과 크기를 비교적 잘 모사하는 것으로 알려져 있다(15). LES 방법으로는 속도변동의 피크와 벽 압력의 실효치 분포예측에 효과적인 DSM(Dynamic Smagorinsky model)을 사용하였다(16). 이후, 두 유동해석 결과를 기반으로 음향상사식(4)을 이용하여 전파되는 음향에 대한 계산을 추가로 진행하여 결과를 비교하였다.
3. 결과 및 고찰
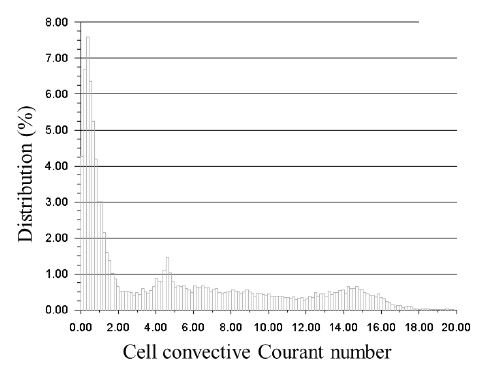
비정상유동해석에 있어서 수렴성을 확인할 수 있는 방법은 각 계산영역에서 Courant 수를 고찰하는 것인데, 이는 다음과 같이 정의된다.
| (7) |
여기서 C는 Courant 수, U는 속도, ∆x는 계산격자 크기, 그리고 ∆t는 계산시간 간격이다.
Fig. 6은 본 연구에서 계산된 Courant 수 분포를 도시하였다. 이는 40이내의 값을 가져야 선정된 설정값과 계산이 안정화 되었다고 알려져 있는데(17), 모든 계산영역에 있어서 20이하의 Courant 수를 갖는 것을 확인하였다.
3.1 유동특성 분포
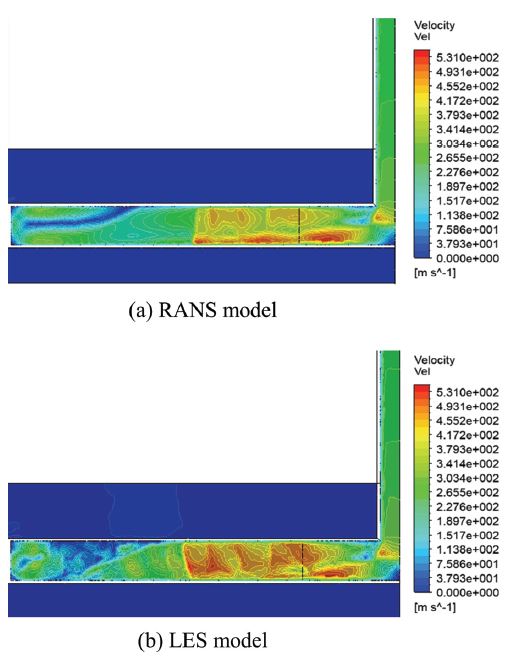
소화노즐 내부 속도와 압력분포를 RANS 모델과 LES 모델을 사용하여 각각 수치적으로 계산하였고, 이를 Fig. 7과 8에 도시하였다. 입구영역에서 계산된 속도는 RANS 모델의 경우 약 267.05[m/s]이며, LES 모델의 경우 262.62[m/s]로 약 1.69 %의 오차로 큰 차이가 없었다. 하지만 내부 간섭에 의한 속도분포는 조금 더 큰 차이를 보였다. LES모델의 경우 벽 근처의 경계층 효과에 의한 eddy형성이 RANS모델 보다 더 뚜렷하게 모사되었는데, 이러한 결과는 방출 유동에 영향을 끼쳤다. 그 결과, 외부로 방출되는 유동의 평균 속도는 RANS 모델의 경우 약 249.73[m/s]로 계산되었고, LES 모델의 경우 약 262.30[m/s]로 계산되었다.
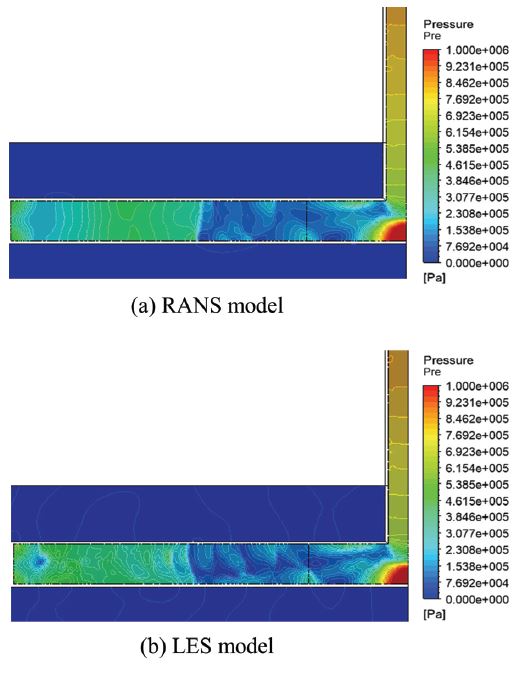
Fig. 8은 소화노즐내부의 압력분포를 도시한 것이다. 속도분포에서 확인하였듯이, 노즐 내부에 존재하는 섭동(fluctuation) 형상을 LES 모델에서는 더 뚜렷하게 확인 할 수 있었다. 입구영역에서의 압력 값은 각각 RANS 모델과 LES 모델이 828.260[kPa]과 842.487[kPa]을 나타내었고, 출구영역에서의 압력은 65.807[kPa]과 58.033[kPa]을 나타내었다.
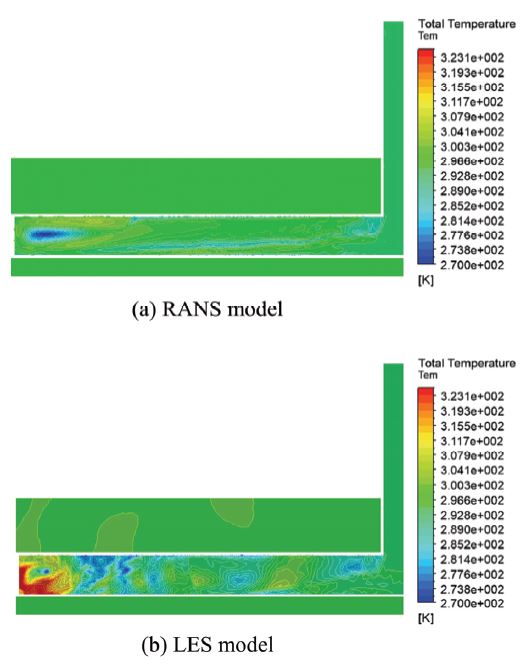
소화노즐 내부 유동특성을 통해 유체의 온도변화를 예측할 수 있는데, Fig. 9에 계산된 온도분포를 도시하였다. 온도분포의 개형은 Fig. 7의 속도분포와 유사한 경향을 보였으며, 그에 따른 차이를 보였다. LES 모델의 경우 노즐 끝단의 온도가 약 323K까지 상승하며, 노즐내부 온도변화가 잘 모사되는 것을 알 수 있지만, RANS 모델의 경우 노즐 끝단의 온도 상승이 크지 않고 노즐내부 온도변화가 상대적으로 작음을 보였다.
유동특성을 분석한 결과, 난류처리기법에 따른 입구영역과 방출영역에서의 속도, 압력 및 온도 값은 미미한 차이를 보였다. 하지만 eddy형성에 의한 유체의 섭동모사에 의한 유동특성은 LES 모델이 더 뚜렷하게 나타내는 것을 확인하였다.
3.2 와동 점도
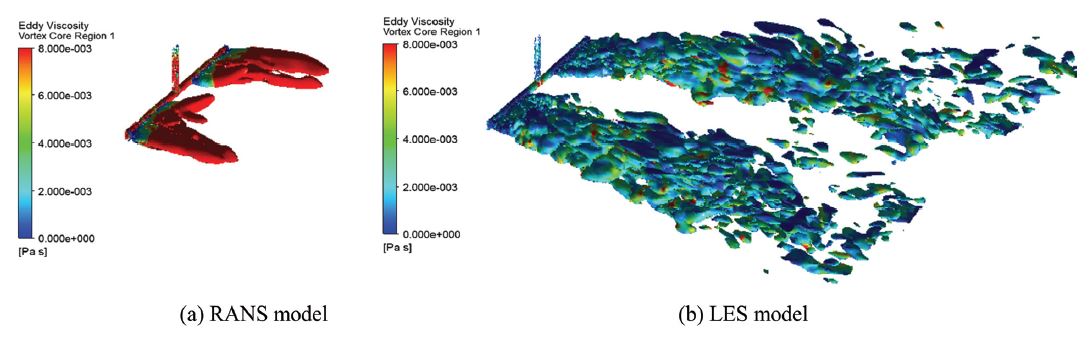
난류에 의한 운동량(momentum) 전달은 유체 내부의 마찰을 유발하며 이에 대한 정도를 와동 점도(eddy viscosity)로 표현할 수 있다. 이에 본 연구에서는 각 난류처리 기법에 대한 결과를 비교하였으며, 그 결과를 Fig. 10에 도시하였다.
와류를 검출하기 위해서는 속도 벡터와 와도 벡터의 내적을 절대값으로 나타낸 헬리시티(helicity)를 고찰하게 된다. 시간평균기법으로 난류응력(turbulent stress)항을 계산하는 RANS 모델의 경우 와동구조의 형태가 LES 모델과 비교하여 볼 때 뭉툭하며 모사되지 못하는 부분이 일부 존재함을 알 수 있다. 이는 LES 모델과 RANS 모델에 따른 난류 모사 정도를 비교할 수 있으며, LES 모델이 난류를 더 세분화하여 넓은 영역에 분포한 것으로 모사함을 알 수 있다. 수치적으로는 헬리시티(helicity) 절대값이 RANS 모델의 경우 72040.9 [m/s2]로써 LES 모델의 116452 [m/s2]보다 약 1.6배 정도 작게 계산되었다. 이 때문에 RANS 모델의 와동 점도는 일부 영역에 집중되어 LES 모델 보다 더 크게 계산됨을 알 수 있으며, 이러한 난류응력 계산의 차이는 소음도 주파수를 분석할 경우 차이를 보일 것으로 사료된다.
3.3 소음도
음향상사식에 의해 계산된 데이터는 FFT(Fast Fourier Transform) 분석 방법을 사용하여 주파수 대비 소음도로 변환할 수 있다. 주파수 대역은 0~20kHz까지 분석하였으며, SPL(sound pressure level)은 다음 식을 이용하여 계산하였다.
| (7) |
여기서, prms는 압력변동의 RMS(root mean square)값을 나타내며, p0는 기준 SPL값인 2×10-5 [Pa] 이다.
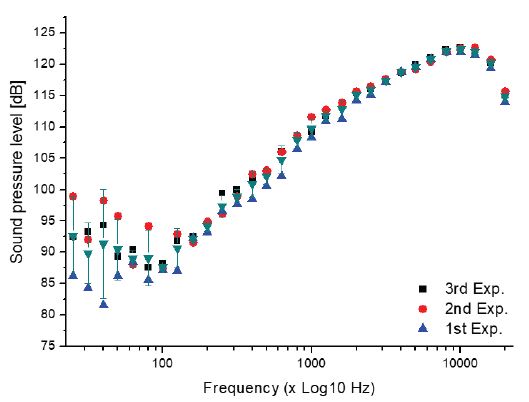
계산된 결과는 실험값과 비교하였으며, 각 데이터는 주파수 영역에 따라 도시하였다. Fig. 11은 측정된 데이터의 신뢰성 검증을 위해 세 번의 실험 결과 값을 도시하였으며, 200 Hz미만의 결과를 제외한 모든 영역에서는 오차범위 5% 이내로 데이터가 측정됨을 확인하였다. 이에 본 연구에서는 200 Hz이상의 주파수 영역에서의 측정된 데이터를 평균화하여 수치해석결과 검증에 사용하였다.
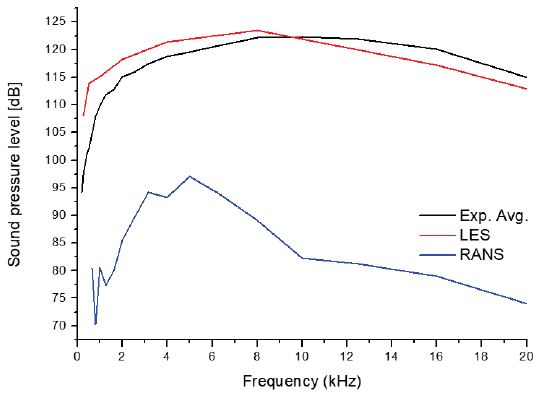
Fig. 12은 RANS와 LES에서 계산된 결과를 실험 평균값과 비교한 결과이다. LES값은 실험 평균값과 비교시 미비한 차이가 있으나, 서로 유사한 경향을 가지는 것에 비해 RANS 모델은 다른 경향을 띄는 것을 알 수 있다.
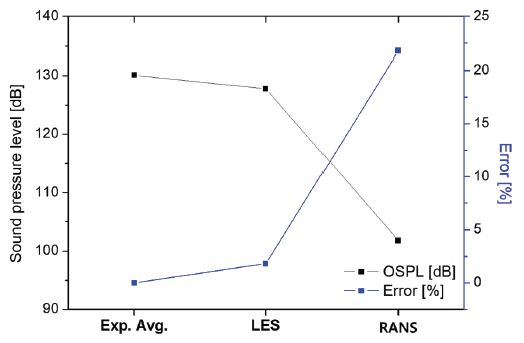
주파수영역에서의 소음도를 평균화하여 OSPL(overall sound pressure level)로 나타내었으며, 각 난류처리방법에 따른 결과와 실험값을 비교하여 Fig. 13에 도시하였다. 실험에서 얻어진 OSPL 값은 130.1 dB이며, LES 모델과 RANS 모델은 각각 127.75 dB, 101.81 dB로 계산되었다. 이에 따른 오차 또한 Fig. 12에 도시하였는데, LES 모델결과와 실험 평균값은 약 1.8%의 오차를 보였지만, RANS 모델결과는 약 21.8%의 큰 오차를 확인할 수 있다.
이러한 이유는 RANS 모델의 경우 난류처리에 있어서 앞서 기술한 것과 같이 모든 난류에 대해 시간평균기법을 사용하여 모델링하게 되고, LES 모델에 비해 난류 섭동을 자세하게 모사하지 못하기 때문이다. 유속과 압력분포 예측에 있어서는 유사한 경향을 모사하는 것을 확인하였지만, 난류 운동량과 점도에 있어서는 큰 차이를 보이는 것을 확인하였다. 이는 RANS 모델이 유동의 섭동과 eddy를 효율적으로 모사하지 못하는 부분이 많아 유동해석 및 소음해석 결과에 반영된 것으로 사료된다. 이러한 결과는 다른 장치를 기반으로 수행된 선행연구결과와 유사한데, Dunham 등(18)은 k-ϵ기반의 RANS 모델은 LES 모델에 비하여 상당한 계산시간 절감 효과를 보이지만, 진폭 및 주파수 영역에 대한 예측을 올바르게 하지 못한다는 결과를 발표하였다.
4. 결 론
본 연구에서는 가스계 소화시스템의 소음도 계산과 소화약제의 유동특성을 상용코드인 ANSYS FLUENT ver. 18.1을 이용하여 계산하였다. RANS 모델과 LES 모델을 이용하여 유동해석을 진행하였고, FW-H(Ffowcs Williams-Hawkings)음향상사식을 이용하여 소화노즐의 배기소음을 수치적으로 계산하였다. 시간평균기법을 사용하는 RANS 모델은 LES 모델과 비교하였을 때, 전체적인 유동특성은 유사하게 모사가 가능하나, 국소적인 부분과 난류 운동량 및 점도에서 많은 차이를 보였다. 따라서 고해상도의 주파수영역의 소음에너지 분석을 위해서는 LES 모델이 더 효과적임을 확인하였다.
Acknowledgments
본 연구는 국토교통기술사업화지원사업의 연구비 지원(18TBIP-C127226-02)에 의해 수행되었습니다.
References
-
Wang, Z., Wang, W., and Qingsheng Wang., 2016, “Optimization of Water Mist Droplet Size by Using CFD Modeling for Fire Suppressions,” Journal of Loss Prevention in the Process Industries, Vol. 44, pp. 626-632.
[https://doi.org/10.1016/j.jlp.2016.04.010]

-
Lee, J., 2018, “Numerical Analysis on the Rapid Fire Suppression Using a Water Mist Nozzle in a Fire Compartment With a Door Opening,” Nuclear Engineering and Technology, Vol. 51, No. 2, pp. 410-423.
[https://doi.org/10.1016/j.net.2018.10.026]

- NFPA, 2008, “Standard on Clean Agent Fire Extinguishing Systems,” NFPA 2001.
- NEMA, 2013, “National Fire Safety Code of Clean Agent Fire Extinguishing System,” NFSC 107A.
-
Saito, N., Saso, Y., Ogawa, Y., Otsu, Y., and Kikui, H., 1997, “Fire Extinguishing Effect of Mixed Agents of Halon 1301 and Inert Gases,” Fire Safety Science, Vol. 5, pp. 901-910.
[https://doi.org/10.3801/IAFSS.FSS.5-901]

-
Rosa, D., Maria, I., and Charles, D. L., 2007, “Effectiveness of Various Concentrations of an Inert Gas Mixture for Preventing and Suppressing Mining Equipment Cab Fires: Development of a Dual Cab Fire Inerting System,” Fire technology, Vol. 43, No. 1, pp. 29-44.
[https://doi.org/10.1007/s10694-006-0002-4]

- Green, K., Nelson, D., Pai, N., and Nickerson, M., 2011, “Hard Drive Performance Degradation Due to High Level Noise in Data Centers,” INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Vol. 2011, No. 6, pp. 1862-1867.
- Siemens, 2011, “Potential Problems With Computer Hard Disks When Fire Extinguishing Systems Are Released,” A White Paper issued by Siemens.
-
Nickerson, M. L., Green, K., and Pai, N., 2013, “Tonal Noise Sensitivity in Hard Drives,” The Journal of the Acoustical Society of America, Vol. 134, p. 4222.
[https://doi.org/10.1121/1.4831506]

-
Lighthill, M. J., 1952, “On Sound Generated Aerodynamically I. General Theory,” Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences Vol. 211, No. 1107, pp. 564-587.
[https://doi.org/10.1098/rspa.1952.0060]

-
Williams, J. F., and Hawkings, D. L., 1969, “Sound Generation by Turbulence and Surfaces in Arbitrary Motion,” Philosophical Transactions of the Royal Society A, Vol. 264, No. 1151, pp. 321-342.
[https://doi.org/10.1098/rsta.1969.0031]

- Ferziger, J. H., and Peric, M., 2012, “Computational methods for fluid dynamics,” Springer Science & Business Media.
-
Smagorinsky, J., 1963, “General Circulation Experiments With the Primitive Equations: I. The Basic Experiment,” Monthly weather review, Vol. 91, No. 3, pp. 99-164.
[https://doi.org/10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2]

-
Deardorff, J. W., 1970, “A Numerical Study of Three-Dimensional Turbulent Channel Flow at Large Reynolds Numbers,” Journal of Fluid Mechanics, Vol. 41, No. 2, pp. 453-480.
[https://doi.org/10.1017/S0022112070000691]

-
Bardina, J. E., Huang, P. G., and Coakley, T. J., 1997, “Turbulence Modeling Validation, Testing, and Development,” NASA Technical Memorandum 110446, p. 97N19942.
[https://doi.org/10.2514/6.1997-2121]

-
Ben-Nasr, O., Hadjadj, A., Chaudhuri, A., and Shadloo, M. S., 2017, “Assessment of Subgrid-Scale Modeling for Large-Eddy Simulation of a Spatially-Evolving Compressible Turbulent Boundary Layer,” Computers & Fluids, Vol. 151, pp. 144-158.
[https://doi.org/10.1016/j.compfluid.2016.07.004]

- ANSYS Help version 18.1, 2018, Ansys Inc.
-
Dunham, D., Spencer, A., McGuirk, J. J., and Dianat, M., 2008, “Comparison of URANS and LES CFD Methodologies for Air Swirl Fuel Injectors,” In ASME Turbo Expo 2008: Power for Land, Sea, and Air, Vol. 3, pp. 187-196.
[https://doi.org/10.1115/GT2008-50278]