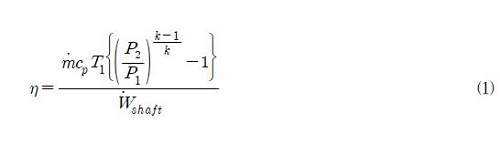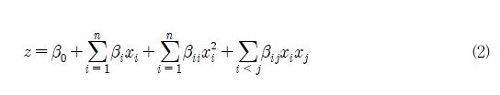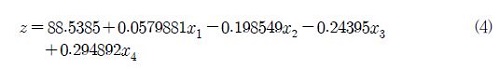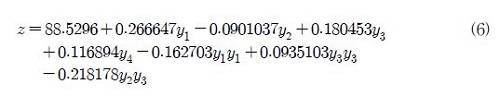A Numerical Study on Shape Design Optimization for an Impeller of a Centrifugal Compressor

2.1. 설계사양

본 연구에서 공기를 작동유체로 하는 원심압축기를 대상으로 최적화를 수행하였다. 대상 원심압축기는 입구부와 임펠러 및 폭까지 줄어드는 구간(pinched)을 포함하는 디퓨저를 가진다. Table 1은 유동조건 및 기존 압축기 임펠러 모델의 세부 설계 사양을 나타낸다.

Table 1.

Flow conditions and design specification

최적화는 압축기 입구부와 디퓨저의 설계값을 고정하고 임펠러의 자오면 형상과 블레이드 각도 θ를 대상으로 한다.

2.2. 수치해석

압축기 기존 모델의 경우, Concepts NREC사의 원심압축기 설계 프로그램인 COMPAL ver. 8.0.1.0 및 AxCent ver. 8.0.1.0 프로그램을 사용하여 설계되었다. 이를 ANSYS사의 유체기계 설계 프로그램인 BladeGen의 포맷으로 전환하여 사용하였다. 실험계획법을 위한 설계변경도 BladeGen ver. 14.5에서 진행하였다.

3D 수치해석을 위한 격자계 생성은 ANSYS사의 TurboGrid ver. 14.5를 이용하였다. 블레이드 표면 인근에는 O형 격자계, 그 외의 영역에는 H/J/C/L형 격자계를 사용하였으며, 모두 육면체 격자계로 구성하였다. 특히 허브, 쉬라우드 및 블레이드(blade) 벽면에서 y⁺가 1을 넘지 않도록 하였다. 격자계 테스트를 통해서 약 60만개의 격자를 사용하기로 결정하였다.

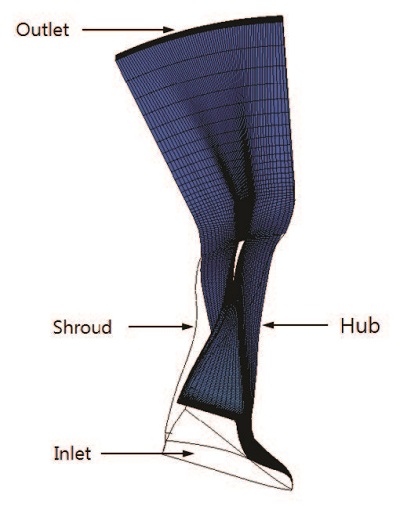
유동해석은 3차원 압축성 난류유동 해석 상용프로그램인 ANSYS사의 CFX ver. 14.5를 사용하였으며, 정상상태(steady state)로 가정하여 수행하였다. 난류유동을 계산하기 위해 k-ω SST 모델을 사용하였다. 경계조건으로는 압축기 입구에서 전압력(total pressure) 및 전온도(total temperature)를 고정하였으며, 출구에서는 질량 유량을 고정하였다. Fig. 1은 기존 임펠러 모형에 대해 수치해석을 위한 경계 및 격자계를 나타낸다.

Fig. 1

Computational boundaries and mesh of impeller

3.1. 목적함수 및 설계변수

최적화를 위해서는 목적함수와 설계변수의 선정이 중요하다. 본 연구에서는 원심압축기 효율향상을 위해 목적함수를 비총효율(specific overall efficiency) η로 선정하였고, 다음과 같이 정의된다(7).

여기서 c_p와 k는 각각 정압비열(constant pressure specific heat)과 비열비(specific heat ratio)를 나타내고, 본 연구에서는 그 값이 각각 1.0082 kJ/kg⋅K과 1.3981이다. P와 T는 각각 전압력과 전온도를 나타내며, 하첨자 1과 2는 각각 입구부와 출구부를 나타낸다. 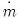과 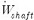는 각각 질량유량(mass flow rate)과 축일(shaft work)을 나타낸다.

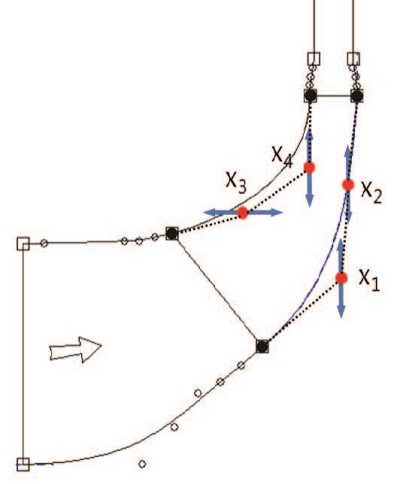
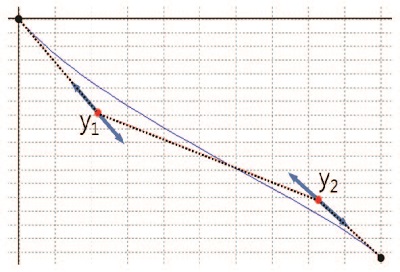
임펠러에는 압축기의 효율에 영향을 미치는 다양한 설계변수들이 있다. 하지만 압축기의 성능을 향상시키기 위한 적절한 형상변수를 선택하여야 한다. 그 중 대표적인 것이 임펠러 자오면(meridional plane) 상의 유로와 허브와 쉬라우드의 블레이드 각도 θ이며 본 연구에서도 이들을 형상변수로 선정하였다. 최적화에서는 설계변수의 개수에 의해 실험점의 개수가 정해지므로, 최적화 시간을 줄이기 위해 설계변수의 개수를 줄이는 것과 적절한 설계변수를 선정하는 것이 매우 중요하다. 허브와 쉬라우드에서 자오면 유로 형상과 블레이드 각도를 각각 변수화(parameterization)하기 위해서 각각 3차 베지어 곡선(Bezier curve)로 표현하였고, 이 때 경계점인 입구부와 출구부에서의 값을 고정할 경우 각각 2개의 통제점(control point)을 가진다. Fig. 2는 임펠러 허브 및 쉬라우드에서의 자오면 형상과 이를 표현하는 베지어 곡선의 통제점을 나타낸다. Fig. 3은 허브에서의 블레이드 각도 θ의 분포와 이를 표현하는 베지어 곡선의 통제점을 나타내며, 쉬라우드에서의 블레이드 각도 θ도 동일한 방식으로 3차 베지어 곡선으로 나타낸다.

Fig. 2

Control points at the meridional plane

Fig. 3

Control points of the blade angle θ at hub

3.2. 반응면기법

본 연구에서는 최적설계를 위해 근사모델기반 최적설계 기법 중 일반적으로 널리 사용되는 반응면기법을 이용하였다. 반응면기법은 설계변수의 집합에 대한 3차원 CFD를 수행한 후 나온 목적함수의 값으로 근사적으로 반응면 함수를 구하는 기법이다. 반응면 함수는 일반적으로 다음과 같은 2차 다항식(quadratic polynomial)으로 나타낼 수 있다.

여기서 z는 반응면 함수이며, x_i, x_j는 설계변수, β₀, β_i, β_ii, β_ij는 미정계수들이며 이 미정계수들은 3차원 CFD 결과로 부터 최소자승법(least square method)을 이용하여 구한다.

반응면기법에서 반응면 함수의 신뢰성을 확인하고 유의하지 않는 미정계수를 제거하여 반응면 함수의 신뢰도를 높일 수 있는데 이를 반응면 모형 축소(pooling)라고 한다. 반응면 모형 축소는 분산분석(ANOVA: analysis of variance)과 회귀분석(regression analysis)를 통해 이루어진다. 분산분석을 통해 반응면 함수의 각 항에 대해 유의한지를 파악하는데 유의성의 확인은 유의확률 p가 p<0.05인 조건으로 확인한다. 유의하지 않은 항들은 블록, 교호항, 제곱항 순으로 제거를 하면서 분산분석을 진행한다. 분산분석이 끝나면 회귀분석을 수행한다. 회귀분석은 반응면 함수가 실제값을 얼마나 잘 나타내는지 적합도를 측정하는 분석 방법이며, 반응면 함수의 R²_adj(수정결정계수)로 판단한다. 즉 R²_adj>0.9면 반응면 함수가 매우 정확하고, 0.9>R²_adj>0.7면 반응면 함수가 비교적 정확하다고 판단할 수 있다⁽⁸⁹⁾.

3.3. 실험계획법

주어진 조건에서 최소의 실험 회수로 정확도가 높은 반응면 함수를 구하기 위해 다양한 실험계획법(DOE: design of experiments)이 사용된다. 본 연구에서는 그 중 2차 회귀방정식을 도출할 수 있고, 직교블록(orthogonal block)을 만들기 용이하며, 3k 요인배치법이나 중심합성법(central composite design)에 비해 실험점(design point)의 수가 많지 않은 Box-Behnken 계획법(10)을 사용하였다. 범위를 무차원화하여 기존 형상값을 0으로 정하고, 설계 변수의 최대 변경 범위를 ±1로 설정한다. 임펠러 자오면 형상과 블레이드 각도 θ의 4개의 설계변수에 대해 각각 2개는 기준점에 고정시키고, 나머지 2개의 변수는 ±1점으로 형상을 변경한다. 이 때 기존 모델점(reference point)를 포함하여 각각 25개의 설계점이 나오며 각각의 경우에 대해 3D CFD를 수행한다.

4.1. 자오면 형상 최적설계

자오면 형상 최적화를 위해 BladeGen에서 허브 및 쉬라우드의 베지어 곡선 통제점의 위치를 변경하여 Box- Behnken 계획법에 따라 25개의 각기 다른 형상을 만들고, TurboGrid로 격자를 생성한 후 CFX를 통해 25개의 해석 결과를 얻었다. 이 해석 결과로 얻은 효율값에 대해 다음과 같은 반응면 함수를 구하였다.

이 반응면 함수의 회귀분석 결과는 R²_adj = 86.9%이다. 이 반응면 함수의 정확도 향상을 위해 반응면 모형 축소를 수행하였다. 분산분석을 통해 유의확률 p가 p<0.05인 항들을 블록, 교호항, 제곱항 순으로 제거를 하면서 분산분석을 진행하였다. 그 결과 다음과 같은 축소된 반응면 함수를 구하였다.

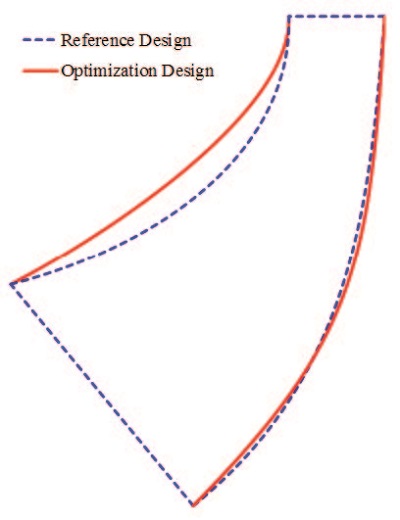
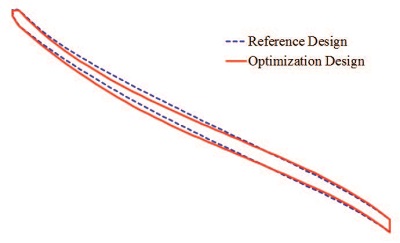
축소된 반응면 함수의 회귀분석 결과는 R²_adj = 88.3%로 축소되기 전 반응면 함수에 비해 신뢰도가 일부 향상되었음을 알 수 있다. 또한 R²_adj 값이 90%에 근접한 값으로 반응면 모델을 상당히 신뢰할 수 있는 것으로 판단된다. 도출된 반응면 함수로 목적함수가 설계변수에 대해 선형적으로 변함을 알 수 있다. 따라서 설계변수 x₁, x₂, x₃, x₄가 각각 1, -1, -1, 1일 때 반응면 함수가 최대값을 가지는 것을 알 수 있다. Fig. 4는 자오면 형상 최적 설계에 따른 형상 변화를 나타낸 그림이다.

Fig. 4

Comparison of geometry by meridional shape optimization

4.2. 블레이드 각도 최적설계

블레이드 각도 θ에 대해서도 자오면 형상 최적화와 동일한 방식으로 진행하였다. 그 결과 다음과 같은 반응면 함수를 구하였다.

이 반응면 함수의 회귀분석 결과는 R²_adj = 94.4%이다. 이 반응면 함수의 정확도를 향상을 위해 반응면 모형 축소를 수행하였다. 그 결과 다음과 같은 축소된 반응면 함수를 구하였다.

축소된 반응면 함수의 회귀분석 결과는 R²_adj = 95.5%로 축소되기 전 반응면 함수에 비해 신뢰도가 일부 향상되었음을 알 수 있다. 또한R²_adj 값이 90% 이상으로 반응면 모델을 매우 신뢰할 수 있는 것으로 판단된다. 반응면 함수의 최적점을 구해보면, 설계변수 y₁, y₂, y₃, y₄가 각각 0.9559, -1, 1, 1일 때, 최대값을 가지는 것을 알 수 있다. Fig. 5는 블레이드 각도 최적 설계에 대한 형상 변화를 나타낸다.

Fig. 5

Comparison of geometry by blade angle optimization

4.3. 설계점 성능 분석

형상 최적 설계를 통해 도출된 형상들을 설계점(design point)에서의 성능 비교를 진행하였다. 성능 비교를 위해 Table 2와 같이 형상을 정의하였다. 특히 design 4의 경우 별도의 형상 최적화를 수행하지 않고 자오면 형상과 블레이드 각도를 앞서 수행한 최적 설계를 동시에 반영한 설계이다. 즉 자오면 형상은 design 2에 적용된 자오면 형상의 최적 설계 결과를 적용하고, 블레이드 각도 θ는 design 3에 적용된 블레이드 각도의 최적 설계 결과를 적용하였다.

Table 2.

Definition and description of design

이 4가지 형상에 대해 설계점에서 성능해석을 수행한 결과를 Table 3에 나타내었다. 반응면기법에 의한 최적설계의 결과는 기존 모델(design 1)에 비해 자오면 형상 최적화에 의한 모델(design 2)과 블레이드 각도 형상 최적화에 의한 모델(design 3) 모두 각각 0.80% 및 0.81% 효율 상승을 보였다.

Table 3.

Comparison of efficiency and pressure ratio by response surface method and 3D CFD at design point

실제 3D 수치해석에 의한 효율 값의 상승은 각각 0.62%, 0.78%로 반응면기법에 의한 예측값보다 조금씩 낮아진 결과를 보여주었다. 특히 블레이드 각도 최적 설계의 경우 거의 정확한 성능 예측값을 나타내었는데 이는 회귀분석에 의한 수정결정계수 R2adj의 값이 95.5%로 R2adj 값이 100%에 근접할수록 반응면 함수의 정확도가 높아진다는 사실과 부합한다. 이와 관련하여 수정결정계수 R2adj의 값이 88.3%인 자오면 형상 최적화의 경우 반응면 함수의 예측 값과 3D CFD 결과 값이 다소 차이가 나는 것을 알 수 있다.

design 4의 경우 효율 상승은 0.91%로 자오면 형상 최적 설계에 의한 결과 0.62% 및 블레이드 형상 최적 설계에 의한 결과 0.78%보다 높은 값을 나타내었다. 이는 자오면 형상 최적화와 블레이드 각도 형상 최적화가 각기 다른 형태로 효율 향상에 영향을 주고 있음을 알 수 있다.

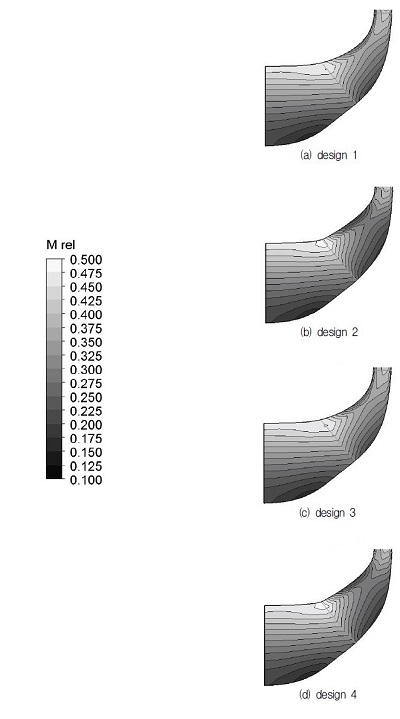
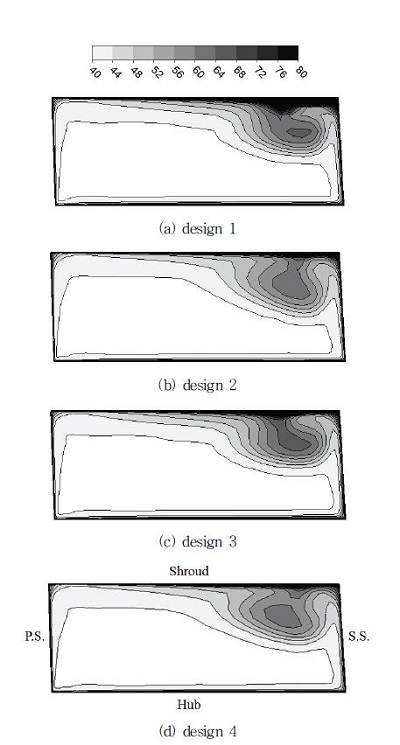
Fig. 6에서 자오면에서의 상대마하수 분포를 살펴보면 임펠러 유로(impeller passage)에서 최적 설계 후 스팬(span) 방향으로의 분포가 균일해졌음을 나타난다. 특히 자오면 형상 최적화가 적용된 design 2와 design 4에서 마하수 분포 균일도의 향상이 높음을 알 수 있다. Fig. 7은 날개 뒷전에 위치한 출구(outlet)에서의 엔트로피 분포를 나타낸다. 엔트로피 분포를 보면 형상 최적화가 적용될 경우 쉬라우드에 인접하여 나타나는 높은 엔트로피 영역이 얇아지고, 흡입면(suction side) 부근에서 국부적으로 나타나는 높은 엔트로피의 값이 낮아진다. 이 경우에도 자오면 형상 최적화가 적용된 design 2와 design 4에서 엔트로피가 많이 낮아진다.

Fig. 6

Contours of relative Mach number at meridional surface

Fig. 7

Contours of static entropy at trailing edge(unit: J/kgK)

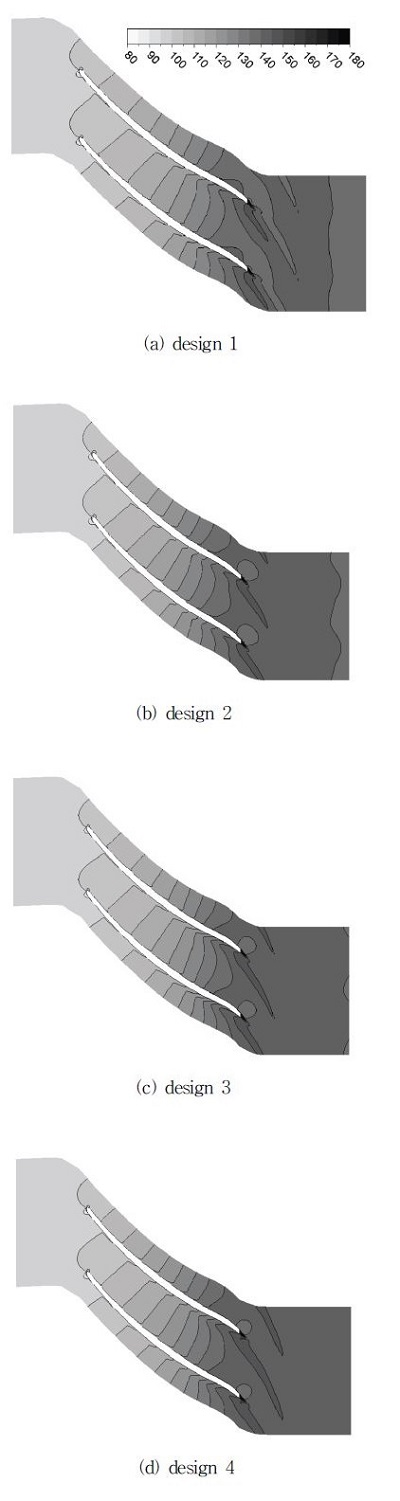
Fig. 8은 미드스팬(mid-span)에서 전압력의 분포를 나타낸다. 형상 설계 최적화가 적용될 경우 출구에서의 전압력이 높게 나온다. 특히 블레이드 각도 최적화가 적용된 design 3과 design 4의 경우 그 값이 높게 나타난다.

Fig. 8

Contours of total pressure at mid-span(unit: kPa)

4.4. 탈설계점 성능 분석

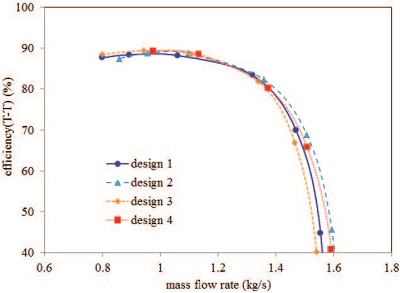
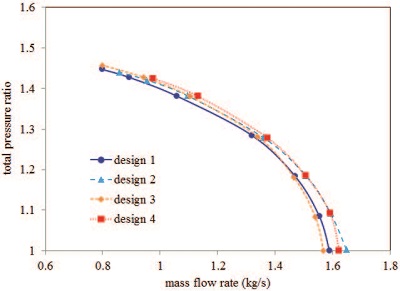
압축기의 형상 최적화는 설계점을 기준으로 수행하였다. 하지만 압축기는 항상 설계점에서만 작동하는 것이 아니며, 탈설계점에서의 성능 변화도 비교해 보아야한다. 설계점에서의 성능 향상 정도에 비해 운전영역 전반의 성능이 현격히 저하된다면 최적 설계의 의미가 없는 것이다. 따라서 탈설계점에서의 성능 분석을 수행하였다. 정격 회전수에 대해 스톨(stall)과 초크(choke) 사이의 범위에서 유량을 변화시키면서 효율 및 전압력비를 구하였다. Fig. 9와 Fig. 10은 각각 탈설계점에서의 효율과 전압력비를 나타낸다. 효율 그래프를 보면 design 3의 경우 설계점인 1kg/s 부근을 기준으로 저유량 영역에서 design 2와 design 4는 고유량 영역에서 기준 모델인 design 1에 비해 효율이 우수하게 나타난다. 전압력비의 경우에도 최적 설계된 모델이 기준 모델과 비교할 때 저유량 영역에서는 유사하게, 고유량 영역에서는 높거나 유사하게 나타난다. 탈설계점 영역의 효율 및 전압력비를 살펴보면 기존 모델과 유사 또는 일부 개선된 것으로 나타나 탈설계점에서의 성능에 문제가 없는 것으로 판단된다.

Fig. 9

Efficiency curves under off-design conditions

Fig. 10

Total pressure ratio curves under off-design conditions