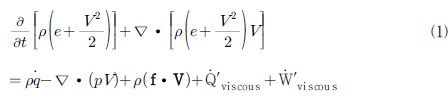A Study on the Numerical Analysis Methodology for Thermal and Flow Characteristics of High Pressure Turbine in Aircraft Gas Turbine Engine

2.1. 난류모델

k-ω based SST(shear stress transport) 난류모델과 RSM(Reynolds stress model) 난류모델은 RANS(Reynolds averaged Navier-Stokes) 방정식을 기반으로 만들어졌다. RANS 방정식에서는 그 변수 값을 찾기 위해서 레이놀즈 응력 텐서(Reynolds stress tensor)를 모델링하여야 하는데, 그 방법에 있어 SST 난류모델은 와점성모델(eddy viscosity model)에 속한다. 와점성모델은 유동에 등방성(isotropic) 가정을 적용한다. 그러나 대다수의 유동은 이방성(anisotropic)이기 때문에 와점성모델은 난류를 모사하는데 한계를 가진다. 바로 이런 와점성모델의 등방성 가정으로 인한 이방성 유동 모사의 어려움을 극복하기 위하여 RSM 난류모델을 사용할 수 있는데, 이 난류모델은 6개의 이송방정식 뿐만 아니라 소산 방정식까지 직접 풀게 된다.

RSM 난류 모델은 와점성 모델에 비하여 더 많은 방정식을 풀기 때문에 RANS 기반 난류모델 중에 가장 많은 계산 시간과 비용이 필요하다고 알려져 있다.(3)

본 연구에서는 SST 난류 모델과 RSM 난류 모델을 천음속 고압터빈인 C3X 베인에 적용하여 전산해석을 수행하였고, 난류모델이 베인 표면의 압력과 온도에 미치는 영향을 연구하였다.

2.2. 점성항

일반적으로 에너지 보존 방정식은 식 (1)과 같이 표현된다.(4)

여기서 ρ, e, V, , p , f 는 각각 밀도, 내부에너지, 속도, 단위질량당 열량, 압력, 체적력을 나타낸다. 특히 식 (1)에서 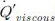와 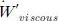을 점성항(viscous work term) 이라 하며, 유동에서 유체가 가지는 점성에 의해 발생하는 에너지를 의미한다. 유동의 속도가 작거나, 온도가 낮을 때, 일반적으로 점성항을 무시하고 계산을 수행하지만 터빈과 같이 유동속도가 매우 빠르고 온도가 높아 상대적으로 점성이 높은 유동에 대하여서는 점성항을 고려해야한다.(5)

본 연구에서는 점성항을 천음속 고압터빈인 C3X 베인에 적용하여 전산해석을 수행하였고, 점성항이 베인 표면의 압력과 온도에 미치는 영향을 연구하였다.

2.3. 천이모델

일반적으로 널리 사용되는 난류모델들은 벽법칙(the law of the wall)에 기반을 둔 벽함수(wall function)를 사용하고, 벽면 근처에서의 경계층 유동을 완전한 난류로 가정하여 계산하게 한다. 이런 벽함수 기법은 계산시간을 단축하고 공학적으로 관심대상이 되는 유체기계의 성능을 타당하게 계산할 수 있지만, 점성저층(viscous sublayer)을 계산하지 않기 때문에 층류에서 난류로의 천이현상과 열전달 현상 등을 완전히 모사하지 못하는 단점이 있다. 이러한 단점을 극복하기 위해 벽면 근처에 충분한 격자를 쌓고, 유동 천이현상을 고려한 천이모델(transition model)의 적용이 필요하다.

ANSYS CFX는 ω 방정식을 사용하는 난류모델에 대하여 γ 천이모델과 γ-Re_θ 천이모델을 지원하고 있다. 특히 γ 천이모델은 임계레이놀즈 수(Onset Reynolds number)를 이용하여 천이가 발생하는 지점을 지정해줄 수 있다.(6) γ-Re_θ 모델은 실험을 통해 얻어진 데이터를 기반으로 천이과정을 국부변수(local variable)로 모델링하는 천이 모델이다.(5)

본 연구에서는 천음속 고압터빈인 C3X 베인에 이들 천이모델들을 적용하여 전산해석을 수행하였고, 천이모델이 베인 표면의 압력과 온도에 미치는 영향을 완전난류(fully turbulent) 모델과 비교하여 연구하였다.

3.1. 검증모델 선정

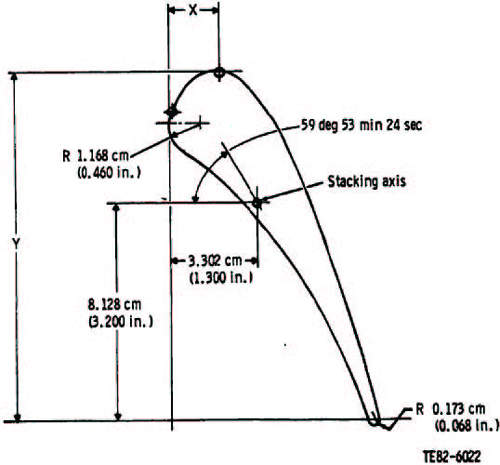
고압터빈의 3차원 전산해석기법 검증모델로써 NASA의 C3X 베인을 선정하였다. C3X 베인은 천음속을 고려한 터빈 노즐인데, Fig. 1 에 본 연구에서 사용한 C3X 베인의 좌표 정보를 나타내었다. Hylton 등(7)은 C3X 베인에 내부 냉각을 적용한 실험을 수행하기도 하였다.

3.2. 전산해석 영역 설정

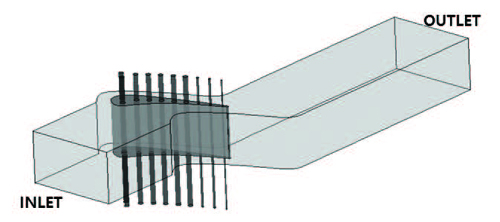
Fig. 2 는 고압터빈 노즐의 전산해석 영역을 나타낸다. 전산해석 영역은 총 12개인데, 주유로(main flow) 영역 1개과 내부 냉각 유로(coolant flow) 영역 10개 그리고 고체(solid) 영역 1개로 구성되었다. 10개의 냉각 유로를 독립적인 영역으로 구성하여 각각의 냉각 유로 영역과 고체 영역을 연결하였다.

3.3. 격자 생성

ANSYS ICEM CFD를 이용하여 격자를 Fig. 3 과 같이 생성하였다. 12개의 해석영역 별로 격자를 구성하였고, 총 138 만 개의 격자를 생성하였다. 해석 영역별 격자수는 Table 1 에 나타내었다.

Fig. 1

C3X vane coordinate system(7)

Fig. 2

Computational domain for the C3X vane

Fig. 3

C3X vane girds

Table 1

The number of grids for the C3X vane

주유동 영역의 격자수가 다른 영역의 격자수보다 많은 이유는 C3X 베인 표면의 경계층 유동을 정확히 예측하기 위하여 C3X 베인 표면 근처에 많은 격자를 쌓았기 때문이다.

C3X 베인 전체 표면에서 무차원 벽면거리(y+)가 1 이하가 되도록 격자를 생성하였다. 이것은 점성저층에 충분한 격자를 넣음으로써 난류모델이 벽함수를 사용하지 않고 난류 유동을 계산하도록 하기 위함이다.

인근 격자 간의 크기 변화를 격자 확장비(grid expansion ratio)로 나타낼 수 있는데, ANSYS CFX Solver에서 허용하는 최대 격자 확장비인 20이다.(8) 본 연구에 사용한 격자계의 최대 격자 확장비는 2.2로써 인근 격자간의 크기가 급격히 증가하는 영역이 없도록 격자를 구성하였다.

3.4. 경계 조건 설정

본 연구에서 사용한 입구와 출구의 경계 조건은 Hylton 등(7)이 실험에서 사용한 경계조건을 참고하여 사용되었다. 하지만 전산해석에 필요한 입구와 출구의 경계조건이 실험보고서에 명확하게 제시되어 있지 않았기 때문에 실험보고서에서 주어진 정보를 기반으로 입출구 조건을 찾아 전산해석을 수행하였다.

주유동 영역의 입구에는 전압력과 전온도, 그리고 난류 강도를 설정하였고, 출구에는 정압력을 설정하였다. 실험에서는 출구의 경계조건으로써 정압력 대신 마하수를 제시하였기 때문에 제시된 출구 마하수인 0.9가 나오도록 출구압을 조절하여 출구 경계조건을 찾았다. 이 때 도출된 출구압은 131.8kPa이다. 주유동에 적용된 경계 조건은 Table 2 에 나타내었다.

내부 냉각 영역의 경계조건은 10개의 냉각 홀 마다 각각 다른 온도와 유량을 설정하였고, 적용된 냉각 홀 별 경계조건은 Table 3 에 나타내었다.

작동유체로 공기를 사용하였는데, 고압 터빈은 아주 높은 온도에서 운용되기 때문에 상온의 공기 물성치를 사용할 수 없다. 따라서 고압터빈의 전산해석에서는 온도에 따른 물성치 변화를 반영하여 보정해야하는데 본 연구에서는 ANSYS CFX에서 기본으로 제공하는 이상기체의 비열과 열전도도 그리고 동점성을 온도의 함수로 보정하여 사용하였다.

C3X 베인의 전산해석을 위한 난류 모델로써 k-ω 기반의 SST 난류모델과 RSM 난류모델을 선정하였다. 또한 천이모델의 영향성을 비교하기 위하여 전체 유동을 난류로 가정하는 Fully Turbulent 모델과 천이 모델인 γ 모델과 γ-Reθ 모델을 적용하였다. 특히 γ 모델은 임계레이놀즈 수를 설정하여 천이가 발생할 지점을 지정할 수 있는데, 본 연구에서는 임계레이놀즈 수를 150으로 설정하였다.

천이모델은 SST 난류 모델과의 조합으로 사용되었고, RSM 난류모델에는 천이모델을 적용하지 않았다.

C3X 베인의 소재는 Hylton 등(7)이 실험에서 사용한 ASTM 310 Stainless Steel을 사용하였고, Table 4 에 베인 소재의 상세한 물성치를 나타내었다.

Table 2

Boundary conditions of the main flow

Table 3

Boundary conditions of the coolant flow

Table 4

Material property of ASTM 310 stainless steel

4.1. 난류모델의 영향성

천음속 노즐에 대해 SST 난류 모델과 RSM 난류모델을 적용하여 그 영향성을 비교하였다.

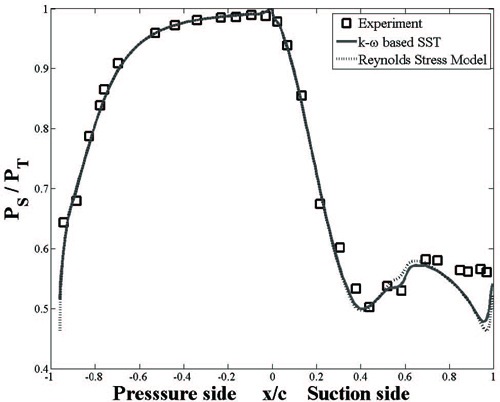
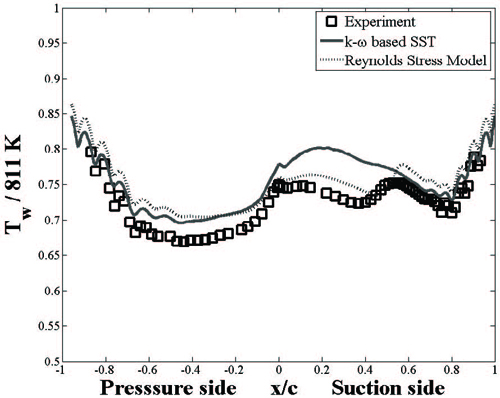
Fig. 4 은 난류모델 별로 베인 표면 압력의 분포를 나타낸 그래프이다. 두 개의 난류모델 모두 흡입면 뒷전 부근에서 실험 결과와 약 10% 정도 차이를 보이는데, 이것은 유동의 비정상성이 강하기 때문에 나타는 현상이다.

Fig. 4

Effect of turbulence model on surface pressure of vane

Fig. 5 는 난류모델 별로 표면온도의 분포를 나타낸 그래프이다. 압력면 후방(-1 < x / c < - 0.3)과 흡입면 후방(0.55 < x / c < 1)에서 SST 난류모델의 결과는 실험결과와 차이가 최대 3% 이내로 RSM 난류모델 보다 잘 일치하였다. 하지만 압력면 앞전 근처(-0.3 < x / c < 0.55)에서는 RSM 난류모델의 결과가 SST 난류모델의 결과보다 실험결과와 유사한 분포를 가지면서 더 유사하게 예측되었다. 이 때 RSM 난류모델과 실험 결과의 차이는 최대 3% 이내이다.

Fig. 5

Effect of turbulence model on surface temperature of vane

RSM 난류모델은 SST 난류모델과 달리 유동을 등방성으로 가정하지 않기 때문에 유동을 모사하기 위해 모델링 된 이송방정식이 SST 난류모델보다 더 많다.

Table 5 는 SST 난류모델과 RSM 난류모델을 적용하였을때의 계산 시간을 나타낸다. RSM 난류모델을 적용한 경우는 계산할 이송방정식이 SST 난류모델보다 많기 때문에 SST 난류모델보다 약 2배의 시간이 더 소요된다.

베인의 표면 온도를 실험결과와 유사하게 계산할 수 있는 난류모델은 베인 영역에 따라 다르다. 하지만 RSM 난류모델은 SST 난류모델보다 약 2배 정도 많은 계산 시간이 소요된다. 따라서 RSM 난류모델은 냉각 요소가 적용되어 형상이 복잡한 터빈 노즐이나 로터의 전산해석용 난류모델로는 적합하지 않다.

4.2. 점성항의 영향성

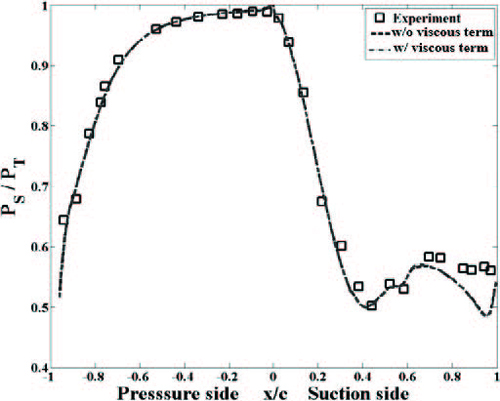
Fig. 6 은 점성항의 적용 유무에 따른 표면 압력 분포를 나타내는데, 점성항을 켜고 끔에 따른 결과 차이가 거의 없다. 즉, 베인 표면 전체 영역에서 점성항의 유무가 표면 압력 에 영향을 주지 않는 것을 알 수 있다. 흡입면 뒷전부근에서 전산해석 결과가 실험 결과와 최대 10% 정도로 확인되었는데, 이는 Fig. 4 에서도 확인하였듯이 비정상성이 강한 영역이기 때문에 나타난 현상이다.

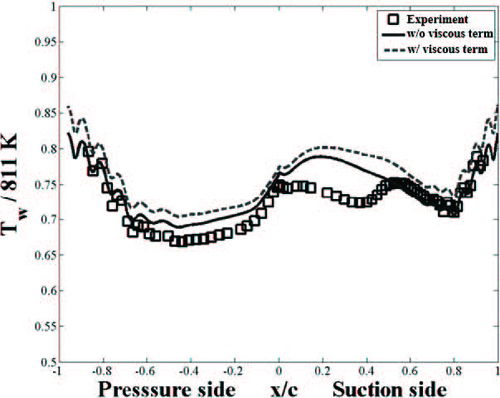
Fig. 7 은 점성항의 적용 유무에 따른 표면 온도 분포를 나타내는데 점성항을 고려하여 계산하면 베인 표면 온도가 점성항을 적용하지 않은 결과에 비해 전체적으로 약 2∼4% 정도 높은 것을 알 수 있다. 이 때 점성항이 표면 온도 분포의 경향은 유지면서 온도 값만 상승시키는 것도 확인할 수 있다.

Table 5

Comparison of computing time in SST and RSM

Fig. 6

Effect of viscous work term on surface pressure of vane

Fig. 7

Effect of viscous work term on surface temperature of vane

Fig. 8

Effect of transition model on surface pressure of vane

Fig. 9

Effect of transition model on surface temperature of vane

4.3. 천이모델의 영향성

천이모델 영향성 연구를 위해 SST 난류모델에서 지원하는 γ 천이모델, γ-Re_θ 천이모델을 선정하고 두 천이모델들과 유동 전체를 난류로 계산하는 Fully turbulent 모델의 비교를 통하여 천이모델이 고압터빈 노즐에 미치는 영향성을 연구하였다. 이때 4.2절에서 언급했던 점성항을 적용하여 전산해석을 진행하였다.

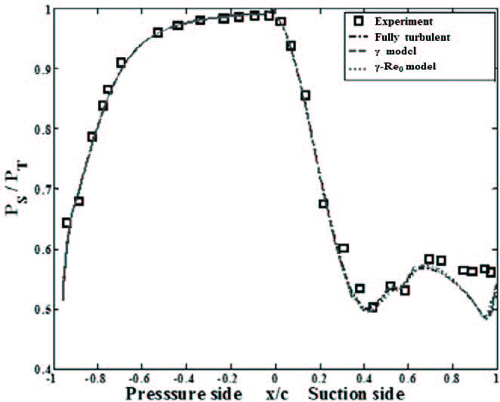
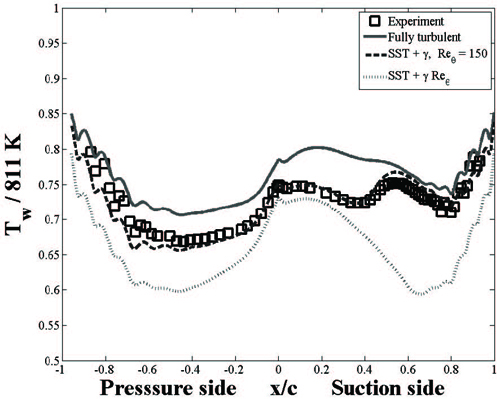
베인의 표면 압력에는 천이 모델이 영향을 주지 않는다는 것을 Fig. 8 을 통해 알 수 있다. 표면 압력에 대한 천이모델의 영향성은 무시할 수 있지만, 표면 온도에 대한 영향성은 그렇지 않은데, Fig. 9 를 보면 베인의 표면 온도가 천이 모델의 종류에 따라 크게 차이가 나는 것을 알 수 있다.

γ 천이모델은 압력면(-1 < x / c < 0)에서 실험 결과보다 표면 온도를 평균 2% 가량 낮게 예측하였고, 흡입면(0 < x / c < 1)에서는 평균 1% 정도 높게 예측하였다. 특히 유동의 천이로 인해 온도를 예측하기 어려운 영역인 흡입면의 x/c가 0.2∼0.4 부근에서 표면 온도를 실험 결과와 유사하게 계산하였다. 또한 표면 온도의 경향을 전체 영역에서 다른 천이모델보다 실험 결과와 가장 유사하게 예측하였다.

Fully turbulent 모델의 결과는 Fig. 7 에서 점성항을 고려한 결과와 같다. 베인 흡입면 전방 영역에서 실험 결과의 경향과 다르게 계산하였지만, 압력면과 흡입면 후방 영역에서는 표면 온도 경향을 잘 예측하였다. 반면 γ-Re_θ 천이모델은 x / c = 0.65에서의 표면 온도를 최대 23% 낮게 계산했고, 경향도 다르게 예측했다. 이 천이모델은 실험으로부터 얻어진 데이터를 기반으로 천이를 예측하게 되는데, 고온, 고압, 고속의 환경에서 운용되는 터빈의 표면 온도 예측에는 적합하지 않은 것으로 판단된다.