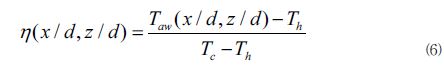A Study on the Film-cooling Characteristics of Gas Turbine Blade with Various Area Ratios and Ejection Angles of the Double Jet Holes

1. 서 론

가스터빈의 열효율 및 출력 향상을 위해 꾸준히 터빈 입구온도를 상승시켜온 결과, 최근에는 1500°C 이상 고온의 터빈 입구온도 조건 하 설계가 이루어지게 되었다. 이에 따른 블레이드의 수명 및 성능저하를 막기 위한 다양한 냉각기법들이 연구되어왔으며, 이 가운데 막냉각 기법이 널리 사용되고 있다. 막냉각 기법에 있어서 냉각유체의 과다 공급은 가스터빈의 효율을 낮추는 작용을 하기 때문에, 높은 효율을 갖는 막냉각 기법을 통하여 가스터빈의 열 손실을 최소화 하는 노력이 필요하다.

Goldstein(1) 연구그룹에 의해 처음 막냉각 방식이 제시된 이후, 막냉각 홀 형상 변화에 따른 냉각성능에 관한 고찰이 다각적으로 이루어지기 시작하였다. Goldstein과 Eckert(2)는 홴 형상을 지닌 막냉각 홀의 냉각성능과 냉각범위가 원형 형상 막냉각 홀에 비해 향상되었음을 확인하였다. 이는 분사홀 내부로부터 냉각유체가 갖기 시작한 운동량 감소가 냉각성능 향상의 원인이 된다고 설명하였다. 이후 지속적으로 관련 연구가 활발하게 진행되었다(3-6).

Andrepulos와 Rodi(7)는 서로 반대방향으로 회전하는 한쌍의 소용돌이인 신장와류(kidney vortex)에 의해 막냉각 홀 하류 유동이 지배됨을 확인하였으며, 이에대한 생성 원리를 고찰하였다. 냉각홀에서 분사된 냉각유체는 소용돌이의 회전 방향에 의하여 냉각표면으로부터 이격되며 고온가스가 냉각유체 아래로 유입되 도록 유도하는데, 이로써 막냉각 효율이 급격히 떨어지게 된다. 따라서 앞서 소개한 홴 형상 냉각 홀이 Goldstein과 Eckert(2)에 의해 제시되었으며, 냉각유체의 운동량 감소를 통해 신장와류의 간섭을 최소화 할 수 있음이 확인되었다.

하지만 홴 형상 막냉각 홀은 실제 가스터빈 블레이드 제품에 적용하기에 다소 복잡하고 생산비용이 증가하는 단점을 지니고 있다. 따라서 엇갈린 방향을 지닌 두 냉각 홀이 배치된 형태의 이중분사(double-jet) 막냉각 홀이 제시되었다(8). 이중분사 막냉각 홀이 형성하는 반 신장와류는 냉각유체 유로 하부로의 고온가스 유입을 차단하며 냉각유체 분포가 넓게 형성되도록 유도한다. Kusterer등(9-11)은 수치해석을 통하여 이중분사 막냉각 홀의 성능 및 반 신장와류를 포함한 유동특성을 고찰하였다. 또한 Lee 등(12)은 이중분사 냉각홀의 홀 간 거리와 측면각 변화에 따른 막냉각 효율 변화를 수치적으로 해석하였으며 이를 RBNN(Radial Basis Neural Network) 모델을 사용하여 최적화 하였다. Gräf와 Kleiser(13)는 비정렬 격자계를 이용한 수치해석 결과와 직교격자계를 이용한 수치해석 결과가 큰 차이가 없다는 결과를 제시하였고, 수치해석 결과와 실험결과가 잘 일치함을 확인하였다.

본 연구에서는 이중분사 막냉각 홀의 분사각 변화와 상류 홀과 하류 홀 면적비 변화에 따른 이중분사 막냉각 홀 주변 유동특성 및 이에 따른 열전달 특성을 고찰하였다.

2. 해석모델 및 경계조건

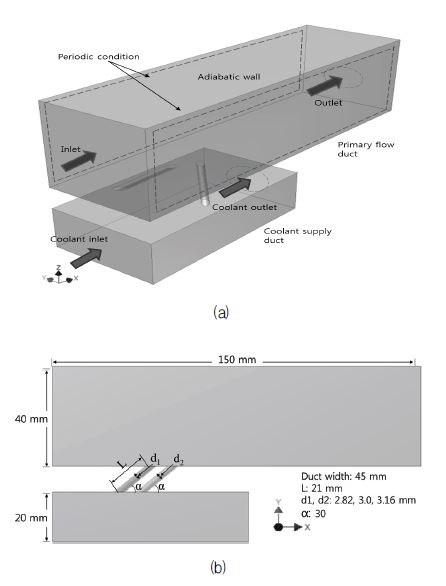
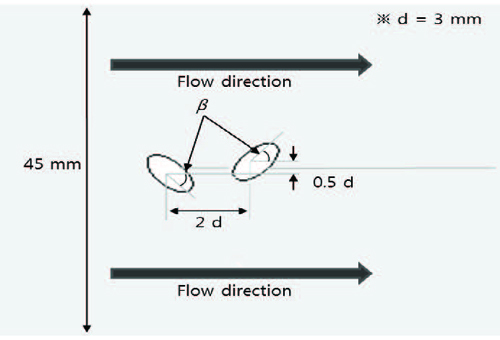
본 연구에서는 정상상태 압축성 RANS(Reynolds-Averaged Navier Stokes) 방정식을 사용하여 이중분사 냉각홀의 형상변수들이 막냉각 특성에 미치는 영향을 수치해석적으로 고찰하였다. 이를 위해 생성된 유동영역은 Fig. 1에 도시하였고, 경계조건을 Table 1에 표시하였다. 유체영역은 냉각유체 공급유로, 막냉각 홀, 고온가스가 흐르는 주유로로 구성하였으며 작동유체는 공기를 사용하였다. 한쌍의 이중분사 막냉각 홀에 의한 열 유동 패턴을 확인하기 위하여 반복(periodicity) 경계조건은 홀 직경 기준 15d값을 갖는 거리를 두어 설정하였다. 냉각홀 형상 변수에 대한 정의는 Fig. 2에 나타내었으며, 한 쌍을 이루고 있는 홀의 직경 변화에 따른 면적비(A₁/A₂)와 측면 분사각(β)을 변수로 선정하였다. 변수 제원들의 변화에 따른 유동특성 및 냉각특성을 파악하기 위한 각 Case의 정의를 Table 2에 명시하였다.

Fig. 1

Schematic of the modeled hole geometry

Table 1

Boundary conditions for the numerical model

Fig. 2

Schematic of the film-cooling hole on the surface of the primary flow duct.

Table 2

Design specifications for the Cases.

3. 수치해석

냉각홀의 측면 분사각과 두 냉각홀 직경비 변화에 따른 유동특성 및 냉각특성을 파악하기 위하여 연속방정식과 운동량 방정식, 에너지방정식을 지배방정식으로 사용하였다.

여기에서 U는 속도, ρ는 밀도, k는 열전도율, τ는 전단력, f 는 단위질량 당 체적력이다.

난류모델은 열전달 예측에 효과적이며 높은 난류강도를 갖는 경계층 내부 열전달 예측에 효과적인 것으로 알려진 SST(Shear Stress Transport) 모델을 사용하였다(14).

이중분사 냉각홀의 형상변수 변화에 따른 냉각특성 및 유동특성을 해석하기 위하여 사면체와 삼각주 형상으로 구성된 비정렬 격자계를 Fig. 3과 같이 구성하였으며 정확한 경계층 모사를 위하여 inflation 조건을 적용한 10겹의 격자층을 구성하였다. 격자의존도 테스트는 Case 2의 냉각홀 면적비 1.0인 모델에 대하여 수행하였으며, 격자수 67만개에서 398만개 사이 격자수를 시험하여 최적 격자수 140만개 격자수를 갖는 격자계를 각 Case에 적용하였다.

4. 결과 및 고찰

수치해석 결과의 타당성을 검증하기 위해 동일한 형상조건에 의한 수치해석 결과와 Kusterer등(11)에 의한 수치해석 결과를 비교하였으며 이를 Fig. 4에 나타내었다. 그림에서 볼 수 있듯, 참고문헌의 분사비 M=1.5와 M=2.0인 결과가 갖는 수치해석 결과와 본 연구의 분사비 M=1.5, M=2.0인 조건 하에서의 수치해석 결과가 서로 유사함을 확인할 수 있다.

Fig. 3

Grid systems of the flow domain.

Fig. 4

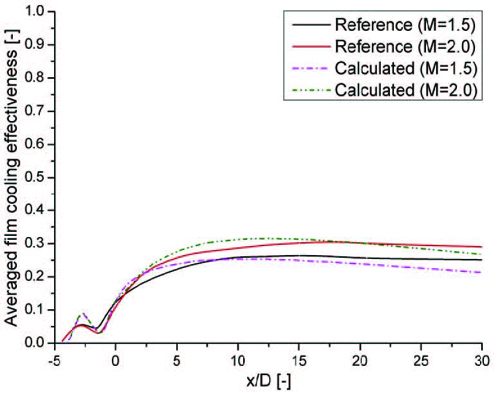
Lateral averaged film cooling effectiveness comparison for the cases at M=1.5 and M=2.0 demonstrates good agreement between reference results and computations

4.2. 2차 유동

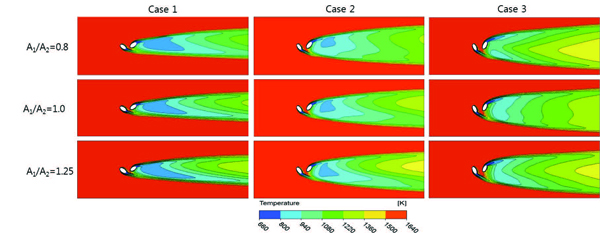
상류 홀과 하류 홀 사이의 면적비와 측면 분사각 변화에 따른 Y-Z 평면상의 온도분포와 속도벡터 분포를 Fig. 5에 도시하였다. 두 변수조건에 따른 2차 유동 패턴 및 냉각유체 분포를 통하여 다음 두 가지 사실을 확인할 수 있다. 첫째로 측면 분사각 증가에 따라서 유로 표면에 냉매가 접촉하는 면적이 증가하는 경향이 있음을 확인할 수 있다. 이는 같은 분사비 조건하에서 측면 분사각 증가에 따라 냉각홀 하류 냉각유체 유속벡터 크기가 X축 방향보다 Y축 방향으로 유도되는 것에 기인한다. 두 번째로, 벡터분포의 경우, 막냉각 홀 하류지점에서 발생하는 반 신장와류의 강도 및 크기가 막냉각 홀 면적 비율증가에 따라서 상류 홀 하류영역으로 편중되는 경향을 나타내었다. 또한, 막냉각 홀 면적비에 따라서 신장와류 쌍의 불균형이 조절되었음을 알 수 있다.

Fig. 5

Temperature contours and velocity vectors on the Y-Z plane at x/D=10(Case 1: β=30°, Case 2: β=45°, Case 3: β=60°) with various cooling hole area ratios(A1/A2=0.8, 1.0, 1.25).

Table 3

Calculated local blowing ratios for holes of the double-jet film cooling configurations.

4.3. 표면 온도분포

상류 및 하류의 막냉각 홀 사이의 면적비와 측면 분사각 변화에 따른 단열 표면상의 온도분포를 Fig. 6에 도시하였다. 두 변수조건에 따른 단열벽 온도분포를 통하여 막냉각 홀 면적비 변화가 온도분포에 영향을 미치고 있음을 확인할 수 있다. 측면 분사각이 30°, 45°인 Case 1과 Case 2의 경우, 상류 홀 하류로 표면냉각이 집중되는 경향을 보였으며, 상류 홀 면적 증가에 따라서 이러한 현상이 더욱 두드러지는 경향을 보였다. 이는 상류 홀에서 분사된 냉각유동이 하류 홀에서 분사된 냉각유동보다 큰 강도로 반 신장와류를 생성하는 데에 기인하며, 따라서 막냉각 홀 직경변화를 통해 반 신장와류의 강도 및 온도분포를 제어할 수 있게 된다. Case 3의 경우에는 막냉각 홀 면적비가 1.0인 형상에서 가장 고른 온도분포를 나타내었으며 냉각유체 측면 확산면적이 증가하였다. 막냉각 홀 면적비 증감이 있는 경우 냉각유체 분포영역 외연으로 냉각지점이 유도되는 경향을 보이는데, 이는 이중분사 중심지점에 고온가스가 유입되는 현상에 기인하는 것으로 해석할 수 있다.

Fig. 6

Temperature contours on the surface of adiabatic wall(Case 1: β=30°, Case 2: β=45°, Case 3: β=60°) with various cooling hole area ratios(A1/A2=0.8, 1.0, 1.25).

4.4. 냉각효율

막냉각 성능을 평가하기 위한 일반적인 막냉각 효율 η은 다음과 같이 정의할 수 있다.

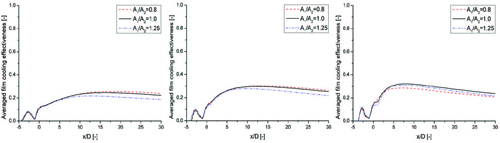
Fig. 7을 통해 A₁/A₂=0.8, 1.0, 1.25인 경우 측면방향 막냉각 효율 값이 각각 최대 0.048, 0.145, 0.287의 변동을 보이며, 상류홀 하류지점에서 최대값을 나타냄을 확인할 수 있다. 이를 통해 상/하류홀 면적비 조건을 변경함으로써 상류홀 하류 표면으로 집중되는 냉각효과를 측면방향으로 균일화 할 수 있는 것을 확인할 수 있는데, 이는 두 막냉각 홀에서 국소적으로 갖는 유량이 홀 면적비 변화를 통하여 조정되었기 때문이다.(Table 4 참조.) 측면방향 냉각효율 균일화와 함께 길이방향으로 갖는 평균 막냉각 효율 또한 변화하였음을 확인할 수 있는데, 이를 확인하기 위해 상류 홀과 하류 홀 사이 면적비에 따른 길이방향 평균 막냉각 효율을 Fig. 8에 도시하였다. Case 1과 Case 2 에서는 x/D=5 인 지점 이후로 면적비 변화에 따른 평균 막냉각 효율 차이가 두드러지는 경향을 나타내었다. Case 1에서는 x/D=15인 지점을 기준으로 분사구 면적 변화에 따라 A₁/A₂=1.25인 경우 막냉각 효율의 약 11.8 %가 감소하였고,A₁/A₂=0.8인 경우는 막냉각 효율의 약 3.2 %가 증대되었음을 확인하였다. Case 2에서도 A₁/A₂=1.25인 경우 막냉각 효율의 약 8.6 %가 감소하였고, A₁/A₂=0.8인 경우는 막냉각 효율의 약 1.9 %가 증대되었음을 확인하였다. 이는 앞서 기술한 바와 같이 막냉각 홀의 상/하류 위치에 따른 반신장와류의 피치 불균형을 상쇄하여주는 유량조절을 막냉각 홀 면적 변화를 통하여 유도할 수 있었기 때문이다. 하지만 분사방향에 의해 반신장와류가 큰 와도를 갖게 되는 Case 3 에서는 분사구 면적에 변화를 준 두 경우 모두 막냉각 효율이 감소하는 경향을 나타내었다. A₁/A₂=1.25인 경우 막냉각 효율의 약 4.6 %가 감소하였고, A₁/A₂=0.8인 경우는 막냉각 효율의 약 11.8 %가 감소하였음을 확인하였다.

Fig. 7

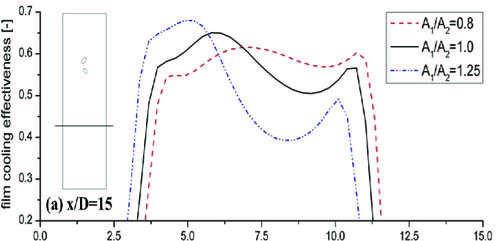
Film-cooling effectiveness(ηl) (Case 2: β=45°) with various cooling hole area ratios(A1/A2=0.8, 1.0, 1.25) on the line x/D=15.

Table 4

Calculated local flow rate(m3/s) for holes of the double-jet film cooling configurations.

Fig. 8

Laterally averaged film-cooling effectiveness(ηl) (Case 1: β=30°, Case 2: β=45°, Case 3: β=60°) with various cooling hole area ratios(A1/A2=0.8, 1.0, 1.25).

5. 결 론

본 연구에서는 가스터빈 블레이드 냉각에 사용되는 이중분사 막냉각 홀 측면 분사각과 냉각홀의 면적 비율에 따른 유동장, 온도분포 및 막냉각 효율에 대한 연구를 수행하였다. 측면 방향 두 분사각이 작을수록 이중분사 막냉각 홀 내부 냉각유체가 Y축에 가까운 방향으로 분사되어 냉각유체의 측면 확산면적이 감소하는 반면, 분사각이 커질수록 측면 확산면적이 넓어짐을 확인할 수 있었다. 이러한 조건 하에서 막냉각 홀 면적비가 0.8, 1.0, 1.25일 때의 열유동장을 수치적으로 해석하였다. 상류 홀 면적을 감소시킨 Case 1과 2 에서는 양측 분사구 유량을 조절하는 효과와 함께 하류영역 막냉각 효율이 향상되는 것을 확인할 수 있었다. 반면에 측면 분사각이 큰 Case 3에서는 이중분사 중심부에 고온가스가 유입되어 막냉각 효율이 감소하였다. 이로써 상류 홀 직경을 축소하여 얻어진 최적 면적비를 통해 낮은 분사각 조건 하에서 막냉각 효율 향상을 기대할 수 있으며, 반면 일정 분사각 이상에서는 그 효과를 잃고 오히려 부정적 요소가 됨을 확인하였다.

References

• R. J. Goldstein, A. Haji-Sheikh, “Prediction of film cooling effectiveness”, Proceedings of Japanese Society of Mechanical Engineers, Semi-International Symposium, (1967), 2, p213.
• R. J. Goldstein, E. R. G. Eckert, “Effects of hole geometry and density on three-dimensional film cooling”, Int. J. Heat Mass Transfer, (1974), 17, p595-607. [https://doi.org/10.1016/0017-9310(74)90007-6]
• Y. Makki, G. Jakubowski, “An experimental study of film cooling from diffused trapezodial shaped holes, AIAA, (1986), 86, p1326.
• B. Sen, D. L. Schmidt, D. G. Bogard, “Film cooling with compound angle holes: heat transfer”, J. Turbomach, (1996), 118, p800. [https://doi.org/10.1115/1.2840937]
• C. Bell, H. Hamagawa, P. Ligrani, “Film cooling from shaped holes”, J. Heat Transfer, (2000), 122(2), p224-232. [https://doi.org/10.1115/1.521484]
• M. Gritsch, W. Colban, H. Schär, K. Döbbeling, “Effect of hole geometry on the thermal performance of fan-shaped holes”, J. Turbomach, (2005), 127, p718-725.
• J. Andreopoulos, W. Rodi, “Experimental investigation of jets in a cross flow”, J. Fluid Mech, (2007), 138, p93-127.
• K. Kusterer, D. Bohn, T. Sugimoto, R. Tanaka, “Double-jet ejection of cooling air for improved film cooling”, J. Turbomach, (2007), 129, p809-815. [https://doi.org/10.1115/1.2720508]
• K. Kusterer, A. Elyas, D. Bohn, “A parametric study on the influence of the lateral ejection angle of double-jet holes on the film cooling effectiveness for high blowing ratio”, Proceedings of ASME Turbo Expo 2009: Power for land, sea and air GT2009 June 8-12, 2009, Orlando, Florida, USA. GT2009-59321, (2009). [https://doi.org/10.1115/GT2009-59321]
• K. Kusterer, D. Bohn, T. Sugimoto, R. Tanaka, “Influence of blowing ratio on the double-jet ejection of cooling air”, Proceedins of ASME Turbo Expo 2007: Power for land, sea and air GT2009 May 14-17, 2007, Montreal, Canada, GT2007-27301, (2007). [https://doi.org/10.1115/GT2007-27301]
• K. Kusterer, D. Bohn, T. Sugimoto, R. Tanaka, M. Kazari, “Fiml cooling effectiveness comparison between shaped- and double jet film cooling holes in a row arrangement”, Proceedins of ASME Turbo Expo 2010: Power for land, sea and air GT2010 June 14-18, 2010, Glasgow, UK, GT2010-22604, (2010).
• K. D. Lee, D. W. Choi, K. Y. Kim, “Optimization of ejection angles of double-jet film-cooling holes using RBNN model”, Int. J. Therm. Sci, (2013), 73, p69-78. [https://doi.org/10.1016/j.ijthermalsci.2013.05.015]
• L. Gräf, L. Kleiser, “Large eddy simulation of double-row compound-angle film cooling: setup and validation”, Computers and Fluids, (2010), 43, p58-67.
• F. R. Menter, M. Kuntz, R. Langtry, “Ten years of industrial experience with the SST turbulence model”, Proceeding of the 4th International Symposium on Turbulence, (2003), p632-652.