스캘럽형상이 구심터빈 효율에 미치는 영향

1. 서 론

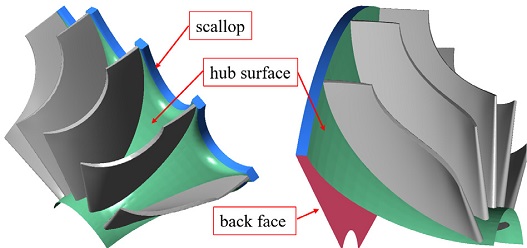
스캘럽(scallop)은 Fig. 1에서 보여주는 것과 같이 구심터빈 팁부분의 일부를 제거하는 것을 의미하는데, 이러한 가공으로 얻을 수 있는 이점으로 중량감소와 극관성모멘트의 감소를 얻을 수 있다. 특히 터보차져와 같이 엔진의 출력에 따라 수시로 회전속도가 변경되어야하는 경우에는 터빈의 응답속도가 엔진의 성능에 영향을 미치게 된다. 따라서 구심터빈의 극관성모멘트 감소는 엔진 성능에 상당한 장점으로 작용한다. 하지만 스캘럽으로 구심터빈 허브영역의 일부제거는 터빈에 효율감소를 초래^(1-3)할 수 있다. 그러므로 스캘럽의 정도는 응답성과 효율감소를 고려하여 결정하게 된다.

Fig. 1

Configuration of scalloped rotor (left) and no-scalloped rotor (right)

스캘럽의 또 다른 중요성은 축추력(axial thrust)의 감소에 있다. 특히 구심터빈이 유기랭킨사이클^(4,5)에 사용되는 경우에는 기존의 작동유체인 공기와 달리 냉매를 작동유체로 사용하여야 때문에 높은 압력에서 작동^(6-8)하게 된다. 작동유체가 냉매이므로 터빈은 외부와 완전히 차단되어 작동하여야 하므로 터빈의 축추력은 상당히 증가하게 된다. 냉매의 경우, 공기와 달리 음속이 낮으므로 터빈의 회전수에도 영향을 미치게 되어 터빈의 크기는 증대하게 된다. 따라서 터빈의 뒷면(back face)이 증대되어, 축추력 증가⁽⁹⁾에 큰 영향을 미치게 된다.

스캘럽은 터빈 뒷면의 면적을 감소하게 되므로, 특히 유기랭킨사이클용 터빈의 경우에는 축추력을 줄이는데 아주 효과적인 방법⁽¹⁰⁾이 된다. 하지만 효율의 감소를 동반하므로 이에 적절한 선정한 필요하다. Baines⁽¹¹⁾은 Galligan⁽¹²⁾의 결과를 참조하여 스캘럽비가 0.8과 0.65인 경우에 효율이 상대적으로 각각 2%와 3∼4% 감소한다고 제시하였다. Hiett and Johnson⁽¹³⁾은 스캘럽으로 관성모멘트가 45%까지 축소된 터빈의 경우 효율이 3∼4% 감소할 수 있으며, 허브표면에 불연속을 줄이면 2%까지 효율감소를 할 수 있다고 하였다. 하지만 명확한 근거가 제시되지 못한 아쉬운 점이 있다.

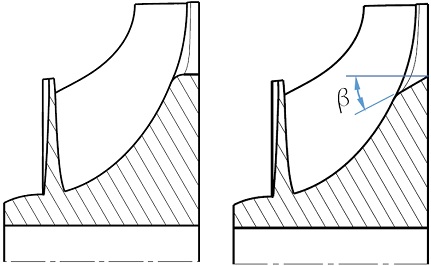
본 연구에서는 100°C 수준의 폐열 열원으로부터 유기랭킨 사이클을 이용하여 150 kW급의 발전을 얻기 위한 1단 구심터빈이 적용되었다. 터빈은 축추력 감소를 위하여 Fig. 1에서 보여주는 것과 같이 스캘럽된 로터로 설계되었으며, 스캘럽의 형상은 유동의 불연속을 완화할 수 있는 세 가지 다른 형상이 추가적으로 적용되었다. 본 연구에서는 Fig. 2에서 보여주는 것과 같이 스캘럽의 형상을 유동의 불연속성이 향상되도록 허브면에서 조정하였을 경우에 터빈의 효율이 어느 정도 향상될 수 있는지를 수치해석적으로 연구하고자 한다. 아울러 본 결과를 바탕으로 대용량의 저온 폐열을 활용할 수 있는 터빈에서 축추력 감소를 달성하면서도 고효율 터빈을 설계하는데 도움이 되고자 한다.

Fig. 2

Basic scalloped rotor (left) and modified scalloped rotor (right)

2. 스캘럽 터빈형상 및 작동조건

Fig. 3은 본 연구에 적용된 네 종류의 터빈 로터 형상을 보여주고 있다. 노즐에서 분사되는 유동이 스캘럽에 의하여 형성되는 불연속적인 흐름을 완화하기 위하여 스캘럽의 각도(β; Fig. 2참조)에 차이를 두었다. 이 각도가 0°에서 15°, 30°, 40°로 증가하면서 A-type, B-type, C-type, D-type으로 분류하였다.

Fig. 3

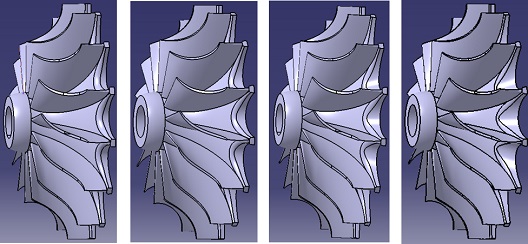
Four different scalloped rotors; A-type (basic), B-type (β=15o), C-type (β=30o) and D-type (β=40o) from left

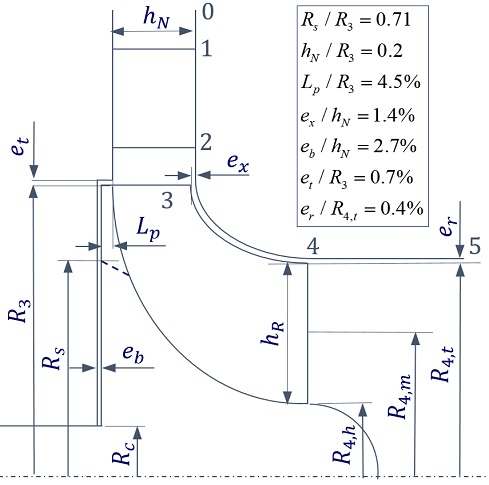
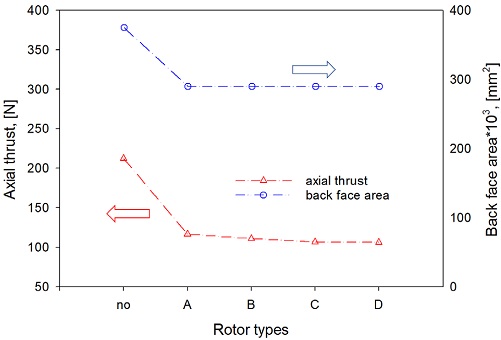
Fig. 4는 터빈의 치수 및 장착과 관련한 간극에 대한 결과를 Table 1과 함께 나타내고 있다. 네 경우 로터의 스캘럽비(R_s/R₃)는 모두 동일하게 0.71을 적용하였다. 이로써 로터 뒷면에서의 축추력에 영향을 미치는 면적은 스캘럽을 하지 않은 경우에 비하여 36.2% 감소하였으며, 극관성모멘트는 27.5% 감소하였다.

Fig. 4

Symbols at the meridional plane of turbine

Table 1

Dimension and flow condition at rotor

이상과 같은 터빈의 형상과 크기 등의 치수는 유기랭킨사이클에서 사이클해석을 통하여 얻어지게 되는데, 기본적으로 작동유체에 따라 달라진다. 유기랭킨 사이클에 적용될 수 있는 작동유체는 상당히 많지만 작동조건에 따라 효율과 친환경적인 요소를 고려하여 작동유체를 선정^(14-16)하여야 한다. 본 연구에서 100°C의 열원에서 효율적으로 작동할 수 있는 친환경적인 냉매인 R245fa를 선정⁽¹⁷⁾하였으며, 사이클해석에서 냉매의 물성치는 RefProp⁽¹⁸⁾을 사이클해석 프로그램에 연계하였다. R245fa의 작동유체로 150 kW의 출력을 얻기 위하여서는 터빈 입구조건으로 전온도와 전압력은 각각 74°C와 626 kPa를 얻었으며, 질량유량은 10.15 kg/s가 필요하였다. 아울러 터빈의 크기와 노즐의 분사속도를 고려하여 회전수는 12,500 RPM으로 결정하였다.

3. 유동해석방법 및 검정

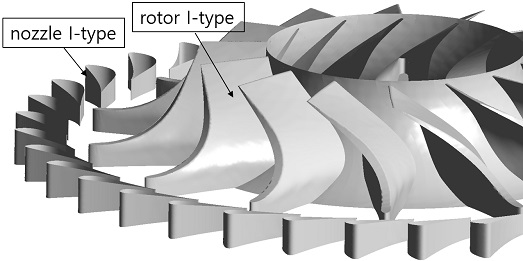
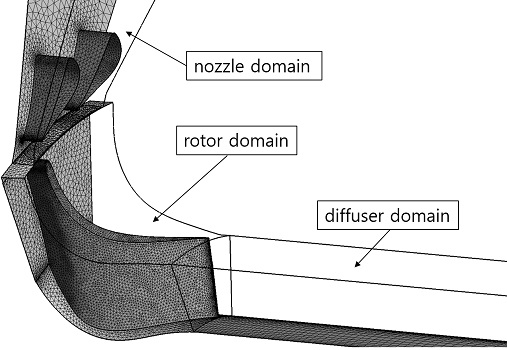
구심터빈의 성능 및 유동장을 측정한 Simonyi의 결과⁽¹⁹⁾를 바탕으로 수치해석 알고리즘의 검정을 수행하였다. Fig. 5는 실험에 적용된 스캘럽된 로터의 형상과 노즐을 보여주고 있다. 작동유체는 가열가압한 공기이며, 노즐과 블레이드의 개수는 36개와 14개이다. 실험에서 사용된 I-type 노즐과 I-type 로터를 기준으로 수치해석을 수행하였다. 로터의 팁반경은 183.6mm이며, 회전수 19,919 RPM으로 실험을 수행하였으므로 이에 맞도록 수치해석을 수행하였으며, 작동조건 및 치수들은 참고문헌에 자세히 기록되어 있다.

Fig. 5

Configuration of nozzle and rotor on the experiment

수치해석은 상용코드인 CFX⁽²⁰⁾를 사용하였으며, 대류항은 high resolution 을 사용하였다. 난류모델은 터보기계의 유동장에 대하여 보다 정확한 결과를 보여주는 SST(shear stress transport)모델을 적용하고, 벽함수는 벽에서부터 격자까지의 거리에 따라 자동으로 전환되어 계산되는 자동전환방식을 사용하였다. 벽면에서의 격자 높이는 난류해석에 문제가 없도록 인플레이션(inflation)을 사용하여 최소격자 높이를 설정하여 형성하였다. 특히, 블레이드와 쉬라우드 사이의 팁간극 및 블레이드 뒷면에서의 간극은 12개 이상의 격자를 형성하였다.

Fig. 6은 스캘럽된 로터를 사용하는 터빈에서의 계산영역(computational domain)과 블레이드 및 노즐에서의 격자를 보여주고 있다. 전체계산 영역은 Fig. 6에서 보여주는 것과 같이 회전영역과 정지영역에 따라서 3개의 세부계산영역으로 분할하여 계산을 수행하였다. 노즐 입구에서의 유동은 실험의 조건과 일치하는 유동속도를 주었으며, 디퓨저의 출구에는 정압력으로 출구 조건을 설정하였다. 계산시간의 단축을 위하여 노즐영역에서는 노즐 블레이드 2개 (피치각 20^o)가 적용되었으며, 로터영역은 하나의 블레이드 (피치각 25.7^o)가 사용되었다.

Fig. 6

Computational domains and grid

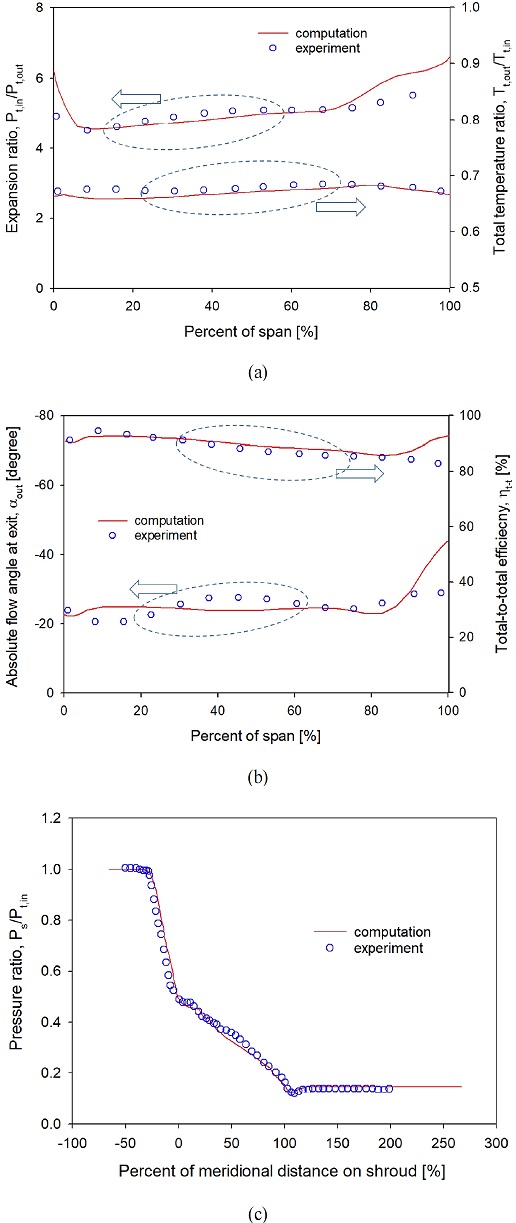
Fig. 7은 실험결과와 비교한 결과를 보여주고 있다. 전효율의 비교 위치는 실험에서와 같이 로터 뒷전에서 로터출구폭의 2.08배의 하류에서 비교한 것이고, 전압력비, 전온도비 및 유동각은 로터출구폭의 3.48배의 하류에서 비교한 것이다. Fig. 7(c)에서 보여주는 정압력비의 경우는 쉬라우드를 따라서 측정한 값이며, 각각의 값들은 원주방향으로 평균하여 얻은 것이다. 정압력은 실험에서 불확도가 가장 적은 인자이므로 두 결과가 상당히 잘 일치하는 결과를 보이고 있으며, 전체적으로 수치해석의 결과는 측정된 결과를 잘 모사하고 있음을 보이고 있다. 단지, 쉬라우드근처에서 전효율의 차이를 보이고 있는데, 로터출구폭의 2.08배의 하류에서도 전온도와 전압력이 감소하는 결과를 Fig. 7(a)처럼 동일하게 보여주었으므로 쉬라우드근처에서의 효율은 계산에서와 같이 증가한 값으로 나타나는 것이 일관된 결과라고 할 수 있다.

Fig. 7

Comparison of computational results and experimental results; (a) expansion ratio and total temperature, (b) flow angle and efficiency, (c) static pressure ratio

4. 결과 및 분석

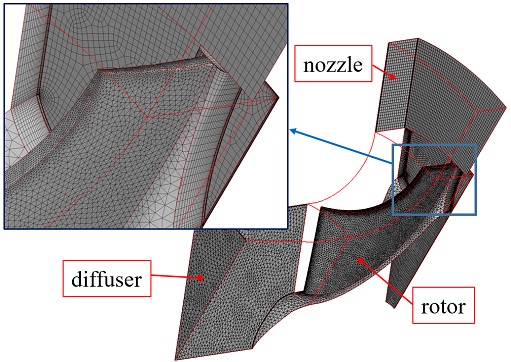
Fig. 8은 본 연구에서의 B-type 스캘럽 로터에서의 계산영역(computational domain)과 블레이드 및 계산영역의 면에서 격자를 보여주고 있다. 격자의 비대칭도(skewness)를 줄이기 위하여 일부 영역은 육각형 격자를 사용하였으며, 이를 위하여 전체계산 영역은 Fig. 8에서 보여주는 3개의 계산영역 외에도, 로터 뒷면 영역에서 3개의 세부계산영역으로 분할하여 총 6개의 세부영역으로 구성하였다. 세부계산영역에서 회전영역과 정지영역과의 경계는 프로젠(frozen)로터 방식을 적용하였으며, 노즐의 입구는 유동각을 고려하여 유동속도를 주었으며, 디퓨저의 출구에는 정압력으로 출구 조건을 설정하였다. 작동유체는 R245fa로 설정하였다.

Fig. 8

Computational domains and surface grid

격자의 개수에 따른 독립성을 확인하기 위하여 계산요소(elements)의 수를 변경하면서 로터의 출력을 확인한 결과 총 계산요소가 60만 이상에서는 출력값의 변화가 일정 범위 내에 있음을 확인하였다. 따라서 네 경우 모두 동일한 격자방법으로 격자를 만들었으며, 계산은 정상상태로 수행하였다. 노즐 계산영역에 노즐의 형상을 설치하지 않고, 노즐 출구에서의 유동 방향을 일치시켰다. 터빈 출구에서의 압력은 작동조건에 맞도록 2 bar의 정압력을 적용하였다. 노즐의 설치 유무에 따른 차이는 계산된 결과에서 노즐입구에서의 전압력 차이가 형성되는 차이이므로 본 연구에서와 같이 스캘럽 형상의 차이에 의한 로터 효율의 비교에는 영향을 미치지 않는다.

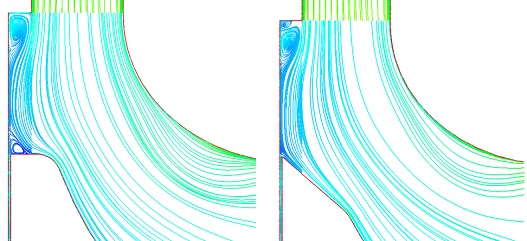
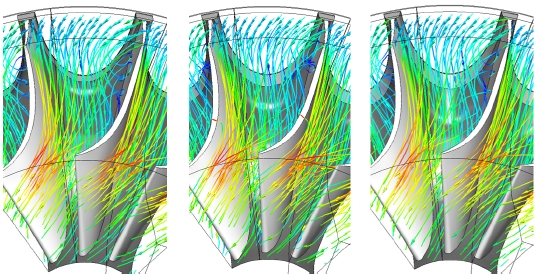
Fig. 9는 로터 자오면에서 유선의 변화를 보여주고 있다. A-type의 경우에 비하여 D-type의 로터에서는 스캘럽이 유동에 연속성을 유지할 수 있도록 설계되었으므로 분사된 작동유체가 스캘럽의 부분에서 박리되지 않고 흐르는 것을 볼 수 있다. 하지만 이러한 유동의 형성이 터빈의 작동에 무조건 좋은 효과를 발생한다고는 할 수 없음을 성능비교를 통하여 알 수 있다.

Fig. 9

Comparison of streamlines on the meridional plane, A-type (left) and D-type (right)

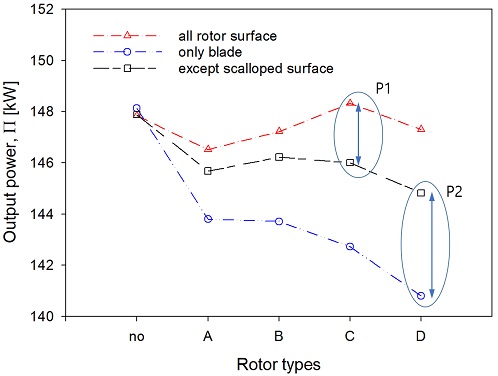
Fig. 10은 각각의 로터에서 얻어진 출력을 비교하고 있으며, Fig. 1에서 보여주고 있는 스캘럽을 하지 않은 로터(no)의 경우도 참고로 보여주고 있다. A-type 의 로터에서 스캘럽의 각도를 적용하여 기울어지게 형상을 만들었을 때 출력은 점차적으로 상승하다가, 가장 큰 각도로 기울어지게 스캘럽을 만든 D-type 의 경우에는 출력이 다시 낮아지게 됨을 보여주고 있다. 이러한 결과는 노즐에서 분사되는 유동이 하류로 잘 배출되도록 무조건 유로를 경사지게 스캘럽의 형상을 조정한다고 하여도 출력이 증가하는 것은 아니라는 것을 알 수 있다. 이 부분에 대한 분석은 뒷부분에서 다루기로 한다.

Fig. 10

Comparison of output powers with no-scalloped rotor

스캘럽의 형상 변화에 따라 출력을 보여주는 Fig. 10에서 P1은 스캘럽된 영역(Fig. 1참조)을 포함하지 않고 출력을 얻을 때와 로터 전체표면을 고려하여 얻어진 출력의 차이를 보여주고 있다. 스캘럽의 각도가 증가하면서 이 차이가 증가하는 특징을 보여주고 있는데, 이는 스캘럽으로 인하여 로터의 회전력을 증가하는 면적이 늘어난 것과 같은 효과가 나타났기 때문이다. P2의 경우는 블레이드만으로 얻어진 출력과 스캘럽된 면적을 제외하고 얻어진 출력의 차이를 나타내는데, 회전하는 로터의 블레이드 외에도 로터의 다른 회전하는 면이 출력을 향상하고 있음을 알 수 있다. 이는 스캘럽으로 허브면이 변경되었으므로 발생된 효과이다. 반면에 스캘럽이 되지 않은 로터에서는 블레이드에서의 출력이 가장 크게 나타나게 되고 나머지는 마찰에 의한 손실로 출력을 감소하는 역할을 하게 된다. 따라서 스캘럽의 차이에 따른 효과는 로터 디스크의 두께에 상당히 영향을 받게 됨을 알 수 있으므로, 재질에 따른 효과를 고려하지 않는다면 스캘럽된 영역을 제외하고 얻어진 결과도 스캘럽의 설계에 참고하여야 함을 알 수 있다.

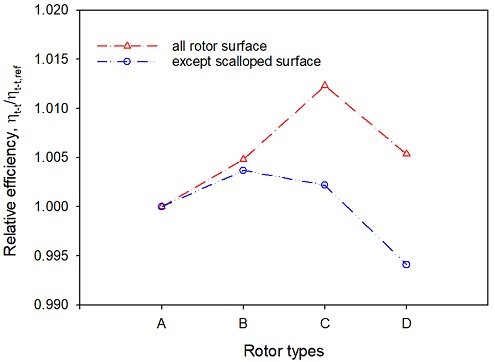
Fig. 11은 A-type 로터를 기준으로 전효율의 상대적인 비교를 보여주고 있다. 전효율은 식(1)에서 보여주는 것처럼 입구와 출구를 기준으로 등엔트로피 과정에서 얻을 수 있는 출력대비 실제 얻어지는 출력의 비로 얻었다. 전효율의 상대적인 비교의 결과도 출력의 결과와 마찬가지로 스캘럽의 기울기가 어느 수준을 넘어서면서부터 효율은 감소하고 있음을 알 수 있다. 스캘럽된 면적을 제외하고 얻어진 결과에서 D-type 의 로터에서는 A-type 에서의 로터 효율보다 감소하고 있음을 알 수 있으며, C-type과 같이 스캘럽의 형상을 적절히 설정하게 되면 상대적으로 1% 이상의 효율 증가를 얻을 수 있음을 알 수 있다.

Fig. 11

Comparison of total-to-total efficiency for the different rotor types

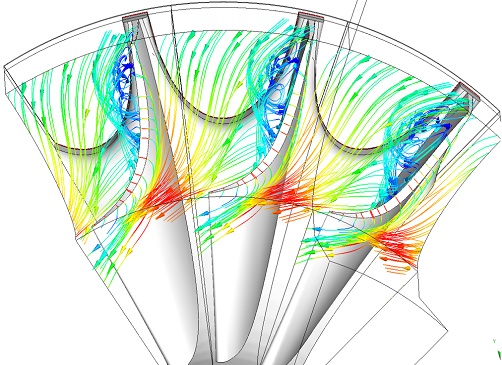
구심터빈 내부유로의 형성에서 주유동장에 영향을 미치는 유동으로 팁간극에 의한 유동과 스캘럽이 되어 있는 경우에 로터 뒷면에서 형성되어진 유동이 있다. 팁간극에 의하여 형성되는 유동을 Fig. 12에서 보여주고 있는데 블레이드의 압력면에서 흡입면으로 흘러들어온 팁간극 유동은 블레이드의 흡입면의 상부를 따라서 하류로 흐르게 되는데 최종적으로 주유동의 흐름과 합하여 하류로 진행된다. 그림에서는 로터 쉬라우드 근처에서의 유동과 함께 팁간극에 의한 유동을 같이 나타내었으며, 스캘럽의 형상이 다른 경우의 로터에서도 비슷한 결과를 보여주었다. 이는 스캘럽의 형상 변화가 팁간극에 미치는 영향이 미미하다는 것을 의미한다.

Fig. 12

Streamlines near shroud with tip clearance flow

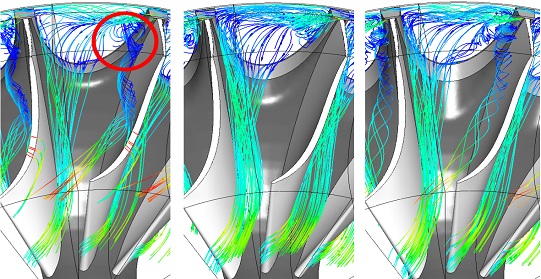
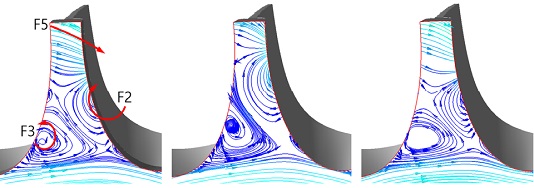
로터 뒷면에서의 간극은 노즐 높이에 비하여 2.7%로 설계되었다. 팁에서의 간극으로 인하여 유동이 형성되는 것과 같이 뒷면에서의 간극은 스캘럽의 설치로 인하여 동일한 현상이 발생될 수 있다. 하지만 본 연구에 사용된 터빈에서는 뒷면에서의 폭이 팁간극의 폭에 비하여 상당히 크기 때문에 넓은 폭의 단면으로 회전하면서 유동이 끌리게 되어(scraping flow) 팁간극에서의 유동과는 다른 현상을 보여준다. Fig. 13은 A-type과 효율이 가장 좋은 C-type 및 효율이 가장 나쁜 D-type의 경우에 대하여 뒷면의 간극에서 형성된 유동에 대한 유선을 보여주고 있다. A-type에서 보여주는 유선에서 원형으로 표시된 와류 부분이 효율이 가장 좋은 C-type에서는 이 와류의 흐름이 억제되고 있으며, 반면에 D-type에서는 다시 나타나는 현상을 보여주고 있다.

Fig. 13

Streamlines started from back face, A-type, C-type and D-type from left

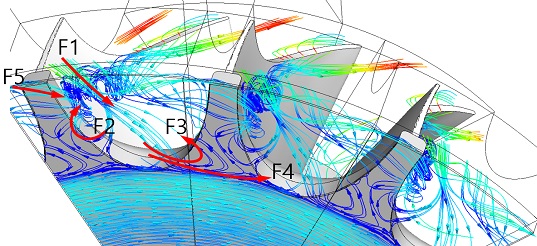
Fig. 14는 로터 뒷면에서 형성된 유선을 보여주고 있는데, 앞선 Fig. 13에서 보여준 와류가 어떻게 형성되었는지에 대한 원인을 명확히 보여주고 있다. 유선은 회전에 따른 상대속도를 기준으로 나타내었으므로 회전방향과는 반대방향으로 나타난다. 따라서 로터 뒷면의 팁부분에서 형성된 유동(F5)은 노즐의 허브측에서 분사되어진 유동(F1)이 스캘럽부분에서 압력면으로 진행한 유동(F2)과 합하여져 와류를 형성하고 있음을 알 수 있다. 반면에 노즐의 허브측에서 분사된 유동(F1) 중에서 흡입면으로 진행한 유동의 일부는 뒷면의 와류(F3)를 거쳐서 흡입면으로 진행하는 유동이 있으며, 일부는 뒷면 아래부분의 유동과 함께 압력면으로 빠져나가는 유동(F4)이 있다.

Fig. 14

Streamlines on the back face of the A-type

Fig. 15는 노즐에서 분사되는 작동유체의 유선을 보여주고 있는데, 기본적으로 Fig. 12에서 보여준 팁간극에서 유동과 Fig. 13에서 보여준 뒷면에서 형성된 유동들이 합쳐져 나타나는 유동이다. 따라서 부분적으로 뒷면에서 형성된 와류가 다소 강한 A-type의 유동이 다소 큰 와류를 압력면의 상부에서 보이고, C-type에서는 이 와류가 완화되었다가 D-type에서 다시 증가함을 보이고 있다.

Fig. 15

Streamlines within the rotor, A-type, C-type and D-type from left

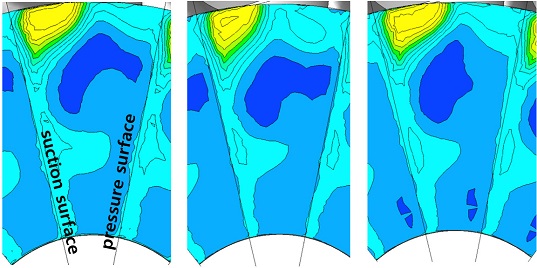
Fig 16에서 보여주는 것은 로터 출구에서의 엔트로피 변화에 대한 결과를 보여주고 있는데, 흡입면 상부에서의 손실은 팁간극의 유동과 쉬라우드 근처에서 형성된 주유동의 와류에 의하여 형성된 것이다. 그리고 흡입면의 중간에 형성되는 손실은 Fig. 14에서 보여주는 F3 유동에 의한 것이며, 압력면 상부에서의 손실영역은 Fig. 14의 F2 유동과 관련이 있음을 알 수 있다. 따라서 로터 출구에서의 엔트로피 분포도에서 효율이 가장 좋은 C-type 로터에서 엔트로피 분포가 가장 낮은 값을 보여주고 있다.

Fig. 16

Entropy contours at the rotor exit, A-type, C-type and D-type from left

로터 뒷면에서의 유동과 혼합된 주유동에서의 미세한 차이는 블레이드의 회전력에 차이를 만들게 되었는데, 이를 Fig. 17의 블레이드 압력면에서의 정압력 분포선도로부터 확인할 수 있다. 가장 높은 효율을 보인 C-type의 블레이드에서는 가장 높은 정압력의 값을 보이고 있으며, D-type으로 가면서 다시 정압력의 분포가 낮은 값을 바뀌어지고 있음을 알 수 있다.

Fig. 17

Static pressure contours on the pressure surface of blade, A-type, C-type and D-type from left

Fig. 18은 로터의 뒷면 간극의 중간 평면에서의 유선을 보여주고 있는데 A-type의 경우는 스캘럽의 각도(β)가 0도 이므로 노즐의 허브측에서 분사된 유동(F1; Fig. 14참조)이 스캘럽의 형상에 의하여 와류를(F2) 만들기 쉬운 구조이며 이 유동이 F5의 유동과 함께 와류를 형성하여 하류로 진행된다. 반면에 효율이 좋은 C-type에서는 분사된 유동(F1)이 스캘럽의 각도에 의하여 하류로 빠져나가기 좋은 구조이므로 분사된 유동은 와류(F3)의 형성에 도움을 주며, 반대로 와류(F2)의 형성에는 약한 영향을 미치고 있다. 스캘럽의 각도를 D-type과 같이 더 많은 형성한 경우에는 분사된 유동이 하류로 진행하기가 때문에 흡입면에 의한 와류(F3)의 세기가 약하여지고, 이로 인하여 압력면에 의한 와류(F2)의 세기가 증가하게 된다. 이러한 차이로 인하여 효율적인 스캘럽의 각도가 있음을 알 수 있다.

Fig. 18

Streamlines on the center plane of rotor back face, A-type, C-type and D-type from left

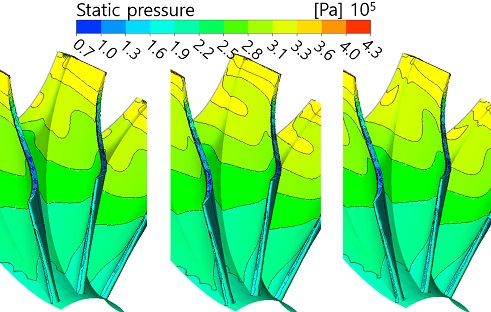
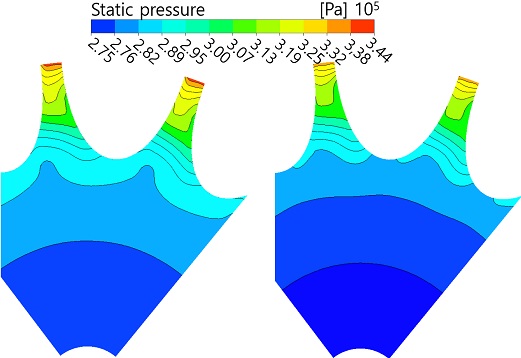
Fig. 19는 로터 뒷면에서의 정압력분포를 보여주고 있다. 축추력에 미치는 영향이 가장 큰 부분이므로 여기에서의 압력 변화는 축추력에 영향을 미치게 된다. 뒷면에서의 압력은 스캘럽 각도에 의하여 영향을 받음을 알 수 있다. 비록 압력의 차이는 크지 않지만, D-type 의 경우 스캘럽 각도가 가장 크므로 노즐의 허브측에서 분사된 유동이 스캘럽의 형상을 따라서 쉽게 하류로 진행되는 구조를 갖고 있으므로 뒷면에 미치는 압력의 영향이 적은 것을 알 수 있다. 아울러 로터 중앙부의 낮은 압력은 원심력으로 인하여 형성된 압력감소임을 알 수 있다.

Fig. 19

Static on the back face of rotor, A-type and D-type from left

Fig. 20에서 보여주는 것과 같이 스캘럽에 의하여 뒷면의 면적은 36.2% 감소하였으며, 로터의 전체 축추력은 50% 정도 감소를 하였음을 보여주고 있다. 아울러 스캘럽의 형상에 따라 추가적인 축추력의 감소가 달성되고 있음을 알 수 있다. 스캘럽을 하지 않은 경우에 비하여 스캘럽을 함으로써 로터의 질량은 6% 감소하였으며, 극관성모멘트는 17% 감소하였다.

Fig. 20

Axial thrust and back face area

5. 결 론

본 연구에서 구심터빈의 스캘럽 형상변화에 따른 효율 변화에 대한 연구를 수행하였다. 스캘럽의 각도를 0^o 기준으로 15^o, 30^o, 40^o의 변화를 주었을 경우에 30^o인 스캘럽의 각도를 갖는 C-type 로터에서 효율은 증가하다가 스캘럽의 각도가 40^o까지 증대한 경우에는 효율이 감소하는 추세로 변경되었다. 따라서 스캘럽의 증대에 따라 로터 내부에서의 유동이 충분히 블레이드에 부하를 주지 못하는 현상이 발생됨을 알 수 있었으므로 최적의 각도를 형성하여야함을 알 수 있었다. 비록 스캘럽의 형상변화에 따라 효율의 증가는 1% 수준의 낮은 값을 보여 주었으나, 스캘럽으로 인하여 스캘럽을 하지 않은 경우에 비히여 축추력은 50% 수준의 감소와 극관성모멘트는 27%의 감소를 달성할 수 있었다. 하지만 이 결과값들은 로터에서 형성되는 뒷면의 간극의 영향을 많이 받게 되었으므로, 차후 이들 값의 변화에 대한 연구를 수행할 필요가 있다.

References

• Cox, G., Wu, J., Finnigna, B., 2007, “A Study on the Flow Around the Scallops of a Mixed-Flow Turbine and its Effect on Efficiency,” ASME Turbo Expo 2007, Montreal, Canada, GT2007-27330. [https://doi.org/10.1115/GT2007-27330]
• Baskharone, E. A., 2006, “Principles of Turbomachinery in Air-Breathing Engines,” Cambridge Univ. Press. 1st ed. [https://doi.org/10.1017/CBO9780511616846]
• He, P., Sun, Z., Zhang, H., Chen, H. and Tan, C., 2012, “Investigation of Clearance Flows in Deeply Scalloped Radial Turbines,” Proceeding Inst. Mech. Engr. Part A: J Power and Energy, Vol. 226, No. 8, pp. 951∼962. [https://doi.org/10.1177/0957650912460361]
• Teguh, B., Suyanto, B., Surana, T., Kurniawan, P., Djubaedah, E. and Ola, K., 2011, “Design of n-Butane Radial Inflow Turbine for 100 kW Binary Cycle Power Plant,” International Journal of Engineering and Technology, Vol. 11, No. 6, pp. 55∼59.
• Robertson, M. C., Costall, A. W., Newton, P. J. and Martinez-Botas, R. F., 2016, “Radial Turboexpander Optimization over Discretized Heavy-Duty Test Cycle for Mobile Organic Rankine Cycle Application,” ASME Paper, GT2016-56754 [https://doi.org/10.1115/GT2016-56754]
• Pasquale, D, Ghidoni, A. and Rebay, S., 2013, “Shape Optimization of an Organic Rankine Cycle Radial Turbine Nozzle,” J. of Engineering for Gas turbines and Power, Vol. 135, 042308-1. [https://doi.org/10.1115/1.4023118]
• Pini, M., Persico, G., Casati, E., and Dossena, V., 2013, “Preliminary Design of a Centrifugal Turbine for Organic Rankine Cycle Applications,” J. of Engineering for Gas turbines and Power, Vol. 135, 042312-1. [https://doi.org/10.1115/1.4023122]
• Pei, G., Li, J., Li, Y., Wang, D. and Ji, J., 2011, “Construction and Dynamic Test of a Small-Scale Organic Rankine Cycle,” Energy, Vol. 36, pp. 3215∼3223. [https://doi.org/10.1016/j.energy.2011.03.010]
• Cho, S. Y., Jung, Y. and Kyun, K., 2018, “Axial Force Prediction and Maneuvering on the Thrust Bearing on a Two-Stage Radial Turbine,” Journal of the Korean Society for Power System Engineering, Vol. 22, No. 5, pp. 51∼61. [https://doi.org/10.9726/kspse.2018.22.5.051]
• Cho S. Y., Choi, B. S. and Lim, H. S., 2019, “Effect of Scallop on the Performance of Radial-Type Turbine,” J. of Fluidmachinery, Vol. 23, No. 1, pp. 56∼64. [https://doi.org/10.5293/kfma.2020.23.1.056]
• Baines, N. C, 2015, “Turbochargers, Advanced Integration and Design for Internal Combustion Engines,” Course Notes, Concepts NREC, 2015.
• Galligan, J. E., 1979, “Advanced Technology Components for Model GTCP 305-2 Aircraft Auxiliary Power System,” Design Report No. 31-2874. AiResearch Manufacturing Co. of Arizona, Phoenix, AZ.
• Hiett, G. F. and Johnston, I. H., 1963, “Paper 7: Experiments Concerning the Aerodynamic Performance of Inward Flow Radial Turbines,” Proceedings of the Institution of Mechanical Engineers, Conference Proceedings, Vol. 178, Pt3, pp. 28∼42. [https://doi.org/10.1243/PIME_CONF_1963_178_214_02]
• Veleza, F., Segoviab, J., Martin, M. C., Antolina, G., Chejnec, F. and Quijanoa, A. 2012, “A Technical, Economical and Market Review of Organic Rankine Cycles for the Conversion of Low-Grade Heat for Power Generation,” Renewable and Sustainable Energy Reviews, Vol. 16, pp. 4175∼4189. [https://doi.org/10.1016/j.rser.2012.03.022]
• Tchanche, B. F., Papadakis, G., Lambrinos, G. and Frangoudakis, A., 2009, “Fluid Selection for a Low-Temperature Solar Organic Rankine Cycle,” Applied Thermal Engineering, Vol. 29, pp. 2468∼2476. [https://doi.org/10.1016/j.applthermaleng.2008.12.025]
• Chen, H., Goswami, D. Y. and Stefanakos, E. K., 2010, “A Review of Thermodynamic Cycles and Working Fluids for the Conversion of Low-Grade Heat,” Renewable and Sustainable Energy Reviews, Vol. 14, pp. 3059∼3067. [https://doi.org/10.1016/j.rser.2010.07.006]
• Cho, S. Y. and Cho, C. H., 2015, “Effect on the Cycle by the Properties of Working Fluids Using Organic Rankine Cycle,” J. of Fluidmachinery, Vol. 18, No. 4, pp. 5∼12. [https://doi.org/10.5293/kfma.2015.18.4.005]
• RefProp, 2010, “Reference Fluid Thermodynamics and Transport Properties,” NIST, Version 9.
• Simonyi, P. S., Roelke, R. J., Stabe, R. G., Nowlin, B. C. and Dicicco, D., 1995, “Aerodynamic Evaluation of Two Compact Radial Inflow Turbine Rotors,” NASA TP-3514.
• CFX, v.18, 2018, ANSYS Inc.