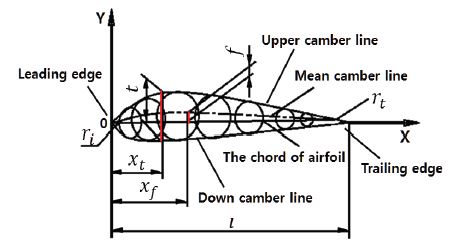
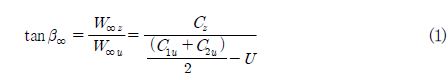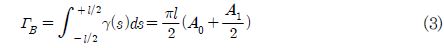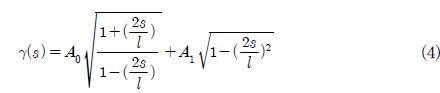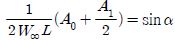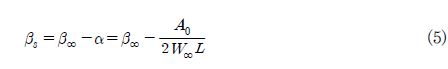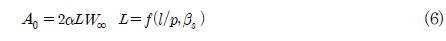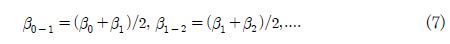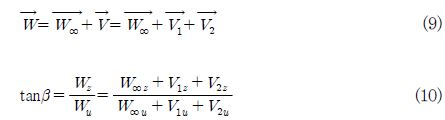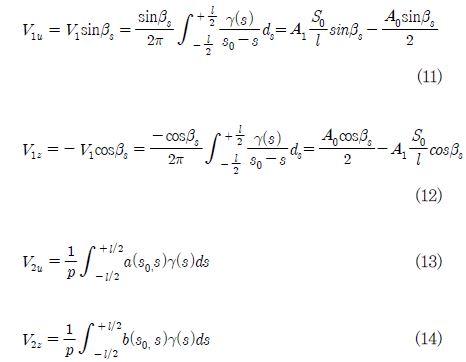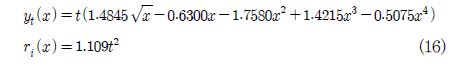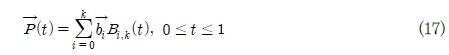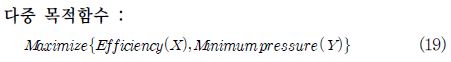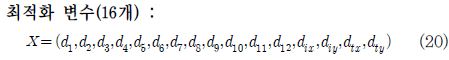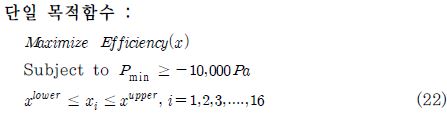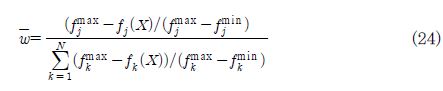Optimization of Micro Hydro Propeller Turbine blade using NSGA-II
In addition to the development of micro hydro turbine, the challenge in micro hydro turbine design as sustainable hydro devices is focused on the optimization of turbine runner blade which have decisive effect on the turbine performance to reach higher efficiency. A multi-objective optimization method to optimize the performance of runner blade of propeller turbine for micro turbine has been studied. For the initial design of planar blade cascade, singularity distribution method and the combination of the Bezier curve parametric technology is used. A non-dominated sorting genetic algorithm Ⅱ(NSGA Ⅱ) is developed based on the multi-objective optimization design method. The comparision with model test show that the blade charachteristics is optimized by NSGA-II has a good efficiency and load distribution. From model test and scale up calculation, the maximum prototype efficiency of the runner blade reaches as high as 90.87%.
Keywords:
Propeller turbine, Runner blade, Multi-objective optimization method, Singularity distribution method, Bezier curve, Nondominate sorting genetic algorithm, 프로펠러 수차, 러너 블레이드, 다목적 최적화 방법, 특이점 분포법, 베지어 곡선, 비지배 분류 유전 알고리즘1. 서 론
최근 일본 후쿠시마 원전 사태 등으로 안전한 발전원에 대한 요구가 신재생에너지 이용 비율 확대 방향으로 글로벌 에너지 정책 변화로 나타나고 있다. 수력자원은 신재생 에너지 중에서 가장 청정한 에너지원이며 에너지 밀도가 높아 수력자원 이용에 대한 관심이 재 고조되고 있다. 수력 자원 중에서 친환경적이고 개발 가능 잠재력으로 볼 때 가장 관심이 집중되고 있는 부분이 마이크로급 소수력 자원 개발이다. 마이크로급 수력 자원의 가장 취약한 점은 경제성이 낮아 마이크로급 수력자원 개발에 가장 중요한 부분이 고효율 수차 시스템 개발이다(1).
저낙차 저유량 환경의 마이크로급 수차 시스템에 적당한 수차는 횡류 수차와 프로펠러 수차가 대표적이다. 횡류 수차는 유량 변동에 강점이 있으나 수차 특성상 고가의 증속 장치가 필요하다. 이에 반해 고정식 프로펠러 수차는 유량 변동 폭이 좁으나 가변속 운전 시스템을 채택함으로써 종래의 프로펠러 수차의 단점을 극복할 수 있고 카플란수차에 비해 저가이고 시스템이 단순하기 때문에 대표적인 마이크로급 수차 시스템으로 주목을 받고 있다(2).
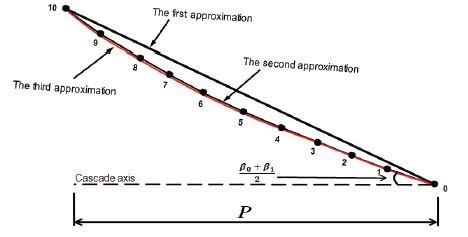
저낙차용 마이크로급 및 피코급 프로펠러 수차에 대한 실험적 연구는 캔터베리대학에서 시도되었다. 이 수차 러너 블레이드는 축류 펌프의 설계 가이드라인에서부터 초기 블레이드를 근사하고 그다음에 입구와 출구각을 변화시켜 2차, 3차 최적화하였지만 러너 블레이드 비틀림 각도를 일정하게 유지하여 흐름에 대한 최적화가 부족하였다(1).
최근 컴퓨터의 급속한 발달과 더불어 수치적 설계기법이 활성화되면서 각종 다중 목적 최적화에 대한 알고리즘이 개발되었다(3). 수차 러너 블레이드처럼 복잡한 형상에 대한 최적화에 대한 연구에 NSGA 및 NSGA-II 알고리즘을 이용하여 다중목적 최적화에 대한 연구가 가능하게 되었다(4). 이 연구는 최적화 방법으로서 생물의 진화 과정을 기반으로 한 최적화 탐색 방법인 유전자 알고리즘을 슈퍼 컴퓨터를 이용하여 수차 설계에 적용하였다(4). 그러나 이 방법은 풍부한 경험적인 지식 바탕과 다년간 축적된 실험 데이터를 토대로 파라미터 선택이 필요하며 경험이 부족한 사용자나 슈퍼 컴퓨터의 이용이 제한적인 일반적 산업현장에서는 연구개발 기간이나 비용 면에서 효율적이지 못한 실정이다(5).
본 연구에서는 고 효율 마이크로 프로펠러 수차 개발 연구의 일환으로 먼저 개발된 축소 모델 10kW 블레이드를 바탕으로 최적화된 수차 블레이드 독자 개발에 그 목적이 있다(6). 블레이드를 최적화하기 위한 초등단계로서 초기 익형 설계를 위해 기존의 직관적인 방법보다는 고전유체역학에 근거한 특이점 분포법(singularity distribution method)을 이용하여 해석적인 해를 구하였다(78). 해석적으로 얻은 익형의 평균 캠버선(mean camber line)을 베지어 곡선(Bezier curve)과 NACA 0012익형을 이용하여 기준형상을 완성하였다. 기준 러너 블레이드 형상을 기초로 상용 CFD 소프트웨어인 STAR CCM+와 Optimate+의 NSGA-II를 이용하여 마이크로 수차 러너 블레이드를 최적화 하였다.
2. 러너 블레이드 최적화
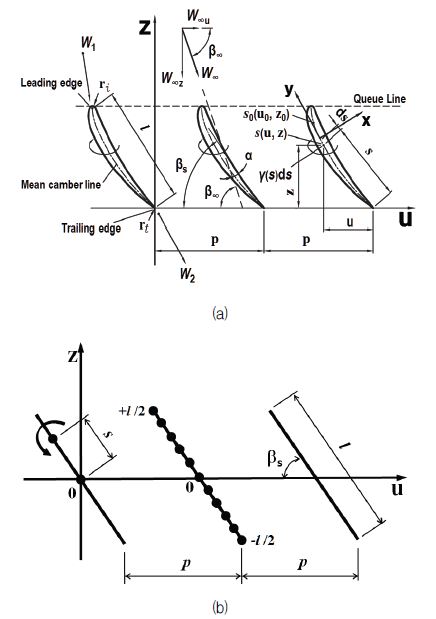
수차 블레이드 최적화 형상 설계에서 소스(source) 및 싱크(sink)를 이용한 특이점 분포법을 통하여 초기 블레이드를 설계하는 순서는 Fig. 1과 같다.
Fig. 1과 같이 초기 블레이드가 결정되면 베지어 곡선을 이용하여 블레이드 형상 모수화를 기하고 블레이드 두께, 비틀림각을 통한 기준 형상을 완성하고 블레이드의 효율, 최소 정압을 목적함수로 선택하여 NSGA-II를 통하여 파레토 최적해를 찾는 최적화 방법을 제시하였다.
Flow chart of initial blade design
2.1. 특이점 분포법을 이용한 초기 익형 설계
비압축성 유체가 작동하는 2차원 익렬(Cascade)이라고 부르는 익형에서 박익이론(thin airfoil theory)을 적용하면 Fig. 2와 같이 U-Z 평면으로 표현할 수 있다.
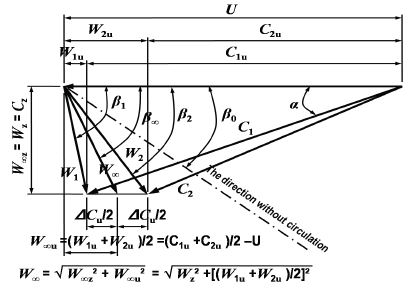
상기 그림에서 p는 피치(p=2πr/Z)이다. 여기서, Z: blades number. Fig. 2처럼 입사하는 익형에 작용하는 흐름의 속도 삼각형은 Fig. 3과 같다.
(a) Blade cascade and its coordiantion system and (b) Approximate blade cascade
Velocity triangles
속도 삼각형으로부터 β∞는 다음과 같이 표현할 수 있다.
여기서, W∞u : u축 방향 속도, W∞z: z축 방향 속도.
W∞로 a영각으로 입사하는 유체속에 단일 평판의 경우에 circulation은 Γ =πlW∞sina. 단일 평판과 같은 영각조건인 경우의 평판열의 경우는 수정 계수 L을 도입하여 표현하면 다음과 같다.
Fig. 2와 같이 익형을 평판으로 근사하고 평판으로 입사하는 흐름으로부터 Kutta-Joukowsky이론을 적용하면 평판열에 작용하는 circulation(ΓB)은 다음과 같다.
여기서, A0, A1는 형상 계수.
식 (3)에서 vortex sheet 밀도 함수 γ(s)는 다음과 같이 전개된다.
식 (2)와 식 (3)으로부터,
평판의 경우, 선단부(leading edge)에서 형상 계수 A1 = 0, 영각이 작다고 하면 sin a ≈ a 이기 때문에
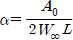로 형상 함수 A0만으로 표기된다. 상기 함수로부터 익형 형상각도는 아래와 같이 표현할 수 있다.
여기서 영각(a)은 블레이드 허브(hub)에서는 3o∼4o, 블레이드 팁(tip)에서는 8o∼10o이며, 형상 계수 A0와 수정 계수 L은 다음과 같다.
계수 A0,L은 참고문헌에서 표로 정리되어 있다(7). Fig. 4에서처럼 익형을 10개의 등간격으로 한 후 각각의 점에서의 형상 각도는 아래식으로부터 구해진다.
식 (3)으로부터 형상 계수 A1은 다음과 같이 구해진다.
여기서, 평판열의 circulation(ΓB)은 평판 선단부와 뒷전(trailing edge) circulation 차이를 평판수로 나눈 값이다.
평판열의 어떤 지점 s0 의 속도는 다음과 같이 표시된다.
여기서, V1 : 기본익형의 s0에서 vortex sheet에 의해서 야기된 속도, V2 : s0뿐만 아니라 익형의 다른 모든 점에서 vortex에 의해 야기되는 속도로서 익렬의 모든 지점에 작용하는 vortex sheet에 의해 야기된 속도 성분은 다음과 같이 계산된다.
상기 속도 성분 계산을 위해 가우스적분공식(Gaussian integral formula)을 이용하면 각 지점에서의 속도 성분이 구해진다(9).
각 구간에서의 곡률을 고려하기 위하여 접선방향 성분인 V1s와 법선방향 성분 V1n에 다음과 같은 보정함수를 사용하였다.
Approximate method of mean camberline
NACA airfoil geometrical construction
여기서, R: 익형 평균 캠버선의 평균 곡률
상기 방식으로 각 구간의 곡률을 구한 후 U, Z축 면에 투사하면 익형의 캠버선은 Fig. 4와 같이 표현할 수 있다.
생성된 평균 캠버선으로부터 초기 블레이드 익형을 Fig. 5처럼 NACA 4-digit의 익형과 익형두께 방정식은 다음과 같다.
NACA 0012 익형의 두께 방정식은 다음과 같다.
완성한 평균 캠버선으로부터 상기의 NACA 0012 두께를 중첩하면 초기 블레이드 익형이 생성된다.
2.2. 베지어 곡선 매개변수화
수차 블레이드 단면을 형상화하기 위하여 조정점 즉 곡선을 근사화하는 순차적인 점들의 집합을 이용하여 사용자가 곡선을 예측 가능한 형상으로 조절할 수 있도록 하는 베지어 곡선을 이용한다. 일반적으로 k+1개의 조정점에 의해 정의되는 k차 베지어 곡선은 다음과 같은 매개 변수식으로 나타낼 수 있다.
Airfoil construction by the composition of bezier curve
여기서,
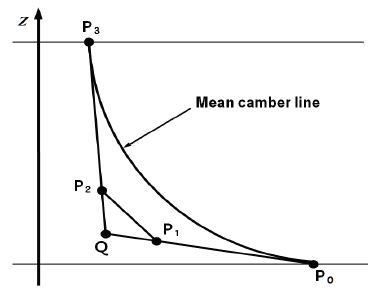
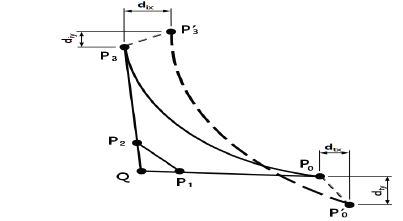
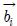: 조정점 벡터, Bi,k(t)는 Bernstein 기저함수.Fig. 6과 같이 평균 캠버선을 3개의 베지어 곡선으로 나타내고 조정점은 P0, P1, P2, P3이다.
가능한 설계 변수들을 줄이기 위하여 무차원변수 d1, d2를 도입하면 다음과 같다.
여기서 0 < d1, d2 < 1.
블레이드 최적수가 6개이므로 전체 블레이드 변수들은 d1, d2, d3, ....d12 12개이다. 12개의 변수들을 블레이드 선단부와 뒷전에서 블레이드 shape invariant 전제하에 변화시킬 수 있다.
축 방향 수차 러너 블레이드에서 블레이드 선단부 위치는 블레이드에 진입하는 흐름의 영각(angle of attack) 변화를 야기하여 블레이드 에너지 변환 효율 및 캐비테이션(cavitation) 성능에 영향을 미치기 때문에 Fig. 7에서처럼 선단부 위치 변화를 최적화하기 위하여 축 방향과 원주 방향으로 dix, diy만큼 변화시키면 P0, P3′가 새로운 평균 캠버선이 된다.
The schematic diagram of the airfoil parameterization
뒷전에서도 같은 방법으로 동시에 dtx, dty 변화시킨다. 이처럼 평균 캠버선에 대한 변수(12개)와 선단부와 뒷전 변화량에 대한 변수(4개) d1, d2,...d12, dix, diy, dtx, dty 등 16개의 변수들을 최적화 하면 최적 블레이드 형상을 얻을 수 있다.
3. 수치 해석
본 연구에서는 러너 블레이드 주위의 비압축성 3차원 나비어 스톡스(Navier-Stokes)방정식을 정상 상태로 가정하고 유동해석을 위해 상용 소프트웨어인 STAR CCM+를 사용하였다(10). 지배방정식은 유한 체적법으로 이산화 하였으며, 난류유동의 해석을 위해 k –Ω SST모델을 사용하였고 벽함수를 사용하였다(11). 블레이드 해석을 위해 Fig. 8과 같이 계산 영역을 설정하였다. 격자계는 비정렬 격자계를 사용하였으며, 격자 크기에 대한 민감도를 검증하기 위해 격자 테스트를 거친 후 약 100만 개의 격자점을 채택하였다. 총 6개의 블레이드 중 1개의 블레이드만을 계산 대상으로 정하고 주기조건을 이용하였다. 입구 조건으로 균일 유량조건을 적용하였고 작동유체는 상온의 물이다. 수렴된 유동 해석 결과를 얻기 위하여 Intel 제온 프로세스 E5-2680에서 약 5시간의 CPU시간이 소요 되었다. 유동 계산을 위한 기초적인 조건은 Table 1과 같다.
Computational grid of the runner blade
Specification of reference blade
4. 다중 목적함수 최적화
4.1. 목적함수와 제약 조건
프로펠러 수차 러너 블레이드의 성능 향상을 위하여 러너 블레이드의 효율 향상과 러너 블레이드면의 최소 압력을 최대로(캐비테이션 발생 가능성을 최소)하는 다중 목적 최적화를 하였다. 블레이드를 구성하는 형상 변수로서 식 (18)을 사용하여 형상 최적화를 도모 하였다. 목적함수는 러너 블레이드 최대 효율과 러너 블레이드의 최소 정압으로 하고 2개를 동시에 최적화하고자 하며 최적화 모델은 다음과 같다.
여기서, X는 블레이드 효율, Y는 최소 정압이다.
러너 블레이드 최적화 변수는 다음과 같이 표기할 수 있다.
설계점에서의 목적함수 값은 비압축성 나비어 스톡스 방정식의 수치해석으로부터 얻어진다.
수치해석으로부터 얻은 결과들은 설계 공간을 표현할 수 있도록 반응 표면법(response surface method)으로 다수의 다항식으로 표현하였다. 면을 구성하기 위해서는 무한대의 점이 필요하지만 근사 모델링이므로 반응 표면의 정교함과 계산 시간 사이에 절충(trade-off)하였다.
본 연구에서는 시간 및 효율성을 위해 다음과 같은 제약 조건을 두었다. 무차원 변수 di∈(0, 1)(여기서, i = 1,2,3,...12)의 제약 조건은 다음과 같다.
다중 목적함수의 최적화에 대한 타당성 검증의 목적으로 다음과 같이 효율이라는 하나의 목적함수로 최적화를 수행 하였다. 다중 목적 최적화에서 최소 압력 최대화는 러너 블레이드의 캐비테이션과 관련이 있으므로 캐비테이션이 발생하지 않는 압력을 지정하여 그 이하로 내려가지 않도록 제약조건을 줌으로써 단일 목적함수 최적화로 바꿀 수가 있다.
단일 목적함수의 최소 압력 값은 모델 시험 결과를 기반으로 러너 블레이드 양면의 캐비테이션이 발생하지 않는 최소 압력 값으로 설정하였다(12).
4.2. NSGA-II를 이용한 다중 목적함수 최적화
다중목적 최적화 문제에서 모든 목적함수를 동시에 최적화 하는 해는 일반적으로 존재하지 않는다. 이러한 다중목적 최적화 문제를 해결하기 위한 대표적인 방법 중의 하나는 어떤 목적함수를 개선하기 위해서 다른 목적함수의 희생이 필요하다. 후보해 중에서 다른 해에 지배되지 않는 해가 선정되는데 이러한 해를 비지배해라고 한다. 비지배해로 분류된 해들을 파레토 최적해(Pareto-optimal solution)라고 하며, 파레토 최적해를 다음과 같이 도입한다.
파레토 최적해의 목적함수들에 의해 생성된 공간을 파레토 최적 프론트(Pareto-optimal front)라 한다.
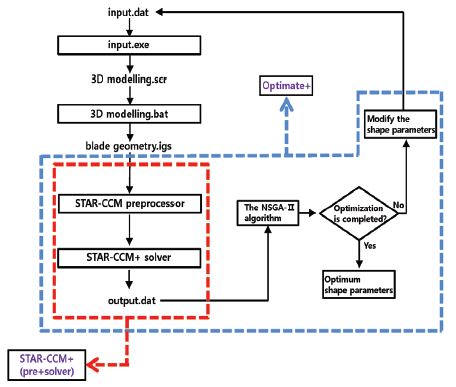
본 연구에서는 프로펠러 수차 러너 블레이드의 설계에서 NSGA-II를 이용한 다중 목적함수 최적화를 수행한다. 다중 목적함수(효율 및 최소 압력)를 최적화하는 계산상의 과정은 Fig. 9와 같다. 초기에 설계 변수가 선택되어지고 기준 블레이드 형상(reference blade profile)이 결정되면 계산 격자를 자동적으로 생성한 후 수치계산을 행한다. 수치계산 결과와 최적화 알고리즘과의 연결은 SHERPA 알고리즘을 사용하는 Optimate+라고 하는 최적화 툴을 통해 구현되며 그림과 같이 만족할 값을 얻을 때까지 최적화 과정을 반복한다(10).
Computational procedure of optimization process
Flow chart of NSGA-II
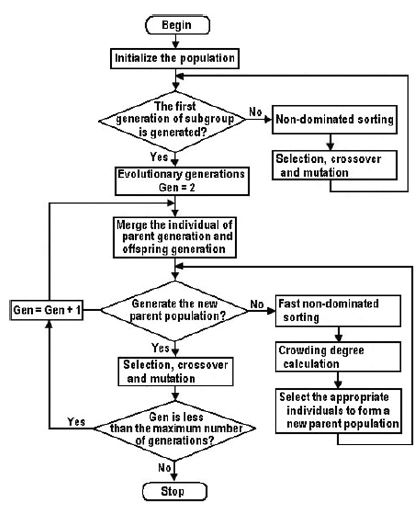
NSGA-II 알고리즘의 순서도는 Fig. 10과 같으며 기본 개념은 다음과 같다. 먼저 랜덤으로 N규모의 초기 개체군이 만들어지고 비지배 분류(non-dominated sorting)후 유전 알고리즘의 선택(selection), 교차(crossover), 변이(mutation) 3가지 기본 조작을 통해 1세대 개체군이 만들어지며, 다음으로 2세대부터 부모 개체군을 자손 개체군과 합쳐서 고속 비지배 분류(fast non-dominated sorting)를 진행하는 동시에 모든 비지배 계층의 각각의 개체에 대해 밀집도를 계산하고 비지배 관계와 개체의 밀집도에 근거하여 적절한 개체를 선택, 새로운 부모 개체군을 만든다. 마지막으로 유전 알고리즘의 기본 조작을 통하여 자손 개체군을 만들어 낸다. 이런 방식으로 프로세스의 종료 조건에 만족할 때까지 지속하여 진행한다. NSGA-II 연산중 서로 다른 변수들을 문제의 특성에 맞게 하나씩 조장되며 본 연구에서 사용된 과정은 다음과 같다.
개체군(population) 수는 100, 유전대(generation) 수 100, 교차(crossover) 수 20, 그리고 변이(mutation) 확률은 0.7로 하였다.
NSGA-II는 근사 파레토 최적해를 제공하고 가중 합계법이 파레토-최적해의 질을 향상시키는데 사용된다. 가중치는 다음 공식을 이용하여 각각의 목적함수에 대해 계산된다.
여기서 W는 jth목적함수의 가중치, N은 목적함수의 개수,ƒjmax,ƒjmin 그리고 ƒjmax(X)는 jth목적함수의 최대, 최소 그리고 초기 값이다.
이와 같은 방법으로 얻은 최적해들은 개체간의 지배성을 정렬하고 엘리티즘(elitism)의 방향으로 탐색하여 최적해를 얻는다.
5. 결과 및 고찰
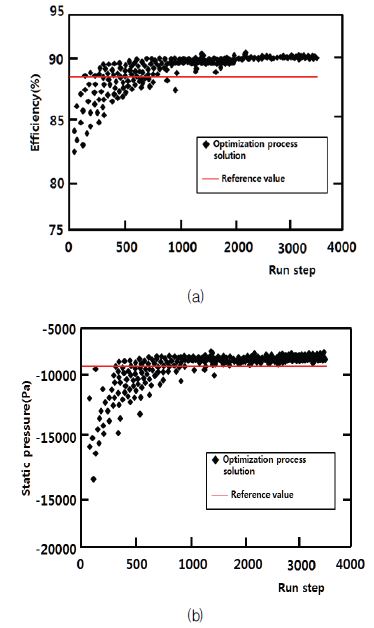
본 연구는 100kW 마이크로 프로펠러 수차 러너 블레이드의 성능 향상을 위해 기준 블레이드(reference blade)를 바탕으로 러너 베인을 최적화 하였다. 목적함수인 러너 블레이드의 효율과 표면 정압의 최적화 이력(history)은 Fig. 11과 같다.
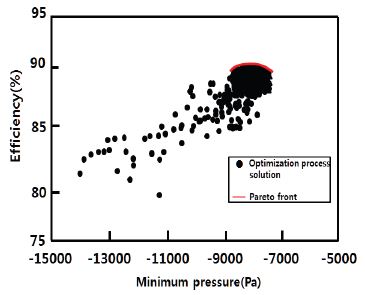
효율 및 최소 정압이 2000회부터 90%, -7,500Pa 정도에서 수렴되는 모습을 볼 수 있다. Fig. 12에 목적함수의 최적화 수렴 과정을 표시하였다. 최적화 수렴도에서 볼 수 있듯이 파레토 해의 분포는 비교적 균일하다. 최적화 후 얻은 파레토 해의 일부를 변수의 초기 값과 대비해 Table 2에 나타내었다. Table 2에서처럼 NSGA-II에 의해 생성된 파레토 최적해에서 목적함수인 효율과 정압 둘 다 만족하는 값은 존재하지 않으며 절충해(trade-off solution)를 효율 90.889%와 최소 정압 -7,530.51Pa로 선택하였다.
Comparision of optimal results and initial value
다중 목적에서 사용한 같은 데이터를 이용하여 압력조건을 제한조건의 10%범위 내에서 여러번 계산한 효율만의 단일 목적함수로 최적해를 Table 3에서 나타내었다. 단일 목적함수 최적해의 경우의 최적화된 효율이 90.57%이다. 이는 다목적함수 최적화가 단일 목적함수 최적화보다도 효과적으로 성능을 향상시킬 수 있음을 보여준다.
다목적함수 최적화의 최소 압력 값은 다목적최적화 결과인 파레토 프론트 중에서 Table 2의 점선으로 표기 한데로 효율과 절충해서 최저압력을 -7,530.51Pa로 선택하였지만, 단일 목적함수의 최저 압력을 선택할 경우 캐비테이션이 발생하는 기준을 모델 시험 결과로부터 러너 블레이드면에 기포가 생성되기 시작하는 임계 캐비테이션 값보다 10% 마진을 두어 -10,000Pa로 결정하였다. 일반적 러너 블레이드 최적화시에는 시험 결과 값을 모르기 때문에 단일 목적함수 최적화의 경우 최저 압력 설정시 수치 캐비테이션 계산 결과를 제한조건으로 설정할 수 있지만, 설계자의 많은 경험적 지식과 노하우에 의존해야 된다. 이에 반해 다중 목적함수 최적화에서는 경험적인 지식 없이도 모든 목적에 대해 동시에 최적화를 수행한다. 그 결과에 대해 설계자는 각 성능지수 간의 최선의 절충을 통해 주어진 상황에서 보다 객관적인 성능 효율을 최대화하는 것이 신빙성 있는 최적 대안을 찾을 수 있는 장점이 있다. 다중 목적함수 최적화와 단일 목적함수 최적화 결과가 단지 효율면에서 0.319%가 차이지만 마이크로급 수차 효율 향상면에서 고려하면 의미가 있는 수치라고 사료된다.
기준 러너와 최적화된 러너의 형상 변화, 최소 정압, 효율을 Table 4에 비교하였다. 효율과 최소 정압에 대해 파레토 최적선이 형성되었을 때 효율은 3.672% 향상 되었고 최소 정압은 17.3% 증가 하였다. 러너 블레이드의 기준 형상과 최적화된 형상과의 차이를 Fig. 13에 비교하였다.
러너의 팁 부근, 중간, 그리고 허브 부근의 2차원 단면과 최적화된 러너의 3차원 형상을 표시하였다.
Fig. 13에서처럼 기준 형상에 비해 최적화된 러너가 반경 방향으로 진행할수록 기울기가 완만하게 형성된다는 것을 볼 수 있다.
Optimal solutions of single objective optimization
(a) Optimization history of objective function efficiency and (b) Minimum static pressure
Convergence history of optimization process
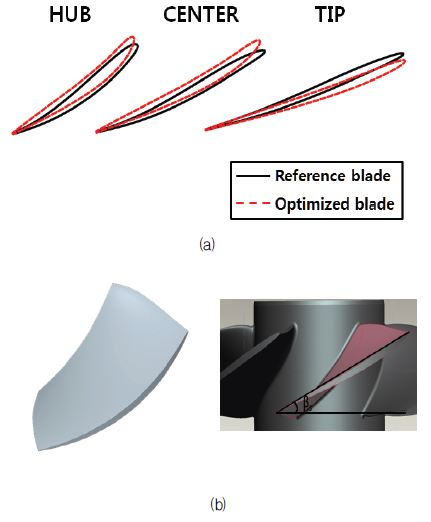
(a) Comparison of reference and optimized runner blade profile (b) Optimized runner blade and geometry of a micro propeller turbine
Comparison of reference and optimized blade
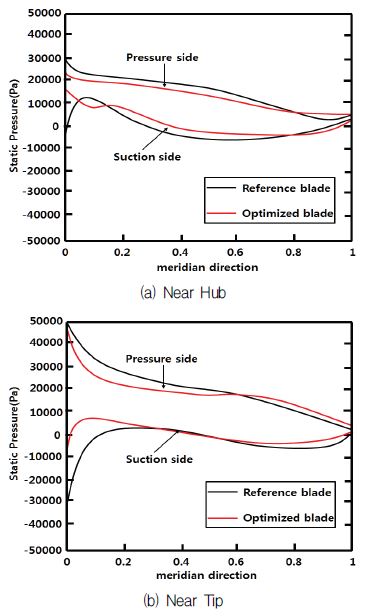
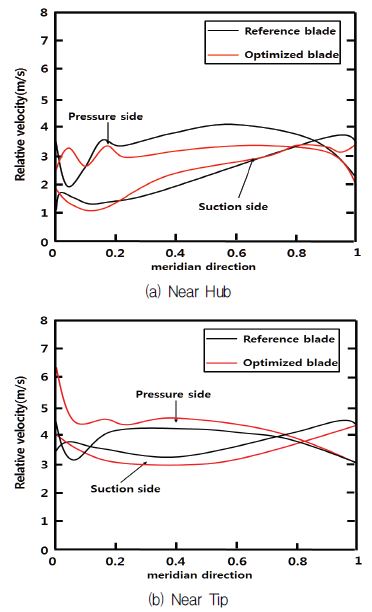
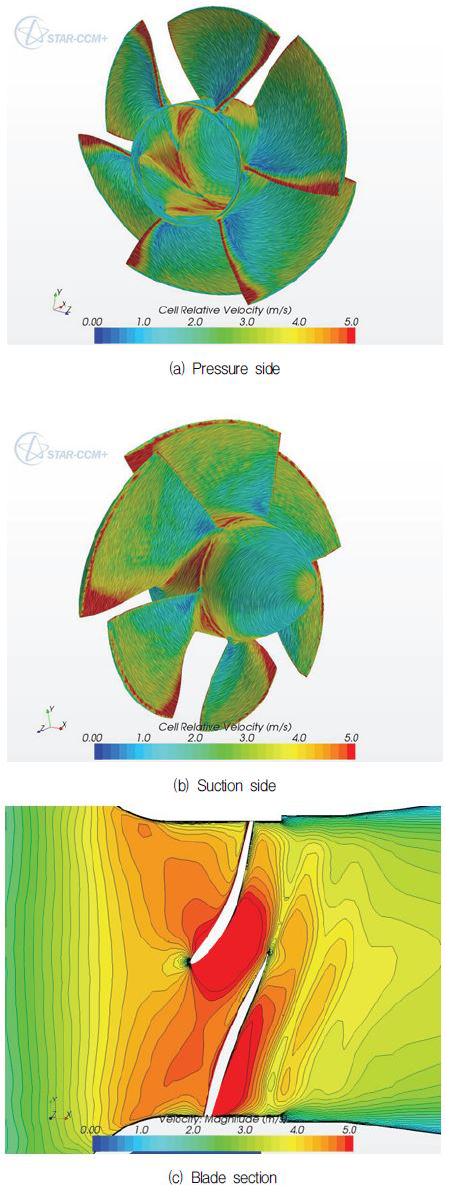
현 블레이드의 성능 특성을 비교하기 위하여 러너 블레이드를 실린더 방향의 단면(허브 근처와 팁 근처)에서의 스팬방향(spanwise) 정압 분포를 Fig. 14에 나타내었다. Fig. 14에서 보는 바와 같이 최적화된 러너 블레이드의 최저 압력 값이 많이 개선되었고 선단부 부근의 부하 특성 및 블레이드가 받는 응력 값도 개선되었다. 캐비테이션과 관련되어 있는 러너의 토출면(suction side)에서의 최소 압력 분포는 확실히 개선된 것을 확인할 수 있다. 따라서 최적화된 러너의 에너지 성능은 최적화되기 전 러너 보다 양호하다 할 수 있다. 압력 분포와 같은 단면에서의 상대 속도 분포를 Fig. 15에 나타내었다. 러너의 허브근처에서의 유동 속도는 압력면에서는 비교적 균일하지만 토출면에서는 스팬방향으로 갈수록(선단부에서 뒷전방향) 서서히 증가한다. 팁 근처에서는 압력면에서 속도는 스팬방향으로 갈수록 단순히 증가하지만, 토출면에서 속도는 선단부에서 최대가 되지만(압력이 최소로 되는 지점) 기준 러너에 비해서 빠르기가 최적화된 러너의 유동 속도가 상대적으로 적음을 알 수 있다. 이것은 압력 선도와 비교해 보면 이 부분에서 캐비테이션 발생 가능성이 제일 높다는 것을 알 수 있다. Fig. 16에는 최적화된 러너 블레이드면의 속도 등고선도를 표시하였다. 그림에서처럼 팁 근처에서 속도는 압력면의 선단부근에서 정체점에 도달하고 러너 베인 사이로 가속(압력은 반대로 하강)되는 전형적인 수차 러너 베인 사이의 유동 특성을 보인다. 즉 물리적으로 러너의 선단부로 입사하는 흐름이 정상적으로 입사한다는 것을 알 수 있다.
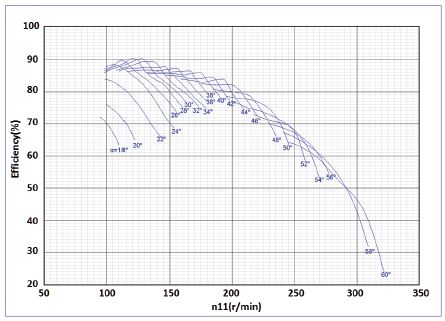
최적화된 러너 블레이드의 성능 특성을 실험적으로 검증하기 위하여 시험 장치에 맞게 러너 직경을 400mm로 5축 가공하였으며 가공 오차는 거의 무시할 수 있다. 제작 시 러너 블레이드 원형과 기하학적, 운동학적 그리고 역학적 상사성을 유지하도록 하면서 가이드 베인 개도를 변수로 실험적으로 연구한 결과중 효율 곡선을 Fig. 17에 나타내었다(11). 모델 블레이드의 단위 회전수 (
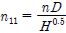) 변화에 대한 최적화된 러너의 효율 특성을 가이드 베인 개도 각에 따라 나타낸 것이다. Fig. 17에서처럼 최적화된 러너 블레이드의 최고 효율은 가이드 베인 개도가 30o일 때 90.27%이고 원형 러너로 척도 변환하면 90.87%이다. 수치 최적화의 최고 효율 값과 비교해보면 최고 값이 0.3% 미세한 차이가 난다. 이것은 모형 시험에서는 가이드 베인 의한 개도 변화에 의한 최고 효율 값을 구하였기 때문에 가이드 베인의 경계층 효과로 사료된다.
Static pressure distribution
Relative velocity distribution
Velocity contours of optimized runner blade
Blade efficiency and unit speed depend on the guide vane opening(12)
6. 결 론
본 연구에서는 고전 유체역학에 입각한 익형의 특이점 분포 방법을 이용한 해석적인 해와 베지어 곡선을 통한 기준 러너 블레이드 형상을 구하였다. 기준 러너 블레이드를 기준으로 수치해석과 NSGA-II를 이용한 다중(효율 및 최소 압력) 및 단일 목적함수 최적화한 러너 블레이드의 성능 결과(효율)와 모델 시험을 통한 실험값과의 비교를 통해 다음과 같은 결론을 도출 하였다.
1) 다중 목적함수 최적화(효율: 90.9%, 최소 압력: -7,530.5Pa)가 단일 목적함수 최적화(효율 90.6%)에 비해 효율 개선면에서 단지 0.319%가 차이지만, 경험적인 지식이나 실험값에 의존해야하는 단일 목적함수 제한조건 대신에 모든 목적에 대해 동시에 최적화를 수행하는 다중 목적함수 최적화가 마이크로 프로펠러급 수차 러너 블레이드의 성능 향상면에서 고려하면 단일 목적함수 최적화에 비해 객관적인 해를 구하기 용이한 현실적인 최적화 방법이라고 사료된다.
2) 최적 러너 블레이드와 기준 러너와의 압력면과 토출면에서의 압력 및 상대 속도를 비교하여 최적화된 러너 블레이드가 성능이 개선되었다는 것을 확인하였고, 최고 효율에 대한 모델 시험 결과 효율 값이 0.3%의 성능 차이를 보일 정도로 본 최적화 방법이 최적 수차 설계에 효과적인 수단임을 확인하였다.
Acknowledgments
본 연구는 2013년도 산업통상자원부(MOTIE)의 재원으로 한국에너지기술평가원(KETEP)의 연구과제(과제명: 마이크로 수차 발전 시스템 개발, No:2011T100200136)의 지원을 받아 수행한 연구과제의 결과입니다.
References
- Faulkner, S. A., “A Simplified Low Head Propeller Turbine for Micro Hydroelectric Power", Master Engineering Thesis, University of Canterbury, (1991).
- Lippold, F., Gode, E., Ruprecht, A., On the “Design of a Variable-Speed Turbine with Fixed Blades and Fixed Guide Vanes”, Proceeding of the International Conference on CSHS03, (2003).
-
Deb, K., Pratap, A., Agarwal, S., Meyarivan, A., A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II, IEEE Transactions on Evolutionary Computation, (2002), 6(2), p182-197.
[https://doi.org/10.1109/4235.996017]
- Ruprecht, A., Maihofer, M., Heitele, M., Helmrich, T., “Massively Parallel Computation of the Flow in Hydro Turbines”, Proceedings of Hydraulic Machinery and Systems 21st IAHR Symposium September 9-12, Lausanne, (2002).
- Ruprecht, A., Ruopp, A., Simader, J., “CFD-ba sed Mathematical Optimization of Hydroturbine Components Using Cloud Computing”, Advances in Hydroinformatics Springer Hydrogeology, (2014), p375-387.
- 박지훈, 김유택, 조용, 김병곤, 이영호, 2014,“CFD를 이용한 10kW급 모델 실험용 프로펠러 수차의 유량 및 러너베인 깃 수 변화에 따른 성능 해석”, 한국유체기계학회 논문집, (2014), 17(2), p5-11.
- Hira, N., Takizawa, E., Principle and Practice of Fluid Mechanics, Hirokawa Publishing Co, Tokyo, (1968).
- Bohl, W., Stromungsmachinen 2, Berchnung und Kakulation: Vogel Fachbuch, (2005).
- Zhang, Z., “Understanding of MATLAB 5.3 version”, Beijing University Aeronautics and Astronautics Publishing House, (2000).
- Introduction to STAR CCM, CD-adapco, (2013).
- Ismail, B.C., Introduction Turbulence Modelling, Lectures Notes, (1999).
- 100kW propeller turbine model test report for DSK, Dongfang Electric Machinery Co., LTD, (2013).