계단 형상의 단차가 적용된 팬 형상 막냉각 홀 하류에서의 막냉각 효율에 관한 실험적 연구

1. 서 론

현대의 가스터빈 엔진은 연소온도를 높여 가며 터빈 입구로 유입되는 작동유체의 온도를 상승시키는 방향으로 발전되어 왔다. 연소 온도를 높이는 과정에서 점차 재료의 물성이 감당할 수 있는 한계치를 넘기 시작했고, 이를 해결할 방안으로 여러 냉각기법들이 연구되어 왔다. 그중 터빈 내 고온부품에는 대표적인 외부 냉각기법인 막냉각(film cooling) 기법이 널리 사용되고 있다. 막냉각 기법은 냉각유체를 터빈외부 표면의 홀을 통해 분사시켜 얇은 막을 형성하는 냉각기법이다. 냉각유체로 형성된 막은 고온으로부터 구성품의 표면을 보호하여 터빈의 수명을 늘려준다.^(1-3) 하지만 과도한 냉각유체의 사용은 가스터빈 엔진의 효율을 저하시키는 요인으로 작용하므로 적은 냉각유체를 사용하며 높은 냉각성능을 갖는 기술개발을 필요로 한다.

막냉각 홀의 성능에 큰 영향을 미치는 요인으로는 막냉각 홀의 형상, 분사각도, 유동조건, 주유동과 냉각유체와의 각도 등이 있다.^(4-6) 이중 막냉각 홀의 형상에 대한 연구는 단순한 형상인 원형형상의 홀에서부터 홀의 출구 부분을 확장시킨 팬 형상(Fan-shaped) 홀^(7-9), 화살촉 형태의 형상(Arrow-head) 홀^(10-12) 등 여러 방면으로 발전해 왔다. 이외에도 유동조건과 냉각유체가 분사되는 표면 상태에 대한 실험결과를 기반으로 최적화된 형상에 대한 개발도 이루어져 왔다.^(13-17)

또한, 막냉각 효율의 개선방안 중 하나로 홀의 형상에 변화 이외에 추가 구조물을 넣어 막냉각의 성능을 높이려는 연구가 수행되었다. 대표적으로 벽면 주변을 이동하는 유체가 벽면에 부착되어 흐르는 현상인 코안다 효과를 이용한 연구가 Kim 등⁽¹⁸⁾과 Benabed⁽¹⁹⁾에 의해 진행되었다. 해당 연구에서는 막냉각 홀의 출구 부분에 경사진 구조물을 설치하여 구조물의 경사 각도에 따른 효율의 변화를 측정하였다.

이외에도 막냉각 홀에 트렌치(trench)를 구현하여 막냉각 성능을 향상시키는 연구가 Lu 등⁽²⁰⁾과 Oguntade 등⁽²¹⁾, 그리고 Wang 등⁽²²⁾에 의해 수행되었다. 막냉각 홀 주위에 구현된 트렌치 형상은 냉각유체를 횡방향으로 분산시키는 특징을 이용하여 막냉각 효율 균일성을 개선시키고 냉각유체의 표면으로부터의 이탈을 억제하여 냉각효율을 증가시키는 효과가 있다.

본 연구에서는 팬 형상 막냉각 홀 내부의 출구영역에 계단형상의 이중 단차를 구현하여 막냉각 홀 하류에서의 막냉각 효율 분포특성을 고찰하였다. 계단형 단차의 효과를 비교하기 위한 기준형상으로 막냉각 홀 출구부분에서의 확장각이 각각 7°이고 직관부가 홀 직경의 2배인 팬 형상의 막냉각 홀을 사용하였다. 계단형 구조물이 적용된 형상은 계단형상의 폭을 변화시켜가며 구조물의 확장 길이에 따른 영향을 분석했다. 실험조건은 밀도비(DR)가 1.0일 때 분사비(M)를 0.5, 1.0, 2.0 으로 변화시키며 진행하였으며 막냉각 효율의 측정은 압력감응페인트(Pressure Sensitive Paint, PSP)기법을 사용하였다.

2. 연구방법

2.1 막냉각 홀 형상

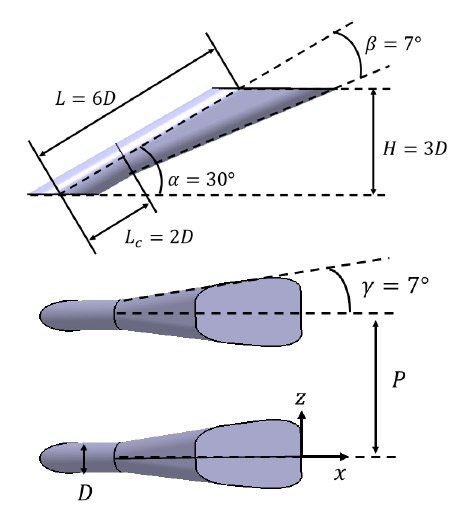
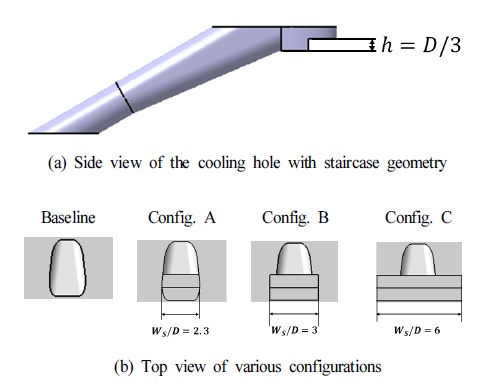
본 실험에서 구조물의 성능을 비교하기 위한 기준형상을 Fig. 1과 Table 1에 나타내었다. 팬 형상 막냉각 홀 중 가장 잘 알려진 형상으로 유동방향과 횡방향으로 7°의 확장각을 갖는 형상이다. 해당 형상을 기준으로 계단형상 단차를 설치하여 막냉각 효율을 비교하였다. 계단형상 단차는 홀 내부의 출구영역 내부에 구현한 형상(Config. A)과 횡방향으로 계단형상의 폭을 변화시켜가며 각각 홀 직경의 3배(Config. B), 6배(Config. C)로 길이를 변화시킨 형상을 실험하여 단차의 길이에 따른 막냉각 효율을 비교하였으며 단차가 적용된 형상에 대한 특징은 Fig. 2에 나타내었다.

Fig. 1

Baseline cooling hole design

Table 1

Geometry parameter of Baseline cooling hole

Fig. 2

Schematics of film cooling holes with various staircase geometries

Lu 등⁽²⁰⁾이 실험한 막냉각 홀에 단차를 형성하여 막냉각 효율을 측정한 실험은 막냉각 효율을 개선시키는 결과를 보여주었다. 단일단차 구조에서는 분사되는 냉각유체가 주유동과 단차 영역에서 혼합되어 분사된다. 이러한 점을 개선하기 위해 냉각유체가 주유동과 상호작용하기 전에 균일한 냉각유체를 분사할 수 있도록 내부에 단차를 추가로 구성한 이중단차 구조를 적용하여 실험을 진행하였다.

2.2 시험설비

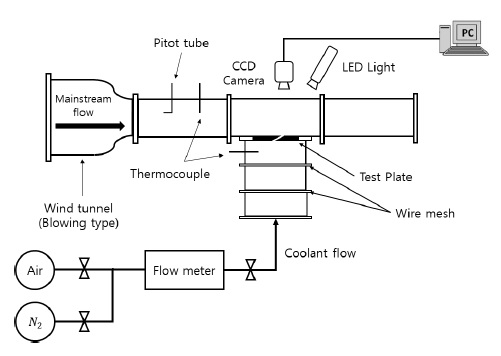
Fig. 3에는 본 연구에서 사용된 평판 막냉각 시험 설비를 나타내었다. 주유동은 방출형(Blowing type) 풍동을 이용하여 공기를 공급했으며, 유속의 측정은 피토관을 이용한 차압을 통해 계산했다. 냉각유체는 공기와 질소를 사용하였고, 냉각유체의 유량은 코리올리 유량계와 밸브를 이용해 측정을 하였다. 시험시편의 각 홀에 균일한 냉각유체를 유입시키기 위해 냉각홀 입구의 플레넘 챔버에 와이어메쉬를 설치하였다. 주유동과 냉각유체 각각 열전대를 이용하여 온도를 측정했다.

Fig. 3

Schematic diagram of the experimental apparatus

시편은 SLA(Stereo-Lithography) 방식의 3D 프린터를 이용하여 제작했으며 각각 시험리그에 탈부착이 가능하도록 설계하였다. 시험리그 외부에는 압력감응페인트에서 발광세기를 측정하기 위해 CCD카메라와 LED를 설치하였다.

2.3 시험조건

Table 2에는 본 시험에서 수행한 실험조건을 나타내었다. 막냉각 유체로는 공기와 질소를 사용하였으며 밀도비는 1.0 이다. 분사비의 경우 주유동의 속도와 풍동의 단면적을 통해 유량을 계산하여 시편의 홀에 유입되는 냉각유체의 유량을 조절하여 각각 0.5, 1.0, 2.0의 시험조건에서 수행했다.

Table 2

Test conditions

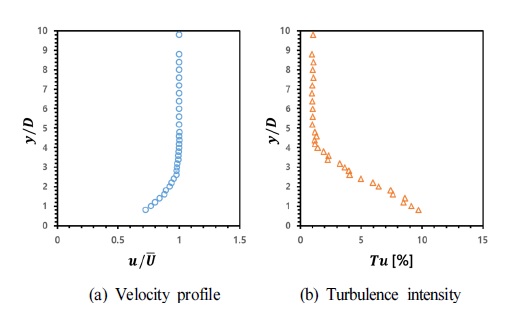
Fig. 4는 막냉각 홀 상류 x/D=-12에서 열선유속계(Dantec Streamline Pro)를 이용하여 측정한 입구유동의 경계층 프로파일이다. 측정한 경계층의 두께는 막냉각 홀 직경의 약 3.6배이며 주유동의 난류강도는 약 1.2%이다.

Fig. 4

Mainstream velocity and turbulence intensity profiles at x/D=-12

2.4 압력감응페인트

막냉각 효율은 식(1)과 같이 정의한다.

$\[ \eta =\frac{T_{gas}-T_{aw}}{T_{gas}-T_{coolant }} \]$

(1)

막냉각 효율은 단열벽면 온도를 측정하여 계산할 수 있으나 완벽한 단열조건이 불가능하다는 문제가 있다. 이런 이유로 막냉각 성능 연구에 있어서 압력감응페인트(PSP)를 이용한 물질전달 실험을 진행하였다. PSP 실험 방법은 Park 등⁽²³⁾에 상세히 기술되어있다.

$\[ \eta \begin{array}{l}=\frac{C_{mix}-C_{air}}{C_{fg}-C_{air}}=\frac{{\left(P_{O_2}\right)}_{air}-{\left(P_{O_2}\right)}_{fg}}{{\left(P_{O_2}\right)}_{air}}\\ =1-\frac{{\left(P_{O_2}\right)}_{fg}/{\left(P_{O_2}\right)}_{ref}}{{\left(P_{O_2}\right)}_{air}/{\left(P_{O_2}\right)}_{ref}}\end{array} \]$

(2)

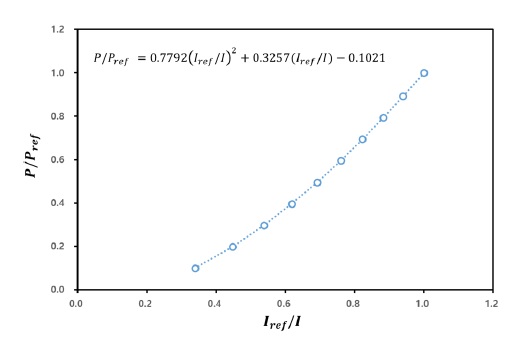
압력감응페인트는 특정 파장의 빛을 쏘는 경우, 산소의 분압정도에 따라 발광의 정도(Intensity)가 달라지는 특성을 갖고 있다. 산소의 농도가 낮아 분압이 적어질수록 발광도가 증가하는 특징을 갖고 있어 주유동에 산소가 흐르게 하여 산소분압이 감소하면 압력감응페인트의 발광강도가 증가하는 현상이 일어난다. 해당 빛의 발광세기를 이용하여 막냉각 효율을 정의하기 위해서는 다음과 같은 식(2)를 사용한다. 식(2)를 이용하여 막냉각 효율을 계산하기 위해서는 산소의 분압과 압력감응페인트의 발광 정도에 대한 상관관계를 알아야한다. 이를 위해 감압이 가능한 챔버를 제작하여시험에 사용된 LED조명(LM2X-DM LED Light Source)과 카메라(PSP-CCD-M)를 이용하여 압력에 따른 발광세기를 측정하였으며, 그 결과를 Fig. 5에 제시하였다. 압력감응페인트는 압력뿐만 아니라 온도에도 영향을 받는다. 그러나 실험에 사용된 압력감응페인트는 ISSI사의 Binary FIB PSP (BF400)로 해당 제품의 사양⁽²⁴⁾을 참고할 때, 본 실험이 수행된 온도 범위(대기온도 15∼25°C)에서는 온도에 따른 영향은 무시할 만한 수준이며, 측정한 데이터를 바탕으로 교정을 수행하여 Fig. 5와 같은 교정커브를 형성하였다.

Fig. 5

PSP Calibration curve

막냉각 효율의 불확실도은 Natsui 등⁽²⁵⁾의 연구결과를 통해 계산을 진행하였다. 본 실험에서 막냉각 효율의 불확실도는 η=0.5에서 약 ±4.5%, η=0.2에서는 약 ±11.0% 으로 계산되었다.

3. 실험 결과

3.1 기존 팬 형상 막냉각 효율 분포와의 비교

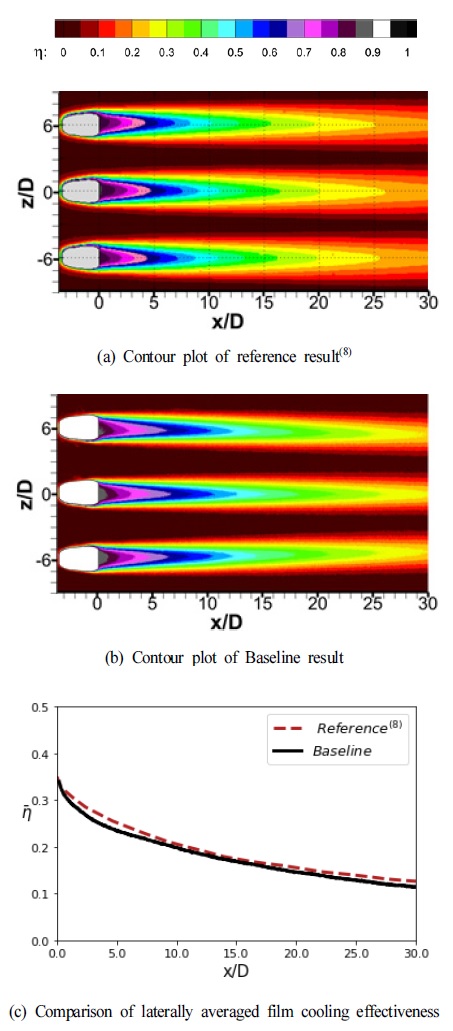
Fig. 6은 Schroeder 등⁽⁸⁾이 실험한 결과와 본 연구에서 수행한 실험의 결과를 나타내고 있다. Schroeder의 실험과 본 연구에서의 실험은 막냉각 홀의 직관부의 길이와 난류강도, 밀도비, 실험기법 등 조건이 달라 다소 차이는 있지만, 동일한 확장각의 팬 형상 홀을 사용하여 시험을 진행했기 때문에 팬 형상 막냉각 홀의 막냉각 효율 분포와 횡방향 평균 효율값이 유사한 것을 볼 수 있다.

Fig. 6

Comparison of cooling effectiveness at M=1.0

3.2 분사비에 따른 막냉각 효율 비교

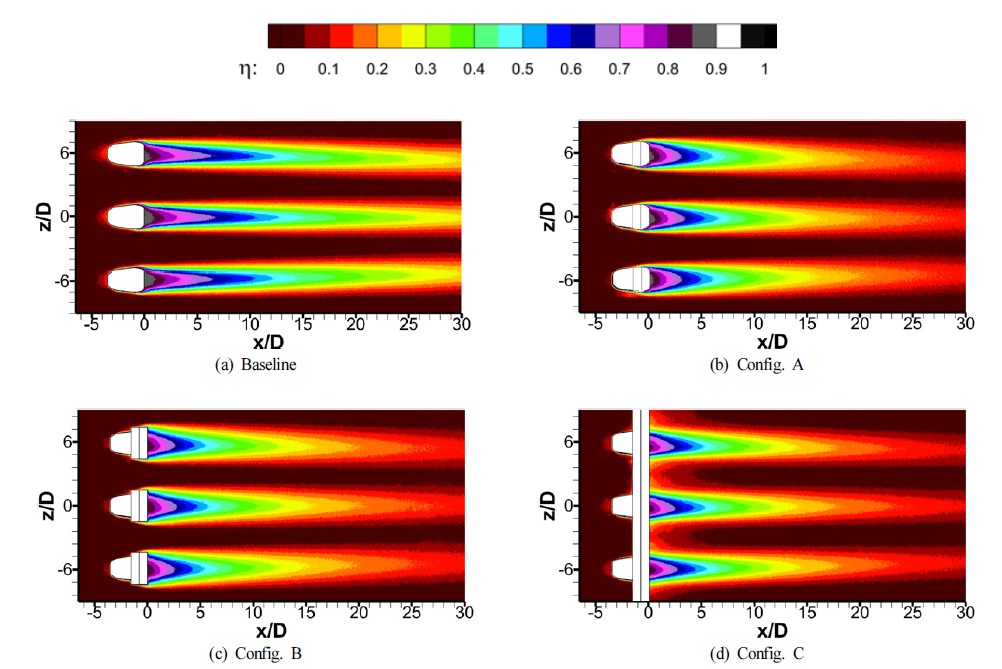
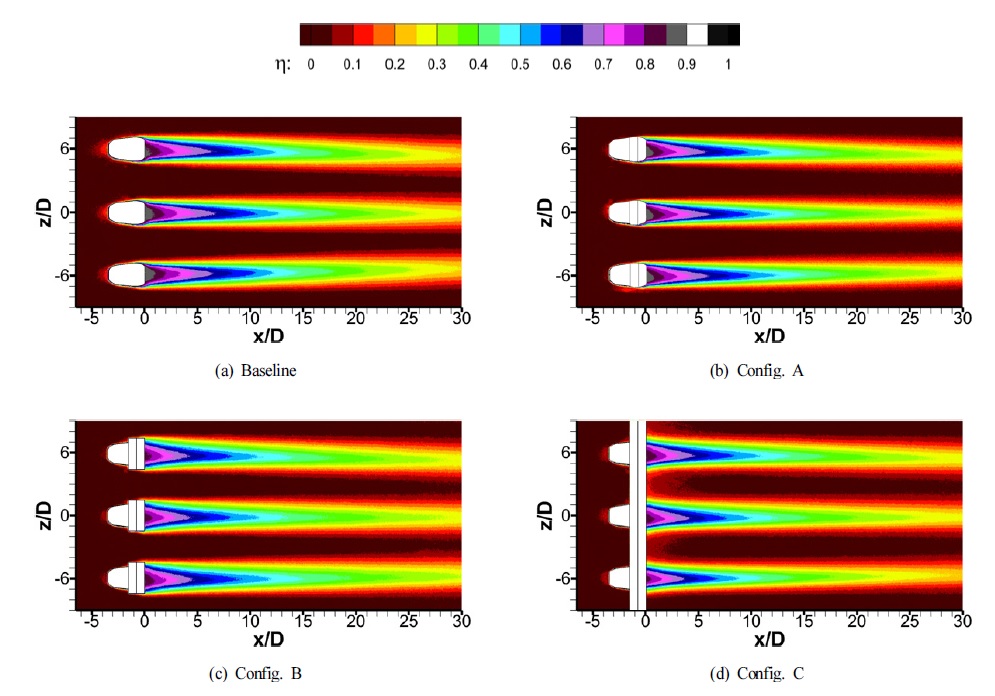
Fig. 7은 M=0.5에서의 막냉각 효율 측정 결과를 나타낸 것이다. Fig. 7(a)는 이번 실험의 기본이 되는 형상이며 Fig. 7(b)는 Config. A이다. Fig. 7(c)와 7(d)는 각각 Config. B와 Config. C 형상으로 홀 형상보다 횡방향으로 더 연장하여 단차를 가공한 형상이다.

Fig. 7

Contour plots of film cooling effectiveness for various hole configurations at M=0.5

막냉각 효율분포를 비교해볼 때, 기본형상과 Config. A에 비해 Config. B와 Config. C가 횡방향으로의 효율의 분포가 더 넓은 것을 확인할 수 있다. 이는 홀 출구가 기본형상과 Config. A는 팬 형상의 막냉각 홀의 형태이지만, Config. B와 Config. C는 홀의 출구부에서 횡방향으로 계단형상의 단차가 연장되어 가공되어 있어 냉각유체의 분사 시 횡방향으로 연장된 단차를 통해 냉각유체가 확산되어 분사되기 때문에 홀 출구에서부터 더 넓은 영역의 표면을 냉각유체가 보호하기 때문이다.

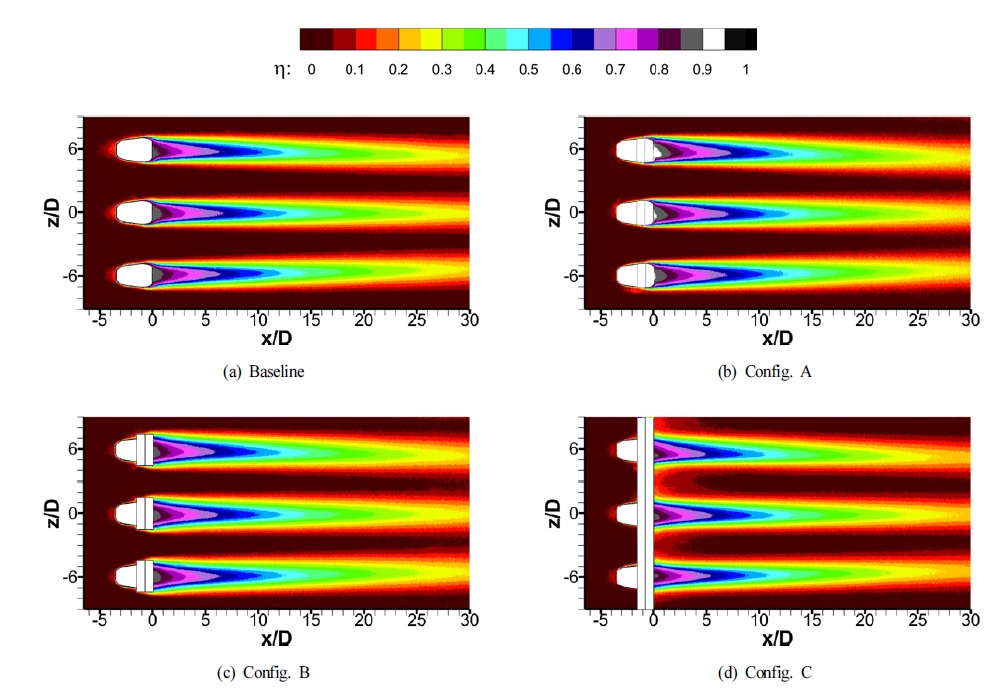
Fig. 8은 M=1.0에서의 막냉각 효율 측정 결과로 M=0.5에 비해 주유동방향으로 진행할수록 동일 위치에서 더 높은 값의 효율을 보여준다. 기본형상과 Config. A, Config. B는 유사한 막냉각 효율 분포를 보인다. Config. C의 경우, 횡방향으로 연장된 단차가 서로 연결되어 있어 홀 출구에서 냉각유체가 Config. A 및 Config. B보다 더 많이 확산된다. 그로인해 홀의 중심부에서는 냉각유체의 유량이 감소하여 x/D>20의 하류구간에서는 다른 형상들에 비해 낮은 효율값의 분포를 보인다.

Fig. 8

Contour plots of film cooling effectiveness for various hole configurations at M=1.0

Fig. 9는 M=2.0에서의 효율 측정 결과로 높은 분사비로 인해 막냉각 유체가 표면으로부터 이탈이 발생하여 다른 분사비에 비해 전체적으로 높은 효율의 영역이 가늘어진 것을 볼 수 있다. 단차 구조는 주유동이 단차 구조에서 냉각유체와의 상호작용으로 인해 냉각유체의 표면으로부터의 이탈을 감소시켜주는 효과가 있어 단차 구조를 넣은 막냉각 홀은 기본형상과 같이 가늘어진 막냉각 효율분포를 볼 수 있지만, 동일 위치에서 기본형상에 비해 더 높은 막냉각 효율값을 보여준다.

Fig. 9

Contour plots of film cooling effectiveness for various hole configurations at M=2.0

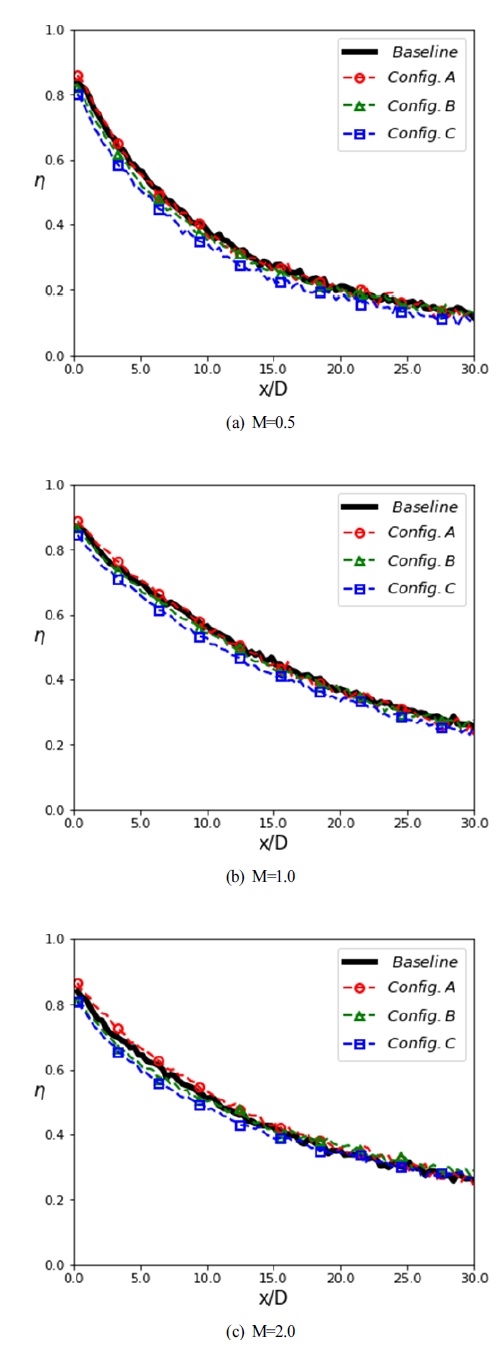
Fig. 10은 분사비별 홀의 중심선에서의 막냉각 효율을 나타낸 그래프로 기본형상과 Config. A가 유사한 막냉각 효율값을 보이며 Config. C의 경우가 가장 낮은 효율값을 보인다. 이는 홀 출구에서의 계단형 단차의 길이가 다른 형상에 비해 길어 막냉각 유체가 넓은 영역에 분사되지만, 중심부에서는 분사유량이 감소하여 낮은 효율값을 보여주기 때문인 것으로 판단된다.

Fig. 10

Film cooling effectiveness on the centerline

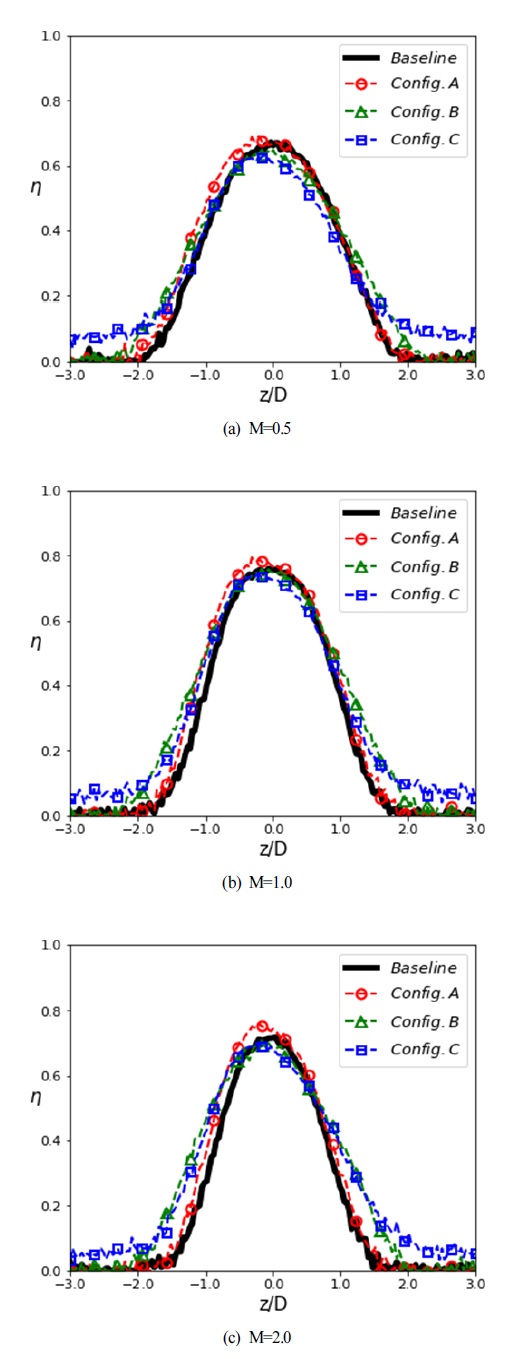
Fig. 11은 각 분사비별 x/D=3에서의 횡방향 막냉각 효율 분포이다. 전체적으로 기본형상에 비해 Config. A 가 높은 효율값을 보여준다. 그러나 홀 출구에서의 형상이 동일하여 M=1.0 에 비해 M=2.0에서 냉각유체의 표면으로부터 이탈로 인해 효율값의 분포가 더 가늘어 지는 것을 볼 수 있다.

Fig. 11

Lateral distribution of film cooling effectiveness at x/D=3

Config. B와 Config. C는 z/D=0 근처에서 Config. A에 비해 낮은 효율값을 보인다. Config. B와 Config.C는 횡방향으로 단차의 연장되어 있어 홀 출구에서 횡방향으로 냉각유체가 확산된다. 그로 인해 z/D=0 주변의 홀 중심부에서는 냉각유체의 유량이 Config. A에 비해 감소하여 낮은 효율값을 보여준다. 그러나 횡방향으로 연장된 단차로 인해 막냉각 유체가 표면을 보호하는 영역이 넓어져 |z/D|>1.6인 영역에서 Config. A 보다 높은 효율값을 보여준다.

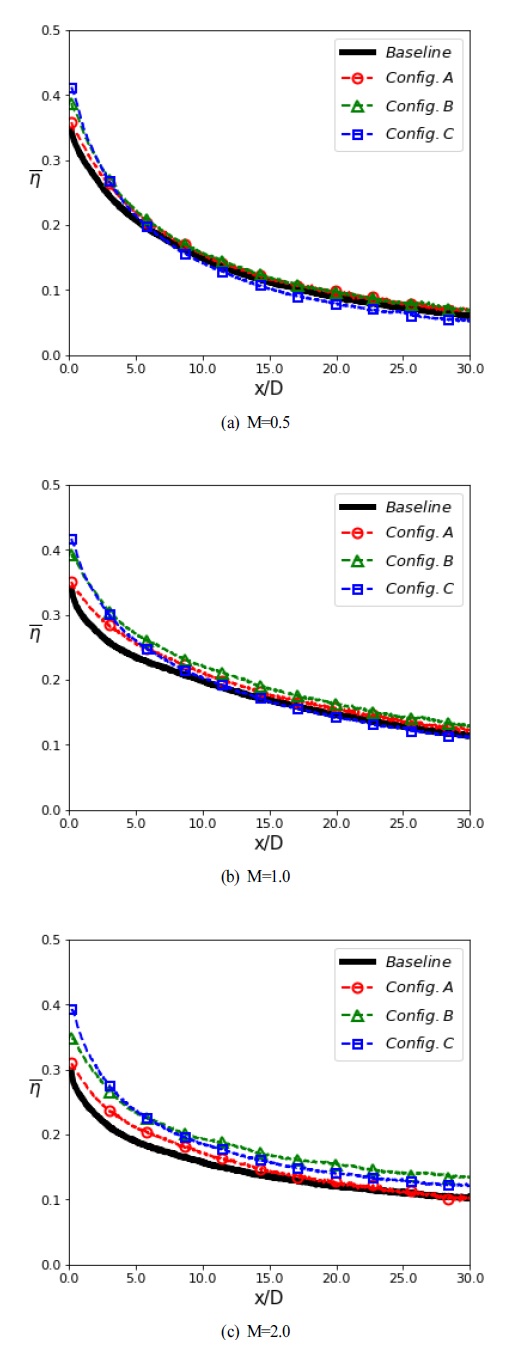
Fig. 12에서 Config. A는 기본형상에 비해 높은 횡방향평균 효율값을 보여준다. 이러한 영향은 계단형상의 단차로인해 발생하였다. 홀 출구부분에서의 계단형상의 단차는 홀 출구 부분에서 냉각유체의 정체가 형성되면서 횡방향으로 냉각유체가 균일하게 분포된다. 또한, 정체로 인한 운동량의 감소는 냉각유체가 표면으로부터 이탈하는 현상을 줄여주어 보다 높은 효율값을 나타나게 한다. 이는 분사비가 증가할수록 잘 나타나며 Fig. 12의 M=2.0의 경우, x/D=5 기준으로 기본형상에 비해 약 11%의 횡방향 평균 효율값이 증가하는 것을 볼 수 있다.

Fig. 12

Comparison of laterally averaged film cooling effectiveness

Config. B. 는 Config. A에 비해 계단형상 단차의 길이가 길어 횡방향 분포가 더 넓게 나타나 횡방향 평균효율값이 높게 나온다. Config. C에 비해서는 단차의 횡방향 길이가 짧아 단차로 인한 냉각유체의 횡방향으로 분산이 적어지며 홀의 중심부에서 냉각유체 유량의 감소가 더 적다. 결과적으로 Config. A보다 더 넓은 범위에 냉각유체가 표면을 보호할 수 있게 하며, Config. C보다 하류까지 냉각유체가 잘 유지되는 것으로 나타난다. Fig. 12의 M=2.0의 경우, 기본형상에 비해 홀 출구근처인 x/D=5에서 약 25% 증가하며 하류영역인 x/D=20에서 약 28%가 증가하는 것을 볼 수 있다.

Config. C는 계단형 단차의 횡방향 길이가 길어 횡방향 평균시 홀 출구부근에서 높은 값을 보여준다. 그러나 단차의 영향으로 인해 냉각유체가 운동량이 다른 형상에 비해 더 크게 감소하게 된다. 주유동방향으로 갈수록 주변과의 상호작용으로 인해 막냉각 효율이 감소하게 되고, Fig. 12(a)와 Fig. 12(b)에서는 기본형상의 횡방향 평균효율값보다 낮은 평균효율값을 보여준다. 그러나 M=2.0와 같은 높은 분사비의 조건에서는 냉각유체가 횡방향으로 확산이 됨에도 홀의 중심 부분에서 충분한 유량이 분사되어 하류까지 막냉각 효율이 잘 유지되는 것을 Fig. 12(c)에서 볼 수 있다.

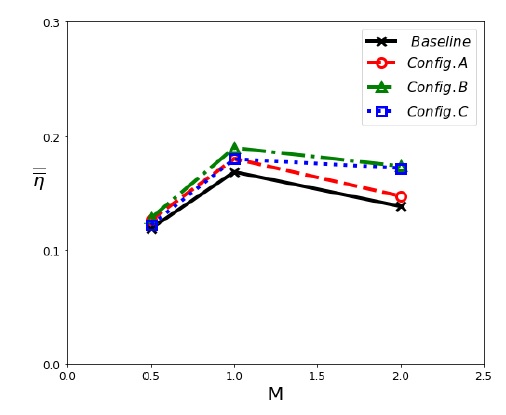
Fig. 13 은 3<x/D<30 에서의 면적평균된 효율의 값을 분사비에 따라 보여준다. M=0.5 에서는 각 형상들이 비슷한 값을 보이며, M=1.0 에서 각 형상들의 가장 높은 면적평균 효율값을 보여주며, 분사비가 높아짐에 따라 기본형상에 비해 계단형상의 단차가 적용된 형상이 더 높은 값을 보여준다. M=2.0 에서는 면적평균 효율값이 M=1.0 에 비해 감소하는데, Config. B와 Config. C의 경우 Config. A에 비해 계단형상의 단차가 횡방향으로 더 확장되어 더 넓은 영역을 냉각유체가 보호하며, 홀 출구에서 냉각유체가 횡방향으로 분산됨에도 하류까지 냉각유체가 퍼질 수 있는 충분한 유량이 분사되기 때문에 면적평균 막냉각 효율값이 완만하게 감소하는 것을 볼 수 있다.

Fig. 13

Area-averaged film cooling effectiveness for various hole configurations

이상으로 계단형상이 적용된 막냉각 홀의 경우, 분사비가 낮은 환경에서 큰 영향이 없지만 분사비가 증가함에 따라 냉각유체의 표면으로부터의 이탈을 감소하여 막냉각 효율을 높이는 경향을 확인할 수 있었다. 또한, 계단형상 단차의 횡방향 길이에 따라 막냉각 효율의 횡방향 분포의 증가를 볼 수 있었으며, 단차의 횡방향 길이에 따른 홀 중심부 근처에서의 냉각유체 유량의 감소와 그에 따른 영향을 확인할 수 있었다.

4. 결 론

본 연구에서는 평판 막냉각 실험을 통해 팬 형상의 막냉각 홀에 계단형상 단차가 막냉각 효율에 미치는 영향을 확인하였다. 단열 막냉각 효율을 측정하기 위하여 압력감응페인트를 이용하였고, 기본 팬 형상 막냉각 홀과 계단형상 단차의 횡방향 길이를 바꿔 적용한 3가지 형상을 평판에 제작하여 단열 막냉각 효율을 비교분석하였다.

시험 결과 계단형상 단차가 적용된 막냉각 홀은 기본 형상에 비해 향상된 막냉각 효율을 보여주었다. 단차형상을 가공한 경우, 홀 출구부분에서 단차의 영향으로 보다 균일한 냉각유체가 분사되도록 하여 막냉각 효율이 증가되었다. 단차의 횡방향 길이는 길어질수록 냉각유체가 보호하는 면적이 넓어져 홀 출구 부분에서 좋은 성능을 보여주었다. 낮은 분사비의 환경에서는 단차구조를 따라 횡방향으로 냉각유체가 분산되어 홀 중심부근에서의 냉각유체 유량의 감소에 의해 냉각유체가 하류까지 잘 전파되지 못해 낮은 막냉각 효율값을 보였다. 그러나 높은 분사비의 환경에서는 단차구조에 의해 횡방향으로 냉각유체가 분산되더라도 낮은 분사비의 환경에 비해 홀 중심부에서 냉각유체 유량이 하류까지 전달될 수 있을 정도로 분사한다. 그로인해 하류까지 냉각유체가 잘 전달되어 기본형상에 비해 높은 막냉각 효율값을 보인다. 횡방향 평균의 경우 x/D=5 기준으로 Config. A의 경우 기본형상에 비해 약 11%이상의 평균 효율값의 증가가 있으며 Config. B의 경우 약 25%의 평균 효율값의 증가가 관찰되었다. 면적 평균 막냉각 효율에서 계단형 단차 형상을 적용하는 경우 최대 27%까지 막냉각 효율이 증가하는 것으로 나타났다.

막냉각 홀에 계단형상 단차를 적용하여 막냉각 성능의 증가를 실험적으로 검증하였고, 성능의 증진을 확인하였다. 향후 다른 형상의 막냉각 홀에 계단형상 단차 이외의 형상정보를 적용하여 개선된 막냉각 홀 형상을 보일 예정이다.

Acknowledgments

본 연구는 산업통상자원부 주관 항공우주부품기술 개발 사업의 지원(과제번호: 10083654)에 의해 수행되었습니다.

2021 한국유체기계학회 하계학술대회 발표 논문, 2021년 7월 7일~7월 9일, 휘닉스 평창

References

• Bunker, Ronald S., 2005, “A Review of Shaped Hole Turbine Film-Cooling Technology,” ASME Journal of Heat Transfer, Vol. 127, pp. 441∼452. [https://doi.org/10.1115/1.1860562]
• Bogard, D. G. and Thole, K. A., 2006, “Gas Turbine Film Cooling,” Journal of Propulsion and Power, Vol. 22, N0. 2, pp. 249∼270. [https://doi.org/10.2514/1.18034]
• Haruyuki, T., Chiyuki, N., Syu, F., Yasuhiro A. and Masato I., 2008, “Development of Simple and High-Performance Technology for Turbine,” IHI Engineering Review, Vol. 41, No. 1, pp. 20∼31.
• Haydt. S., 2018, “Cooling Effectiveness for a Shaped Film Cooling Hole at a range of Compound Angles,” Proceedings of ASME Turbo Expo 2018, GT2018-75726 [https://doi.org/10.1115/GT2018-75726]
• Haydt. S. and Lynch. Stephen, 2018, “Flowfield of a Shaped Film Cooling Hole over a range of Compound Angles,” roceedings of ASME Turbo Expo 2018, GT2018-75728 [https://doi.org/10.1115/GT2018-75728]
• Kim, Y. J., Park, S. S., Rhee, D. H. and Kwak, J. S., 2016, “Comparative Study on the Film Cooling Effectiveness of 15° Angled Anti-Vortex Hole and 30-7-7 Fan-Shaped Hole Using PSP Technique,” The KSFM Journal of Fluid Machinery, Vol. 19, No. 4, pp. 13∼18. [https://doi.org/10.5293/kfma.2016.19.4.013]
• Park, S. H., Kang, Y. J., Seo, H. J., Kwak, J. S. and Kang, Y. S., 2019, “Experimental optimization of a fan-shaped film cooling hole with 30 degrees-injection angle and 6-hole length-to-diameter ratio,” International Journal of Heat and Mass Transfer 144 (2019) 118652 [https://doi.org/10.1016/j.ijheatmasstransfer.2019.118652]
• Schroeder, R. P., Thole, K. A., 2014, “Adiabatic Effectiveness Measurements for a Baseline Shaped Film Cooling Hole,” Proceeding of ASME Turbo Expo 2014, GT2014-25992 [https://doi.org/10.1115/GT2014-25992]
• Wang, H. and Wright, L. M., 2021, “Effect of Inlet Geometry on Flat Plate, Film Cooling Effectiveness from Shaped Holes,” Proceedings of the ASME 2021, IMECE2021-73135
• Elyas, A., Kusterer, K., Bohn, D., Sugimoto, T., Tanaka, R. and Kazari, M., 2011, “The NEKOMIMI Cooling Technology: Cooling Holes with Ears for High-Efficient Film Cooling,” Proceeding of ASME Turbo Expo 2011, GT2011-45524 [https://doi.org/10.1115/GT2011-45524]
• Kusterer, K., Tekin, N., Wüllner, T., Bohn, D., Sugimoto, T., Tanaka, R. and Kazari, M., 2014, “NEKOMIMI Film Cooling Holes Configuration under Conjugate Heat Transfer Conditions,” Proceeding of ASME Turbo Expo 2014, GT2014-25845 [https://doi.org/10.1115/GT2014-25845]
• Okita, Y., Ideta, T., and Fujimoto, S., 2020, “Multi-Objective Shape Optimization of Arrowhead-shaped Film Cooling Hole on Transonic Turbine Blade,” Proceedings of ASME Turbo Expo 2020, GT2020-14721 [https://doi.org/10.1115/GT2020-14721]
• Schmidt, D. L., Sen, B., and Bogard, D. G., 1996, “Effects of Surface Roughness on Film Cooling,” American Society of Mechanical Engineers, ASME Paper 96-GT-299. [https://doi.org/10.1115/96-GT-299]
• Goldstein, R. J., Eckert, E. R. G., Chiang, H. D., and Elovic, E., 1985, “Effect of Surface Roughness on Film Cooling Performance,” Journal of Engineering for Gas Turbines and Power, Vol. 107, pp. 111∼116. [https://doi.org/10.1115/1.3239669]
• Cutbirth, J. M., and Bogard, D. G., 2002, “Evaluation of Pressure Side Film Cooling with Flow and Thermal Field Measurements, Part I: Showerhead Effects,” Journal of Turbomachinery, Vol. 124, pp. 670∼677. [https://doi.org/10.1115/1.1504441]
• Mehendale, A. B., and Han, J. C., 1992, “Influence of High Mainstream Turbulence on Leading Edge Film Cooling Heat Transfer,” Journal of Turbomachinery, Vol. 114, pp. 707∼715. [https://doi.org/10.1115/1.2928023]
• Moore, J. D., Horner, M. J. and Bogard, D. G., 2020, “Adiabatic Effectiveness and Thermal Field Measurements of a Shaped Hole in the Showerhead of a Model Turbine Blade,” Proceeding of ASME Turbo Expo 2020, GT2020-15016 [https://doi.org/10.1115/1.0003240V]
• Kim, G. M., Kim, Y. J. and Kwak, J. S., 2017, “Improvement of Film Cooling Performance of a Slot on a Flat Plate Using Coanda Effect,” The KSFM Journal of Fluid Machinery, Vol. 20, No. 2, pp. 05∼10. [https://doi.org/10.5293/kfma.2017.20.2.005]
• Benabed, M., 2015, “Computational Optimization of Coanda Effect on Film-Cooling Performance,” J. Thermophysics and Heat Transfer, Vol. 29, Issue 4. [https://doi.org/10.2514/1.T4487]
• Lu, Y., Dhungel, A., Ekkad, S. V. and Bunker, R. S., 2009, “Effect of Trench width and depth on film cooling from cylindrical holes embedded in trenches,” ASME Journal of Turbomachinery, Vol. 131, 011003 [https://doi.org/10.1115/1.2950057]
• Oguntade, H. I., Andrews, G. E., Burns, A. D., Ingham D. B. and Pourkashanian, M., 2013, “Improved trench film cooling with shaped trench outlets,” ASME Journal of Turbomachinery, Vol. 135, 021009 [https://doi.org/10.1115/1.4006606]
• Wang, C., Sun, X. and Zhang, J., 2019, “Uncertainty analysis of trench film cooling on flat plate,” Applied Thermal Engineering 156, 562-575 [https://doi.org/10.1016/j.applthermaleng.2019.04.099]
• Park, S. D., Lee, K. S., Kim, H. B., Kwak, J. S., and Kim, J. H., 2008, “Measurement of the Film Cooling Effectiveness on a Flat Plate using Pressure Sensitive Paint,” The Korean Society of Propulsion Engineers, Vol. 12, No. 5, pp. 67∼72.
• “Binary FIB PSP Data Sheet,” Innovation Scientific Solution, Inc., 2012, https://innssi.com/binary-pressure-sensitive-paint, /.
• Natsui, G., Little, Z., Kapat, J. S., Dees, J. E. and Laskowski, G., 2016, “A Detailed Uncertainty Analysis of Adiabatic Film Cooling Effectiveness Measurements Using Pressure-Sensitive Paint,” ASME Journal of Turbomachinery, Vol. 138, 081007 [https://doi.org/10.1115/1.4032674]