휴대용 수력 터빈 이노마드 우노의 성능향상을 위한 최적설계

1. 서 론

전 세계적으로 탄소 배출을 저감하기 위한 제도 개선, R&D 투자 등 정부와 민간의 노력이 지속적으로 확대되고 있다. 우리나라 역시 ‘2050 탄소중립’ 추진전략을 공표한 바 있고, 친환경⋅저탄소⋅에너지산업 분야 유망기술 보유기업 발굴 및 지원하여 저탄소산업 생태계를 조성하기 위한 정책을 추진 중이다.

전 세계 인구의 20%는 에너지원을 이용하지 못하며 이러한 에너지 취약계층은 개발도상국에서 상대적으로 높은 비율을 차지하고 있다. 개발도상국 내 도서산간 및 오지 지역주민들의 에너지 빈부 격차는 지속적으로 증가하고 있으며, 이들은 주로 케로신, 디젤 등의 화석연료를 사용하여 환경오염을 유발하고 있다.

에너지산업은 현대사회에서 매우 중요한 비중을 차지하고 있으며, 기존의 전통적 에너지자원인 화석연료의 의존도를 줄이고 친환경⋅저탄소 재생에너지원을 활용한 산업으로 변화하고 있다.

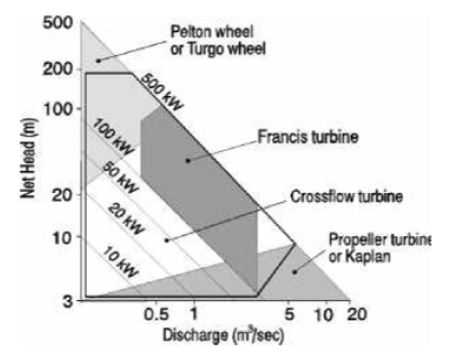
수력 발전은 탄소 배출이 ‘0’으로, 탄소중립을 실현하기에 매우 적합한 발전 방식이며, 최근에는 낙차가 거의 없는 강이나 하천 또는 건물의 오수 등 미활용 에너지원을 활용한 소수력 발전에 대한 연구¹⁾가 활발히 이루어지고 있다. 일반적으로 저낙차 조건에서 설치하는 수차는 마이크로(Micro) 수차로 분류하여 소규모 수원지 및 관로 등에 적용한 연구가 주를 이루고 있다.²⁾ 사용 환경(유량 및 낙차)에 따라서 수차의 형식을 분류한 Fig. 1과 같이 저낙차 조건에서는 프로펠러(Propeller) 형태의 수차가 적합하며,³⁾ 러너(Runner)와 가이드 베인(Guide vane)에 의해 수력학적 성능이 결정된다.^4,5) Park 등⁴⁾은 10 kW급 프로펠러형 수차를 대상으로 러너의 깃 수 변화에 따른 수차의 성능을 전산유체해석을 통해 분석하였고, 설계유량을 기준으로 저유량에서 깃 수가 증가할수록 높은 효율을 얻을 수 있고, 고유량에서는 깃 수의 영향이 거의 없음을 확인하였다. Li 등⁵⁾은 벌브(Bulb)형 수차의 가이드 베인의 개도 변화에 따른 수차의 수력학적 성능을 분석하였다. 이처럼 소수력 발전용 수차를 대상으로 가이드 베인의 개도율, 러너의 깃 수 변화 및 유량(낙차) 조건 변화에 따른 연구들은 많이 수행되었지만, 낙차가 거의 없는 사용 환경에서 사용될 수 있는 조류형 소수력 수차에 대한 연구는 거의 수행되지 않았다. 조류형 수차는 주로 바닷속에 설치되어 해류를 이용해 발전한다. 따라서 직경이 매우 크고, 낙차 없이 발전이 가능하다. 이러한 특징을 착안하여 낙차가 거의 없는 환경에서도 발전이 가능하도록 조류형 소수력 수차를 ㈜이노마드에서 기개발하였다.

Fig. 1

Classification of the hydraulic turbines according to the usage conditions3)

본 연구에서는 캠핑용 휴대용 수차로 개발된 ㈜이노마드의 Enomad UNO를 대상으로 다양한 미활용 에너지원을 활용하여 범용 발전이 가능하도록 수력학적 성능을 향상시키고자 하였으며, 이를 위하여 머신러닝 기반 최적설계를 접목하여 러너의 최적형상을 도출하였다.

2. 수치해석 및 최적설계 방법

2.1 수치해석 방법

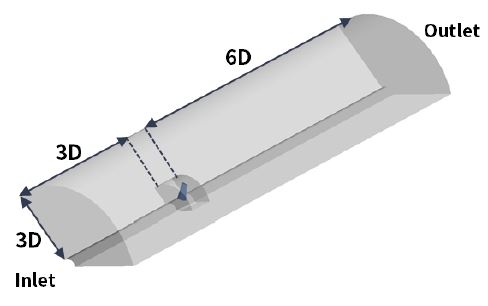
본 연구에서는 기존 Enomad UNO의 수력학적 성능을 분석하기 위해 정상상태 Reynolds-averaged Navier-Stokes (RANS) 해석을 수행하였고, 상용코드인 ANSYS-CFX 19.0⁶⁾을 사용하였다. 기존 Enomad UNO의 형상은 Fig. 2와 같이 조류형 익형으로 설계되었다. 계산 시간의 단축과 수렴성 향상을 위해 계산영역은 Fig. 3과 같이 회전축을 중심으로 주기조건을 부여하여 설정하였으며, 러너를 기준으로 입구부, 출구부 및 외부 경계면은 각각 러너 직경(D)의 3배, 6배 및 3배로 구성하였다.⁷⁾

Fig. 2

Enomad UNO Reference model

Fig. 3

Computational domain for the numerical analysis

작동유체는 25°C의 물을 사용하였으며, 입구 경계조건은 사용 환경에 따른 유속범위를 부여하였고, 출구 경계조건은 표준상태 대기압으로 가정하였다. 회전 영역과 정지 영역 사이의 경계조건은 Frozen rotor 방식⁶⁾을 적용하였다.

수치해석을 위해 계산영역의 격자는 Fig. 4와 같이 구성하였고, 회전 영역과 정지 영역은 각각 Turbo-grid와 ANSY-ICEM⁶⁾을 사용하였다. 러너의 표면에는 O형 격자를 사용하여 격자계를 구성하였고, Low-Reynolds number SST 난류모델 사용을 위해 y⁺가 11 미만으로 유지되도록 하였다.

Fig. 4

Grid system obtained by using GCI method

격자의존성을 제거하기 위해 Richardson 외삽법을 기반으로 한 이산화 오류 예측법⁸⁾을 사용하여 최적의 격자계를 선정하였다. 이를 위하여 3개의 서로 다른 격자계(N₁, N₂ 및 N₃)를 구성하였고, 격자 세분화 인자를 약 1.3으로 설정한 격자 의존성 시험 결과를 Table 1에 나타내었다. 이를 위해 다음과 같이 정의된 수차의 발전계수(C_p)를 사용하였고, N₁의 발전계수 값으로 나누어 무차원화하였다.

$\[ C_p=\frac{\tau \omega }{\frac{1}{2}\rho A{U}^3} \]$

(1)

Table 1

Grid dependency test using grid convergence index

여기서 τ와 ω는 각각 러너에 작용하는 토크와 회전 속도를 의미하며, ρ, A 및 U는 각각 작동 유체의 밀도, 입구부 면적과 입구 유속을 의미한다.

Table 1에 나타낸 바와 같이 격자수가 증가할수록 러너의 발전계수가 점차 수렴하는 경향을 보이며, N₁을 사용한 경우의 외삽 상대오차(e_ext²¹)와 격자 수렴 지표(GCI_fine²¹)가 각각 0.024 및 0.0003으로 예측되어 매우 작은 수치적 불확실성이 확인되었다. 이 결과를 바탕으로 N₁을 최적의 격자계로 선정하여 최적설계를 수행하였다.

2.2 최적설계 방법

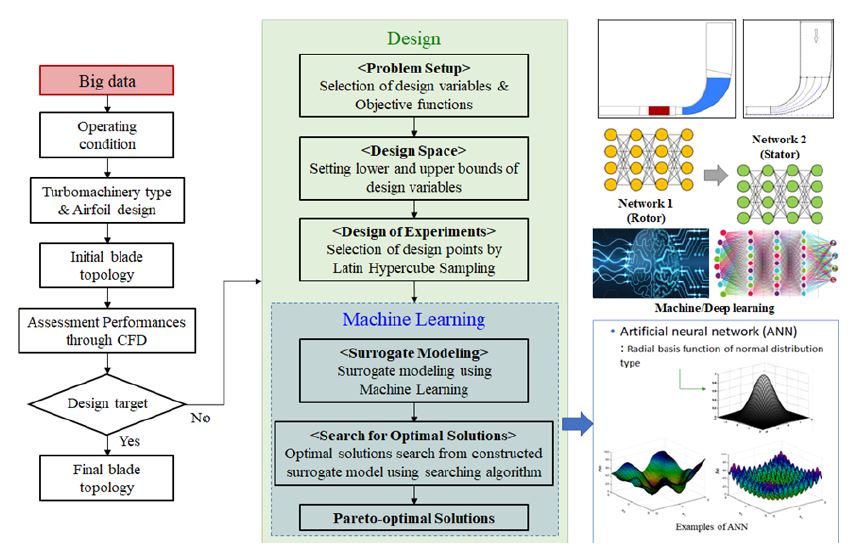
머신러닝 기반 최적설계의 과정을 Fig. 5에 순서도로 나타내었다. 먼저 설계변수와 목적함수를 결정하는 최적설계 문제 정의를 시작으로 설계영역을 구성하여 실험계획법(Design of experiment)을 통해 실험점을 도출한다. 이 실험점에서의 목적함수 값들을 수치해석을 통해 계산하여 머신러닝을 위한 입력값(Input data)을 만들고, 인공신경망(Artificial neural network) 기법을 사용하여 대리모델을 구축한다. 인공신경망의 예측 정확도를 향상시키기 위해 머신러닝을 적용하여 훈련된 대리모델 상에서 유전 알고리즘(Genetic algorithm)을 사용해 최적해를 찾아 설계영역 내에 값이 존재하면 최적설계 과정이 종료된다.

Fig. 5

Procedure of the optimization based on machine learning

2.2.1 설계변수

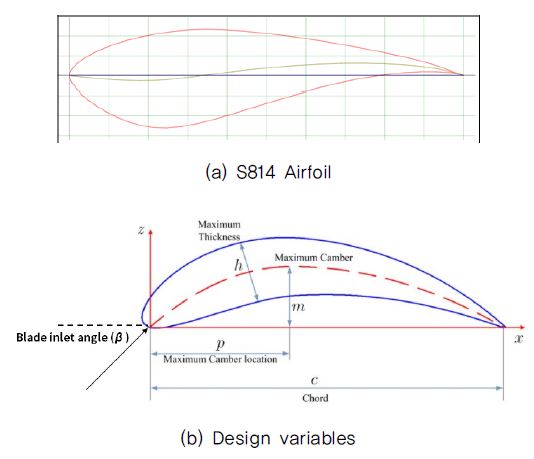
본 연구에서 사용된 러너 블레이드의 단면은 Fig. 6에 나타낸 바와 같이 S814 airfoil이 사용되었고, 수차의 발전계수를 극대화하기 위하여 70% 및 팁 스팬(Tip span)에서 입구 각도(β)와 최대 두께 위치(σ)를 설계변수로 선정하였다. 총 4개의 설계변수가 최적설계를 위해 선정되었으며, 각 설계변수의 범위는 Table 2에 나타내었고, 기준 형상의 값으로 나누어 무차원화하였다.

Fig. 6

2D cross-sectional view of the runner

Table 2

Range of the design variables

각 설계변수의 범위는 러너 블레이드의 주물 제작을 고려하여 선정하였고, 추후 유체-구조 연성해석을 통해 구조적 안정성을 분석할 예정이다.

전술한 바와 같이 실험계획법을 사용하여 설계영역 내 실험점을 도출하였고, 본 연구에서는 Latin hypercube sampling (LHS) 기법을 사용하여 48개의 설계점을 도출하여 각 실험점에서 목적함수인 수차의 발전계수를 계산하여 Table 3에 나타내었고, 각 값들은 기준 형상의 값으로 나누어 무차원화하였다.

Table 3

Design of experiment

2.2.2 대리모델

본 연구에서는 인공신경망 기법 중 하나인 Radial basis neural network (RBNN)을 사용하여 대리모델을 구축하였다. 인공신경망은 경험과 기존 자료로부터 학습하는 인간의 기능을 묘사한 기법으로 신경회로망의 기본요소인 각 뉴런(Neuron)의 출력은 뉴런에 저장되었거나 도착하는 국부적인 정보에만 의존한다. 따라서 망의 예측 능력은 가중치들에 의해 반영되고, 망의 훈련은 자료를 통한 반복에 의해 수행된다. 이 과정에서 머신러닝을 통해 인공신경망의 예측 능력을 향상시키고, 본 연구에서는 K-fold cross validation⁹⁾을 사용하여 망의 학습을 수행하였다.

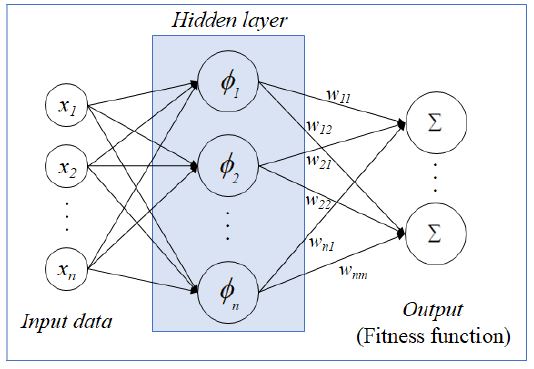
RBNN은 Fig. 7에 나타낸 바와 같이 입력층, 출력층 및 은닉층(Hidden layer)으로 구성되어 있으며, 은닉층과 출력층은 방사형 기저 전달함수와 선형 출력으로 이루어진다. 본 연구에서는 Matlab¹⁰⁾의 내장함수인 ‘newrb’을 사용하였고, 방사형 기저 전달함수는 다음과 같이 정의되었다.

$\[ a=radbas\left(‖w_i-p‖b\right) \]$

(2)

$\[ radbas\left(n\right)=e^{-n^2} \]$

(3)

Fig. 7

Construction of the RBNN model

여기서 b는 바이어스이고, w는 각 뉴런의 가중치 벡터, p는 입력값을 의미한다. 각 뉴런들은 출력 가중치가 결합되어 선형결합으로 출력되며, 다음과 같이 나타낼 수 있다.

$\[ f\left(x\right)=\sum _{j=1}^N{\left(w_{\mathrm{o}}\right)}_j{\varphi }_j \]$

(4)

여기서 (w_o)_j는 가중치이고, φ_j는 방사형 기저 함수를 나타낸다. RBNN의 가장 큰 장점은 선형 출력으로 구성된 출력망으로 인해 계산시간을 감축시킬 수 있다는 것이다.

3. 결과 및 검토

3.1 최적설계

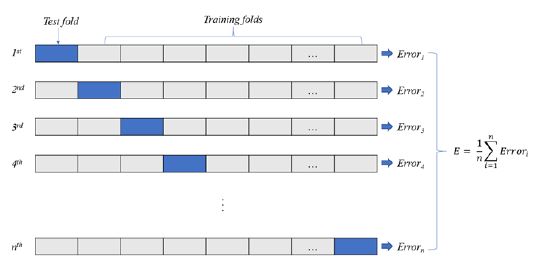
RBNN 모델을 구축하기 위해 각 층의 가중치(w_i, w_o), 뉴런의 수(n)와 확산 상수(Spread constant, SC)가 필요하며, 이 변수 값들은 머신러닝을 통해 도출된다. 머신러닝은 반복적인 학습을 통해 예측오차가 최소가 되는 변수 값들을 찾는 과정이다. 이를 위해 K-fold cross validation 방법을 적용하였다. 이 방법은 Fig. 8과 같이 입력값을 K개의 분리된 부분집합으로 분할하고, 각 부분 집합에서 Test fold를 선정하여 Training fold로 RBNN을 훈련한다. 이 때 훈련된 RBNN의 예측값은 Test fold의 실제 값과 비교하여 상대오차를 계산하고, 이 과정을 K번 반복하여 각 부분 집합의 상대오차를 합산한다. 본 연구에서 사용된 머신러닝은 이러한 과정을 통해 합산된 상대오차를 최소화할 수 있는 변수 값들을 찾도록 반복 수행된다.

Fig. 8

K-fold cross-validation

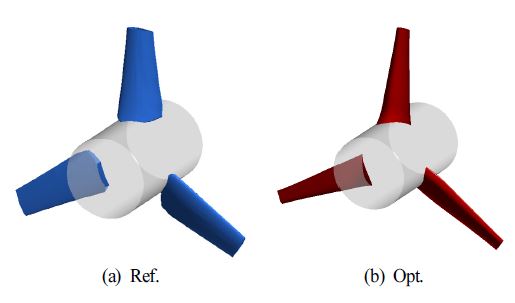
Table 4와 Fig. 9에 본 연구에서 수행한 최적설계 결과를 나타내었다. 최적설계를 통해 70% 및 팁 스팬에서의 러너 입구 각도가 증가하였고, 러너 단면인 Airfoil의 최대 두께의 위치가 팁 스팬에서는 하류 방향으로 이동하고, 70% 스팬에서는 상류 방향으로 이동한 것을 확인할 수 있다. 이러한 러너 형상의 변화를 통해 발전계수가 약 5% 향상된 것으로 예측되었고, 수치해석을 통해 예측값과 비교한 상대오차는 약 7% 미만으로 최적설계의 예측 결과가 매우 정확한 것을 알 수 있다.

Table 4

Optimization results

Fig. 9

Comparison of the 3D geometries

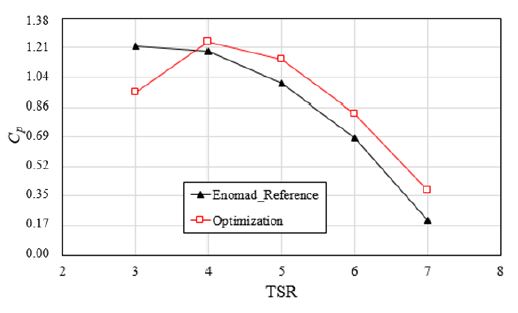
Fig. 10은 기준 형상과 최적 형상의 주속비(Tip speed ratio, TSR)에 따른 발전계수를 비교한 결과를 보여주고 있으며, 주속비는 다음과 같이 정의하였다.

$\[ TSR=\frac{r\omega }{U} \]$

(5)

Fig. 10

Comparison of the performance curves

여기서 r, ω 및 U는 각각 러너 블레이드의 반지름, 회전 속도 및 입구 유속을 의미한다,

주속비가 3일 때를 제외하고, 모든 주속비 영역에서 최적 형상의 발전계수가 기준 형상과 비교하여 향상된 것을 확인할 수 있다. 특히, 목적함수인 주속비 5일 때의 발전계수는 기준 형상과 비교하여 약 5% 향상되었으며, Enomad UNO의 배터리 완충시간을 기준으로 약 1시간 이상 감축시킨 것으로 환산할 수 있다.

3.2 수력학적 성능

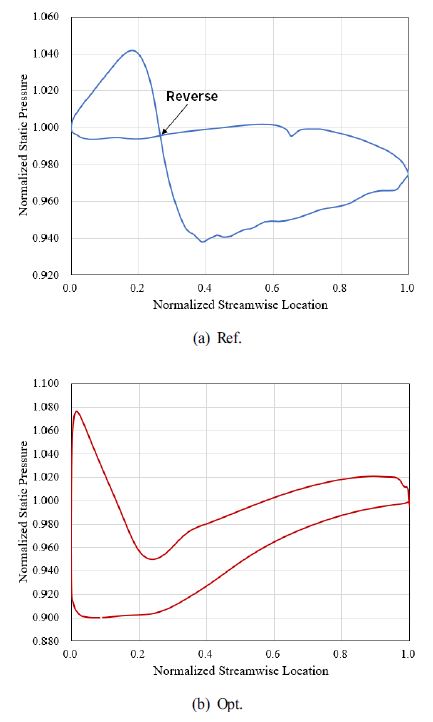
Fig. 11은 기준 형상과 최적 형상의 70% 스팬에서 러너에 작용하는 정압 분포를 비교하고 있다. Fig. 11 (a)에서 보는 바와 같이 기준 형상의 경우 정압 분포가 전연(Leading edge)에서부터 약 20% 위치에서 역전되는 현상이 관찰되었다. 이러한 현상은 러너의 받음각(Angle of attack)이 초기 설계 의도와 다르게 형성되었을 때 발생하며, 발전 효율이 현저히 저하되게 된다. 반면, 최적 형상의 경우 러너의 받음각이 최적화되어 압력면과 흡입면에서의 정압 분포가 Fig. 11 (b)와 같이 형성되는 것을 관찰할 수 있다.

Fig. 11

Static pressure distribution on the runner surface at 70% span

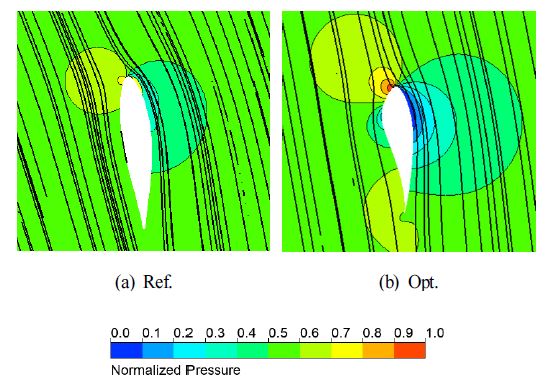
주속비가 5일 때 러너의 70% 스팬에서 유선분포를 Fig. 12에 나타내었다. 앞서 설명한 바와 같이 기준 형상의 경우 Fig. 12 (a)에 나타난 바와 같이 받음각이 초기 설계 의도와 다르게 되어 압력면에서 정체점이 형성되는 것을 확인할 수 있다. 최적 형상의 경우 Fig. 12 (b)에 나타난 바와 같이 러너의 전연에서 정체점이 형성되었고, Airfoil의 최대 두께 위치가 상류 방향으로 이동하여 압력면과 흡입면의 압력차이가 발생한 것을 알 수 있다.

Fig. 12

Static pressure distribution with streamline at 70% span

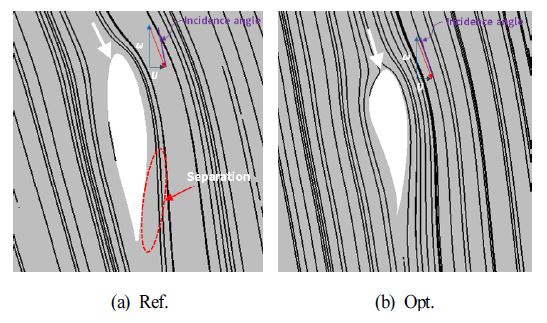
Fig. 13은 앞선 유동특성을 반영한 속도 삼각형 분석 결과를 보여준다. 기준 형상의 러너 입구 각도와 유동 각도가 차이가 발생하여 붙임각(Incidence angle)이 최적 형상과 비교하여 상대적으로 큰 것을 알 수 있다. 이로 인해 Fig. 12 (a)에서 관찰된 바와 같이 러너의 후연(Trailing edge) 부근에서 유동박리가 발생한 것을 확인할 수 있다. 이와는 반대로 최적 형상의 경우 받음각이 기준 형상보다 작게 설계되어 붙임각 또한 비교적 작게 형성된 것을 알 수 있다.

Fig. 13

Velocity triangle diagram with streamline at 70% span

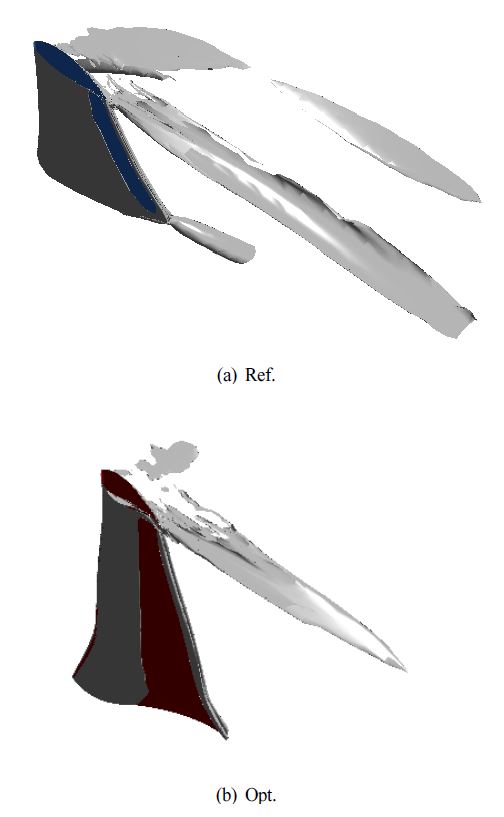
Fig. 14는 러너 회전에 따른 계산영역 내부의 선회 강도(Swirling strength)를 나타내고 있다. 기준 형상의 경우 앞서 설명한 바와 같이 붙임각이 상대적으로 크게 형성되어 심한 유동박리 현상이 발생하고, 그로 인한 선회 현상이 발달하여 Fig. 14 (a)에 나타난 바와 같이 러너 회전 반대방향으로 선회 현상이 지속되는 것을 알 수 있다. 최적 형상의 경우 붙임각이 기준 형상과 비교하여 상대적으로 작기 때문에 유동박리 현상이 억제되었고, 선회 현상 또한 감소된 것을 관찰할 수 있다.

Fig. 14

Comparison of the velocity swirling strength (s=100s-1)

4. 결 론

본 연구에서는 휴대용 수력 터빈으로 개발된 Enomad UNO를 대상으로 다양한 사용 환경에서도 사용이 가능하도록 수력학적 성능을 향상시키기 위한 머신러닝 기반 최적설계를 수행하였다. 기존 형상의 러너를 최적설계의 대상으로 하여 발전 성능과 관련 있는 팁 부근 4개의 형상변수를 설계변수로 선정하였다. 대리모델로 사용된 RBNN의 예측정확도를 향상시키기 위해 머신러닝을 적용하였고, 최적설계의 예측 값과 RANS 해석 결과의 상대오차는 7% 미만으로 매우 정확한 예측 성능을 보여주었다. 최적설계를 통해 넓은 주속비 범위에서 발전계수가 향상된 결과를 보여주었으며 특히, 주속비가 5일 때 발전효율이 5% 이상 향상되었다.

본 연구를 통해 도출된 최적설계 형상은 성능을 검증하기 위해 시제품으로 제작될 예정이며, 후속 연구를 통해 입구 가이드 베인 설계를 수행하여 더욱 넓은 운전 범위에서 고효율로 발전이 가능한 휴대용 수력 터빈을 개발할 예정이다.

Acknowledgments

본 연구는 과학기술정보통신부의 재원인 융합연구사업(No.ES200006)과 기획재정부의 재원인 한국생산기술연구원의 중소⋅중견기업 생산기술 실용화 및 기술지원 사업(No. JE210011)의 일환으로 수행되었음을 밝히며, 이에 감사드립니다.

References

• Lee, S. Y., Choi, Y. D., Hwang, Y. C., and Lee, Y. H., 2009, “A study on internal flow characteristics and performance analysis of a micro hydro tubular turbine,” Proceedings of the Korean Society for New and Renewable Energy, pp. 606-609.
• Park, N. H., and Rhee, Y. W., 2013, “Output optimization of microhydro kaplan turbine by double regulating runner and guide vane,” The KSFM Journal of Fluid Machinery, Vol. 16, No. 1, pp. 17-23. [https://doi.org/10.5293/kfma.2013.16.1.017]
• Gatte, M. T., and Kadhim, R. A., “Hydro power,” Open access peer-reviewed chapter. [https://doi.org/10.5772/52269]
• Park, J. H., Kim, Y. T., Cho, Y., Kim, B. K., and Lee, Y. H., 2014, “Performance analysis of 10kW class propeller hydro turbine by the change of flow rates and the number of runner vane using CFD,” The KSFM Journal of Fluid Machinery, Vol. 17, No. 2, pp. 5-11. [https://doi.org/10.5293/kfma.2014.17.2.005]
• Li, K. M., Kwon, W., and Lee, Y. W., 2019, “Numerical study on effects of guide vane opening of a bulb turbine,” Journal of the Korean Society of Marine Engineering, Vol. 43, No. 7, pp. 528-534. [https://doi.org/10.5916/jkosme.2019.43.7.528]
• ANSYS Inc., 2018, “ANSYS CFX-19.0, ANSYS CFX-solver theory guide,” Canonsburg, PA, USA.
• Lee, K. H., 2016, “Analysis of horizontal axis tidal turbine performance and turbine efficiency deficit from blade deformation,” Ph.D. Thesis, Inha University.
• Celik, I., and Karatekin, O., 1997, “Numerical experiments on application of richardson extrapolation with nonuniform grids,” Journal of Fluids Engineering, Vol. 119, No. 3, pp. 584-590. [https://doi.org/10.1115/1.2819284]
• Stone, M., 1974, “Cross-Validatory Choice and Assessment of Statistical Predictions,” Journal of the royal statistical society: Series B Methodology, Vol. 36, pp. 111-133. [https://doi.org/10.1111/j.2517-6161.1974.tb00994.x]
• Math Work, Inc., 2014, “MATLAB 2014, The Language of Technical Computing,” Natic, MA, USA.