A Study on the Flow around a D-shape Bluff Body with Arc-Groove

1. 서 론

물체 표면의 유동을 제어하여 항력을 저감시키면 비행기, 자동차, 선박 등의 효율을 증가시켜 에너지 절감에도 효과가 크다. 따라서 물체 주위의 유동장 제어에 관한 응용연구는 유체역학적으로 중요한 연구과제이다.(1)

특히 외부에너지의 공급 없이 물체의 기하학적 형상을 변경하여 물체의 항력을 저감하는 것은 공학적 측면과 실용적인 측면에서 중요하다고 할 수 있다.

이러한 외부에너지의 공급 없이 수동적 유동 제어 방법 중에서 대표적인 예가 골프공의 딤플(dimple)을 들 수 있다. 골프공의 표면에 압입의 방법으로 딤플 형상을 구현하고, 구현된 딤플형상은 외부 유동에 의해 딤플 내부에 캐비티 유동이 발생한다. 이렇게 발생된 캐비티는 표면 경계층이 교란을 받아 운동에너지가 혼입되어 골프공 표면의 유동 박리를 지연되는 것으로 알려져 있다.

Bearman and Harvey(2)는 딤플을 원주 표면에 형성하여 2 ×10⁴ ≤Re ≤ 3×10⁵ 범위에서 항력계수(Drag Coefficient, C_D)와 스트로할수(Strouhal Number, S_t)를 측정하여 항력계수의 변화를 측정하였고, 노기덕과 박지태(3)는 정방형 딤플에 의해 원주의 항력이 28 % 감소함을 확인하였다.

딤플 대신 그루브(groove)에 의한 유동제어를 통해 항력감소를 위한 연구 또한 다양하게 이루어지고 있다. Takeyoshi and Michihisa(4)는 원주 표면에 하나의 호형 그루브(arcgroove)를 설치하여 항력 감소 효과를 연구하였고, Shinichi 등(5)은 Groove의 깊이가 원주의 항력과 유동장 변화에 미치는 영향을 연구하였다. 그리고 Robarge and Stark(2004)(6)는 익형 NACA 0015에 하나의 호형 Groove를 설치하여 실험한 결과, 최적의 Groove 깊이는 경계층 두께의 0.6에서 1.0의 범위이며, Groove의 폭 대비 깊이의 비는 0.1에서 0.15가 최적값임을 밝힌 바 있다. Suresh et al(7)은 D-형상의 물체 표면에 거칠기를 두어 전산해석을 통해 항력 저감 효과를 관찰하였다.

본 연구에서는 D-형상의 물체 표면에 Arc-Groove를 형성하여 물체 표면에서의 후류 경계층과 유동장의 변화 그리고 와유출 현상을 살펴봄으로써 과연, D-형상에서 Arc-Groove가 항력 저감에 효과가 있는지를 확인하고자 한다.

2. 실험장치 및 방법

본 실험은 풍동을 이용하여 수행하였으며, 풍동은 개회로형 아음속 풍동으로 측정부의 크기는 305mm×305mm(가로×세로)이다. 실험구간의 난류강도는 약 1%로 균일유동을 유지하도록 하였다. 후류 유동장 측정에는 정온형 열선풍속계(TSI, model IFA300)와 I형 열선과 X형 열선(Kanomax)을 사용하였으며, 열선풍속계에서 나오는 전압신호는 5㎑의 저역통과 필터를 거쳐 A/D변환기를 통해 PC로 저장하였다. 자료의 추출간격을 100 μs(10 kHz)로 하여 측정 지점당 40,960개의 데이터를 획득하여 통계 처리하였다. X형 열선 프로브의 이송은 정밀도가 0.01 mm인 자동이송장치를 사용하였다.

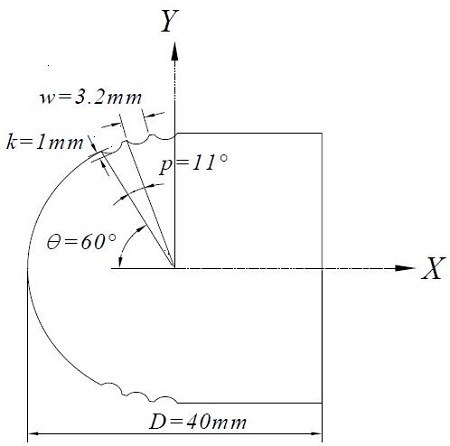
실험에 사용한 D-형상 실린더와 좌표계를 Fig. 1에 나타내었다. 실험에 사용한 모델은 표면이 매끈한 형상의 실린더를 포함하여 총 3가지이다. Groove의 깊이는 1 mm이며, Groove의 폭은 3.2 mm로 원주 직경 대비 8 %이다. Groove간 피치는 11°로 설정하였다. 실린더의 직경은 40mm이다. 자유유동속도는 6.5m/s에서 21m/s까지 변화시켰으며, 이에 대응하는 레이놀즈수(Re)는 1.72×10⁴ ≤Re≤5.54×10⁴ 이다.

Fig. 1.

D-shape bluff body

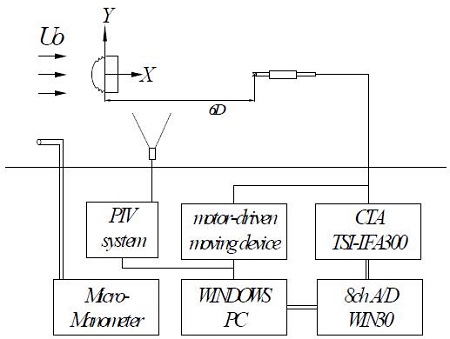
Fig. 1에서 보는 바와 같이 Groove의 각도는 X 좌표상에서 가장 가까운 첫 번째 Groove의 중심을 기준으로 60°로 고정하였다. 후류 유동장은 X=6D 지점에서 Y=+3D ∼ -3D 범위로 0.8mm 간격으로 31지점에서 X형 열선브로프로 측정하였으며, 실린더 표면의 경계층 유동은 I형 열선 프로브를 이용하여 속도를 측정하였다. 그리고 측정시스템의 개략도는 Fig. 2와 같다.

Fig. 2.

Diagram of measuring and data processing

3. 실험 결과 및 고찰

3.1 시간평균 후류 유동장

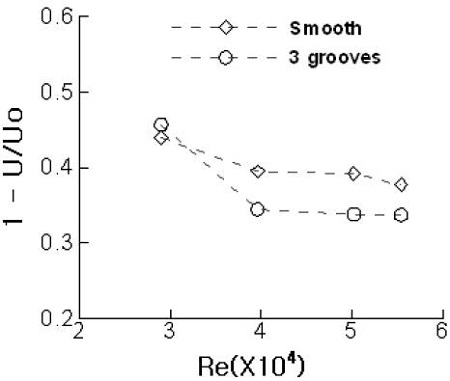
Fig. 3은 후류 유동장에서 최대 속도 결손(maximum velocity defect)을 비교한 것이다. 최대 속도 결손은 Y=0에서 U속도의 결손량으로 자유유동 속도(U_o)와의 차이값이다. Re ≥ 4×10⁴에서는 표면이 매끈한 물체와 Groove가 형성된 물체와의 최대 속도 결손량에 차이가 다소 커지고 있고, 그 차이값도 일정하게 유지되고 있다.

Fig. 3.

Maximum velocity defect

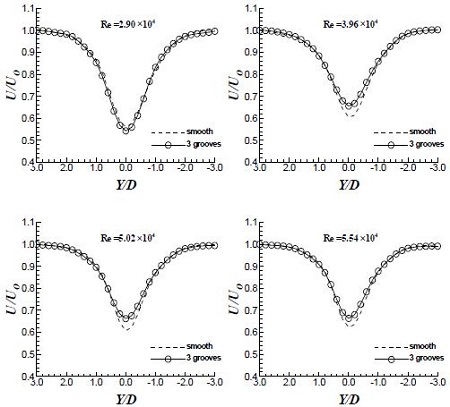
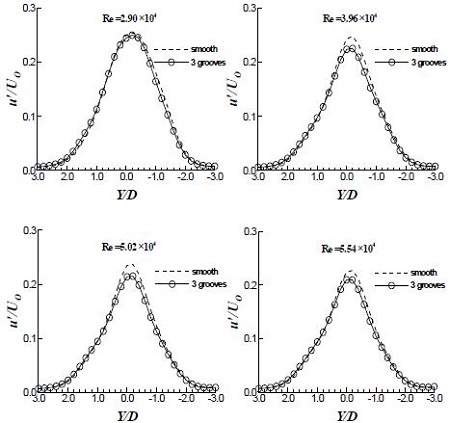
Fig. 4는 후류 유동장의 U/U_o를 분석한 결과이다. Re ≥ 4×10⁴에서 Groove가 3개인 경우, 후류유동장에서 속도 회복이 조금씩 나타나고, 이후의 Re 범위에서 모두 비슷한 속도 회복 양상을 보이고 있다. 속도 회복은 항력 저감의 효과를 정성적으로 판단할 수 있는 인자(parameter)로 Groove에 의한 항력 저감 효과가 나타나고 있음을 알 수 있다. 하지만 속도 회복량은 크지 않은 것으로 보인다.

Fig. 4.

Streamwise time mean velocity distributions

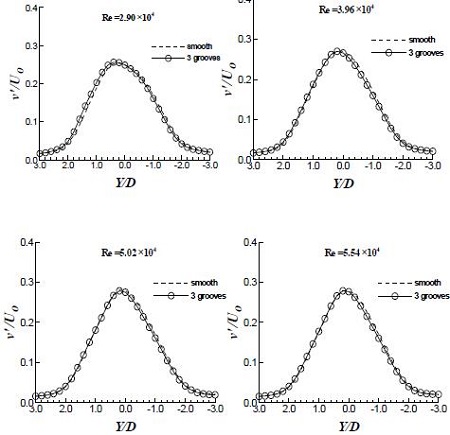
Fig. 5와 Fig. 6은 난류강도(u′/U_o, v′/U_o)를 나타낸 그림이다. 매끈한 원주와 비교하여 큰 변화를 볼 수는 없지만, u′/U_o의 경우 Re ≥ 4×10⁴에서 Groove가 있는 물체의 경우 다소 감소한 결과를 얻었다. 난류폭은 줄어들지 않았다. 난류강도는 소규모 난류구조로 변화를 감지하여 에너지의 소산의 영향을 볼 수 있는 인자로서, 본 실험의 경우에는 이러한 영향을 관찰할 수 없었다.

Fig. 5.

Comparisons of streamwise turbulent intensity

Fig. 6.

Comparisons of lateral turbulent intensity

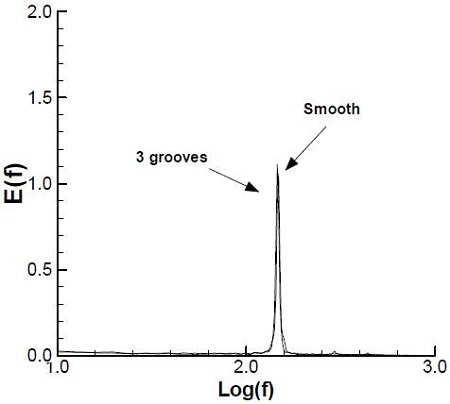
자유유동속도를 24 m/s로 하여 조직적인 와에 해당하는 조건부 신호의 위상과 동일한 속도신호를 추출(sampling)한 후 앙상블 평균(ensemble average)을 하여 한 지점에서의 위상평균화된 데이터를 얻었다. Y방향 속도성분인 V신호의 파워스펙트럼을 Fig. 7에 나타내었다. 표면이 매끄러운 경우와 Groove 3개의 경우 비슷한 와유출주파수에서 뾰족한 첨두치를 보이고 있고, 이 주파수를 기준으로 조건부 신호를 추출한 후 위상평균화하였다.

Fig. 7.

Power spectrums of V-velocity at X/D=6, Y/D=0

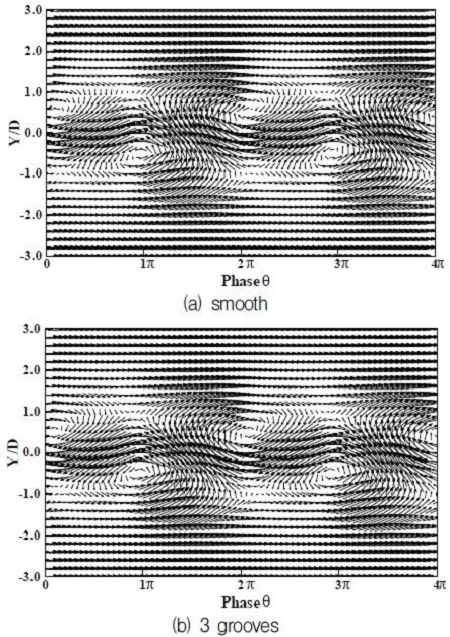
Fig. 8은 위상평균된 속도를 와 이동속도(Ua)로 감하여 나타낸 속도벡터장이다. 응집와의 중심과 새들(saddle)을 확연히 볼 수 있다. Groove가 3개인 원주의 경우와 매끈한 원주의 경우 차이가 나지 않는다. 이는 Groove의 영향이 후류 유동장까지 미치지 못하고 있음을 나타낸다고 생각된다.

Fig. 8.

Velocity vector fields (<U-Ua>, <V>)

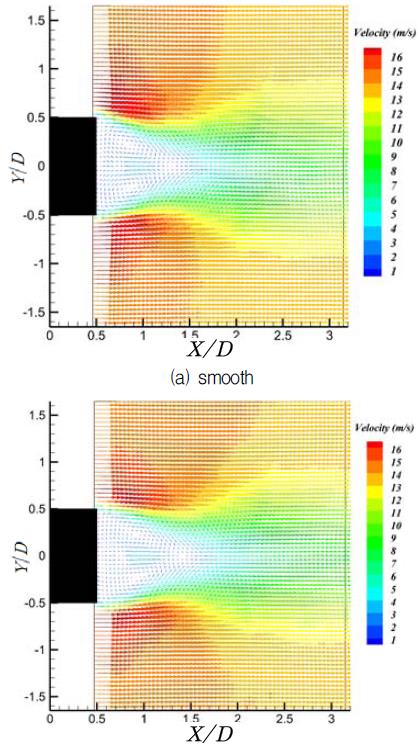
원주의 근접 후류 유동장을 살펴보기 위해 PIV 계측을 수행하였다. PIV 계측은 0.5≤X/D≤3.0, -1.5≤Y/D≤1.5의 유동장 범위에서 수행하였으며, 자유유동 속도는 16m/s로 고정하였다. Fig. 9는 근접 후류에 대한 시간평균유동장을 나타내고 있다. 매끄러운 형상과 Groove가 있는 형상간의 차이가 없음을 알 수 있다.

Fig. 9.

The time mean velocity field at 0 ≤ X/D ≤ 3.0

Groove에 의한 유동제어 효과가 후류 유동장에는 많은 영향을 미치지 않는 이유를 좀 더 자세히 알아보고자 물체 상부 벽면 근처의 경계층 유동을 측정하였다. Fig. 10은 Groove 형상 모델과 경계층 속도 측정 개시점(starting point)의 개략도를 보여주고 있다. X=0, Y/D=0.51를 개시점으로 하여 X방향으로 2 mm 이동하고 Y방향으로는 0.1 mm씩 이동하면서 X 위치당 Y방향으로 20개 지점에서 I형 프로브로 속도를 측정하였다.

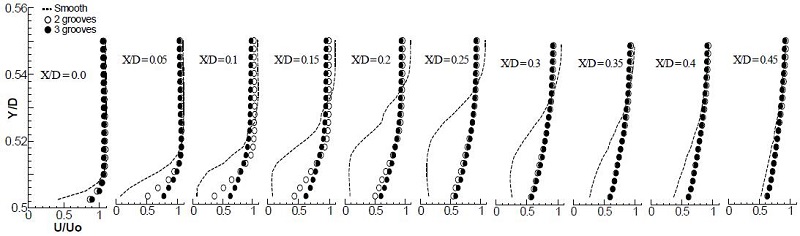
Fig. 11은 표면 부근에서의 유동방향 시간평균속도를 나타낸 그림이다. 시간평균속도분포에서 전단부에서는 Groove의 영향이 크게 나타나면서 표면 근처에서의 평균속도가 매끈한 원주의 경우보다 많이 회복되어 있다. 이는 Groove내에서 형성된 박리기포(separation bubble)와 유동교란(turbulence generation by the shear layer instability)에 의해 표면 근처 유동으로 운동량이 공급되기 때문이다. 후단부로 가면서 매끈한 경우와 Groove가 있는 경우의 평균속도 분포는 비슷한 양상으로 수렴되고 있다. 이렇게 표면 근처에서의 속도 회복이 지속되지 못함으로 인해 후류 유동장에서의 후류폭 감소와 속도 결손량의 감소 효과를 가지오지 못하고, 결과적으로 항력 저감이라는 유동 제어 목적을 달성하지 못한 것으로 판단된다.

Fig. 11.

Streamwise time mean velocity distribution near the surface of the D-shaped body

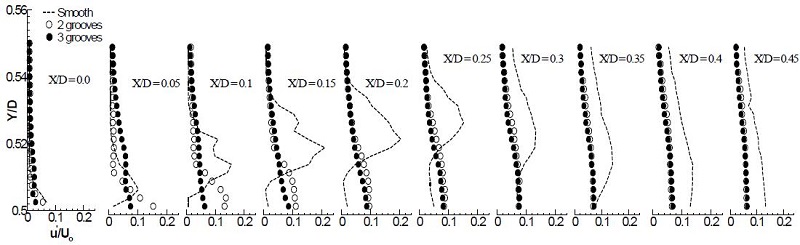
Fig. 12는 유동방향 난류강도를 표시한 그림이다. 매끈한 원주는 난류강도의 최대지점인 Y/D=0.52～0.53에서 난류전단층 중심이 확연히 나타나고 있다. 이에 반해 Groove가 형성된 원주는 난류전단층의 형성이 지연되고, 크기도 상당히 감소하고 있음을 알 수 있다.

Fig. 12.

Streamwise turbulent intensity distribution near the surface of the D-shaped body

이처럼 경계층 유동장에서 관찰된 Groove 영향에 의한 유동장의 변화가 후류 유동장에서는 크게 나타나지 않았다. 이는 Groove에 의해 물체 전단부에서 유동 박리가 지연되었으나 운동에너지의 부족으로 유동이 벽면 후단부까지 진행되지 못한 결과, 후류 유동장에서 매끈한 원주와 비슷한 유동 형태를 보여주었다.

4. 결 론

본 연구에서는 D-형상의 물체 표면에 Arc-Groove를 형성하여 물체 표면에서의 후류 경계층과 유동장의 변화 그리고 와유출 현상을 살펴보았다.

물체 표면 후류 경계층은 초기에는 Groove내 캐비티 유동에 의해 평균속도 회복이 일어나면서 유동박리가 다소 지연되고, 표면이 매끈한 경우에 나타난 난류전단층의 크기도 상당히 감소하였지만, 물체 표면 후단까지 Groove의 영향이 미치지 못함을 확인하였다.

Groove가 있는 경우, Groove가 없는 경우에 비하여 후류 유동장에서 시간평균속도 회복은 다소 이루어졌으나, 미미한 수준이었으며 후류 폭 감소도 크게 보이지 않았다. Groove가 있는 경우와 없는 경우에서 후류 와유출 주파수는 비슷하게 나타났으며, 와의 구조 또한 큰 변화를 나타내지 않았다.

따라서 본 연구에서 Arc-Groove를 가진 D-형상에서는 후류 유동제어를 통한 항력 저감 효과는 아주 미미한 것으로 판단된다.

마지막으로 D-형상 물체의 유동 제어를 위한 본 연구는 향후 추가적인 연구와 함께 폭넓은 레이놀즈 수 범위에서의 후속 연구가 계속 이어져야 될 것으로 판단된다.

Acknowledgments

이 논문은 2012년 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NO.2012R1A1A2007814).

References

• Bearman, P. W., and Trueman, D. M., (1972), An Investigation of the Flow around Rectangular Cylinders, aeronautic, 23, p229-237.
• Bearman, P. A, and Harvey, J. K., (1993), Control of circular cylinder flow by the use of dimples, AIAA Journal, 31(10), p1753-1756. [https://doi.org/10.2514/3.11844]
• 노기덕, 박지태, (2002), 표면에 정방형 딤플을 가진 원주의 항력저감 특성, 한국박용기관학회지, 26(2), p233-239.
• Takeyoshi, K., and Michihisa, T., (1991), Fluid dynamic effects of grooves on circular cylinder surface, AIAA Journal, 29, p2062-2068.
• Shinichi, T., Takuya, S., and Katsumi, A., (2004), Drag Reduction Mechanism of a Circular Cylinder by Arc Grooves, Transactions of JSME B, 70(697), p2363-2370.
• Robarge, T. W., and Stark, A. M., (2004), Design Considerations for Using Indented Surface Treatments to Control Boundary Layer Separation, 42nd AIAA Aerospace Sciences Meeting and Exhibit, AIAA 2004-425. [https://doi.org/10.2514/6.2004-425]
• Suresh1, V., Prasad1, R. A., Pillai, S. N., and Kumar, C. S., (2012), Influence of surface roughness on drag and flow field of D-shape model, VI National Conference on Wind Engineering.