LNG 펌프의 누설 유량 최소화를 위한 래버린스 실 형상의 수치적 연구

1. 서 론

최근 들어 LNG의 수요량이 전 세계적으로 증가하고 있다. 대용량 LNG를 운반하는 LNG 수송선은 탱크 내에 있는 액체상태의 LNG를 가압하여 육상 인수기지로 운반하기 위해 LNG 카고 펌프를 사용한다. LNG 수송선이 대형화되는 추세에 따라 카고 펌프도 점차 대용량화 되고 있고, 이에 따라 펌프의 효율 개선과 진동, 소음, 캐비테이션, 안전성 확보가 필요하다. 펌프 내의 회전체와 고정체 사이, 부품 사이의 틈새에서 일어나는 누설 손실은 펌프의 효율을 감소시킬 수 있다. 이러한 손실을 줄이기 위해 틈새 사이에 미로 형상의 패턴을 적용하여 작동 유체의 흐름에 대한 저항을 증가시키는 래버린스 실을 적용할 수 있다. 래버린스 실은 비접촉 실로서 높은 밀봉 성능과 내구성, 제작의 용이성으로 인해 누설 저감을 위한 용도로 널리 쓰이고 있는데, 특히 고정체와 회전체 사이(inducer와 suction bell, impeller와 wearing ring, impeller와 balance seat)에 적용된다. 본 연구에 사용한 직선형의 See-Through labyrinth seal 외에도 더 복잡한 유로를 가지거나 다양한 형태의 캐비티를 가진 실도 존재한다. CFD를 이용하면 이러한 래버린스 실 내에서의 유동 특성을 분석할 수 있고, 이를 통해 더 나은 형태의 실을 개발하기 위한 연구가 가능하다. 현재는 전산 해석을 이용한 연 구가 활발히 진행되고 있지만 전산 해석이 발전하기 훨씬 이 전에도 래버린스 실은 연구되었다. Becker⁽¹⁾는 래버린스 실 내부의 유동을 Poiseuille 유동으로 생각하여 마찰 계수를 구하고자 하였고, Martin⁽²⁾은 처음으로 비압축성 기체 유동이 흐르는 래버린스 실의 질량 유량을 구하기 위한 식을 제안하였다. 이후에는 Martin⁽²⁾의 식을 개선하기 위한 많은 연구가 이루어지기도 하였다. Egli⁽³⁾는 교축작용에 의한 운동에너지의 전달을 고려할 수 있도록 유량 식을 개선하였고, Hodkinson⁽⁴⁾은 간극을 통과한 유동이 다음 간극을 지나기 전 부분적으로 벽에 부딪혀 캐비티 내의 회전 유동에 합류함에 따른 운동 에너지 소산을 고려한 식을 제안하였다. 이러한 래버린스 실 유량의 해석적인 해를 구하기 위한 시도가 계속되었고, 실험 기구 및 방법과 전산 해석이 발전한 이후에는 Witting⁽⁵⁾의 연구와 같이 수치 해석에 의한 결과와 실험 결과를 비교하는 연구가 이뤄지기도 하였다. Wang⁽⁶⁾은 Reynolds-Averaged Navier Stokes (RANS) 난류 모델을 사용하여 stepped labyrinth seal이 interlocking seal에 비해 더 우수한 성능을 보인다는 것을 밝혀냈다. Zhao⁽⁷⁾는 stator와 rotor 중 한 쪽에만 래버린스 형상 패턴을 주는 것 보다 양 쪽 모두 패턴을 주는 것이 효율적이라는 결과를 보여주었으며, 캐비티의 깊이와 길이가 증가하거나 혹은 캐비티의 수가 늘어날수록 실의 누설 감소 효과가 개선된다고 하였다. Marsis⁽⁸⁾ 는 물과 공기를 작동 유체로 하여 다양한 형태의 캐비티를 가진 래버린스 실의 누설 및 동적 특성을 연구하여 효율적이고 안정적인 형상의 실을 제안하였다. Beak⁽⁹⁾은 직선형 래버린스 실의 형상에 따라 내부 유동의 흐름을 연구하여 누설 유량 변화의 원인을 분석하였고, 누설 유량 및 누설 계수(Discharge Coefficient)를 줄이기 위한 최적의 형상을 제안하였다. Hur⁽¹⁰⁾는 계단형 래버린스 실의 간극과 캐비티 형상에 따른 누설 특성을 연구하였으며 압력장과 속도장을 분석하여 유량 감소 원리를 설명하였다. 본 연구에서는 보편적으로 LNG의 성분 중 90% 이상을 차지하는 액화 메테인을 작동 유체로 하여 CFD 해석을 수행하였고, Marsis⁽⁸⁾ 와 Beak⁽⁹⁾ 이 사용한 직선형 래버린스 실의 형상에 따른 누설 특성을 연구하였다.

2. 해석 방법

2.2 해석모델

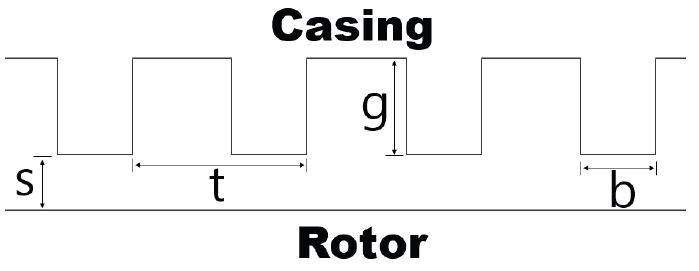
본 연구는 Fig. 1과 같이 패턴이 새겨진 casing과 회전하는 rotor 사이의 래버린스 실에 주기 조건을 사용하기 위해 원주방향으로 1˚ 크기에 해당하는 폭을 고려하여 해석 영역으로 선정하였다. 그리고 같은 그림에는 직선형 래버린스 실 형상의 주요 형상 파라미터를 함께 표시하였다. 각 파라미터에 대한 정보는 Table 1에 나타내었다. 해석은 상용 코드인 ANSYS CFX 19.4⁽¹¹⁾를 사용하였고, 해석에 사용한 조건은 Table 2에 나타내었다.

Fig. 1

Geometry and parameters of labyrinth seal

Table 1

Design parameters of the labyrinth seal

Table 2

Operating Conditions

2.3 격자 생성 및 경계 조건

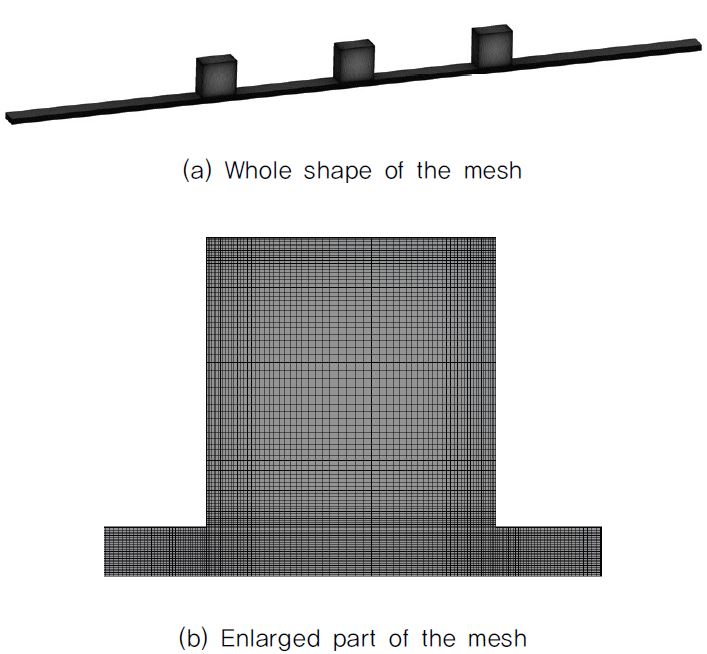
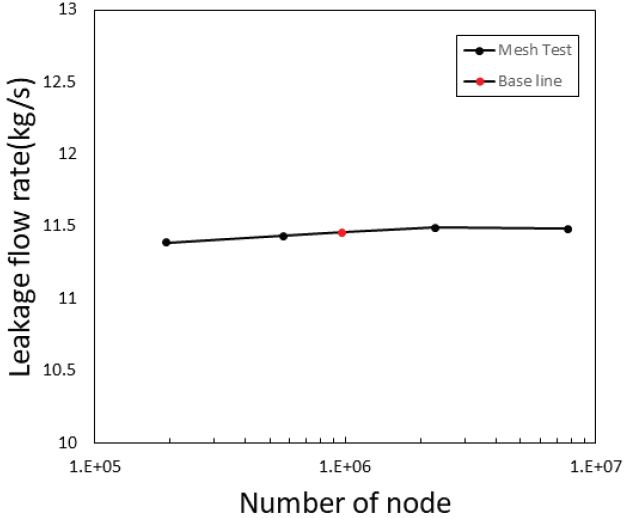
래버린스 실을 포함하는 해석 영역의 격자는 정렬 격자를 이용하여 생성하였다. 형상 파라미터의 변화에 따라 격자의 질이 달라질 수 있기 때문에 모든 영역에서 인접한 노드 간의 길이를 약 0.1mm 이상 벗어나지 않도록 생성하였다. 벽면에서의 점성의 영향을 고려하기 위해 벽면에 가까울수록 노드간의 간격이 작아지도록 만들었다. 그리고 회전하는 shaft 벽에서의 y⁺ 는 k-ε 모델 적용 시 적정 값이 30∼300 인 점을 고려하여 대체적으로 145∼150 정도의 범위를 가지도록 하였으며, 벽면 처리 방법은 Scalable wall function을 사용하였다. 해석에 사용한 각 형상 파라미터 값 범위의 평균값으로 제작한 격자를 Fig. 2 에 나타내었다. 해석 모델의 입구에는 pressure inlet, 출구에는 pressure outlet의 경계 조건을 사용하였고, shaft 벽은 rotating wall(no slip), 절단면에서의 경계 조건은 periodic condition을 사용하였다. 해석에 사용한 격자 민감도 분석은 Fig 2.에 나타낸 격자를 기준 격자로 하여 격자 개수를 줄이거나 늘리는 방향으로 해석을 진행하였으며 기준 격자가 해석에 충분히 사용 가능한 격자라고 판단하였다. 격자 테스트의 결과는 Fig. 3에 나타내었다.

Fig. 2

Baseline mesh of the labyrinth seal

Fig. 3

Result of mesh test

2.4 수치해석 모델의 검증

수치해석 결과의 검증을 위해 본 연구와 동일한 모델을 사용한 Marsis⁽⁸⁾의 CFD 해석 결과 값과 비교 하였다. 본 해석은 작동 유체로 액화메테인을 사용하였으나 Marsis⁽⁸⁾는 청수(water)를 사용하였으므로 동일하게 해석을 수행하였다. 비교에 사용한 형상은 Table 3에 나타내었다.

Table 3

Two types of reference seal design

Table 4에 입구와 출구의 압차에 따른 누설 유량 값을 비교한 결과를 나타내었다. 비교 결과 최대 4.9% 의 오차 수준으로 유사하게 나타났다.

Table 4

Comparison with reference[8]

3. 수치 해석 결과

본 연구의 목적은 CFD를 통해 래버린스 실의 형상에 따라 바뀌는 누설 유동의 특성에 대해 분석하고, 주어진 변수 값의 범위 내에서 누설 유량을 최소화 하는 형상을 찾는 것에 있다. 이를 위해 parametric study와 완전요인설계 분석을 수행하였고, 추가하여 주요 형상 파라미터 값에 대한 누설 유량을 예측할 수 있는 근사식을 만들었다.

3.1 Parametric study

앞서 설명한 바와 같이 래버린스 실의 성능은 형상에 따라 바뀐다. 본 해석에서는 See-Through labyrinth seal 형태의 직선형 래버린스 실을 사용하였다. 이 실의 형상을 결정짓는 주요 형상 파라미터를 바꿔가며 수치 해석을 수행하여 각 파라미터가 누설 유동에 어떤 영향을 미치는지 알아보았다.

3.1.1 간극 크기(s)의 영향

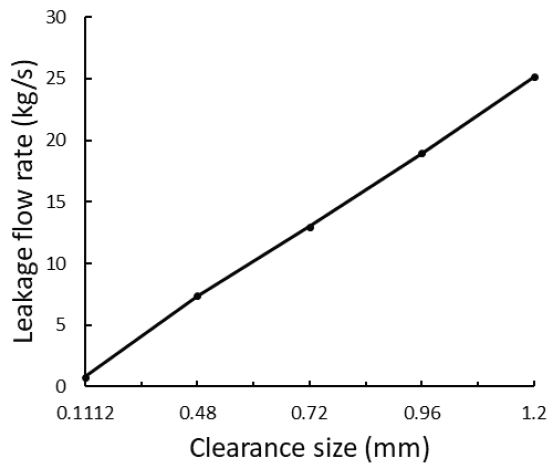
간극이 커지면 그만큼 유량이 지나갈 수 있는 영역이 확대되므로 누설유량은 증가할 것이다. 그리고 교축작용에 의해 잃게 되는 운동에너지의 비율이 줄어들어 래버린스 실의 누설 성능은 더욱 감소하게 된다.

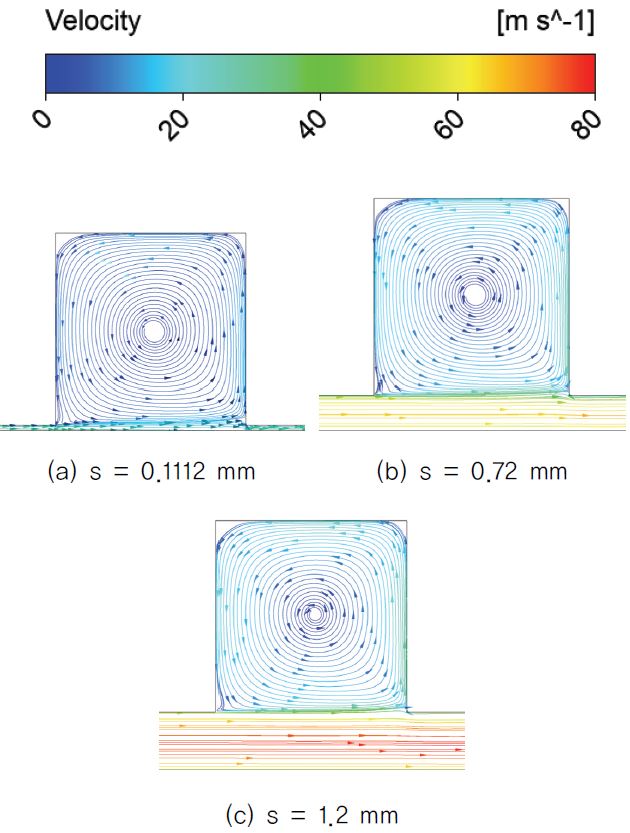
이때의 래버린스 실 내부의 유동특성을 CFD를 통해 해석하여 jet divergence angle(β)과 누설 유량과의 관계에 대해 분석하였다. Hodkinson⁽⁴⁾의 연구에 따르면 throat를 통해 캐비티로 유체가 빠져나오면서 확산하게 되는데 이때 Fig. 4와 같이 jet divergence angle 각이 생긴다. 이 각이 클수록 다음 throat로 빠져나가는 유동이 캐비티 벽에 부딪혀 충돌이 일어나게 되고 누설유량이 감소하게 된다. Fig. 5는 간극의 크기에 따른 래비린스 실 내부 유동의 유선을 나타낸 것이다. 그림으로 크기를 가늠하기는 힘들지만 jet divergence angle이 형성된 것을 확인할 수 있다. Table 5는 간극에 따른 jet divergence angle을 측정한 값과 outlet에서의 누설 유량 값을 나타낸 것이다. 간극이 커질수록 jet divergence angle이 작아지고 누설유량이 증가하였다.

Fig. 4

Jet divergence angle(β)

Fig. 5

The effect of changing the clearance(s) on the streamlines of the labyrinth seal

Table 5

Jet divergence angles and leakage flow rate for several clearances

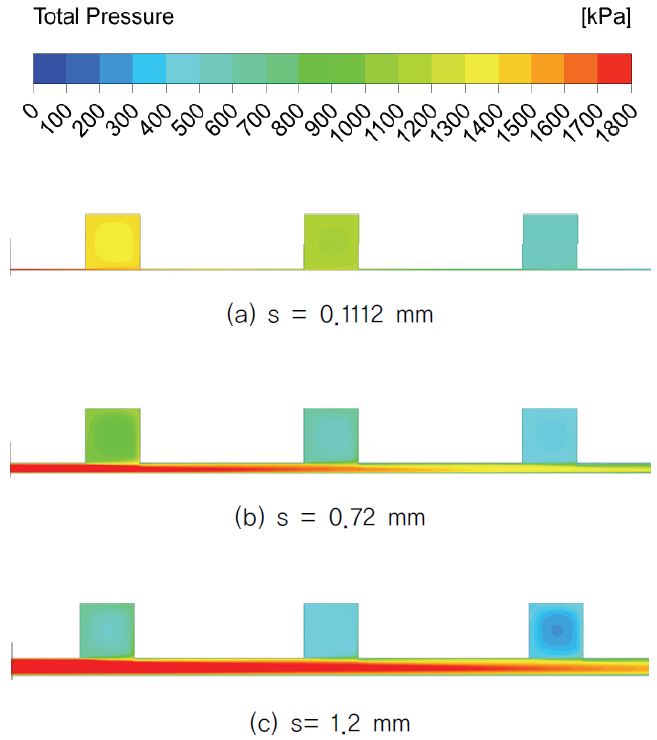
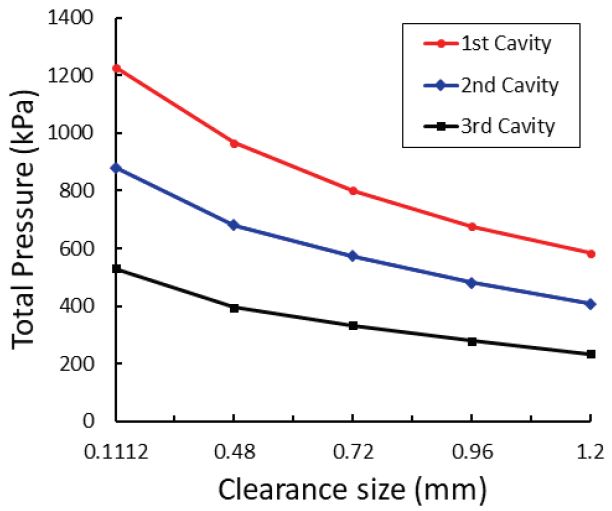
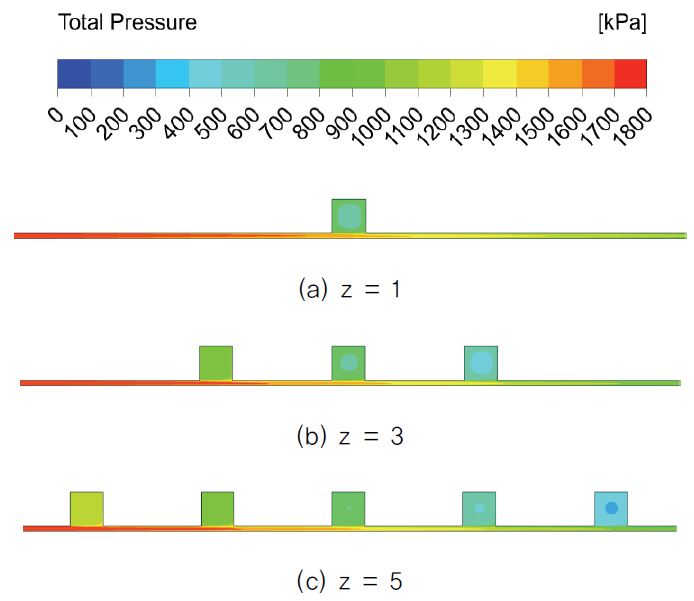
다음으로 간극의 크기가 증가함에 따라 래버린스 실 내부의 전압의 양상이 어떻게 나타나는지 분석하였다. 래버린스 실 내부에서의 유동은 크게 캐비티를 제외한 간극을 지나는 고속의 유동과 캐비티 내부에 갖힌 채로 회전 하는 유동으로 나눌 수 있다. 이에 따라 Fig. 6에서 전압 또한 마찬가지로 간극과 캐비티의 영역이 서로 차이를 보이고 있다. 여기서 캐비티 내부의 전압은 회전 유동이 얼마나 강한지를 나타는데, Fig. 6을 보면 간극이 커질수록 같은 위치의 캐비티 내부의 전압이 감소하는 경향을 보이고 있다. 전압이 감소하므로 회전 유동이 약해지고 간극을 방해하는 힘도 그에 따라 작아진다. 결과적으로 누설 유량은 증가하였다. 세 경우의 그림에서 간극이 커질수록 간극에서의 고속 유동이 나타내는 전압이 강해지는 것을 확인할 수 있다. 간극에 따른 각 캐비티 내부에서의 전압과 누설 유량을 Fig. 7 과 Fig. 8 에 각각 나타내었다.

Fig. 6

Total pressure contour plots for various clearance(s) sizes

Fig. 7

Variation in the averaged total pressure inside the cavity with clearance sizes

Fig. 8

Variation in the leakage flow rate with clearance size(s)

3.1.2 캐비티 높이(g)의 영향

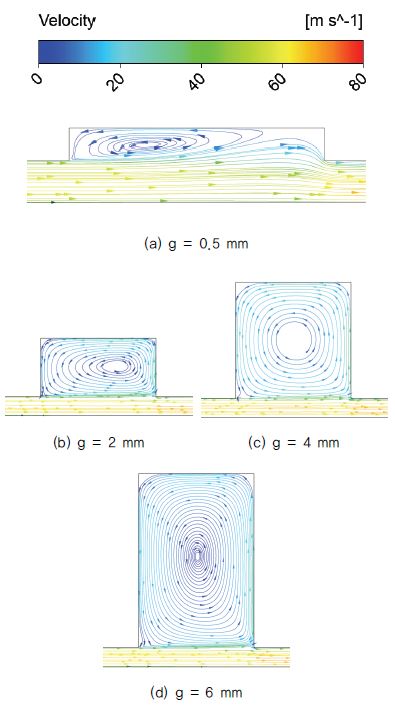
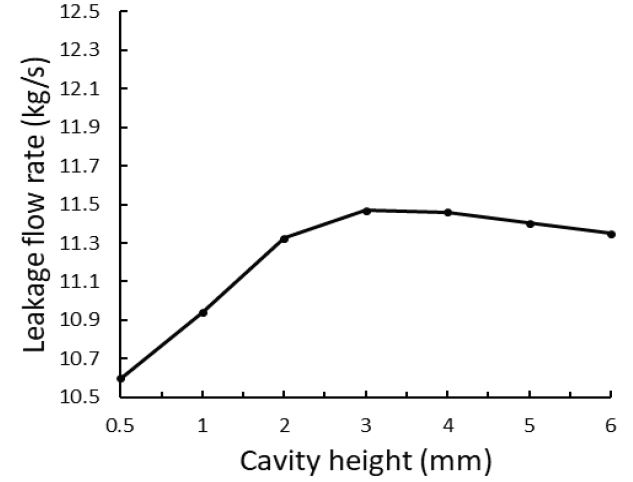
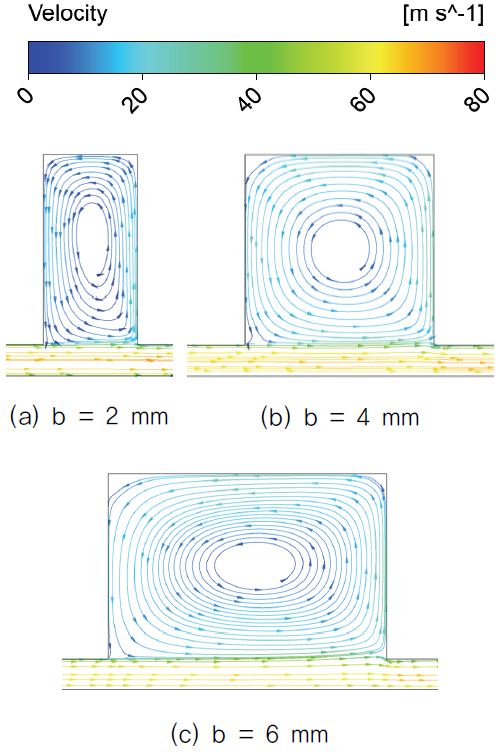
Fig. 9는 캐비티 높이에 따라 각 래버린스 실 내부에서 나타는 유선도이다. 캐비티의 높이가 커짐에 따라 vortex 또한 높이 방향으로 확장되면서 운동 에너지가 소산되는 양이 더욱 증가하게 되는데 Fig. 10에서 캐비티 높이가 커질수록 누설 유량이 줄어드는 것을 볼 수 있다. g=3mm에서 캐비티 높이가 작아지는 경우에는 반대의 경향을 보여주는 것을 볼 수 있다. Fig. 9 (a)의 유선도를 보면 캐비티 내의 vortex가 캐비티를 완전히 채우지 못하고 있으며, 이로 인해 다음 간극을 지나는 지점에서 jet divergence angle이 커지게 되고, 충돌이 크게 일어나 높이가 큰 경우에 비해 누설 유량이 적게 나타난다. 이 경우에서 캐비티의 높이가 커지면 vortex의 크기가 증가하면서 누설 유량은 증가할 것으로 예상된다. g=2mm인 케이스는 그 사이에 있기 때문에 g=3mm인 케이스에 비해 누설 유량이 적게 나타나고 있다.

Fig. 9

The effect of the cavity height(g) on the streamlines of the labyrinth seal

Fig. 10

Variation in the leakage flow rate with cavity height(g)

3.1.3 캐비티 너비(b)의 영향

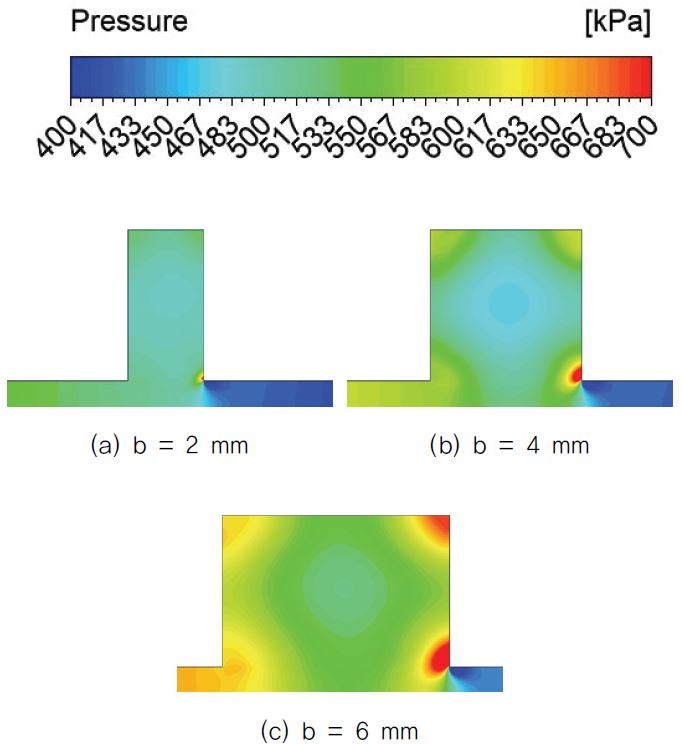
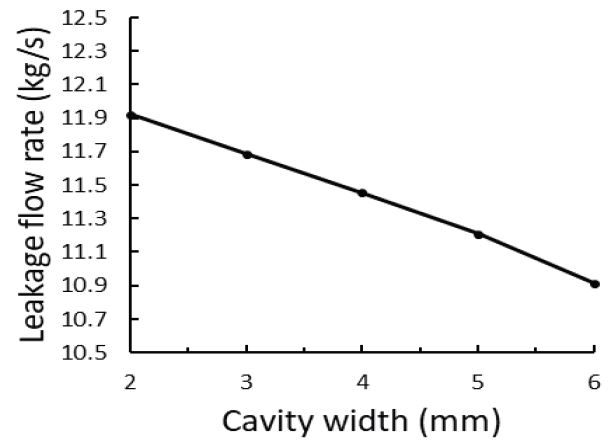
캐비티의 너비가 누설 유량에 미치는 영향은 캐비티 높이의 영향에 비해 크게 나타났다. 먼저 Fig.11을 보면 캐비티 너비가 넓어지면서 vortex가 캐비티를 차지하는 비율이 조금씩 줄어들게 된다. 이러한 현상이 캐비티의 너비가 높이에 비해 극단적으로 넓은 Fig. 9(a) 와 같이 되면, 마찬가지로 jet divergence angle이 커져 다음 간극으로 넘어가는 목에서 더욱 강한 충돌이 일어나 유동은 운동 에너지를 잃게 된다. Fig. 12 를 보면 캐비티 너비가 가장 큰 b=6인 케이스에서 충돌이 가장 크게 일어나는 것을 확인할 수 있다. 이 결과로 Fig. 13과 같은 결과가 나오게 된다. 그리고 캐비티 너비 방향으로의 vortex의 확장에 의해 운동에너지가 소산되는 양이 증가하는 것 또한 누설 유량 감소의 원인이 되고 있다.

Fig. 11

The effect of changing the cavity width(b) on the streamlines of the labyrinth seal

Fig. 12

Static pressure contour for various cavity width(b)

Fig. 13

Variation in the leakage flow rate with number of cavity width(b)

3.1.4 캐비티 개수의 영향

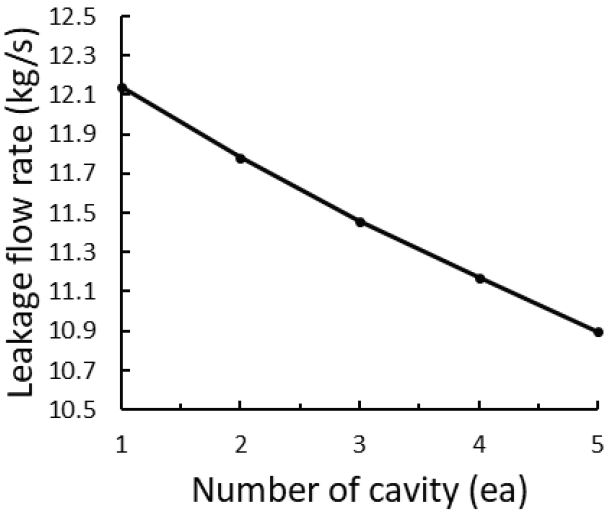
다음으로 캐비티의 개수가 누설 유량에 미치는 영향을 살펴보았다. 래버린스 실을 지나는 유동은 반복적인 교축작용을 겪으면서 압력 손실이 일어나는데, 이에 의해 Fig. 15에서는 캐비티의 개수(z)가 많을수록 누설 유량이 줄어드는 결과를 보여주었다.

또, 캐비티 내의 vortex는 간극을 지나는 유동을 방해하하는데, 캐비티의 형상이 동일하다면 캐비티의 수가 많을수록 유동은 더 많은 에너지를 잃게 된다. Fig. 14를 보면 캐비티의 수가 많아질수록 간극에서의 전압이 약해지는 것을 확인할 수 있다.

Fig. 14

Total pressure contour plots for various number of cavity(z)

Fig. 15

Leakage flow rate with the number of cavity(z)

4. 완전요인설계를 이용한 분석

앞선 parametric study 통해서 각 형상 파라미터가 누설 유동에 미치는 영향을 분석해보았다. 형상 파라미터는 간극의 크기(s), 캐비티 높이(g), 캐비티 너비(b), 캐비티 개수(z) 로 총 4 가지이다. 하지만 완전요인설계를 사용하였을 때의 샘플의 수를 고려하여 간극의 크기(s)를 제외한 3가지 파라미터만을 이용하였다. 간극의 크기는 누설 유량에 가장 큰 영향을 미치고, 작을수록 누설 유량을 줄일 수 있다. 하지만 래버린스 실의 열전달과 윤활, 마모 등을 포함한 여러 가지 요소를 고려하여 결정해야하기 때문에 요인 분석에서는 제외하였다. 사용한 샘플의 수는 총 125개 이다. 아래의 분석은 Minitab 21.1⁽¹²⁾을 이용하였다.

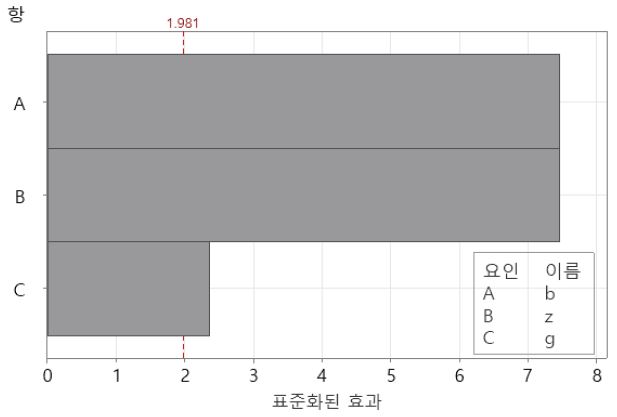
Fig. 16은 세 가지 형상 파라미터가 누설 유량에 미치는 영향 크기를 정량화하여 비교한 Pareto chart이다. 캐비티의 높이(g)에 의한 영향이 가장 작으며, 캐비티의 너비(b)와 개수(z)에 의한 영향은 서로 동등한 수준으로 캐비티 높이(g)에 의한 영향에 비해 세 배 가량 높게 나타났다.

Fig. 16

Pareto chart of three parameters

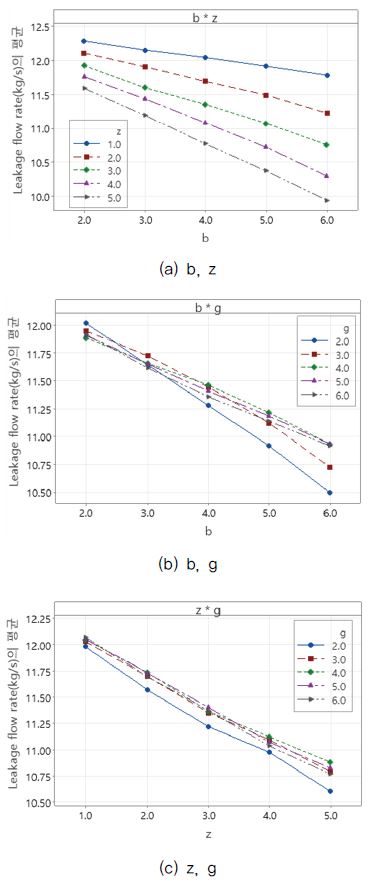
Fig. 17은 두 가지 파라미터의 누설 유량에 대한 영향이 서로 어떤 관계를 가지는지 보여주는 교호작용도를 나타낸 그림이다. 그래프의 선들이 평행할수록 각 파라미터의 영향은 서로 독립적인 관계를 보이는 것이다. 세 가지 조합의 교호작용도 모두 강하게 연관성이 있지는 않지만 캐비티 너비(b)와 개수(z)는 서로의 크기가 커질수록 누설 저감 효과를 확대시켜주는 것으로 나타났다.

Fig. 17

Interaction plot of three parameters

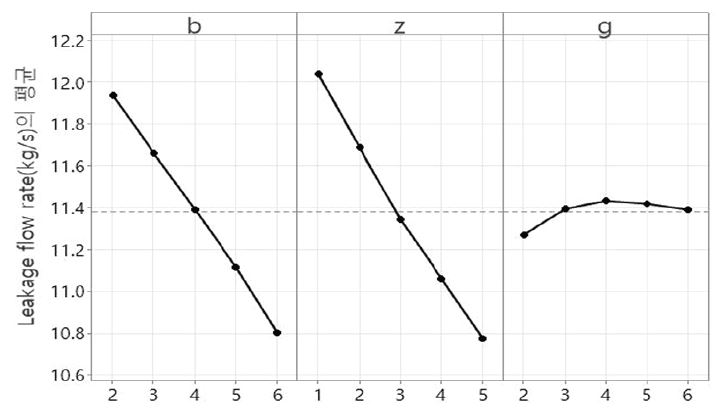
마지막으로 Fig. 18은 각 파라미터의 서로 다른 수준에서 유량 평균값이 어떻게 나타는지를 보여주는 주효과도를 나타낸 것이다. 이 그림에서는 파라미터가 누설 유량에 어떠한 영향을 미치는지에 대한 경향을 쉽게 확인할 수 있다. 캐비티 너비(b)와 개수(z)의 영향은 선형적으로 감소하는 경향을 보여주고 있다. 하지만 높이(g)의 영향은 최고점을 가지고 있으며 비선형적인 경향을 보여주고 있다. 이 그림을 통해서도 캐비티 높이의 영향은 상대적으로 작다는 것을 확인하였다.

Fig. 18

Main effects plot of three parameters

5. 최적 형상 제시

앞서 설명한 분석의 결과는 다음과 같다. 캐비티 너비(b) 와 캐비티 개수(z)는 그 값이 클수록 누설 저감 효과가 증대되고, 캐비티 높이(g)에 대한 누설 유량의 결과는 비선형적인 경향을 보이지만 주어진 범위 내에서는 캐비티 높이(g)가 가장 작은 값에서 최소의 유량 값을 가진다. 따라서 Fig. 19에 나타낸 형상과 같이 b=6, z=5, g=2 일 때의 래버린스 실이 누설 유량을 최소화 할 수 있는 최적 형상이다. 누설 유량은 9.45 kg/s 로 125개 케이스의 결과 중 가장 작은 값이며, 이는 래버린스 실의 패턴이 없는 경우의 유량에 비해 23.85% 감소한 결과이다.

Fig. 19

Suggested design

6. Response surface와 누설 유량 근사식

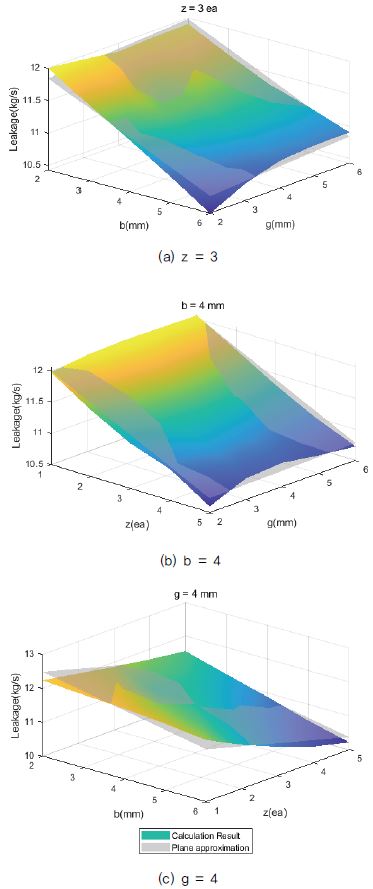
Fig.20은 Fig.17 의 교호작용도를 3차원으로 나타낸 반응 표면이다. 세 가지의 반응 표면이 모두 평면에 가깝게 나타났으며, 앞서 확인한 것과 같이 b, g, z 세 가지 형상 파라미터의 변화에 대한 유량의 반응은 거의 독립적인 관계를 보인다. 이를 통해 다중 선형 회귀분석을 수행하여 식(5)와 같은 근사식을 구하였다. 125개 케이스의 해석 값과의 오차는 최소 0.01%, 최대 6.79%, 평균 1.20% 로 나타났다.

Fig. 20

Response surfaces of leakage flow rate

누설 유량을 예측 할 수 있다는 것은 불필요한 가공과 실험을 줄여 소비되는 자원을 크게 절약할 수 있다는 것을 의미한다.

7. 결 론

래버린스 실은 비접촉 환형 실로서 압축기나 터빈과 같은 기계에서 효율을 높이기 위해 주로 쓰인다. 래버린스 실은 연속된 캐비티를 지나면서 점성 및 난류 효과와 반복적 교축 작용으로 인해 출구로 유출되는 유량이 줄어들게 된다. 본 연구는 CFD를 통해 래비린스 실의 형상에 따른 누설 유동의 변화를 관찰하였다.

• 1) 간극의 크기는 래버린스 실의 누설 유량에 가장 큰 영향을 주는 것으로 나타났다. 간극이 커질수록 소산되는 운동에너지의 양이 감소하기 때문이며, jet divergence angle이 작아지고, 캐비티 내에서의 전압이 감소한다.
• 2) 캐비티의 높이에 대한 누설 유량의 변화는 특이점이 존재하였다. 이 때의 경우에 비하여 캐비티 높이가 작으면 vortex가 캐비티 전체를 채우지 못하여 jet divergence angle이 매우 커지고 누설 유량은 줄어든다. 하지만 vortex가 충분히 캐비티를 채울 만큼 캐비티 높이가 큰 경우에는 높이 커질수록 vortex가 높이 방향으로 확장되면서 운동 에너지의 소산이 커져 유량이 줄어들게 된다.
• 3) 캐비티의 너비는 커질수록 누설 유량이 줄어들었다. Vortex의 확장에 의한 운동에너지 소산과 jet divergence angle의 증가로 인한 결과로 판단된다.
• 4) 캐비티의 개수가 많을수록 누설 유량이 줄어들었다. 반복적인 교축 작용에 의한 압력 손실과 vortex의 더 많은 방해를 받기 때문이다.
• 5) 완전요인설계를 통한 분석의 결과는 b, z 에 의한 누설 유량 변화는 선형적인 경향을 보였고, g에 의한 영향은 가장 작으나 비선형적인 경향을 보였다. 교호작용도는 b, z 의 조합에서 적지만 유의미한 영향을 보여주었다.
• 6) 결과 분석을 통해 누설 유량을 최소화하기 위한 형상을 선정하였고, 그 결과 래버린스 실의 패턴이 적용되지 않은 경우에 비해 누설 유량이 23.85% 감소하였다.
• 7) 각 파라미터가 누설 유량에 미치는 영향이 선형적이고 서로 독립적이라고 가정하여 누설 유량 근사식을 구한 결과 평균적으로 1.20% 의 오차를 보였다.

Acknowledgments

본 과제는 2021년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신 사업의 결과입니다.(2021RIS-003)

References

• Becker, E., 1907, “Stromungsvergange in Ringformigen Spalten”, V.D.I., Vol. 51, pp.1133-1141.
• Martin, H.M., 1908, “Labyrinth Packings’, Engineer, 85, pp. 35-36. [https://doi.org/10.1175/1520-0493(1908)36<85:FAW>2.0.CO;2]
• Egli, A., 1935, “The Leakage of Steam Through Labyrinth Seals”, Trans. ASME, 57, pp. 115-122.
• Hodkinson, B., 1939, “Estimation of the Leakage Through a Labyrinth Gland”, Proc.Inst.Mech.Engrs., 141, pp.283-288. [https://doi.org/10.1243/PIME_PROC_1939_141_037_02]
• Wittig S., Schelling, U., Kim, S., and Jacobsen, K., 1987, “Numerical Predictions and Measurements of Discharge Coefficients in Labyrinth Seals,” ASME 87-GT-188. [https://doi.org/10.1115/87-GT-188]
• W. Wang, Y. Liu, P. Jiang, and H. Chen, 2007, “Numerical analysis of leakage fow through two labyrinth seals,” Journal of Hydrodynamics, vol. 19, no. 1, pp. 107–112. [https://doi.org/10.1016/S1001-6058(07)60035-3]
• Zhao, W.; Nielsen, T.K.; Billdal, J.T., 2010, “Effects of Cavity on Leakage Loss in Straight-Through Labyrinth Seals”. In Proceedings of the 25th IAHR Symposium on Hydraulic Machinery and Systems; Timi¸soara, Romania, 20–24 September 2010, IOP Publishing Ltd.:Bristol, UK, 2010; Volume 12, p. 012002. [https://doi.org/10.1088/1755-1315/12/1/012002]
• Marsis, E, & Morrison, G., 2013, "Leakage and Rotordynamics Numerical Study of Circular Grooved and Rectangular Grooved Labyrinth Seals." Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition. Volume 7A: Structures and Dynamics. San Antonio, Texas, USA. June 3–7, 2013. V07AT29A028. ASME. [https://doi.org/10.1115/GT2013-96001]
• Baek, Seung I., and Joon Ahn. 2021. "Optimizing the Geometric Parameters of a Straight-Through Labyrinth Seal to Minimize the Leakage Flow Rate and the Discharge Coefficient" Energies 14, no. 3: 705. [https://doi.org/10.3390/en14030705]
• Hur, Min S., Soo I. Lee, Seong W. Moon, Tong S. Kim, Jae S. Kwak, Dong H. Kim, and Il Y. Jung. 2020. "Effect of Clearance and Cavity Geometries on Leakage Performance of a Stepped Labyrinth Seal" Processes 8, no. 11: 1496. [https://doi.org/10.3390/pr8111496]
• ANSYS, Inc. ANSYS CFX-Pre User’s Guide, Release 2019 R2.
• Minitab, LLC. (2021). Minitab. Retrieved from https://www.minitab.com