전기자동차 배터리팩 내부 자연대류 열전달 특성에 관한 수치해석적 연구
Abstract
This study primarily aimed to explore the natural convection heat transfer characteristics inside the battery pack of electric vehicle equipped with effusion holes and rectangular fins. Three-dimensional numerical simulations were performed to examine the effects of effusion hole diameter, rectangular fin thickness and height, and effusion hole and rectangular fin arrangements. The local and average heat transfer coefficients on the inner surface of the battery pack upper cover were obtained from numerical simulations. The results showed that the flow velocities between the battery modules and under the battery pack upper cover increased with the aid of the effusion holes and rectangular fins. This increased flow velocity has a significant influence on the improvement of the natural convection heat transfer of the battery pack upper cover.
Keywords:
Effusion Hole, Rectangular Fin, Polyamide 6, Average Heat Transfer Coefficient, Computational Fluid Dynamics키워드:
유출홀, 직사각형 핀, 폴리아미드 6, 평균열전달계수, 전산유체역학1. 서 론
최근 지구 온난화와 각종 환경 오염 문제로 인해 배기가스 규제가 강화되면서 화석연료가 아닌 친환경적인 에너지원을 활용하는 에너지 저장 시스템(Energy storage system)의 필요성이 더욱 증가하였다. 최근 자동차 시장도 내연기관에서 전기 자동차, 수소 자동차와 같은 친환경 자동차로 변해가는 추세이며, 전기 자동차의 판매량이 2020년에 전체 자동차 시장의 약 4.7%를 차지하였고, 2030년에는 약 48%까지 성장할 것으로 예측된다(1). 이처럼 에너지 저장 시스템 시장이 급성장하고 있고, 이에 따라 전기를 저장하는 배터리의 안정성을 확보하기 위한 연구가 활발히 진행되고 있다(2). 전기 자동차의 배터리는 성능 및 주행거리를 확보하기 위하여 높은 에너지 밀도가 요구되기 때문에 높은 에너지 밀도, 긴 수명, 가벼운 무게 등의 장점을 가지는 리튬 이온(Li-ion) 배터리를 가장 많이 사용하고 있다. 하지만, 리튬 이온은 특성상 충격과 고온에 취약하다는 단점이 있다. 배터리는 산화⋅환원 반응과 전류의 흐름으로 인해 열이 발생하는데, 고온에 약한 리튬 이온이 높은 온도에 장시간으로 노출하게 되면 수명이 짧아지게 되고, 심할 경우 열 폭주 현상(Thermal runway phenomenon)으로 폭발을 야기할 수도 있다(3). 또한, 배터리팩 내 발열로 인한 자연대류 현상에 의해 배터리팩 커버의 온도가 상승하여 배터리팩 커버의 열변형이 일어나는 원인이 되기도 한다. 이처럼 배터리 발열은 해결해야 할 중요한 과제이기 때문에 효율적인 열관리 기술이 필요하다. 그중에서도 자연대류는 경제성, 간편성으로 인하여 냉각에서 매우 유용하게 활용할 수 있어 열 유동 시스템의 중요한 요소 중 하나이다. 자연대류 특성을 산업기기에 널리 적용할 수 있도록 다음과 같은 자연대류에 관한 연구가 활발히 진행되고 있다. Nada(4)는 전자 장비에 적용하는 수평⋅수직 히트싱크의 직사각형 핀 간격 및 길이에 대한 자연대류 열전달 및 유체 흐름 특성에 대해 실험을 수행하였고, 핀 길이가 증가함에 따라 Nusselt 수와 핀 효율이 증가하는 것을 확인하였다. Bocu(5)는 발열되는 장치의 고온부 표면에 원통형 핀을 적용하여 원통형 핀 개수, 직경, 길이에 따라 층류 자연대류 열전달 및 유동 특성에 대한 수치해석을 수행하였고, 원통형 핀이 열전달 성능 향상의 효과를 얻을 수 있다는 것을 확인하였다. Fontana(6)는 개방된 캐비티 내부의 자연대류 특성과 개방된 구멍 근처의 유동 특성을 분석함으로써 Rayleigh 수와 구멍 크기가 열에너지 교환에 큰 영향을 미치는 것을 확인하였다. 또한, 캐비티의 기울기, 핀의 형상, 위치 등 다양한 설계인자에 따른 자연대류 특성에 대해 분석하는 기초 연구가 활발히 진행되고 있다(7–9). 하지만 기존 연구들은 자연대류 특성을 단순한 캐비티 내부 형상에서 분석했기 때문에 실제 기기에 적용하여 분석하는 연구가 필요하다.
본 연구에서의 주요 목표는 배터리팩 내부의 유동과 자연대류 열전달 특성을 확인하기 위해 3차원 수치해석을 수행하였다. 평면으로 단순화한 배터리팩 상부 커버의 안쪽 표면에 유출홀 및 직사각형 핀의 설계 인자를 고려하여 열전달 특성에 미치는 영향을 확인하였다. 또한, 유출홀과 직사각형 핀 배열 및 치수 변화에 따른 배터리팩 상부 커버의 안쪽 표면 평균 및 국부 열전달계수의 변화를 확인하였다.
2. 수치해석
2.1 수치해석 형상 및 경계조건
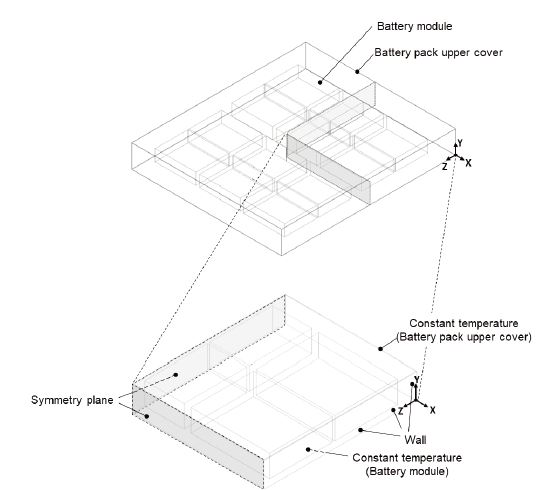
Fig. 1은 배터리팩 시스템의 3차원 수치해석 모델 계산영역을 나타내며, 배터리팩 내부 자연대류 열전달에 대한 해 석을 수행하였다. 수치해석의 계산시간을 단축하기 위해 전체 배터리팩 시스템의 대칭성을 고려하여 1/4만 모델링하여 계산영역으로 선정하였다. Fig. 2는 배터리팩 상부 커버 형상에 대한 계략도이다. 배터리팩 상부 커버는 기존 형상을 평면으로 단순화한 형상과 유출홀(Fig. 2(a)), 핀(Fig. 2(b)), 유출홀과 핀이 모두 설치된(Fig. 2(c)) 형상 총 4가지이며, 배터리팩 내부 치수를 고려하여 유출홀의 직경(De)은 4, 5, 6, 7 mm, 직사각형 핀의 두께(tfin)는 3, 6, 9 mm, 핀의 높이 (Hfin)는 7, 10, 13 mm로 선정하였다. 유출홀과 직사각형 핀은 단순화한 배터리팩 상부 커버 형상으로 수치해석을 수행한 결과에서 배터리 발열이 많이 분포되어 있는 고온부 위치로 선정하였다. 유출홀 배열(Fig. 2(a))에서 Cases-2, 3은 배터리 모듈 위, Case-4는 배터리 모듈 간격 위, Cases-5, 6은 배터리 모듈과 모듈 간격 위쪽으로 구분하여 유출홀의 위치를 선정하였다. 직사각형 핀 배열(Fig. 2(b))에서 핀은 배터리 모듈 간격 위쪽에 위치하고 Cases–7, 8은 x축 방향, Cases-9,10은 y축 방향으로 배치하였다. Cases-8, 10 형상은 Cases-7, 9의 직사각형 핀을 끊어서 배치한 형상이다. 유출홀과 핀을 모두 설치한 형상(Fig. 2(c))은 유출홀과 핀 형상을 기반으로 해석한 것에서 배터리팩 상부 커버의 안쪽 표면 평균 열전달계수가 높은 형상을 조합한 것이다. Case-12 형상은 Case-11 형상과 동일한 유출홀 위치에서 직사각형 핀을 끊어서 배치한 형상이다. Case-14 형상은 Case-13 형상과 동일한 직사각형 핀 형상에서 핀 사이에 유출홀을 추가한 형상이다.
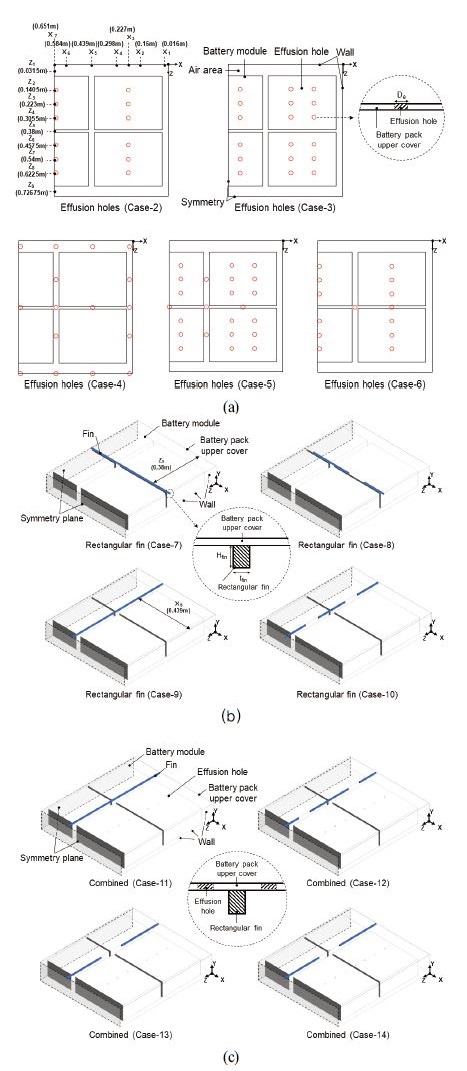
Battery pack system with (a) effusion holes, (b) rectangular fins, and (c) both effusion holes and rectangular fins
배터리 모듈에는 배터리 적정온도(10)인 313.15 K, 배터리팩 상부 커버 안쪽 표면에 상온 293.15 K의 일정 표면 온도를 경계조건으로 주었다. 대칭이 되는 면은 대칭 조건을 적용하였고, 그 외에 모든 벽면 경계에서는 점착 조건(No-slip condition)을 가정하였다. 중력을 적용하기 위해 배터리팩 시스템의 높이 방향인 –y 방향으로 설정하였다. 온도에 따른 공기의 밀도 변화에 의한 부력을 계산하기 위해 Boussinesq 모델(11)을 사용하였고 다음과 같이 표현된다.
| (1) |
이때, β와 ρo는 T0에서의 체적 열팽창계수와 밀도를 의미한다. 공기의 열전도율, 점성계수, 정압비열과 같은 물성치는 NIST (National Institute of Standards and Technology)의 REFPROP 9.1(12) 프로그램을 사용하여 얻었고, 배터리팩 상부 커버의 물성치는 폴리아미드 6의 물성치를 적용하였다. 관련하여 수치해석을 위한 경계조건 및 치수는 Table 1에 정리하였고, 수치해석 Case는 Table 2에 정리하였다.
2.2 수치해석 기법
본 연구에서는 3차원 정상상태 해석을 위해 상용 전산유체역학 소프트웨어인 ANSYS Fluent 20.1(13)을 사용하였다.배터리팩 내부의 자연대류 열전달 및 유체 특성을 분석하기 위해 층류 유동, 정상상태 비압축성으로 가정하였고 질량, 운동량, 에너지 보존에 대한 지배방정식은 다음과 같이 표현된다.
| (2) |
| (3) |
| (4) |
수치해석의 이산화기법은 압력-속도 연성 기법인 Semi-implicit method for pressure linked equations–consistent (SIMPLEC)(14) 해석기법을 사용했다. 압력은 2차 정확도(Second-order)를 사용하였고 운동량, 에너지에 대한 이산화기법은 2차 정확도 상류 차분법(Second-order upwind)을 사용하였다. 수치해석 해의 수렴은 연속, 운동량, 에너지 방정식의 잔차가 10-4 미만의 값에 도달할 때까지 반복하여 계산을 진행하였다.
2.3 수치해석 격자 독립성 검증
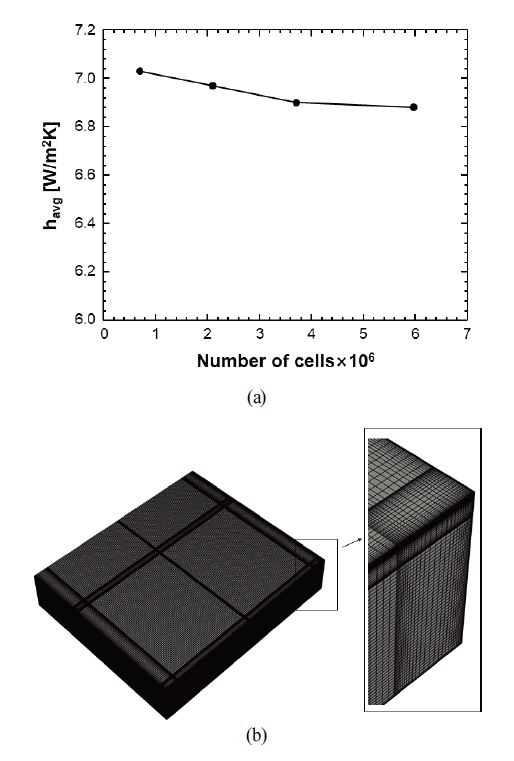
기존 배터리팩 상부 커버 형상일 때, 0.84×106, 2.11×106, 3.83×106, 5.96×106개의 총 4가지 격자를 포함하는 계산 영역에 대한 격자 독립성 검사를 수행하였다. 계산의 수렴성을 향상시키기 위해 격자 구조는 정렬 격자로 구성하였다. 4가지 격자에 대해 배터리팩 상부 커버 안쪽 표면의 국부 열전달계수는 다음 식을 이용하여 계산하였고, 계산한 국부 열전달계수를 평균하여 비교하였다.
| (5) |
이때, qc’’는 배터리팩 상부 커버 안쪽 표면에서의 국부 열유속, Tavg는 배터리팩 내부의 평균 온도, Ts는 배터리팩 상부 커버 안쪽 표면에서의 국부 온도이다. Fig. 3(a)은 4가지 격자에 대해 배터리팩 상부 커버 안쪽 표면에서의 평균 열전달계수를 비교하여 나타낸 그래프이다. 3.83×106개와 5.96×106개 격자 간 배터리팩 상부 커버 안쪽 표면에서의 평균 열전달계수 차이가 0.29%로 나타나 3.83×106개의 격자수로 선정하였고, 본 연구에서 사용한 수치해석 모델의 격자 구조는 Fig. 3(b)과 같다.
3. 수치해석 결과
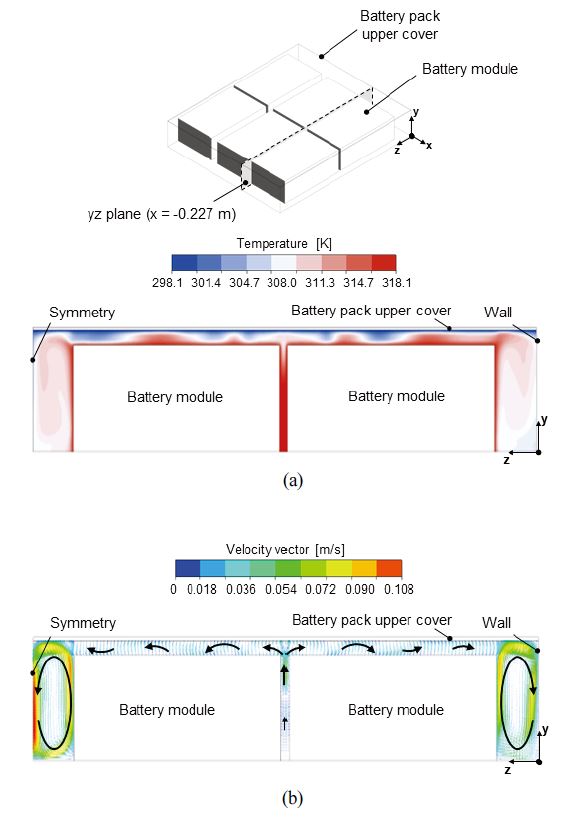
Fig. 4는 평면으로 단순화한 배터리팩 상부 커버 형상으로 수치해석을 진행한 것이며, yz 평면(x = -0.227 m)에서의 온도, 속도벡터의 분포이다. Fig. 4(a)는 yz 평면(x = -0.227 m)에서의 온도 분포를 나타내며, 배터리에서 발생하는 열로 인해 배터리 모듈 사이 및 배터리 모듈, 배터리팩 상부 커버 사이에서 온도가 비교적 높게 나타나는 것을 확인할 수 있었다. Fig. 4(b)는 yz 평면(x = -0.227 m)에서의 속도벡터 분포를 나타내며, 배터리에서 발생하는 열에 의해 공기의 밀도가 감소하여 밀도차에 의한 부력으로 배터리 모듈 주위에서 위로 상승하는 기류가 형성된다. 배터리 모듈 사이에서 상승하는 공기는 배터리 모듈 측면으로 이동하고 배터리 모듈 측면에서 상승되는 공기는 배터리팩 상부 커버와 만나 바닥면으로 하강하면서 순환하게 된다. 속도 벡터는 배터리 모듈과 우측의 벽면 사이보다 배터리 모듈과 좌측의 대칭되는 면 사이에서 더 빠른 분포를 보였다.
3.1 유출홀의 효과
Fig. 5는 평면으로 단순화한 배터리팩 상부 커버 형상과 유출홀이 있는 배터리팩 상부 커버 형상에 대한 yz 평면(x = -0.227 m)에서의 온도, 속도벡터의 분포이다. 배터리에서 발생하는 발열이 외부로 유출되는 공기의 흐름을 나타내기 위해 유출홀 출구는 대기압으로 가정하여 수치해석을 진행하였다. Fig. 5(a)는 yz 평면(x = -0.227 m)에서의 온도 분포를 나타내며, 유출홀이 있는 배터리팩 상부 커버 형상에서 유출홀로 인해 내부 유동 속도가 증가되어 배터리팩 상부 커버와 배터리 모듈 사이에서 온도가 높은 고온부를 최소화할 수 있었다. Fig. 5(b)는 yz 평면(x = -0.227 m)에서의 속도벡터 분포를 나타내며, 유출홀이 있는 배터리팩 상부 커버 형상에서 유출홀로 인해 배터리팩 상부 커버와 배터리 모듈 사이, 배터리 모듈 측면에서 유동 속도가 증가하는 것을 확인할 수 있었다.
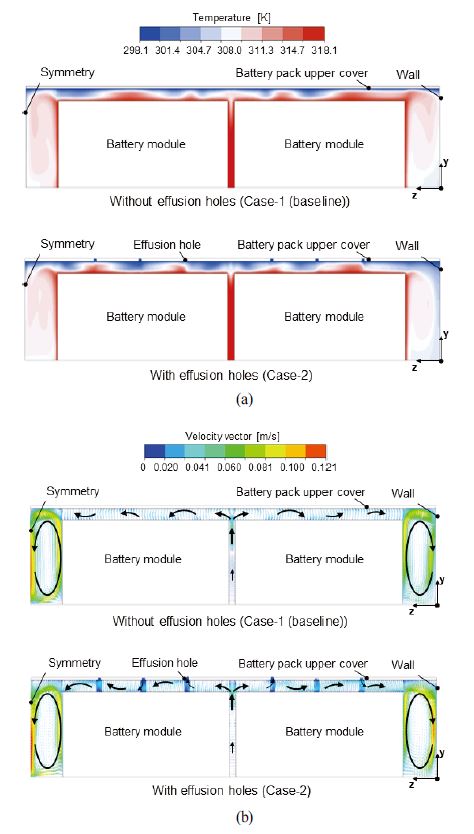
Comparison of (a) temperature and (b) velocity vector distributions on yz plane (x = -0.227 m) without and with effusion holes
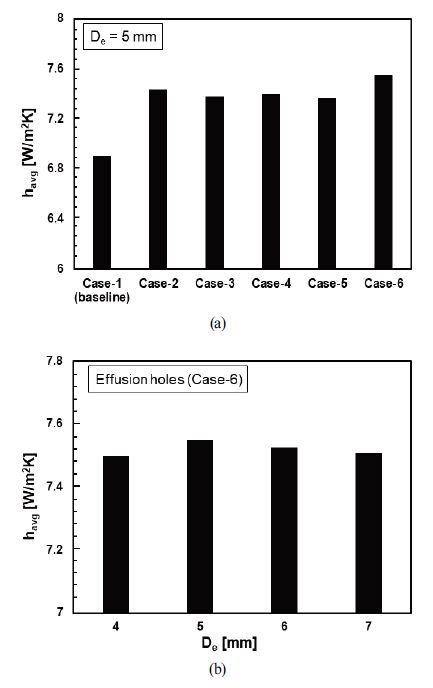
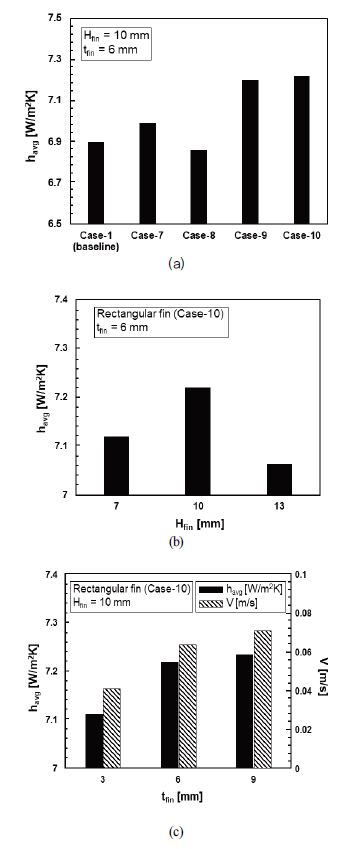
Fig. 6은 유출홀의 배열(Fig. 6(a)) 및 유출홀의 직경(Fig. 6(b))에 따른 배터리팩 상부 커버 안쪽 표면의 평균 열전달계수를 나타낸 그래프이다. 배터리팩 상부 커버의 안쪽 표면 평균 열전달계수는 유출홀의 위치가 배터리 모듈 간격 위쪽보다 배터리 모듈 위에 위치할 때 증가하는 것을 확인할 수 있었다. 또한, 배터리팩 상부 커버에 유출홀을 설계했을 경우 단순화한 배터리팩 상부 커버 형상보다 평균 열전달계수가 평균적으로 7.1% 향상되는 것을 확인할 수 있었고, 유출홀이 배터리 모듈과 배터리 모듈 간격 위쪽에 위치한 유출홀 Case-6 형상이 평면으로 단순화한 형상보다 8.6% 증가하여 가장 높은 평균 열전달계수로 나타났다. Fig. 6(b)는 유출홀 Case-6 형상을 기준으로 유출홀의 직경을 달리하여 계산해서 얻어진 평균 열전달계수 값을 나타낸다. 유출홀의 직경이 5 mm보다 작을 경우 유출홀에 의한 영향이 줄어들었고, 유출홀의 직경이 5 mm보다 클 경우 유출홀의 직경 단면적이 커지기 때문에 배터리 모듈과 배터리팩 상부 커버 사이의 유동 속도가 감소하여 배터리팩 상부 커버 안쪽 표면의 평균 열전달계수가 감소하는 것을 확인할 수 있었다.
3.2 직사각형 핀의 효과
Fig. 7은 평면으로 단순화한 배터리팩 상부 커버 형상과 직사각형 핀을 추가로 설치한 배터리팩 상부 커버 형상에 대한 yz 평면(x = -0.227 m)에서의 온도, 속도벡터의 분포이다. 직사각형 핀의 온도 조건은 배터리팩 상부 커버 안쪽 표면과 동일한 상온 293.15 K의 일정 표면 온도를 경계조건으로 부여하였다. Fig. 7(a)는 yz 평면(x = -0.227 m)에서의 온도 분포를 나타내며, 핀으로 인한 내부 유동 속도 증가로 오른쪽 배터리 모듈과 배터리팩 상부 커버 사이에서 온도가 높은 고온부를 최소화할 수 있었다. Fig. 7(b)는 yz 평면(x = -0.227 m)에서의 속도벡터 분포를 나타낸다. 직사각형 핀에 의해 배터리 모듈과 배터리 상부 커버 사이의 유동 속도가 증가하는 것을 확인할 수 있었고, 좌측의 대칭되는 면과 배터리 모듈 사이의 공간에서 가장 빠른 속도벡터 분포가 나타나는 것을 확인할 수 있었다.
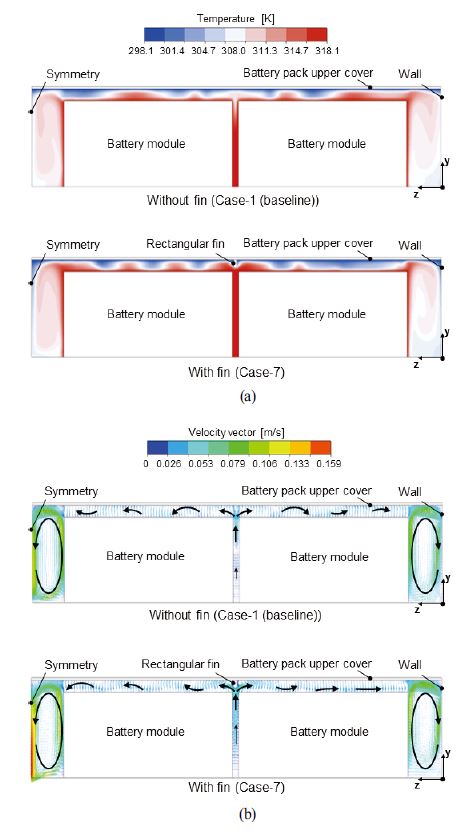
Comparison of (a) temperature and (b) velocity vector distributions on yz plane (x = -0.227 m) without and with fins
Fig. 8은 직사각형 핀 배열(Fig. 8(a)), 핀 높이(Fig. 8(b)), 핀 두께(Fig. 8(c))의 변화에 따른 배터리팩 상부 커버 안쪽 표면의 평균 열전달계수를 나타낸 그래프이다. 배터리팩 상부 커버의 안쪽 표면 열전달계수는 직사각형 핀 Case-8을 제외한 모든 형상이 평면으로 단순화한 형상보다 높게 나타나는 것을 확인할 수 있었다. 또한, 핀을 x축 방향(Cases-7, 8)보다 z축 방향(Cases-9, 10)으로 설치하였을 때, 더 높은 평균 열전달계수가 나타나는 것을 확인할 수 있었다. 그 이유는 x축 방향보다 z축 방향으로 배치한 핀의 길이가 더 길어 내부 유동에 대한 영향을 많이 받기 때문이다. 그러므로 z축 방향으로 배치된 직사각형 핀 Case-10 형상이 가장 높은 평균 열전달계수를 나타내며 평면으로 단순화한 형상보다 4.4% 향상되었다. Fig. 8(b)는 직사각형 핀 Case-10 형상을 기준으로 핀 두께(tfin)를 6 mm로 고정하고 핀 높이(Hfin)를 변화하여 얻어진 평균 열전달계수 값을 나타낸다. 직사각형 핀의 높이가 10 mm보다 작을 경우 열전달 면적이 줄어들어 평균 열전달계수가 감소하였다. 핀의 높이가 10 mm보다 클 경우 열전달 면적은 증가하지만, 배터리 모듈과 배터리팩 상부 커버 사이의 간격이 15 mm로 줄어들어 배터리 모듈과 배터리팩 상부 커버 사이로 흐르는 내부 유동 속도를 감소시켜 평균 열전달계수가 감소하는 것을 확인할 수 있었다. Fig. 8(c)는 직사각형 핀 Case-10 형상을 기준으로 핀 높이(Hfin)를 10 mm로 고정하고 핀 두께(tfin)를 변화하여 얻어진 평균 열전달계수 및 속도 값을 나타낸다. 직사각형 핀의 두께가 증가할수록 열전달 면적 및 배터리 모듈과 배터리팩 상부 커버 사이에서의 유동 속도 증가로 인해 평균 열전달계수는 증가하지만, 증가량은 감소하여 핀의 두께가 6, 9 mm에서의 평균 열전달계수는 크게 차이가 없는 것을 확인하였다.
3.3 복합된 유출홀과 직사각형 핀의 효과
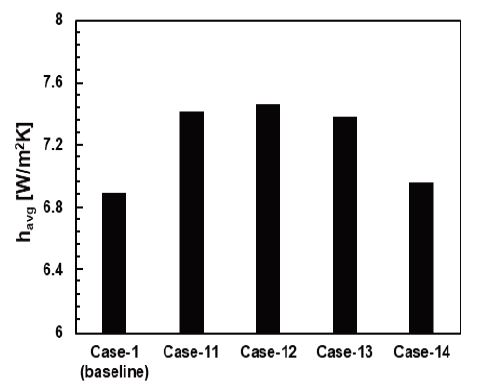
유출홀과 직사각형 핀이 모두 설치된 배터리팩 상부 커버 형상은 평균 열전달계수가 높은 유출홀 Cases-2, 6과 직사각형 핀 Cases-9, 10을 조합하였다. Fig. 9는 평면으로 단순화한 배터리팩 상부 커버 형상과 유출홀과 핀이 모두 설치된 배터리팩 상부 커버 형상에 대한 안쪽 표면의 평균 열전달계수를 나타낸 그래프이다. 유출홀과 핀이 모두 설치된 배터리팩 상부 커버 형상은 유출홀과 핀으로 인해 배터리 모듈과 배터리팩 상부 커버 사이의 유동 속도 증가로 인해 평면으로 단순화한 배터리팩 상부 커버 형상보다 평균 열전달계수가 향상되는 것을 확인할 수 있었다. 그중에서도 Case-12 형상이 평면으로 단순화한 배터리팩 상부 커버 형상보다 평균 열전달계수가 7.6% 향상되었다.
3.4. 국부 열전달계수 비교
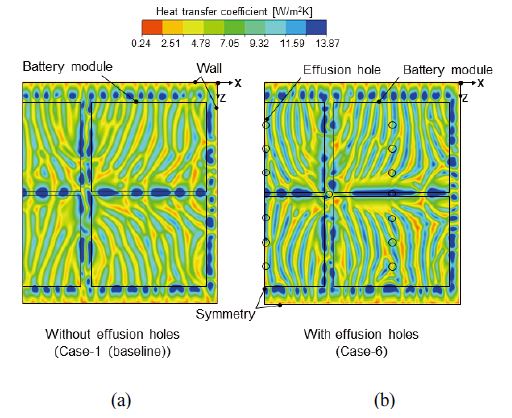
본 연구에서 평면으로 단순화한 배터리팩 상부 커버 형상에 유출홀과 직사각형 핀을 설치하여 수치해석을 진행한 결과, 배터리팩 상부 커버 안쪽 표면의 평균 열전달계수는 유출홀, 유출홀과 핀이 모두 설치된 형상, 핀 순으로 높게 나타났고, 수치해석을 진행한 14가지 형상 중에서 유출홀을 설치한 Case-6 형상이 가장 높은 평균 열전달계수를 보였다. Fig. 10은 평면으로 단순화한 배터리팩 상부 커버 형상과 유출홀이 설치된 Case-6 형상에 대한 배터리팩 상부 커버 안쪽 표면의 국부 열전달계수 분포를 나타낸 것이다. 유출홀이 없는 형상(Fig. 10(a))보다 유출홀이 있는 형상(Fig. 10(b))에서 높은 열전달계수 분포가 나타나는 것을 확인할 수 있었고, 유출홀 근처에서 유동 속도가 증가하기 때문에 가장 높은 열전달계수는 유출홀 근처에서 나타나는 것을 확인할 수 있었다. 또한, 전반적으로 유동 속도가 빠른 배터리 모듈 간 사이, 배터리 모듈과 벽면, 대칭면 사이에서 높은 열전달계수 분포를 나타내는 것을 확인하였다.
4. 결 론
본 연구에서는 배터리팩 내부의 유동과 자연대류 열전달 특성을 확인하기 위해 3차원 수치해석을 수행하였다. 평면으로 단순화한 배터리팩 상부 커버의 안쪽 표면에 유출홀과 직사각형 핀의 배열 및 치수 등 다양한 설계 인자를 고려하여 배터리팩 상부 커버의 안쪽 표면 평균 열전달계수의 수치해석 결과를 요약하면 다음과 같다.
- 1) 유출홀을 설치한 배터리팩 상부 커버 형상에서 유출홀로 인해 배터리 모듈과 배터리팩 상부 커버 사이의 유동 속도가 증가되어 평균 열전달계수가 향상되었다. 배터리팩 상부 커버 안쪽 표면의 평균 열전달계수는 유출홀 직경이 5 mm인 Case-6 형상에서 가장 높았으며, 평면으로 단순화한 배터리팩 상부 커버보다 8.6% 향상되었다.
- 2) 직사각형 핀을 설치한 배터리팩 상부 커버 형상에서 핀으로 인한 배터리 모듈과 배터리 상부 커버 사이의 유동 속도 증가로 인해 평균 열전달계수가 향상되었다. 핀 두께 6 mm, 높이 10 mm, z축 방향으로 배치한 Case-10 형상의 평균 열전달계수가 가장 높게 나타났고, 평면으로 단순화한 배터리팩 상부 커버보다 4.4% 향상되었다.
- 3) 유출홀과 직사각형 핀이 모두 설치된 배터리팩 상부 커버 형상 중, Case-12 형상의 평균 열전달계수는 평면으로 단순화한 배터리팩 상부 커버보다 7.6% 향상되었다.
- 4) 배터리팩 상부 커버 안쪽 표면의 평균 열전달계수는 유출홀만 설치한 형상, 유출홀과 직사각형 핀을 모두 설치한 형상, 직사각형 핀만 설치한 형상 순으로 높게 나타났다. 본 연구에서는 배터리팩 상부 커버 내부의 자연대류 열유동 특성을 파악하였으며, 향후 배터리팩 상부 커버의 구조 및 내충격성 해석을 함께 고려하여 배터리팩 상부 커버의 형상 설계를 진행하고자 한다.
Acknowledgments
이 연구는 2020년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(20013794).
References
- Johnny, X., Chris, J., and Marcy, R., 2021, “Global Electric Vehicle Market 2020 and Forecasts,” Canalys Newsroom.
-
Park, K. M., Kim, J. H., Park, J. Y., and Bang, S. B., 2018, “A Study on the Fire Risk of ESS through Fire Status and Field Investigation,” Korean Institute of Fire Science and Engineering, Vol. 32, No. 6, pp. 91∼99.
[https://doi.org/10.7731/KIFSE.2018.32.6.091]

- Kim, M. S., 2019, “The Importance of Integrated Thermal Management System for Electric Vehicle,” Auto Journal, Journal of the Korean Society of Automotive Engineers, Vol. 41, No. 6, pp.62∼64.
-
Nada, S.A., 2007, “Natural convection heat transfer in horizontal and vertical closed narrow enclosures with heated rectangular finned base plate,” International Journal of Heat and Mass Transfer, Vol. 50, No. 3–4, pp. 667∼679.
[https://doi.org/10.1016/j.ijheatmasstransfer.2006.07.010]

-
Bocu, Z. and Altac, Z., 2011, “Laminar natural convection heat transfer and air flow in three-dimensional rectangular enclosures with pin arrays attached to hot wall,” Applied Thermal Engineering, Vol. 31, No. 16, pp. 3189∼3195.
[https://doi.org/10.1016/j.applthermaleng.2011.05.045]

-
Fontana, E., Capeletto, C. A., Silva, A. d., and Mariani, V. C., 2013, “Three-dimensional analysis of natural convection in a partially-open cavity with internal heat source,” International Journal of Heat and Mass Transfer, Vol. 61, pp. 525∼542.
[https://doi.org/10.1016/j.ijheatmasstransfer.2013.02.047]

-
Sert, Z., Tekkalmaz, M., and Timuralp, C., 2017, “Combined Natural Convection and Thermal Radiation in an Inclined Cubical Cavity with a Rectangular Pins Attached to Its Active Wall,” Periodicals of Engineering and Natural Sciences, Vol. 5, No. 3, pp. 347∼354.
[https://doi.org/10.21533/pen.v5i3.122]

-
Saeid, N. H., 2017, “Natural Convection in a Square Cavity with Discrete Heating at the Bottom with Different Fin Shapes,” Heat Transfer Engineering, Vol. 39, No. 2, pp. 154∼161.
[https://doi.org/10.1080/01457632.2017.1288053]

-
Chen, H. T., Lin, M. C., and Chang, J. R., 2018, “Numerical and experimental studies of natural convection in a heated cavity with a horizontal fin on a hot sidewall,” International Journal of Heat and Mass Transfer, Vol. 124, pp. 1217∼1229.
[https://doi.org/10.1016/j.ijheatmasstransfer.2018.04.046]

- Jeon, W. H., 2016, “Integrated Thermal Management with Thermal Mapping and Heat Dissipation,” M.Sc. Thesis, University of seoul national.
- Bergman, T. L., Incropera, F. P., DeWitt, D. P., and Lavine, A. S., 2011, “Fundamentals of heat and mass transfer,” John Wiley & Sons.
- Lemmon, E. W., Huber, M. L., and McLinden, M. O., 2013, “REFPROP 9.1,” NIST Standard Reference Database 23.
- ANSYS Inc., ANSYS Fluent Theory Guide, Canons burg, PA: release 20.1, 2019.
-
Van Doormaal, J. P. and Raithby, G. D., 1984, “Enhancements of the SIMPLE method for predicting incompressible fluid flows,” Numerical heat transfer, Vol. 7, No. 2, pp. 147∼163.
[https://doi.org/10.1080/01495728408961817]