2차원 등각 원심형 임펠러에 대한 미끄럼 계수

1. 서 론

미끄럼 현상은 전향력에 의한 불균일한 유동장에 의해 발생한다. 전향력은 점성 유무에 상관없이 존재하므로, 미끄럼 현상은 점성 유동뿐만 아니라 비점성 유동에서도 발생한다.

전향력에 의해 블레이드 압력면 상대 속도는 느려지고, 흡입면 상대 속도는 빨라진다. 비점성 유동에서는 이러한 상대 속도 구배로 인해 임펠러 회전 방향과 반대로 순환하는 상대 와류가 발생하며, 이는 임펠러 출구에서 미끄럼 속도를 발생시킨다. 점성 유동에서는 전향력에 의해 블레이드 흡입면 위에 두꺼운 경계층이 형성된다. 경계층의 두께는 유속에 비례하므로, 블레이드 앞전 흡입면에는 두꺼운 경계층이 형성된다. 흡입면 경계층 내의 유속은 점점 느려지며, 압력도 표면 마찰에 의해 낮아진다. 이에 따라 임펠러 출구 흡입면에는 두꺼운 경계층과 저속의 후류가 발생한다. 따라서 임펠러 출구에서는 흡입면에서 압력면 쪽으로 미끄러지는 유동이 형성된다.

미끄럼 현상의 정도를 나타내기 위해 미끄럼 속도가 정의되었다. 미끄럼 현상은 임펠러 출구 유동의 각운동량을 감소시킨다. 이로 인해 임펠러로부터 얻을 수 있는 이론적인 양정이 감소하게 된다. 미끄럼 속도의 크기를 산출하는 방법은 크게 두 가지 방법으로 나눌 수 있다. 이론 양정을 대수적으로 구하여 미끄럼 속도를 산출하는 방법과 미끄럼 속도를 상대 와류의 기하학적 크기로부터 유추하는 방법으로 나눌 수 있다.

기하적 방법의 대표적인 예로는 Stodola⁽¹⁾와 팽기석 등⁽²⁾이 있다. Stodola는 상대 와류의 회전 각속도는 임펠러 회전 각속도와 같으며, 상대 와류의 형상은 원형으로서 직경은 블레이드 출구 너비로 간주하였다. 미끄럼 속도를 상대 와류의 원주 속도와 같다고 간주하여 식(1)과 같이 나타내었다.

식(1)에서 V_s는 미끄럼 속도, U₂는 임펠러 출구 원주 속도, β는 블레이드 각도(원주 방향 기준), Z는 블레이드 개수이다. 식(1)은 블레이드 각도가 작고 블레이드 개수가 많은 경우에는 잘 맞지만, 그렇지 않으면 과도하게 예측하는 경향이 있다. 팽기석 등은 이러한 문제를 개선하고자 상대 와류의 지름을 임펠러 출구 너비 대신 임펠러 외경과 블레이드에 내접하는 원의 지름으로 간주하여 미끄럼 속도를 식(2)와 같이 나타내었다.

where, $$ f=0.833+\frac{0.21}{e^{\frac{Z^3}{32.3}}}+0.024\left(1-\frac{1}{e^{\frac{Z^{41}}{336}}}\right)e^{\frac{{90}^{\circ }-{\beta }^{\circ }}{24.2}\frac{1}{1-e^{-Z^{1.31}/3.04}}}$$

대수적 해법은 유동 해석을 통해 이론 양정을 계산하여 미끄럼 속도를 산출하는 방법이다. 이론 양정이란 단위 유량당 각운동량의 변화량으로서, 임펠러 손실이 배제된다. 대수적 연구 방법에도 두 가지 부류가 있었는데, 2차원 포텐셜 유동 해석으로 이론 해를 구하거나 임펠러 유동을 단순화하여 지배 방정식으로부터 근사 해를 구하는 방법이 있다.

Busemann⁽³⁾은 등각 사상을 통한 포텐셜 유동 해석으로 2차원 원심형 등각 블레이드에서 발생되는 이론 양정을 계산하였다. 등각 블레이드의 두께는 무한히 얇다고 가정하고, 블레이드 개수와 각도에 따라 이론 양정을 계산하여 미끄럼 속도를 산출하였다. 미끄럼 속도는 임펠러 출구 유동이 원주 방향으로 불균일할수록 커진다는 것을 밝혀내었다. 하지만 이론 해를 수식 형태가 아닌 그래프 형태로 제시하였기 때문에 사용에 불편한 점이 있다. 이러한 문제를 해결하고자 Wiesner⁽⁴⁾는 Busemann의 계산 결과를 추세식으로 표현하였다. Wiesner는 실제 점성 유동에서 측정된 실험 데이터와 여러 미끄럼 계수 모델들을 비교한 결과, Busemann의 이론 해가 가장 잘 맞는다는 것을 검증한 후 이에 대한 추세식을 다음과 같이 표현하였다.

근사적인 해법으로 이론 양정을 구한 연구에는 Kearton⁽⁵⁾과 Sheets⁽⁶⁾ 등이 있다. 이들은 단일 원호 블레이드를 해석 대상으로 하였기 때문에 블레이드 곡률 반경이 모든 위치에서 동일하다. 모든 유체의 상대 유동각이 블레이드 각도와 동일하다는 가정 하에 운동량 방정식과 에너지 방정식으로부터 상대 속도와 압력 분포를 구하였으며, 이로부터 이론 양정을 산출하였다.

본 연구에서는 Sheets의 근사적인 방법을 활용하여 등각 블레이드에서 발생하는 미끄럼 속도를 수식 형태로 유도하였다. Busemann의 이론 해와 비교하여 미끄럼 속도 및 미끄럼 계수에 대한 보정식을 제안하였으며, Wiesner 모델과 팽기석 모델과 정합성을 비교하였다.

2. 상대 속도 분포 유도

2.1 블레이드 중심부 상대 속도 분포

블레이드에 작용하는 회전력이 온전히 유체에 전달된다면 블레이드 회전력과 유체의 각운동량 변화량은 동일하다. 이론 양정은 단위 유량당 각운동량 변화량이므로, 블레이드 회전력으로부터 이론 양정을 산출할 수 있다. 블레이드 회전력은 블레이드 압력면과 흡입면에 작용하는 압력 분포를 적분하여 구할 수 있다.

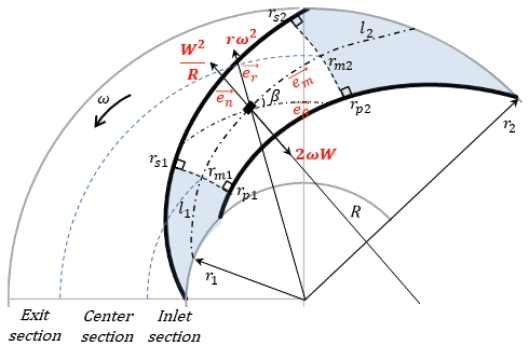
본 연구에서는 Sheets가 제안한 근사적인 방법으로 블레이드 주위의 상대 속도 분포를 유도하였다. 블레이드 유로를 Fig. 1과 같이 입구부과 중심부, 출구부의 세 구간으로 나누어 해석한다. 블레이드 상류와 하류는 원주 방향으로 균일한 비회전 유동이지만, 블레이드 중심부에는 불균일한 회전 유동이 형성된다고 가정한다. 입구부는 블레이드 입구의 비회전 유동에서 중심부의 회전 유동으로 상대 속도를 연속적으로 연결하기 위한 조정 영역이다. 출구부 또한 중심부와 블레이드 출구를 연결하는 조정 영역이다. 이로써 블레이드 전 영역에 걸쳐 불균일한 속도 분포를 만들 수 있다. 하지만 이 방법은 블레이드 유로를 세 영역으로 나눌 수 있을 만큼 충분히 길어야만 적용할 수 있다. 따라서 본 해석 결과는 현절비(Solidity)가 한계 현절비보다 큰 경우에만 유효하다.

Fig. 1

Forces in a rotating channel

블레이드 폭(b)이 일정한 2차원 블레이드의 중심부를 통과하는 비점성 유동의 수직 방향 힘 평형 방정식은 다음과 같다.

$\[ \frac{1}{\rho }\frac{\partial p}{\partial n}=\frac{W^2}{R}+r{\omega }^2\mathrm{c}\mathrm{o}\mathrm{s}\beta -2\omega W \]$

(4)

식(4)에서 ρ와 p는 유체의 밀도와 압력이며 W는 상대 속도, R은 블레이드 곡률 반경, ω는 블레이드 회전 각속도이다. 유선에 수직한 방향으로 작용하는 압력구배(∂p/∂n)는 블레이드 곡률에 의한 원심 가속도(W²/R)와 블레이드 회전에 의한 원심 가속도의 수직 방향 성분(rω²cosβ), 코리올리 가속도(2ωW)의 영향을 받는다. 유선을 따라 상대 유동의 전체 에너지는 식(5)와 같이 일정하게 유지된다.

$\[ \frac{p}{\rho }+\frac{W^2}{2}-\frac{r^2{\omega }^2}{2}= const\text{.} \]$

(5)

식(5)로부터 유선 위의 한 점에서의 에너지 방정식은 다음과 같다.

$\[ \frac{1}{\rho }\frac{\partial p}{\partial n}+W\frac{\partial W}{\partial n}-r{\omega }^2\frac{\partial r}{\partial n}=0 \]$

(6)

식(6)에서 dr/dn=cosβ 이다. 식(4)와 식(6)을 연립하면 상대 속도에 대한 지배 방정식은 다음과 같다.

$\[ \frac{\partial W}{\partial n}+\frac{W}{R}-2\omega =0 \]$

(7)

식(7)은 1계 비제차 미분방정식이므로 적분 인자 $$ e^{\int \frac{dn}{R}}$$을 도입하여 적분하면, 유선의 수직 방향 상대 속도 분포 함수는 다음과 같다.

$\[ W\left(n\right)=e^{-\int \frac{dn}{R}}\left[2\omega \int e^{\int \frac{dn}{R}}dn+C\right] \]$

(8)

식(8)에서 블레이드 압력면의 위치를 n=0, 그리고 압력면 상대 속도를 W_ps라 하면 적분 상수는 C=W_ps가 된다.

등각 블레이드의 곡률 반경은 r과 β의 함수로서, 다음과 같다.

$\[ R=\frac{r}{\left|\mathrm{c}\mathrm{o}\mathrm{s}\beta \right|} \]$

(9)

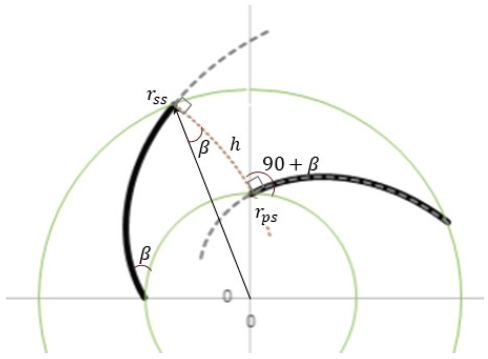
Fig. 2는 등각 블레이드에 수직한 직교선을 도시한 것이다. 이웃 블레이드는 기준 블레이드로부터 2π/Z 만큼 회전 이동하면 된다. 직교선은 원주 방향을 기준으로 90°+β의 각도를 갖는 등각선이다. 직교선과 기준 블레이드 및 이웃 블레이드가 만나는 교점을 구하면 압력면 반경 r_ps에 대응하는 흡입면 반경 r_ss는 다음과 같다.

$\[ \frac{r_{ss}}{r_{ps}}=E=\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{2\pi }{Z}\mathrm{s}\mathrm{i}\mathrm{n}\beta \mathrm{c}\mathrm{o}\mathrm{s}\beta \right) \]$

(10)

Fig. 2

A line orthogonal to the flow lines in an equiangular impeller

등각 블레이드는 블레이드 각도가 β로 일정하므로, 식(9)를 미분하면 dR=dr/cosβ 이다. 그리고 블레이드의 미소 너비는 dn=dr/cosβ 이므로, 등각 블레이드에서는 dR=dn 이 성립한다. 압력면의 곡률 반경을 R_ps라 할 때, 등각 블레이드의 곡률 반경은 직교선을 따라 다음과 같이 변한다.

$\[ R=R_{ps}+n \]$

(11)

식(11)을 식(8)에 적용하면 상대 속도는 직교선을 따라 다음과 같이 분포한다.

$\[ W\left(n\right)=\frac{R_{ps}{W}_{ps}+\omega \left(n^2+2R_{ps}n\right)}{n+R_{ps}} \]$

(12)

블레이드 폭이 b로 일정한 2차원 등각 블레이드에서 직교선을 따라 상대 속도의 평균값 $$ \stackrel{-}{W}$$를 구하면 다음과 같다.

$\[ \stackrel{-}{W}\begin{array}{l}=\frac{Q}{Zbh}=\frac{1}{h}{\int }_0^h Wdn\hfill \\ =\frac{\omega }{2}\left(h+2R_{ps}\right)+\frac{R_{ps}{W}_{ps}-\omega R_{ps}^2}{h}\ln \frac{h+R_{ps}}{R_{ps}}\hfill \end{array} \]$

(13)

이웃한 두 블레이드 사이의 거리 h는 식(11)로부터 곡률 반경의 차이와 같으므로, h=R_ss-R_ps 이다. 또한 식(10)으로부터 R_ss/R_ps=E 로 치환하여 식(13)을 정리하면 압력면 상대 속도는 다음과 같이 나타낼 수 있다.

$\[ W_{ps}=\frac{E-1}{\ln E}\stackrel{-}{W}-\omega R_{ps}\left(\frac{E^2-1}{2\ln E}-1\right) \]$

(14)

식(14)를 식(12)에 대입한 후 n=R-R_ps로 치환하면, 직교선 위의 상대 속도 분포는 다음과 같다.

$\[ W=\frac{E-1}{\ln E}\frac{R_{ps}}{R}\stackrel{-}{W}-\omega R\left(\frac{R_{ps}^2}{R^2}\frac{E^2-1}{2\mathrm{l}\mathrm{n}E}-1\right) \]$

(15)

흡입면 속도 W_ss는 R=R_ss에서의 속도이므로 식(15)로부터 다음과 같다.

$\[ W_{ss}=\frac{E-1}{E\mathrm{l}\mathrm{n}E}\stackrel{-}{W}+\omega R_{ss}\left(1-\frac{E^2-1}{2E^2\mathrm{l}\mathrm{n}E}\right) \]$

(16)

직교선에 대한 평균 속도 $$ \stackrel{-}{W}$$는 연속 방정식을 이용하여 임펠러 출구 속도 성분으로 치환할 수 있다.

$\[ Q=2\pi r_{2}b{V}_{2m}=2\pi r_{2}b{W}_{2\mathrm{\infty }}\mathrm{s}\mathrm{i}\mathrm{n}\beta =Zbh\stackrel{-}{W} \]$

(17)

$\[ \stackrel{-}{W}=\frac{2\pi \mathrm{s}\mathrm{i}\mathrm{n}\beta }{Z}\frac{r_2}{h}{W}_{2\mathrm{\infty }}=\frac{\ln E}{E-1}\frac{r_2}{r_{ps}}{W}_{2\mathrm{\infty }} \]$

(18)

식(18)을 식(14)와 식(16)에 대입한 후 임펠러 원주 속도 U₂ 로 무차원화 하면 다음과 같이 표현할 수 있다.

$\[ \frac{W_{ps}}{U_2}=\frac{W_{2\mathrm{\infty }}}{U_2}\left(\frac{r_2}{r_{ps}}\right)-P\left(\frac{r_{ps}}{r_2}\right) \]$

(19)

$\[ \frac{W_{ss}}{U_2}=\frac{W_{2\mathrm{\infty }}}{U_2}\left(\frac{r_2}{r_{ss}}\right)+S\left(\frac{r_{ss}}{r_2}\right) \]$

(20)

where, $$ P=\frac{1}{\cos \beta }\left(\frac{E^2-1}{2\mathit{ln}E}-1\right)$$

　　　 $$ S=\frac{1}{\cos \beta }\left(1-\frac{E^2-1}{2E^2\mathit{ln}E}\right)$$

식(19)과 식(20)은 블레이드 중심부 내의 압력면 및 흡입면 상대 속도 분포 함수이다. 두 식의 우변 첫째 항은 비회전 유동의 평균 속도이고, 두 번째 항은 회전 유동에 의한 속도 변화량을 나타낸다.

3. 이론 양정 산출

블레이드에 작용하는 회전력이 온전히 유체에 전달된다면 모든 회전력은 유체의 각운동량 변화량과 같다. 이론 양정은 단위 유량당 각운동량 변화량과 같으므로, 이론 양정(H_E)과 회전력의 관계는 다음과 같다.

블레이드의 회전력은 모든 블레이드 표면에 작용하는 압력에 의한 모멘트와 같다.

비점성 유동인 경우 에너지 방정식은 다음과 같다.

식(26)에서 압력은 비점성 에너지 방정식에 의해 상대 속도로 변환할 수 있다. 이로부터 식(26)을 적분하면 블레이드 회전력을 구할 수 있다.

식(28)을 적분한 다음, 수식을 보다 간단히 만들기 위해 r_p1과 r_s1은 r_m1으로, r_p2와 r_s2는 r_m2로 치환하여 정리하였다. 평균 유선을 상대 와류의 중심을 통과하는 궤적으로 간주하면 평균 유선에서는 비회전 유량만 존재한다. 따라서 r_m은 식(15)의 우변 두 번째 항인 회전 유동이 0이 되는 위치이다.

따라서 등각 블레이드 회전력은 다음과 같다.

블레이드 입구 유동에 입사각이 발생하지 않는 경우, W_2∞는 연속 방정식을 이용하여 r₂/r₁의 함수로 치환할 수 있다.

식(30)과 식(31)을 식(25)에 대입하면 무차원 이론 양정은 다음과 같다.

식(32)는 근사적 해법으로 구한 이론 양정이다. 각 항들의 계수들을 전개하면 모두 E에 대한 함수이다. 계수들의 크기를 비교하기 위해 추세식으로 구해보면 lnE에 대한 2차 다항식으로 표현할 수 있다.

$$ \mathrm{l}\mathrm{n}E=\frac{\pi }{Z}\mathrm{s}\mathrm{i}\mathrm{n}2\beta \le 1$$인 경우, 식(35)∼식(38)은 작은 값이므로 무시할 수 있다. 따라서 식(32)는 다음과 같이 간략화 할 수 있다.

where, $$ \begin{array}{c}{\nu }_2=\frac{3}{2}F+\left(1+\frac{3}{2}G\right)\frac{r_{m2}}{r_2}\hfill \end{array}$$

　　　 $$ {\nu }_1=\frac{3}{2}F+\left(1+\frac{3}{2}G\right)\frac{r_{m1}}{r_1}$$

4. 미끄럼 계수 유도

임펠러 입구 유동은 비회전 균일 유동이므로, 임펠러 입구 수두는 속도 선도에 의해 다음과 같이 나타낼 수 있다.

비점성 유동인 경우 임펠러 출구 수두는 입구 수두와 이론 양정의 합이므로, 식(39)와 식(40)을 더하면 다음과 같다.

임펠러 출구 속도 선도로부터 출구 수두는 미끄럼 속도와 다음의 관계가 있다.

미끄럼 계수(σ₀)를 다음과 같이 정의할 경우 식(42)로부터 다음과 같이 나타낼 수 있다.

식(43)은 근사적 해법으로 유도한 미끄럼 계수식이다. 이 식에는 ν₁과 ν₂ , 두 개의 미지수가 포함되어 있다. 본 연구에 사용된 근사적 해법은 블레이드 유로를 입구부와 중심부, 출구부의 세 구역으로 나눌 수 있을 만큼 현절비가 충분히 큰 임펠러에서만 유효하다. Busemann은 현절비가 한계 현절비 이상인 경우 미끄럼 계수가 유량 및 반경비(r₁/r₂ )와 무관하게 일정한 값을 갖는다고 하였다. 따라서 식(43)이 반경비와 무관한 값을 가지려면 ν₁ = 1 이 되어야 한다.

ν₂는 F와 G, 그리고 출구부의 입출구 반경비인 r_m2/r₂의 함수이다. F와G는 E에 대한 함수이므로 β와 Z의 함수이다. 본 연구에서는 ν₂를 등각 블레이드의 현절비 공식에 비례 계수 Γ 를 도입하여 다음과 같은 모형으로 나타내었다.

식(44)에서 Γ는 출구부의 현절비에 상응한다. 식(44)를 식(43)에 적용하면 본 연구를 통해 제안하는 미끄럼 계수식의 최종 형태는 다음과 같다.

식(45)를 보면 미끄럼 계수는 블레이드 각도와 개수의 제한된 변수만의 영향을 받으며, 유량과는 무관한 함수로 표현된다. Busemann은 한계 현절비 이상에서는 미끄럼 계수가 유량 변화와 무관하다고 하였는데, 이는 등각 블레이드의 특성이다. 따라서 등각 블레이드가 아니거나 입사각이 존재한다면 양상은 달라질 수 있다. 오종식⁽⁸⁾은 유량에 따라 미끄럼 계수가 변하는 특성은 블레이드 하중이 변하는 모습과 유사하게 나타난다고 하였다.

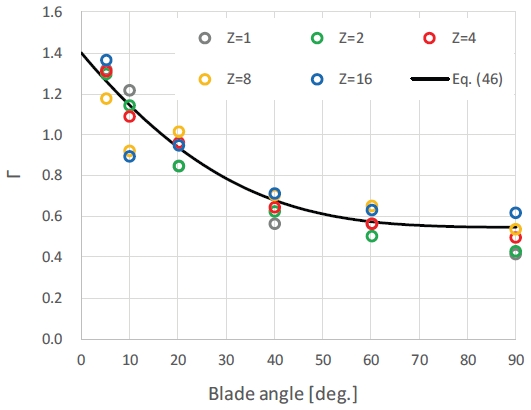
Γ 에 대한 모형을 만들기 위해 식(45)에 Busemann의 미끄럼 계수를 대입하여 Γ 값을 역산해보았다. Fig. 3은 역산한 Γ 값을 도시한 것으로서, 다음의 추세식을 구하였다.

Fig. 3

Γ fitting to Busemann’s solutions

5. 모델식의 검증

5.1 기존 미끄럼 계수 모형들과 비교

본 연구에서 제안하는 미끄럼 계수를 Wiesner와 팽기석의 모델과 비교하였다. Wiesner는 Busemann의 이론 해를 기반으로 하여 식(3)과 같은 경험식을 제안하였고, 팽기석은 상대 와류의 크기를 모델링하여 식(2)를 제안하였다.

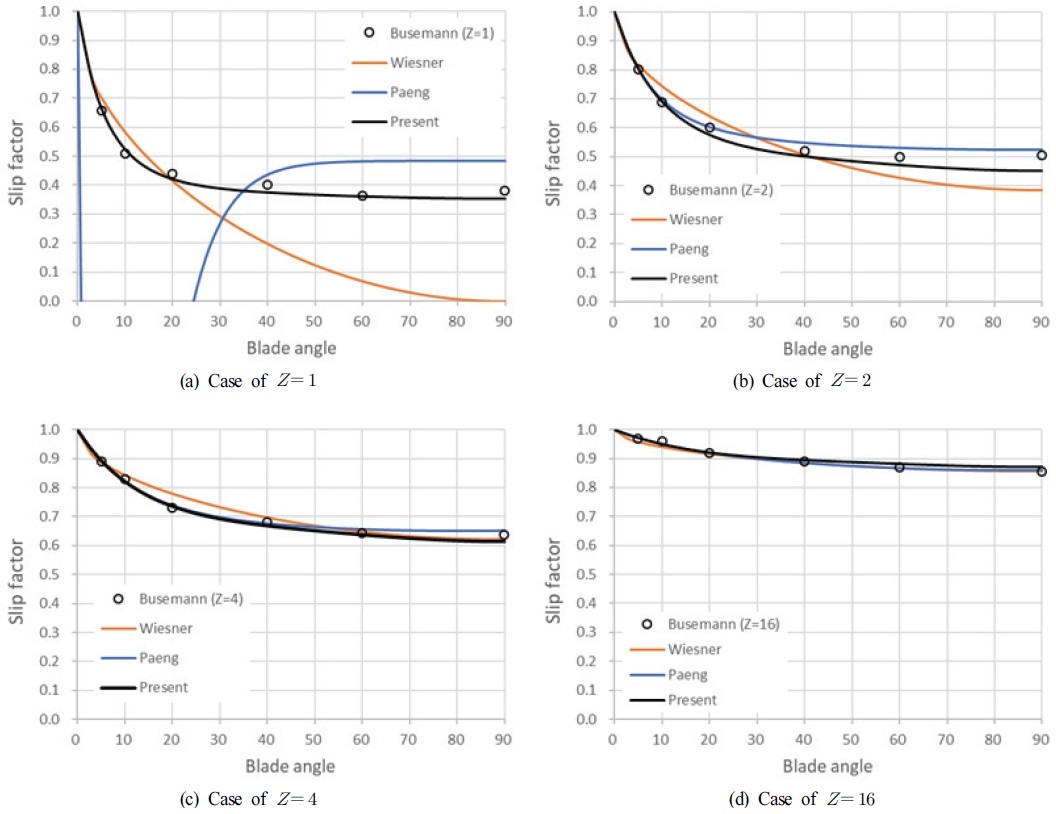
Fig. 4는 Busemann의 이론 해와 세 개의 모델을 블레이드 개수와 각도에 따라 비교한 결과이다. Wiesner와 팽기석 모델 모두 블레이드 개수가 4 이상이면 Busemann의 이론 해와 잘 일치하였다. 하지만, 블레이드 개수가 적어지면 오차가 증가하였다. 본 모델은 lnE≤1 조건에서 제작되었지만, Z=1과 Z=2를 포함한 모든 경우에 대해 잘 일치함을 볼 수 있다.

Fig. 4

Comparison between Busemann and slip factor models

5.2 현절비의 영향 보정

미끄럼 계수가 현절비의 영향을 받는 임계값을 한계 현절비라 하는데, Busemann은 한계 현절비를 1이라고 하였으며, Wienser는 1.3으로 간주하였다. 본 연구에서는 Busemann의 제안대로 한계 현절비를 1로 간주하였다. 현절비는 임펠러 입출구 반경비의 함수이므로, 현절비 대신 입출구 반경비를 사용하기도 한다. Wiesner는 현절비의 영향을 한계 반경비와 반경비의 함수로 표현하였으며, 반경비가 한계 반경비보다 큰 경우에만 감소율을 곱하는 형태로 미끄럼 계수를 보정하였다.

$\[ \sigma ={\sigma }_0\times \left[1-{\left(\frac{ϵ-{ϵ}_{cr}}{1-{ϵ}_{cr}}\right)}^3\right] ;ϵ>{ϵ}_{cr} \]$

(47)

where, $$ ϵ=\frac{r_1}{r_2},{ ϵ}_{cr}=\text{exp}\left(-\frac{2\pi \text{sin}\beta }{Z}\times 1.3\right)$$

Wiesner는 반경비의 3승에 비례하여 미끄럼 계수가 감소한다고 하였다. 하지만 이는 블레이드 개수가 많거나 블레이드 각도가 큰 경우에는 Busemannn의 이론 해와 잘 어울리지만, 그렇지 않은 경우에는 편차가 커진다. 따라서 본 연구에서는 지수를 3 대신 Z와 β의 함수로 다음과 같이 수정하였다.

$\[ \sigma ={\sigma }_0\times \left[1-{\left(\frac{ϵ-{ϵ}_{cr}}{1-{ϵ}_{cr}}\right)}^x\right],{ϵ}_{cr}=\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{2\pi \mathrm{s}\mathrm{i}\mathrm{n}\beta }{Z}\right) \]$

(48)

where, $$ x=3\times \frac{Z^{0.2}\sqrt{\text{sin}\beta }}{2}$$

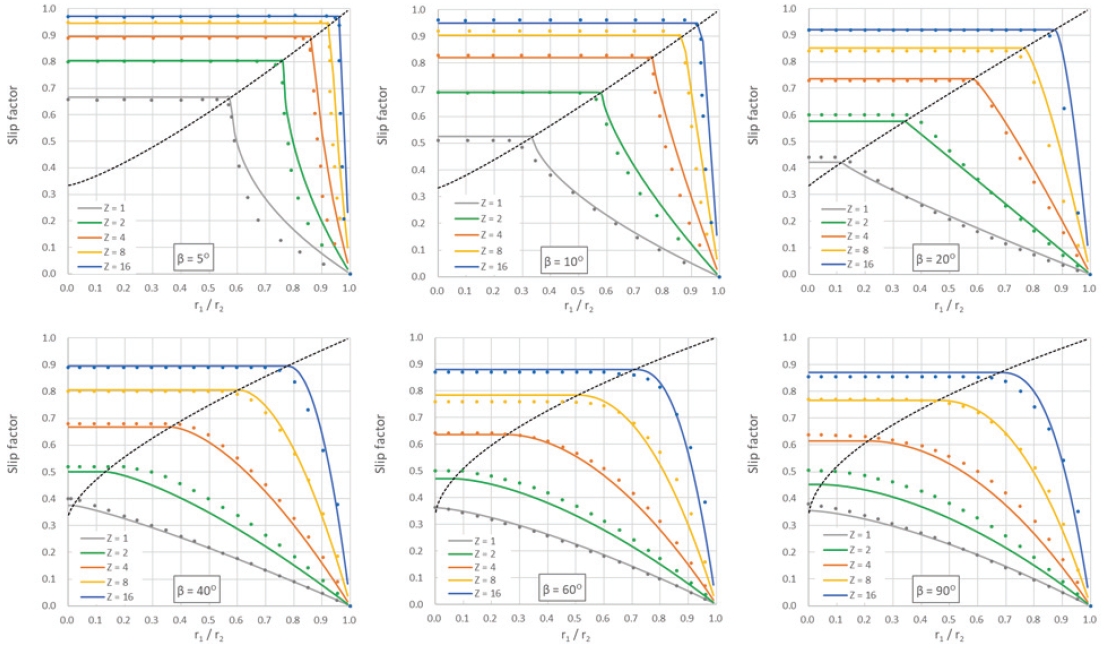
Fig. 5는 식(48)과 Busemann의 이론 해와 비교한 결과이다. 블레이드 개수가 적거나 블레이드 각도가 작은 경우에도 Busemann의 이론 해와 잘 일치하였다.

Fig. 5

Comparison of slip factor with Busemann’s exact solutions

6. 결 론

Sheets가 제안한 근사적 해법을 이용하여 2차원 등각 블레이드에 대한 미끄럼 계수식을 유도하였다.

Wiesner 식보다 더 넓은 범위의 블레이드 개수 및 각도에서 잘 일치하였다. 또한 현절비 보정식을 반경비와 블레이드 개수, 각도의 함수로 수정하여 정확성을 향상시켰다.

Acknowledgments

본 연구는 산업통상자원부 소재부품패키지형기술개발사업의 일환으로 한국산업기술평가관리원의 지원을 받은 과제(20010867)에 의해 수행되었습니다.

References

• Stodola, A., 1927, “Steam and Gas Turbines,” McGraw-Hill Book Company, New York.
• Paeng, K. S., and Chung, M. K., 2001, “A New Slip Factor for Centrifugal Impellers,” Proc. Inst. Mech. Eng., Part A, pp. 645-649. [https://doi.org/10.1243/0957650011538776]
• Busemann, A., 1928, “Das Forderhohenverhaltniss Radialer Kreiselpumpen mit Logarithmischspiraligen Schaufeln,” Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 8, pp. 372∼384. [https://doi.org/10.1002/zamm.19280080504]
• Wiesner, F. J., 1967, “A Review of Slip Factors for Centrifugal Impellers,” Trans. ASME, J. Engineering for Power, Vol. 89, pp. 558-572. [https://doi.org/10.1115/1.3616734]
• Kearton, W. J., 1933, “The Influence of the Number of Impeller Blades on the Pressure Generated in a Centrifugal Compressor and on its General Performance,” Proc. Inst. Mech. Eng., Vol. 124, pp. 481-568. [https://doi.org/10.1243/PIME_PROC_1933_124_017_02]
• Sheets, H. E., 1950, “Flow through Centrifugal Compressors and Pumps,” Trans. ASME, Vol. 72, pp. 1009-1015. [https://doi.org/10.1115/1.4016896]
• Helmholtz, H., 1858, Jourmal für die reine und angewandte Mathematik, Vol. 55, pp. 25-55. [https://doi.org/10.1515/crll.1858.55.25]
• Oh, Jongsik, 1999, “A Numerical Study on Slip Factor Variations in Centrifugal Compressor Impellers,” The KSFM Journal of Fluid Machinery, Vol. 2, No. 3, pp. 17-23. [https://doi.org/10.1115/IMECE1999-1221]