하이브리드 프랙탈격자에서 발달된 저선회 화염의 난류강도 특성화에 관한 연구
Abstract
This study investigated the low swirl turbulent flow characteristics combined with the hybrid fractal grid, and studied the correlation between the turbulence intensity of the combustion reaction field and structural variables of the grid. The turbulence intensity before the nozzle outlet showed the characteristics of the cross grid. Turbulence intensity increased in the descending order of reduced ratio of bar thickness(RRBT), and the maximum point was located in the down stream. The Borghi-Peter diagram confirmed that the flame region was location in the thin reaction zone, and the height at which the flame floats from the nozzle exit was determined with the number of grid iterations was quantified with an OH* chemiluminescence image. The combustion reaction field was characterized by variable(x*) containing structural information of the grid, and the correlation between the characterized flow and I2/(I2)peak was identified. The coefficient of determination(R2) differed with the number of iteration and shape of the grid, and at I3, it was the highest in xs* including the square grid variable.
Keywords:
Low swirl injector, Hybrid fractal grid, Iteration Number, Turbulence intensity, Borghi-Peter diagram, Integral length scale, Energy cascade, Structural variable, Coefficient of determination키워드:
저선회 인젝터, 하이브리드 프랙탈 격자, 반복횟수, 난류강도, 보기피터선도, 적분 길이스케일, 에너지 캐스케이드, 구조적 변수, 결정계수1. 서 론
최근 탄소중립 및 환경 규제 정책이 엄격해짐에 따라, 가스터빈 발전기 운용 시 대기오염을 유발하는 연소 생성물의 감축 필요성이 대두되고 있다. 기존 가스터빈 연소기의 대부분이 강선회 인젝터(high swirl injector)에서 희박 예혼합 연소를 적용하여 운용하고 있는데, 강선회 인젝터는 선회유동으로 중심축 방향에 내부재순환영역(inner recirculation zone)이 생성되고 이 영역은 예혼합기에 지속적인 열원을 공급하여 노즐 팁에 화염을 부착시켜서 안정성을 유지한다. 하지만 내부재순환영역은 고온인 연소 생성물의 체류시간을 증가시켜 열적 질소산화물(thermal NOx) 생성을 촉진시킨다.
한편 R. K. Cheng은 난류생성기로 원형의 타공판(perforated plate)을 사용한 저선회 인젝터(low swirl injector)를 통해 연소생성물의 감축을 위한 새로운 연소기법을 제안하였다(1). 이들에 따르면 저선회 연소는 바깥의 약한(weak) 선회유동과 난류생성판에서 형성된 중앙의 난류유동이 상호작용된 확대유동장(divergence flow field)을 형성하고 확대유동의 자기상사성(self similarity)은 수식으로 표현이 가능하였다. 그리고 난류생성판에서 발달된 중심 유동은 높은 난류강도의 등방성 유동을 생성하는 특징을 가지는데 공급되는 예혼합기의 유속변화에 대해서 부상된 위치가 변하지만, 이에 유동적으로 대응함으로써 화염이 안정화된다. 하지만 난류생성판에서 토출된 예혼합기의 속도가 난류 연소속도를 초과할 경우 안정화 된 부상 화염을 형성할 수 없다. 따라서 저선회에 적용되는 난류생성판에서 격자의 면적을 일정 수준 이상으로 증가 시키거나 유지하여 중심영역과 선회영역에 적절한 유량이 공급되어야한다. 결과적으로 난류생성판에서 적절히 공급된 예혼합기는 인젝터 출구 이후 유동속도와 난류 연소속도가 같아지는 정체점(stagnation point)을 형성하는데, 이 지점에서 안정적으로 부상된 화염을 형성하게 된다(1).
저선회 인젝터는 종래 강선회기반의 가스터빈 인젝터에서 내부재순환영역에 따른 연소생성물 체류시간 증가에 따라 질소산화물 절감의 한계에 대한 대안으로 제시됨에 따라 많은 연구가 진행되었다. 대표적으로 Johnson 등은 강선회 인젝터와 저선회 인젝터의 유동장 및 NOx와 CO 배출물에 대하여 조사하였고, PIV기법을 통해 저선회의 유동장은 축 방향 유동이 모두 양(+)의 값을 가지며 내부재순환영역을 후류로 밀어내는 것을 확인하였다. 그 결과로 강선회보다 저선회화염에서 배기가스 체류시간을 감소시키며 열적 NOx가 크게 감소하는 것을 보였다(2). D. Littlejohn 등은 저선회 화염에서 다양한 탄화수소 계열의 예혼합 연료에서 NOx 및 CO 배출특성과 난류 연소속도와의 상관관계를 관찰함으로써 탄화수소계열의 연료들이 유사한 배기가스 배출 특징을 가지는 것을 확인하였다(3). 최근에는 무탄소 연료에 대한 관심이 높아짐에 따라 기존 가스터빈 연소기에 무탄소 연료를 적용하기 위한 연구가 활발하게 진행되고 있다. R. K. Cheng 등은 저선회 연소기에서 수소혼소 및 전소 시 부상화염의 거동 및 역화발생 조건을 파악하였고 수소 함량에 따라 난류연소속도와 속도섭동의 관계를 보여주었고 강선회와 저선회 연소의 NOx거동을 비교하였다(4).
프랙탈(fractal)이란 일정한 규칙을 가지는 형상이 자기상사성(self similarity)을 가지며 끝없이 반복되는 기하학적 구조이다. 이때 프랙탈격자는 초기 형상의 규칙이나 크기에 따라 서로 다르게 배치되는 흥미로운 특징을 가지게 된다. 프랙탈격자에서는 서로 다른 크기의 격자에서 다양한 난류길이와 동적 에너지를 생성함으로써 효과적으로 난류강도를 증가시키는 효과를 가진다. 이러한 특징을 가진 프랙탈격자는 유체역학자들에 의하여 다양한 프랙탈 형상에 따라 난류특성과 난류강도 증대에 대한 연구가 수행되었는데 대표적으로 D. Hurst와 J. C. Vassilicos는 사각풍동에서 세 가지 형상(cross, I, square)의 격자를 조사하였고 난류생성판의 등방성(isotropy)과 균일성(homogeneity)을 평가하고 난류생성과 소멸의 특성을 보고하였다(5). 스퀘어 프랙탈격자에서 발달된 에디들 중 가장 큰 격자의 영향을 나타낸 웨이크 상호작용길이(wake interaction length, x*)를 통해 다양한 길이스케일의 상호작용의 개념을 제안하였다. 또한 스퀘어 프랙탈격자에서 생성된 난류강도 분석을 통해 난류강도의 생성과 소멸의 평가 및 변곡점 위치와 유동장 특성화에 대한 관계를 보고하였다(6). Koji Nagata 등은 스퀘어 프랙탈격자를 반복횟수에 따라 x*를 포함한 구조적 정보가 담긴 변수들을 통하여 유동장을 무차원화 하였고, 무차원화 된 유동장과 작은 길이스케일과 소산계수특성의 상관관계를 보고하였다(7). Nicolleau 등은 원형, 삼각형, 별형의 프랙탈격자가 적용된 파이프유동에서 프랙탈격자의 반복횟수에 따라 압력손실과 유동의 특성에 대한 연구를 진행하였다(8). Sylvain Laizet 등은 스퀘어 프랙탈격자와 일반적인 격자인 그리드격자를 사각풍동의 유동장 DNS 해석을 보고하였는데, 이 연구에서 난류강도가 후류에서 증대되는 웨이크 상호작용 현상이 명확하게 나타나는 것을 확인하였다(9).
앞서 설명한 비반응장인 난류 유동장에서 프랙탈격자에 관한 연구와 별도로 반응 유동장인 예혼합 난류화염에서 프랙탈격자를 적용한 다양한 연구들이 보고되었다. T. Sponfeldner 등은 프랙탈격자를 이용한 V-shape 화염 연구에서 기존 그리드격자보다 화염의 표면밀도(flame surface density)와 난류 연소속도가 증가된 것을 확인하였다(10,11). Kang 등은 크로스 프랙탈격자를 저선회 인젝터에 결합하여 종래 타공판과의 난류특성을 비교하였고, LDV로 계측한 난류 연소속도와 난류 레이놀즈 수의 상관관계에 대해 보고하였다(12). A. A. Verbeek 등은 먼저 원형의 타공판과 크로스 프랙탈격자를 저선회기와 결합하여 OH-PLIF으로 난류 연소속도 및 화염의 표면밀도가 증대되는 것을 보고하였고, 이후 수소연료를 첨가하여 OH-PLIF을 통하여 크로스 프랙탈격자와 종래의 난류생성판과 속도 섭동과 국부 난류 연소속도를 비교하였는데, 크로스 프랙탈그리드에서 개선된 것을 확인하였다(13,14). 이처럼 저선회 인젝터 화염에 대한 선행 연구가 다수 보고되었지만 대부분의 저선회 인젝터 중심 채널은 타공판 타입의 난류생성판을 적용되었다. 일부 저선회 인젝터에 프랙탈격자를 적용한 시도가 있었지만 그것도 크로스격자에 국한되었다(12-14).
그런데, J. C. Vassilicos 등의 연구에 의하면 크로스격자와는 달리 스퀘어격자에서는 발달된 난류강도가 상류에서 후류로 갈수록 천천히 증대되나 이후 빠르게 감소되는 특징을 보였다. 또한 스퀘어격자에서 웨이크 상호 작용길이로 유동장이 재편되어 타 형상보다 유동장과 격자 구조에 대한 연관성이 존재하는 것을 보였고 x*로 재편된 유동장과 다양한 난류특성들과의 상관관계에 대해서도 보고하였다. 이러한 특성이 저선회 화염의 난류특성에 미치는 영향을 파악하기 위하여 Vassilicos가 제안한 스퀘어격자를 저선회 인젝터에 적용하려고 하였으나 구조적 한계로 저선회 연소기에서 화염이 안정화되기 위한 충분한 막힘률을 만족하질 못하고 있다.
한편, 두 가지 형상을 결합한 프랙탈격자에 대한 연구는 보고된 바가 없는데, 본 연구팀에서는 스퀘어격자의 다양한 난류특성과 구조적 변수의 영향을 관찰하기 위해서 스퀘어와 크로스 형상을 결합한 하이브리드 프랙탈격자를 고안하게 되었다. 앞서 기술한 바와 같이 난류생성판의 격자형상에 의한 난류강도 증대는 난류화염의 연소성능을 향상시키는 역할을 하게 된다. 하지만 난류생성판의 격자형상과 저선회 화염의 난류강도간의 관계에 대한 연구는 전무한 실정이다.
따라서 본 연구에서는 저선회 인젝터의 난류 생성판에 하이브리드 프랙탈격자를 적용하여 격자가 생성하는 유동장의 난류특성에 대해 실험적으로 면밀히 조사하고자 한다. 이를 위하여 하이브리드 프랙탈격자에서 생성된 유동의 균일성(homogeneity)과 등방성(isotropy)을 살펴보고, 다양한 길이스케일의 상호작용 효과와 난류강도를 조사한다. 또한 격자 반복횟수에 따라 난류 연소속도와 밀접한 관계를 가지는 난류강도의 거동과 격자의 구조적 변수로 특성화된 유동장의 상관관계를 파악하고자 한다.
| (1) |
2. 실험방법 및 장치
2.1 저선회 인젝터
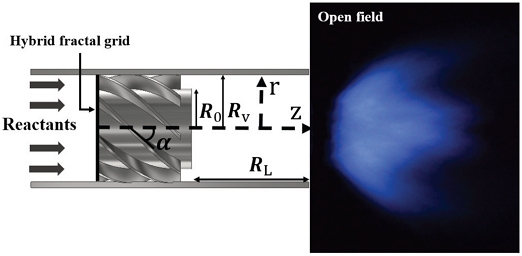
저선회 인젝터(low swirl injector)의 축 방향과 반경 방향을 각각 z, r로 정의하였고, 하이브리드 프랙탈격자를 결합한 저선회 인젝터의 단면도를 Fig. 1에 도시하였다. 본 연구에서 저선회 인젝터의 선회영역 반경(Rv)과 중심영역 반경(Ri)는 각각 Rv = 14 mm, Ri = 10 mm이다. 또한 저선회 인젝터의 선회각도(swirl angle) α는 37 °이고 중심유동과 선회유동이 적절하게 상호작용할 수 있는 완화길이(recess length, RL)는 선회 반경(Rv)의 약 2.4 배로 34 mm이다.
선회강도를 나타내는 swirl number(S)의 수식을 식 (1)에 나타내었다. 식 (1)의 α는 선회각도, R 은 저선회 인젝터의 선회영역 반경과 중심영역 반경 비(ratio)로 Ri/Rv으로 나타내며, 본 연구에서는 0.714의 값을 가진다. m은 각 영역의 혼합기의 질량플럭스 비(mass flux ratio)로 이다. 는 난류생성판을 통과하는 중심축 방향의 질량유량, 는 난류생성판 바깥의 선회익을 통과하는 선회영역의 질량유량이다. 선회영역과 중심영역의 유동이 통과하는 면적을 CATIA V5로 도출하여 값을 계산하였고 본 연구에서는 0.384의 값을 가진다. 따라서 식 (1)에 의하여 계산된 swirl number의 값은 0.571이다.
2.2 하이브리드 프랙탈격자
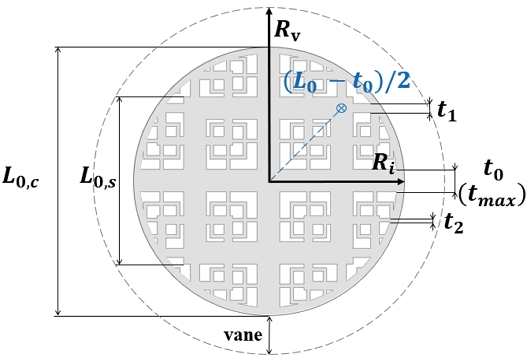
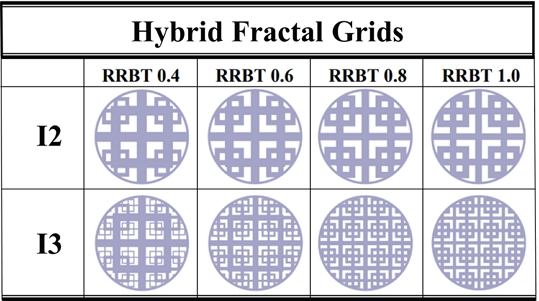
하이브리드 프랙탈격자(hybrid fractal grid) 구조와 격자 정보를 Fig. 2에 도시하였다. 하이브리드 프랙탈격자는 스퀘어와 크로스형상을 결합한 구조로 격자의 길이를 L로 정의하였고, 각 형상의 최대 길이를 각각 L0,s, L0,c로 나타내었다. 격자 반복의 기준점을 각 형상의 중심에 위치시키기 위하여 J. C. Vassilicos가 제안한 격자 생성규칙을 따라 제작하였고, 프랙탈격자의 유효격자길이(effective mesh size, Meff)를 제안하였는데, 원형격자에 적용을 위해선 정의된Meff의 수식 에서 사각격자 면적에 대한 부분인 T2(사각격자의 단면적)의 변경이 필요하였다. 본 연구에서는 상기 수식을 원형 프랙탈에 대한 면적으로 수정하였는데 수정된 수식을 식 (2)에 나타내었다(5). 식 (2)는 원형 프랙탈격자의 유효격자길이로 격자의 프랙탈화를 판단할 수 있는 격자의 중요한 구조적 변수 중 하나이다. A는 격자가 차지하는 면적, σ는 막힘률, P는 프랙탈격자의 둘레길이(perimeter’s length)를 의미한다. 하이브리드 프랙탈격자 전체 면적대비 격자가 차지하는 면적의 비율을 막힘률(blockage ratio, σ)로 정의하는데, 모든 격자는 막힘률 70 %로 고정하였다.
격자의 직경은 20 mm이고 각 격자는 식 (3)의 규칙에 따라 분류된다. 식 (3)은 격자의 바 두께 감소비율 (reduced ratio of bar thickness, RRBT)을 나타내며 tn+1와 tn의 비율을 의미한다. 여기서 t는 격자의 두께를 나타내고, 0.2 단위로 0.4∼1.0까지 제작되었다. 반복 횟수(iteration number, I)는 하이브리드 프랙탈격자가 반복된 횟수를 의미하며, 식 (2)의 tn의 하첨자인 n을 반복 횟수로 정의한다. 반복 횟수 두 번과 세 번은 각각 I2, I3로 표기하였다. RRBT와 반복 횟수는 격자생성에 주요한 변수들이며, 고정된 막힘률(σ)로 제작된 8개의 하이브리드 프랙탈격자를 Table 1에 나타내었다.
| (2) |
| (3) |
| (4) |
2.3 실험장치 구성
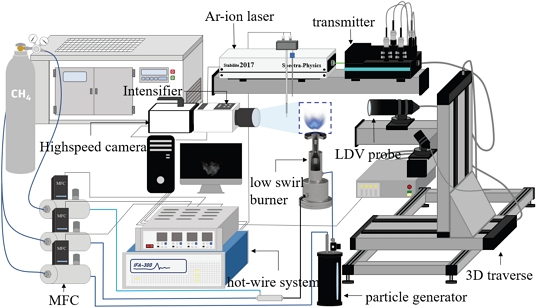
저선회 버너의 부분 단면도 및 실험장치의 개략도를 Fig. 3에 도시하였다. 실험 시 주변온도를 20 ℃로 유지하였으며 비반응장 및 반응장 모두 벌크유속(bulk velocity, U0)이 7.5 m/s인 조건에서 진행하였다. 연료는 고순도 메탄 (CH4, 99.999 %)을, 산화제는 압축공기를 사용하였고 공기와 연료의 비율인 당량비(equivalence ratio, φ)는 0.85로 고정하였다. 공기와 연료는 버블 메타로 교정된 질량유량계(mass flow controller, Air : M3500V, CH4 : MCR-100slpm-D/5M)를 통하여 제어했으며 혼합 챔버에서 혼합된 예혼합기를 버너의 플래넘 하단부에 공급하였다. LDV에 사용된 입자는 오일 입자생성기에서 분사되며 버너의 플래넘 상단부 출구를 통하여 공급되었다. 예혼합기와 입자는 버너 내부에서 혼합된 후 수축노즐을 통하여 방출된다.
각 격자에서 발달되는 비반응 난류유동을 계측하기 위하여 열선유속계(hot wire anemometer HWA, TSI-IFA300)를 사용하였다. 본 연구에서는 직경 3.8 μm인 텅스텐 선에 백금이 코팅된 2차원 센싱 프로브를 사용하였으며, CTA(constant temperature anemometer) 타입으로 동적 응답특성이 우수하여 중심 축 방향의 2차원 속도섭동(u′, v′)과 다양한 난류스케일 및 에너지 스펙트럼을 조사하기 적합하였다(15). 열선유속계는 20 kHz의 취득률(sampling rate)으로 약 14초 동안 측정하여 난류 유동의 정보를 취득하였다. 다만 에너지 스펙트럼(energy spectrum)은 가장 작은 길이스케일인 콜모그로브 길이 스케일(Kolmogorov length scale, η)까지 관찰하기 위하여 30초 동안 50 kHz의 높은 취득률로 측정하였다. 또한 저선회 화염의 거동을 이미지 계측을 통해 분석하기 위하여 고속카메라로 OH 화학자발광 이미지(OH* chemiluminescence image)를 취득하였다. 본 연구에서 사용된 고속카메라는 nac-MEMRECAM HX-7s이며 Invisible vision사의 UVi Camera Intensifier와 동기화하여 4000 fps로 취득하였고 이미지의 크기는 896×1112 pixel이며 픽셀당 길이는 0.133 mm/pixel이다. 여기에 AVR OPTICS의 320/40 nm BrightLineⓇ single bandpass filter와 UV-lens(Nikon Rayfact PF10545MF)를 사용하여 OH 라디칼(radical)을 취득하였다.
반응장 유동(reaction flow)의 정보는 레이저 진단기법(laser diagnostics method)으로 이용한 레이저 도플러 속도계(Laser-Doppler Velocimetry, 이하 LDV)를 사용하여 계측하였다. LDV 광원으로는 6 W Argon–Ion 가스레이저 (Spectra physics, Stabilite 2017)를 사용하였고 트랜스미터(transmiter)를 통해 각각 514.5 nm(녹색)와 488.6 nm(청색)의 파장으로 분기된 시스템을 사용하였다. 분기된 레이저는 dual beam 방법을 통해 한 축 방향의 입자 속도 성분을 취득하기 위해 일정한 각도로 조사되었다. 입자의 속도(U)는 식 (5)의 수식을 통해 구할 수 있고 θ는 두 레이저가 이루는 각도, λ는 레이저의 파장이며 ∆f는 입자에 의한 주파수 변화의 차이이다. 플린지 영역(fringe spacing)의 길이는 5.27 μm 이며 400 mm 초점거리를 가지는 프로브(probe)를 통하여 유동 정보를 취득하였다.
2.4 입자의 유동 추종성을 위한 스토크스 수
본 연구에 사용된 LDV용 입자는 올리브 오일(olive oil)이며 분무 미립화(atomization) 방식의 오일입자 생성기(TSI oil droplet generator 9307)를 통해 평균 직경 0.5-1.0 μm로 생성된 입자를 사용하였다. LDV는 유체를 따르는 입자의 속도를 계측하여 유체의 속도로 판단한다. 특히 난류유동은 다양한 길이스케일의 에디(eddy)가 상호작용하며 복잡한 운동을 하므로 입자의 유동 추종성 검증이 반드시 필요하다. 따라서 입자가 유동을 따르는 정확성을 판단하기 위하여 스토크스 수 (Stokes Number, Stk)를 확인한다.
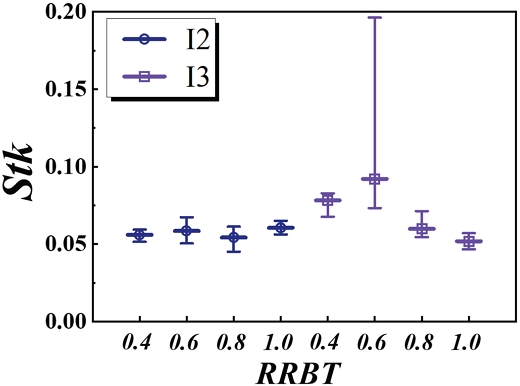
식 (6)은 스토크스 수를 나타내며 식 (7)과 식 (8)의 비(ratio)로 계산된다. 식 (7)은 특성 응답 시간과 식 (8)은 특성 유동시간 스케일이다. Fig. 4는 각 격자에 대한 스토크스 수를 도시하였고 에러바(error bar)로 각각 최대, 평균, 최솟값을 나타내었다. 일반적으로 스토크스 수의 값이 1미만이면 유동을 충분히 추종하게 되는데, 스토크스 수가 0.1 이하의 값을 가질 때 유동과 입자와의 거동 오차가 1 % 미만을 충족하게 된다(16). 본 조사결과에서 I3의 RRBT 0.6에서 스토크스 수의 최댓값이 0.1을 초과하였지만 이는 유동장의 후류부분에서 적분길이스케일이 감소함으로써 나타난 것으로 판단되며 본 실험조건에서 RRBT에 따라 계산된 스토크스 수의 평균값은 모두 0.1이하의 값을 나타내었다. 따라서 입자의 거동이 유동을 충분히 따르는 것을 알 수 있고 LDV로 측정된 물리량은 높은 신뢰성을 가지는 것으로 확인되었다.
| (5) |
| (6) |
| (7) |
| (8) |
3. 실험결과 및 고찰
3.1 비반응장 유동 특성
J. C. Vassilicos는 프랙탈격자에서 프랙탈 차원(fractal demension, Df)을 도입하여 유동의 균일성을 확인하였다. 식 (4)은 프랙탈 차원에 대한 수식이며 B 는 반복 횟수, RL은 반복 횟수에 따른 격자의 절반길이이다. Vassilicos가 제안한 1 ≤ Df ≤ 2인 프랙탈 차원에 대해서는 유동의 균일성과 등방성이 검증되어있다(5). 그러나 본 연구에 사용된 격자는 스퀘어와 크로스 형상이 겹쳐진 하이브리드 타입의 격자이기 때문에 다른 RL 값을 가지게 된다. 따라서 하이브리드 프랙탈격자에서는 프랙탈차원을 도입할 수 없기 때문에 유동장에 대한 직접적인 조사가 필수적이다. 이를 위해 본 연구에서는 CTA 타입의 열선유속계를 사용하여 하이브리드 프랙탈격자가 적용된 저선회 인젝터 출구에서의 유동 균일성과 저선회 인젝터의 축 방향 유동 등방성을 조사하였다.
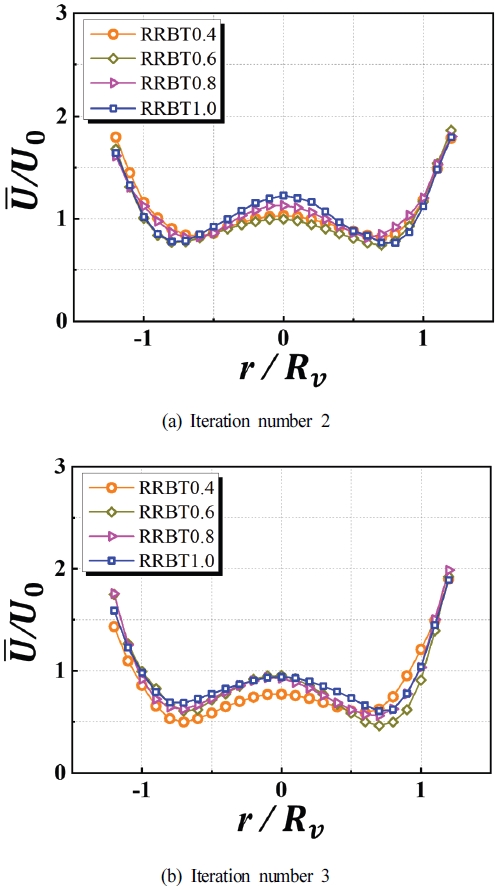
먼저 유동의 균일성(homogeneity)을 판단하기 위해서 측정된 위치는 프로브 보호를 위해 노즐 출구에서 z-축 방향으로 3 mm 올린 지점에서 열선유속계를 통해 r-방향으로 측정하였으며, 벌크유속으로 정규화 된 평균유속()을 Fig. 5에 도시하였다. Fig. 5의 가로 축은 반경방향인 r-방향의 길이를 프랙탈격자의 반지름(Rv)으로 정규화한 값이다. 그리고 본 논문에 나타낸 Figure들의 (a),(b)는 각각 격자 생성 반복이 두 번과 세 번인 I2, I3를 의미한다.
그림에서 보는 바와 같이 Fig. 5 (a), (b)는 저선회 인젝터의 중심(r/Rv = 0)에서 격자 반복횟수와 무관하게 가장 높은 유속을 보였다. (a)는 RRBT 0.4에서 1.0에 따른 중심 축에서 유속변화로 내림차순에 따라 유속의 값이 상승하는 것을 볼 수 있는데, 이는 격자의 초기 두께인 t0에 의한 영향으로 판단된다. 즉, 유동이 공급되는 격자의 빈 공간은 스퀘어와 크로스의 t0에 따라 형성되기 때문이다. 반면 (b)는 RRBT 0.4를 제외한 격자에서 유사한 유속 값을 가진다. (b)의 중심 축 유속의 경향은 격자의 tn, 즉 반복 횟수의 영향으로 판단되는데, RRBT의 감소로 tn의 두께가 증가하면서 격자의 빈 면적이 감소하였고 반복 횟수가 증가함에 따라 프랙탈화(fractality) 되어 격자가 더 조밀하여 그 효과가 증대하였기 때문으로 사료된다. Fig. 5 (a), (b)를 통해 비록 축 중심에서는 다소 높은 유속분포를 가지나 격자의 반복 횟수와 무관하게 노즐 출구에서 유속분포가 중심을 기준으로 대칭적으로 균일하게 분포하고 있음을 볼 수 있다. 따라서 하이브리드 프랙탈격자가 적용된 저선회 유동은 높은 유동 균일성을 형성함을 알 수 있다.
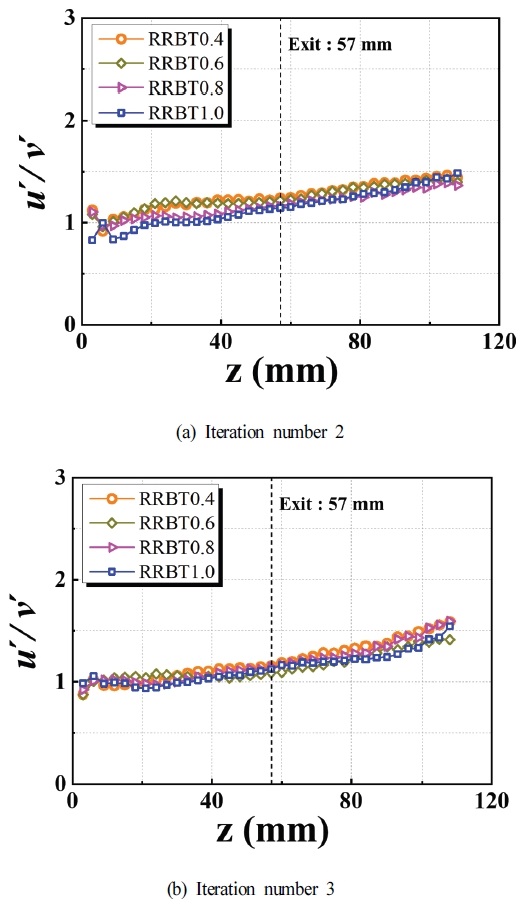
Fig. 6은 유동의 중심축 방향의 등방성(isotropy, u′/v′)을 보여주는 그래프로, 하이브리드 프랙탈격자의 3 mm 위 지점부터 3 mm 간격으로 약 5 L0인 108 mm까지 측정하였다. 여기서 u′과 v′은 각각 z-방향과 r-방향의 속도 섭동을 의미한다. Fig. 6에서 보이는 바와 같이 (a), (b) 전체 격자들에서 노즐 출구 전인 z = 57 mm 이전에서는 모두 1.0에 가까운 값을 보였다. 또한 노즐 출구(z = 57 mm)에서 (a), (b) 각각 1.24, 1.15 이하의 값을 보이며 하이브리드 프랙탈격자에서 발달된 저선회 중심 축 유동이 노즐 출구에서 이상적인(ideal) 등방성 난류유동에 가깝게 나타냄을 확인하였다. I3는 I2와 동일한 막힘률을 가지지만 더 큰 둘레길이(P)로 구성됨으로서 더 조밀한 격자에서 생성되는 작은 크기의 적분 길이스케일(integral length scale)을 가지게 된다. 따라서 Fig. 6에서 알 수 있듯이 I3는 I2보다 1에 더 가까운 등방성의 경향을 보이는 것은 난류생성판 격자 이후 작은 적분 길이스케일을 생성되며 u′과 v′이 유사한 운동성을 보여준 것으로 판단된다. 또한 난류화염의 해석을 위한 대부분의 방정식은 등방성과 균일성을 가정하여 정의되며 저선회 화염에서는 식 (9)와 같이 Damkhöler가 제안한 저선회 화염에서 난류 연소속도에 대한 모델식이 대표적이다. 따라서 본 조사를 통해 하이브리드 프랙탈격자에서 발달된 저선회 화염은 난류화염에 대한 이론적 물리량과 실험적 물리량을 비교 또는 검증에 적합한 모델이 될 수 있음이 확인되었다.
| (9) |
Fig. 7은 중심축에서 측정된 로 정의되는 난류강도 값(turbulence intensity, I)을 격자 반복 횟수별로 보여주고 있다. Fig. 7에서 보는 바와 같이 (a), (b) 모두 공통적으로 노즐 출구(z = 57 mm) 이전인 상류(upstream)에서 높은 난류강도를 보이고 있다. 유동장의 상류에서 I2, I3 모두 RRBT 0.4부터 1.0까지 내림차순으로 난류강도가 증가하였으며 최댓값 위치는 난류강도의 크기에 따라 후류로 밀려나는 것을 볼 수 있는데, RRBT별로 일관성을 가지며 후류로 밀려나는 것을 통해 RRBT별 경향성을 가지는 것이 확인되었다. 상류의 난류강도 증가는 하이브리드 프랙탈격자 중심에 위치한 크로스격자의 두께(t0) 효과로, 격자의 두께가 두꺼워지며 격자에서 발달 된 유동의 에디들이 상호작용 하는 위치가 후류로 밀리면서 큰 값의 강도를 가진다. 본 결과로 난류강도가 유지되거나 증가되는 웨이크 상호작용 이론을 확인할 수 있었다. 반면 Fig. 7(b)에서 노즐출구 이후의 후류에서 I3의 난류강도가 급격히 상승하는 특이한 거동을 보였다. 노즐 중심 유속은 확대유동으로 감소하지만 속도섭동은 웨이크의 상호작용과 선회유동의 효과 때문에 상승됨으로써 난류강도가 지속적으로 상승되는 것으로 판단된다. 노즐 출구 이후 높은 난류강도를 보이는 특성에 대해서는 다음절인 반응장에서 자세히 살펴보기로 한다.
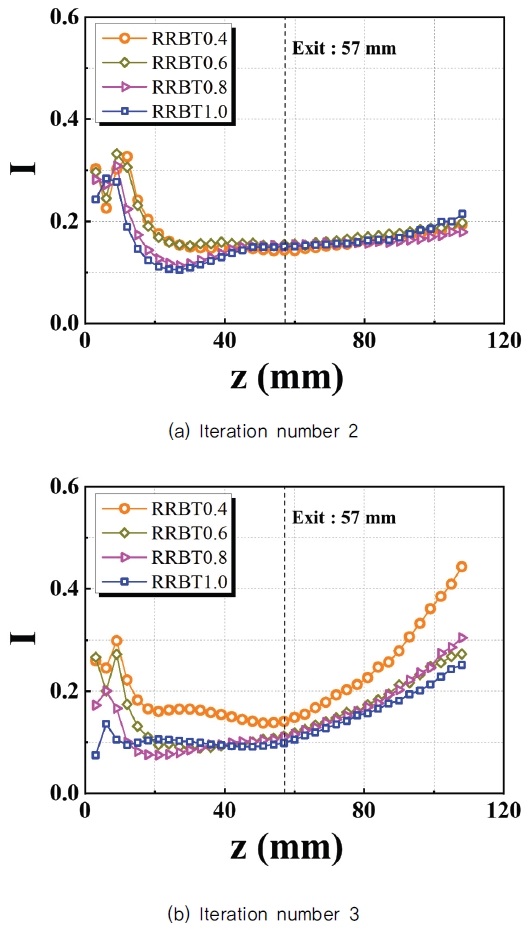
Turbulence intensity of low swirl center flow, I = u'/U-, dotted line at z = 57 mm denotes nozzle outlet
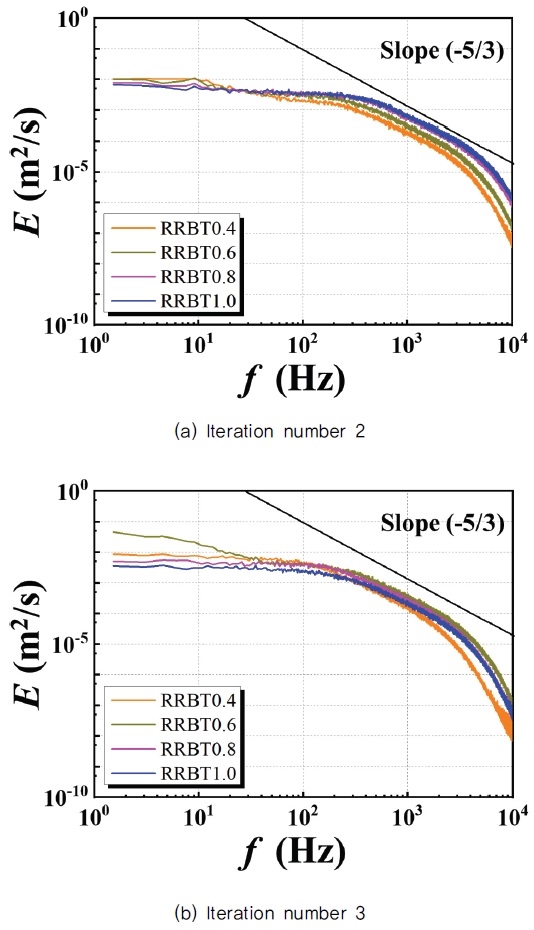
난류유동의 에너지전달 거동을 파악하고자 에너지스펙트럼을 Fig. 8에 도시하였다. 에너지 스펙트럼은 노즐출구 이후 부상화염이 평균적으로 위치하는 중심축 방향의 z / D = 0.36(z = 10 mm)에서 측정되었고 Kolmogorov 스케일의 파장영역까지 분석하기 위해서 앞서 실험방법에서 설명한 바와 같이 50 kHz의 높은 취득률로 측정되었다. Fig. 8의 세로축은 에너지의 크기를 나타내며 가로축은 주파수를 나타내는데, 주파수가 커질수록 작은 에디를 의미한다. I2에서 관찰된 특징은 큰 에디의 영역에서 에너지의 크기는 약 30 Hz까지 RRBT의 오름차순으로 낮아졌고, 이후의 에너지 크기는 RRBT에 내림차순으로 낮게 나타났으며 낮은 주파수에서 역전된 경향이 나타났다. 반면 I3에서는 약 100 Hz 부근에서 RRBT 0.4의 격자만 에너지 크기가 역전되었고, 나머지 I3격자들은 오름차순으로 작은 에너지를 가지며 감소하였다. 또한 난류 에너지가 관성아영역(inertial subrange)에서 콜모그로브의 멱 법칙(Kolmogorov’s power law)으로 –5/3승의 기울기를 가지며 큰 에디에서 작은 에디로 에너지가 전달되는 에너지 전달과정이 확인되었다(20). 본 과정에서 나타난 반복 횟수에 따른 특징은 에너지 전달이 일어나는 주파수와 에너지의 크기가 I3 보다 I2에서 더 큰 것으로 나타났다. 더 큰 주파수에서 –5/3승의 기울기를 따르는 것은 작은 에디에서 에너지 전달이 일어남을 의미하며 I2가 I3보다 큰 에디의 운동이 활발하며, 에너지를 더 오랫동안 유지하고 있음을 보여준다. 본 실험결과에서 관찰된 에너지 역전현상 및 에너지전달과정은 향후 난류의 생성 및 소산특성과의 연관성을 추가적인 연구를 통하여 면밀히 관찰하고자 한다.
3.2 반응장 유동 특성
본 절에서는 하이브리드 프랙탈격자의 구조적 변수에 따른 연소반응장 특성을 파악하고 저선회 화염에 미치는 영향을 분석하였다. 먼저, 보기피터 선도(Borghi-Peter diagram)를 통해 하이브리드 프랙탈격자의 저선회 난류화염이 갖는 난류화염 영역대(regime)를 표시하여 화염의 특징을 살펴볼 수 있었으며, 이를 Fig. 9에 도시하였다. 여기서 화염기저에서 LDV로 취득된 난류화염의 정보(u′,LT)는 층류화염의 정보(SL,δL)로 정규화하여 나타내었다. 본 연구에서 사용된 층류화염의 정보는 층류연소속도(SL)와 층류화염두께(δL)이며 각각 PREMIX코드(17)와 GRI 3.0(18) 상세반응 메커니즘을 사용하여 계산되었다.
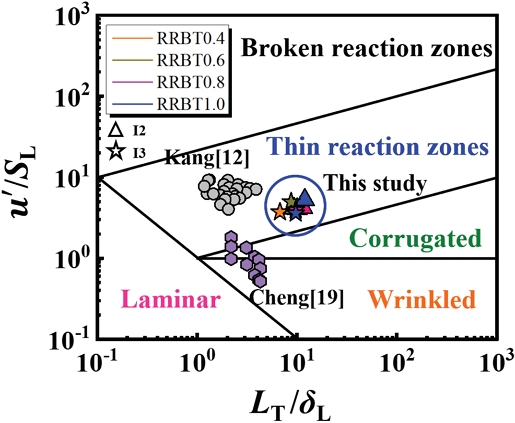
Borghi-Peter diagram regime of flame developed in hybrid fractal grid, cross fractal grid[12], perforated plates[19]
Fig. 9를 통하여 하이브리드 프랙탈격자에서 생성된 저선회 화염은 얇은 반응영역대(thin reaction zones)에 위치함을 알 수 있다. 선행연구인 타공판(perforated plate)(19) 및 크로스 프랙탈격자(12)의 난류생성판과 본 연구의 하이브리드 프랙탈격자에서 발달된 화염영역을 비교하였다. 분석결과 속도섭동은 타공판 형상의 비해 증가되었지만 크로스 프랙탈 형상에 비해 감소된 것이 확인되었다. 그리고 적분 길이스케일은 비교된 두 격자에 비해 본 연구에서 모두 증가된 것을 확인할 수 있다. 따라서 하이브리드 프랙탈격자는 타공판 형상보다 효과적으로 난류화 된 것을 확인 할 수 있었다. 다만 하이브리드 프랙탈격자가 동일한 직경과 막힘률의 크로스 프랙탈격자(12)의 t0보다 작기 때문에 크로스 형상의 영향이 감소한 것으로 판단되며, 스퀘어 형상과 크로스 형상으로 인해 다양한 길이스케일의 난류가 생성되고 상호작용하여 더 큰 적분 길이스케일을 갖는 것으로 나타났다.
본 연구에서 취득된 직접 화염사진에서 격자 반복 횟수에 따라 부상화염의 높이 차이가 발생하였는데, 부상된 높이를 정량적으로 분석하기 위하여 OH 라디칼(radical)의 화학자발광 이미지를 취득하였다. Fig. 10은 이렇게 측정한 OH* 자발광 이미지들을 보여주고 있는데, 고속카메라로 취득된 이미지는 Matlab을 통해 이진화(binarization)한 후 평균하여 나타내었다. r, z-방향의 길이를 저선회 인젝터 직경으로 나누었고 하단에 노즐 출구를 표시하였다. 화염의 부상높이는 노즐 출구중심에서부터 중심축 방향으로 평균 진행변수(mean progress variable, )가 0.1의 값을 가지는 위치까지의 길이로 정의하였다. 각 격자에서 도출된 부상화염의 높이를 Table. 2에 나타내었는데 저선회 화염의 부상높이는 모든 I2가 I3보다 높게 위치한 것을 알 수 있다. 한편 Fig. 9에 나타낸 층류화염 두께로 정규화 된 적분 길이스케일은 I2가 I3보다 큰 값을 가지는 경향을 확인하였다. 난류 화염속도에 비례하는 속도섭동은 격자반복 횟수에 따른 경향을 확인할 수 없었지만 적분 길이스케일은 반복 횟수에 따른 경향이 나타났다. 앞서 언급하였던 격자 간격의 차이로 다양한 난류스케일이 생성되며 I2는 I3보다 더 큰 적분 길이스케일을 생성하여 부상화염의 높이에 영향을 미친다고 판단되었다. Fig. 8에서 I2가 I3보다 작은 에디에서 큰 에너지를 가지는 것을 확인했지만 추후 연구를 통해 유동의 작은 스케일(small scale)의 정량적인 값을 도출하여 저선회 화염의 부상된 높이와 유동의 작은 스케일과의 연관성을 추가적으로 파악되어야 할 것으로 판단된다.
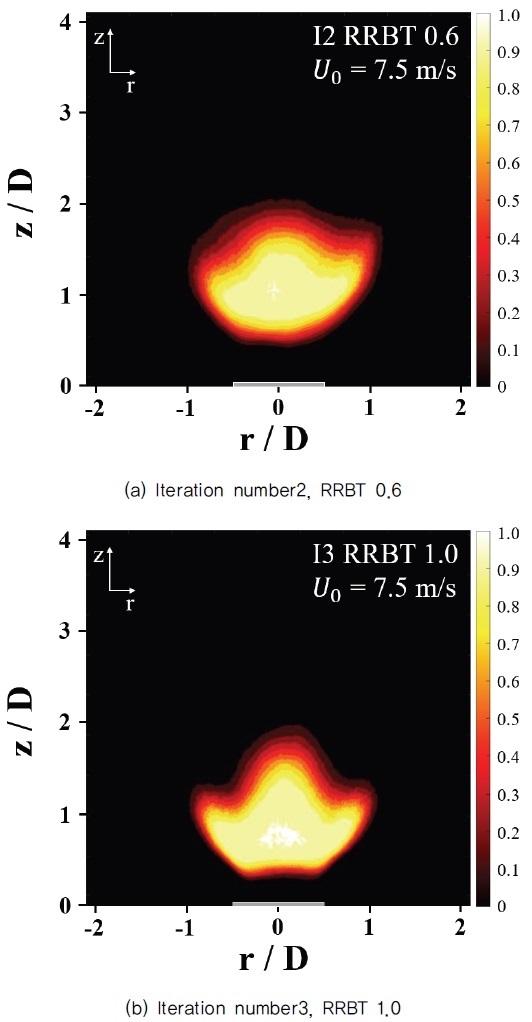
OH* Chemiluminescence images Averaging 4000 photo low swirl flame, length of r, z-axial normalized to nozzle diameter(D), mean progress variable value on the right color bar
3.3 유동장 특성화
J. C. Vassilicos 등은 프랙탈격자의 다양한 구조적 변수와 프랙탈격자에서 발달된 난류유동장의 정보의 관계성에 대해 보고하였다. 이들의 연구에 의하면 사용된 사각 프랙탈격자의 구조적 변수는 Meff, x* 등이며 L0=Lmax, t0=tmax을 이용해 x*를 나타내었고 격자의 가장 긴 길이성분인 L0가 유동장과 높은 연관성을 갖는 것으로 보고하고 있다. 하지만 앞서 언급하였듯이 하이브리드 프랙탈격자는 L0에 대해서 L0,c(cross)와 L0,s(square)의 두 가지 격자의 정보를 가지고 있다. 따라서 본 절에서는 LDV로 조사된 반응 유동장 특성화에 기여하는 격자타입을 확인하고, 하이브리드 프랙탈격자에서 생성된 난류강도와 격자의 구조적변수로 특성화된 유동장의 상관관계에 대하여 관찰하고자 한다.
본 연구에서 사용된 x*를 식 (10)과 식 (11)에 나타내었다. 식 (10)과 (11)에서 Meff는 식 (2)의 유효 격자크기이며, Ri로 각 격자 형상의 L0와 t0를 정규화 하였고 mm의 단위로 나타내어진다.
| (10) |
| (11) |
Fig. 11의 (a),(b),(c)와 (d),(e),(f)는 각각 I2, I3에 대한 정보이다. Fig. 11의 세로 축은 난류강도 제곱을 난류강도 제곱의 최댓값(I2/(I2)peak)으로 정규화 한 정보를 도시하였고 (a),(d)의 가로 축은 중심 축 방향의 길이이며 z = 0은 노즐 출구로 나타내었다. 또한 (b),(e) 및 (c),(f)의 가로 축에는 각 격자의 L0,c, L0,s가 포함된 xc*,xs*로 중심축 길이를 특성화 한 값을 도시하였다. x*로 무차원화 된 중심 축 길이는 하이브리드 프랙탈격자의 구조적 정보를 포함하여 재편되었다. 그리고 x*로 특성화 된 값과 정규화 된 난류강도의 상관관계를 파악하기 위한 지표는 결정계수(coefficient of determination, R2)로 나타내었다. 각 그래프들의 R2의 값은 RRBT 0.4에서 1.0까지의 모든 격자의 데이터를 다항식 피팅을 통해 도출하였다.
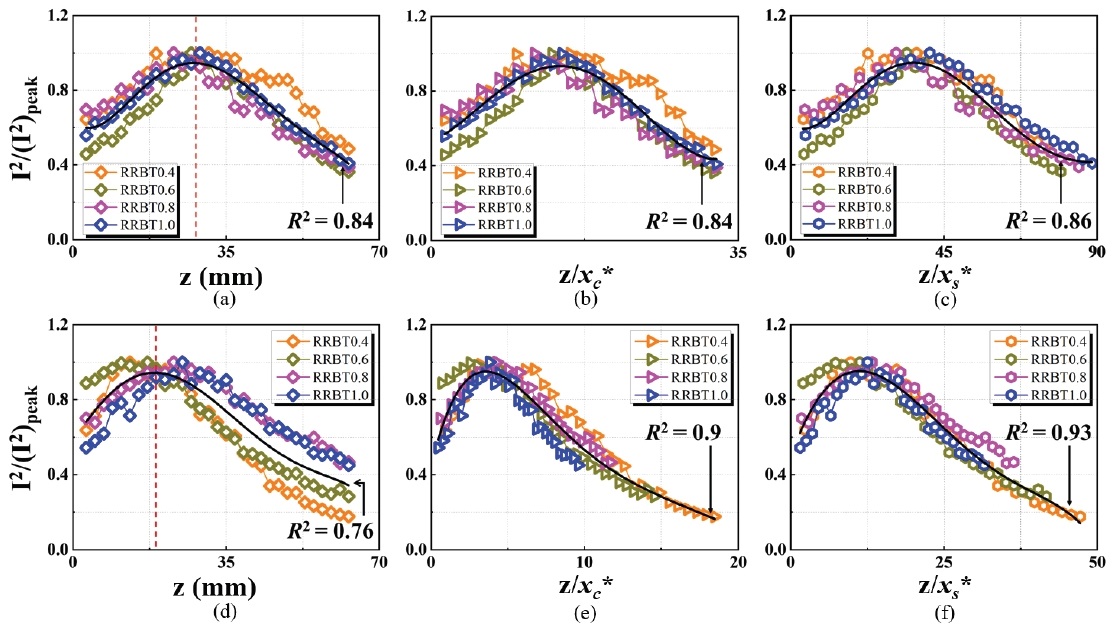
Characterization of flow field by geometry variables of hybrid fractal grid, {(a),(b),(c)} = Iteration number 2 {(d),(e),(f)} = Iteration number 3, characterized grid type {non-characterized : (a), (d)} {L0,c : (b), (e)} {L0,s : (c), (f)} Red dotted line denotes maximum value of I2/(I2)peak, R2 is coefficient of determination
Fig. 11에서 I2의 (a),(b)와 (c)의 R2는 각각 0.84, 0.86의 값을 가졌는데 (b),(c)의 중심축 길이를 각각의 x*로 유동장 특성화를 시도했지만, R2는 (a)와 동일하거나 비슷한 값을 가졌다. 한편 I3의 R2는 (d)가 0.76, (e)가 0.9 그리고 (f)가 0.93으로 나타났다. I3에서 x*로 유동장을 특성화함에 따라 특성화 시키지 않은 (d)와 비교하여 더 높은 R2를 가진 것을 확인 할 수 있다. 본 결과로 유동장 특성화 시 I2보다 I3일 때 더 높은 R2를 가졌고, 반복 횟수의 증가가 유동특성화에 높은 연관성이 있음을 파악할 수 있다. 그리고 유동장 특성화 시 고려된 격자 형상과 유동 특성화의 연관성을 파악하였다. (c)와 (f)는 스퀘어격자의 구조적 변수가 포함된 식 (11)을 사용했으며, 각 격자 반복 횟수에서 가장 높은 R2를 가졌다. 특히 (d)는 RRBT에 따라 I2/(I2)peak의 값이 분산되어있지만 (f)에서 모든 격자의 데이터가 한 커브(curve)로 재편된 것을 확인할 수 있다. 본 결과로 스퀘어격자의 구조적 변수와 I2/(I2)peak가 높은 연관성이 있음을 알 수 있다. 따라서 하이브리드 프랙탈에서 발달된 난류강도는 격자의 구조적 변수와 높은 연관성을 보이며, 반복 횟수가 증가된 스퀘어 격자에서 특성화되는 것을 확인 할 수 있다.
Fig. 11의 (a),(d)에 다항식 피팅된 곡선의 최댓값의 위치를 적색 점선으로 나타내었다. I2/(I2)peak의 최고점은 (d)가 (a)보다 노즐 출구에서 더 가까운 것을 볼 수 있는데, 이는 Fig. 10에서 보여진 격자 반복 횟수에 따른 난류 화염의 부상된 높이 차이에서도 확인할 수 있다. Fig. 11에서 보여진 I2/(I2)peak 최고점을 기준으로 이전 유동은 양의 기울기, 이후 유동은 음의 기울기가 관찰되었는데 각 기울기를 가지는 영역은 난류의 생성과 소멸의 영역을 의미한다. 그리고 Fig. 11의 (a), (d)에서 I3가 I2보다 노즐에서 더 가까운 위치에서 소멸의 거동을 보임으로써, I3가 더 빠르게 소산됨을 알 수 있다. 이러한 현상을 Fig. 8의 에너지 스펙트럼을 통한 난류 소멸의 조사 결과에서 확인할 수 있다. 즉, I3가 I2보다 더 낮은 주파수에서 Kolmogorov 멱법칙의 –5/3승 기울기를 따르는 것을 통해 더 빠르게 소산의 과정이 진행되는 것을 알 수 있다. 본 결과를 통해 격자의 반복 횟수는 적분 길이스케일 및 난류소산의 차이를 만들고, 이는 부상화염 높이에 영향을 미치는 인자로 작용함을 알 수 있다.
4. 결 론
본 연구에서는 하이브리드 프랙탈격자를 적용한 저선회기에서 발달된 유동의 난류특성 및 격자의 구조적 변수와 반응장에서 난류강도와의 상관관계에 대하여 살펴보았다. 동일한 조건의 유속을 공급했을 때 모든 격자에서 중심축 방향의 등방성이 1.0에 가깝게 나타났고 반경방향의 평균유속이 대칭적으로 분포되는 것을 확인하였다. 비반응 유동장 조사를 통해 노즐 이전의 난류강도의 경향은 크로스격자의 특징을 보였고, RRBT의 값이 줄어듦에 따라 웨이크 상호작용으로 난류강도가 증대되는 것을 확인하였다. 에너지스펙트럼 분석을 통해 에너지 캐스케이드 과정에서 Kolmogorov의 –5/3 법칙을 따르는 것이 확인되었고, I3가 I2보다 빠르게 소산되는 특징이 관찰되었다.
하이브리드 프랙탈격자에서 발달된 저선회 화염은 Borghi-Peter 선도에서 thin reaction zone 영역에 위치하는 것을 파악하였고, 이 선도로 난류화염의 영역과 구조적 특성을 파악하였으며, 기존연구의 크로스 프랙탈격자보다 더 큰 적분 길이스케일의 영역에 위치함을 확인하였다. OH* 자발광 이미지를 통해 부상된 화염의 높이를 정량적으로 도출하였고, I3보다 I2에서 높았으며 적분 길이스케일과 같은 경향이 관찰되었다. 반응장에서 중심 축 방향 길이는 하이브리드 프랙탈격자의 구조적 변수를 포함한 x*를 통해 재편되었고, I2/(I2)peak와 z/x*에 대한 결정계수(R2)는 I3의 스퀘어 격자에서 가장 높게 나타났으며, 노즐 출구 이후 반응장은 스퀘어격자의 형상의 특성과 높은 연관성을 나타내었다. 이러한 R2를 통해 격자와 유동장의 관계에 대한 특성화는 반복 횟수가 높아짐에 따라 연관성이 높아지는 것으로 파악되었다. 또한 I3는 I2보다 I2/(I2)peak의 최고점이 비교적 상류에 위치한 것을 확인할 수 있었고 에너지 케스케이드 과정이 더 빠르게 일어나는 것을 확인할 수 있었다.
Acknowledgments
본 연구는 2022년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의(20206710100060, 분산발전 가스터빈용 수소전소 저 NOx 연소기 개발) 지원 및 2022년 한국산업기술평가관리원 산업소재 핵심기술개발사업(20005788)의 지원을 받아 수행되었으며 이에 감사드립니다.
References
- R. K. Cheng, 2006, “The Gas Turbine Handbook,” pp. 242∼253.
-
M. R. Johnson, D. Littlejohn, W. A. Nazzer, K. O. Smith and R. K. Cheng, 2005, “A comparison of the flowfields and emissions of high-swirl injectors and low-swirl injectors for lean premixed gas turbines,” Proceedings of the Combustion Institute, Vol. 30, pp. 2867∼2874.
[https://doi.org/10.1016/j.proci.2004.07.040]

-
D. Littlejohn and R. K. Cheng, 2007, “Fuel effects on a low-swirl injector for lean premixed gas turbines,” Proceedings of the Combustion Institute, Vol. 31, pp. 3155∼3162.
[https://doi.org/10.1016/j.proci.2006.07.146]

-
R. K. Cheng, D. Littlejohn, P.A. Strakey and T. Sidwell, 2009, “Laboratory investigations of a low-swirl injectors with H2 and CH4 at gas turbine conditions,” Proceedings of the Combustion Institute, Vol. 32, pp. 3001∼3009.
[https://doi.org/10.1016/j.proci.2008.06.141]

-
D. Hurst and J. C. Vassilicos, 2007, “Scalings and decay of fractal-generated turbulence,”Physics of Fluids, Vol.19, No. 035103, pp.1∼31
[https://doi.org/10.1063/1.2676448]

-
N. Mazellier and J. C. Vassilicos, 2010, “Turbulence without Richardson-Kolmogorov cascade,” Physics of Fluids, Vol. 22, No. 075101, pp. 1∼25.
[https://doi.org/10.1063/1.3453708]

-
Koji Nagata, Teppei Saiki, Yasuhiko Sakai, Yasumasa Ito and Koji Iwano, 2007, “Effect of grid geometry on non-equilibrium dissipation in grid turbulence,” Vol.29, No.015102, pp. 1∼12
[https://doi.org/10.1063/1.4973416]

-
F.C.G.A. Nicolleau, S.M.M. Salim and A. F. Nowakowski, 2011, “Experimental study of a turbulent pipe flow through a fractal plate”, Journal of Turbulence, Vol.12, No. 44, pp. 1∼20
[https://doi.org/10.1080/14685248.2011.637046]

-
Sylvain Laizet and John Christos Vassilicos, 2011, “DNS of Fractal-Generated Turbulence,” Flow Turbulence Combustion, Vol. 87, pp. 673∼705.
[https://doi.org/10.1007/s10494-011-9351-2]

-
Thomas Sponfeldner, Nikolaos Soulopoulos, Frank Beyrau, Yannis Hardalupas, Alex M. K. P. Taylor, J. Christos Vassilicos, 2015, “The structure of turbulent flames in fractal-and regular-grid-generated turbulence,” Combustion and Flame, Vol. 162, pp. 3379∼3393.
[https://doi.org/10.1016/j.combustflame.2015.06.004]

-
A. A. Verbeek, P. A. Willemsa, G.G.M. Stoffels, B.J. Geurts, T. H. van der Meer, 2015, “Enhancement of turbulent flame speed of V-shape flames in fractal grid genetated turbulence,” Combustion and Flame, Vol. 167, pp. 97∼112.
[https://doi.org/10.1016/j.combustflame.2016.02.022]

-
Yeonse Kang and Keeman Lee, 2021, “The Study of Turbulent Flame Characteristics by plate Shape of Turbulence Generator,” The Korea Society of combustion, Vol. 26, No. 3, pp. 20∼34.
[https://doi.org/10.15231/jksc.2021.26.3.020]

-
Anton A. Verbeek, Thijs W. F. M Bouten, Genie G. M. Stoffels, Bernard J. Geurts and Theo H. van der Meer, 2014, “Fractal turbulence enhancing low-swirl combustion,” Combustion and Flame, Vol. 162, pp. 129∼143.
[https://doi.org/10.1016/j.combustflame.2014.07.003]

-
G. D ten Thij, A. A. Verbeek, T. H. van der Meer, 2016, “Application of Fractal Grids in Industrial Low-Swirl Combustion”, Flow Turbulence Combustion, Vol. 96, pp. 801∼818
[https://doi.org/10.1007/s10494-015-9670-9]

- Dongho Lee, 1981, “The principle of hot-wire anemometer and its application,” The Korea Society of Mechanical Engineers, Vol. 21, No. 2 pp. 119∼126.
-
Cameron Tropea, Alexander L. Yarin and John F. Foss 2007, “Springer Handbook of Experimental Fluid Mechanics,” pp. 242∼253.
[https://doi.org/10.1007/978-3-540-30299-5]

- R.J. Kee, J.F. Grcar, M.D. Smooke, J.A. Miler, E, Meeks, 1985, Premix : A fortran Program for Modeling Steady Laminar One-Dimensional Premixed Flames, Sandia National Laboratories Report;SAND:, 85-8540
- G.P. Smith, D.M. Golden, M. Frenklach, N.W. Moriarty, B. Eiteneer, M. Goldenberg, 1999, GRI mech. 3.0. http://combustion.berkeley.edu/grimech/
-
R. K. Cheng, 1995, “Velocity and Scalar Characteristics of Premixed Turbulent Flames Stabilized by Weak Swirl,” Combustion and Flame, Vol. 101, pp. 1∼14.
[https://doi.org/10.1016/0010-2180(94)00196-Y]

- Myung Kyoon Chung, 1984, “Understanding turbulent flow using spectrum analysis,” The Korea Society of Mechanical Engineers, Vol. 24, No. 4 pp. 246∼254.