Hydraulic Characteristics of a Single-channel Pump Designed by the Affinity Law
Abstract
Recently single–channel pumps are widely applied for wastewater treatment in Korea. To be able to apply this type of pump in the world, which is different in power frequency, this study uses the affinity law to redesign the impeller geometry of the single–channel pump optimized from the previous work. Meanwhile, the volute is designed by two methods which are the affinity law and the cutting diameter method. The numerical approach is performed by using steady and unsteady Reynolds-averaged Navier-Stokes equations and a shear stress transport reattachment modification (SST k–ω) turbulence model. The hydraulic efficiency curves and internal flow field including contours and streamlines are investigated and evaluated thoroughly. The numerical result is verified by the experimental test based on the 11th API610 standard. At the design flow rate condition, the novel pump models meet the design requirement with a minimum total head coefficient. The efficiency of the novel models remains almost unchanged compared to the base model. The sweep area of the unsteady radial force distribution in the novel models is smaller than that of the base model at low flow rate and design flow rate conditions while at high flow rate conditions show the opposite. In addition, the distance between the center of the radial force and the origin of the novel models is also reduced compared to the base model. The pressure amplitudes of the novel models are also decreased significantly. These improvements in the novel models mostly result in the reduction in noise and vibration in pump operation.
Keywords:
Wastewater treatment, Single–channel pump, Hydraulic performance, Unsteady radial force, Pressure fluctuation1. Introduction
In order to fulfill the rising demands of the populace, submerged pumps have expanded in variety and popularity today. Submerged pumps are frequently used in home water pumping, subterranean drainage systems, pumping for fountains, etc. because of their compact design and ease of installation and movement. In addition, wastewater comprising several foreign elements and extremely harmful chemicals is frequently handled by submerged pumps for environmental cleanup(1). Submerged pumps have the advantage of working stably underwater, which helps prevent cavitation(2). However, if not designed appropriately, it is also more prone to corrosion and failure than other pumps. These properties make the crushing and flow-path-securing types of submersible pumps the most common for wastewater handling.
The crushing pump has specialized impeller blades that make it easier to crush and shred unwanted objects caught in the pump, preventing blockage(3). Contrarily, these unique impeller blades add complexity, expense, and low performance to the system. Meanwhile, flow-path-securing pumps with a straightforward design that is inexpensive to produce and install are being developed to generate a big space for waste circulation. Because it is not pressured by blades, this sort of pump has a lower head but is highly effective at handling huge wastes.
Single-channel pumps (SCP) of the flow-path-securing variety run without an impeller blade and are pressured by the revolving impeller’s centrifugal force. Because of this, SCP operates with great durability and efficiency without harming anything. These advantages have led to a rapid increase in demand for SCP used in wastewater treatment systems, which have expanded around the world. The SCP has been extensively studied and improved via a number of prior research articles(4-7) and is currently in use all over the world. However, using the same type of pump will result in a decrease in efficiency because of the difference in power frequency. This calls for investigation into and revision of pump geometry.
The affinity law is a well-liked and practical approach in the development of pumps. In reality, because many pumps are so huge in size and capacity, it is sometimes impossible to perform an experimental test on actual pumps. As a result, it is crucial to research and creates smaller pumps utilizing the affinity law. The affinity law was used by Matsushita et al.(8) to build the centrifugal pump. In-depth research was done on the affinity laws for blade height, rotational speed, and impeller diameter. GonzG lez et al.(9) utilized affinity law for the pump manufacturer in a different investigation. The results only revealed a very slight variation in particular speeds. Based on the affinity law, Cai et al.(10) found that the flow rate and head had linear and quadratic proportions of the rotating speed, respectively. Many other kinds of pumps have also successfully used the affinity law(11–15). As a result, using the already-optimized models as a reference, the affinity law may also be used to develop a novel SCP model.
The SCP with novel impeller and volute geometries created using the previously optimized model is presented in this study, and its impact on radial force (RF) and pressure fluctuations on hydraulic performance is thoroughly investigated. The impeller shape is redesigned using the affinity law, whereas the volute is developed using the affinity law and the cutting diameter approach. In this work, the experimental findings are first thoroughly presented together with the numerical steady result. In order to present the tendency of the hydraulic performance curves, steady results are employed. Additionally, it is utilized for a fundamental analysis of the characteristics of the flow field at the BEP, low, and high flow rates inside the pump. Finally, based on the unsteady numerical results at various flow rate conditions, the RF and pressure fluctuation are thoroughly examined.
2. Methodology
2.1 Experiment
Fig. 1 presents the experimental test at the Korea Institute of Industrial Technology, Korea. The water utilized in the testing system was waste-free and pure. Through the data collecting system, the hydraulic performance of the pump under various flow rates were acquired. The butterfly valve was adjusted to achieve different flow rate conditions, which led to the generation of the hydraulic performance curves. In more detailed experiment was presented in the previous study(16).
2.2 Numerical approach
Utilizing the computer, computational fluid dynamics (CFD)(17) expands the capability of fluid mechanics analysis. The skilled engineer can use CFD to provide cost-effective, precise predictions that are very insightful and flexible. In actuality, the experimental test cannot reveal many complicated phenomena. The analytical procedure is made much simpler with the assistance of CFD. The ANSYS software is utilized in the current study to examine the internal flow characteristics and determine the efficiency of the pump. The steady and unsteady RANS equations for 3D incompressible flow are used to achieve numerical analysis. The finite volume approach is used to discretize these governing equations.
2.3 Turbulence model
The SST k-ω reattachment modification, which is utilized as a turbulence closure model in this work, is used to get an understanding of the internal flow taking place inside the pump. The SST turbulence model established by Menter(18) was able to fairly accurately predict the turbulent flow near wall areas with adverse pressure gradients. However, it is prominent that the reattachment points are frequently forecasted to be too far downstream of what is seen in the experiment. By including the source term “P_reattach” in the transport equation, the SST turbulence model is updated to address this and improve the predictability of the reattachment point(19).
3. Numerical modeling and boundary condition
3.1 Single-channel pump model
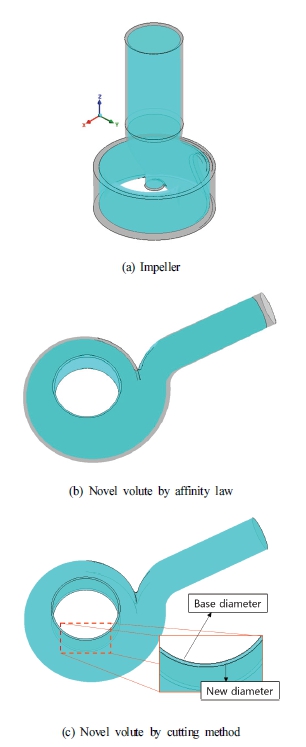
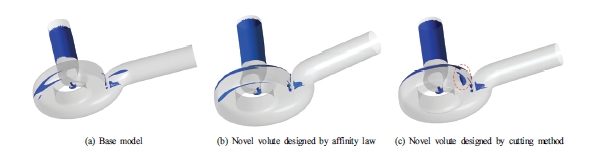
The demand for the SCP model for waste water treatment is rising in the world. Nevertheless, the power frequency in use in the majority of nations is just 50Hz as opposed to 60Hz in a few. Because of this, the pump’s rotating speed is different, and its hydraulic properties are completely different. To keep similar performance characteristics, changing the pump design based on the affinity laws is necessary and efficient. In the present work, the novel SCP model is redesigned based on the earlier optimum model(4-7). By using the affinity law, the impeller is scaled in the three-dimensional directions as long as the lowest total head coefficient of the novel pump model is larger than 3.022 (by Eq. (3)) at the BEP. In order to account for the drop in total head when the rotating speed is slowed down because of the decline in power frequency, the novel model’s impeller diameter is larger than 1.053 times that of the base model. However, due to the manhole’s size restriction, the total size of the SCP cannot be too huge. In addition, to be able to operate at different power frequencies, there were many SCPs which are manufactured and installed. Therefore, to easily manage the impeller and volute prototypes in the storage, it is essential to reduce the number of prototypes. Based on real demands, the novel volute is proposed to redesign based on the base volute by the cutting diameter method instead of the affinity law. The novel volute model designed by the cutting method uses the base volute. However, the inlet diameter of the volute is enlarged to accommodate the diameter of the new impeller. Therefore, the novel volute designed by the cutting method has a bigger diameter than the base volute. The novel and base models are presented in Fig. 2(c) with a change in volute diameter. Consequently, in this study, there are two models are investigated to compare with the base model. In the first model, both impeller and volute geometries are designed by the affinity law. The second model, the impeller is designed by the affinity law and the volute is designed by cutting method.
In the present work, the specific speeds computed based on Eq. (1) are 370 and 379 corresponding to the base and novel pump models, respectively. The impeller without a vane and the volute are the main parts of the model pump. The base and novel pump models use power frequencies of 60Hz and 50Hz, respectively. According to equations (2) and (4), the novel pump design’s design flow rate coefficient and rotational speed coefficient are 0.114 and 0.575, respectively. In addition, some other parameters are shown in Table 1.
3.2 Boundary condition
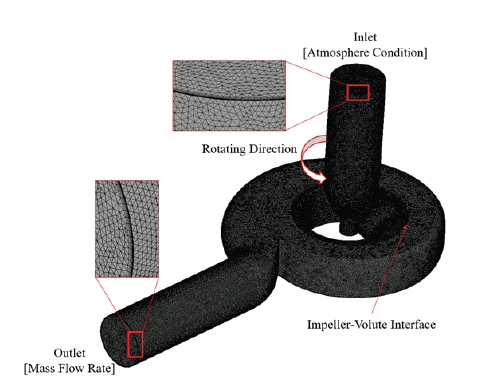
The water in a single phase operates at 25℃. In the computational domain, adiabatic and no-slip conditions are employed for the wall surfaces. The revolving and stationary domains are referred to as the impeller and volute, respectively. The stage model (mixing plane) is used in the steady simulation to convey the data by circumferential averaging at the boundary between the stationary and revolving domains while the transient rotor/stator is employed in the unsteady simulation. At the inlet and outlet of the SCP, respectively, the atmospheric pressure and the mass flow rate are established. The convection term(20) and the turbulence numeric are discretized using high-resolution and the first order, respectively.
The convergence process is hastened by using a physical time scale(21) The convergent status of the calculation is verified by using the performance functions monitored in the CFX-Solver with a fluctuation range of beneath 0.5% during 100-time steps. Additionally, the Root Mean Square value is set 10-6 to drop under for the standard of the time-dependent convergence.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where n, Q, H, D, Ψ, g, ω, and nb are the rotating speed, discharge rate, pressure head, impeller diameter, the total head coefficient, the gravity acceleration, the angular velocity, and the number of impeller blade, respectively.
The steady result is utilized as the initial value for the unsteady calculation. The overall computation time set to 10 times the impeller’s rotational period is about 0.411 s. The time step is established as 5.7 ×10-4 s which is the time required for 5⁰ of the impeller revolution. For further convergence, a loop with a maximum coefficient of four is established.
3.3 Mesh generation
The mesh systems for the impeller and volute have been constructed and shown in Fig. 3. Tetrahedron mesh type is used to create an unstructured mesh. To ensure that the averaged value of y+ is less than 20, the mesh is heavily refined at wall regions using multi-layer prism mesh with a first layer thickness of 2×10-5 m.
In order to create the best mesh, it is crucial to check the mesh dependencies. To confirm the mesh dependency, the grid convergence index method (GCI) developed by Celik et al.(22) is used. The GCI approach uses three separate meshes to assess the numerical uncertainty brought on by the discretization mistake. The extrapolations are carried out with a mesh refinement factor of 1.326 and 1.343 corresponding to the medium and fine meshes. The mesh test is carried out at the BEP. The efficiency and total head are chosen as the key variables and their values are normalized by the values of the fine mesh, respectively. With the rise of the number of mesh, the performance values in Table 2 indicate a monotonic convergence. The key variables, according to Celik et al.(22), should have index values of less than 1% with smaller error values. Therefore, the low values of the and indicate that the mesh system is ideal and further mesh refining is not required. Consequently, the optimum mesh of the impeller and volute includes 1.9×106 and 1.2×106, respectively.
4. Results and discussions
4.1 Numerical validation
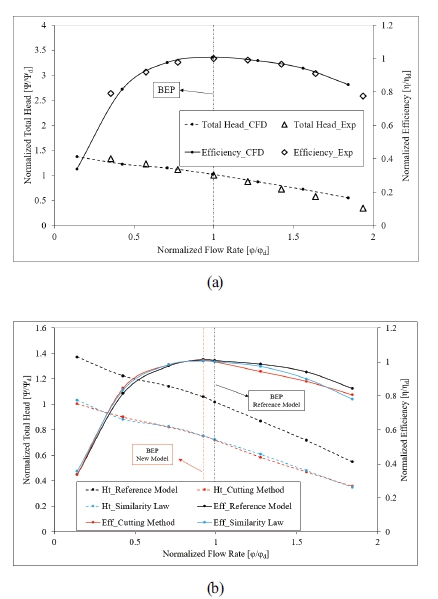
Validation is an essential step in ensuring the precision of the numerical approach. Fig. 4(a) shows the comparison of the hydraulic performance between the experiment and numerical calculation for the base model. According to their respective values at the BEP in the experiment, the values of the flow rate, efficiency, and total head are normalized. The efficiency and total head values that were obtained experimentally for the base model are essentially compatible with the results of the numerical simulation. The small deviations under low and high flow rates can be caused by errors in measurement, instrumentation, and errors in CFD calculations. Additionally, the inlet conditions of the CFD model differ somewhat from those of the real model utilized in the experiment. In order to avoid the effect of the complex inflow, the inlet section of the CFD model was expanded to about the same impeller diameter whereas it was not extended in the real model. This contributes to the difference between the results of the experiment and simulation. Due to the flow instability that results in oscillations and a significant inaccuracy at high flow rate conditions, there are relatively big differences in the total head between the numerical and experimental results. These validations confirmed the extremely high accuracy and dependability of the numerical simulation findings achieved in this work. This validation confirmed that the simulations obtained in this work have very high accuracy and reliability. For this reason, the numerical approach is employed for steady and unsteady simulations of the novel design model.
4.2 Hydraulic characteristics
The efficiency and total head curves of the novel models are presented in Fig. 4(b). The values of the flow rate, efficiency, and total head are normalized using their values at the BEP of the base model, respectively. The novel model’s efficiency and total head follow the same trend as the base model. At high flow rates, the efficiency of the novel models is lower than the base model due to the turbulent flow occurring in the pump channel. Because of the large rotational speed, the total head of the base model is much larger than the novel models. However, at BEP of the novel models (0.92Qd), the hydraulic performance still satisfies design requirements as the minimal total head coefficient is greater than 3.022 while the efficiency is nearly unchanged compared to the base model. The efficiency curves of the novel models seem to shift to the left with higher efficiency than the base model. As can be seen, the hydraulic performance of the novel models created by affinity law and cutting method is almost unchanged. There is only a slight difference in efficiency at the high flow rate conditions. As a result, using the cutting diameter method instead of affinity law to manufacture the volute is completely feasible and brings high management efficiency. The hydraulic performance curves also show the effectiveness of using the affinity law in pump design.
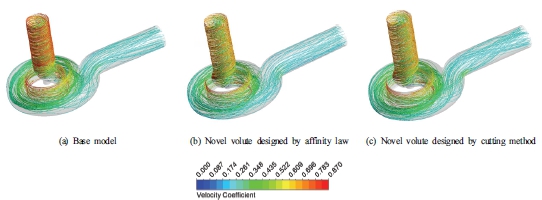
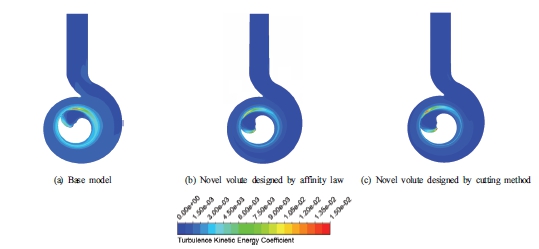
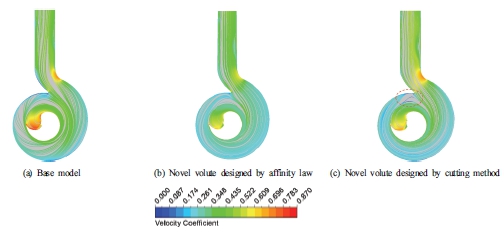
Fig. 5 shows the 3D streamline velocity distribution in the SCP at the BEP of the novel models among base model, novel model using affinity law, and novel model using the cutting method. The velocity coefficient is determined by the ratio to the velocity at the outlet of the impeller in the base model. At the flow rate of 0.92Qd, the fluid flow inside the volute is stable and almost the same in all three models. There seems to be no instability occurring inside the volute. Therefore, the efficiency is almost the same in all models. The velocity field of the base model is higher than the novel models because of the higher rotational speed of the impeller. This also makes the total head of the base model greater than the novel models as can be seen in Fig. 4(b). Fig. 6 presents the turbulence kinetic energy (TKE) distribution in the middle plane of the SCP at the BEP of the novel models among the three models. The TKE coefficient is determined as being proportional to the square of the velocity at the impeller outlet of the base model. At the BEP, the high TKE hardly occurs in the volute channel resulting in high efficiency. The TKE of the base model is slightly larger than the novel models because its high rotational speed leads to a high-velocity field resulting in a greater turbulent potential. The TKE of the two novel models is almost the same showing the positive effect of using affinity law and cutting method in volute design.
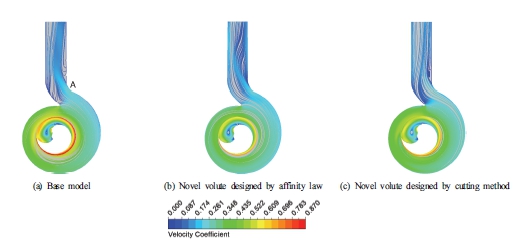
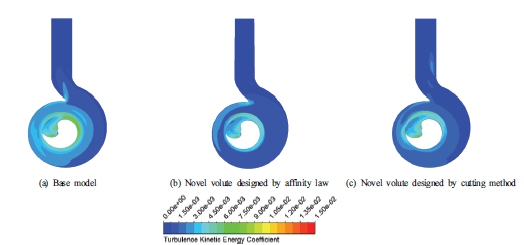
Fig. 7 depicts the 2D streamline velocity distribution in the middle plane in the SCP at 0.43Qd among the three models. At low flow rate condition, the flow field in the SCP still has good stability except for the outlet area. The velocity field around the impeller is stable and free of turbulence. There is a small swirl with a low velocity that forms inside the core of the impeller as the impeller rotates around its axis resulting in the formation of a swirl flow at the center. This swirl flow is similar in the three models. In the tongue area of the base model, the flow becomes complicated and a bit turbulent because of the mismatching between the flow angle and the tongue angle. This is significantly improved in the novel models. However, due to the strong acceleration of the flow around point A, turbulence is formed leading to instability in the flow field at the outlet region, especially the volute design by the affinity law. To better understand the intensity of turbulent flow inside the SCP, Fig. 8 shows the TKE distribution in the middle plane at 0.43Qd among the three models. At low flow rate, the TKE is increased slightly in comparison to that at the BEP. The TKE in the base model is still the highest, concentrated around the outlet of the impeller. In the tongue region of the base model, there is a small TKE that forms due to the mismatching between the flow and tongue angle. In the volute model designed by affinity law, the tongue region also has a small TKE extending inside the volute channel. This results in a slight decrease in efficiency compared to the volute model designed by the cutting method. Due to the strong acceleration of the velocity, a small TKE occurs at point A in the volute model designed by the cutting method.
Fig. 9 shows the 2D streamline velocity distribution in the middle plane of the SCP at the flow rate of 1.56Qd among the three models. The velocity field of the models at high flow rate condition is quite stable and smooth. Additionally, the acceleration of the flow at point A can be clearly seen in high flow rate condition. There is an instability in the tongue region, especially in the volute model designed by the cutting method. The flow is strongly separated in the tongue region causing efficiency to be degraded. However, this separation is not widespread in the volute channel resulting in a not-so-strong reduction of efficiency. To quantify the effect of this separation flow, Fig. 10 shows the low-velocity distribution in the SCP at the 1.56Qd among the three models. The low-velocity region is presented in blue color with velocity coefficient of 0.09.
There is a low-velocity region that forms in the tongue region of the volute model designed by the cutting method due to the separation flow. However, this low-velocity region is relatively small. Except for the low-velocity region at the tongue, no other low-velocity regions appear to occur inside the pump channel. This keeps the pump performance at a high level.
4.3 Radial force analysis
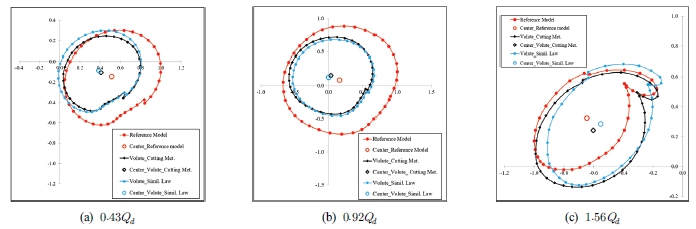
Theoretically, the asymmetrical momentum fluxes at the impeller’s outlet as well as the asymmetric pressure distribution surrounding the impeller have an impact on the RF sources of the impeller. Fig. 11 depicts the distribution of the unsteady RF at the impeller’s outlet within one rotation of models under the flow rate of 0.43Qd, 0.92Qd, and 1.56Qd. At each flow rate, the RF is non-dimensionalized by the maximum values of the base model. At all three flow rates, the distribution of the RF tends to be the same in the two novel models. At the BEP and low flow rates, the RF distribution of the base model is larger than that of the two novel models while the opposite is presented at the high flow rate. The sweep area(4-7) of the novel model with the volute designed by cutting method at 0.43Qd is smaller than 1.174 times the novel model with the volute designed by affinity law. On the other hand, at 1.56Qd, the sweep area of the volute designed by the cutting method is 1.05 times bigger than that of the volute designed by affinity law. At the BEP of the novel models, the sweep area of the two novel models is almost the same. According to Guelich et al.(23), the surface area and pressure distribution surrounding the impeller influence the RF.
This makes the RF distribution of the base model bigger than the novel models. Under the flow rate of 0.92Qd, the distributions of the RF in all models are stable close to the origin because of the stability in flow characteristics inside the pump channel. At the flow rate of 0.43Qd and 1.56Qd, the center position of RF is much better in the novel models. As a result, this significantly helps to improve the operating condition of the pump by reducing the bearing and seal fatigue.
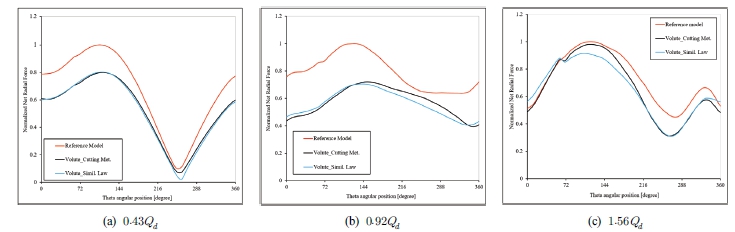
Fig. 12 presents the net RF distribution within one rotation of the impeller at 0.43Qd, 0.92Qd, and 1.56Qd. The net RF is non-dimensionalized based on the maximum value of the base model at each flow rate. The net RF value of the base model is almost higher than the two novel models because of the large RF distribution. At the flow rate of 0.92Qd, the oscillation range of the three models is notably reduced in comparison with the flow rate of 0.43Qd and 1.56Qd. Because the RF in the two novel models is uniformly distributed around the origin and their sweep areas are also smaller than that of the base model, the distribution of the net RF likewise becomes more uniform and smaller. The trend of the net RF distribution of the base and two novel models is similar to the sinusoidal periodic pattern at 0.43Qd. At the flow rate of 0.43Qd, the upward or downward trend of net RF for each theta angular location of the three models is also evident. The net RF of the base model should be lower than the novel model because of its tiny sweep area at 1.56Qd. However, since the RF distribution of the base model is skewed too much toward the first quadrant, the net RF is drastically raised and bigger than the two novel models from the theta angular locations of 72 to 350 degree. Fig. 13 shows the frequency spectra of the amplitude values at measuring points for the base model and two novel models at the flow rate of 0.43Qd, 0.92Qd, and 1.56Qd. A Fast Fourier Transformation (FFT) algorithm is used to establish the spectra based on the pressure fluctuation time series. The largest amplitude value among the measuring points of the base model for each flow rate condition is used to normalize the amplitude data.
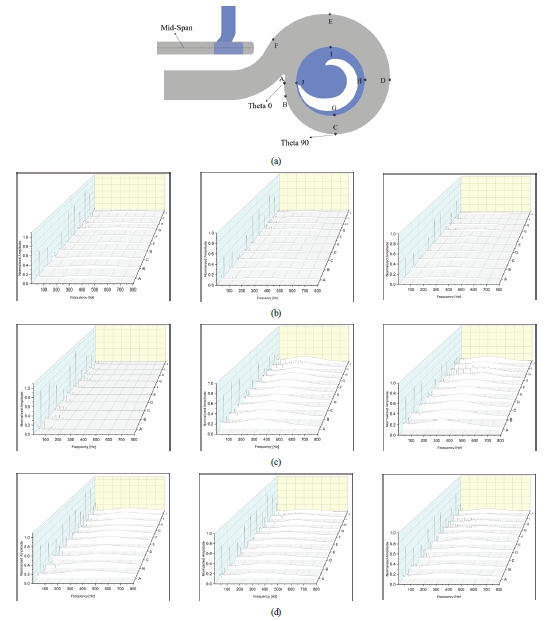
Spectra of the amplitude values at measuring points. (left: base model, middle: Cutting method, right: Affinity law) (a) Position of the measuring points, (b) 0.43Qd, (c) 0.92Qd, (d) 1.56Qd
For the base model and the two novel models, the blade passing frequencies (BPF) derived using Eq. (6) are roughly 29.33 Hz and 23.83 Hz, respectively, conditions. This indicates that the volute design by the cutting method is feasible and has a positive effect on vibration and noise. The significant reduction in the unsteady pressure pulsation of two novel models at are roughly 29.33 Hz and 23.83 Hz, respectively, conditions. This indicates that the volute design by the cutting method is feasible and has a positive effect on vibration and noise. The significant reduction in the unsteady pressure pulsation of two novel models at these three flow rate conditions indicates a considerable effect of the impeller-volute interaction and it helps to reduce the vibration and noise during the operation.
| (6) |
5. Conclusion
This study shows the hydraulic performance and the internal flow characteristic of the SCP for wastewater treatment. The impeller is redesigned by using the affinity laws based on the earlier optimum model while the volute is redesigned by two methods which are affinity law and the cutting diameter method. Detailed analysis is performed in both steady and unsteady simulations at various flow rates. Some conclusions are drawn as follows:
(1) In comparison to the base model, the efficiency of the two novel models is nearly constant at the design flow rate condition, and the total head coefficient meets the minimum design requirement. At the low flow rates, the hydraulic performance of the novel models is slightly increased compared to the base model while at high flow rates show the opposite trend. The hydraulic performance of the two novel models which are by affinity law and cutting method is almost the same.
(2) The distribution trend of the RF in the two novel models for unsteady results is almost identical to that of the base model. In comparison to the base model, the sweep area of the novel models is smaller, and the space between the center of RF and the origin is also shrunk. In addition, the fluctuation range in the net RF distribution of the two novel models is smaller. The pressure pulsation at measuring points gets almost reduced compared to the base model resulting in the reduction of vibration and noise during the operation.
With the hydraulic performance and the internal flow characteristic as shown in this study, the novel models of the SCP totally can meet the demand of users around the world. In order to save production costs and management resources, the volute made by the cutting method completely meets the requirements of hydraulic performance as well as vibration compared to the volute made by the affinity law.
Acknowledgments
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (2021021010003D, Construction of Open Platform for Turbine Design Data Base) and partially supported by a grant (No. JB230001) from the Korea Institute of Industrial Technology (KITECH).
References
-
H. Zhang, B. Chen, W. D. Shi, Z. Y. Pan, and W. D. Cao, “Effects of contraction-type impeller on non-overloaded performance for low-specific-speed sewage pump,” Journal of Mechanical Science and Technology, Vol. 28, No. 3, pp. 937~944, 2014.
[https://doi.org/10.1007/s12206-013-1165-9]

-
D. A. Nguyen, S. B. Ma, S. Kim, and J. H. Kim, “Influence of inflow directions and setting angle of inlet guide vane on hydraulic performance of an axial‑flow pump,” Scientific Reports, Vol. 13, p. 3468, 2023.
[https://doi.org/10.1038/s41598-023-30511-4]

-
B. Corwin and M. Nation, “New Pumps Solve Ragging Problems,” Proceedings of the Water Environment Federation, Vol. 2011, No. 5, pp. 388~394, 2011.
[https://doi.org/10.2175/193864711802837525]

- J. H. Kim and Y. S. Choi, “State-of-the-Art Design Technique of a Single-Channel Pump for Wastewater Treatment,” Wastewater and Water Quality, Chapter 10, pp. 183~199, 2018.
-
J. H. Kim, S. B. Ma, S. Kim, Y. S. Choi, and K. Y. Kim, “Design and Verification of a Single-Channel Pump Model based on a Hybrid Optimization Technique,” Processes, Vol. 7, No. 747, pp. 1~21, 2019.
[https://doi.org/10.3390/pr7100747]

-
J. H. Kim, S. B. Ma, Y. S. Choi, and K. Y. Kim, “Simultaneous Optimization of Impeller and Volute of a Single-channel Pump for Wastewater Treatment,” International Journal of Fluid Machinery and Systems, Vol. 12, No. 2, pp. 99~108, 2019.
[https://doi.org/10.5293/IJFMS.2019.12.2.099]

-
J. H. Kim, B. M. Cho, Y. S. Kim, Y. S. Choi, J. H. Kim, K. Y. Kim, and Y. Cho, “Optimization of a Single-Channel Pump Impeller for Wastewater Treatment,” International Journal of Fluid Machinery and Systems, Vol. 9, No. 4, pp. 370~381, 2016.
[https://doi.org/10.5293/IJFMS.2016.9.4.370]

-
N. Matsushita, A. Furukawa, S. Watanabe, and K. Okuma, “Study on Design of Air-water Two-phase Flow Centrifugal Pump Based on Similarity Law,” International Journal of Fluid Machinery and Systems, Vol. 2, No. 2, pp. 127~135, 2009.
[https://doi.org/10.5293/IJFMS.2009.2.2.127]

-
J. González, J. Parrondo, C. Santolaria, and E. Blanco, “Steady and Unsteady Radial Forces for a Centrifugal Pump With Impeller to Tongue Gap Variation,” Journal of Fluids Engineering, Vol. 128, No. 3, pp. 454~462, 2006.
[https://doi.org/10.1115/1.2173294]

-
J. Cai, J. Pan, and A. Guzzomi, “The flow field in a centrifugal pump with a large tongue gap and back blades,” Journal of Mechanical Science and Technology, Vol. 28, No. 11, pp. 4455~4464, 2014.
[https://doi.org/10.1007/s12206-014-1013-6]

-
H. Zhu, G. Bo, Y. Zhou, R. Zhang, and J. Cheng, “Pump Selection and Performance Prediction for the Technical Innovation of an Axial-Flow Pump Station,” Mathematical Problems in Engineering, Vol. 2018, pp. 1~9, 2018.
[https://doi.org/10.1155/2018/6543109]

-
T. S. Lee and S. Pejovic, “Air Influence on Similarity of Hydraulic Transients and Vibrations,” Journal of Fluids Engineering, Vol. 118, pp. 706~709, 1996.
[https://doi.org/10.1115/1.2835499]

-
Y. Pei, Q. Liu, C. Wang, and G. Wang, “Energy efficiency prediction model and energy characteristics of subsea disc pump based on velocity slip and similarity theory,” Energy, Vol. 229, No. 2021, pp. 1~18, 2021.
[https://doi.org/10.1016/j.energy.2021.120690]

-
D. A. Nguyen, S. B. Ma, S. Kim, and J. H. Kim, “The influence of inlet guide vane and diffuser vane on internal flow characteristics in an axial flow pump,” Journal of Energy Engineering, Vol. 30, No. 4, pp. 94~104, 2021.
[https://doi.org/10.5855/ENERGY.2021.30.4.094]

-
D. A. Nguyen, S. B. Ma, S. Kim, and J. H. Kim, “Hydrodynamic optimization of the impeller and diffuser vane of an axial-flow pump,” Journal of Mechanical Science and Technology, Vol. 37, No. 3, pp. 1~16, 2023.
[https://doi.org/10.1007/s12206-022-1217-0]

-
D. A. Nguyen, M. S. Roh, S. Kim, and J. H. Kim, “Hydrodynamic and radial force characteristics with design of a single-channel pump for wastewater treatment based on the similarity law,” Process Safety and Environmental Protection, Vol. 170, pp. 1137~1150, 2023.
[https://doi.org/10.1016/j.psep.2022.12.090]

-
A. W. Date, “Introduction to Computational Fluid Dynamics,” Cambridge university press, Chapter 1, 2005.
[https://doi.org/10.1017/CBO9780511808975]

-
F. R. Menter, “Two-equation eddy-viscosity turbulence models for engineering applications,” AIAA journal, Vol. 32, No. 8, pp. 1598~1605, 1994.
[https://doi.org/10.2514/3.12149]

-
B. Liu, G. An, and X. Yu, “Assessment of curvature correction and reattachment modification into the shear stress transport model within the subsonic axial compressor simulations,” Journal of Power and Energy, Vol. 229, No. 8, pp. 1~18, 2015.
[https://doi.org/10.1177/0957650915595168]

- ANSYS, “ANSYS CFX-Pre User’s Guide,” Software Handbook, Release 15.0, ANSYS Inc, Canonsburgre, PA, USA, 2013.
- ANSYS, “ANSYS CFX Tutorials,” Software Handbook, Release 14.0, ANSYS Inc, Canonsburgre, PA, USA, 2011.
-
I. B. Celik, U. Ghia, P. J. Roache, C. J. Freitas, H. Coleman, and P. E. Raad, “Procedure for estimation and reporting of uncertainty due to discretization in CFD applications,” Journal of Fluids Engineering, Vol. 130, No. 7, 2008.
[https://doi.org/10.1115/1.2960953]

-
J. Guelich, W. Jud, and S. F. Hughes, “Review of parameters influencing hydraulic forces on centrifugal impellers,” Proceedings of the Institution of Mechanical Engineers, Vol. 201, No. A3, pp. 163~174, 1987.
[https://doi.org/10.1243/PIME_PROC_1987_201_021_02]