OPR1000 원전의 냉매 열수력 종합효과 실험장치 척도설계

1. 서 론

원전의 신뢰성 및 설계검증을 위해서, 열수력 종합효과 실험장치는 기준원전과 동일한 형상으로 설계하는 것이 이상적이다. 그러나, 예산 및 공간적 제약을 고려하여 일반적으로 축소된 규모로 설계되며, 높이 혹은 직경을 축소하여 냉각재상실사고(LOCA) 모의를 주목적으로 설계된다. 열수력 종합효과 실험장치는 다양한 능동 및 수동 안전 시스템을 평가해왔는데, 각종 열수력 현상이 중력에 영향을 받기 때문에 실험장치는 현상 발생의 시간비를 동일하게 유지하기 위해 참조원전과 유사하게 높이를 갖도록 해왔다. 국내의 경우 대표적으로 ATLAS⁽¹⁾ 실험장치는 APR1400/OPR1000 원전의 다양한 사고 시나리오에 대한 열수력 종합효과 실험을 수행해왔다. 다만, 기존 대형 종합효과 실험장치는 큰 규모와 높은 압력/온도 조건 때문에, 설계 변경이 어려운 특징이 있으며, 이로 인한 열수력 실험 교육이나 새로 제안되는 피동안전계통 혹은 4차 산업혁명 기술기반 계통의 적용/평가 시 많은 예산과 인력이 필요하여 선제적 적용/평가에 어려움이 있다.

본 연구의 목적 및 목표는 기존 대형 열수력 종합효과 실험장치에서 수행하기 어려운 다양한 원자력 안전 신기술을 선제적/통합적으로 시험하고, 실험과 관찰을 통한 교육의 기회를 제공하기 위한 다목적 소형 열수력 종합효과 실험장치를 구축하는 것이다. 실험장치의 기준원전은 1000 MW급 경수로(PWR) 원전으로 국내에서 가장 보편적으로 가동 중인 원전인 OPR1000(Optimized Power Reactor 1000)이며, OPR1000을 높이비 1/8, 직경비 1/10로 축소 설계하였다. 본 실험장치는 높이와 직경을 크게 줄여 소형화하고, 원전의 이상유동 현상을 재현하기 위해 작동 유체로 물 대신 프레온 냉매를 사용하였다. 냉매 사용의 이점은 훨씬 낮은 압력과 낮은 온도 조건에서 실험할 수 있어 필요한 전력을 크게 줄이고 낮은 압력 조건에서 내부 열수력 현상을 가시화할 수 있다는 것이다.

냉매 기반 실험은 낮은 운전조건에서 원전의 열수력 현상을 모의할 수 있는 점 때문에 원자력 열수력 분야에서 널리 사용되었다. 예를 들어, 핵연료봉에 대한 임계열유속(CHF) 현상 척도는 유체 대 유체 실험에서 냉매를 사용하여 수행되었으며, 이는 CHF 값을 정확하게 변환하고 결정하는 상사성을 유지하면서 비용과 작동 요구사항을 크게 줄였다^(2-4). 또한, EPRI⁽⁵⁾에서는 R11 냉매를 사용하여 증기발생기의 비등 및 유동 분포/패턴을 분석하였고, 일본 Y. Kondo et al.⁽⁶⁾는 증기발생기의 기공률, 계면 속도 및 유동 분포를 파악하기 위해 R123을 사용하여 척도 설계하였다.

냉매로 척도설계 하여 실험을 수행할 때 서로 다른 유체가 사용되기 때문에 실험결과의 왜곡을 피할 수 없는데, 연구자들은 냉매 기반 열수력 루프가 이상유동에 대한 종합적인 척도가 효과적으로 수행될 수 있지만, 그 이외의 단상 유동 현상과 종합효과 실험 관련 무차원 수를 모두 일치시키는 것은 불가능하다고 지적하였다^(7-9). 관련 연구^(10-12)에서 파악한 바와 같이 동일한 L/D 형상에서 CHF 냉매 실험의 잠재적 왜곡은 냉매는 물에 비해 고유량 조건에서 마찰 및 위치 에너지의 더 큰 영향을 받으며, 이는 압력강하로 인해 플래싱이 더 쉽게 발생할 수 있다. 또한, 냉매를 사용하면 시설의 높이와 폭을 크게 줄일 수 있지만, 높이가 낮아질수록 속도와 가속도가 증가하므로 가속도 영향을 최소화할 수 있는, 느린 천이 현상을 모의하는 것이 더 적합하다고 지적하였다⁽⁹⁾. 따라서, 본 연구에서는 냉매를 사용하는 다목적, 소형 열수력 종합효과 실험장치를 설계하고자 하며, 앞서 문헌에서 지적한 바와 같이 상대적으로 느린 과도상태를 포함하는 사고인 SBLOCA와 SBO를 실험 대상으로 선정하였다. 본 실험장치는 냉매 기반 모의의 장점과 원전 계통의 열수력 현상을 최대한 보존하는 것을 목표로 한다.

본 논문에서는 OPR1000을 기준원전으로 한 다목적 소형 열수력 종합효과 실험장치를 ‘URILO-II’ (UNIST Reactor Innovation Loop II)로 명명하였으며, 프레온 냉매 R134a의 유체 대 유체 척도 설계법을 이용하여 URILO-II의 주요 설계 결과를 소개한다.

2. 척도설계 및 해석

2.1 척도설계

URILO-II 실험장치의 설계는 기준원전 OPR1000의 일차계통, 이차계통, 그리고 안전주입계통을 포괄하며, 모든 시스템은 열수력 현상을 최대한 정확히 모의하기 위해 적절한 척도법과 유사성을 따르도록 설계하였다. 설계 과정에서 가장 중요한 목표 중 하나는 자연순환, SBLOCA, SBO와 같은 사고에서 나타나는 이상 유동 자연순환을 모사하는 것이었다. 작동유체로는 냉매 R134a를 선택하였으며, 냉매의 사용은 몇 가지 중요한 이점을 가져다준다. 첫째, 기준원전 압력의 약 1/6로 운영하면서도 원전 사고 모의 중 압력 천이에서 발생하는 이상 유동 현상을 수력학적으로 비교할 수 있다. 둘째, 운전압력이 낮아져서 내부 시각화를 통해 현상을 관찰할 수 있다. 셋째, 저 점성 특성으로 인해 루프 압력강하의 유사성을 쉽게 확보할 수 있다. 따라서, URILO-II는 냉매를 활용함으로써, 내부 현상을 관찰할 수 있다는 점이 가장 큰 장점이 될 것이며, 수력학적 상사가 가능하므로 사고 실험 시 기준원전의 압력 천이 거동을 잘 맞출 수 있을 것으로 기대하였다.

Ishii의 3단계 척도법을 사용하여 축소된 높이와 이상유동 자연순환, 그리고 다른 유체의 특성을 고려하는 방식으로 URILO-II 실험장치의 설계를 진행하였다. 많은 무차원수를 포함하는 단상유동과 이상유동의 상사를 완벽하게 맞추는 것은 굉장히 복잡하고 도전적인 일이기 때문에, URILO-II의 척도해석 및 설계 과정에서는 압력 천이를 정확히 상사하는 것을 목표로 설정하였다. 이를 위해, 고압 계통을 다른유체-저압계통으로 척도할 수 있는 Ishii 3단계 척도법⁽¹³⁾과 Kocamustafaofullari and Ishii⁽⁷⁾ 척도법을 활용하였다.

열원, 열교환기, 배관, 펌프 등으로 구성된 기준원전의 일차계통과 유사한 일반적인 폐쇄 순환계통에서, 단상 유동의 상사변수는 전체 루프에 대한 1차원 국부 평형 방정식 (연속방정식, 운동량방정식, 에너지방정식)의 적분효과를 통해 결정된다⁽⁷⁾. 1차원 국부 평형 방정식으로부터 계통의 대표속도, 열원의 길이, 유동 단면적 등의 무차원화 변수가 도출된다. Table 1은 단상유동에 대한 무차원 변수를 정리한 내용이며, 각 변수의 의미는 다음과 같다; l_iR=실험장치 길이비/기준원전 길이비, a_iR=실험장치 유동 면적비/기준원전 유동 면적비, Time ratio 수=유체 수송시간/열전도 시간, Heat source 수= 열원/축 방향 에너지 교환, Richardson 수=부력/관성력, Biot 수= 벽면 대류/전도, Stanton 수=벽면 대류/축방향 대류, Friction 수=마찰력/관성력, Pump characteristic 수=펌프 수두/관성력을 의미한다. 여기서 실험장치의 상사조건은 다음 식(1)과 같이 모든 무차원수가 기준원전과 일치해야 한다.

$\[ F_{iR}=R_R=S{t}_{iR}=T_{iR}^{*}=B_{iR}=Q_{siR}=F_d=1 \]$

(1)

Table 1

Dimensionless numbers for single-phase flow(7)

이상 자연순환의 상사조건은 유체 및 증기의 혼합물에 대한 면적 평균 1차원 국부 평형 방정식에 Drift-Flux 모델을 적용하여 미분방정식으로부터 상사변수를 도출하고, 노심 입구의 작은 섭동에 의한 전체 시스템 반응을 고려하여 국부 반응의 미분방정식으로부터 적분효과로 상사변수를 도출한다. 이상유동 무차원 변수는 Table 2에 정리하였는데, 각 변수에 대한 의미는 Phase change 수=상변화 열유속/인가 열유속, Subcooling 수=미포화도/잠열, Froude 수=관성력/중력, Drift-flux 수=Drift 이동/대류 속도, Time ratio 수=유체 이동시간/열전도 시간, Thermal inertia 수=고체 열관성/유체 열관성이다. 식 (1)과 마찬가지로, 이상유동의 상사 조건은 Table 2의 무차원수의 값이 모두 기준원전과 일치되도록 하는 것이다.

Table 2

Dimensionless numbers for two-phase flow(7)

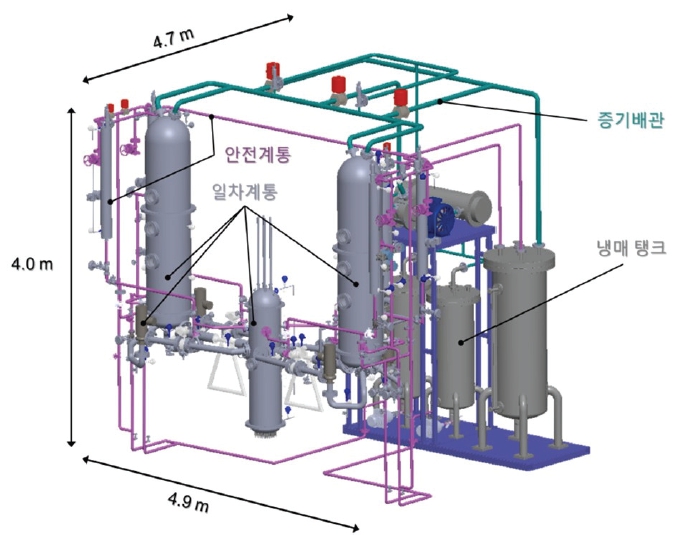
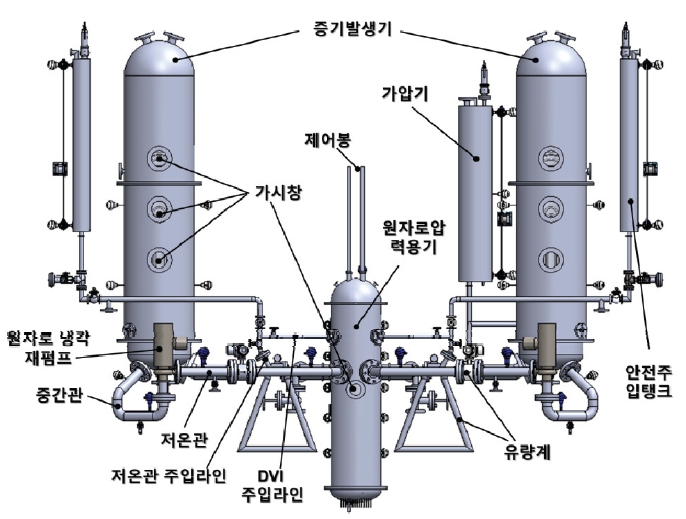
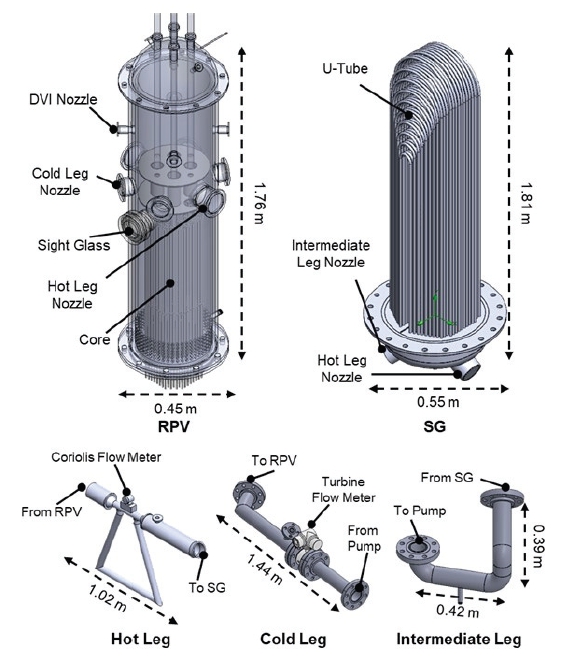
Table 1과 Table 2에 도시된 무차원수를 최대한 보존할 수 있도록 URILO-II의 기하학적 형상비는 높이비와 직경비를 1/8, 1/10으로 선정하였으며, 형상비에 기반하여 Fig. 1, Fig. 2와 같이 URILO-II 실험장치를 설계하였다.

Fig. 1

Schematic overall design of URILO-II

Fig. 2

Schematic design of primary system and safety injection system of URILO-II

URILO-II는 너비 4.9 m, 높이 4.0 m, 길이 4.7 m의 규모이며, 설계범위는 OPR1000의 일차계통, 이차계통, 안전주입계통을 포함한다. 계통 구성에 사용된 기본 재료는 기준원전과 동일한 SS304이며, 냉매 R134a의 액체-기체 밀도비가 동일한 압력인 26.5 bar를 운전압력으로 선정하였고, 설계 여유도를 고려하여 전체 파이프는 40 Sch. 이상으로 선택하였다. 원자로압력용기와 증기발생기는 운전압력을 고려하여 가시창을 설계하였고, 이를 통해 노심 내 냉각재 유동과 U-tube 외벽에서의 비등 현상을 관찰할 수 있도록 하였다. 노심의 경우, 간접 전기가열법을 이용하여 척도된 정상출력의 10 % 수준을 모의할 수 있게 설계하였다. 안전주입계통은 기존 OPR1000의 저온관 주입방식의 특징을 보존하면서, 차세대 원전 관련 연구를 위해, 원자로 직접주입방식(Direct vessel injection, DVI)을 가능하게 하는 방식으로 설계하였다.

설계의 기준이 되는 OPR1000의 설계값은 한울 3, 4호기의 FSAR와 MARS-KS input에서 취득하였으며, Table 3은 척도 설계된 URILO-II 일차계통의 정상운전 조건이다. URILO-II는 척도된 전출력은 정상운전 조건에서 1.7 MW이며, 본 실험장치는 전출력의 10 % 수준인 0.17 MW를 실험장치의 최대출력으로 설계하였다. 이는 저출력 정상운전 실험에 적절한 출력 수준이며, 사고 실험에서 잔열을 충분히 모의할 수 있는 조건이다. 실험장치의 고온관 기준 운전압력은 26.5 bar이고 재료의 안전 여유도를 고려하여 설계 압력은 35 bar로 선정하였다.

Table 3

Scaled design operating conditions of URILO-II compared to OPR1000

노심 입구 온도는 기준 원전의 Subcooling 수의 상사를 고려하여 도출되는 변수로, 미포화도 비율에 의해 입구온도 61℃가 도출되었고, 노심 온도증가비 1/2.11를 고려하여 출구온도는 75 ℃가 도출되었다. 계통 및 노심의 유량비는 노심입구의 유체 밀도와 유동 면적비 및 유속비를 곱하여 구할 수 있으며, 계통 유량은 기준원전의 1/195.8인 70.5 kg/s로 설계하였다. 기준원전의 원자로압력용기는 강수관-상부헤드, 고온관 노즐틈, 노심 shroud, 노심 안내관으로의 우회 유로가 있으며, 계통 유량의 3 %가 우회하기 때문에, 노심유량은 계통유량의 97 % 수준이다. 반면, URILO-II의 원자로압력용기 설계에는 우회 유로의 비율과 사고 실험에 주는 영향이 적을 것으로 판단하여, 강수관-상부헤드 및 고온관 노즐틈, 노심 안내관 우회유로를 설계하지 않았으며, 노심 shroud 우회 유로만 고려하였다. 계통 유량은 모의 출력이 10 %이므로, 계통의 초기 온도분포를 맞추기 위해 유량도 10 % 수준으로 설계하였다. 결과적으로 원자로압력용기의 총 높이는 1.76 m로 기준원전 대비 1/7.67 크기이고, 체적은 1/845으로 축소 설계하였다.

2.2 척도해석

축소 비율이 큰 URILO-II 실험장치는 작동유체로 냉매 R134a를 활용하므로, 축소비와 다른 유체 사용에서 발생하는 왜곡을 최소화하기 위한 면밀한 척도해석과 설계가 필요하다. URILO-II의 단상유동 및 이상유동에 대한 척도해석 결과를 Table 4와 Table 5에 집약적으로 나타냈다. Table 4를 살펴보면 Time ratio 수, Heat source 수, Richardson 수, Friction 수, Pump 특성 수는 기준원전과 일치하게 유지할 수 있지만, 고체 내부와 표면의 열전달과 관련된 무차원수인 Heat transfer rate 비, Biot 수, Stanton 수는 매우 왜곡된 무차원수를 보여준다. 이 왜곡은 열전달 관점에서, 냉매 R134a의 물보다 1/10정도 낮은 열전달 계수 때문이며, 낮은 단상 열전달로 인해 단상 자연순환 모의에 왜곡이 발생할 가능성이 큼을 예상할 수 있다.

Table 4

Scale analysis results for single-phase flow

Table 5

Scale analysis results for two-phase flow

이상유동과 관련하여, Table 5에 따르면, Phase change 수, Subcooling 수, Drift flux 수, Froude 수, Quality 비, Void fraction 비는 모두 기준원전과 동일하게 나타나므로, 이상유동에 대한 거시적인 현상은 유사하게 상사가 가능하다. 그러므로, URILO-II는 이상유동이 발생하는 사고 모의에서는 OPR1000에서 발생하는 열수력 현상들을 효과적으로 실험할 수 있을 것이다. 그러나, 단상 열전달에 대한 정확한 상사는 어렵기 때문에, 열전달이 발생하는 단상영역에서 열전달과 온도분포 등에 있어 왜곡이 발생할 가능성이 높다. 따라서, 본 실험장치는 사고 모의 실험에 있어, 모의 범위를 이상유동이 지배적인 범위로 실험 조건을 조절하여, 초기조건을 맞추고 사고 모의를 적절히 수행할 수 있을 것으로 예상한다.

3. 척도설계 평가

3.1 노심 국부 현상 평가

앞서 소개된 URILO-II의 설계와 척도해석은 거시적인 상사성을 파악할 수 있었다. 세부적인 현상에 대한 모의를 위해, 국부 현상에 대한 상사성을 평가하면, 사고 모의실험에서 가장 중요한 현상은 냉각재 재고량과 압력천이 등에 따라 노심에서 발생하는 열수력 현상이다. 노심의 국부적 현상 중에서, 노심 내의 이상 자연순환, 성층화, 혼합물의 수위, 열전달률 등과 같은 핵심 열수력 현상을 좌우하는 주요 요소는 이상 유동 패턴과 이를 유지하는 건도비이다⁽¹⁴⁾.

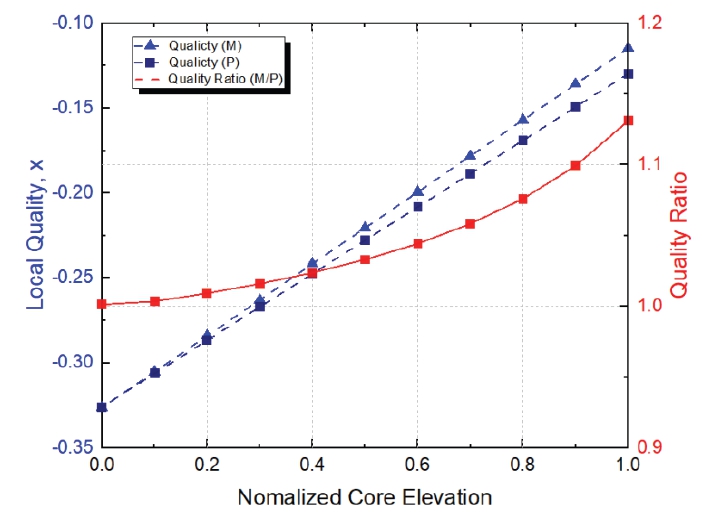
Mishima 및 Ishii⁽¹⁴⁾의 유동양식 천이 이론을 참조하여 건도비와 이상 유동 양식의 천이 비를 비교했고, 그 결과를 Fig. 3에 나타냈다. 노심 높이에 따른 건도의 상관성을 분석한 결과, 노심 입구에서는 건도비가 1.0으로 유지되지만, 노심의 높이가 증가함에 따라 건도비가 1.13까지 증가함을 확인하였다. 이는 노심 높이가 증가함에 따라 이상 유동 패턴에 약간의 왜곡이 발생할 가능성이 있음을 의미한다.

Fig. 3

Comparison of void fraction according to core height

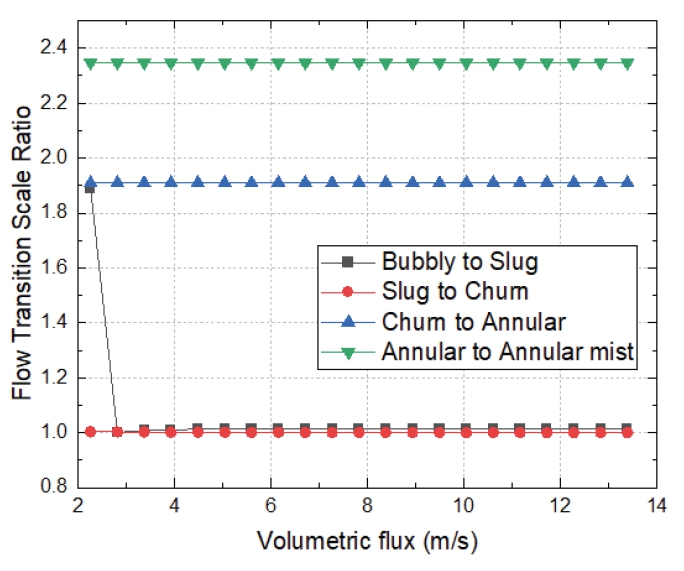
Fig. 4는 증기의 표면 속도에 따른 이상 유동 양식의 천이 비율을 정리한 것이다. 건도와 기공율이 유지된다고 가정할 때, bubbly-slug flow 천이 및 slug-churn flow 천이는 참조원전과의 상사성이 있지만, churn-annular flow 및 annular-annular mist flow 천이는 약 2∼3배의 왜곡이 있어 이 영역의 전환은 더 늦게 일어날 것으로 예상된다.

Fig. 4

Comparison of two-phase flow regime transition in the core

3.2 CFD 해석

통상적으로, 척도 설계한 실험장치의 왜곡도의 검증은 대표적으로 MARS-KS나 SPACE와 같은 열수력 시스템 코드나 전산유체역학(CFD)을 사용하여 실험장치의 성능을 예비 검증하는 방식으로 평가된다. 설계된 URILO-II는 MARS-KS 코드로 분석이 필요하지만, MARS-KS의 R134a 냉매에 대한 물성치 데이터가 불안정하므로, 시스템 코드 분석에 앞서 전산유체역학(CFD, Solidworks Flow Simulation) 분석을 통해 실험장치의 설계 성능을 예비 검증하였다. URILO-II는 다수의 시스템 및 구성 요소를 가지고 있지만, 모든 구성 요소를 CFD로 분석하는 것은 컴퓨팅 능력에 제약이 있으므로, 가장 핵심적인 요소인 원자로 압력용기와 증기발생기의 1차측, 1차계통 배관을 해석하여, 척도 설계값인 온도 및 압력분포를 비교하였다.

3.2.1 해석 형상

URILO-II에서 해석할 영역인 원자로 압력용기(Reactor Pressure Vessel, RPV)와 증기발생기(Steam Generator, SG)의 1차측, 1차계통 배관의 형상은 Fig. 5에 도시하였다. 구체적으로, 원자로 압력용기는 상단 헤드에 제어봉 노즐을 통해 제어봉이 삽입되며, 원자로 본체 상단에는 4개의 DVI 노즐이 있고, 중간 부분에는 고온관(Hot Leg) 및 저온관(Cold Leg) 노즐이 위치하며, 내부에는 156개의 간접 전기 가열봉으로 구성된 노심(Core)과 환형 강수관(Down-comer), 원형의 가시창 등으로 구성된다. 정상운전 조건에서는 원자로 압력용기의 저온관으로 저온의 작동유체가 들어와 강수관을 따라 하강하고, 유동 홀을 지나 노심으로 상승하여 열전달을 통해 작동유체의 온도가 상승하며, 노심 상부에서 고온관으로 유체가 빠져나간다.

Fig. 5

CFD analysis component of URILO-II

URILO-II의 1차계통 배관은 고온관, 저온관, 중간관으로 구성되며, 원자로 압력용기에서 빠져나온 고온의 작동유체가 고온관으로 흐르고, 고온관에서 증기발생기 1차계통 전열관 내에서 열교환을 통해 저온의 작동유체로 나온다. 증발생기에서 나온 저온의 작동유체는 중간관을 지나, 펌프를 거쳐 저온관으로 흐르고, 이는 다시 원자로 압력용기로 들어가는 순환 루프를 형성한다.

3.2.2 CFD 해석 조건

설계된 컴포넌트의 온도 및 압력 분포 경향을 파악하기 위해, 작동 유체인 R134a의 물성치와 단상 유동 및 열유속 조건, 입구 유동 조건을 바탕으로 분석을 시행하였다. 본 해석에서는 고체의 거칠기에 따른 압력 강화 영향과 노심 고체 가열봉에서 작동 유체로의 열전달 효과, 증기발생기 고체 전열관과 작동 유체 간의 열전달 효과를 종합적으로 파악하기 위해, 고체-유체 영역을 동시에 해석하였다. 단상 유체 영역은 유한체적법에 기반하여 질량, 운동량, 에너지방정식과 k-ε 난류 모델을 이용하여 해석한다. 고체 영역은 열전도 방정식만 해석하며, 고체와 유체 간의 에너지 교환은 유체의 에너지방정식과 고체의 열전도 방정식에 열유속 및 면적의 곱으로 계산되는 열량 항을 추가함으로써 해석된다. 해석 격자는 Cartesian Meshing 기법에 따라 생성하였으며, 원자로 압력용기, 증기발생기, 1차계통 배관은 최소 2.74 mm∼최대 5.83 mm 크기로 생성하였다.

각 해석의 경계조건은 Table 6에 정리한 것과 같이, 원자로압력용기는 입구 조건이 저온관에서 61 ℃의 R134a 작동유체가 17.625 kg/s이고, 출구 조건이 고온관에서 2.65 MPa로 압력 경계이며, 노심에서 156개의 가열봉에 10.89 kW 열출력 조건으로 설정하였다. 증기발생기의 경우, 입구 조건은 고온관 노즐에서 35.25 kg/s 및 75 ℃로 작동 유체가 유입되며, 출구 조건은 중간관 노즐에서 압력 경계로 나가고, 2차측의 증기 발생에 따른 열제는 열유속 조건으로 설정하였다. 저온관과 중간관, 고온관의 해석 조건은 원자로 압력용기 및 증기발생기의 입구, 출구 조건과 같은데, 저온관과 중간관은 61 ℃ 및 17.625 kg/s의 질량 유량 조건이고, 고온관은 35.25 kg/s 및 75 ℃의 질량 유량 조건이다.

Table 6

Boundary Conditions and mesh information

3.2.3 CFD 해석 결과

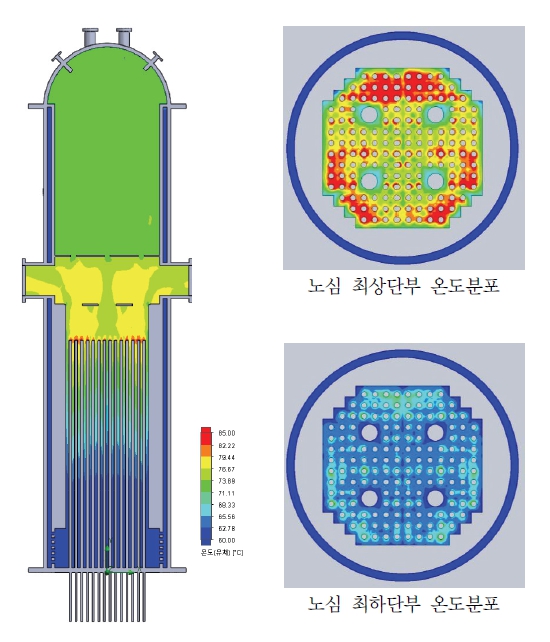
내부 작동 온도의 분포는 Fig. 6에 나타내었으며, 저온관에서 들어온 61 ℃의 작동 유체가 강수관을 따라 내려가고, 하부 플레넘 및 노심 입구를 통과한 후, 모의 노심에서 가열되어 고온관으로 나가는 과정에서 온도분포의 경향을 확인할 수 있었다. 온도분포의 경우, 척도 설계값인 입구온도 61 ℃와 출구온도 75 ℃를 분석 결과와 비교하며, 내부 온도 분포 경향을 살펴보았다. 출력 100 % 운전조건에서 온도분포를 확인한 결과, 출력 1.7 MW, 입구온도 61 ℃ 및 계통 유량 70.5 kg/s에서 출구온도는 76.1 ℃로 해석되었으며, 이는 설계값인 75 ℃보다 1.1 ℃ 더 높은 결과를 보였다. Fig. 6에서 노심 최상단부에서 가열봉 부근 작동유체의 온도가 비등 온도인 80 ℃ 이상인 영역이 발생하였고, 이는 노심 가열봉 상단부에서 비등이 발생할 것으로 예상할 수 있는 결과이다. 본 해석은 단상 유동 및 열전달 해석을 비등 및 응축에 의한 열전달이 고려되지 못해 출구온도가 1.1 ℃ 더 높은 결과를 보인 것으로 분석된다.

Fig. 6

Temperature analysis result of URILO-II’s RPV at normal operating conditions (100 % thermal power)

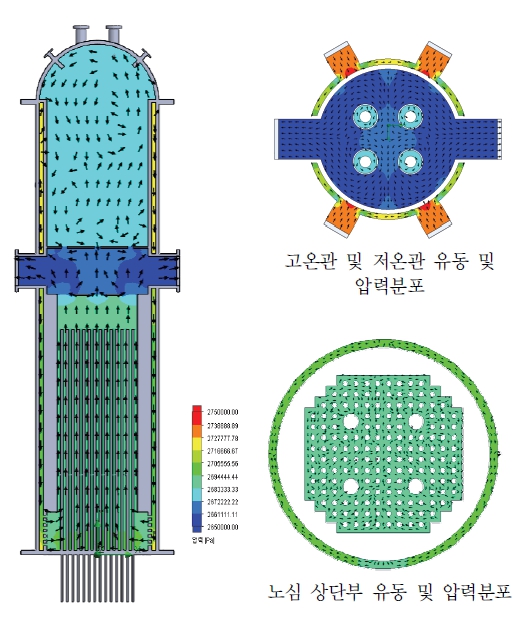
압력 분포에 대해서는 RPV의 압력강하를 척도 설계값과 해석값을 비교하여 설계 예비 검증을 수행했다. 각 컴포넌트의 압력강하는 척도값과 같게 설계되어야, 각종 사고 모의 실험에서 발생하는 단상, 이상 자연순환의 경향을 잘 모의할 수 있으므로 컴포넌트 및 전체 루프에 대한 압력강하를 맞추는 것은 중요하다. 압력강하에 대한 척도값은 OPR1000의 MARS-KS 해석 결과와 Table 2의 Pump characteristic number로부터 도출하였다. 원자로 압력용기의 압력분포 해석 결과는 Fig. 7과 같으며, 압력강하 척도값인 77,806 Pa보다 10 % 낮은 70,667 Pa로 해석되었다. 설계된 원자로 압력용기는 이상적 설계보다 약간 압력강하가 더 작을 것으로 예상되며, 추가적으로 원자로 압력용기에는 가시창 모듈과 열전대 등의 삽입으로 압력강하가 다소 상승할 것으로 예상한다. 아울러, Fig. 7의 vector는 유체 속력과 방향을 의미하며, 압서 설명한 바와 같이, 원자로 압력용기의 저온관에서 유입된 저온, 고압의 작동유체가 강수관을 따라 하강하고, 유동 홀을 지나 노심을 거처 압력이 낮아진 상태로 고온관으로 나간다. 여기서, 원자로 압력용기 상부 구조물의 홀을 통해 상부 및 헤드쪽으로 작동유체 일부가 우회하는 하는 것 확인할 수 있다.

Fig. 7

Pressure analysis result of URILO-II’s RPV at normal operating conditions (100 % thermal power)

URILO-II 증기발생기의 CFD 해석은 1차측 영역의 단상유동 열전달만 해석하였으며, 비등이 발생하는 2차측 영역은 본 해석에서는 전열관 열유속(-37.604 kW/m²) 경계조건으로 대체하여 해석하였다. Fig. 8은 증기발생기 1차측의 온도분포와 압력분포 해석 결과이다. 좌측 고온관으로 75 ℃, 35.25 kg/s의 R134a 작동유체가 유입되어, 전열관을 통한 열전달이 발생하고, 우우측 저온관으로 61.1 ℃, 17.625 kg/s으로 빠져나가는 것으로 해석되었다. 압력강하의 경우, 고온관 유입압력 2.65 MPa일 때, 저온관 출구압력은 2.6148 MPa이며, 총 압력강하는 35,248 Pa로 해석되었다.

Fig. 8

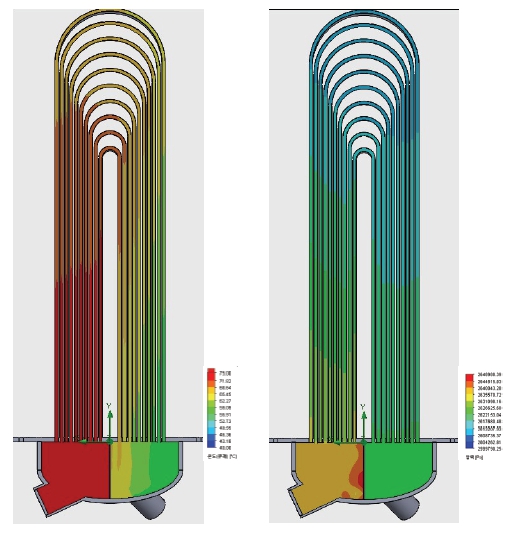
Temperature and pressure analysis result of URILO-II’s steam generator at normal operating conditions (100 % thermal power)

URILO-II 일차계통의 전체 압력강하는 Table 7에 정리하였는데, 정상운전 조건에서 이상적인 압력강하 값인 127,825 Pa에 비해 해석된 URILO-II의 전체 압력강하는 116,904 Pa로 약 8.5 % 낮은 결과가 도출되었다. 압력강하 해석의 결과는, 실제 실험장치 제작에서 각종 온도, 압력, 차압 측정 센서가 유로 내로 삽입됨에 따라 해석 결과보다 더 높은 압력강하가 발생할 가능성이 크기 때문에, 척도 설계값보다 8.5 % 낮은 해석 결과는 실험장치 실제 제작 관점에서 조정 가능한 적절한 결과라고 할 수 있다. 본 연구에서 보인 온도 분포와 압력강하 해석은 추후 열수력 해석 코드인 MARS-KS의 해석을 수행하여 면밀한 예비 검증을 수행할 계획이다.

Table 7

Scale analysis results for single-phase flow

4. 결 론

본 연구는 복합적인 원자력 안전 기술들을 종합적 테스트하고, 동시에 실험과 관찰을 기반한 열수력 전문가 교육의 기회를 제공을 목적으로, 냉매 열수력 종합효과 실험장치인 URILO-II를 설계하고 예비 검증을 수행하였다. URILO-II의 기준 원전은 국내에서 가장 많이 운영되는 OPR1000 원전으로, 높이는 1/8, 직경은 1/10으로 축소 설계하였다. 실험장치의 작동 유체로는 원전의 이상 유동 현상을 상사할 수 있도록 냉매 R134a를 사용하여, 26.5 bar에서 참조원전의 열수력 현상을 재현할 수 있었다. 또한, 낮은 작동 온도 덕분에 소비 전력이 낮아지며, 운영 및 재료적 측면에서 설계 및 구현이 용이하게 되었다.

실험장치의 척도해석 결과, 이상유동에 대한 상사성은 잘 확보되었으며, 단상 유동의 경우, 질량 및 운동량에 대한 상사성이 존재하나, 냉매의 낮은 단상 열전달률 때문에 천이상황에서의 열전달과 온도 분포에 왜곡이 있음이 확인되었다. 이를 바탕으로, 본 실험장치를 사고 모의에 사용하는 것에 있어 주요 모의 대상을 이상 유동 현상에 초점을 맞추는 것이 중요하다는 사실을 확인하였다.

세부적인 국부 현상에 대한 상사성 비교와 CFD 해석을 통해, 척도 설계값과 거의 일치하는 결과가 도출되었다. 압력강하의 경우, 척도 설계값보다 약 8.5 % 더 낮게 계산되었으며, 앞으로의 연구에서는 열수력 해석 코드를 활용한 계통 전체 해석을 통해 예비 검증을 이어나갈 계획이다.

Acknowledgments

2023 한국유체기계학회 하계학술대회 발표 논문, 2023년 7월 5일~7월 7일, 평창 알펜시아

이 논문은 2022년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구입니다.(No.2022M2D6A1063101)

References

• Baek, W. P., Song, C. H., Yun, B. J., Kwon, T. S., Moon, S. K., and Lee, S. J., 2005, "Kaeri integral effect test program and the atlas design,” Nucl. Technol., Vol. 152, pp. 183∼195. [https://doi.org/10.13182/NT05-A3669]
• Kim, S. J., Zou, L., and Jones, B. G., 2015, “An experimental study on sub-cooled flow boiling CHF of R134a at low pressure condition with atmospheric pressure (AP) plasma assisted surface modification,” Int. J. Heat Mass Transf., Vol. 81, pp. 362∼372. [https://doi.org/10.1016/j.ijheatmasstransfer.2014.10.032]
• Kim, C. H., and Chang, S. H., 2005, “CHF characteristics of R-134a flowing upward in uniformly heated vertical tube,” Int. J. Heat Mass Transf., Vol. 48, pp. 2242∼2249. [https://doi.org/10.1016/j.ijheatmasstransfer.2004.12.025]
• Bang, I. C., Chang, S. H., and Baek, W. P., 2004, “Visualization of the subcooled flow boiling of R-134a in a vertical rectangular channel with an electrically heated wall,” Int. J. Heat Mass Transf., Vol. 47, pp. 4349∼4363. [https://doi.org/10.1016/j.ijheatmasstransfer.2004.04.030]
• Adams, G., Duffy, D., Lapson, B., Lundberg, R., 1979, “Integral experiments for PWR U-tube steam generators. Part 1: freon facility description and performance test results,” Acurex Corp., Mountain View, CA (USA). Alternate Energy Div. [https://doi.org/10.2172/5847671]
• Kondo, Y., Hirao, Y., Suzuta, T., Ueno, T., Tsuge, A., Kawanishi, K., and Tomomatsu, K., 2000, “Development of thermal-hydraulic computer code (two-fluid model) for steam generator.”, Proc. of the 4th JSME-KSME Therm. Eng. Conf., Vol. 2, pp. 149~154.
• Kocamustafaogullari, G., and Ishii, M., 1987, “Scaling of two-phase flow transients using reduced pressure system and simulant fluid,” Nucl. Eng. Des., Vol. 104, pp. 121∼132. [https://doi.org/10.1016/0029-5493(87)90293-7]
• Yadigaroglu, G., and Zeller, M., 1994, “Fluid-to-fluid scaling for a gravity- and flashing-driven natural circulation loop,” Nucl. Eng. Des., Vol. 151, pp. 49∼64. [https://doi.org/10.1016/0029-5493(94)90033-7]
• Khonsha, B., Jahanfarnia, G., Sepanloo, K., and Nematollahi, 2019, M., “Scaling and thermal-hydraulic design of a test loop for the VVER-1000 reactor,” Prog. Nucl. Energy., Vol. 113, pp. 18∼27. [https://doi.org/10.1016/j.pnucene.2019.01.007]
• Tain, R. M., Groeneveld, D. C., and Cheng, S. C., 1995, “Limitations of the fluid-to-fluid scaling technique for critical heat flux in flow boiling,” Int. J. Heat Mass Transf., Vol. 38, pp. 2195∼2208. [https://doi.org/10.1016/0017-9310(94)00344-U]
• Groeneveld, D. C., 1972, “The thermal behavior of a heated surface at and beyond dryout,” University of Western Ontario, London, Ontario, Canada.
• Yang, B. W., Anglart, H., Han, B., and Liu, A., 2021, “Progress in rod bundle CHF in the past 40 years,” Nucl. Eng. Des., Vol. 376, 111076. [https://doi.org/10.1016/j.nucengdes.2021.111076]
• Ishii, M., and Kataoka, I., 1984, “Scaling laws for thermal-hydraulic system under single phase and two-phase natural circulation,” Nucl. Eng. Des., Vol. 81, pp. 411∼425. [https://doi.org/10.1016/0029-5493(84)90287-5]
• Mishima, K. and Ishii, M., 1984, “Flow regime transition criteria for upward two-phase flow in vertical tubes,” Int. J. Heat Mass Transf., Vol. 27, pp. 723∼737. [https://doi.org/10.1016/0017-9310(84)90142-X]