CFD와 인공신경망을 활용한 허니컴 래버린스 실 성능 예측
Abstract
There is a growing interest in sealing technology, as the demand for gas turbine performance improvements increases. The honeycomb labyrinth seal is the most popular sealing technology, but it takes a lot of time to exactly predict its leakage performance considering various geometrical parameters and operating conditions. This study investigated a method to reduce computational costs involved in predicting the performance of honeycomb labyrinth seals using artificial neural networks(ANN) and computational fluid dynamics(CFD). Firstly, the central composite design, one of the design of experiment(DOE), was used to analyze the effects of various geometrical parameters on the leakage performance. The influences of geometric parameters were comparatively analyzed using a Pareto chart, and it was confirmed that clearance, tooth width, pitch, and honeycomb cell diameter were statistically significant(i.e. influential) parameters. Then, CFD simulation was performed using the combination of the selected geometric parameters and operating conditions, generating the database for the ANN to train. The high accuracy of the ANN’s prediction was confirmed by comparing its results with CFD simulations using mean squared error(MSE) and root mean squared error(RMSE). The MSE and RMSE values for the training data within the generated database were 1.475 × 10-5 and 0.003841, respectively. For the new unseen data, the MSE and RMSE values determined to be were 0.00021 and 0.01452 respectively.
Keywords:
Gas turbine, Labyrinth seal, Discharge coefficient, Leakage, Computational Fluid dynamics, Feed forward neural network키워드:
가스터빈, 래버린스 실, 토출계수, 누설, 전산유체역학, 순방향 신경망1. 서 론
래버린스 실은 블레이드 팁(blade tip)과 케이싱(casing) 사이의 공간에 여러 개의 이빨을 두어 누설을 방지하는 밀봉 기술이다. 래버린스 실은 이빨의 배치 구조에 따라 계단처럼 층을 이루고 있는 계단형 래버린스 실과 층이 없이 일직선으로 이어진 직선형 래버린스 실로 분류할 수 있다. 또한 케이싱 표면의 구조에 따라 매끄러운 면을 가진 솔리드 래버린스 실(solid labyrinth seal)과 벌집 형태의 빈 공간을 가진 허니컴 래버린스 실(honeycomb labyrinth seal)로 분류된다. 이와 같이 여러 종류의 실들이 누설 유동 저감에 활용되고 있으며, 실의 성능을 정확히 예측하기 위한 다양한 연구가 수행되고 있다(1-3).
래버린스 실은 실의 종류, 간극, 이빨 개수 등 다양한 변수들의 영향을 받기 때문에, 실을 정밀하게 설계하기 위해서는 넓은 범위에서 다양한 형상 변수의 영향이 반영된 실의 성능 데이터가 필요하다. 따라서 다양한 형상 변수들이 래버린스 실의 누설 특성에 미치는 영향을 파악하기 위해, 다음과 같은 기초적인 연구가 수행되었다. Vermes(4)는 직선형 래버린스 실과 계단형 래버린스 실 그리고 혼합된 형태의 실(combination seal)의 누설 유동 특성을 실험을 통해 분석하고, Martin(5)의 식을 수정하여 새로운 상관식을 제안하였다. Zimmermann, 등(6)은 Hodkinson(7)의 carry-over factor 식을 수정하여 새로운 carry-over factor를 제안하고, 이를 활용하여 새로운 누설 유량 상관식을 개발하였다. Kim, 등(8-10)은 직선형 래버린스 실과 계단형 래버린스 실의 누설 특성을 CFD로 분석하고, 간극, 압력비 그리고 실의 종류에 따른 실의 성능 변화를 확인하였다. 또한, 실험 결과나 KTK(knife-to-knife)와 같은 analytic model로 얻은 결과와 CFD 결과를 비교하여 CFD 결과의 정확성을 확인하였다. Hur, 등(11, 12)은 계단형 래버린스 실의 간극에 따른 누설 유동의 특징을 CFD로 분석하고, 계단형 래버린스 실의 누설 특성을 기반으로 케이싱에 립(rib)이 추가된 실의 형상을 제안하였다.
Schramm, 등(13)은 계단형 허니컴 래버린스 실의 누설 특성을 실험과 CFD 분석을 통해 연구하였으며, 간극과 허니컴 셀 지름 그리고 이빨 두께 간의 상관관계가 누설 유동에 중요한 영향을 미치는 변수임을 확인하였다. 또한 세 가지 변수들 간의 상관관계를 하나의 식으로 정리하여 유효 간극(effective clearance)이라 정의하였다. Yan, 등(14)은 계단형 허니컴 래버린스 실의 허니컴 셀 지름과 허니컴 셀 깊이에 따른 누설 유량의 변화를 CFD와 실험을 통해 예측하였다. 예측 결과 동일한 압력비에서 허니컴 셀 지름이 증가할수록 누설 유량이 증가하지만, 허니컴 셀 깊이는 2.7 mm 이상 증가하면 누설 유량에 영향을 미치지 않음을 확인하였다. Nayak, 등(15)은 직선형 래버린스 실의 간극과 허니컴 셀 지름의 영향을 CFD로 분석하였으며, 간극이 증가할수록 유량 함수(flow function)가 감소하는 경향을 확인하였다. 그러나 간극이 계속해서 증가하는 경우 유량 함수가 다시 증가하는 경향을 보였다. Jo, 등(16)은 계단형 허니컴 래버린스 실의 유효간극을 좁히는 혼합된 허니컴 실(mixed honeycomb seal)을 제안했으며, 간극 1.204 mm에서 기존의 형상보다 토출계수가 19 % 저감된 효과를 확인하였다.
위와 같이 래버린스 실의 형상 변수와 누설 특성 간의 영향을 파악하기 위한 다양한 연구들이 진행되었다. 대부분의 연구들은 형상 변수의 영향을 중점적으로 연구하였으며, 실험 및 계산의 편의성을 위해 래버린스 실을 정적 상태(stationary state)로 가정하여 누설 특성을 분석하였다. 그러나 래버린스 실을 보다 정밀하게 설계하기 위해서는 정적상태에서만 누설 특성의 변화를 고려하는 것이 아니라, 회전 중에 발생하는 다양한 누설 특성의 변화를 고려할 필요가 있다. 따라서 형상 변수의 영향뿐만 아니라 실질적인 운전 조건을 실제로 반영하여 원주방향으로의 회전효과를 고려한 연구도 수행되었다. W. Waschka, 등(17)은 회전 속도가 계단형 허니컴 래버린스 실의 누설 특성에 미치는 영향을 확인하고자 실험을 수행하였다. 실험 결과 테일러 수 와 레이놀즈 수의 비(Ta/Re)가 0.2 이상으로 증가할 경우 토출계수가 감소하는 효과를 확인하였다. Roger Paolillo, 등(18)은 회전 속도에 의한 계단형 허니컴 래버린스 실의 토출계수 변화를 예측하였으며, 축 방향 속도와 회전 속도의 비가 1 이상 증가할 경우, 회전 속도가 실의 성능에 영향을 미친다는 결론을 얻었다. Nayak, 등(19)은 직선형 허니컴 래버린스 실의 회전 속도에 따른 누설 유동의 특성 변화를 연구하였으며, 회전 속도가 증가할수록 공동(cavity)에서 회전하는 소용돌이(swirl)가 크게 발달하여 토출계수가 감소하는 것을 확인하였다.
이처럼 기존의 연구들은 실험과 수치해석 방법을 통해 다양한 형상 변수 및 회전 효과에 따른 래버린스 실의 성능 변화에 초점을 맞추어 진행되어왔다. 그러나 최근에는 실의 성능 예측과 형상 최적화에 소요되는 시간을 절감하고자 인공신경망과 CFD를 활용한 연구가 수행되고 있다. Pychynski, 등(20)은 데이터 마이닝(data mining) 방법 중 하나인 인공신경망을 활용하여 래버린스 실의 성능을 예측하였다. 이때, 래버린스 실의 다양한 형상변수를 입력변수로 실의 성능을 출력변수로 설정하였으며, 인공신경망의 예측결과와 CFD 결과를 비교하여 예측 정확도를 확인하였다. 학습에 소요된 시간은 5 분 이내이며, 학습이 잘 수행된 케이스에서 평균 오차 1.4 %를 확인하였다. Ruilk, 등(21)은 래버린스 실의 이빨 두께, 이빨 높이, 이빨 간격, 이빨 각도를 입력변수로, 토출계수를 출력 변수로 설정하였다. 인공신경망으로 예측된 데이터를 메타모델(metamodel) 구축에 활용하고, 구축된 메타모델에 최적화 알고리즘을 적용하여 실의 형상을 최적화하였다. 이를 통해, 기존의 형상보다 토출계수가 17.5 % 저감된 효과를 확인하였다. 이와 같이 인공신경망을 활용하여 실의 성능을 예측하거나, 예측된 성능데이터를 활용하여 실의 형상을 최적화하는 연구가 수행되었다.
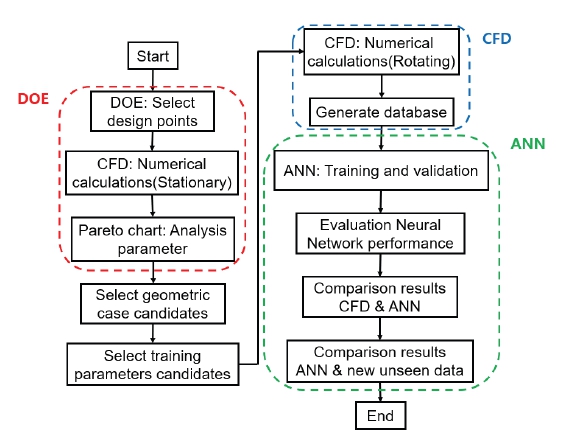
이처럼 인공신경망과 CFD를 활용한 래버린스 실 성능 예측은 다양한 형상 변수의 영향을 반영할 수 있으며, 성능 예측에 소요되는 시간을 절감할 수 있다. 이러한 특성은 형상 변수와 운전 조건의 영향을 모두 고려해야 하는 실의 성능을 예측하는데 효과적이다. 특히, 허니컴 래버린스 실과 같이 상관식이 잘 알려져 있지 않거나 구축이 어려운 경우에도 인공신경망과 CFD를 활용한 방법을 적용할 수 있다. 따라서 본 논문에서는 인공신경망과 CFD를 활용한 허니컴 래버린스 실의 성능 예측 방법을 제안하였으며, 일련의 연구과정을 Fig. 1에 정리하여 나타내었다. 먼저 허니컴 래버린스 실의 주요 형상 변수를 선정하기위해 실험계획법(DOE)을 활용하였다. 중심합성설계법을 활용하여 설계점을 선정하였고, 이를 Pareto chart로 분석하여 주요 형상 변수를 선정하였다. 그 다음, 선정된 주요 형상 변수를 조합하여 형상 케이스를 구성하고, 이를 운전 조건과 조합하여 학습 변수를 선정하였다. 선정된 학습 변수들을 CFD로 해석하였고, 이를 인공신경망의 학습에 활용하였다. 이때, 인공신경망의 학습 성능을 확인하기 위해 평균제곱오차(Mean Squared Error, MSE)를 활용하였으며, MSE와 평균제곱근오차(Root Mean Squared Error, RMSE)를 통해 CFD 결과와 인공신경망의 예측 결과를 비교하였다. 또한, 예측된 성능데이터의 실용성을 확인하고자, 학습에 활용되지 않은 ‘new unseen data’의 CFD 해석결과와 인공신경망의 예측 결과를 비교하였다.
2. 모델링
2.1 해석 모델 및 형상 변수
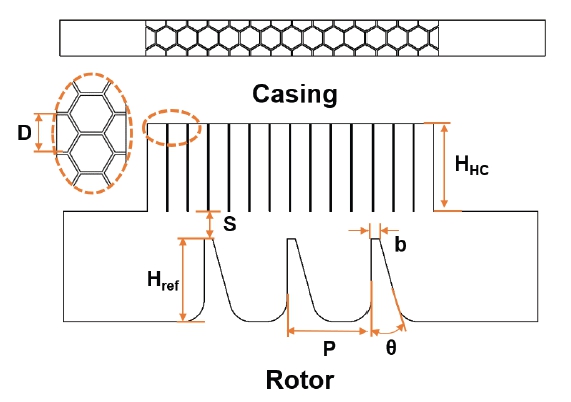
본 연구에서는 케이싱(casing)과 로터(rotor) 사이에서 발생하는 누설을 방지하기 위한 허니컴 래버린스 실을 해석 모델로 선정하였고, 변수들의 정보와 형상을 Fig. 2에 도식화하여 나타내었다. 주요 변수는 간극(S), 허니컴 셀 지름(D), 이빨 두께(b), 이빨 높이(H), 그리고 이빨 간격(P)이며 그 외 변수들은 허니컴 셀 깊이(HHC)와 이빨 각도(θ)로 구성되었다. 주요 변수들을 무차원화하기 위해, 기준 이빨 높이(Href)를 정의하였으며, 이를 기반으로 간극(S), 이빨 두께(b), 이빨 간격(P), 이빨 높이(H)들은 각각 기준 이빨 높이(Href)에 대한 비율로 표현하였다. 허니컴 셀 지름(D)은 허니컴 셀 높이(HHC)에 대한 비율로 나타내었으며, 허니컴 셀 지름(D/HHC)은 0.252와 0.504 두 가지 종류를 설정하였다. 또한, 간극(S/Href)은 0.083에서 0.33까지, 이빨 두께(b/Href)는 0.1에서 0.183까지, 이빨 간격(P/Href)은 0.917에서 1.167까지 그리고 이빨 높이(H/Href)는 0.75에서 1까지 범위를 선정하였다. 무차원변수의 종류와 범위는 Table 1에 정리하여 나타내었다.
2.2 실험계획법
본 논문에서는 형상 변수의 영향을 최소한의 결과로 분석하기 위해 상용프로그램인 Minitab(22)을 활용하여 실험계획법을 수행하였다. 직선형 허니컴 래버린스 실의 경우 간극이 증가할수록 유량 함수가 감소하는 경향을 보이지만, 일정 간극 이상에서는 유량 함수가 증가하는 비선형적인 경향을 보이므로(15), 변수의 비선형성을 잘 반영할 수 있는 중심합성설계법(central composite design)으로 설계점을 선정하였다. 중심합성설계법은 완전요인설계점(full factorial design points) 2x, 축 점(axial points) 2x, 중심점(center point) n으로 구성된다. 이때, x는 요인(factor)의 개수를 나타내며, 요인은 +1 과 -1로 두 개의 수준(level)을 가진다. 완전요인설계법은 2 개의 수준으로 조합되는 모든 경우의 수를 나타내며, 축 점은 각 수준의 중심 0 을 표현하고, 중심점은 두 요인 간의 중심을 나타낸다. 중심합성설계법의 총 실험 횟수는 완전요인설계점 2x 개, 축 점 2x 개, 그리고 중심점 n 개의 합으로 식(1)과 같이 구성된다.
| (1) |
본 논문의 경우 5 가지의 요인 요소(허니컴 셀 지름, 간극, 이빨 두께, 이빨 간격, 이빨 높이)를 기반으로 중심합성설계법을 적용하였다. 이때, 허니컴 셀 지름을 범주형 요인으로, 간극, 이빨 두께, 이빨 간격, 이빨 높이를 연속 요인으로 설정하였다. 4 개의 연속 요인에 대해 완전요인설계점 16 개, 축 점 8 개, 중심점 7 개가 선정되었으며, 2 개의 범주형 요인을 곱해 총 62 개의 설계점을 선정하였다. 각 해석모델의 자세한 정보는 Table 2에 간략히 나타내었다.
2.3 격자 구성 및 경계조건
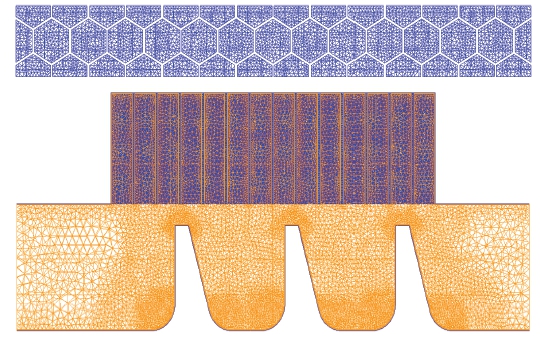
직선형 허니컴 래버린스 실의 격자 구성은 상용 프로그램인 ANSYS ICEM CFD 2020R2(23)를 활용하였으며, 벽면(허니컴, 케이싱, 로터) 근처의 영역에 정렬 격자(prism layer)를 그 외의 누설 유로에는 비정렬격자(tetra)를 구성하였다. 또한, 누설 유동을 보다 정밀하게 계산하고자 Fig. 3와 같이 이빨 끝에 고밀도 격자를 설정하였으며, 벽면에서의 y+를 2이하로 유지하였다. 유동 해석은 ANSYS CFX 2020R2(24)를 활용하였으며, 작동 유체는 이상기체 공기, 난류 모델은 SST 모델을 적용하였다. 입구의 전온도와 출구의 대기온도(opening temperature)는 300 K으로 동일하게 설정하였으며, 출구의 압력은 정압으로 대기압 조건을 적용하였다. 입구의 압력은 출구압력에 대한 압력비(PR) 2.5 를 설정하였다. 래버린스 실형상의 측면에는 주기성 경계조건(periodic boundary condition)을 설정하였으며, 정적상태로 해석을 수행하였다. 벽면은 단열(adiabatic)과 점착 조건(no slip condition)을 설정하였다. 이산화기법(advection scheme)은 고해상도기법(high-resolution)을 활용하였으며, 수렴조건으로는 평균제곱근(root mean square, RMS)을 10-4 이하로 설정하였다. 해석 방법과 경계조건의 수치에 대한 정보는 Table 3에 정리하였다.
본 연구에서는 토출계수(CD)로 실의 밀봉 성능을 평가하였으며, 식의 구성은 다음과 같다:
| (2) |
| (3) |
는 질량유량, To,in는 입구 전온도, Ac는 간극을 지나는 누설 유동의 단면적, Po,in는 입구 전압력, k 는 비열비, R 은 이상기체상수, Pout은 출구 압력이다. 동일한 간극 및 압력비에서 토출계수의 수치가 낮을수록 실의 성능이 우수함을 나타낸다.
2.4 격자 민감도 분석 및 CFD 해석 검증
격자수에 따른 토출계수의 수렴도를 확인하고, 격자 구성의 경제성을 확보하기 위해 격자 민감도 분석을 수행하였다. Fig. 4 는 허니컴 셀 지름(D/HHC) 0.252, 간극(S/Href) 0.083, 이빨 두께(b/Href) 0.1, 이빨 간격(P/Href) 0.917, 압력비(PR) 2.5 조건에서 토출계수의 수렴도를 나타내었다. 이러한 결과를 통해 약 320∼330 만 개의 격자로 허니컴 래버린스 실을 해석하였다.
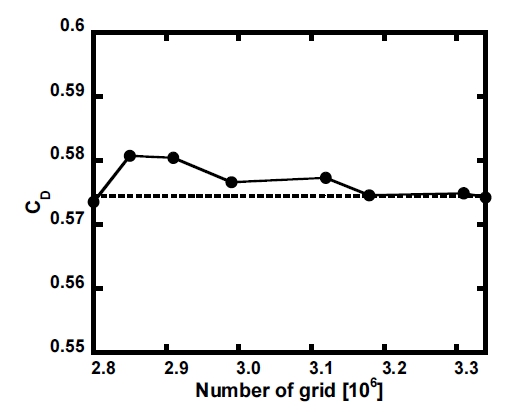
Example of grid dependence test results of the stationary seal(D/HHC=0.252, S/Href=0.083, b/Href=0.1, P/Href=0.917, PR=2.5)
본 논문에서의 수치해석 기법과 해석 결과에 타당성을 확인하기 위해 Schramm(13)의 래버린스 실 형상을 CFD로 해석한 뒤, Schramm의 실험결과와 비교하였다. 이때, 허니컴 래버린스 실의 토출계수와 솔리드 래버린스 실의 토출계수의 비(CD, honeycomb / CD, solid)를 활용하여 결과를 비교하였다. 간극과 허니컴 셀 지름 비(S/D)= 0.187, 0.309, 0.496에서 결과를 비교하였으며, 이를 Table 4에 정리하여 나타내었다. 비교 결과 평균오차 1.15 %로 해석 결과가 Schramm의 실험 결과와 잘 일치함을 확인하였다. 이를 통해 본 논문에서 제시된 수치해석 기법과 해석 결과에 타당성을 확인하였다.
2.5 인공신경망 구조
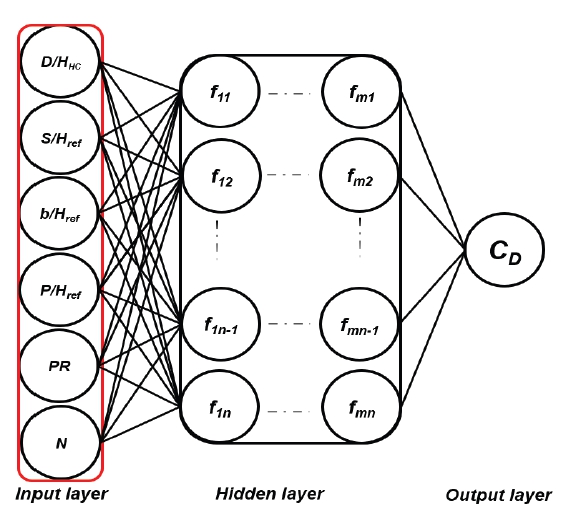
인공신경망(ANN)은 여러 개의 연결된 노드(node)점들이 여러 개의 층(layer)들을 이루는 구조로, 각각 입력 층, 은닉 층, 그리고 출력 층으로 구성된다. 입력 층에서 입력된 독립 변수에 가중치를 곱한 후, 은닉 층을 거치며 가중치 업데이트를 반복하고, 마지막으로 최적의 가중치를 선정하여 출력 층에서 결과를 예측한다.
본 논문에서는 MATLAB R2020a(25)에서 지원하는 deep learning toolbox로 순방향 신경망(feed forward neural network, FFNN)을 활용하였다. 순방향 신경망은 입력 층에서 입력된 학습데이터를 은닉 층을 거쳐 출력 층으로 결과를 출력하는 단방향 구조로, 비선형 결과를 학습 및 출력하는데 적합한 특징을 가지고 있다. 인공신경망의 과적합을 방지하고 일반화성능을 평가하기 위해 학습데이터를 training set 60 %, validation set 20 %, test set 20 %로 학습데이터를 분할하였다. 이는 인공신경망이 학습데이터의 60 %를 학습에 활용하고, 20 % 학습데이터로 예측 결과를 검증하고 나머지 20 % 학습데이터로 인공신경망의 학습 성능을 평가하는 방법이다. Validation set은 과적합이 발생하지 않는 적절한 epochs의 수를 결정하기 위해 학습에 관여하는 반면, test set은 학습과 검증이 끝난 모델의 최종 성능을 평가하는데 활용된다. 또한, test set은 학습에 전혀 관여하지 않아 인공신경망의 일반화 성능을 평가하는데 활용된다. 이와 같은 학습방법을 통해 unseen data(validation, test)를 검증함으로써 일반화성능을 확인한다. 학습데이터의 분할은 무작위로 이루어졌으며, 학습 알고리즘으로는 손실함수의 기울기를 빠르고 안정적으로 수렴할 수 있는 장점이 있어 다양한 연구(20, 21, 26, 27)에서 학습 알고리즘으로 활용되고 있는 Levenberg-Marquardt(28, 29) 알고리즘을 사용하였다. 인공신경망의 성능은 평균제곱오차(mean squared error, MSE)로 평가하였으며, ANN의 예측결과와 CFD 결과 비교는 MSE와 평균제곱근오차(root mean squared error, RMSE)를 활용하였다. 식의 구성은 다음과 같다:
| (4) |
| (5) |
각 변수는 다음과 같이 구성되어 있다. y0 는 CFD 해석 결과, yi 는 ANN의 예측 결과, Z는 데이터 수이다. MSE와 RMSE 값 모두 0에 가까울수록 학습 성능과 예측 정확도가 우수하다는 것을 의미한다.
3. 결 과
3.1 래버린스 실 주요 형상변수 선정
본 논문에서는 CFD를 활용하여 중심합성설계로 선정된 62 개의 설계점에서 토출계수 값을 예측하였다. 그 다음 Minitab에서 지원하는 Pareto chart를 활용하여 변수들의 중요도를 분석하였다. Pareto chart는 입력변수의 중요도를 통계적으로 분석하는 방법으로, 변수들의 중요도를 최솟값부터 최댓값까지 표준화하여 절댓값으로 나타낸다. 이 과정에서 Lenth(30)의 방법을 통해 기준선을 설정하고, 기준선 이상의 값을 가진 변수를 통계적으로 유의한 변수라고 선정한다. 이러한 방법을 통해 허니컴 래버린스 실의 주요 형상 변수를선정하였다.
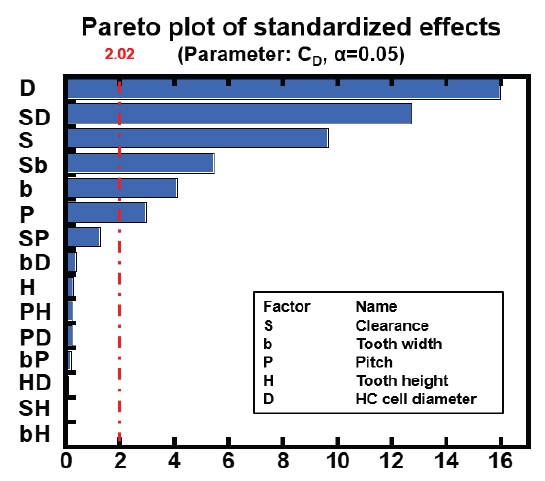
Fig. 5에 간극(S), 이빨 두께(b), 이빨 간격(P), 이빨 높이(H), 허니컴 셀 지름(D)이 실의 성능에 미치는 영향을 Pareto chart로 나타내었다. 분석 결과 기준선 2.02 이상의 값을 가진 유의한 변수는 허니컴 셀 지름, 간극, 이빨 두께, 그리고 이빨 간격이며, 이빨 높이는 유의하지 않은 변수임을 확인하였다. 허니컴 래버린스 실의 성능에 영향을 미치는 정도는 허니컴 셀 지름, 간극, 이빨 두께, 이빨 간격 순으로 컸다. 또한, 허니컴 셀 지름과 간극, 그리고 간극과 이빨 두께 간의 교호작용 또한 유의한 변수임을 확인하였다. 이는 간극과 허니컴 셀 지름 그리고 이빨 두께 간의 상관관계를 정의한 유효 간극(13)에 의한 결과이다. 이를 통해 Pareto chart가 변수들의 중요도를 잘 분석하였다고 사료된다. 이러한 결과를 바탕으로 3 개의 수준을 가진 간극, 이빨 두께, 이빨 간격으로 조합되는 모든 경우의 수인 33에 두 가지 허니컴 셀 지름을 곱해 총 54 개의 형상 케이스를 선정하였다.
3.2 인공신경망 데이터베이스 생성
실험계획법을 통해 선정된 54 개의 형상 케이스에 압력비 3 가지와 회전 속도 6 가지를 조합하여 총 972 개의 학습 변수를 선정하였다. 압력비는 1.5에서 2.5까지, 회전 속도는 0에서 7500 RPM까지 설정하였으며, 선정된 학습 변수의 자세한 정보는 Table 5에 정리하여 나타내었다. 이때, 래버린스 실에 회전효과를 반영하기 위해 이전 연구(31)결과를 참고하여 블레이드 반경과 회전 속도를 고려하여 계산한 선속도를 회전부의 경계조건으로 부여하였다. 또한, 학습이 완료된 순방향 신경망의 예측데이터가 실용성을 가지고 있는지 평가하기 위해, training set, validation set, 그리고 test set에 활용되지 않는 new unseen data를 선정하였다. 2 개의 경우를 가지는 5 가지 변수의 조합으로 총 25 가지 경우의 수를 선정하고, 이에 2 가지 허니컴 셀 지름을 곱하여 총 64 개의new unseen data를 무작위로 선정한 뒤, 이를 CFD로 해석하였다. 이때, 변수의 수치는 무작위로 선정하였다.
3.3 인공신경망 학습 결과
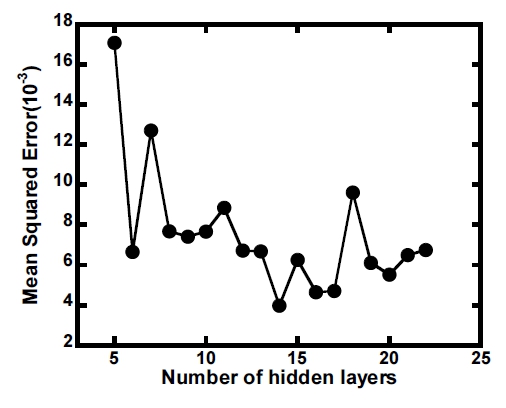
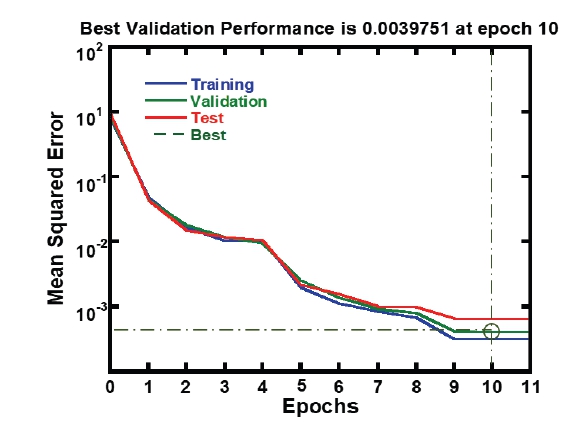
선정된 학습 변수들을 CFD로 해석하여 생성된 데이터베이스를 순방향 신경망(FFNN)의 학습데이터로 활용하였다. 입력변수는 간극(S/Href), 허니컴 셀 지름(D/HHC), 이빨 두께(b/Href), 이빨 간격(P/Href), 압력비(PR), 그리고 회전 속도(N)로 출력변수는 토출계수로 학습을 수행하였다. FFNN의 입력변수와 출력변수에 대한 정보는 Fig. 6에 정리하여 나타내었다. 높은 학습 성능을 가진 은닉 층의 개수를 선정하고자, 5 개에서 22 개의 은닉 층으로 학습을 수행하였다. 이때, 각 경우에서의 학습 성능을 MSE로 평가하였으며, 평가 결과를 Fig. 7에 나타내었다. 이를 통해 14 개의 은닉 층에서 학습 성능 MSE가 0.0039751로 우수한 학습 성능을 확인하였다. Fig. 8에 FFNN의 학습 성능을 나타내었고, epoch 10에서 학습 성능이 우수한 결과를 보였으며, 학습에는 약 4 초의 시간이 소요되었다.
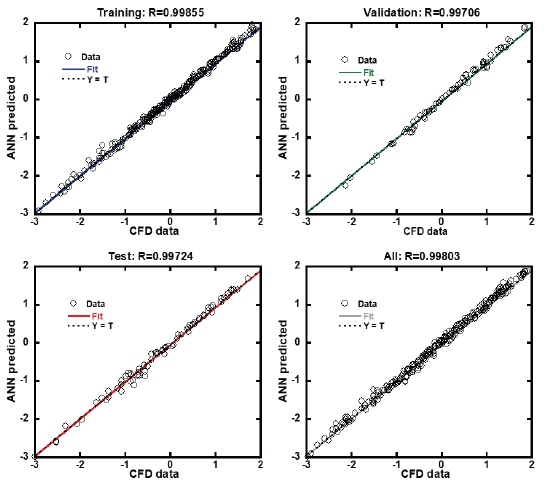
Fig. 9은 training, validation, test set에서 예측된 결과와 입력 결과의 회귀 및 상관관계(R)를 나타낸다. R 값으로 인공신경망에 의해 도출된 예측 값이 실제 입력 데이터 값과 어느 정도 일치하는 지를 확인할 수 있다. R 값이 1에 가까울수록 예측 정확도가 높은 것을 의미하며, 각 점들이 선에 가까울수록 R 값이 1에 가까워진다. Fig. 9에서 볼 수 있듯이 validation set과 test set에서 unseen data를 잘 예측하였으며, 이를 통해 우수한 일반화성능을 확인하였다.
허니컴 래버린스 실의 다양한 입력 변수가 가지는 고유한 경향성을 인공신경망이 잘 예측할 수 있는지 확인하기 위해, 먼저 인공신경망이 데이터 학습에 활용된 training data에서 CFD 결과와 인공신경망의 예측 결과를 비교하였다. 그 다음 예측 데이터의 실용성을 평가하기 위해 학습에 활용되지 않은 데이터인 new unseen data에서 CFD 결과와 인공신경망의 예측 결과를 비교하였다. 이러한 결과를 각 입력 변수에 따라 두 가지 허니컴 셀 지름에 대해 Fig. 10∼14에서 나타내었다. 총 972 개의 학습 변수들을 비교한 결과, MSE가 1.475 × 10-5, RMSE가 0.003841로 매우 높은 정확도를 보였다. 또한, 64 개의 new unseen data를 비교한 결과 MSE가 0.00021, RMSE가 0.01452로 마찬가지로 높은 정확도를 보였다.
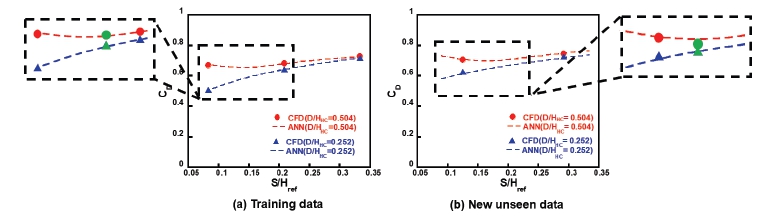
Comparison of CFD & ANN predictions for clearance effect. (a) b/Href= 0.1, P/Href= 1.167, PR= 2.5, N= 7500 RPM, (b) b/Href= 0.167, P/Href= 1, PR= 2.3, N= 3500 RPM
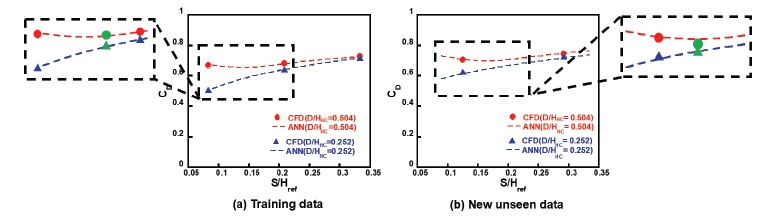
Comparison of CFD & ANN predictions for tooth width effect. (a) S/Href= 0.083, P/Href= 0.917, PR= 2.5, N= 7500 RPM, (b) S/Href= 0.125, P/Href= 1, PR= 2.3, N= 3500 RPM
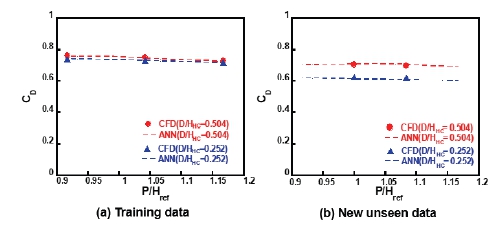
Comparison of CFD & ANN predictions for pitch effect. (a) S/Href= 0.083, b/Href= 0.1, PR= 2.5, N= 7500 RPM, (b) S/Href= 0.125, b/Href= 0.167, PR= 2.3, N= 3500 RPM
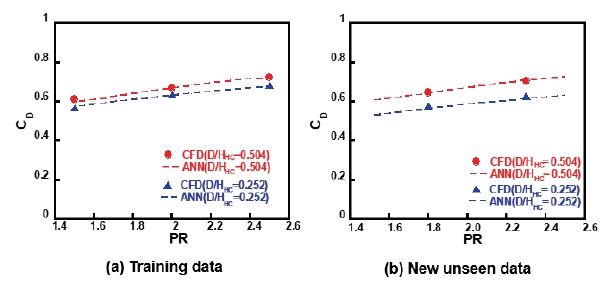
Comparison of CFD & ANN predictions for pressure ratio effect. (a) S/Href= 0.208, b/Href= 1.042, P/Href= 0.1417, N= 7500 RPM, (b) S/Href= 0.125, b/Href= 0.167, P/Href= 1, N= 3500 RPM
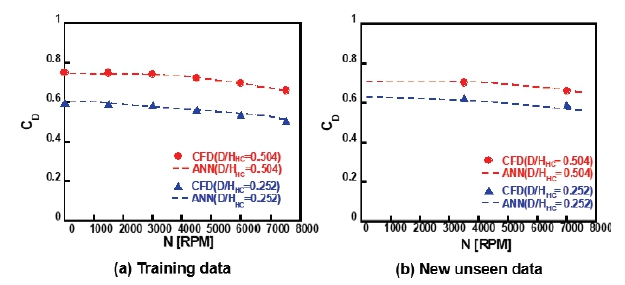
Comparison of CFD & ANN predictions for rotation speed effect. (a) S/Href= 0.208, b/Href= 1.042, P/Href= 0.1417, PR= 2.5, (b) S/Href= 0.125, b/Href= 0.167, P/Href= 1, PR= 2.3
Fig. 10(a)는 이빨 두께 0.1, 이빨 간격 1.167, 압력비 2.5, 회전 속도 7500 RPM에서 간극의 변화에 따른 토출계수의 변화를 나타내었다. 그리고 Fig. 10(b)는 이빨 두께 0.167, 이빨 간격 1, 압력비 2.3, 회전 속도 3500 RPM에서 간극에 따른 토출계수의 변화를 표현하였다. 두 그래프 모두 공통적으로, 허니컴 셀 지름이 0.252인 경우 간극이 증가함에 따라 토출계수가 선형적으로 증가하는 경향을 보였다. 또한, 허니컴 셀 지름이 0.504인 경우 간극이 증가할수록, 토출계수가 감소한 후 다시 증가하는 경향을 확인하였다. 이러한 경향성을 인공신경망이 학습데이터와 new unseen data에서 모두 잘 예측하였다. 그러나 CFD 결과에서는 간극이 증가할수록 토출계수가 감소한 후 다시 증가하는 경향을 확인하기 어려워, 경향성을 명확히 하기 위해 간극(S/Href) 0.167에 CFD 해석 점을 추가하였다.
Fig. 11(a)는 간극 0.083, 이빨 간격 0.917, 압력비 2.5, 회전 속도 7500 RPM에서 이빨 두께의 변화에 따른 토출계수의 변화를 나타내었다. 그리고 Fig. 11(b)는 간극 0.125, 이빨 간격 1, 압력비 2.3, 회전 속도 3500 RPM에서 이빨 두께의 변화에 따른 토출 계수의 변화를 표현하였다. 두 허니컴 셀 지름 모두 이빨 두께가 증가할수록 토출계수가 감소하는 경향을 확인하였다. 마찬가지로, 이러한 경향성을 인공신경망이 학습데이터와 new unseen data에서 모두 잘 예측할 수 있음을 확인하였다.
Fig. 12(a)는 간극 0.083, 이빨 두께 0.1, 압력비 2.5, 회전 속도 7500 RPM에서 이빨 간격의 변화에 따른 토출계수의 변화를 표현하였고, Fig. 12(b)는 간극 0.125, 이빨 두께 0.167, 압력비 2.3, 회전 속도 3500 RPM에서 토출계수의 변화를 나타내었다. 두 허니컴 셀 지름 모두 이빨 간격이 증가할수록 토출계수가 감소하는 경향을 보였다. 학습데이터와 new unseen data에서 모두 인공신경망이 이빨 간격에 따른 토출계수의 변화를 잘 예측한 것을 확인하였다. 위와 같은 결과들을 통해 인공신경망이 형상 변수의 변화에 따른 토출계수의 변화를 잘 예측할 수 있음을 확인하였다.
Fig. 13(a)는 간극 0.208, 이빨 두께 0.1417, 이빨 간격 1.042, 회전 속도 7500 RPM에서 압력비의 변화에 따른 토출계수의 변화를 나타내었고, Fig. 13(b)는 간극 0.125, 이빨 두께 0.167, 이빨 간격 1, 회전 속도 3500 RPM에서 압력비의 변화에 따른 토출계수의 변화를 표현하였다. 두 그래프에서 모두 압력비가 증가함에 따라 토출계수가 선형적으로 증가하는 경향을 보였다. 이러한 경향성을 인공신경망이 학습데이터와 new unseen data에서 모두 잘 예측하였으며, 압력비가 토출계수에 미치는 영향을 잘 예측할 수 있음을 확인하였다.
Fig. 14(a)는 간극 0.208, 이빨 두께 0.1417, 이빨 간격 1.042, 압력비 2.5에서 회전 속도의 변화에 따른 토출계수의 변화를 표현하였다. 그리고 Fig. 14(b)는 간극 0.125, 이빨 두께 0.167, 이빨 간격 1, 압력비 2.3에서 회전 속도의 변화에 따른 토출계수의 변화를 나타내었다. 두 그래프 모두 회전 속도가 증가함에 따라 토출계수가 감소하는 경향을 보였으며, 이를 인공신경망으로 예측하였다. 이러한 경향성을 학습데이터와 new unseen data에서 모두 잘 예측하였으며, 위와 같은 결과를 통해 인공신경망이 운전 조건의 영향을 잘 예측할 수 있음을 확인하였다.
Training data와 new unseen data의 결과에서 CFD와 인공신경망이 예측한 결과를 비교하여 인공신경망이 다양한 입력 변수들이 가지는 고유한 경향성을 잘 예측한 것을 확인하였다. 또한, 학습에 전혀 활용되지 않은 new unseen data와 결과 비교를 통해 인공신경망의 예측 데이터가 허니컴 래버린스 실의 성능을 예측하는데 실용성이 있음을 확인하였다.
4. 결 론
본 논문에서는 허니컴 래버린스 실의 형상 변수와 운전 조건의 영향을 모두 반영한 실의 성능을 예측하고자, CFD와 인공신경망을 활용한 성능 예측 방법을 연구하였다. 실험계획법을 통해 선정된 형상 케이스와 운전 조건을 조합하여 학습 변수를 선정하였으며, 이를 순방향 신경망으로 학습하였다. 또한, 순방향 신경망의 학습 성능과 일반화성능을 확인하고자 다양한 지표를 활용하였다.
1) 실험계획법을 활용하여 허니컴 래버린스 실의 해석 모델을 선정하였고, 이를 Pareto chart로 분석하여 변수들의 중요도를 확인하였다. 분석 결과 허니컴 셀 지름(D), 간극(S), 이빨 두께(b), 이빨 간격(P)이 주요 형상 변수이며, 이빨 높이(H)는 유의하지 않은 변수임을 확인하였다. 이러한 결과를 통해 선정된 형상 케이스와 운전 조건을 조합하여 학습데이터를 선정하였다. 임의의 범위 내에서 선정된 각 점들을 CFD로 해석하였고, 이를 활용하여 데이터베이스를 생성하였다. 그 다음, 인공신경망을 활용하여 데이터베이스를 학습하였고, 이를 통해 각 점들 사이의 결과를 예측하였다. 이러한 결과를 통해 인공신경망이 다양한 입력 변수를 수용할 수 있음을 확인하였다.
2) 인공신경망의 학습 성능과 일반화성능을 다양한 지표를 통해 확인하였다. Epochs 10에서 MSE가 0.003975로 우수한 학습 성능을 보였으며, 회귀 및 상관관계(R) 분석을 통해 인공신경망의 일반화성능을 평가하였다. 또한, CFD 결과와 인공신경망의 예측 결과를 비교하여, 인공신경망이 형상 변수와 운전 조건의 영향을 잘 예측한 것을 확인하였다. 학습 변수 비교 결과 MSE가 1.475 × 10-5, RMSE가 0.003841로 높은 예측 정확도를 보였다. 또한, 인공신경망을 통해 예측된 성능 데이터의 실용성을 확인하고자 training, validation, 그리고 test set에 활용되지 않은 new unseen data와 결과를 비교하였다. 비교 결과 MSE가 0.00021, RMSE가 0.01452로 높은 예측 정확도를 확인하였으며, 이를 통해 인공신경망을 통한 실의 성능 예측 데이터의 실용성을 확인하였다.
3) CFD와 인공신경망을 활용하여 효과적으로 허니컴 래버린스 실의 성능을 예측하였다. New unseen data를 예측하기 위해 CFD는 새로운 수치해석을 수행하였고, 인공신경망은 학습된 결과를 기반으로 new unseen data를 빠르게 예측하였다. 인공신경망의 학습데이터 생성에는 상당한 시간이 소요되었으나, 새로운 결과를 예측하는 데 소요되는 시간과 계산 비용을 절감할 수 있음을 확인하였다. 추후에는 이러한 특성을 활용하여 허니컴 래버린스 실의 형상을 개선하기 위한 연구를 수행할 계획이다.
Acknowledgments
본 연구는 2023년도 산업통산자원부의 한국산업기술평가원(KEIT)의 지원을 받아 수행한 연구과제입니다.(NO. 20002700)
References
- Zimmermann, H., A. Kammerer, and K. H. Wolff., 1944, “Performance of worn labyrinth seals,” ASME Turbo Expo, Power for Land, Sea and Air. Vol. 78835, pp. V001T01A042.
-
Michaud, M., Vakilli, A., Meganathan, A., Zielke, R., Shuster, L., and Terrell, J., 2003, “An experimental study of labyrinth seal flow,” International Joint Power Generation Conference, Vol. 36924, pp. 497~504.
[https://doi.org/10.1115/IJPGC2003-40097]

-
Oettinger, M., Kluge, T., and Seume, J., 2022, “Influence of honeycomb structures on straight-through labyrinth seal aerodynamics,” Journal of the Global Power and Propulsion Society, Vol. 6, pp. 290~303.
[https://doi.org/10.33737/jgpps/152697]

-
Vermes, G., 1961, “A fluid mechanics approach to the labyrinth seal leakage problem.”
[https://doi.org/10.1115/60-GTP-12]

- Martin, H. M., 1908, “Labyrinth packings,” Engineering Vol. 85, pp. 35.
-
Zimmermann, H, and K. H. Wolff., 1998, “Air system correlations: Part 1 – Labyrinth seals,” ASME Turbo Expo, Power for Land, Sea and Air, Vol. 78651, pp. V004T09A048.
[https://doi.org/10.1115/98-GT-206]

-
Hodkinson, B., 1939, “Estimation of the Leakage through a Labyrinth Gland,” Proceedings of the institution of Mechanical Engineers, Vol. 141, No. 1, pp. 283~288.
[https://doi.org/10.1243/PIME_PROC_1939_141_037_02]

-
Kim, T. S., Kang Y., and Moon H. K., 2009, “Aerodynamic performance of double-sided labyrinth seals,” Fluid Machinery and Fluid Mechanics: 4th International Symposium, Springer Berlin Heidelberg, pp. 377~382.
[https://doi.org/10.1007/978-3-540-89749-1_60]

-
Kim, T. S., and Cha, K. S., 2009, “Comparative analysis of the influence of labyrinth seal configuration on leakage behavior,” Journal of Mechanical Science and Technology Vol. 23. No. 10, pp. 2830~2838.
[https://doi.org/10.1007/s12206-009-0733-5]

-
Kim. T. S., and Kang. S. Y., 2010, “Investigation of leakage characteristics of straight and stepped labyrinth seals,” International Journal of Fluid Machinery and Systems, Vol. 3, No. 3, pp. 253~259.
[https://doi.org/10.5293/IJFMS.2010.3.3.253]

-
Hur, M. S., Lee, S. I., Moon, S. W., Kim, T. S., Kwak., J. S., Kim, D. H., and Jung, I. Y., 2020, Effect of clearance and cavity geometries on leakage performance of a stepped labyrinth seal. Processes,” Vol. 8, No. 11, pp. 1496.
[https://doi.org/10.3390/pr8111496]

-
Hur, M. S., Moon, S. W., and Kim, T. S., 2021, “A study on the leakage characteristics of a stepped labyrinth seal with a ribbed casing,” Energies, Vol. 14, No. 13, pp. 3719.
[https://doi.org/10.3390/en14133719]

-
Schramm, V., Willenborg, K., Kim, S., and Witting, S., 2002, “Influence of a honeycomb facing on the flow through a stepped labyrinth seal,” J. Eng. Gas Turbines Power, Vol. 124, No. 1, pp. 140~146.
[https://doi.org/10.1115/1.1403460]

-
Yan, X., Li, J., and Feng, Z., 2010, “Effect of inlet preswirl and cell diameter and depth on honeycomb seal characteristics,” Journal of engineering for gas turbines and power, Vol 132, No. 12, pp. 122506.
[https://doi.org/10.1115/1.4001296]

-
Nayak, K. C., and Dutta, P., 2016, “Numerical investigations for leakage and windage heating in straight-through labyrinth seals,” Journal of Engineering for Gas Turbines and Power, Vol. 138, No. 1, pp. 012507.
[https://doi.org/10.1115/1.4031343]

-
Jo, S. Y., Hur, M. S, Moon, S. W., and Kim, T. S., 2023, “Numerical study on the leakage characteristics of a stepped labyrinth seal with mixed honeycomb cell diameters,” Journal of Mechanical Science and Technology, Vol. 37, No. 1, pp. 465~475.
[https://doi.org/10.1007/s12206-022-1244-x]

-
Waschka, W., Wittig., and Kim, S., 1992, “Influence of high rotational speeds on the heat transfer and discharge coefficients in labyrinth seals,” pp. 462~468.
[https://doi.org/10.1115/1.2929166]

-
Paolillo, R., Moore, S., Cloud, D., and Glahn, J. A., 2007, “Impact of rotational speed on the discharge characteristic of stepped labyrinth seals.” Turbo Expo, Power for Land, Sea, and Air, Vol. 47394, pp. 1291~1298.
[https://doi.org/10.1115/GT2007-28248]

-
Nayak, K. C., 2020, “Effect of rotation on leakage and windage heating in labyrinth seals with honeycomb lands,” Journal of Engineering for Gas Turbines and Power, Vol. 142, No. 8.
[https://doi.org/10.1115/1.4047180]

-
Pychynski, T., Dullenkopf, K., Bauer, H. J. R., and Mikut, R., 2010, “Modeling The Labyrinth Seal Discharge Coefficient Using Data Mining Methods,” Turbo Expo, Power for Land, Sea, and Air, Vol. 43994, pp. 1013~1023.
[https://doi.org/10.1115/GT2010-22661]

-
Rulik, S., Wròblewski, W., and Fraczek, D., 2017, “Metamodel-based optimization of the labyrinth seal,” Archive of Mechanical Engineering, Vol. 64, No. 1.
[https://doi.org/10.1515/meceng-2017-0005]

- Minitab, Getting Started with Minitab Statistical Software (Minitab, 2022).
- ANSYS Inc, ANSYS ICEM 2020R2, (2019).
- ANSYS Inc, ANSYS CFX 2020R2, (2019).
- The Math Works, Inc. MATLAB. Version 2020a.
-
Selimfendigil, F., and Öztop,H. F., 2021, “Thermoelectric generation in bifurcating channels and efficient modeling by using hybrid CFD and artificial neural networks,” Renewable Energy, Vol. 172, pp. 582~598.
[https://doi.org/10.1016/j.renene.2021.03.046]

-
Lira, J. O., Riella, H. G., Padoin, N., and Soares, C., 2022, “Computational fluid dynamics (CFD), artificial neural network (ANN) and genetic algorithm (GA) as a hybrid method for the analysis and optimization of micro-photocatalytic reactors: NOx abatement as a case study,” Chemical Engineering Journal, Vol. 431, pp. 133771.
[https://doi.org/10.1016/j.cej.2021.133771]

-
Levenberg, K., 1944, “A method for the solution of certain non-linear problems in least squares. Quarterly of applied mathematics,” Vol. 2, No. 2, pp. 164~168.
[https://doi.org/10.1090/qam/10666]

-
Marquardt, D. W., 1963, “An algorithm for least-squares estimation of nonlinear parameters,” Journal of the society for Industrial and Applied Mathematics, Vol. 11, No. 2, pp. 431~441.
[https://doi.org/10.1137/0111030]

-
Lenth, R. V., 1989, “Quick and easy analysis of unreplicated factorials,” Technometrics, Vol. 31, No. 4, pp. 469~473.
[https://doi.org/10.1080/00401706.1989.10488595]

- Hur, M. S., W., Kim, T. S., Kim, D. H., and Jung, I. Y., 2022, “A numerical investigation of leakage characteristics of the rotating labyrinth seal with solid and honeycomb lands,” Asian Congress on Gas Turbines 2022. Korean Society for Fluid Machinery, GT-2022-0082.