난류모델에 따른 SMART BLADE 공력 특성 연구

1. 서 론

지난 수십년 동안 풍력에너지는 화석 연료로 인한 기후 변화를 억제하기 위한 대체 에너지 자원으로 큰 관심을 받고 있다. 전 세계 풍력에너지의 누적 용량은 2001년 23.9 GW에서 2022 년 906 GW로 약 38 배의 증가율을 달성했으며, 세계적으로 유망한 지속 가능한 에너지 시스템 중 하나로 수요가 많다. 유체 행동의 이해, 복합재 및 블레이드 설계 기술의 향상으로 LCOE(Levelized Cost of Energy)의 감소로 인해 2030년까지 풍력에너지의 전체 누적 용량은 최대 1787 GW에 이를 것으로 예상된다.^(1-4)

풍력발전기는 일반적으로 로터 블레이드. 나셀 및 타워와 같은 세 가지 주요 구성 요소로 구성된다. 로터 블레이드는 풍력에너지를 효율적으로 수집하는 역할을 수행하며, 블레이드의 공력 특성은 풍력발전기 전체 성능에 큰 영향을 미친다. 최근의 풍력발전기는 블레이드의 길이를 증가시켜 보다 많은 AEP(Annual Energy Production) 확보를 통해 사업성을 향상시키고자 한다.⁽⁵⁾ 풍력발전기의 공력 특성 연구 방법은 풍동 실험, 수치 해석 등으로 나눠진다. 풍동 실험 결과의 경우 신뢰도가 크나 실험적, 기술적 조건에 의해 제한되며 비용과 시간이 많이 소모된다. 이로 인해, 연구자들은 CFD 등의 수치해석기법을 통해 공력 특성 연구를 수행하고 있다. 또한 최근에는 계산 능력 및 CFD 기술의 발전에 의해, 대형화된 풍력발전기 블레이드의 공력 특성 연구에서 중요한 부분이 되고 있다.^(6-8) 다만, CFD 해석은 난류 모델, 경계 조건 등에 따라 결과의 차이가 발생할 수 있으므로, 난류 모델과 레이놀즈 수에 따른 특성 연구가 필요하다.⁽⁹⁾

Sorensen⁽¹⁰⁾ 등은 RANS SST k-ω 난류 모델을 사용하여 풍력발전기의 운영 조건에 따른 공력 특성 연구를 수행했다. Kody⁽¹¹⁾ 등은 3D 블레이드를 대상으로 S-A 난류 모델과 k-ω 난류 모델을 사용하여 가장 적합한 난류 모델을 조사하고, 블레이드의 다양한 위치에서 압력 계수를 비교하였다. CFD를 활용한 풍력발전기 블레이드 대상 공력 특성 연구는 참고 문헌^(12-18)에서 더 확인할 수 있다.

현재까지 와류 중심 가시화 기법을 이용한 풍력발전기 블레이드에 대한 연구는 수행된 바가 없다. 따라서 본 논문에서는 와류 식별 기법을 적용하여 블레이드에 발생하는 3차원 와류 형상을 난류 모델 변화에 따라 비교하였다. 풍력발전기 블레이드의 공력 특성을 다양한 난류 모델에서 비교 분석하기 위해 유한 체적법에 근거한 CFD 해석 소프트웨어 ANSYS CFX⁽¹⁹⁾ 2021 R1을 활용하여 RANS 기반 3차원 CFD 해석을 수행하였다. 또한 레이놀즈수 변화에 따른 공력 특성 비교를 위해 다양한 운영 조건에 대해서 연구를 수행했다.

2. 수치해석 방법론

2.1 해석 대상

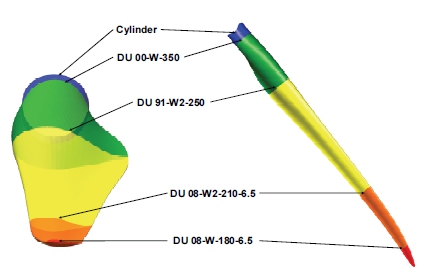
본 연구에서는 SMART BLADES 및 SMART BLADES 2 프로젝트^(20,21)(두 프로젝트는 독일 연방경제부의 지원을 받았다.(펀딩 번호:0325601, 0324032))에서 개발한 20 m 길이의 로터 블레이드를 연구 대상으로 선정했다. 블레이드의 3차원 형상은 아래에 제시된 Fig. 1과 같으며, 제원은 Table 1과 같다. 블레이드에 적용된 익형은 DU 00-W-350, DU 91-W2-250, DU 08-W2-210, DU-08-W2-180로 블레이드 루트에서 끝단까지 순차적으로 배치되었다.

Fig. 1

3-D shape of the blade

Table 1

Blade design specification

2.2 난류 모델

난류 유동의 수치해석기법은 일반적으로 DNS(Direct Numerical Simulation), LES(Large Eddy Simulation), RANS의 3 가지 종류로 나눌 수 있다.⁽²²⁾ DNS는 크고 작은 다양한 스케일(scale)의 와류가 혼재하는 난류 유동장에서 전체 완류의 거동을 정확히 해상하기 위해서는, 계산 격자 크기를 와류구조의 최소 공간스케일이하로 하면서, 시간간격을 와류 변동의 최소시간 스케일이하로 할 필요가 있다. 이것에 비해 LES에서는 공간적으로 평균화된 Navier-Stokes방정식을 계산하는 것으로, 격자스케일보다 큰 와류는 직접계산하고 작은 와류는 SGS모델에 의해 계산하게 된다. 하지만, DNS와 LES는 와류 해상을 위해, 방대한 계산 자원을 필요로 하여, 공학적인 실용문제 적용에 있어, 불가능하다.

이에 비해, RANS는 시간적으로 앙상블 평균화된 Navier-Stokes 방정식을 계산하며, 난류의 모든 영향을 모델링한다. RANS는 DNS나 LES와 비교할 때, 유동장의 해상도는 낮지만, 고해상도 계산격자가 필요하지 않기 때문에 엔지니어링 실무적인 관점에서 가장 많이 적용된다.

본 연구에서는 RANS 수치해석에서 블레이드 공력 성능을 예측할 때 주로 사용되는 3종류의 난류 모델을 비교 분석하였다. 그 중 1-방정식 난류 모델인 S-A 모델은 1992년 Spalart와 Allmaras^[23]에 의해 개발되었으며, 난류 점성을 단일 수송방정식으로 표현하여 계산 효율이 뛰어나고, 항공우주공학 분야에서 성공적으로 적용되고 있다. S-A 모델의 수송 방정식과 에디 점성계수의 식은 식 (1)과 같다.

$\[ \begin{array}{l}\frac{\partial \left(\rho \tilde{\nu }\right)}{\partial t}+div\left(\rho \tilde{\nu }U\right)=\frac{1}{{\sigma }_{\nu }}div\left[\left(\mu +\rho \tilde{\nu }\right)grad\left(\tilde{\nu }\right)+C_{b2}\rho \frac{\partial \tilde{\nu }}{\partial x_k}\frac{\partial \tilde{\nu }}{\partial x_k}\right]\\ +C_{b1}\rho \tilde{\nu }\widetilde{ohm}-C_{w1}\rho {\left(\frac{\tilde{\nu }}{\kappa y}\right)}^2{f}_w\\ {\mu }_t=\rho \stackrel{-}{\nu }{f}_{\nu 1}\end{array} \]$

(1)

여기에서 ρ는 밀도, $$ \tilde{\nu }$$는 에디 동점성계수, U는 평균 풍속, $$ \tilde{\mathrm{\Omega }}$$는 국소 평균 와도, κy는 길이 스케일이며, f_w와 f_v1은 벽-감쇠 함수이다.

Standard k-ω 모델은 Daly와 Harlow⁽²⁴⁾가 2-방정식 난류 모델을 제안한 이후로 Wilcox⁽²⁵⁾에 의해 개발되었다. 이 모델은 역 압력구배에 대한 예측 정확도가 높지만, 외부 유동에 대한 민감도가 높은 단점이 있다. Standard k-ω 모델의 수송 방정식과 에디 점성계수 식은 식 (2)와 같다.

$\[ \begin{array}{l}\frac{\partial \left(\rho k\right)}{\partial t}+div\left(\rho kU\right)=div\left[(\mu +\frac{{\mu }_t}{{\sigma }_k}) grad\left(k\right)\right]+P_k-{\beta }^{*}\rho k\omega \\ \frac{\partial \left(\rho \omega \right)}{\partial t}+div\left(\rho \omega U\right)=div\left[(\mu +\frac{{\mu }_t}{{\sigma }_{\omega }}) grad\left(\omega \right)\right]\\ \begin{array}{c}+{\gamma }_1\left(2\rho S_{ij}\cdot S_{ij}-\frac{2}{3}\rho \omega \frac{\partial U_i}{\partial x_j}{\delta }_{ij}\right)\\ -{\beta }_1\rho {\omega }^2\\ {\mu }_t=\rho k/\omega \end{array}\end{array} \]$

(2)

여기에서 k는 난류 운동에너지, P_k는 난류 운동 에너지 생성항, ω는 난류 비 소산률이다.

외부 유동에 대한 예측 정확도 개선을 위해 Menter⁽²⁶⁾는 standard k-ε과 standard k-ω 모델의 장점을 결합한 SST k-ω 모델을 제안했다. 이 모델은 자동 벽 처리법을 도입하여 벽면에 인접한 영역에서는 k-ω 모델을 적용하고, 자유 흐름 영역에서는 k-ε 모델을 적용한다. 이를 통해 외부 유동에 대한 안정성을 확보하고 역 압력구배에 의한 재순환 영역 크기 및 박리지점을 비교적 정확하게 예측하는 것으로 알려져 있다. SST k-ω 모델의 수송 방정식과 에디 점성계수 식은 식 (3)과 같다.

$\[ \begin{array}{l}\frac{\partial \left(\rho k\right)}{\partial t}+div\left(\rho kU\right)=div\left[(\mu +\frac{{\mu }_t}{{\sigma }_k}) grad\left(k\right)\right]+P_k-{\beta }^{*}\rho k\omega \\ \frac{\partial \left(\rho \omega \right)}{\partial t}+div\left(\rho \omega U\right)=div\left[(\mu +\frac{{\mu }_t}{{\sigma }_{\omega , 1}}) grad\left(\omega \right)\right]\\ \begin{array}{c}+{\gamma }_2\left(2\rho S_{ij}\cdot S_{ij}-\frac{2}{3}\rho \omega \frac{\partial U_i}{\partial x_j}{\delta }_{ij}\right)\\ -{\beta }_2\rho {\omega }^2+2\frac{\rho }{{\sigma }_{\omega ,2}\omega }\frac{\partial k}{\partial x_k}\frac{\partial \omega }{\partial x_k}\\ {\mu }_t=\frac{a_1\rho k}{\mathrm{m}\mathrm{a}\mathrm{x}\left(a_1\omega ,S{F}_2\right)}\end{array}\end{array} \]$

(3)

여기에서 F₂는 혼성함수이며, k-방정식은 Wilcox의 standard k-ω 모델과 동일하지만, ε-방정식은 ϵ=kω의 치환으로 ω-방정식으로 변환된다. 따라서 식 (2)와 비교하면 식 (3)은 우변에 추가적인 항을 가지며 이는 ε-방정식에서 확산 항의 ϵ=kω 변환에 따른 횡-확산(cross-diffusion) 항이다.

이들 난류모델들은 유동장을 완전난류(fully turbulent)로 가정하므로, 층류 경계층에서의 유동박리가 난류 경계층에서의 유동박리보다 빠르게 진행되어, 천이 현상을 정확히 해상하지 못하는 한계가 있다.⁽²⁷⁾ 이러한 결과는 실제 실험 결과와 차이를 발생시키는 중요한 원인이 된다.

본 연구에서는 SMART BLADE 프로젝트에서 개발한 블레이드를 대상으로 하여 S-A, standard k-ω, SST k-ω 모델을 적용하여 난류 모델에 따른 공력 특성을 비교하였다. 또한 레이놀즈 수에 따른 공력 특성을 비교하기 위해 Table 2와 같이 정격 출력 속도 12.5 m/s 이하의 5가지 조건에서 연구를 수행하였다. 이 연구에서는 프라운호퍼에서 수행한 실험기반의 FAST⁽²⁸⁾ 해석 결과를 기준값으로 삼아 CFD 해석결과의 신뢰성 검증 및 난류 모델에 따른 공력 특성 비교를 실시하였다.⁽²⁹⁾ 수렴판정은 RMS 오차가 10^-7 이하인 조건을 1차 수렴 상태로 설정하였으며, 이후 주기적인 블레이드 축 출력(Shaft Power)의 발생을 확인하여 수렴을 판단하였다.

Table 2

Simulated cases - overview

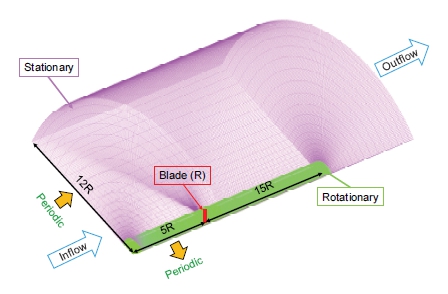
Fig. 2는 블레이드 계산 영역을 나타낸다. 계산 영역은 로터 블레이드로부터 유입방향으로 로터 반경의 5배, 후류방향으로는 로터 반경의 15배, 반경 방향으로는 로터 반경의 12배의 공간 해상도를 확보하였다. 본 계산에서 블레이드 표면은 점착조건 (no-slip condition), 입구에서는 자유류 (free-stream) 조건을 적용하였으며, 3개의 블레이드 중 1개의 블레이드에 해당하는 120° 주기적 경계조건 (periodic boundary condition)을 적용하여 Fig. 2와 같이 단일 블레이드의 유동장을 모사하였다. 고정밀도로 풍력발전기 블레이드의 공력 특성을 분석하기 위해, 정렬 격자로 전체 격자계를 구성하였다. 블레이드 벽면 경계층 내부 유동의 정확한 모사를 위해, 모든 계산 격자의 y+가 5 이하가 되도록 설정하였고, SST k-ω 난류 모델을 활용하여 유입 풍속 10 m/s 조건에서 격자 의존성 검토를 수행하여 계산 격자의 신뢰성 및 계산 효율성을 향상시켰다. Table 3에 나타낸 격자 의존성 검토 결과를 바탕으로, 프라운호퍼 FAST 결과 대비 축 출력의 상대 오차율이 10% 미만이 되도록 조정하였다. 해석은 총 1.0 x 10⁷개의 격자로 수행되었으며, Blade region에 4.6 x 10⁶개와 그 외 5.4 x 10⁶개(rotationary region : 4.4 x 10⁶ + stationary region : 1.0 x 10⁶)로 구성되었다.

Fig. 2

Blade analysis grid

Table 3

Mesh convergence test at 10 m/s wind speed

2.3 와류 식별 기법

1995년 Sawada가 개발한 와류 식별 방법⁽³⁰⁾을 사용하여 블레이드 팁과 허브 근방에서 발생하는 와류 구조를 특이점 이론, 와류 구조의 확률적 정의, 전산 유체 해석 결과를 이용하여 시각화하였다. 또한 시각화된 와류 중심에 정규화된 helicity로 색을 입혀 와류의 회전 방향을 시각화하였다. 정규화된 helicity는 식 (4)에 의해 정의되었다.

$\[ H_n=\overrightarrow{\zeta }\cdot \overrightarrow{\omega }/\left(\right|\overrightarrow{\zeta }|\cdot |\overrightarrow{\omega }\left|\right) \]$

(4)

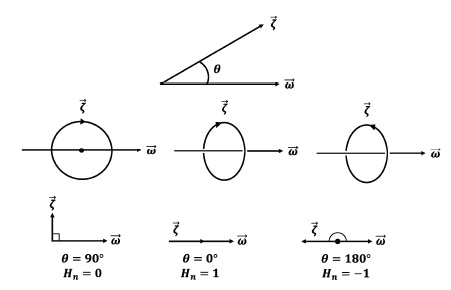
여기에서 H_n은 정규화된 helicity이고, ζ는 절대 와류 벡터, ω는 상대 속도 벡터이다. Fig. 3은 정규화된 helicity 변화에 따른 회전 방향을 나타낸다. H_n은 다음과 같은 물리적 의미를 갖는다. H_n>0이라면, 와류가 오른손의 법칙에 따라 축 방향으로 회전하며 이동한다는 의미이다. H_n=0은 와류가 정체 및 회전 상태에 있음을 의미하며, H_n<0은 와류가 오른손 법칙에 따라 회전하며 축 방향의 반대 방향으로 이동한다는 것을 의미한다.

Fig. 3

Rotation direction according to normalized helicity

3. 결과 및 고찰

3.1 축 출력 예측 및 블레이드 표면 유선 비교

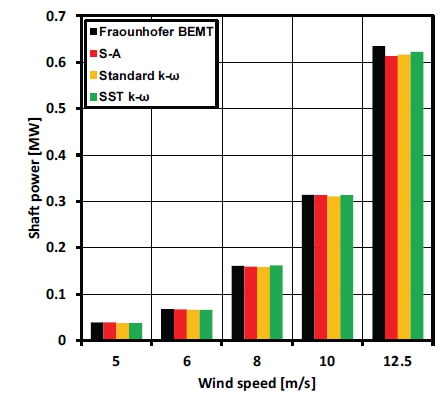
Fig. 4는 프라운호퍼의 FAST 해석 결과와 CFD 해석결과의 축 출력 비교 결과를 보여준다. 유입 풍속 10 m/s 이하에서는 모든 난류 모델이 프라운호퍼의 FAST 해석 결과에 근접한 결과를 나타내었다. 하지만 유입 풍속 12.5 m/s에서는 블레이드 루트부에서 발달하는 3차원 재부착 영역의 발생으로 인해 각 난류모델이 박리영역과 재부착 영역의 크기를 예측하는데 차이가 발생하였다. SST k-ω 모델은 유입 풍속 12.5 m/s에서 다른 난류 모델보다 축 출력 상대 오차율이 낮은 것을 확인할 수 있다.

Fig. 4

Comparison of shaft power

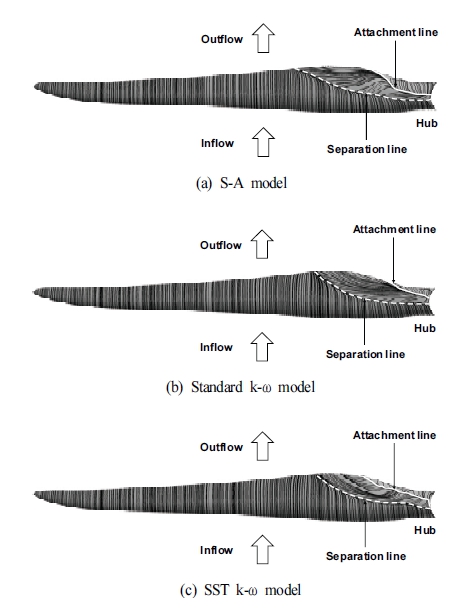
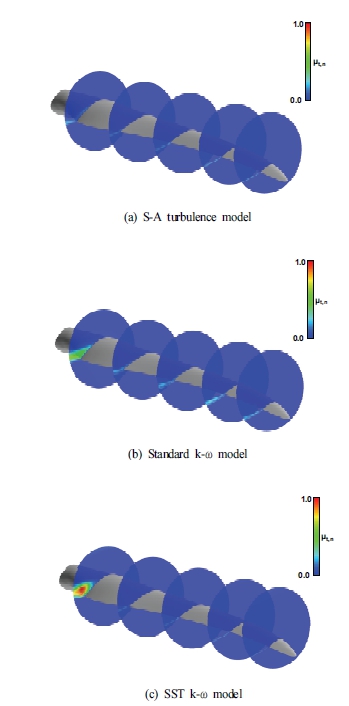
본 연구에서는 난류 모델에 따른 블레이드 루트부에서 발달하는 박리영역과 재부착 영역의 크기를 유입 풍속 12.5 m/s에서 분석하였다. 이를 위해 블레이드 흡입면 (suction surface)에서 형성되는 표면 유선을 Fig. 5에 나타내었다. Fig. 5(a)는 S-A 모델을 적용한 해석 결과이며, Fig. 5(b)와 (c)는 각각 standard k-ω, SST k-ω 모델을 적용한 해석결과이다. Fig. 5를 통해 블레이드 허브 근방에서 허브로부터 팁 반경방향으로 스팬 약 40%인 8 m에 걸쳐 박리 영역이 형성됨을 알 수 있다. 박리 영역에 걸친 표면 유선을 통해 허브로부터 팁 반경방향으로 경계층의 2차 흐름 (secondary flow)이 발생함을 알 수 있다. 이러한 2차 흐름은 블레이드 표면에서 발생하는 저 에너지 (low energy) 상태의 경계층이 원심력 (centrifugal force), 코리올리력 (Coriolis force), 스팬 방향으로 형성된 압력차에 의해 허브로부터 팁 반경방향으로 발달한다.

Fig. 5

Surface streamlines on the suction surface of the blade at wind speed 12.5 m/s

Fig. 5에서 확인할 수 있듯이 S-A 모델이 가장 큰 박리 영역을 예측한 반면, SST k-ω 모델이 가장 작은 박리 영역을 예측하였다. 유입 풍속 12.5 m/s 조건에서, 각각의 모델이 예측한 결과는 서로 다른 특징을 보이며, 특히 SST k-ω 모델은 박리 영역이 더 작은 영역에 걸쳐 형성되었으며, 다른 두 모델의 결과에 비해 더 큰 출력을 예측하였다.

3.2 블레이드 표면 압력 계수 비교

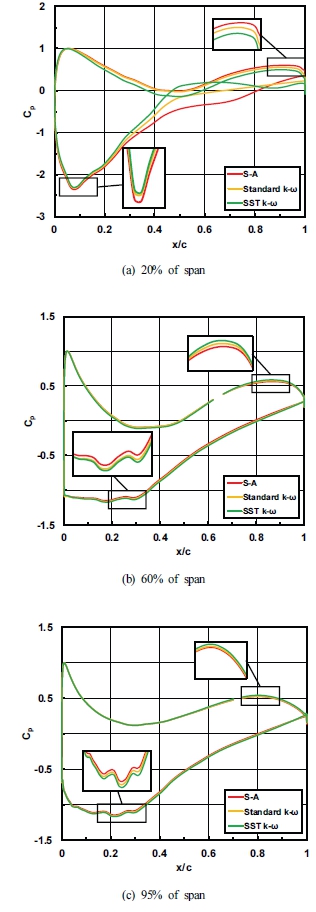
유입 풍속 12.5 m/s일 때 블레이드 스팬위치가 각각 20%, 60%, 95% 지점에서의 표면 압력계수를 Fig. 6 에 나타내었다. 압력계수는 다음과 같이 정의된다.

$\[ C_p=\frac{P-P_{\infty }}{0.5{\rho }_{\infty }\left(U_{\infty }^2+\left(r{\omega }^2\right)\right)} \]$

(5)

Fig. 6

Comparison of pressure coefficient of numerical simulation results as inlet wind speed 12.5 m/s

여기서 P_∞, U_∞는 자유류의 정압과 풍속, r은 해당 스팬위치에 대한 로터 반경방향의 거리, ω는 로터의 회전 각속도를 나타낸다.

Fig. 6을 통해 흡입면 및 압력면에서 x/chord=0.5 위치를 기준으로 층류박리가 발생하고 있으며, 그 후 난류 재부착이 발생함에 따라 압력이 급격히 상승함을 알 수 있다. SST k-ω 모델의 경우 다른 두 개의 난류모델에 비해 층류박리 및 재부착 지점의 비교적 정확한 예측을 하는 것으로 사료된다.

블레이드 루트부(Fig. 6(a))에서는 회전 속도가 상대적으로 낮기 때문에 모든 난류 모델의 호환성이 좋아 보인다. 그러나 블레이드 단면의 앞전(leading edge)과 뒷전(trailing edge)에서 결과를 자세히 평가하면 난류 모델 간의 차이가 더 명확해진다. Fig. 6(a)를 통해 S-A 모델의 예측 결과가 다른 두 난류 모델의 결과에 비해 다소 과대 예측되었으며, 특히 뒷전에서 SST k-ω 난류 모델에 비해 약 26% 과대 예측함을 확인하였다. 그러나 블레이드 중간 위치(Fig. 6(b))와 블레이드 팁(Fig. 6(c))에서 S-A 모델이 다른 두 난류 모델에 비해 약 4% 과소 예측하는 것을 확인할 수 있다. 이는 계산 결과를 통해 모든 난류 모델이 압력면(pressure surface)에 대한 압력 계수 예측 기능이 유사한 것으로 확인되지만, 흡입면에 대해서는 다소 차이를 나타내고 있다. 이는 난류를 일으키는 흡입면에서 발생하는 흐름의 분리에 의해 난류 모델에 따라 예측 정확도가 영향을 받는 것으로 사료된다.

3.3 블레이드 3차원 와류 형상 비교

유입 풍속 12.5 m/s일 때 블레이드 팁 근방 흡입면 및 허브 근방에서 발생하는 3차원 와류를 나타내는 유선과 와류 근방 와도의 세기 분포를 각각 Fig. 7, 8에 나타내었다.

Fig. 7

Vortex flow structure near the tip at wind speed 12.5 m/s

Fig. 8

Vortex flow structure near the hub at wind speed 12.5 m/s

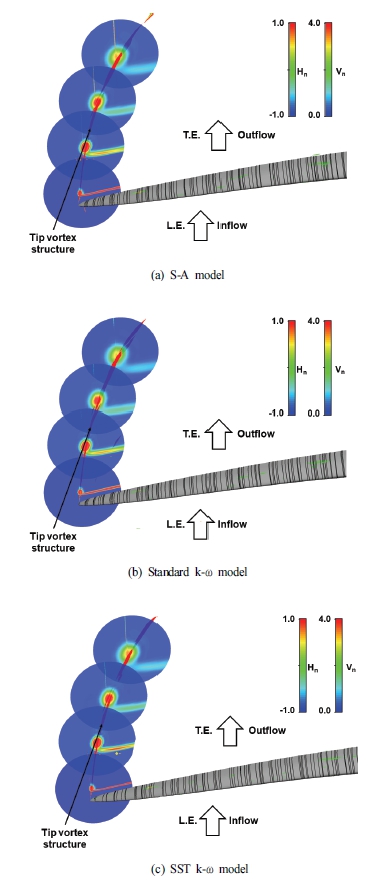
Fig. 7에서 빨간색 유선은 블레이드 팁 흡입면 앞전에서 발달한 와류 중심(vortex core)을 지나는 유선을 나타낸다. 그리고 Fig. 7에서 블레이드 팁 뒷전보다 하류 위치에서 와도의 세기 분포 및 블레이드 표면 유선을 나타내고 있다. 일반적으로 블레이드 팁 와류는 블레이드 팁의 코드(chord) 방향으로 블레이드 로딩이 가장 큰 코드위치에서 발생된다.⁽³¹⁾

Fig. 7(a)와 Fig. 7(b), Fig. 7(c)의 블레이드 팁 와류의 와도 세기를 비교하면, Fig. 7(b)의 높은 와도 영역이 Fig. 7(a), (c)의 높은 와도 영역에 비해 좁은 것을 알 수 있다.

이는 Fig. 7(b)가 Fig. 7(a), (c)보다 와류 중심을 형성하는 블레이드 팁 전연의 박리(빨간 유선)를 과소 예측하기 때문이다.

Fig. 7을 통해 모든 난류 모델이 블레이드 팁 근방 흡입면에서 발생하는 3차원 와류에 대한 예측 기능이 유사한 것으로 확인되지만, 와도 영역 예측에 있어 S-A 모델과 SST k-ω 모델이 팁 전연의 박리 예측에 있어 standard k-ω 모델에 비해 우수한 성능을 보였다. Standard k-ω 모델의 경우, 경계층 내부와 외부의 난류 특성 차이로 인해 경계층 외부의 난류 현상을 정확하게 예측할 수 없다. 하지만 S-A 모델은 경계층 외부의 난류 현상을 효과적으로 모델링 할 수 있으며, SST k-ω 모델은 standard k-ω의 이러한 한계를 극복하기 위해 경계층 외부의 난류 현상을 k-ε 모델을 활용하여 모사하기에 블레이드 팁 근방의 3차원 와류 예측 기능이 우수한 것으로 판단된다.

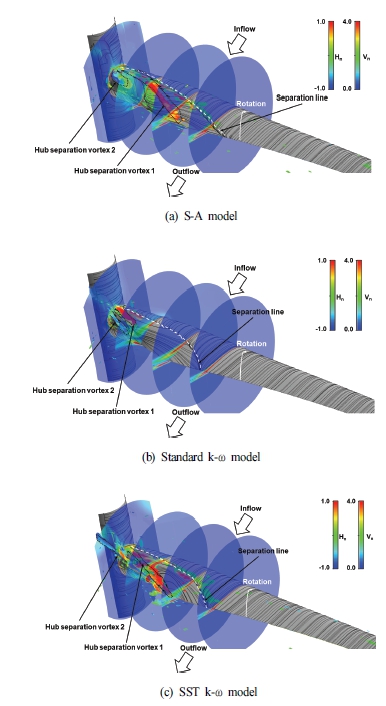
Fig. 8은 블레이드 허브 근방에서 와류를 나타내는 유선과 와류 근방의 와도의 세기 분포를 나타낸다. Fig. 8의 빨간색 유선은 블레이드 흡입면에서 발달한 경계층의 박리에 의해 형성된 와류를 나타내며, 파란색 유선은 블레이드 압력면에서 발달한 경계층의 박리에 의해 형성된 와류를 나타낸다. Fig. 8에서 빨간색과 파란색 유선으로 나타낸 와류의 중심은 허브에서 시작되며, 허브로부터 팁 반경방향으로 발달함을 알 수 있다. Fig 8을 통해 블레이드 허브 근방의 와류 예측에 있어 SST k-ω 모델이 다른 난류 모델에 비해 블레이드 압력면에서 발달한 경계층의 모사 능력이 우수하여 와류의 규모 예측 성능이 우수한 것으로 사료된다.

3.4 Eddy viscosity 비교

유입 풍속 12.5 m/s일 때 블레이드 스팬위치가 각각 20%, 40%, 60%, 80%, 95% 지점에서의 eddy viscosity를 정규화(Normalization)하여 Fig. 9에 나타내었다. 정규화된 eddy viscosity는 다음과 같이 정의된다.

$\[ {\mu }_{t,n}=\frac{{\mu }_t-{\mu }_{t,\mathrm{m}\mathrm{i}\mathrm{n}}}{{\mu }_{t,\mathrm{ }\mathrm{m}\mathrm{a}\mathrm{x} }-{\mu }_{t, \mathrm{m}\mathrm{i}\mathrm{n}\mathrm{ }}} \]$

(6)

Fig. 9

Comparison of eddy viscosity at wind speed 12.5 m/s

Eddy viscosity는 난류 운동 에너지 전달을 특성화하는 난류 모델의 핵심 매개변수이다. RANS 난류 모델에서 확산 항과 소산 항은 eddy viscosity를 예측하는데 기여한다. S-A 난류 모델에서 소산 항은 난류 운동 에너지와 그 소산율에 대한 추가 수송 방정식을 사용하여 모델링된다. Standard k-ω 모델의 확산 항과 소산 항은 모두 특정 난류 소산율에 영향을 받으며, SST k-ω 모델에서는 난류 운동 에너지와 그 소산율에 대한 운송 방정식을 풀어서 eddy viscosity를 결정한다. SST k-ω 모델은 경계층 효과를 설명하는 turbulent viscosity에 대한 추가 방정식을 포함하는 standard k-ω 모델의 수정된 버전으로 k-ω 모델과 k-ε 모델의 혼합 기능을 활용하여 외부 영역의 정확한 예측 및 난류 흐름의 벽 근처 유동을 정확하게 모사할 수 있다. 일반적으로 S-A 모델과 standard k-ω 모델은 유동 분리와 같은 복잡한 유동 현상을 포착하는데 한계가 있으며, SST k-ω 모델은 두 모델에 비해 정확하게 모사하는 것으로 간주된다. Fig 9를 통해 SST k-ω 모델이 eddy viscosity의 예측 성능이 우수한 것으로 확인되었다. 이는 2.2절에 서술한 바와 같이 SST k-ω 모델의 수송방정식에는 S-A, standard k-ω 모델과는 달리 추가적인 횡-확산항이 포함되어 있어 난류확산에 의한 eddy viscosity 예측 정확도가 높은 것으로 사료된다.

4. 결 론

본 연구에서는 SMART BLADES 및 SMART BLADES 2 프로젝트에서 개발한 20m 길이의 로터 블레이드를 대상으로 CFD 해석을 수행하였으며 다음과 같이 요약할 수 있다.

CFD 해석결과, 풍력발전기의 정격출력 속도 이전의 저풍속 조건에서 모든 난류 모델이 비교적 정확한 공력 특성 예측을 보여주지만, 정격출력 풍속 조건의 경우 SST k-ω 난류 모델이 블레이드 공력 특성 예측에 있어 우수한 성능을 보였다. S-A 난류 모델과 Standard k-ω 난류 모델은 정격출력 풍속 조건의 경우 블레이드 허브 근방의 유동 박리지점 및 재순환 영역의 크기 과대 예측으로 공력성능이 낮게 예측하는 특징을 보였다. 따라서 정격출력 풍속 조건에서는 블레이드 3차원 와류 구조 및 eddy viscosity 비교를 통해 경계층 내, 외부의 난류 현상을 정확히 모사하는 SST k-ω 난류 모델을 적용하는 것이 블레이드 공력성능예측에 유리할 것으로 판단된다.

후속 연구에서는 본 연구에서 수행한 공력 해석 결과와 프라운호퍼에서 수행한 정적 하중 시험 결과를 활용하여 유체-구조 연성해석 기법을 적용하여 블레이드 변형으로 인한 공력 특성 영향 분석 및 이에 따른 블레이드 구조건전성 평가를 수행하고자 한다.

Acknowledgments

이 논문은 2022년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원(20223030020070, 풍력발전용 블레이드 피뢰시스템 유지보수를 위한 X-ray기반 비파괴검사플랫폼 개발)과 2023년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임.(P0020612, 2023년 산업혁신인재성장지원사업)

References

• Global Wind Energy Council, “Global Wind Statics 2011”; GWEC: Brussels, Belgium, 2012.
• IRENA, “Future of Wind: Deployment, Investment, Technology, Grid Integration, Socia-Economic Aspects; IRENA”: Abu Dhabi, UAE, 2019; ISBN 978-92-9260-155-3.
• Konstantinidis, E.I.; Botsaris, P.N., “Wind Turbines: Current status, obstacles, trends, and technologies”, In IOP Conference Series: Materials Science and Engineering, Proceedings of the 20th Innovative Manufacturing Engineering and Energy Conference (IManEE 2016), Kozani, Greece, 23–25 September 2016; IOP Publishing: Bristol, UK, 2016.
• Stevens, R.J.; Meneveau, C., “Flow Structure and Turbulence in Wind Farms”, Annu. Rev. Fluid Mech. 2017, 49, 311–339. [https://doi.org/10.1146/annurev-fluid-010816-060206]
• Schubel, P.J.; Crossley, R.J., “Wind Turbine Blade Design: Review”, Energies 2012, 5, 3425–3449. [https://doi.org/10.3390/en5093425]
• Lin, L., “BEMT and CFD-Based Unsteady Aerodynamic Analyses of Floating Offshore Wind Turbine”, Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2016.
• Bangga, G.; Lutz, T.; Jost, E.; Kramer, E., “CFD studies on rotational augmentation at the inboard sections of a 10MW wind turbine rotor”, J. Renew. Sustain. Energy 2017, 9, 023304. [https://doi.org/10.1063/1.4978681]
• Jeong, J.; Kim, S., “CFD investigation on the flatback airfoil effect of 10 MW wind turbine blade”, J. Mech. Sci. Technol. 2018, 32, 2089–2097. [https://doi.org/10.1007/s12206-018-0418-z]
• Montazeri, H.; Montazeri, F., “CFD simulation of cross-ventilation in buildings using rooftop wind-catchers: Impact of outlet openings. Renew”, Energy 2018, 118, 502–520. [https://doi.org/10.1016/j.renene.2017.11.032]
• N. Sørensen, F. Zahle, K. Boorsma, G. Schepers, “Cfd computations, in: Proceedings of the Second Round of Mexico Rotor Measurements”, Journal of Physics: Conference series 753, 2016, 022054-1-10. [https://doi.org/10.1088/1742-6596/753/2/022054]
• Soyadı, Yazar & Alpman, Emre & Yilmaz, Baris & Kody, Sebit. (2014)., “Computational Studies of Horizontal Axis Wind Turbines Using Advanced Turbulence Models”, MARMARA UNIVERSITY JOURNAL OF SCIENCE. 2. 36-36. 10.7240/MJS.2014266488. [https://doi.org/10.7240/MJS.2014266488]
• N. Mandas, F. Cambuli, C. E. Carcangiu, “Numerical prediction of horizontal axis wind turbine flow, in: Proceedings of European Wind Energy Conference and Exhibition, Athens, Greece, 2006.
• D. Hu, O. Hua, Z. Du, “A study on stall-delay for horizontal axis wind turbine, Renew.”, Energy 31 (2006) 821–836. [https://doi.org/10.1016/j.renene.2005.05.002]
• T. Fletcher, R. Brown, D. Kim, O.J. Kwon, “Predicting wind turbine blade loads using vorticity transport and rans methodologies”, in: Wind Energy Conference and Exhibition, Marseille, France, 2009.
• K. Mansour, M. Yahyazade, “Effects of turbulence model in computational fluid dynamics of horizontal axis wind turbine aerodynamic”, wseas transactions on applied and theoretical mechanics 6 (3), 2011, pp. 108–118.
• G. Yu, X. Shen, X. Zhu, Z. Du, “An insight into the separate flow and stall delay for hawt”, Renew. Energy 36 (1) (2011) 69–76. [https://doi.org/10.1016/j.renene.2010.05.021]
• R. Lanzafame, S. Mauro, M. Messina, “Wind turbine cfd modeling using a correlation-based transition model”, Renew. Energy 52 (2013) 31–39. [https://doi.org/10.1016/j.renene.2012.10.007]
• A. AbdelSalam, V. Ramalingam, Wake prediction of horizontal-axis wind turbine using full-rotor modeling, J. Wind Eng. Ind. Aerodyn. 124 (2014) 7–19. [https://doi.org/10.1016/j.jweia.2013.11.005]
• Ansys, C.F.X. “ANSYS CFX-Solver Theory Guide”; ANSYS Inc.: Canonsburg, PA, USA, 2018.
• Willberg, C. Smartblades 2 Finite Element Reference Rotorblade Model. 2020. Available online: https://zenodo.org/record/3628356#.YILQpVARWMo, (accessed on 22 April 2021).
• Haller, B.; Noever-Castelos, P. Full Scale Blade Test of a 20 m Wind Turbine Blade within the SmartBlades2 Project; 2021. Available online: https://zenodo.org/record/4605409#.YILPVlARWMo, (accessed on 22 April 2021).
• Svorcan, J.; Pekovi’c, O.; Ivanov, T., “Estimation of wind turbine blade aerodynamic performances computed using different numerical approaches.”, Theor. Appl. Mech. 2018, 45, 53–65. [https://doi.org/10.2298/TAM171130004S]
• Spalart, P., and Allmaras, S., 1992, “A one-equation turbulence model for aerodynamic flow,” 30th Aerospace sciences meeting and exhibit, Reno, NV, U.S.A., 01/06-01/09, pp. 439-455. [https://doi.org/10.2514/6.1992-439]
• Daly, B. J., and Harlow, F, H., 1970, “Transport equations in turbulence,” The physics of fluids, Vol. 13(11), pp. 2634-2649. [https://doi.org/10.1063/1.1692845]
• Wilcox, D. C., 1988, “Reassessment of the scale-determining equation for advanced turbulence models,” AIAA Journal, Vol. 26(11), pp. 1299-1310. [https://doi.org/10.2514/3.10041]
• Menter, F. R., 1994, “Two-equation Eddy-viscosity Turbulence Models for Engineering Applications,” AIAA Journal, Vol. 32(8), pp. 1598-1605. [https://doi.org/10.2514/3.12149]
• Kim, B.-S., Kim, M.-E. and Lee, Y.-H. (2008) “Predicting the Aerodynamic Characteristics of 2D Airfoil and the Performance of 3D Wind Turbine using a CFD Code,” Transactions of the Korean Society of Mechanical Engineers B. The Korean Society of Mechanical Engineers. [https://doi.org/10.3795/KSME-B.2008.32.7.549]
• Jonkman J and Jonkman B, 2016, NWTC, “information portal (FAST v8)”, https://nwtc.nrel.gov/FAST8
• Bastian Dose. Smart Blades Projet Report – Task 1.2.5.3 – FSI simulation of the 20 m blade. Technical report, 2016.
• Sawada, K. Convenient visualization method for identifying vortex centers. Trans. Jpn. Soc. Aeronaut. Space Sci. 1995, 38, 102–116.
• Furukawa, M., Nakano, T., and Inoue, M., 1992, “Unsteady Navier-Stokes Simulation of Transonic Cascade Flow Using an Unfactored Implicit Upwind Relaxation Scheme With Inner Iterations,” ASME Journal of Turbomachinery, Vol. 114, No.3, pp. 599-606. [https://doi.org/10.1115/1.2929184]