질량유량 증폭기의 직렬 배치조건에 따른 유동특성 연구

1. 서 론

다양한 산업 분야에서 가스 이송 및 배출 시스템으로 압축기를 사용하고 있다. 하지만 물리적인 설치 공간 부족, 전력 부족, 경제성 등 여러가지 문제로 압축기를 사용하지 못하는 경우도 많다. 특히 반도체 공정 중 발생하는 부산물 가스를 가스처리 장치까지 전달하는 시스템에서는 기체가 고체로 상변화하여 배관을 막는 현상을 방지하기 위해서 기체를 빠르게 이송해야만 한다. 하지만 압축기를 설치하기엔 부족한 공간과 경제적인 문제로 압축기 역할을 대신할 수 있는 소형의 유체기계가 필요한 상황이다.

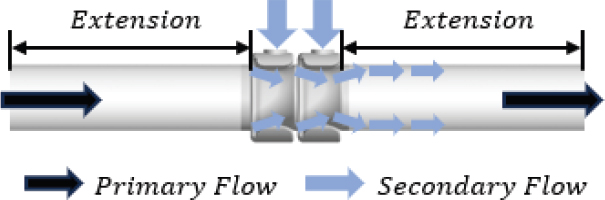
질량유량 증폭기는 벤츄리(Venturi) 효과를 활용한다는 점에서는 일반 이젝터와 원리는 같다. 하지만 부유동을 주유동 중심에 분사하는 방식의 이젝터와 다르게 질량유량 증폭기는 부유동을 코안다(Coanda) 효과를 통해 벽면을 타고 흐르게 분사한다는 점에서 차이가 있다. 즉, 질량유량 증폭기는 코안다 효과와 벤츄리 효과를 복합적으로 활용한 소형 장치이다. 코안다 효과는 속도를 가진 유체가 물체 근처에 흐르게 되면 점성력에 의해 물체 표면에 달라붙어 흐르게 되는 효과이다. 벤츄리 효과는 유동이 지나는 단면적이 좁아질 때 발생하는 유속 증가를 통해 압력강하를 유발하는 효과이다.

코안다 효과와 벤츄리 효과를 활용하면 질량유량 증폭기 내부에 강한 음압력을 생성하여 압력차를 유발하고, 작동유체를 빠르게 이송할 수 있다. 일반적인 압축기와 비교했을때 증폭기가 생성하는 압력차의 절대적인 크기는 작다. 하지만 작동조건이 소량의 기체만 있으면 된다는 점과 장치가 차지하는 부피가 작다는 점 등의 장점이 있다. 따라서 장치가 필요한 위치에 공간 제한이 있지만, 기체의 빠른 이송이 필요한 영역에서는 이 질량유량 증폭기 설치는 경제성이 높다고 할 수 있다.

다수의 연구자들이 코안다 효과와 벤츄리 효과, 그리고 이를 활용한 장치에 대한 연구를 수행하였다. Imants¹⁾는 다양한 장치에 대한 코안다 효과의 활용에 대한 연구를 수행하였다. Trancossi 등²⁾은 코안다 효과에 대한 적합한 수치해석 모델에 대한 연구를 진행하였고, Fišer 등³⁾은 코안다 효과에 대한 CFD와 실험 결과를 비교하여 유동특성을 연구하였다. Mamou 등⁴⁾은 에어포일에서 발생하는 코안다 효과와 성능에 대한 연구를 진행하였고, Jeong⁵⁾은 지하철 선로 먼지제거 장치에서 공기 분사기(air knife) 형상에 코안다 형상을 활용하여 균일한 속도를 형성하는 수치적인 연구를 진행하였다. Bashir 등⁶⁾은 벤츄리 관로 형상에 따른 유동 특성에 대해 연구하였다. Xu 등⁷⁾은 이젝터 내부에 벤츄리 효과를 발생시키는 형상을 추가하여 입자의 이송 속도에 대한 수치적인 연구와 실험 결과를 비교하였다.

다양한 분야에서 코안다 및 벤츄리 효과, 각 효과를 활용한 다양한 장치의 유동에 대해서 연구가 수행되었다. 하지만 질량유량 증폭기를 배관 시스템에 적용하기 위한 유량 증폭률 및 유동 특성에 대한 연구는 미미하다. 더불어 증폭기 2기를 조합했을 때 어떤 현상이 일어나는지에 대한 연구도 미미하다. 본 연구에서는 직선으로 구성된 관에 질량유량 증폭기 2기를 직렬 배치하고, 배치조건으로 형상 변수와 유동 변수를 설정하여 변화하는 증폭률과 유동 특성을 연구하였다.

2. 해석모델과 경계조건

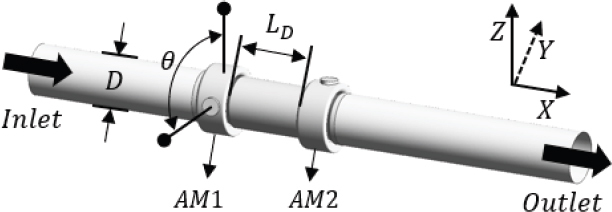
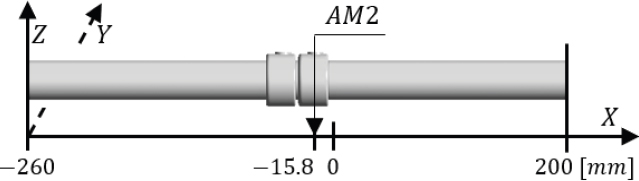
질량유량 증폭기 1(AM1)과 2(AM2), 총 2기를 Fig. 1과 같이 배치하는 모델을 설정하였다. 그리고 배관에 질량유량 증폭기를 설치하여 활용할 가능성을 확인하기 위해 입구와 토출구 방향으로 각각 200 mm 확장하여 유동특성을 고찰하였다.

Fig. 1

Flow domain of amplifiers

부유동은 각 증폭기의 유입구로 주입되어 노즐을 통해 분사되고, 분사된 기체는 코안다 효과가 발생하여 배관 벽면에 붙어 흐르게 된다. 이 코안다 흐름의 속도와 벤츄리 효과의 복합적인 작용으로 인하여 증폭기가 위치한 관 내부에서 압력강하가 발생하여 전방유동 영역에 흡입력을 발생시킨다. 주유동은 입구까지 전달된 흡입력으로 인하여 입구를 통해 들어와 증폭된다.

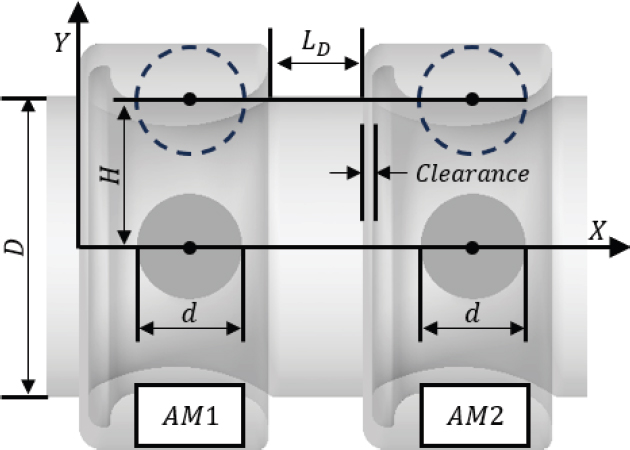
변수는 증폭기 사이 거리 L_D, 증폭기 주입구의 Y축 방향 위치 H, 이 두 가지 요소를 관 지름 D를 기준으로한 비율로 무차원화 하여 사용하였다. 그리고 AM1의 회전 각도 θ를 사용하였다. 이외 상세한 변수와 형상 정보는 Figs. 2∼3과 Tables 1∼2에 정리하였다.

Fig. 2

Parameter description

Fig. 3

Parameter description of AM1 and AM2

Table 1

Boundary conditions applied in this study

Table 2

Geometrical parameters

본 연구에서는 질량유량 증폭기 2기를 배치함으로써 나타나는 유동특성을 총 세 가지로 나누어 해석하였다.

첫 번째 Case는 관 지름에 대해 비율로 무차원화된 간격비(distance ratio, L_D /D) 0, 1, 2, 4를 기준으로, 질량유량 증폭기 1(AM1)의 회전 각도를 나타낸 θ 값을 각각 0 °, 90 °, 180 °로 나누어 해석하였다(Table 3 참조).

Table 3

Boundary conditions for the rotational angles with different values of distance ratio

두 번째 Case는 간격비(L_D /D) 0, 1, 2, 4를 기준으로, 무차원화된 구경비(port ratio, H /D)를 각각 0, 0.25, 0.5로 나누어 해석하였다(Table 4 참조).

Table 4

Boundary conditions for the port ratio with different values of distance ratio

세 번째 Case는 간격비(L_D /D) 0, 4에 대하여 주유동의 유량 증폭률이 가장 높으며, 가장 안정적인 유동을 발생시키는 조건(θ = 180 °, H /D = 0.5)을 적용한 후, 추가로 각 증폭기에 주입되는 부유동의 유량비를 변수로 하여 해석하였다(Table 5 참조).

Table 5

Boundary conditions for the different secondary flow rates through AM1 and AM2

3. 수치해석

유동특성을 고찰하기 위해 다음과 같은 지배방정식을 사용하였다.

- 연속방정식 :

- 운동량방정식 :

위 식에서 ρ는 밀도, u_i는 속도, p는 정압, μ는 점성계수를 나타낸다. 수치해석은 ANSYS Fluent 2023 R1을 사용하였다. 난류모델은 SST(Shear Stress Transport)로 설정하여 벽면 근처에서는 k-ω 모델을, 내부유동에는 k-ϵ 모델을 사용하여 유동해석의 정합성을 높였다.

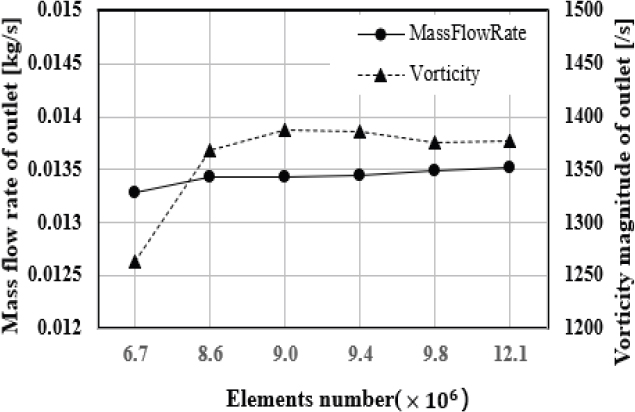
정확한 해석을 위해 격자 조건은 인플레이션 조건을 적용하여 벽면에 5개의 층을 적용하였고, 질량유량 증폭기 형상 내에는 격자 생성 조건에 first aspect ratio를 25로 추가하였다. 결과적으로 Fig. 4에 도시한 질량유량의 격자 의존성 시험에서 기준 지표인 질량유량은 작은 변화폭을 보였으며, 보조 지표로 와류 크기를 설정하여 적절한 격자계 조건을 확보하였다. 따라서 약 940만개를 기준으로 노즐 간극과 벽면에 조밀한 격자계를 적용하였다. 해의 수렴조건으로 잔류값은 10^-4 이하로 설정하였고, 수행된 전체 Case에서 질량유량 증폭기의 벽면 평균 Y⁺는 1 수준임을 확인하였다.

Fig. 4

Grid dependency test

4. 결과 및 고찰

4.1 질량유량 증폭기 사이 거리에 대한 영향

4.1.1 거리에 대한 흡입력 및 전방유동 속도장 결과

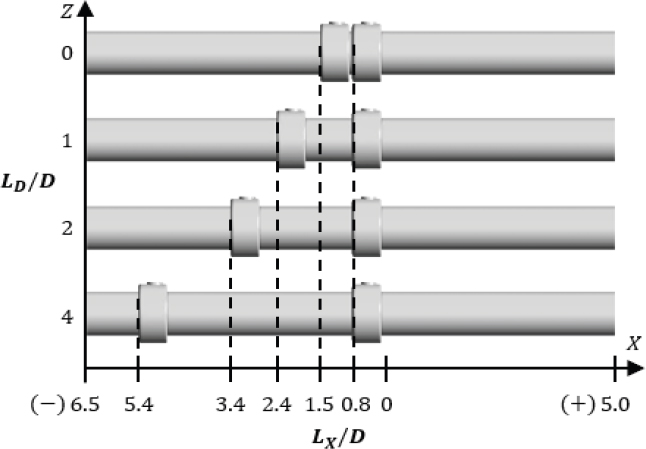
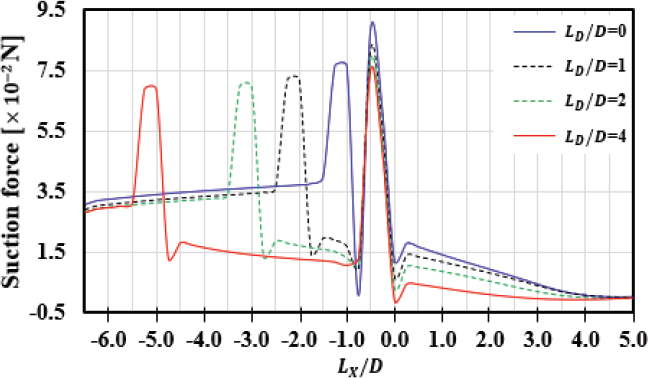
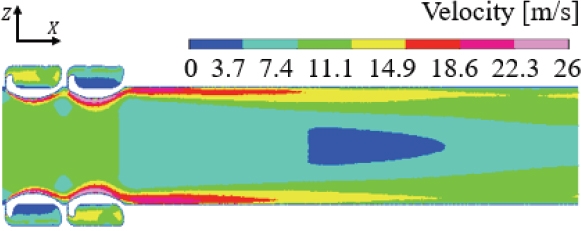
질량유량 증폭기 사이 거리 조건과 증폭기의 X축 위치에 대한 정보를 각각 관 지름에 대한 비율(L_D /D, L_X /D)로 무차원화 하여 Fig. 5에 도시하였다. 그리고 흡입력(suction force, F_Suction) 결과 그래프를 Fig. 6에 도시하였고, 전방유동 영역의 XZ 평면 속도장을 Fig. 7에 도시하였다.

Fig. 5

Dimensionless location for different values of distance ratio(LD /D) with θ = 0 ° and H /D = 0

Fig. 6

Suction force versus LX /D for different values of distance ratio(LD /D) with θ = 0 ° and H /D = 0

Fig. 7

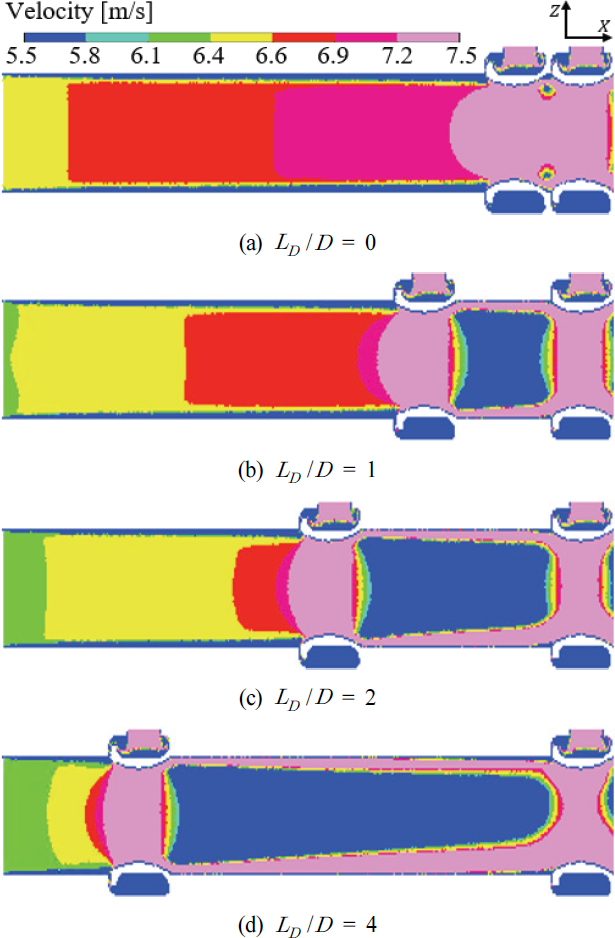
Velocity contour on XZ-plane in front area for different values of distance ratio(LD /D) with θ = 0 ° and H /D = 0

- 흡입력 :

$\[ F_{Suction }=-p_{avg }\times A_c \]$

(3)

위 식에서 A_c는 X축 방향의 단면적, p_avg는 단면적에 대한 평균 정압력을 나타낸다.

결과를 보면, 모든 조건에서 주유동 입구(L_X /D = -6.5)와 질량유량 증폭기 1(AM1) 사이에는 완전발달된 유동이 형성되었으며, 전방유동 영역에 X축 양의 방향으로 흡입력이 발생하였다. 이 흡입력은 증폭기로부터 분사되어 후방유동 영역의 벽면에서 발생하는 코안다 흐름의 속도와 관 내부 직경이 좁아지는 형상에서 일어나는 벤츄리 효과의 복합적인 작용으로 발생하였음을 알 수 있다.

결과적으로 질량유량 증폭기 1(AM1)과 질량유량 증폭기 2(AM2)의 사이 거리 조건(L_D /D)이 작아질수록 주유동 입구(L_X /D = -6.5)부터 AM1 사이에서 발생하는 흡입력과 각각의 AM1, AM2의 위치에서 발생하는 흡입력 크기가 커졌다. 이때 주유동 입구까지 전달된 흡입력은 주유동을 증폭시키는데 사용되는 반면에 AM1과 AM2 사이에서 발생하는 흡입력은 증폭기간 상호작용으로 인하여 유동 증폭에는 큰 영향을 주지 못하였다.

4.1.2 거리에 대한 후방유동 속도장 결과

질량유량 증폭기 사이 거리 조건(L_D /D)에 대한 후방유동 영역의 XZ 평면 속도장을 Fig. 8에 도시하였다.

Fig. 8

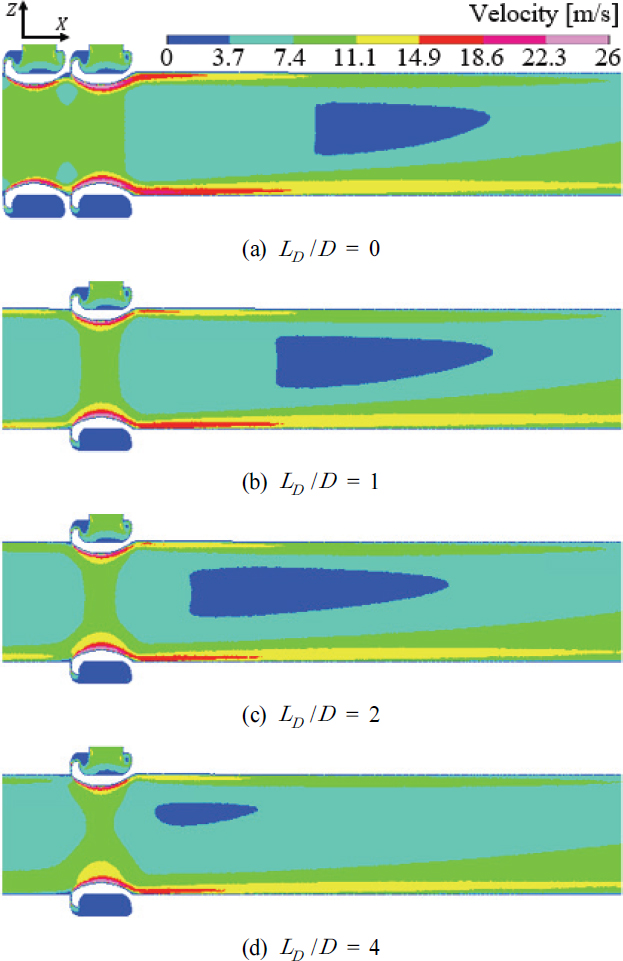
Velocity contour on XZ-plane in rear area for different values of distance ratio(LD /D) with θ = 0 ° and H /D = 0

속도장 결과를 Fig. 6과 비교하여 보면, L_D /D 값이 작아질수록 AM1과 AM2의 사이에서 상호작용으로 인하여 손실되는 힘이 작아지면서 후방유동 벽면의 코안다 흐름 중 빠른 유속을 가진 영역이 상대적으로 길어짐을 알 수 있다. 그리고 증폭기 공압실 내부 고리 모양 형상으로 인하여 모든 L_D/D에서 증폭기 부유동 주입구의 반대 방향에서 상대적으로 유속이 빠른 영역이 넓고 길게 형성되었고, 결과적으로 비대칭성 유동이 형성됨을 알 수 있다.

4.1.3 거리에 대한 흡입력과 증폭률 결과 비교

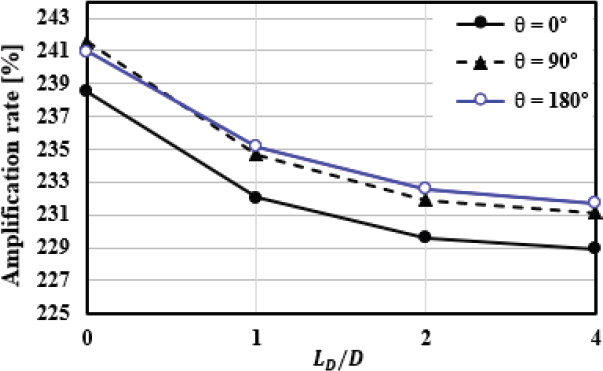
질량유량 증폭기 사이 거리 조건(L_D /D)에 대한 주유동 증폭률(Amplification rate, η) 결과를 주유동의 입구(L_X /D = -6.5)에서의 흡입력 결과와 함께 Fig. 9에 도시하였다.

Fig. 9

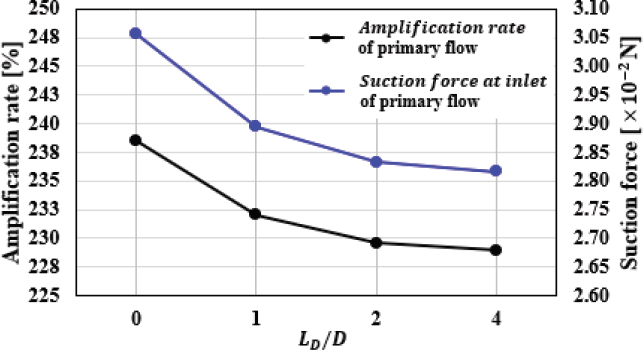
Comparison of amplification rate of primary flow and suction force at inlet for different values of distance ratio(LD /D)

- 주유동 증폭률 :

$\[ \eta =\frac{{\dot{Q}}_{outlet }-{\dot{Q}}_{\mathrm{s}\mathrm{e}\mathrm{c}ondary }}{{\dot{Q}}_{\mathrm{s}\mathrm{e}\mathrm{c}ondary }}\times 100\left(\%\right) \]$

(4)

위 식에서 $$ {\dot{Q}}_{outlet }$$은 토출구로 나오는 질량유량, $$ {\dot{Q}}_{\mathrm{s}\mathrm{e}\mathrm{c}ondary }$$는 부유동 유입구로 주입하는 질량유량을 나타낸다.

결과를 보면, L_D /D 값이 작아질수록 큰 흡입력이 주유동 입구에 전달되었다. 이 흡입력의 크기에 증폭률은 비례하는 경향을 보였다. 증폭률 결과값을 확인하면, L_D /D = 4 조건에서 증폭률은 약 229 % 였으나, L_D /D = 0 조건으로 증폭기간 사이 거리를 최대한 가깝게 배치하면 증폭률이 약 239 %로 약 10 % 정도 증가하였다. 따라서 AM2를 기준으로한 200 mm 이내 영역에서 AM1을 배치하는 경우에는 각 증폭기의 상호작용으로 인한 흡입력 손실이 발생하고, 이에 따라 증폭률도 변화하기 때문에 이를 고려한 배치가 필요함을 알 수 있다.

4.2 질량유량 증폭기 1의 회전 각도에 대한 영향

AM2는 고정하고, AM1을 X축 중심으로 θ = 0 °, 90 °, 180 ° 회전시킨 형상 조건을 적용하였을 때 결과를 Figs. 10∼12에 도시하였다.

Fig. 10

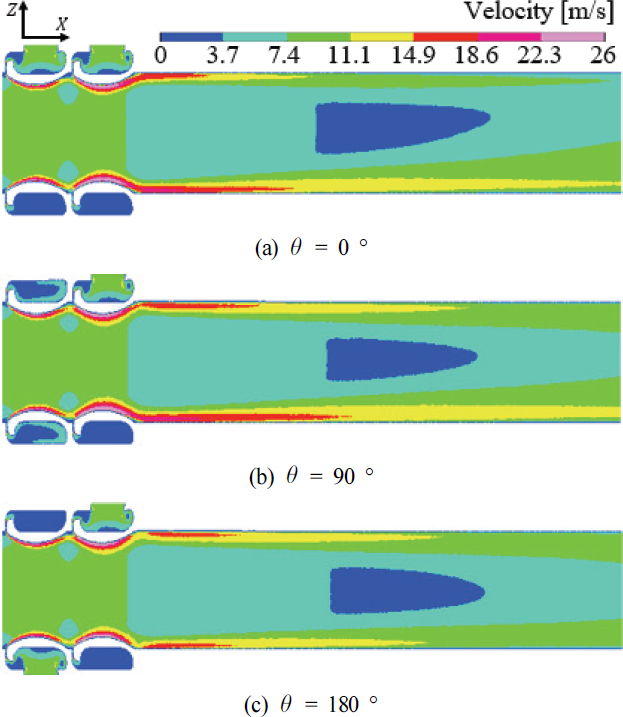
Velocity contour on XZ-plane in rear area for different values of rotation angles(θ) with LD /D = 0 and H /D = 0

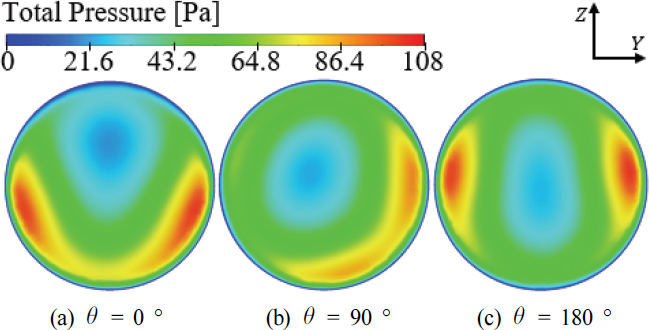
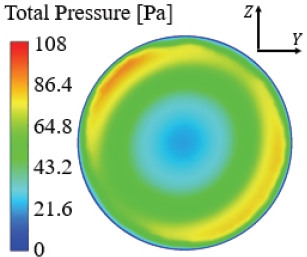
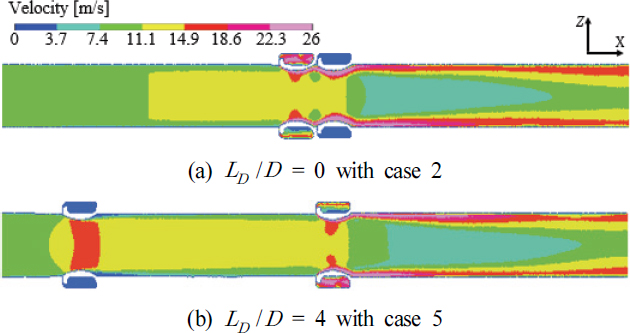
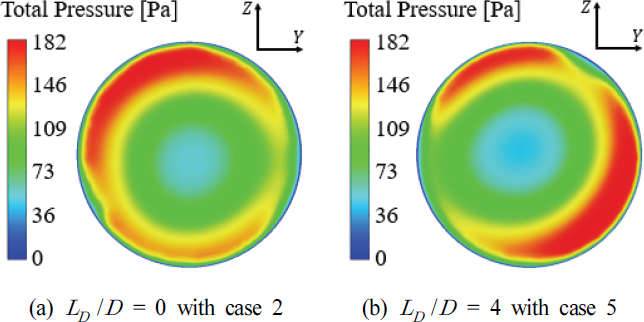
먼저 XZ 평면 속도장 해석결과인 Fig. 10과 토출구 기준 압력장 해석결과인 Fig. 11을 비교하여 보면, θ = 0 ° 조건에서는 증폭기 부유동 주입구 반대 방향에서 유속이 빠른 비대칭성 유동이 형성되었다. 그리고 토출구에서 압력이 낮은 코어 위치가 상단 벽면에 근접하는 결과를 나타내었다. θ = 90 ° 조건에서는 θ = 0 ° 조건에서 보였던 비대칭성이 개선된 결과를 나타내었다. 그리고 토출구에서 압력이 낮은 코어 위치는 관 내부 중심부로 이동하며 안정성이 증가되었다. θ = 180 ° 조건에서는 각 증폭기로부터 생성되는 비대칭성 유동이 완전히 반대 방향으로 유도되어 벽면을 포함한 전반적인 대칭성이 형성되었다. 그리고 토출구에서 압력이 낮은 코어는 관 내부 중심부에 위치하고, 좌우 대칭성을 띄며 안정적인 후방유동이 형성됨을 알 수 있다.

Fig. 11

Pressure contour of outlet for different values of rotation angles(θ) with LD /D = 0 and H /D = 0

증폭률 결과인 Fig. 12을 보면, θ = 90 °와 θ = 180 ° 조건에서 증폭률은 비슷하게 평균 3% 향상되었다. 이 결과는 유동의 비대칭성과 불안정한 압력장을 개선한 결과이다. 따라서 회전 각도는 θ = 180 ° 조건이 증폭률을 높이면서 유동의 안정성을 확보할 수 있는 조건임을 알 수 있다.

Fig. 12

Amplification rate of primary flow versus LD /D for different values of rotation angles(θ) with H /D = 0

4.3 질량유량 증폭기의 부유동 주입구 위치에 대한 영향

AM1과 AM2의 부유동 주입구의 위치가 H /D = 0, 0.25, 0.5 조건으로 설정된 형상에서 나타나는 결과를 Figs. 13∼17에 도시하였다.

Fig. 13

Cross-sectional location of AM2

먼저 Fig. 13에 도시한 절단면 위치와 Fig. 14의 속도 벡터장을 보면, H /D = 0 조건에서는 주입된 기체가 공압실 내부 벽면에 충돌한 뒤에 좌우로 나뉘어 흐르는 것을 알 수 있다. H /D = 0.25 조건에서도 H /D = 0 조건과 유사한 흐름을 보였으나, 좌측 상단부에서는 유동이 방향성을 잃고 불안정한 흐름이 형성되었다. H /D = 0.5인 경우에는 공압실 내부 벽면과 충돌하는 현상이 최소화되고, 시계방향으로 안정적인 회전유동이 생성되었다.

Fig. 14

Cross-sectional velocity vector of AM2 for different values of port ratio(H /D) with LD /D = 0 and θ = 0 °

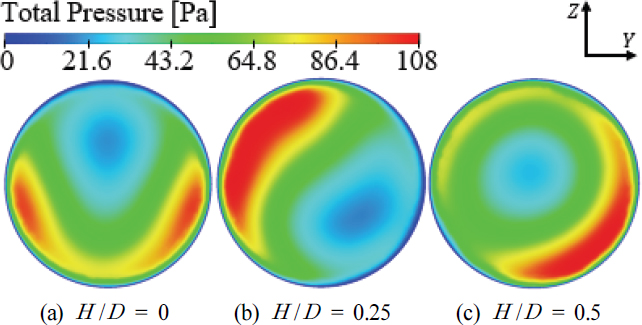
XZ 평면 속도장 해석결과인 Fig. 15와 토출구 기준 압력장 해석결과인 Fig. 16을 비교하여 보면, H /D = 0 조건에서는 부유동 주입구 반대 방향에 속도가 빠른 영역이 형성되었기 때문에 비대칭성 유동을 형성하였고, 토출구에서 압력이 낮은 코어 위치가 상단 벽면에 근접하는 결과를 나타내었다. H /D = 0.25 조건에서는 부유동 주입구 방향에 속도가 빠른 영역이 확장되며 토출구까지 유지되며 비대칭성이 강해졌다. 그리고 회전유동으로 인하여 좌측 상단에 높은 압력이 형성되고, 압력이 낮은 압력 코어 위치가 우측 하단부 벽면에 근접하는 결과를 나타내며 상대적으로 불안정하였다. 반면에 주입구 위치 조건이 H /D = 0.5인 경우 상대적으로 비대칭성이 개선되었고, 회전유동으로 인하여 우측 하단에 높은 압력이 형성되지만, 낮은 압력 코어 위치가 관 내부 중심부로 이동하며 안정성이 증가되었다.

Fig. 15

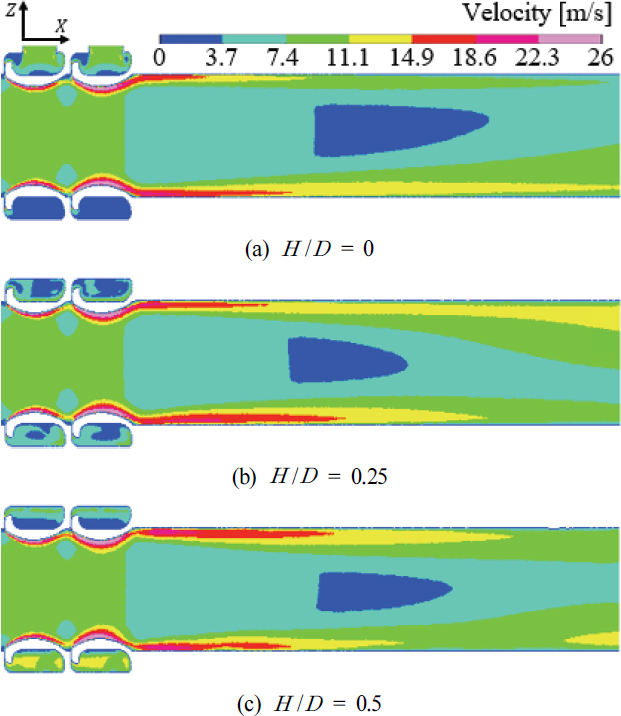
Velocity contour on XZ-plane in rear area for different values of port ratio(H /D) with LD /D = 0 and θ = 0 °

Fig. 16

Pressure contour of outlet for different values of port ratio(H /D) with LD /D = 0 and θ = 0 °

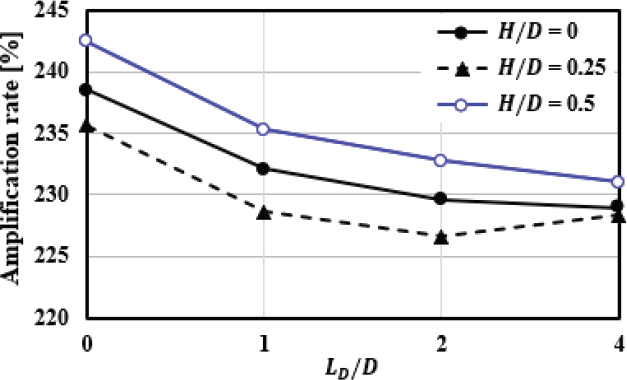
증폭률 결과인 Fig. 17을 보면, H /D = 0.25 조건에서 증폭률이 평균 2% 정도 하락하는 경향을 보였다. 이 결과는 부유동이 증폭기로부터 불안정하게 토출되었고, 이후 후방유동에서도 비대칭성이 강하며 안정성이 떨어졌기 때문이다. 반면에 부유동이 증폭기로부터 안정적으로 토출되었고, 후방유동의 비대칭성과 안정성이 개선된 H /D = 0.5 조건에서는 증폭률이 평균 3% 정도 향상되는 경향을 보였다. 따라서 주입구 위치 조건이 H /D = 0.5인 경우가 증폭률을 향상시키고 유동 안정성을 증가시킬 수 있는 조건임을 알 수 있다.

Fig. 17

Amplification rate of primary flow versus LD /D for different values of port ratio(H /D) with θ = 0 °

4.4 회전 각도와 주입구 위치에 대한 최적 조건

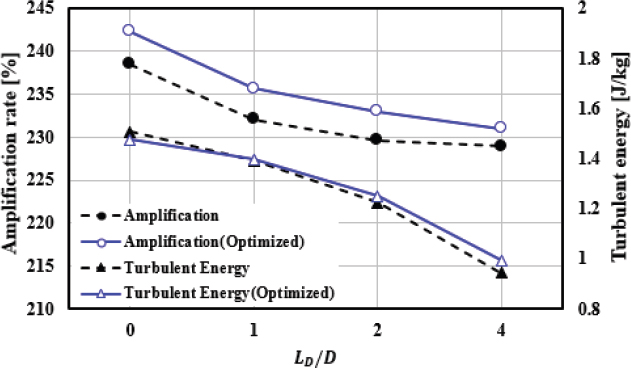
증폭률과 안정성 측면을 모두 고려한다면, 회전 각도와 주입구 위치는 해석 결과에 따라서 각각 θ = 180 °, H /D = 0.5 조건이 최적이라고 할 수 있다. 이 조건을 모두 적용한 상태에서 증폭기 사이 거리 조건에 따른 증폭률과 토출구 난류에너지 결과값을 4.1.항에서 고찰하였던 기준 조건(θ = 0 °, H /D = 0)에 대한 결과값과 함께 Fig. 18에 도시하였다. 최적 조건(θ = 180 °, H /D = 0.5)에서 증폭률은 모든 증폭기 사이 거리 조건(L_D /D = 0, 1, 2, 4)에서 기준 결과값보다 평균 4 % 향상된 결과값이 산출되었다. 반면에 난류에너지는 기준 조건(θ = 0 °, H /D = 0)의 결과와 유사한 수준으로 확인되었다.

Fig. 18

Amplification and turbulent energy comparison of reference and optimized case

증폭률이 향상되었다는 것은 평균 유동속도가 상승했다는 것을 의미한다. 하지만 난류에너지는 거의 비슷한 수준이었기 때문에 유동 안정성은 오히려 증가했다고 볼 수 있다.

이 결과는 AM1의 회전 각도를 활용하여 관 벽면에서 흐르는 부유동 기체 속도를 대칭적으로 생성하고, 부유동 주입구 위치를 활용하여 회전유동을 발생시켜 내부 압력 코어를 관 중심으로 유도한 결과이기 때문이다(Figs. 19∼20 참조).

Fig. 19

Velocity contour on XZ-plane in rear area for LD /D = 0 with θ = 180 ° and H /D = 0.5

Fig. 20

Pressure contour of outlet for LD /D = 0 with θ = 180 ° and H /D = 0.5

4.5 부유동 유량비에 대한 영향

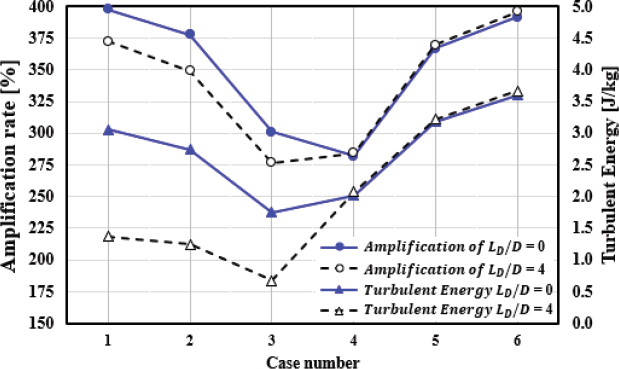
앞서 해석된 결과에 의하면 주유동 증폭률을 가장 안정적으로 향상시킬 수 있는 조건은 각각 θ = 180 °, H /D = 0.5 조건이었다. 이 조건을 모두 적용한 상태에서 L_D /D = 0, 4 조건에 대하여 질량유량 증폭기 1과 2에 주입되는 부유동 유량의 총합을 200 LPM으로 제한하고, 비율을 나누어 해석하였다. 주입되는 비율에 대한 Case 1(1:0), Case 2(19:1), Case 3(3:1), Case 4(1:3), Case 5(1:19), Case 6(0:1)의 증폭률과 난류에너지에 대한 결과를 Fig. 21에 도시하였다.

Fig. 21

Amplification and turbulent energy versus case number for LD /D = 0 and LD /D = 4

Case 1은 비율에 대한 경향성을 확인하기 위해 AM2에 부유동을 주입하지 않았고, Case 6은 같은 이유로 AM1에 부유동을 주입하지 않았다. 이를 고려하여 결과를 보면, L_D/D = 0 조건에서는 AM2에 투입되는 유량비가 높은 Case 4∼6 보다 AM1에 투입되는 유량비가 높은 Case 1∼3에서 상대적으로 증폭률은 높은 경향을 보였고, 난류에너지는 낮은 경향을 보였다. L_D /D = 4 조건에서는 AM1에 투입되는 유량비가 높은 Case 1∼3 보다 AM2에 투입되는 유량비가 높은 Case 4∼6 에서 상대적으로 증폭률은 높은 경향을 보였다. 난류에너지는 상대적으로 낮은 경향을 보였다.

수행한 조건에서 높은 증폭률을 우선으로 보면 L_D /D = 0 조건의 Case 2(19:1)와 L_D /D = 4 조건의 Case 5(1:19)가 유리한 조건이라고 볼 수 있다. Fig. 21 결과를 참조하면, L_D /D = 0 조건의 Case 2와 L_D /D = 4 조건의 Case 5(1:19) 증폭률은 각각 약 378 %와 370 %로 유량비를 조절하지 않은 동일조건(Fig. 18 참조) 보다 각각 약 136 %, 139 % 정도 증가하였다.

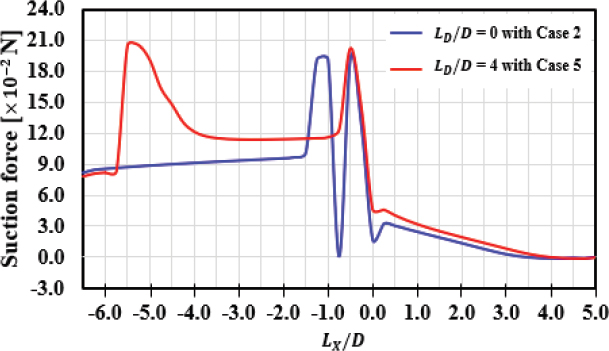
흡입력 결과인 Fig. 22을 보면, L_D /D = 0 조건의 Case 2(19:1)와 L_D /D = 4 조건의 Case 5(1:19)에서 최종적으로 L_X /D = -6.5부터 각 조건의 AM1 위치 사이에서 발생하는 흡입력과 주유동 입구에 전달되는 흡입력의 차이는 근소하였기 때문에 Fig. 21의 증폭률 결과값 차이도 근소하였음을 알 수 있다.

Fig. 22

Suction force versus LX /D for LD /D = 0 with case 2 and LD /D = 4 with case 5

난류에너지는 Fig. 21 결과값을 참조하면, L_D /D = 0 조건의 Case 2(19:1)에서 약 2.7 [J/Kg] 이고, L_D /D = 4 조건의 Case 5(1:19)에서 약 3.2 [J/Kg]로 두 결과값은 큰 차이를 보였다. 이 결과는 Figs. 23∼24를 참조하면, 두 경우 모두 속도장의 대칭성은 형성되었지만 L_D /D = 4 조건의 Case 5(1:19)에서 토출구 압력장이 상대적으로 불안정했기 때문에 나타난 차이임을 알 수 있다.

Fig. 23

Velocity contour on XZ-plane for for LD /D = 0 with case 2 and LD /D = 4 with case 5

Fig. 24

Pressure contour of outlet of LD /D = 0 with case 2 and LD /D = 4 with case 5

따라서 AM2를 기준으로한 200 mm 이내 영역에서 AM1을 L_D /D = 0 조건으로 배치하는 경우에는 AM1의 유량비를 높게 설정하는 것이 다른 Case에 비하여 증폭률 향상하면서 상대적으로 안정적인 후방유동을 형성하는 방향임을 알 수 있다. 그리고 AM1을 L_D /D = 4 조건으로 배치하는 경우에는 AM2의 유량을 높게 설정하는 것이 다른 Case에 비하여 증폭률 향상을 위해서 유리한 방향이지만 안정성이 하락한다는 것을 고려해야 함을 알 수 있다.

5. 결 론

본 연구에서는 질량유량 증폭기 2기를 직렬로 배치하여 배치조건에 따른 유동특성을 수치해석 결과로 분석하여 연구하였다. 증폭률과 유동 안정성을 중점으로 증폭기 성능을 평가하였다. 형상 변수로써 증폭기 사이 거리(L_D /D), 증폭기 2를 기준으로 한 증폭기 1의 회전 각도(θ), 증폭기에 장착되는 부유동 주입구의 위치(H /D)에 따른 결과를 분석하였다. 그리고 유동 변수로써 각각의 증폭기에 주입되는 부유동의 유량비에 따른 결과를 고찰하였다.

• 1) 증폭기 사이 거리에 대한 증폭률 결과는 L_D /D = 0과 L_D /D = 4 조건에서 각각 239 %와 229 %로 최대 10% 차이를 보였다. 증폭기 사이 거리가 가까울수록 흡입력의 작용점이 가까워져 증폭기 1과 2의 상호작용으로 발생하는 힘의 손실이 감소하였고, 주유동이 시작하는 입구부터 증폭기까지 전방유동 영역에 작용하는 흡입력의 크기 또한 커졌다. 결론적으로 주유동 입구에 전달되는 흡입력의 증가는 증폭률 향상으로 이어졌다. 200 mm 범위 내에서는 질량유량 증폭기 2기를 최대한 가깝게 배치하는 것이 흡입력 손실을 방지하여 증폭성능을 향상하는 방향이었다.
• 2) 증폭기 1의 회전된 각도에 대한 증폭률 결과는 θ = 90 °와 180 ° 조건에서 증폭률이 평균 3 % 향상되었다. 이 결과는 부유동의 주입구 반대쪽 벽면의 유동속도가 다른 지점에 비해 빠르다는 비대칭성을 활용한 결과이다. 특히 θ = 180 ° 조건에서 벽면유동을 포함한 속도장이 대칭성을 띄며 안정적이었고, 후방유동 또한 압력장 코어 위치가 중심에 위치하면서 더 안정적인 압력장을 나타내었다. 증폭기 2기를 배치하는 경우 부유동 주입구를 서로 반대 방향으로 회전시켜 배치하는 것이 증폭성능 향상과 유동 안정성 증가에 효과적임을 알 수 있었다.
• 3) 증폭기 부유동 주입구 위치에 대한 증폭률 결과는 H /D = 0.5 조건에서 평균 3 % 향상되었다. 이 결과는 증폭기 내부에 회전유동을 생성하여 후방영역의 압력장을 안정적으로 형성한 결과이다. H /D = 0.25 조건에서는 평균 2 % 하락하였다. 이 결과는 증폭기 내부에서 공압실 내부에서 유동이 불균일하여 에너지 손실이 발생하여 불안정하게 토출되어 후방유동도 불안정하게 형성된 결과이다. 부유동 주입구는 증폭기 접선 방향에 위치시키는 것이 증폭성능 향상과 유동 안정성 증가에 효과적임을 알 수 있었다.
• 4) 증폭기 1의 회전 각도를 θ = 180 °, 부유동 주입구 위치를 H /D = 0.5 조건으로 배치하는 것이 증폭률을 향상하고 유동을 안정적으로 흐르게 하는 방법이다. 두 조건을 모두 적용하면 기존 조건보다 평균 4 % 향상된 값을 나타내었다.
• 5) 증폭기 1의 회전 각도를 θ = 180 °, 부유동 주입구 위치를 H /D = 0.5, 사이 거리를 L_D /D = 0 조건으로 배치하는 경우에는 입구에 가까운 증폭기 1의 유량비를 높은 비율로 설정하는 것이 반대의 경우에 비해 증폭률을 향상시키면서 상대적으로 안정적인 후방유동을 형성하는 방향임을 알 수 있었다. 그리고 θ = 180 °, H /D = 0.5, L_D /D = 4 조건으로 배치하는 경우에는 토출구에 가까운 증폭기 2의 유량비를 높은 비율로 설정하는 것이 반대의 경우에 비해 상대적으로 증폭률을 향상시키는 방향이었으나, 안정성이 하락한다는 것을 고려해야 함을 알 수 있었다.

Acknowledgments

본 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었음(과제번호 RS-2023-00245737).

References

• Imants, R., 1996, “Applications of the Coanda effect,” Scientific American, Vol. 214, No. 6, pp. 84∼921. [https://doi.org/10.1038/scientificamerican0666-84]
• Trancossi, M., Dumas, A., and Vucinic, D., 2013, “Mathematical Modeling of Coanda Effect,” SAE Technical Paper Series, Id. 2013-01-2195. [https://doi.org/10.4271/2013-01-2195]
• Fišer, J., Jedelský, J., Vach, T., Forman, M., and Jicha, M., 2012, “Comparison of CFD Simulations and Measurements of Flow Affected by Coanda Effect,” EPJ Web of Conferences, Vol. 25, Id. 01015. [https://doi.org/10.1051/epjconf/20122501015]
• Mamou, M., and Khalid, M., 2007, “Steady and Unsteady Flow Simulation of a Combined Jet Flap and Coanda Jet Effects on a 2D Airfoil Aerodynamic Performance,” Revue des Energies Renouvelables CER, pp. 55∼60.
• Jeong, W. T., 2017, “Flow Control of Air Blowing and Vacuuming Module Using Coanda Effect,” Journal of the Korea Academia Industrial Cooperation Society, Vol. 18, No. 3, pp. 115∼121.
• Bashir, T. A., Soni, A. G., Mahulkar, A. V., and Aniruddha, B. P., 2011, “The CFD Driven Optimization of a Modified Venturi for Cavitational Activity,” The Canadian Journal of Chemical Engineering, Vol. 89, No. 6, pp. 1366∼1375. [https://doi.org/10.1002/cjce.20500]
• Xu, J., Liu, X., and Pang, M., 2016, “Numerical and Experimental Studies on Transport Properties of Powder Ejector Based on Double Venturi Effect,” Vacuum, Vol. 134, pp. 92∼98. [https://doi.org/10.1016/j.vacuum.2016.10.007]
• Lee, D. W., Lee, S., Kim, B. G. and Kwon, S. B., 2007, “A Study on Jet Characteristic using a Coanda Effect in a Constant Expansion Rate Nozzle,” Journal of the Korean Society for Aeronautical & Space Sciences, Vol. 35, No.8, pp. 706∼713. [https://doi.org/10.5139/JKSAS.2007.35.8.706]
• Zhang, J. X., 2017, “Analysis on the Effect of Venturi Tube Structural Parameters on Fluid Flow,” AIP Advances, Vol. 7, Issue. 6, Id. 065315. [https://doi.org/10.1063/1.4991441]
• Jitschin, W., Ronzheimer, M., & Khodabakhshi, S., 1999, “Gas Flow Measurement by Means of Orifices and Venturi Tubes,” Vacuum, Vol. 53, pp. 181∼185. [https://doi.org/10.1016/S0042-207X(98)00352-2]