[ Original Paper ]

The KSFM Journal of Fluid Machinery - Vol. 27, No. 1, pp.33-43

ISSN: 2287-9706 (Print)

Print publication date 01 Feb 2024

Received 12 Oct 2023 Revised 24 Nov 2023 Accepted 26 Dec 2023

DOI: https://doi.org/10.5293/kfma.2024.27.1.033

상변화물질 기반 수평 핀 배치 원통형 히트싱크의 열성능에 대한 수치해석적 연구

이석용^* ; 최원우^** ; 김성민^*^{, †}

*성균관대학교 기계공학부
**성균관대학교 대학원 기계공학과

Numerical Study on Thermal Performance of Phase Change Material Based Horizontal Finned Cylindrical Heat Sink

Seok-Yong Lee^* ; Won-Woo Choi^** ; Sung-Min Kim^*^{, †}

*School of Mechanical Engineering, Sungkyunkwan University
**Graduate School of Mechanical Engineering, Sungkyunkwan University

Correspondence to: ^†E-mail : smkim@skku.edu

Abstract

The primary objective of this study is to examine the melting rate of phase change material (PCM), the natural convection characteristics, and the bottom temperature distributions of the PCM-based cylindrical heat sinks with horizontal fins. A two-dimensional numerical analysis was performed, and the effect of various horizontal fin positions on the cooling performance of the heat sink was investigated. Compared to the cases without horizontal fins, adding horizontal fins increased the surface area for heat conduction and increased heat absorption into the PCM, resulting in a lower bottom temperature rise. Horizontal fins impede natural convection, but the effect of reducing the rate of increase in the bottom temperature of the heat sink was more significant due to the increased surface area. The set point temperature (SPT) arrival time increased by up to 44% in the case with horizontal fins compared to the case without horizontal fins. Depending on the arrangement of the horizontal fins, SPT arrival time showed a difference of up to 11%. The results showed that the position of the horizontal fins inside the cylindrical heat sink is a significant geometrical parameter that affects the PCM melting rate and the bottom temperature of the heat sink.

Keywords:

Phase Change Material, Thermal Management, Horizontal Fin, Cylindrical Heat Sink, Melting, Computational Fluid Dynamics

키워드:

상변화물질, 열관리, 수평 핀, 원통형 히트싱크, 융해, 전산유체역학

1. 서 론

전자기기의 소형화와 고집적화 같은 현대 기술의 발전으로 다양한 응용 분야^(1–5)에서 시스템의 성능과 효율을 증가시키려는 시도가 증가하고 있다. 전자기기 같은 시스템의 높은 성능을 유지하기 위한 요소 중 하나는 작동 가능한 온도 범위를 벗어나지 않는 것이다. 하지만 높은 성능을 가진 시스템은 필연적으로 높은 발열을 갖기 마련이다⁽⁶⁾. 이에 따라 고성능 시스템의 성능을 유지시키는 열관리 시스템 또한 중요해지고 있고, 많은 연구자는 열 관리를 중요한 주제로 인식하고 있다.

열관리 시스템(Thermal management systems)은 현열 에너지 저장 시스템, 잠열 에너지 저장 시스템 그리고 열ㆍ화학 에너지 저장 시스템으로 크게 3가지가 있다⁽⁷⁾. 그중 잠열 에너지 저장 시스템은 다른 시스템에 비해 몇 가지 장점을 가지고 있다. 첫 번째로 잠열을 이용하기 때문에 높은 열전달 계수를 갖고 있어 부피 당 에너지 저장 면에서 큰 이점을 가지고 있다. 다른 능동 냉각 시스템은 더 높은 성능을 위해 크고 복잡해지지만 잠열 에너지 저장 시스템과 같은 피동 냉각 시스템은 작동을 위한 시스템이 상대적으로 단순하여 소형화가 가능하기 때문에 고집적화된 기기에도 사용할 수 있다. 두 번째로 상변화 중 냉각 물질은 잠열을 흡수하며 일정 온도를 유지하기 때문에 작동 온도 범위를 유지해야 하는 전자기기에 큰 이점이 있다⁽⁸⁾.

잠열 에너지 저장 시스템은 상변화물질(Phase Change Material, PCM)을 사용한다. 위에서 언급한 것처럼 PCM은 큰 잠열 에너지 흡수가 가능하다는 장점을 가지고 있다. 그러나 순수 PCM은 대부분 열전도율이 낮기 때문에^(8,32,33) 시스템의 형태에 따라 일정한 열 흡수를 이루지 못하고 시스템의 작동 온도 범위를 벗어날 수 있다. 열전도율이 낮아 PCM 내 융해 속도가 크게 변하고 시스템의 발열에 따른 즉각적인 대응이 어려울 수 있기 때문이다⁽⁹⁾. 따라서, 이러한 PCM의 단점을 보완하고자 다양한 방법이 고안되었는데, 크게 다양한 형상을 가진 금속 핀, 금속 다공체 그리고 나노입자 등이 있다⁽¹⁰⁾. 이러한 열전도율 향상제(Thermal Conductivity Enhancer, TCE)를 사용하여 PCM의 단점을 보완하는 것이 잠열 에너지 저장 시스템 성능 향상 방법이고 관련된 연구^(34–36)가 활발히 진행되고 있다.

PCM의 낮은 열전도율을 보완하기 위해 금속 핀을 사용한 잠열 에너지 저장 시스템에 관한 연구가 다음과 같이 활발하게 이루어지고 있다. Jeong⁽¹¹⁾ 등은 PCM 기반 원통형 히트싱크에 대해 판형 수직 핀에 대한 핀 높이, 캐비티 각도, 핀 두께, 베이스 높이 등의 다양한 기하학적 변수와 열유속 등의 열적 변수에 따른 융해 속도 변화를 분석하기 위해 단위 셀에 대한 2차원 수치해석을 진행하였다. 캐비티를 채우는 PCM의 양을 늘리고 히트싱크 재료의 질량을 늘림으로써 PCM 융해 시간을 늘릴 수 있음을 확인하였다. 또한, 캐비티 각도가 커질수록 자연대류가 향상하여 일정한 융해 속도를 보여주었다. Kim⁽¹²⁾ 등은 PCM 기반 히트싱크의 열성능에 대한 수평 핀 배열의 영향에 대해 수치해석을 진행하였고, 정렬된 경우와 엇갈린 경우, 그리고 수평 핀의 설치 높이가 자연대류 및 융해 속도에 영향을 주는 것을 확인하였다. Bondareva⁽¹³⁾ 등은 PCM 기반 히트싱크의 열성능에 대한 수평 핀 길이의 영향에 대해 수치해석을 진행하였고, 같은 열유속에 대하여 수평 핀의 길이가 길수록 PCM과 맞닿는 표면적이 증가하기 때문에 열성능이 높아진다는 것을 보여주었다. 이외에도, 수평 핀의 길이, 두께, 개수, 각도, 종횡비 등 다양한 인자에 따른 자연대류의 특성, PCM 융해 속도 또는 히트싱크의 바닥 온도 분포에 대해 분석하는 기초 연구가 활발히 진행되고 있다^(14–18). 하지만 기존 연구들은 대부분 직육면체 히트싱크에 대한 PCM 융해와 성능에 대해 분석한 것들이고, 원통형 히트싱크에 설치되는 다양한 수평 핀 위치에 대한 연구가 필요하다.

본 연구의 주요 목표는 PCM을 기반으로 한 원통형 히트싱크에 대해 동일한 판형의 수직 핀과 다양한 위치에 수평 핀을 설치하여 자연대류 특성, PCM의 융해 속도, 그리고 히트싱크의 바닥 온도 분포를 확인하는 것이다. 이를 위해 2차원 수치해석을 진행하였고, 수평 핀의 배열 위치 변화가 히트싱크의 냉각 성능에 미치는 영향을 확인하였다. 또한, PCM 내부의 자연대류 특성과 PCM의 융해 속도를 비교⋅분석하였다.

2. 수치해석 모델링

2.1 수치해석 모델 설명

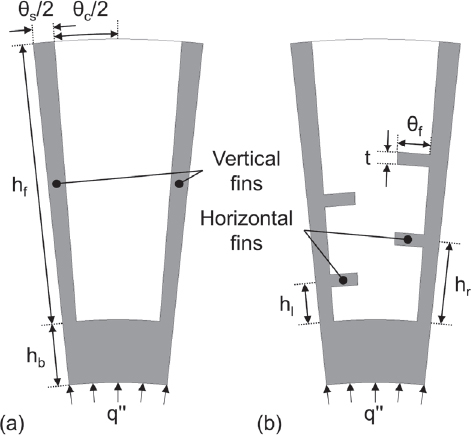
Fig. 1(a)는 본 연구에 사용된 PCM 기반 원통형 히트싱크를 등축 투영한 모습이다. 직육면체가 아닌 원통형이기 때문에 두께는 각도로 표현된다. 지름이 30 mm이고 높이가 2 mm인 원통형 바닥에 일정 간격으로 두께가 3°이고 높이가 9 mm인 수직 핀이 설치되어 있고, 그 사이에 두께가 9°인 캐비티가 만들어져 있다. Fig. 1(b)는 수치해석을 위해 설정한 단위 셀의 단면이다. 단위 셀이기 때문에 인접한 두 개의 수직 핀의 두께는 각각 절반이다. 또한, 대칭이기 때문에 단열인 것으로 가정하였다. 히트싱크의 바닥면에서 일정한 열유속이 주어지고 있고, 히트싱크의 윗면은 단열되어 있다. 수직 핀의 길이와 높이보다 z축 방향의 길이가 충분히 길고, 이전 연구^(19,20,37)를 통해 z축 방향에 대하여 단면이 일정한 경우, z축 방향으로의 효과는 무시할 수 있는 것을 확인하였다. 또한, Jeong⁽¹¹⁾ 등은 히트싱크의 전체 셀과 단위 셀에 대한 비교를 수행하였고 두 경우 간에 유의미한 차이가 없는 것을 확인하였다. 따라서, 본 연구에서는 한 가지의 캐비티 위치 각도의 단위 셀에 대하여 2차원 수치해석을 진행하였다.

Fig. 1

(a) Schematic of PCM-based cylindrical heat sink and (b) cross-sectional view of heat sink unit cell

Fig. 2는 수평 핀이 없는 형상과 있는 형상에 대한 단위 셀의 단면도를 나타낸 그림이다. Fig. 2(a)는 수평 핀이 없는 형상을 나타낸 것이고, Fig. 2(b)는 수평 핀이 있는 형상을 나타낸 것이다. 모든 경우에 대하여 수평 핀은 4개가 설치되어 있다. 수평 핀 설치 위치가 단위 셀의 수직 핀에 대하여 좌, 우측에 다른 높이로 설치되었기 때문에 각각의 길이를 무차원화 하였고 총 6가지의 경우를 분석하였다. 수평 핀의 위치 및 배치는 Table 2와 3에 정리되어있다.

Fig. 2

Schematic of cross-sectional view of heat sink unit cell (a) without horizontal fin case (Case a) and (b) with horizontal fin case (Case b)

Table 1

Geometrical dimensions of cylindrical heat sink

Table 2

Location parameters of horizontal fins placed in cylindrical heat sink

Table 3

Simulation cases for various combinations of horizontal fins presented in Table 2

본 연구에서 사용된 PCM은 n-eicosane(이코산)이다. PCM의 열물성치는 이전 연구^(21,22)를 통해 얻었다. 공기의 열물성치는 NIST(National Institute of Standards and Technology)의 REFPROP 10.0⁽²³⁾ 프로그램을 사용하여 얻었다. 또한, 히트싱크는 알루미늄으로 설정하였다. 본 연구에서 쓰인 물질의 열물성치는 Table 4에 요약되어 있다.

Table 4

Thermophysical properties of aluminum, n-eicosane(21,22), and air(23) used in this study

모든 Case에 설정된 PCM의 질량은 동일하고, 캐비티와 캐비티 내부에 있는 고체 PCM의 부피 비는 Case에 따라 85–90%로 나머지 부분은 공기로 채워져 있다. PCM이 액체로 융해할 때 밀도가 감소하므로 부피 증가를 고려한 여유 공간이 필요하기 때문이다. 히트싱크, 공기 그리고 PCM의 초기 온도는 모두 298K으로 설정하였다. PCM의 융해 전, 중, 후 과정을 고려하여 융해 온도보다 약간 낮게 설정하였고 융해 후도 일정 시간 관찰하였다.

2.2 수치해석 기법

본 연구에서는 2차원 비정상상태 해석을 위해 상용 전산유체역학 소프트웨어인 ANSYS Fluent 20.1⁽²⁴⁾을 사용하였다. 작동 유체인 공기와 액체 PCM은 모두 압축성, 층류 유동을 가지는 뉴턴 유체로 가정하였다. 연속성, 운동량 및 에너지 방정식 계산을 통해 PCM의 2차원 비정상 융해 현상과 액체 PCM의 특성을 연구했다. 공기와 PCM 사이의 경계를 모사하기 위해 Volume-of-Fluid (VOF) 모델⁽²⁵⁾을 사용하였고, PCM의 융해 현상을 나타내기 위해 Brent⁽²⁶⁾ 등에 의해 정의된 enthalpy-porosity 기법을 사용하였다. 공기와 PCM의 연속 방정식은 다음과 같이 나타낼 수 있다.

∂ ∂ t α n + ∇ ⋅ α n V n → = 0

(1)

이때, α_n과 $V n →$ 은 각각 n번째 유체의 부피 비율과 속도 벡터를 나타낸다. 1번째 유체는 공기, 2번째 유체는 액체 PCM이고, 다음의 식이 성립한다.

∑ k = 1 n α k = 1

(2)

공기와 PCM의 운동량 방정식은 다음과 같이 나타낼 수 있다.

∂ ∂ t ρ n V n → + ∇ ⋅ ρ n V n → V n → = ρ n g → - ∇ p + μ n ∇ 2 V n → + S n →

(3)

이때, ρ_n, μ_n 그리고 $S n →$ 은 각각 n번째 유체의 밀도, 점성 계수 그리고 운동량 생성항을 나타낸다. 공기는 상변화가 없기 때문에 운동량 생성항이 없다. 반면에, PCM의 운동량 생성항은 다음과 같이 나타낼 수 있다.

S 2 → = - A ϵ V 2 →

(4)

이때, ε는 전산해석의 단위 셀에 있는 액체 PCM의 비율로 정의되고 다음과 같이 나타낼 수 있다.

ϵ = 0 T < T s T - T s T l - T s T s < T < T l 1 T > T l

(5)

이때, T는 전산해석의 단위 셀의 현재 온도이고, T_s와 T_l는 각각 PCM의 고상선 온도와 액상선 온도이다. 이에 따라, 다공성 함수 A(ε)는 다음과 같이 나타낼 수 있다.

A ϵ = A m u s h 1 - ϵ 2 ϵ 3 + b

(6)

이때, b는 ε가 0일 때 함수 A의 분모가 0이 되는 것을 방지하기 위해 0.001로 정의된 작은 상수이다. 또한, A_mush는 mushy zone 상수로 대류 속도 감쇠의 크기에 영향을 주며, 크기가 커질수록 상변화 속도가 느려지는 경향이 있다^(27–29). 주로 사용되는 값의 범위는 10⁴–10⁷이며, 본 연구에서는 기본값인 10⁵로 설정하였다⁽²⁴⁾.

공기와 PCM의 에너지 방정식은 다음과 같이 나타낼 수 있다.

∂ ∂ t ρ n H n + ∇ ⋅ ρ n V n → H n = ∇ ⋅ k n ∇ T

(7)

이때, H_n과 k_n은 각각 n번째 유체의 전체 엔탈피와 열전도율을 나타낸다. 전체 엔탈피는 다음과 같이 현열 엔탈피(h)와 잠열 엔탈피(ΔH)의 합(H)으로 나타낼 수 있다.

H = h + Δ H

(8)

h = h r e f + ∫ T r e f T c p d T

(9)

Δ H = ϵ L

(10)

이때, h_ref, T_ref, c_p 그리고 L은 각각 기준 엔탈피, 기준 온도, 비열 그리고 잠열 용량이다. 또한, PCM의 상이 mushy zone에 있는 경우, 모든 열물성치는 고상선 및 액상선 온도에서 특성 값의 액체 분율 가중으로 계산된다. 열전도율의 경우는 아래와 같이 나타낼 수 있다.

k m u s h = (1 - ϵ) k T s + ϵ k T l

(11)

히트싱크의 에너지 방정식은 다음과 같이 나타낼 수 있다.

∂ ∂ t ρ a l H a l = ∇ ⋅ k a l ∇ T

(12)

이때, ρ_al, H_al 그리고 k_al은 각각 알루미늄의 밀도, 엔탈피 그리고 열전도율이다.

압력-속도 연성을 위해 Pressure-Implicit with Splitting of Operators (PISO)⁽³¹⁾ 해석기법을 사용하였고, 압력 보정을 위해 PREssure STaggering Option (PRESTO)⁽²⁴⁾을 적용하였다. 또한, 압력의 이산화에는 Second order를 사용하였고, 운동량 및 에너지 방정식의 이산화에는 Second order upwind를 사용했다.

2.3 수치해석 검증

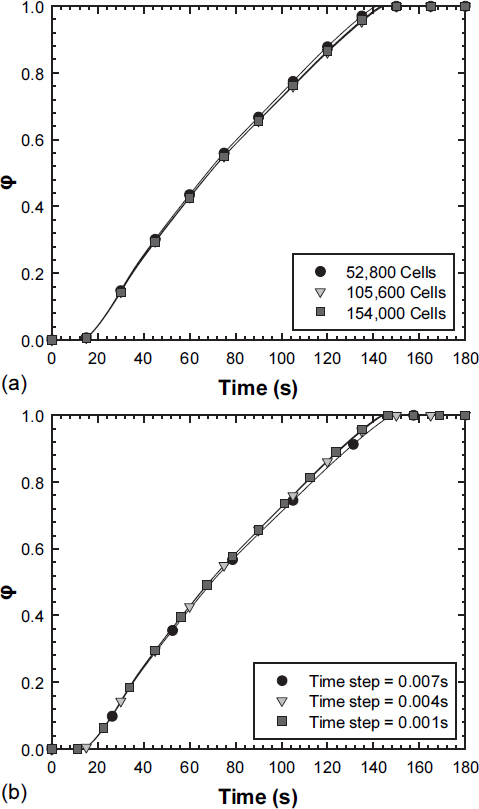
Fig. 3(a)는 Case a에 대하여 52,800, 105,600, 154,000개를 가진 격자 시스템을 이용한 격자 독립성 검증을 수행한 그림이다. 시간에 따른 PCM의 융해 비율 값이 105,600개보다 조밀한 격자일 때 차이가 거의 없는 것을 알 수 있다. 또한, Fig. 3(b)는 (a)와 같은 Case에 대하여 0.007, 0.004, 0.001 초의 총 3가지 단위 시간을 이용한 단위 시간 독립성 검증을 수행한 그림이다. 시간에 따른 PCM의 융해 비율 값이 0.004 초보다 작은 단위 시간일 때 차이가 거의 없는 것을 알 수 있다. 따라서, 본 연구에서는 105,600개의 격자와 0.004 초의 단위 시간을 선택하여 연구를 수행하였다.

Fig. 3

Time variations of liquid fraction of PCM for different (a) number of cells and (b) time step size

본 연구에서 사용된 수치해석 모델에 대한 검증은 Jeong⁽¹¹⁾ 등의 이전 연구에서 이루어졌다. Fig. 4는 Zivkovic과 Fujii⁽³⁰⁾가 이전 연구에서 얻은 PCM(CaCl₂⋅6H₂O)의 온도 변화 실험 데이터를 수치해석 모델과 비교한 그림이다. 이들은 측면을 단열한 스테인리스 재질의 직육면체 용기를 고체 PCM으로 채웠다. 그 후 등온 수조에 용기를 수직으로 넣고 용기 중앙에서 PCM의 온도 변화를 측정하였다. 수치해석을 통한 PCM의 융해 전, 중, 후 온도 변화는 실험⁽³⁰⁾으로 측정된 온도 변화와 잘 일치함을 보여주었다⁽¹¹⁾.

Fig. 4

Comparison of experimental data of the central temperature of PCM in the container measured by Zivkovic and Fujii(30) and numerical data using the current numerical model(11)

3. 수치해석 결과

3.1 PCM 유동 및 열전달 특성 분석

Fig. 5는 원통형 히트싱크 위에 있는 수직 핀의 서로 다른 위치에 수평 핀을 추가하였을 때 여러 특정 시각(40, 90, 140초)에서 PCM의 융해 비율 분포를 나타낸 것이다. 이때, 흰 배경색에 검은색 테두리는 히트싱크의 단위 셀이다. 먼저, 고체 PCM이 융해하여 액체 PCM이 되며 밀도가 줄기 때문에 공기-PCM의 경계선이 시간이 지남에 따라 상승했다. 40초가 경과하였을 때, 모든 Case에서 히트싱크의 표면부터 고체 PCM이 녹기 시작했는데, 이는 주요 열전달 방법이 전도인 것에 기인한다. 이에 따라, 시간이 지나면서 히트싱크의 표면에서 수직 방향으로 액체 PCM 층이 생기고 그 높이가 증가한다. 또한, 액체 PCM의 층이 히트싱크의 바닥과 가까울수록 높이가 더 큰 것을 알 수 있다. 일정한 열유속이 바닥을 통해 전달되므로 바닥과 인접한 PCM이 먼저 융해하며 열을 흡수하기 때문이다. 90초가 경과하였을 때, 가장 상단에 위치한 수평 핀과 공기 및 PCM 경계 사이에서 액체 PCM의 두께가 공기 방향으로 줄어들다 증가하는 것을 모든 Case에서 관찰할 수 있다. 이것은 하단에서 녹은 액체 PCM이 낮은 밀도로 인한 자연 대류로 상승한 결과이다. 또한, 상대적으로 히트싱크 수직 핀 벽면 근처의 액체 PCM이 고체 PCM과 가까운 액체 PCM보다 온도가 높기 때문에 히트싱크 주변에서 유체가 상승하고 고체 PCM 주변에서 유체가 내려가는 흐름을 보이게 된다. 그리고, 수평 핀의 하단에 위치한 액체 PCM의 양이 상단보다 많은 것을 알 수 있는데, 히트싱크의 벽면 주변에서 올라가는 액체 PCM의 유동을 수평 핀이 방해하기 때문이다. 수평 핀의 상단은 더 이상 수평 핀이 액체 PCM의 유동을 방해하지 않기 때문에 다음 수평 핀 혹은 공기와의 경계면 주변까지 올라가게 된다. 이처럼, 초기 주 열전달은 전도를 통해 이루어지지만 고체보다 2배 이상 낮은 열전도율을 가진 액체 PCM 층이 두꺼워질수록 주 열전달이 자연 대류로 변화하게 된다. 140초가 경과하였을 때, 모든 Case에서 주를 이루는 열전달 방법은 대류이다. 액체 PCM의 유속은 상당히 느리고 열전도율 또한 매우 낮기 때문에 액체 PCM 층이 두꺼운 부분일수록 녹는 속도는 느려지고, Case에 따라 남은 고체 PCM의 위치가 달라지게 된다. Case a의 경우, 히트싱크의 벽면 주변의 고체 PCM이 녹으며 점차 중앙 부분만 남게 되는 것을 알 수 있다. 벽면 주변에서 상승했던 액체 PCM은 중앙의 고체 PCM의 표면을 따라 내려가며 열을 전달하고 융해한다. PCM의 열전도율이 매우 낮고, 액체 PCM이 벽면 주변에서 상승하고 중앙 부분에서는 내려가는 특성으로 인해 벽면과 먼 중앙 바닥 부분에서 자연 대류의 흐름은 열유속의 반대 방향을 이루게 된다. 이러한 현상은 히트싱크 중앙 바닥 부분의 PCM이 완전히 융해되는데는 다른 Case에 비해 상대적으로 긴 시간이 소요된다. Case b의 경우, 바닥에서 열이 올라오고 핀 또한 상대적으로 바닥 가까이 위치하고 있기 때문에, 상단의 액체 PCM의 두께가 매우 두껍고 이로 인해 가장 늦게 융해하게 된다. Case c의 경우, PCM의 하단 왼쪽과 상단 오른쪽이 상대적으로 넓은 공간을 가지고 있는데, 일정한 열유속이 바닥을 통해 올라오기 때문에 왼쪽을 포함한 하단이 먼저 녹고 마지막으로 상단에만, 특히 오른쪽 근처로 고체 PCM이 남게 된다. Case d의 경우, 모든 핀이 상대적으로 상단에 위치하고 있기 때문에 하단에 위치한 고체 PCM은 수평 핀의 열전도의 향상을 얻을 수 없다. 이로 인해, 상단에 위치한 고체 PCM이 모두 녹은 이후 융해 속도가 크게 감소한다. Case e의 경우, 핀이 하단과 상단에 위치하고 있고 중단이 가장 공간이 넓기 때문에 중앙 부분에 고체 PCM이 남게 된다. Case f의 경우, 핀의 위치가 하단 왼쪽, 상단 오른쪽에 위치하고 있고 각각에 상대적으로 넓은 공간이 형성된다. 일정한 열유속이 바닥을 통해 올라오며 PCM으로 열이 전달되기 때문에 상단에만 고체 PCM이 남게 된다.

Fig. 5

Liquid fraction distributions of PCM at different specific times for (a) Case a, (b) Case b, (c) Case c, (d) Case d, (e) Case e, and (f) Case f

Fig. 6은 원통형 히트싱크 위에 있는 수직 핀의 서로 다른 위치에 수평 핀을 추가하였을 때 여러 특정 시각(40, 90, 140초)에서 시스템의 온도 분포를 나타낸 것이다. 바닥에서 열이 전달되고 히트싱크는 PCM보다 상당히 높은 열전도율을 가졌기 때문에 시스템 전반적으로 상단보다 하단의 온도가, PCM보다 히트싱크의 온도가 높다. 시간이 지나며 전체적인 온도가 상승하는데, 고체 PCM은 상변화를 하는 과정에서 잠열을 흡수하며 온도를 일정하게 유지하기 때문에 시간이 지나도 온도 변화가 거의 없게 된다. 히트싱크의 벽면에서 고체 PCM으로 열이 전달되며 완전히 융해된 액체 PCM은 잠열 흡수 과정을 끝내고 현열 흡수로 다시 온도가 오르게 시작한다. 또한, PCM의 열전도율은 상당히 낮기 때문에 시간이 지남에 따라 히트싱크 벽면의 수직 방향으로 PCM의 온도 구배가 커지는 것을 알 수 있다. 40초가 경과하였을 때, Case a의 경우만 온도가 비교적으로 높은 것을 알 수 있다. 다른 경우에 비해 히트싱크의 작은 부피로 열용량이 작기 때문이다. 90초가 경과하였을 때, Case a를 제외하고 모두 비슷한 온도 분포를 보이지만, 140초가 경과하였을 때, 즉, 대부분의 PCM이 녹았을 때, Case에 따라 온도 분포가 다른 것을 알 수 있다. Case a가 시스템의 상⋅하단 모두에서 가장 높은 온도를, Case c가 가장 낮은 온도를 갖는다.

Fig. 6

Temperature distributions of system at different specific times for (a) Case a, (b) Case b, (c) Case c, (d) Case d, (e) Case e, and (f) Case f

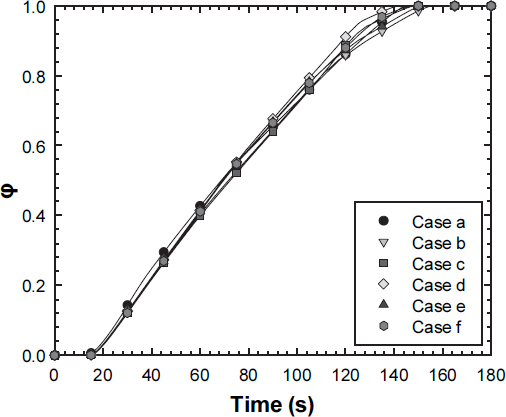
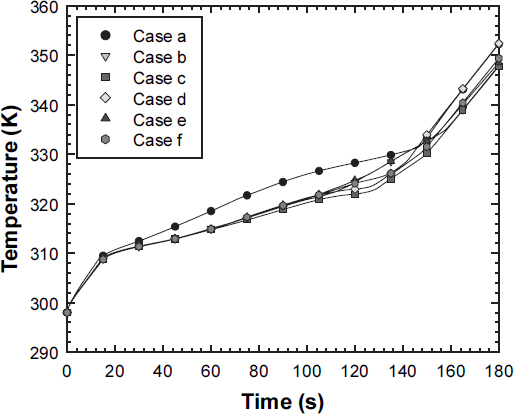
Figs. 7과 8은 원통형 히트싱크 위에 있는 수직 핀의 서로 다른 위치에 수평 핀을 추가하였을 때 시간에 따른 PCM의 융해 비율 변화와 히트싱크 밑면 바닥의 온도 변화를 나타낸 것이다. 초기 온도는 모두 25°C로 PCM의 융해점보다 낮기 때문에 융해점에 도달할 때까지 히트싱크의 온도는 일정하게 상승한다. PCM은 열전도율이 낮기에, 히트싱크의 벽면 근처에서 전달된 열은 매우 느리게 중앙 부분의 PCM으로 전달된다. Case a가 온도가 더 빠르게 상승하는데, 이는 수평 핀을 추가하면서 그만큼 히트싱크의 열용량이 증가했기 때문이다. PCM의 융해점에 도달하면 PCM이 융해하며 잠열을 흡수하기 때문에 히트싱크 바닥의 온도 변화 기울기가 줄게 된다. 융해 시작부터 40초 부근까지 Case a의 융해 비율이 더 빠르게 상승하는데, 이는 히트싱크의 작은 열용량으로 인해 더 빠르게 열이 PCM으로 전도되기 때문이다. 40초 이후부터 Case a는 전도의 영향은 줄기 시작하고 자연 대류의 영향이 커지면서 융해 비율 증가 기울기는 감소하고 히트싱크의 바닥 온도 상승은 빨라지게 된다. Case d, e 그리고 f는 공통적으로 Fin 6을 가지고 있다. Fin 6은 가장 높은 곳에 위치해 있고 그보다 위에 있는 PCM의 양은 적기 때문에 빨리 융해된다. 하지만 이는 히트싱크의 바닥과 거리가 가장 크고 이로 인해 온도 불균형을 이루어 히트싱크의 바닥 온도에 영향을 주지 못한다. Case b의 경우, 모든 핀이 하단에 위치하고 있어 90초 이후부터 바닥에서 올라오는 열이 상단에 남은 고체 PCM에 느리게 전달된다. 하단의 액체 PCM 또한 수평 핀으로 인해 자연 대류에 방해를 받게 되고 온도 상승은 빨라지게 된다. Case e의 경우 또한 하단 두 개의 수평 핀으로 인해 큰 온도 분포의 불균형을 만들어 온도 상승이 빨라졌다. Case d의 경우 상단 고체 PCM이 모두 녹은 이후 융해 속도가 가장 크게 감소하기 때문에 바닥 온도 상승 속도가 크게 증가한다. 또한, PCM이 모두 녹기 전까지 가장 빨리 모두 융해하기 때문에 융해 이후 Case a와 비슷한 온도를 갖게 된다. Case c의 경우, Fin 1과 6이 없어서 다른 Case와 비교했을 때 하단에서의 열 정체와 초기 상단에서의 급격한 융해 이후 감소가 없어, 비교적 일정한 융해 속도를 보이며 바닥에서의 열전달도 효과적으로 이루어졌다. 그 결과, Case c가 가장 낮은 온도를 유지하였다.

Fig. 7

Time variations of liquid fraction of PCM for different horizontal fin locations

Fig. 8

Time variations of base temperature of heat sink for different horizontal fin locations

3.2 히트싱크 냉각 성능 평가

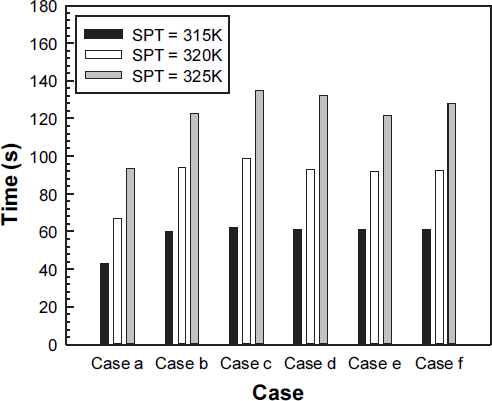
Fig. 9는 특정 온도에 도달하는데 걸리는 시간을 나타낸 것이다. Case a는 모든 특정 온도에 도달하는데 걸리는 시간이 가장 빠르다. 나머지 Case는 모두 수평 핀 추가로 생기는 표면적 증가로 열전도 면적이 증가했고 비슷한 도달 시간을 보였다. Case c의 경우, 상대적으로 낮은 온도 상승을 보였고, 320K와 325K에 도달하는데 걸리는 시간이 가장 긴 것을 알 수 있다. Case b와 e의 경우, Fin 1과 2가 하단에서 올라오는 열을 상승하지 못하게 막는 역할을 하게 되었고 온도가 빠르게 상승하여 온도 도달 시간이 비교적 짧은 것을 알 수 있다.

Fig. 9

Time to reach three different SPTs (315K, 320K, and 325K) for different horizontal fin locations

4. 결 론

본 연구에서는 PCM 기반 원통형 히트싱크의 수평 핀 위치에 따른 융해 비율과 히트싱크의 바닥 온도 분포 특성을 확인하기 위해 2차원 수치해석을 진행하였다. 원통형 히트싱크의 단위 셀을 이용하여 분석하였고, 일정한 간격의 수평 핀을 다양하게 배치하였을 때 PCM의 융해 비율 속도와 히트싱크의 바닥 온도 변화에 대한 결과를 요약하면 다음과 같다.

1) 수평 핀이 없는 형상보다 수평 핀이 있는 형상에서 열전도에 대한 표면적이 증가하고 PCM으로의 열 흡수 증가하므로 낮은 온도 상승을 보였다.
2) 초기 융해 속도에 영향을 미치는 것은 열전도를 위한 히트싱크의 표면적이며 히트싱크의 표면 근처에 있는 PCM이 모두 녹은 시점부터 전도보다 자연 대류로 인한 영향이 증가하였다.
3) 수평 핀은 자연 대류를 방해하지만 표면적 증가로 인한 히트싱크의 바닥 온도 증가율 감소 효과가 더 크다.
4) 하단에 수평 핀이 비슷한 위치에 있을 경우, 하단에서 올라오는 열이 PCM의 낮은 열전도율과 하단 수평 핀의 자연 대류 방해로 인한 액체 PCM의 정체 효과로 불균일한 온도 분포를 보이고 히트싱크 바닥의 높은 온도를 이룬다.
5) 상단에 수평 핀이 비슷한 위치에 있을 경우, 초기 상단에 효과적인 융해 속도를 보이지만 히트싱크 바닥과 가장 먼 위치에 있어 바닥의 온도에 큰 영향을 주지 못한다.
6) 수평 핀이 있는 형상이 수평 핀이 없는 형상보다 SPT 도달 시간이 최대 44%가 증가하였다(Case a와 c의 325K 도달 시간).
7) 수평 핀의 배치에 따라 SPT 도달 시간이 달라질 수 있고, 최대 11%의 차이를 보였다(Case c와 e의 325K 도달 시간).
8) 본 연구에서는 한 가지의 캐비티 위치 각도의 단위 셀에 대한 자연대류 특성, PCM의 융해 속도, 그리고 히트싱크의 바닥 온도 분포를 분석하였으며, 향후 다른 위치 각도에 대한 캐비티 내 PCM의 특성을 조사하고자 한다.

Acknowledgments

본 연구는 2021년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. NRF2021R1A6A1A03039696).

References

Fok, S. C., Shen, W., and Tan, F. L., 2010, “Cooling of portable hand-held electronic devices using phase change materials in finned heat sinks,” International Journal of Thermal Sciences, Vol. 49, No. 1, pp. 109-117. [https://doi.org/10.1016/j.ijthermalsci.2009.06.011]
Geng, J., Wu, J., Yang, J., Fu, M., and Weng, W., 2023, “Numerical simulation of cooling effect of human-PCM-clothing model in hot environments,” International Journal of Thermal Sciences, Vol. 192, pp. 108393. [https://doi.org/10.1016/j.ijthermalsci.2023.108393]
Souayfane, F., Fardoun, F., and Biwole, P. H., 2016, “Phase change materials (PCM) for cooling applications in buildings: A review,” Energy and buildings, Vol. 129, pp. 396-431. [https://doi.org/10.1016/j.enbuild.2016.04.006]
Algarni, S., 2023, “Evaluation and optimization of the performance and efficiency of a hybrid flat plate solar collector integrated with phase change material and heat sink,” Case Studies in Thermal Engineering, Vol. 45, pp. 102892. [https://doi.org/10.1016/j.csite.2023.102892]
Raj, C. R., Suresh, S., Bhavsar, R. R., Singh, V. K., and Govind, K. A., 2020, “Influence of fin configurations in the heat transfer effectiveness of Solid solid PCM based thermal control module for satellite avionics: Numerical simulations,” Journal of Energy Storage, Vol. 29, pp. 101332. [https://doi.org/10.1016/j.est.2020.101332]
Murshed, S. S., and De Castro, C. N., 2017, “A critical review of traditional and emerging techniques and fluids for electronics cooling,” Renewable and Sustainable Energy Reviews, Vol. 78, pp. 821-833. [https://doi.org/10.1016/j.rser.2017.04.112]
Atear, O. E., 2006, “Storage Of Thermal Energy, Encyclopedia of Life Support Systems,” Mechanical Engineering Department, Gazi University.
Dinker, A., Agarwal, M., and Agarwal, G. D., 2017, “Heat storage materials, geometry and applications: A review,” Journal of the Energy Institute, Vol. 90, No. 1, pp. 1-11. [https://doi.org/10.1016/j.joei.2015.10.002]
Qureshi, Z. A., Ali, H. M., and Khushnood, S., 2018, “Recent advances on thermal conductivity enhancement of phase change materials for energy storage system: a review,” International Journal of Heat and Mass Transfer, Vol. 127, pp. 838-856. [https://doi.org/10.1016/j.ijheatmasstransfer.2018.08.049]
Maqbool, Z., Hanief, M., and Parveez, M., 2023, “Review on performance enhancement of phase change material based heat sinks in conjugation with thermal conductivity enhancers for electronic cooling,” Journal of Energy Storage, Vol. 60, pp. 106591. [https://doi.org/10.1016/j.est.2022.106591]
Jeong, J. H., Hah, S., Kim, D., Lee, J. H., and Kim, S. M., 2020, “Thermal analysis of cylindrical heat sinks filled with phase change material for high-power transient cooling,” International Journal of Heat and Mass Transfer, Vol. 154, pp. 119725. [https://doi.org/10.1016/j.ijheatmasstransfer.2020.119725]
Kim, S. H., Park, S. H., Pandey, S., and Ha, M. Y., 2023, “Effects of fin positioning on the thermal performance of a phase change material–filled heat sink with horizontal fins,” Journal of Energy Storage, Vol. 68, pp. 107756. [https://doi.org/10.1016/j.est.2023.107756]
Bondareva, N. S., Ghalambaz, M., and Sheremet, M. A., 2021, “Influence of the fin shape on heat transport in phase change material heat sink with constant heat loads,” Energies, Vol. 14, No. 5, pp. 1389. [https://doi.org/10.3390/en14051389]
Mao, Q., Li, Y., Li, G., and Badiei, A., 2021, “Study on the influence of tank structure and fin configuration on heat transfer performance of phase change thermal storage system,” Energy, Vol. 235, pp. 121382. [https://doi.org/10.1016/j.energy.2021.121382]
Izadi, M., Hajjar, A., Alshehri, H. M., Saleem, A., and Galal, A. M., 2022, “Analysis of applying fin for charging process of phase change material inside H-shaped thermal storage,” International Communications in Heat and Mass Transfer, Vol. 139, pp. 106421. [https://doi.org/10.1016/j.icheatmasstransfer.2022.106421]
Sharifi, N., Bergman, T. L., and Faghri, A., 2011, “Enhancement of PCM melting in enclosures with horizontally-finned internal surfaces,” International journal of heat and mass transfer, Vol. 54, No. 19-20, pp. 4182-4192. [https://doi.org/10.1016/j.ijheatmasstransfer.2011.05.027]
Kalbasi, R., and Salimpour, M. R., 2015, “Constructal design of horizontal fins to improve the performance of phase change material rectangular enclosures,” Applied Thermal Engineering, Vol. 91, pp. 234-244. [https://doi.org/10.1016/j.applthermaleng.2015.08.024]
Mosavi, A., Mehdizadeh, H., Abbasian-Naghneh, S., Kalbasi, R., Karimipour, A., and Cheraghian, G., 2020, “Incorporation of horizontal fins into a PCM-based heat sink to enhance the safe operation time: applicable in electronic device cooling,” Applied Sciences, Vol. 10, No. 18, pp. 6308. [https://doi.org/10.3390/app10186308]
Hosseinizadeh, S. F., Tan, F. L., and Moosania, S. M., 2011, “Experimental and numerical studies on performance of PCM-based heat sink with different configurations of internal fins,” Applied Thermal Engineering, Vol. 31, No. 17-18, pp. 3827-3838. [https://doi.org/10.1016/j.applthermaleng.2011.07.031]
Kozak, Y., Abramzon, B., and Ziskind, G., 2013, “Experimental and numerical investigation of a hybrid PCM–air heat sink,” Applied Thermal Engineering, Vol. 59, No. 1-2, pp. 142-152. [https://doi.org/10.1016/j.applthermaleng.2013.05.021]
Humphries, W. R., and Griggs, E. I., 1977, “A design handbook for phase change thermal control and energy storage devices,” No. NASA-TP-1074.
Vélez, C., Khayet, M., and De Zárate, J. O., 2015, “Temperature-dependent thermal properties of solid/liquid phase change even-numbered n-alkanes: n-Hexadecane, n-octadecane and n-eicosane,” Applied Energy, Vol. 143, pp. 383-394. [https://doi.org/10.1016/j.apenergy.2015.01.054]
Lemmon, E. W., Huber, M. L., and McLinden, M. O., 2018, “REFPROP 10.0,” NIST Standard Reference Database 23.
ANSYS Inc., ANSYS Fluent Theory Guide, Canons burg, PA: release 20.1, 2019.
Hirt, C. W., and Nichols, B. D., 1981, “Volume of fluid (VOF) method for the dynamics of free boundaries,” Journal of computational physics, Vol. 39, No. 1, pp. 201-225. [https://doi.org/10.1016/0021-9991(81)90145-5]
Brent, A. D., Voller, V. R., and Reid, K. T. J., 1988, “Enthalpy-porosity technique for modeling convection-diffusion phase change: application to the melting of a pure metal,” Numerical Heat Transfer, Part A Applications, Vol. 13, No. 3, pp. 297-318. [https://doi.org/10.1080/10407788808913615]
Cabeza, L. F., 2021, “Advances in thermal energy storage systems: Methods and applications,” Woodhead Publishing. [https://doi.org/10.1016/B978-0-12-819885-8.00002-4]
Kumar, M., and Krishna, D. J., 2017, “Influence of mushy zone constant on thermohydraulics of a PCM,” Energy Procedia, Vol. 109, pp. 314-321. [https://doi.org/10.1016/j.egypro.2017.03.074]
Fadl, M., and Eames, P. C., 2019, “Numerical investigation of the influence of mushy zone parameter Amush on heat transfer characteristics in vertically and horizontally oriented thermal energy storage systems,” Applied Thermal Engineering, Vol. 151, pp. 90-99. [https://doi.org/10.1016/j.applthermaleng.2019.01.102]
Zivkovic, B., and Fujii, I., 2001, “An analysis of isothermal phase change of phase change material within rectangular and cylindrical containers,” Solar energy, Vol. 70, No. 1, pp. 51-61. [https://doi.org/10.1016/S0038-092X(00)00112-2]
Issa, R. I., 1986, “Solution of the implicitly discretised fluid flow equations by operator-splitting,” Journal of computational physics, Vol. 62, No. 1, pp. 40-65. [https://doi.org/10.1016/0021-9991(86)90099-9]
Agyenim, F., Hewitt, N., Eames, P., and Smyth, M., 2010, “A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS),” Renewable and sustainable energy reviews, Vol. 14, No. 2, pp. 615-628. [https://doi.org/10.1016/j.rser.2009.10.015]
Velmurugan, K., Kumarasamy, S., Wongwuttanasatian, T., and Seithtanabutara, V., 2021, “Review of PCM types and suggestions for an applicable cascaded PCM for passive PV module cooling under tropical climate conditions,” Journal of Cleaner Production, Vol. 293, pp. 126065. [https://doi.org/10.1016/j.jclepro.2021.126065]
Abdulateef, A. M., Mat, S., Abdulateef, J., Sopian, K., and Al-Abidi, A. A., 2018, “Geometric and design parameters of fins employed for enhancing thermal energy storage systems: a review,” Renewable and Sustainable Energy Reviews, Vol. 82, pp. 1620-1635. [https://doi.org/10.1016/j.rser.2017.07.009]
Ali, H. M., Janjua, M. M., Sajjad, U., and Yan, W. M., 2019, “A critical review on heat transfer augmentation of phase change materials embedded with porous materials/foams,” International Journal of Heat and Mass Transfer, Vol. 135, pp. 649-673. [https://doi.org/10.1016/j.ijheatmasstransfer.2019.02.001]
Tariq, S. L., Ali, H. M., Akram, M. A., Janjua, M. M., and Ahmadlouydarab, M., 2020, “Nanoparticles enhanced phase change materials (NePCMs)-A recent review,” Applied Thermal Engineering, Vol. 176, pp. 115305. [https://doi.org/10.1016/j.applthermaleng.2020.115305]
Saha, S. K., Srinivasan, K., and Dutta, P., 2008, “Studies on optimum distribution of fins in heat sinks filled with phase change materials,” Journal of Heat Transfer, Vol. 130, pp. 034505. [https://doi.org/10.1115/1.2804948]

Fin location	h_l/h_f	h_r/h_f
Fin 1	1/7	-
Fin 2	-	2/7
Fin 3	3/7	-
Fin 4	-	4/7
Fin 5	5/7	-
Fin 6	-	6/7

Case	Fin arrangement
a	No fin
b	Fin 1－4
c	Fin 2－5
d	Fin 3－6
e	Fin 1, 2, 5, 6
f	Fin 1, 3, 4, 6

Aluminum
Density (kg/m³), ρ_al	2719
Specific heat (kJ/kg⋅K), c_p,al	0.871
Thermal conductivity (W/m⋅K), k_al	202.4
n-eicosane
Density (kg/m³), ρ_PCM	838 (Solid) 749 (Liquid)
Dynamic viscosity (kg/m⋅s), μ_PCM	1.73 × 10^-3
Specific heat (kJ/kg⋅K), c_p,PCM	1.85 (Solid) 2.45 (Liquid)
Thermal conductivity (W/m⋅K), k_PCM	0.40 (Solid) 0.15 (Liquid)
Melting temperature (K), T_s–T_l	308.10–310.94
Latent heat (kJ/kg), L	247
Air
Density (kg/m³), ρ_air	1.061
Dynamic viscosity (kg/m⋅s), μ_air	2.021 × 10^-5
Specific heat (kJ/kg⋅K), c_p,air	1.007
Thermal conductivity (W/m⋅K), k_air	0.0285