오토인코더 기반의 머신러닝을 통한 가스터빈 연소기에서의 연소불안정 진단
Abstract
Various diagnostic models for combustion instability based on statistical techniques and machine learning using measured or monitored data are being developed to suppress instabilities in power generation gas turbines. In this paper, we proposed a combustion state diagnosis model using an auto-encoder, one of machine learning approaches. This model has been trained using two main input components; magnitude and waveform pattern of time series dynamic pressure which is measured from a real-scale single nozzle gas turbine combustor. As a result of training, the model could successfully classify the pre-processed input data into stable, transition, and unstable states onto the feature map of the latent space. Especially, in contrast with existing combustion instability monitoring tools based on statistical techniques, the current auto-encoder model provided accurate combustion state diagnosis performance for stable and transition states of dynamic pressure.
Keywords:
Combustion Instability, Dynamic Pressure, Waveform Pattern, Auto-Encoder키워드:
연소 불안정, 동압, 파형 패턴, 오토인코더1. 서 론
가스터빈 연소기의 연소상태를 안정적으로 유지하는 것은 엔진 운전효율의 극대화와 운영비용 감소 측면에서 매우 중요하다. 연소상태는 다양한 운전 인자에 민감하게 기인하는 특징이 있으며, 비정상적 연소의 발생 시 연소 진동이 발생하거나 질소산화물이나 일산화탄소와 같은 대기오염물질의 발생량이 증가하는 현상(1-3)이 나타나게 된다. 여기서, 연소상태의 이상 유무는 가스터빈 연소기의 연소실 부근에 장착된 센서들로부터 계측되는 신호들의 모니터링을 통해 파악하고 있으며 특히, 연소 진동의 경우 동압 신호를 고속으로 샘플링하여 얻은 크기와 주파수 정보를 통해 이상 유무를 감지한다. 하지만, 이 방법은 연소 동압 신호가 과도 응답 상태(transient response states)일 때 좋지 않은 분해 성능을 보이며 빠른 시간에 변화하는 연소상태의 과도적 특성(4)을 파악하기 어렵다.
최근에는 이러한 어려움에 대응하여 연소상태를 진단하기 위한 다양한 연구가 시도되고 있다. 특히, 샘플링한 동압 신호의 통계적 특성을 파악하여 연소상태의 이상 상태를 기존의 모니터링 방법보다 조기에 진단하는 연구 결과들(4-7)이 발표되고 있으며, 이 기법들은 기존의 모니터링 기법과 비교하였을 때 동압 신호가 불안정 상태로의 천이 시에 나타나는 큰 진폭의 정현파(sinusoidal wave)에 가까울 때 의미 있는 조기 감지 성능을 보였다. 하지만, 신호가 간헐적인 불안정을 보이거나 낮은 진폭을 보일 때는 감지 성능이 악화되는 것으로 나타났다.
이와 더불어 머신러닝(machine learning)을 활용한 가스터빈 연소불안정 조기 감지에 관한 연구도 활발하게 진행되고 있다(8,9). 이들 연구에서는 실험실 규모에서 광계측이 가능하도록 설계된 연소기로부터 취득한 화염 이미지를 머신러닝 기술에 적용하였을 때 연소불안정 특성을 효과적으로 진단할 수 있다고 보고하였다. 그러나, 발전용 가스터빈의 경우 연소실 내부 화염 계측이 어렵기 때문에 해당 기술은 실제 적용 측면에서 한계점이 존재한다.
본 연구에서는 발전용 가스터빈의 실시간 모니터링 인자인 연소실 내부 동압 신호 데이터를 활용한 머신러닝 기반의 연소상태 진단모델을 소개하고자 한다. 일부 연구기관에서도 가스터빈 연소기에서 동압 신호 데이터에 대한 머신러닝 모델 적용 연구가 발표되었으며(10), 본 논문은 오토인코더(auto-encoder) 모델을 활용하였다. 오토인코더 모델은 입력 데이터가 가진 특성을 잠재 공간으로 저차원화시켜 이를 분류 및 분석할 수 있는 특징을 갖고 있으며 이러한 특징으로 인하여 이미지의 특징을 추출 및 분류(11)하는 등 다양한 분야에 적용되고 있는 머신러닝 기법이다. 현재의 연구는 이러한 오토인코더의 기본적인 특징을 가스터빈에서 발생하는 연소불안정 신호에 적용하여, 계측 동압 신호의 특성을 분류 및 분석하여 연소상태 진단모델을 구축하고자 한다.
2. 오토인코더 및 동압 데이터의 통계적 처리
2.1 오토인코더(auto-encoder)
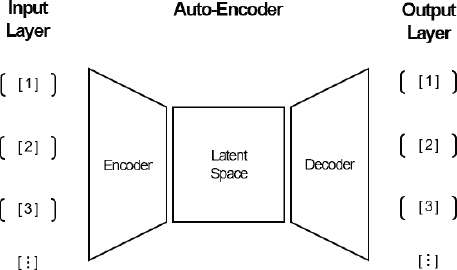
본 연구에서 연소불안정 진단모델 구축을 위하여 채택한 오토인코더 모델은 Fig. 1에 나와 있는 것과 같이 구조적으로 크게 인코더(encoder)와 잠재 공간(latent space) 그리고 디코더(decoder) 세 가지의 구성요소로 이루어진다. 이 모델의 학습 방식은 우선, 입력 데이터의 고차원 정보를 인코딩 과정을 통해 잠재 공간에 축소하여 저차원화시키고, 축소된 정보를 다시 디코딩 과정을 거쳐 원래 형태와 가깝게 복원시키는 방식으로 진행되며 이 과정에서 각 층(layer)에 있는 학습 파라미터들을 최적화시킨다. 이 방법은 입력 데이터가 가진 특성을 잠재 공간에 저차원 정보로 압축시키는 역할을 하는 인코더의 파라미터를 학습하는 것이 목표이다(11). 여기서 인코더란 Fig. 1에서 보이듯 입력층(input layer)과 잠재 공간(latent space) 사이에 존재하며, 입력층으로부터 일정한 데이터 크기를 갖고 튜플(tuple)화 된 입력 데이터를 전달받아 인코더를 구성하는 차원 축소 층에 통과시킴으로써 입력 데이터의 크기를 감소시키며 최종적으로, 잠재 공간으로 이를 출력하는 역할을 한다. 인코더는 구조적으로 여러 개의 은닉층(hidden layer)을 가지며, 입력 데이터의 크기나 목표로 하는 잠재 공간의 크기에 따라 자유로운 구조의 변경이 가능하다. 잠재 공간은 인코더와 디코더 중간에 존재하는 하나의 은닉층이며, 인코더의 출력 및 디코더의 입력 역할을 담당한다. 마지막으로 디코더는 잠재 공간과 출력층 사이에 존재하며, 구조적으로 인코더의 은닉층을 반대로 뒤집은 구조를 갖는다. 잠재 공간으로부터 데이터를 입력받아 출력층(output layer)으로 데이터의 크기를 원시 상태의 입력 데이터 즉, 인코더 이전의 입력 데이터가 갖고 있던 데이터의 크기로 복원시키는 역할을 한다.
본 연구는 실제 발전용 가스터빈에서 모니터링 인자로 활용되고 있는 동압 신호 데이터를 입력 데이터로 활용하여 오토인코더 모델에 학습시킨다. 이는 과거에 연소기의 운전과정에서 축적된 빅데이터(big data)를 기반으로 진단모델을 구축하는 것으로써, 기존에 연소기 운전 과정에서 얻어진 연소불안정 발생 상황을 학습시켜 차후의 연소기 운전과정에서 발생한 연소불안정과의 유사성을 비교 및 분석할 수 있는 특징이 있다. 즉, 경험적인 판단 기준(empirical criterion)을 오토인코더 모델에 학습시킬 수 있으며, 이를 통해 연소불안정의 발생을 조기에 진단하여 이를 회피하는 제어전략을 수립할 수 있다. 이를 위하여, 연소 동압 데이터의 전통적인 분석 기법인 RMS(Root Mean Square)를 포함한 다양한 통계적 데이터 처리 방법을 입력층(input layer)의 활용 인자로 검토하였고, 다음 절에 이를 자세히 소개할 예정이다.
2.2 연소 동압 측정 리그 및 조건과 데이터의 통계적 처리
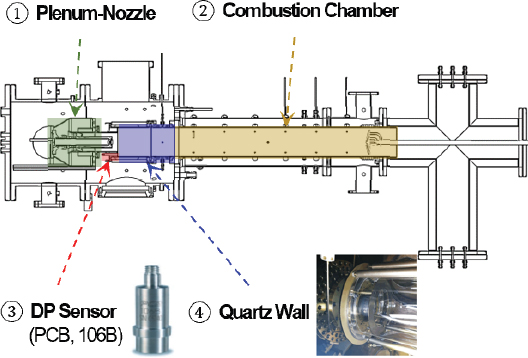
본 연구에서 연소불안정 진단모델 개발을 위하여 사용한 실험데이터의 대상 연소기는 한국기계연구원(Korea Institute of Machinery & Materials)에서 300 MWe급 대형 발전용 가스터빈을 대상으로 50 % 수소혼소 연구를 진행할 목적으로 제작한 실스케일 단일노즐 연소시험 설비이며, 해당 연소기에 대한 개략도를 Fig. 2에 나타내었다. 그림과 같이 덤프면(dump plane)에 장착된 동압 센서(106B, PCB사)에서 측정된 동압 신호를 진단모델 개발에 활용하였으며 이때 샘플링 주파수는 10 kHz였다. 연소시험은 정압 130 kPa과 흡기온도 445 ℃, 당량비 0.419∼0.503 조건에서 운전되었으며, 연료는 수소-천연가스 혼합 연료로, 연료 중 수소의 부피비를 0∼50 %로 가변하여 얻은 동압 데이터를 계측하였다. 특히 연료 조성의 변화는 연소불안정 특성에 큰 영향을 미치게 되는데, 이에 대한 세부 분석 결과는 저자들의 이전일련의 연구 결과들(12)에 자세히 기술되어 있다. 본 연구에서는 운전 조건에 따른 불안정 특성 그 자체의 해석보다는 운전 조건과 관계없이, 동압 신호의 진폭 및 파형과 같은 신호 고유의 특징에 착안한 불안정 특성 진단모델 개발을 관심 대상으로 선정하였기에, 연료 조성에 따른 불안정 특성의 상관 관계에 대한 설명은 저자들의 이전 결과를 참고하기를 바란다.
최근 국내외 다양한 연구 그룹(5-7)에 의하여 연소불안정에 대한 선제적 예측 및 정밀한 분석을 위해 동압 신호의 크기와 주파수를 모니터링하는 기존의 방법 이외에 다양한 통계적 기법들을 활용하여 동압 신호를 진단 및 분석하는 연구가 이루어지고 있다. 대표적으로 RMS, TK(5)(Temporal Kurtosis), PE(6)(Permutation Entropy), 그리고 ZCR(7)(Zero Crossing Rate) 등의 기법이 연소불안정 조기 진단에 적용되어 그 실효성이 분석된 바가 있으며, 본 논문의 저자들은 이전 연구(13)를 통하여 이들의 특징을 비교한 바가 있다. 현재 논문에서는 이 기법들에 대한 간략한 설명 및 대상 동압 신호의 분석 결과만을 소개하며, 각 기법에 대한 세부적 설명은 저자들의 비교 논문(13)과 각 해당 기법의 기존 연구(5-7)를 참고하기를 바란다.
Fig. 3은 대상 연소기로부터 얻은 1초 동안의 서로 다른 4가지의 동압 신호 데이터(Stable, Transition 1, Transition 2, Unstable)에 대해 RMS, TK, PE 및 ZCR을 적용하여 연소상태를 분석한 결과를 나타낸 것이다. 결과의 분석은 서로 다른 크기의 진폭을 갖는 동압 신호에 대하여 각각 이루어졌으며, “Stable”은 매우 작은 진폭을 가지며 노이즈(noise)에 가까운, 즉 안정한 경우를 대표하는 데이터이고, “Unstable”은 데이터 구간 내에서 모두 RMS 기준 1.3 kPa 이상(p′/ 기준 1 % 이상)으로써, 신호가 정현파(sine wave)에 가까운 불안정한 경우를 대표한다. 반면에, “Transition-1”과 “Transition-2”는 앞선 두 신호의 과도기적(transitional) 성격을 보이는 구간을 나타낸다.
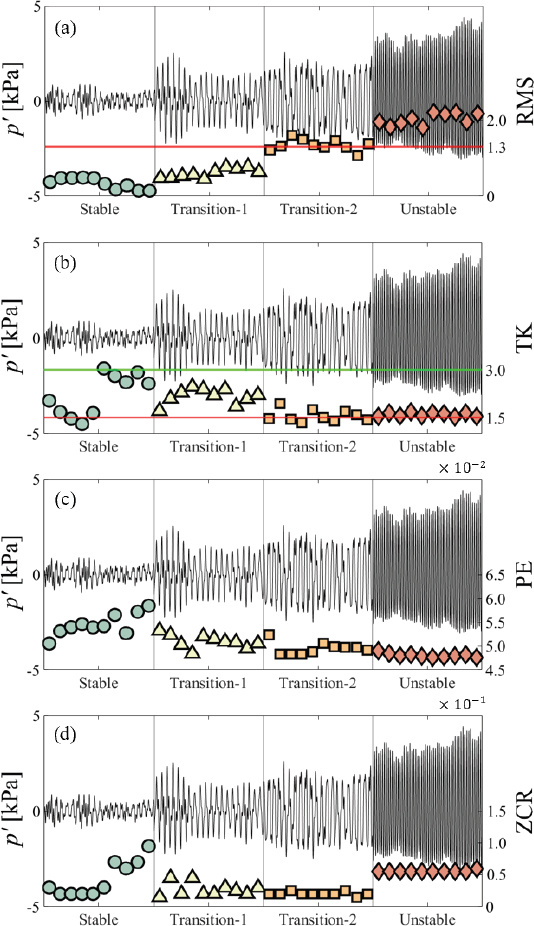
Statistical analysis results for four different dynamic pressure data; (a) RMS, (b) TK, (c) PE, (d) ZCR
우선, Fig. 3(a)는 전통적인 연소 동압 신호 모니터링 기법인 RMS 기법의 적용을 통해 각각의 상태영역에서 동압 신호의 크기를 컷오프(cutoff) 레벨과 비교하여 나타낸 것이다. 이때, 컷오프 레벨은 연소기 운전 정압인 130 kPa의 1 %인 1.3 kPa로 정의하였다. 동압 신호의 크기는 안정 상태인 “Stable” 조건과 낮은 크기로 천이 상태를 보이는 “Transition-1”에서 컷오프에 못미치는 값을 보였으며, 반대로 높은 크기를 갖으며 천이 상태를 보이는 “Transition-2”와 불안정 상태인 “Unstable “에서 컷오프를 넘어서는 값을 보였다. Fig. 3(b)의 TK 분석 방법은 샘플 신호의 첨도(kurtosis) 값을 추출하는 기법으로 신호가 정현파(즉, 불안정한 데이터)일 경우 TK가 1.5에 가까운 값을 갖고 반대로, 노이즈 신호일 때 3.0에 가까운 값을 갖는 특징이 있다(5). 각각의 동압 신호 데이터에 TK를 적용하여 분석한 결과, 불안정 상태인 “Unstable” 조건에 대해서는 TK 값이 모두 1.5에 가까운 것으로 나타났으나, 안정 상태인 “Stable”에서는 TK의 값이 넓게 분산되는 것으로 나타났다. Fig. 3(c)의 PE 기법은 샘플 신호 파형의 패턴을 순열-패턴(permutation-pattern)의 가짓수에 기반하여 통계적으로 추출하고 이에 대한 무질서도(randomness)를 정량화한 방법이다(16). 동압 신호 데이터에 대해 계산된 PE 값은, “Unstable” 조건과 같이 동압 신호의 파형 패턴이 일정한 한계 진동 상태를 보일 때 일률적인 값을 보였다. 그러나, “Stable”과 같이 안정한 상태의 조건에 대해서는 매우 다양한 범위의 PE 값을 가지는 것으로 나타났다. 끝으로, Fig. 3(d)의 ZCR은 신호가 영점을 통과하는 빈도를 정량화한 기법이며, “Unstable”과 같이 동압 신호가 정현파를 띄며 주기적 특징을 보일 때 산출되는 값이 일률적인 특성을 보이며 반대로, 노이즈의 파형을 보이며 소폭의 크기 변화만 있는 신호에 대해서는 산출되는 값이 수렴하지 못하는 결과가 나타났다. 정리하면, 최근에 연소 동압 신호에 대한 분석 수단으로써 제시되고 있는 TK, PE, ZCR는 모두 불안정 데이터에 대해서는 각각의 기법이 가진 원리에 부합하여 일관된 값으로 수렴하는 특성을 보여주었으나, 안정 데이터에 대해서는 세 가지 기법 모두 일정한 값이 아닌 큰 폭의 분포를 보이는 것으로 나타났다. 이러한 특징을 머신러닝에 적용하여 진단모델을 구축할 경우, 동압 신호가 안정한 상태임에도 불구하고 불안정으로 진단하는 이상치(outlier)가 초래될 수밖에 없다.
이렇듯 기존의 3가지 통계적 기법을 활용하여 머신러닝 기반의 진단모델 구축 시 감지 성능의 한계 발생이 예상됨에 따라, 현재 연구에서는 새로운 신호 분석 기법인 파형 패턴(Waveform Pattern, WP) 개념을 도입하였다. WP 기법은 샘플링한 이산(discrete) 신호의 임의 구간에서의 파형 패턴을 분석하는 방법으로, 동압 신호의 진폭을 나타내는 RMS 크기와 더불어 동압 신호가 갖는 파형의 패턴 정보를 활용하고자 고안하게 되었다. Fig. 4는 본 연구에 사용된 WP 분석의 개념도이다. 우선, Fig. 4(a)에서 보이듯, WP 계산을 위해서는 분석 대상이 되는 패턴 데이터의 크기(pattern data size, k)를 정해야 하고, 이로부터 샘플 데이터 내에 임의의 i번째 지점부터 i+1, i+2, ..., i+(k-1)까지 총 k개의 데이터가 WP 분석 대상으로 선정된다. 이때, 주어진 k로부터 데이터가 가질 수 있는 파형 분포 패턴의 경우의 수는 kPk-1개와 같이 순열로 표현할 수 있다. WP 개념의 직관적 이해를 위해 Fig. 4(b)에 k가 4일 때를 선정하여 개념도를 나타내었다. 오른쪽 그림에서와 같이, 샘플 데이터 내의 임의의 지점 i에서 i+3까지를 분석 구간으로 선정할 수 있다. 이때 파형 분포 패턴에 대한 모든 경우의 수는 24로 계산되며, 예시로 선정된 WP(20)은 샘플 데이터의 크기 패턴이 pi+3>pi>pi+2>pi+1일 때를 나타낸다.
그러나, WP는 단순히 데이터가 분포하는 경우의 수를 나타낼 뿐 Fig. 3의 TK, PE, ZCR과 같은 다른 통계적 기법들처럼 연소불안정을 직접적으로 평가하는 기준으로 활용될 수는 없다. 하지만, 진폭의 크기(예, RMS)와 함께 동압의 변화 패턴(예, WP)에 대한 동시 정보는 본 연구에서 제안하는 오토인코더 모델에 적절한 입력 데이터로 활용될 수 있으며, 이 방법을 다음 절에 자세하게 기술하였다.
3. 오토인코더 모델 구축 및 학습 방법
3.1 입력 데이터
머신러닝 기반 연소상태 진단모델의 개발 및 검증을 위하여 2.2.1절에서 언급하였던 서로 다른 운전 조건에서 10 kHz의 샘플링 주파수로 3초 동안 계측한 동압 신호 데이터를 사용하였다(즉, 하나의 동압 신호 샘플은 30,000개의 이산 데이터로 구성). 총 40개의 동압 신호 샘플을 대상으로 각각의 샘플에서 2초(즉, 샘플 당 20,000개의 이산 데이터)는 학습을 위하여 사용되고, 나머지 각각의 샘플에서 1초(즉, 샘플 당 10,000개의 이산 데이터)는 개발된 모델의 검증에 사용되었다. 또한, 오토인코더 모델은 입력 데이터에 대한 라벨링(labeling) 과정이 필요하며, 본 연구에서는 샘플 동압 신호의 RMS 기준 평균압력(=130 kPa) 대비 섭동(p′)의 크기를 기준으로 상태를 정의 및 라벨링 하였다. 해당 샘플 데이터에서 p′/(RMS 기준) 값이 1 % 이상(즉, p′=1.3 kPa 이상)일 경우를 불안정(unstable) 상태로 정의하였고, 0.3 % 미만을 안정(stable)으로 정의하였으며, 이 중간 상태를 천이(transition)로 정의하였다.
오토인코더 모델의 인코더(encoder)는 데이터가 가진 정보를 잠재 공간(latent space)으로 축소하는 저차원화 역할을 수행하며, 이 과정은 잠재 공간에 데이터의 주요 특성이 효율적으로 압축될 수 있도록 입력 데이터를 최적화하는 과정이 매우 중요하다. 현재의 연구는 진단모델의 개발을 위하여 동압 신호로부터 얻을 수 있는 여러 정보를 이용 및 조합하여 다양한 구조의 입력 데이터를 선별하였고, 이로부터 얻어지는 학습 결과(즉, 잠재 공간에서의 특성 지도)를 비교하였다. Table 1은 현재 연구에서 검토되었던 입력 데이터의 구성을 요약한 것이다. 크게 두 가지 case로 구분될 수 있는데, 먼저 기존에 보고되었던 통계적 기법을 통하여 얻을 수 있는 정보들인 RMS, TK, PE, 그리고 ZCR 4가지 정보를 통한 입력 데이터의 구성을 case 1로 정의하였다. 이 4가지 정보 중에서 각각 2개만 선택할 때(4C2(=6), C는 조합(combination)을 의미 : Case 1-1)부터, 3개를 선택(4C3(=4) : Case 1-2), 4개 모두를 선택(4C4(=1) : Case 1-3) 하느냐에 따라 다양한 경우의 수가 존재한다. 단, 4가지의 정보 중 1개만을 선택하는 경우는 입력 데이터가 단일 차원으로, 입력 데이터를 축소 시킬 수 없어 구성에서 생략하였다. Case 1은 총 11가지의 경우의 수가 고려되어 입력 데이터 구성에 따른 잠재 공간 형성의 영향성이 평가되었다.
반면에, Case 2는 본 연구에서 새롭게 제안하는 신호의 진폭(RMS)과 신호의 파형(WP)을 활용하는 방안으로써, 패턴 데이터의 개수(k)에 따라 Case 2의 입력 데이터 차원이 결정된다. 예상되듯이 k값의 증가는 데이터 전처리 과정에서의 계산 시간 증가를 초래하기 때문에, 데이터의 유의미한 특성 지도를 도출할 수 있는 최소 k값의 선정이 중요하다. 현재의 연구에서는 k=3, 4, 5 일 때인 3가지 k값에 대하여 주어진 동압 신호를 비교하였고, 그 결과로부터 k=4가 입력 데이터의 특성을 효과적으로 추출함과 동시에 가장 적은 계산 시간을 갖는다는 결과를 도출하였다. 이때, WP가 갖는 패턴의 경우의 수는 4P3=24가 되며, 따라서 WP는 24차원의 크기를 갖는다. 이때 1행은 RMS가 WP 차원에 맞추어 배치되고, 2행에는 WP 값으로 구성된다.
3.2 학습 방법
본 연구에 사용된 오토인코더 모델의 네트워크 구조 및 하이퍼 파라미터를 Table 2에 요약하여 나타내었다. 이 모델은 인코더와 디코더가 각각 4개의 층(layer)으로 구성되어 있다. 오토인코더 세부 모델 셋업은 Wang 등(11)의 연구에서 적용하였던 방법을 동일하게 사용하였는데, 모든 층에서 패딩(padding)은 VALID를, 활성화 함수(activation function)는 Leaky ReLU(Rectified Linear Unit)을 사용하였다. 학습에 사용된 하이퍼 파라미터로 옵티마이저(optimizer)는 Adam(Adaptive moment estimation)을, 손실함수(loss function)는 MSE(Mean Squared Error)를 사용하였으며, 배치 사이즈(batch size)는 1로 고정하였다. Table 2는 Table 1의 Case 2를 학습시키는 과정에서 은닉층의 하이퍼 파라미터 정보를 나타낸 것이며 이외에 Case 1의 하이퍼 파라미터는 커널 사이즈(kernel size)만 입력 데이터의 크기에 맞게 변형하여 인코더와 디코더를 각각 단일 층으로 구성해 학습하였다. 마지막으로, 학습을 위해 얻어야 할 최소 손실 값(minimum loss value)은 1⨯10-4 이하로 선언하였다.
학습에 사용된 하드웨어의 구성은 다음과 같다. CPU : Intel i9-12900K, RAM : DDR4 128 GB, GPU : RTX 3090 1 way. 학습에 사용된 소프트웨어는 MATLAB과 VS Code를 UI로 하는 Jupyter Notebook이다. 이들은 각각 입력 데이터 전처리 및 모델 학습을 위해 사용되었다. 모델 학습을 위해 사용된 Python의 버전은 3.9.12이고, tensorflow-gpu의 버전은 2.9.0이며, CUDA는 11.2 버전을 사용하였다.
4. 머신러닝 학습 및 진단 결과
4.1 학습을 통한 잠재 공간 특성 지도 도출
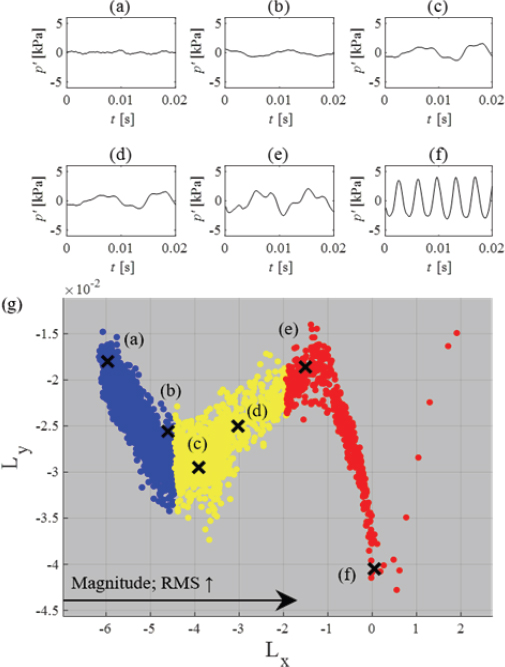
본 절에서는 Table 1에서 설명하였던 두 종류의 입력 데이터를 사용하여 오토인코더 모델을 학습하였을 때의 결과를 소개하고자 한다. 우선 Case 1(Case 1-1∼3 모두)을 이용하였을 경우, 잠재 공간에서의 어떠한 의미 있는 특성 지도를 도출하는 것은 불가능한 것으로 나타났다. 그 이유는 Fig. 3을 통해 언급하였듯이, TK, PE, ZCR과 같은 통계적 기법들은 모두 연소 동압 신호의 불안정 상태를 진단하는 데는 효과적이었지만, 진폭이 작고 노이즈에 가까운 파형(즉, 안정 상태)에 대해서는 불확실성(uncertainty)이 매우 높은 진단 특성을 보였으며, 그 결과 학습 잠재 공간에 형성된 특성 지도를 원활하게 도출하지 못했다. 반면에 본 연구에서 제안한, RMS와 WP의 정보를 동시에 이용하여 학습한 Case 2의 경우 신호의 크기와 파형 분포 패턴 분석으로부터 입력 데이터의 정보를 성공적으로 잠재 공간에 축소하여 특성 지도를 형성할 수 있는 것으로 나타났다. Fig. 5는 Case 2를 입력 데이터로 하여 학습된 결과를 도시한 것이다. 여기서 잠재 공간의 x축을 Lx, y축을 Ly라고 정의할 때, 이 공간 내에 축소된 입력 데이터는 Lx의 증가에 따라 Ly 값의 증가와 감소가 반복되는 “W” 형태의 분포를 나타내었다. 3.1.1절에서 정의한 데이터 라벨링 기준에 따라 파란색 점은 안정한 경우(p′/<0.3 %), 노란색 점은 과도기(0.3 %≤p′/<1.0 %), 빨간색 점은 불안정한 경우(p′/≥1.0 %)로 구분하였는데, 그림에서 보이듯이 해당 점들은 동압 진폭의 증가에 따라 Lx가 증가하는 방향으로 분포하였다. 더욱 명확한 이해를 위하여 잠재 공간의 점을 인덱싱(indexing)하여 해당 포인트에 대응하는 동압 신호의 파형을 Fig. 5(a)∼(f)에 나타내었다. 해당 동압 신호는 서로 다른 진폭을 가지며, 인덱스 된 점이 (a)에서 (f)로 갈수록(즉, Lx가 증가할수록), 동압 신호의 크기는 커지고 그 파형은 점차 정현파에 가까워지며 불안정성이 커지는 것으로 나타났다. 즉, 특성 지도에는 동압 신호의 크기와 파형 정보를 나타내는 RMS와 WP의 특성이 나타났으며 특히, Lx의 증가는 RMS의 크기 증가를 나타낼 뿐만 아니라 동시에 WP를 적용해 추출된 동압 신호의 파형 패턴 정보도 점차 정현파에 가까운 값을 갖는 것으로 나타났다. 따라서, 본 진단 모델은 신호의 크기뿐만 아니라 파형의 특성 역시 고려한다는 점에서 신호의 크기만을 컷오프와 비교하여 분석하는 기존의 모니터링 방법과는 차별화되게 WP를 기반으로 하는 파형 특성이 모니터링 요소로 고려됨으로써, 신호의 크기가 컷오프 도달하기 이전의 상황에서 연소불안정의 발생을 조기에 진단할 수 있음이 나타났다.
4.2 연소불안정 진단 성능
전체 동압 신호 데이터 샘플 중 진폭이 서로 다른 3가지의 동압 신호를 선별하여 아직 학습에 사용되지 않은 나머지 10,000개 즉, 총 30,000개의 데이터로 오토인코더 모델의 성능을 검증하였으며 이를 Fig. 6에 나타내었다. 이 중, 가장 진폭이 작은 Fig. 6(a)는 학습 과정에서 라벨링을 위한 정량적 기준으로 구분하였던 안정 상태(p′/<0.3 %, 즉 |p′|<0.39 kPa)와 과도기(0.3 %≤p′/<1.0 %, 즉 0.3 kPa≤|p′|<1.3 kPa)의 데이터가 혼재하고 있다. Fig. 6(b)의 동압 데이터는 (a)보다 신호의 평균 진폭이 증가하였지만, 여전히 불안정 상태(p′/≥1.0 %, 즉 |p′|≥1.3 kPa)로 정의한 조건보다는 진폭이 낮은 과도기 상태에 머무르고 있다. 마지막으로 Fig. 6(c)는 한계 진동 상태를 대표하는 동압 신호이며, 최소 1.3kPa 이상(즉, p′/≥1.0%)의 큰 진폭 값을 갖는다. Fig. 6(d)는 (a)∼(c) 데이터를 Fig. 5에서 도출한 잠재 공간의 특성 지도에 투영한 결과이다. Fig. 6(a)의 데이터는 그림에서 파란색 부분(학습 특성 지도에서 안정 영역)과 노란색 부분(과도기 영역) 걸쳐서 데이터의 진폭에 따라 분포하고 있음이 확인되었으며, Fig. 6(b)의 데이터 역시 불안정 구간을 나타내는 빨간색 선보다 왼쪽에 분포하였다. 반대로, Fig. 6(c)의 동압 신호 데이터는 빨간색 선보다 오른쪽에 분포하였으며, 해당 신호 데이터를 불안정 상태로 적절하게 진단하는 것으로 나타났다. 이러한 검증 과정으로부터 본 연구에서 개발된 연소상태 진단모델이 원활하게 학습되었음이 확인되었으며, 또한, 오토인코더 기반의 연소상태 진단모델은 기존의 통계적 기법과는 다르게 불명확한 진단 기준이나 이상치가 발생하지 않는 것으로 나타났다.
5. 결 론
본 연구에서는 가스터빈 연소기의 연소불안정 진단을 위해 가스터빈 연소기에서 얻어진 연소 동압 신호 데이터를 이용하여, 머신러닝 기법인 오토인코더 모델에 그 특성을 학습시켜 연소상태를 진단할 수 있는 모델을 고안하였다. 모델 개발과 검증을 위하여 사용된 동압 데이터는 발전용 수소혼소 가스터빈의 싱글노즐 시험 리그에서 다양한 연료 조성 및 운전 조건에서 취득되었다. 모델의 입력 데이터로는 기존 연구들에서 연소불안정 평가를 위해 활용되고 있는 RMS, TK, PE, ZCR 및 현재 연구에서 제시하는 WP 등 다양한 통계적 기법의 조합이 사용되었다. 오토인코더 모델의 학습 과정을 통하여 입력 데이터의 학습 특성을 분석한 결과, TK, PE, ZCR 등 기존의 통계적 기법의 데이터를 입력층으로 적용하였을 경우 잠재 공간에서 유의미한 특성 지도를 도출하지 못하는 것으로 나타났는데, 이는 이러한 기존 통계적 기법들이 불안정한 경우(즉, 동압의 진폭이 커서 정현파의 특성을 보이는 경우)에는 각 기법의 정의에 부합하는 일관된 값에 수렴할 수 있으나, 안정한 경우(즉, 노이즈에 가까운 신호 파형을 갖는 경우)의 데이터에 대해서는 무질서한 분포를 가지기 때문이다. 반면에 RMS와 WP 기법을 통한 데이터를 입력층으로 구성할 경우, 사전에 라벨링 된 안정/천이/불안정 영역을 적절하게 구분하는 의미 있는 특성 지도를 도출할 수 있었다. 진단모델의 검증은 학습에 사용되지 않은 데이터 중 안정, 천이, 불안정을 대표하는 동압 신호 데이터를 사용하여 이루어졌으며, 해당 데이터들을 진단모델에 입력시켰을 때 연소상태의 이상 유무를 명확히 판별 해내는 것으로 나타났다.
Acknowledgments
본 연구는 2023년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행된 연구 결과(RS-2023-00270080)입니다.
References
-
Joo, S., Kwak, S., Kim, S., Lee, J., and Yoon, Y., 2019, “High-frequency transition characteristics of synthetic natural gas combustion in gas turbine,” The Aeronautical Journal, Vol. 123, No. 1259, pp. 138-156.
[https://doi.org/10.1017/aer.2018.150]

-
Choi, B., Kim, H. S., Cho, J. H., 2010, “Large Gas Turbine Combustor Development,” The KSFM Journal of Fluid Machinery, Vol. 13, No. 4, pp. 63-69.
[https://doi.org/10.5293/KFMA.2010.13.4.063]

-
Kim, J. S., Park, Y. K., Kim, T. S., 2022, “Modeling for thermal performance Analysis of power generation gas turbines using 1D simulation programs,” Vol. 25, No. 5, pp. 5-11.
[https://doi.org/10.5293/kfma.2022.25.5.05]

-
Meher-Homji, C. B. and Bhargava, P. E., 1994, “Condition Monitoring and Diagnostic Aspects of Gas Turbine Transient Response,” International Journal of Turbo and Jet Engines, Vol. 11, No. 1, pp. 99-111.
[https://doi.org/10.1515/TJJ.1994.11.1.99]

-
Song, W. J., and Cha, D. J., 2019, “Temporal kurtosis of dynamic pressure signal as a quantitative measure of combustion instability,” Applied Thermal Engineering, Vol. 104, pp. 577-586.
[https://doi.org/10.1016/j.applthermaleng.2016.05.094]

-
Kobayashi, H., Gotoda, H., Tachibana, S., and Yoshida, S., 2017, “Detection of frequency-mode- shift during thermoacoustic combustion oscillations in a staged aircraft engine model combustor,” Journal of Applied Physics, Vol. 122, No. 22, 224904.
[https://doi.org/10.1063/1.5003912]

-
Joo, S. P., Cho, J. W., Kim, N. K., Lee, M. C., 2021, “Zero-crossing rate method as an efficient tool for combustion instability diagnosis,” Experimental Thermal and Fluid Science, Vol. 123, 110340.
[https://doi.org/10.1016/j.expthermflusci.2020.110340]

- Sarkar, S., G Lore, K., Sarkar, S., Ramana, V., Chakravarthy, R. S., Phoha, S., and Ray, A., 2015, “Early detection of combustion instability from hi-speed flame images via deep learning and symbolic time series analysis,” Annual Conference of the prognostics and health management society.
- Sarkar, S., G Lore, K., and Sarkar, S, 2015, “Early detection of combustion instability by neural-symbolic analysis on hi-speed video,” Proceedings of the 2015th International Conference on Cognitive Computation: Integrating Neural and Symbolic Approaches, Vol. 1583, pp. 93-101.
- Gangopadhyay, T., De, S., Liu, Q., Mukhopadhyay, A., Sen, S., and Sarkar, S., 2022, “A deep learning approach to detect lean blowout in combustion systems,” arXiv:2208.01871
- Luo, W., Li, J., Yang, J., Xu, W., and Zhang, J., 2018, “Convolutional sparse autoencoders for image classification,” IEEE Transactions on Neural Networks and Learning Systems, Vol. 29, No. 7, pp 3289-3294.
-
Wang, Y., Yao, H., Zhao, S., 2016, “Auto-encoder based dimensionality reduction,” Neurocomputing, Vol. 184, pp. 232-242.
[https://doi.org/10.1016/j.neucom.2015.08.104]

-
Son, J. C., Hong, S. M., Hwang, J. J., Kim, M. K., and Kim, D., 2021, “Acoustic Modeling in a Gas Turbine Combustor with Backflow Using a Network Approach,” Journal of the Korean Society of Propulsion Engineers, Vol. 25, No. 5, pp. 18-26.
[https://doi.org/10.6108/KSPE.2021.25.5.018]

-
Choi, S. K., Baek, J. M., and Kim, D., 2022, “Early diagnosis of combustion instability using statistical methods,” Journal of Korean Society of Combustion, Vol. 27, No. 3, pp. 1-7.
[https://doi.org/10.15231/jksc.2022.27.3.001]

- O’Shea, K., and Nash, R., 2015, “An introduction to convolutional neural networks,” arXiv:1511.08458
-
Bandt, C., and Pompe, B., 2002, “Permutation entropy: A natural complexity measure for time series,” Vol. 88, No. 17, 174102.
[https://doi.org/10.1103/PhysRevLett.88.174102]