수처리 교반기의 프로펠러 허브 볼텍스 제어

3.1 전산 해석 격자 및 경계조건

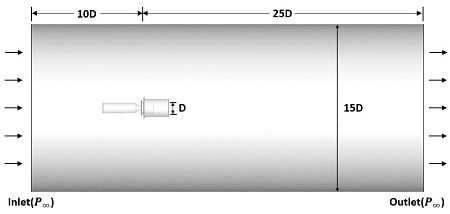
전산 해석은 직경 D를 갖는 프로펠러로 구성된 교반기 형상을 사용하였으며, 중력에 의한 수압 효과는 고려하지 않았다. 본 연구에서는 Fig. 1에 도시된 실린더 형태의 전산 해석 도메인을 사용하였으며, 유동 상류 방향으로 프로펠러 직경 대비 10D의 유동 공간을, 유동 하류 방향으로 25D만큼의 충분한 유동 공간을 모델링하였다. 전산 해석을 위한 도메인은 프로펠러를 감싸는 원형의 회전 도메인과 교반기 모터를 포함하고 있는 정지 도메인으로 구성하였다. 회전 도메인은 성긴 격자를 사용하여 계산하였을 경우 유동 및 성능 수치에 큰 차이는 보이지 않았으나, 프로펠러 팁 볼텍스와 같은 유동 특성의 정확한 분석을 위해 약 500만개의 조밀한 격자를 사용하였고, 사면체 격자와 벽 주변 영역에 대해서는 전단응력에 의해 발생하는 유동을 고려하기 위해 프리즘 격자 구조를 혼합하여 사용하였다. 정지 도메인은 프로펠러 허브에서 발생되는 볼텍스 유동의 정확성을 높이기 위하여 회전 도메인 앞쪽으로 실린더 모양의 조밀한 격자 블록을 사용하였으며, 이후 유동 출구로 갈수록 성긴 격자를 사용하여 계산 시간의 효율성을 높였다.

Fig. 1

Schematic of computational domain

사용한 경계조건은 회전 도메인에 대하여 sliding mesh를 사용하였으며, 도메인 입구 및 좌우측 경계면에서는 정체 입구(stagnation inlet) 조건을, 출구면에서는 압력 출구(pressure outlet) 조건을 사용하였다. 정체 입구 조건은 멀리 떨어진 경계면의 초기 유동이 정지 상태인 조건으로, 무한한 크기의 수조 속에 잠겨있는 교반기를 모델링하였다. 압력 출구 조건은 유동 출구 경계면에서 압력이 정확히 명시되어 사용된다.

3.2 허브 형상에 따른 프로펠러 허브 볼텍스 유동 특성

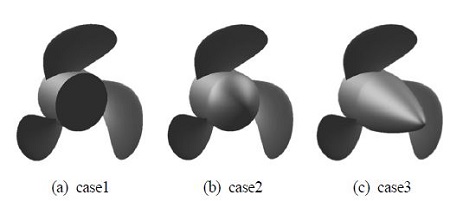
본 절에서는 교반기용 프로펠러 허브 형상에 따른 허브 볼텍스 유동과 프로펠러 성능에 대한 분석을 통해, 프로펠러의 허브 선정 시 고려해야할 유동 특성을 확인하고자 한다. 유동 해석에 사용한 프로펠러의 정보는 Table 1 정리하였다. 허브 형상 결정은 선박이나, 교반기 프로펠러에서 대표적으로 사용되는 형태의 허브인 실린더 형태의 case1, 둥근 형태의 case2, 뾰족한 형태의 case3에 대하여 수행하였으며, Fig. 2에 그 형상을 도시하였다.

Table 1

Propeller specifications

Fig. 2

Profiles of propeller hub

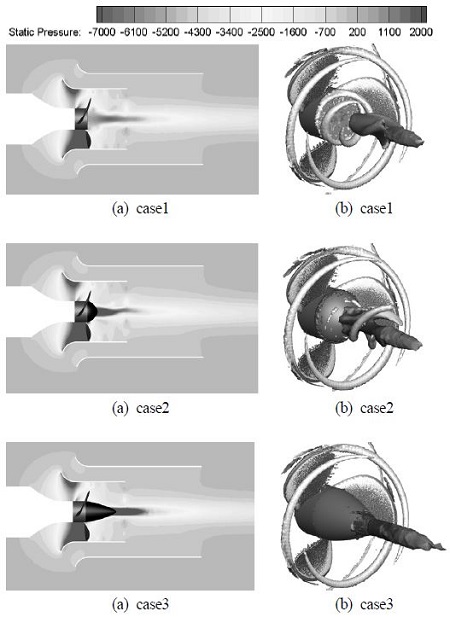
프로펠러 허브 형상에 따른 허브 볼텍스 유동의 분석을 위하여 x축을 기준으로 자른 평면에서의 압력 선도와 3차원 iso-surface에 Q-criterion을 가시화하여 비교를 하였으며, Fig. 3에 각 case에 대하여 표현하였다. 허브 끝단 주변으로 부터 하류 방향에 이르는 압력 분포를 살펴보면, case1에서 가장 높은 압력을, case3에서 가장 낮은 압력 분포를 보여준다.

Fig. 3

(b) Pressure contours (a) Iso-surface of Q-criterion ( Q-criterion value = 6000 [1/s2] )

따라서, 허브 볼텍스가 가지고 있는 회전 성분의 크기는 case3에서 가장 크고, case1에서 가장 작게 나타난다. 이러한 유동 특성을 Fig. 3에서 도시한 iso-surface로 표현하였으며, 모든 case의 허브 형상에 대하여 낮은 압력의 강한 허브 볼텍스가 생성되는 것을 확인할 수 있다. 이는 프로펠러 블레이드의 윗면과 아랫면을 통과하는 유동이 서로 다른 속도를 갖게 되고, 그로 인해 블레이드 끝단으로부터 아래쪽으로 향하게 되는 유동을 만들게 된다. 이 유동은 허브를 통과한 후 강력한 허브 볼텍스를 만들게 되고, 통과 경로 상에서 더 많은 유체와의 상호작용을 통해 전단류에 의한 손실 발생시켜 프로펠러의 효율을 감소시킨다. 각 case별로 프로펠러의 유량 및 소요 동력을 이용하여 정의한 프로펠러 효율을 Table 2에 정리하였다.

Table 2

Performance of various shape of propeller hub

결과를 살펴보면, case2와 case3은 서로 유사한 성능 및 효율을 보였으며, 반면에 case1은 적은 유량과 많은 소요 동력을 보이며 프로펠러의 효율 또한 약 1.9 % 감소하였다. Fig. 4에서 표현된 허브 끝단에서의 압력 분포에서도 세 가지 case 중 case1이 가장 높게 나타났지만, 허브 끝단의 위치가 프로펠러 근처에 위치하여 프로펠러의 유동이 하류 방향으로 매끄럽게 이동하지 못해 손실이 발생하였다.

Fig. 4

Surface pressure contours

반면에, case2와 case3의 경우 허브 끝단에서의 압력은 매우 낮아 허브 볼텍스의 회전 성분은 더 강하게 나타나지만, 프로펠러의 유동이 허브 형상을 따라 매끄럽게 이동하며 프로펠러 근처에서의 압력 분포가 높게 나타나게 되어 전체적인 효율은 case1에 비해 높게 나타났다. 위 결과를 통해, case1 형상의 허브를 적용할 경우 허브 볼텍스의 강도는 줄일 수 있지만, 유동이 허브 형상을 따라 매끄럽게 이동할 수 없고, 압력 손실이 발생하여 효율을 감소시키게 된다. 따라서, 허브 볼텍스의 강도가 증가함에도 불구하고, 둥근 형태의 허브 형상을 적용하는 것이 프로펠러의 효율을 증가시킬 수 있음을 확인하였다. 그러나 모든 case의 허브 끝단에서 매우 낮은 압력 분포를 보이며, 강한 허브 볼텍스가 생성되었기 때문에, 프로펠러의 효율 증가에는 한계가 존재한다.

3.3 허브 볼텍스 제어를 위한 PBCF

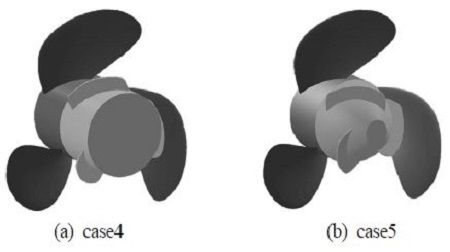
앞 절의 분석을 통해 모든 case에서 허브 볼텍스가 발생하므로, 단순히 허브 형상의 변경만을 통해서는 허브 볼텍스의 제어와 프로펠러의 효율을 증가시킬 수는 없다. 본 절에서는 허브 볼텍스 유동을 효과적으로 제어하여 프로펠러의효율을 증가시키고자 앞 절에서 사용한 허브인 실린더 형태의 case1과 비교 대상으로 둥근 형태의 허브와 뾰족한 형태의 허브 중 단위 동력당 유량값이 큰 case2에 PBCF를 적용하여 유동해석을 진행하였다. 유동해석에 사용한 형상은 Fig. 5에 도시하였고, 두 case에서 동일 크기의 핀을 사용하였으며, 핀의 정보는 Table 3에 나타내었다.

Fig. 5

PBCF

Table 3

Fins specifications

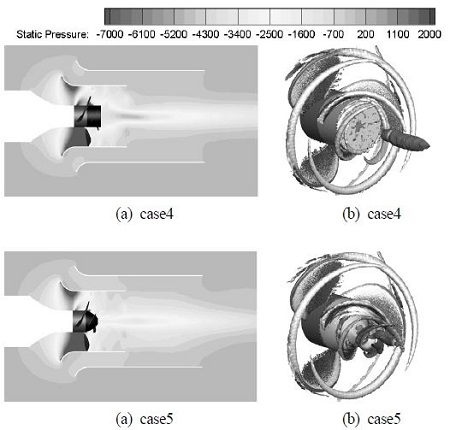
Fig. 6을 살펴보면, PBCF의 설치에 의해 모든 케이스에 서 허브 끝단 근처부터 하류 방향으로 앞 절의 허브 형상 대비 압력이 크게 상승한 것을 확인할 수 있다. Iso-surface의 결과에서도 허브 볼텍스는 크게 감소하였으며, 특히 case5의 경우 핀에 의한 스월(swirl) 성분만 존재하였다.

Fig. 6

Pressure contours (b) Iso-surface of Q-criterion ( Q-criterion value = 6000 [1/s2] )

PBCF 형상에 따른 프로펠러의 성능 특성을 Table 4에 정리하였으며, case4의 경우 PBCF의 설치에도 불구하고, 앞 절의 case보다 더 낮은 효율을 보였다. 반면에 case5의 경우 핀 설치에 의해 약 5.2%의 효율 상승을 보였으며, 모든 case 중 가장 많은 유량과 낮은 소요 동력을 확인하였다.

Table 4

Performance of various shape of PBCF

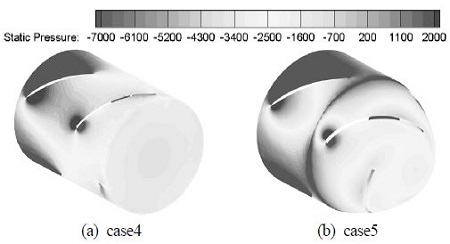
Fig. 7의 압력 분포를 살펴보면, PBCF를 설치한 두 case 모두 허브 끝단에서의 압력은 높게 나타났으나, case4의 핀 근처의 압력을 살펴보면 case5와 큰 차이점을 확인할 수 있다. 프로펠러의 압력 분포와 가장 반대 성향을 보이는 case4의 경우 큰 추력을 보였으나, 핀에 의해 생성되는 반대방향 추력이 매우 크게 작용하였다. 또한, 핀이 프로펠러의 유동을 방해하고 프로펠러의 토크를 상쇄시켜주지 못하여 가장 낮은 유량 및 효율을 보였다. 핀에 의해 허브 볼텍스가 감소하였으나, 실린더 형태의 보스캡에 적용된 핀의 구조 상 유동의 흐름을 방해하여 프로펠러의 효율을 감소시켰다.

Fig. 7

Surface pressure contours

반면에 case5는 보스캡의 형상을 하류 방향으로 갈수록 직경이 작아지는 둥근 형태로 모델링함으로써, 프로펠러 유동이 허브 형상을 따라 매끄럽게 이동하였고, 이는 핀 주변의 압력 분포에 의해 확인할 수 있다. case5의 핀에서도 PBCF의 특징인 역방향 추력을 발생시켰지만, case4와 달리 핀에 의해 프로펠러의 토크를 상쇄시켜 시스템 전체 토크를 낮추었고, 핀에 의해 허브 볼텍스가 약화된 유동은 유량의 증가 및 전체 효율의 증가를 일으켰다.

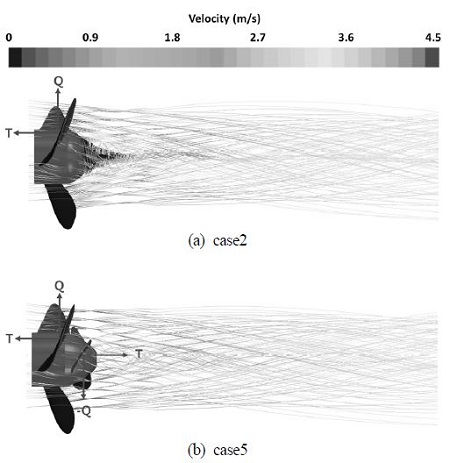
Fig. 8은 3.3절을 통해 분석된 둥근 형태의 허브를 갖는 case2와 PBCF가 적용된 case5의 실제 거동을 가시화한 유선(streamline)이다. 먼저, case2의 유선은 허브 끝단에 강한 허브 볼텍스가 형성되어 있으며, 이는 전단류 손실에 의해 추력을 감소시킨다. case5의 유선에서는 핀에 의해 허브 끝단의 허브 볼텍스가 대부분 제거되었고, 허브 주변에서 회전 유동의 운동 에너지가 회복되어 프로펠러의 효율을 증가시켰다. PBCF는 프로펠러에 의한 정방향 추력과 토크가 작용하는 일반 프로펠러와 달리 핀에 의해 발생하는 역방향 추력과 토크가 추가적으로 작용한다. 하지만, 허브 볼텍스의 약화를 통해 시스템 전체적으로 토크의 감소와 추력의 증가를 가져오며, 이를 통해 전체 효율이 증가한다.

Fig. 8

Streamlines (colors represent velocity magnitude)