원심압축기 임펠러의 형상 변화에 따른 저유량 영역에서 발생하는 불안정 유동 평가

1. 서 론

원심압축기(centrifugal compressor)는 운전 중에 발생할 수 있는 비정상적인 유동현상이 존재한다. 특히 낮은 부하에서 흡입되는 공기량에 과도한 저항이 발생하게 되면 시스템의 압력저항보다 압축기가 더 큰 압력을 생산하지 못하여 압축된 고압부의 유체가 저압부로 역류하는 불안정한 유동현상이 발생하게 되는데, 이를 서지(surge)현상이라고 한다. 서지현상을 압축기의 제어 및 여러 가지 운전상의 제약을 발생시키며, 압력과 유량이 진동하여 큰 소음과 진동을 동반하기 때문에 압축기에 매우 치명적이다. 그렇기 때문에 압축기의 내구성 및 정상적인 작동을 위하여, 서지현상이 발생하면 반드시 바로 벗어날 수 있도록 무부하 상태로 만들어야 한다⁽¹⁾.

최근 컴퓨터의 성능과 다양한 계산방법의 발달로 인하여, CFD를 이용하면 실험에 비해 시간 및 경제적으로도 매우 효율적이기 때문에 많은 선행 연구자들에 의해 수행되고 있다^(2-4). Ding 등⁽⁵⁾은 상용코드 CFX를 사용하여 원심압축기의 수치해석을 수행하였으며 mixing plane interface⁽⁶⁾가 적용된 탈설계점의 정상상태 해석은 매우 낮은 회전속도에서 비정상상태 현상이 두드러지게 나타나는 문제가 발생하게 되는데, 이때 mixing plane 가정의 유효성이 낮음을 확인하였다. 또한 비정상상태 해석을 통해 서지와 같은 불안정한 유동에 대한 성능 예측은 높은 회전속도에서 더 높은 정확성을 보임을 확인하였다. Choi⁽⁷⁾는 원심압축기 최적설계를 위해 수치최적화 기법을 적용하여 서지마진을 증가시킬 수 있는 방안을 찾고자 목적함수로 설계점에서 유량대 압력비의 기울기를 사용하는 것을 제시하고 이를 검증하였다. 그리고 이를 최적화 문제의 목적함수로 사용한다면 서지점에 대한 직접적인 예측이 없더라도 서지마진의 증가를 고려할 수 있을 것이라고 설명하였다. Stein 등⁽⁸⁾은 설계점과 탈설계점에서의 성능곡선을 수치해석을 통해 작성 후 실험과 비교하였다. 또한 처음으로 LE(leading edge)를 넘어서는 유동이 발생하는 조건까지 계산을 진행하였고, 비정상상태 해석을 통해 이 유동이 순간적으로 성장하여 스톨(stall)로 전이되어 압력과 유량 섭동을 야기함을 보였다. 그리고 부가적으로 부유동을 추가하여 스톨을 제어함으로써 안정화된 운전 상태로 만드는 것을 확인하였다.

본 연구에서는 CFD를 이용해 임펠러 블레이드 입구 각도 변화가 저유량 영역에서의 불안정한 유동에 어떠한 영향을 미치는지를 확인하였고, 스톨 및 서지마진의 변화가 어떤 경향으로 나타나는지를 정량적으로 비교 및 분석하였다.

2. 유동해석

2.1 해석대상

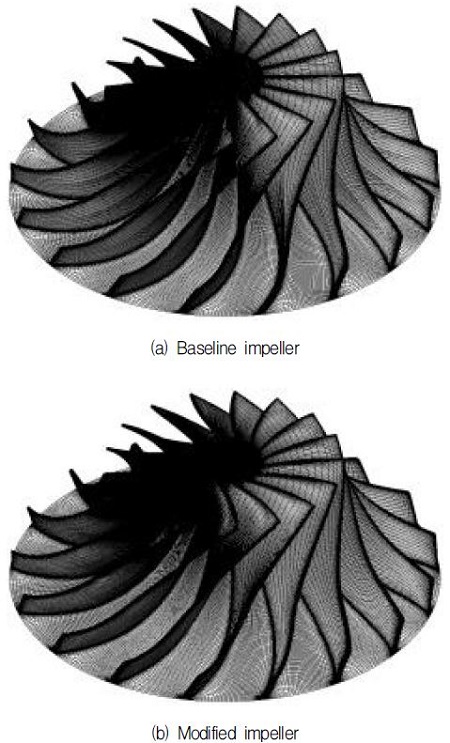
본 연구대상의 압축기는 ㈜세아엔지니어링에서 제작한 터보압축기이며 Table 1에 자세한 설계사양을 기술하였다. 이 압축기는 총 3단으로 구성되어 있으며 그중에 1단부에 대해 정상상태 해석을 수행하였다. Fig. 1은 압축기 1단부의 3차원 모델링 형상이며 본 연구에서는 디퓨져(diffuser)와 볼류트(volute)를 제외한 임펠러 단일 해석을 수행하였고, 기존의 임펠러와 입구 각도를 변경한 임펠러의 해석 결과를 서로 비교 및 분석 하였다. 본 논문에서는 기존의 임펠러를 기본형 임펠러(baseline impeller), 그리고 입구 각도를 변경한 임펠러를 수정된 임펠러(modified impeller)로 명명하였다.

Table 1

Design specification of the present compressor

Fig. 1

Geometry of centrifugal compressor

2.2 계산격자

Fig. 2는 해석대상인 임펠러들의 형상 및 격자를 보여주며 총 17개의 블레이드로 이루어져 있고, 그중에 하나의 블레이드에 대해 주기성(periodic) 조건을 사용하여 해석을 수행하였다. Fig. 2 (b)의 수정된 임펠러 는 Fig. 2 (a)의 기본형 임펠러 블레이드 입구 각도가 회전방향으로 15° 기울어진 형상이며, 선행 연구⁽⁹⁾를 통해 다른 형상 변화보다 저유량에서 더 안정적인 경향을 보인 임펠러이다. 격자 생성은 유체기계 해석에 특화된 격자생성기인 TurboGrid를 사용하였으며 격자 의존성테스트를 통해 입구 도메인에 약 3.6만개, 출구 도메인에 약 4.4만개, 블레이드에 약 42만개로 총 약 50만개의 육면체(hexahedral) 격자를 사용하였다.

Fig. 2

Computational grid of impellers

2.3 해석방법

본 연구에 사용된 CFX⁽¹⁰⁾는 터보기계를 포함한 유체기계 해석에 최적화된 CFD 상용코드이다. 선행 연구⁽¹¹⁾를 통해 기본형 임펠러에 대한 해석 결과와 성능시험 결과를 비교하여 해석방법을 검증하였으며 본 연구에도 적용하였다. 입구조건은 전압력과 전온도로 설정하였고 출구조건은 질량유량으로 설정하였다. 난류모델은 역압력구배로 인한 유동 박리 예측에 효과적인 RANS(Reynolds-averaged Navier-Stokes equation)기반의 SST(shear stress transport) 모델을 사용하였고, 도메인과 블레이드 사이에는 frozen-rotor interface를 적용하였다. 작동유체는 35℃의 이상상태의 공기이며 유량 변화에 따른 기본형 임펠러와 수정된 임펠러의 유동장 분석과 성능곡선을 통해 비교하였다. 성능시험 결과를 통해 서지영역으로 알려진 저유량의 불안정한 영역과 설계점에서의 안정한 영역에서의 유동특성을 비교하여 불안정한 영역에서만 확인할 수 있는 유동특성을 확인하고, 그러한 유동특성이 발생하지 않는 영역까지만 해석을 진행하여 성능곡선을 작성하였다. Table 2에는 자세한 경계조건을 도시하였으며 설계회전수(N_d) 대비 100%와 60%에 대하여 해석을 수행하였다.

Table 2

Boundary conditions

3. 결과 및 고찰

3.1 유량에 따른 비교

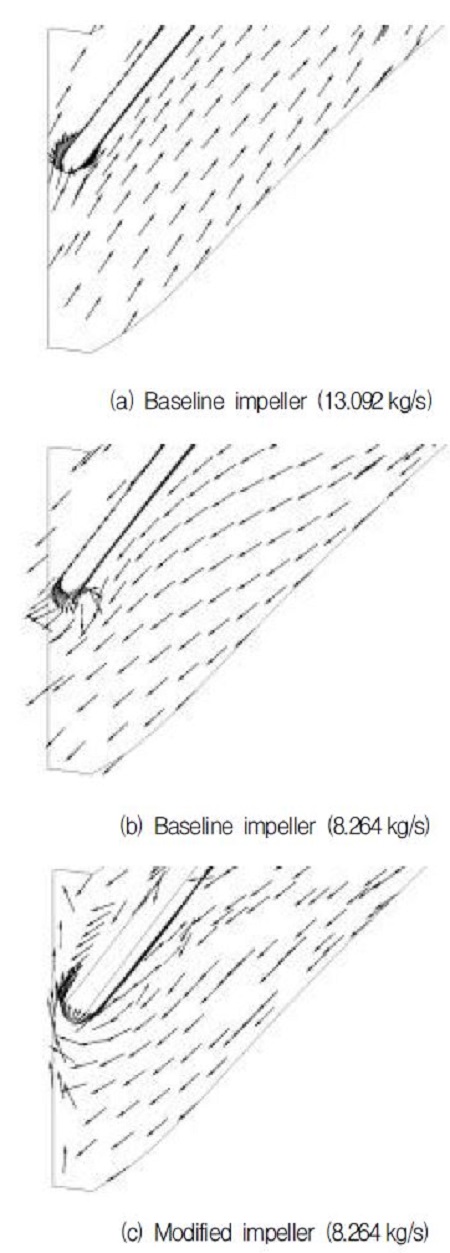
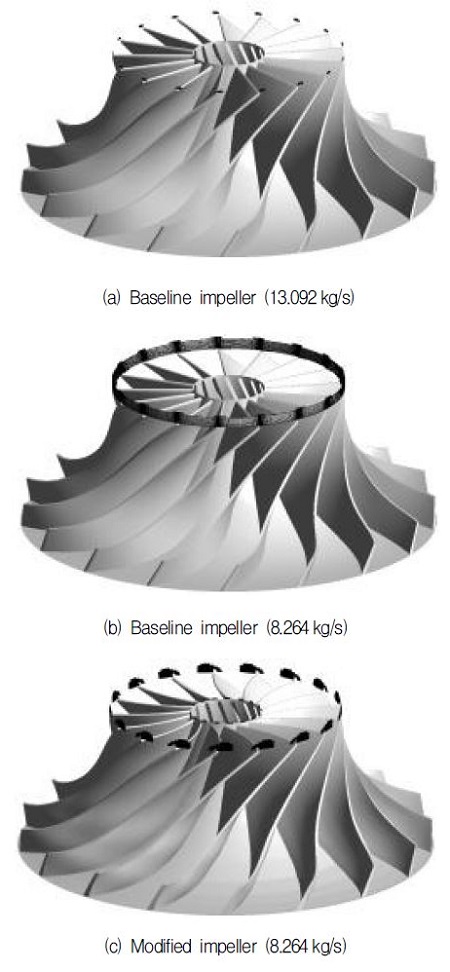
설계점의 안정한 영역과 저유량의 불안정한 영역에서의 해석결과를 비교해보았다. Fig. 3의 (a)와 (b)는 두 영역에서의 임펠러 입구 근처의 속도 벡터를 비교한 것이다. 실제로 불안정한 영역에서 발생하는 스톨과 서지와 같은 비정상상태의 현상은 정상상태 해석결과로는 의미 있는 데이터를 얻을 수 없는 것으로 알려져 있다⁽⁵⁾. 본 연구에서도 Fig. 3 (a)와 달리 불안정 영역인 (b)에서는 유동의 방향과 반대(negative)의 속도성분이 예측되었다. 이 역류하는 유동은 순간적으로 성장하여 스톨과 서지로 전이되고 비정상상태의 현상이 되므로 비정상상태 해석을 통해서만 현상을 예측할 수 있다. 하지만 본 연구에서는 비정상상태 해석을 수행하지 않고 이러한 역류하는 유동의 발생의 유무에 대한 확인을 통해 안정한 영역과 불안정한 영역 구분의 기준으로 사용하였다. Fig. 4의 (a)와 (b)는 이러한 역류가 발생하는 영역의 체적을 도시한 것이다. 불안정한 영역에서는 임펠러 전체에서 고리 모양으로 역류가 발생하는 것을 확인할 수 있다. 안정한 영역에서 보여지는 약간의 체적은 LE에서의 정체구간과 쉬라우드(shroud)의 벽면 영향으로 발생한 것으로 판단된다.

Fig. 3

Comparison of velocity vector

Fig. 4

Comparison of backflow volume

3.2 임펠러 형상에 따른 비교

동일한 유량의 저유량 영역에서 기본형 임펠러와 수정된 임펠러의 해석결과를 비교해보았다. Fig. 3의 (b)와 (c) 두 임펠러의 속도 벡터를 비교한 결과에서 볼 수 있듯이 수정된 임펠러의 속도장이 역류 없이 상대적으로 안정적임을 볼 수 있다. 앞서와 동일한 방법으로 수정된 임펠러에서도 역류가 발생하는 영역을 Fig. 4의 (b)와 (c)에서 살펴보면, 고리 모양으로 전체적으로 역류하던 현상이 줄어들면서 LE 부근으로 국한된 것을 확인할 수 있다. Fig. 4에 도시한 체적을 Table 3에 정리하여 나타내었다. 그 결과 기본형 임펠러의 안정한 영역보다 불안정한 영역의 체적이 더 증가하였고, 동일한 유량에서 수정된 임펠러가 기본형 임펠러보다 체적이 감소한 것을 확인할 수 있다.

Table 3

Comparison of backflow volume

3.3 서지점 예측

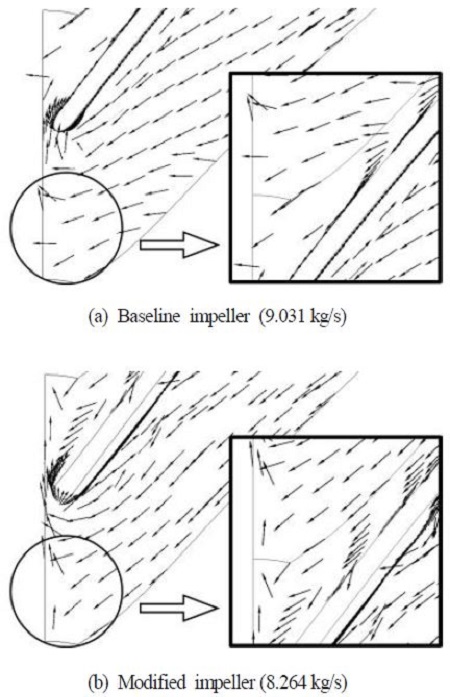
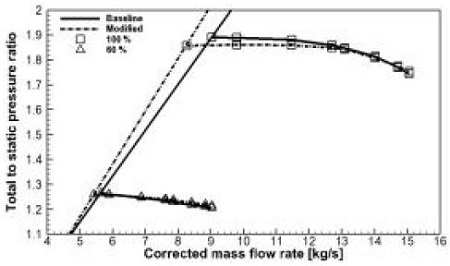
두 임펠러에 대한 성능시험 데이터가 없기 때문에 서지점을 예측하기 위해서는 해석을 통해 접근하는 방법이 필요하다. Fig. 3 (c)의 입구 속도 벡터는 유입이나 역류가 아닌 임펠러 회전방향과 평행한 분포를 보여준다. 이 조건보다 적은 유량이 공급되면 Fig. 3 (b)와 같이 역류하는 속도 벡터를 보일 것이며, 많은 유량이 공급되면 Fig. 3 (a)와 같이 유입되는 속도 벡터를 보일 것이다. 이분법(bi-section method)을 이용한 반복 계산을 통해 Fig. 3 (c)에서처럼 회전방향과 평행한 분포를 보이는 속도 벡터를 찾아가는 방법으로 안정 혹은 불안정을 판단하였고, 해석 결과는 Fig. 7과 같다. Fig. 7 (a)의 기본형 임펠러는 (b)의 수정된 임펠러에 비해 역류하는 속도 벡터가 더 증가한 것을 확인할 수 있지만, 수정된 임펠러보다 고유량 영역에 위치하므로 계산시간 단축을 위해 이 두 지점을 압축기 성능곡선의 스톨 및 서지점으로 가정하여 성능곡선을 작성하였다. 설계점 회전속도 11018rpm을 100%로 하여 60%에 해당하는 회전속도 6611rpm에 대하여 같이 작성하고 Fig. 8에 도시하였다. 수정된 임펠러가 기본형 임펠러에 비해서 압력비는 약간 감소하는 경향을 나타내지만 회전속도 60%도 100%와 마찬가지로 수정된 임펠러가 저유량에서 좀 더 안정적으로 운전 가능할 것으로 판단된다.

Fig. 5

Comparison of velocity vector at last calculated point according to the impeller shape

Fig. 6

Comparison of performance curve

4. 결 론

본 연구에서는 상용코드 CFX를 이용하여 임펠러 형상 변화를 통해 저유량 영역에서 발생하는 불안정 유동에 어떤 영향을 미치는지에 대해 수치적으로 평가 및 정량화 방법을 제시하였다.

• 1) 성능시험에 포함된 운전 조건 중에서 서지영역으로 알려진 불안정한 영역에 대한 해석결과를 통해 유동이 역류하는 것을 확인할 수 있었다. 정상상태 해석의 한계로 인하여 정확한 유동특성을 확인할 수는 없었지만 스톨로 전이되기 이전에 발생하는 역류 이용하여 안정한 영역과 불안정한 영역 구분의 기준으로 사용 가능할 것으로 판단된다.
• 2) 임펠러 블레이드 입구 각도를 변경한 수정된 임펠러와 기본형 임펠러를 동일한 유량에서의 해석결과 비교를 통해, 수정된 임펠러의 입구 부근에서의 속도 벡터 분포가 역류하는 경향을 적게 보이므로 저유량 영역에서 좀 더 안정적으로 운전 가능할 것이라 판단된다.
• 3) 임펠러 입구의 속도 벡터를 비교하며 반복계산을 통해 서지점을 예측하였고, 이를 토대로 성능곡선을 작성하였다. 그 결과 수정된 임펠러의 압력비는 약간 감소하는 경향을 보이지만, 저유량에서 운전 시 비교적으로 더 많은 안정성이 확보될 것이라 예측 가능하다.
• 4) 앞서 작성된 성능곡선을 통해 서지마진을 평가하였다. 그 결과 기본형 임펠러보다 수정된 임펠러의 서지마진이 약 5% 가량 증가한 것을 알 수 있었고, 이 결과는 수정된 임펠러의 서지마진 증가가 압력비 변화에 의한 영향보다 유량 변화에 의한 영향이 더 크다는 것을 의미한다.

Acknowledgments

이 논문은 2012년 교육부와 한국연구재단의 지역혁신인력양성사업의 지원을 받아 수행된 연구임(NRF-2012H1B8A2026181).

References

• Pinsley, J. E., Guenette, G. R., Epstein, A. H., and Greitzer, E. M., (1991), “Active Stabilization of Centrifugal Compressor Surge”, Journal of Turbomachinery, 113(4), p723-732. [https://doi.org/10.1115/1.2929139]
• Kim, J. H., Choi, J. H., and Kim, K. Y., (2010), “Surrogate Modeling for Optimization of a Centrifugal Compressor Impeller”, International Journal of Fluid Machinery and Systems, 3(1), p29-38. [https://doi.org/10.5293/IJFMS.2010.3.1.029]
• Zhu, C., and Qin, G., (2012), “Performance Prediction of Centrifugal Compressor Based on Performance Test, Similarity Conversion and CFD Simulation”, International Journal of Fluid Machinery and Systems, 5(1), p38-48. [https://doi.org/10.5293/IJFMS.2012.5.1.038]
• Kang, Y. S., Park, T. C., and Yang, S. S., (2009), “Centrifugal Compressor Performance Assessment by Experimental and Numerical Simulations”, KSPE Spring Conference, p341-344.
• Ding, M. Y., Groth, C., Kacker, S., and Roberts, D., (2006), “CFD Analysis of Off-design Centrifugal Compressor Operation and Performance”, International ANSYS Conference.
• Sanders, D. D., O'Brien, W. F., Sondergaard, R., Polanka, M. D., and Rabe, D. C., (2008), “A Mixing Plane Model Investigation of Separation and Transitional Flow at Low Reynolds Numbers in a Multistage Low Pressure Turbine”, AIAA Paper No. 2009-1467.
• Choi, J. H., (2008), “A Study on Centrifugal Compressor Design Optimization for Increasing Surge Margin”, The KSFM Journal of Fluid Machinery, 11(2), p38-45. [https://doi.org/10.5293/KFMA.2008.11.2.038]
• Stein, A., Niazi, S., and Sankar, L. N., (2000), “Computational Analysis of Stall and Speration Control in Centrifugal Compressor”, Journal of Propulsion and Power, 16(1), p65-71. [https://doi.org/10.2514/2.5532]
• Jo, S. H., Kim, H. J., and Lee, M. H., (2014), “A Numerical Study on the Performance Assessment and Surge of a Centrifugal Compressor”, 2014 KSME Spring Conference, p561-566.
• ANSYS, v15 CFX Theory Guide.
• Jo, S. H., Kim, H. J., and Lee, M. H., (2013), “A Numerical Study on the Performance Assessment of a Centrifugal Compressor”, 2013 KSME Fall Conference, p106-111.