능동형 케이싱 트리트먼트의 형상 변화가 원심압축기의 공력성능에 미치는 영향

1. 서 론

최근 미세먼지를 동반한 대기오염과 같은 환경문제에 대한 관심이 증가하며 이를 해결하고자 하는 노력들이 폭 넓게 진행되고 있다. 이러한 노력의 일환으로 자동차 배기가스의 규제 방안은 지난 수년간 단계적으로 강화되어 왔다. 국내외 자동차 업체들은 배기가스 규제를 만족하는 엔진을 개발하기 위해 엔진의 소형화와 같은 방법을 통해 배기가스를 저감하였으나 이로 인해 엔진의 출력과 효율이 감소하는 부작용이 발생하였다. 이러한 문제를 해결하기 위해 터보차저(turbocharger)를 사용하여 엔진의 출력과 효율을 유지한 소형 엔진을 개발하여 배기가스 규제에 대응하고 있다.

터보차저는 대기로 버려졌던 배기 에너지를 배기 통로에 설치된 터빈(turbine)으로 회수하고, 흡기 통로에 설치된 압축기를 사용하여 혼합가스의 충전 효율을 높이는 과급기이다. 가변형상 터보차저(Variable Geometry Turbo charger, VGT)는 터빈 입구 베인(inlet vane)의 각도를 조절하여 최적의 과급 특성을 확보하기 위해 고안된 방법이다.^(1-2) 저유량 배기 조건에서는 과급 압력을 증가시켜 저속 토크 증대가 가능하고, 고속 조건에서는 압력손실의 감소로 인하여 고출력이 가능하다는 장점이 있다.⁽²⁾ 그러나 배기가스의 압력에 따라 압축기의 회전속도가 영향을 받으며 급격한 운전 조건의 변화로 인해 압축기의 유동이 불안정해지는 스톨(stall) 및 서지(surge)현상이 발생할 수 있고 엔진의 성능이 급격히 감소하여 고장의 원인이 될 수 있다.⁽³⁾

터보차저에 사용되는 원심압축기의 효율을 향상시키고, 작동 영역을 개선하기 위한 연구들이 그간 활발히 수행되어왔다. Halawa 등⁽⁴⁾은 임펠러(impeller)와 디퓨저(diffuser)의 경계면에 공기 분사 방식을 적용하여 원심압축기의 작동안정성을 증가시켰다. 이들은 공기 분사기의 수, 공기 분사의 각도 및 분사 유량을 설계 변수로 하여 작동안정성을 최대화하기 위해 최적설계를 수행하였으며, 공기 분사 방식을 통해 디퓨저 입구부에서 역류가 발생하는 구간을 감소시켜, 작동안정성을 향상시켰다. Kim 등⁽⁵⁾은 원심압축기의 임펠러자오면을 고려하여 유로의 형상을 최적화하고자 베지어 곡선(Bezier curve)을 적용한 설계변수를 사용하여 신경회로망기법(Radial basis neural network)을 이용한 수치최적설계를 통해 등엔트로피 효율을 향상시켰다. Park 등⁽⁶⁾은 원심압축기의 작동영역 개선을 위해 적용한 링 그루브(ring groove)의 유동특성을 수치해석적으로 분석하였고, 유동특성 분석을 통해 링 그루브의 위치를 변경하여 새로운 형상을 제시하였다. Sun 등⁽⁷⁾은 원심압축기의 운전 상태에 따라 위치가 변화하는 캐비티(cavity)를 이용한 능동형 케이싱 트리트먼트(active casing treatment)를 제안하였고, 이를 수치해석적으로 분석하였다. 그러나 이 연구에서는 원심압축기의 초킹(choking) 및 서지 조건에서 캐비티의 위치에 따른 원심압축기의 공력성능을 분석하였을 뿐, 각 운전 조건에서 캐비티의 형상 변화가 공력성능에 미치는 영향에 대한 연구는 수행되지 않았다.

본 연구에서는 캐비티를 이용한 능동형 케이싱 트리트먼트가 적용된 원심압축기에 대해 초킹 및 서지 조건에서의 공력성능을 수치해석적으로 분석하고, 캐비티의 길이, 입구 및 출구부의 폭, 출구부(분사구)의 각도 등의 캐비티 형상 변화가 원심압축기의 공력성능에 미치는 영향을 분석하였다.

2. 유동해석방법

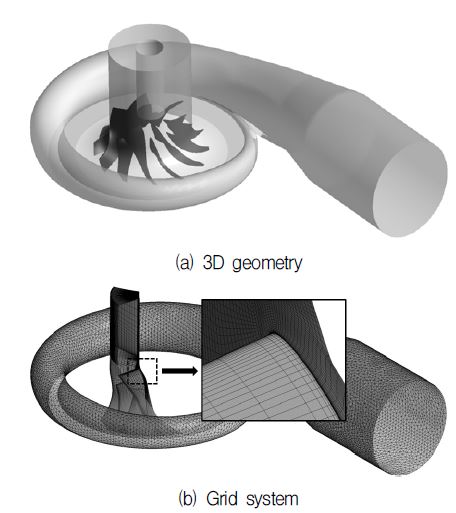
본 연구에서는 원심압축기의 공력성능 분석 및 유동장 해석을 위해 전산유체역학 상용 코드인 ANSYS-CFX15.0⁽⁸⁾을 사용하였다. 해석을 위해 Reynolds-averaged Navier-Stokes(RANS) 방정식을 유한체적법을 사용해 수치해석하였으며 난류닫힘(Turbulence closure) 모델로는 SST 모델을 사용하였다. 일반적으로 SST 모델은 유동박리 예측에 효과적이고, 정확성이 우수하다고 알려져 있다.⁽⁹⁾ 본 연구에서 사용된 원심압축기 모델은 Fig. 1에 나타난 바와 같이 볼류트(volute)와 주날개(main blade)와 스플리터(splitter)를 각각 6개씩 포함하는 임펠러로 구성되어 있으며 자세한 설계사양은 Table 1에 나타난 바와 같다.

Fig. 1

Centrifugal compressor

Table 1

Design specifications of the centrifugal compressor

Fig. 1(b)와 같이 본 연구의 계산 영역은 계산시간의 경제성과 수렴성의 향상을 위해 임펠러 상의 단일 유로와 볼류트를 포함하는 영역으로 설정하여 정상상태 해석을 수행하였다. 정상 상태 해석의 경우 압축기의 축 비대칭성은 무시할 수 있기 때문에 단일 유로에서 양측 경계면을 회전방향으로 주기조건을 부여하여 계산하여도 전체 도메인의 계산 결과와 좋은 일치성을 보여준다고 알려져 있다.⁽¹⁰⁾

원심압축기의 작동유체는 이상기체로 가정하였다. 원심 압축기의 계산영역의 입구부에는 1 atm의 전압과 288.15 K의 전온도를 경계조건으로 설정하였고, 출구부에는 고유량 구간에서는 정압조건을, 저유량 구간에서는 질량유량을 부여하여 계산을 수행하였다. 회전하는 임펠러와 정지한 볼류트 사이의 경계면에는 Frozen-rotor 방식을 적용하였고, 임펠러와 볼류트의 상대적 위치를 고정하여 연구를 수행하였다.⁽¹⁰⁾

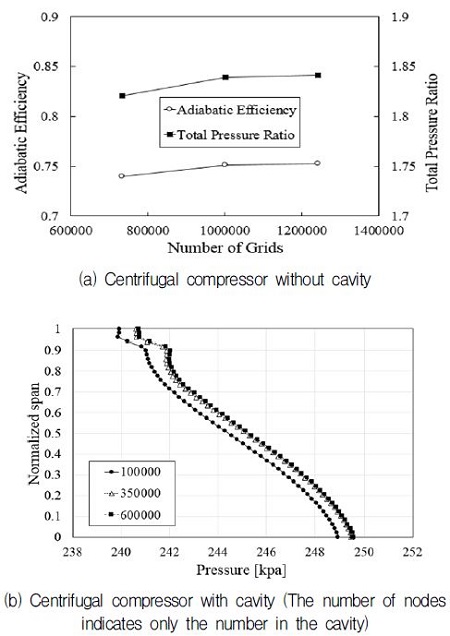
원심압축기의 블레이드 표면에는 O형 격자계를 사용하여 격자계를 구성하였고, 격자의존성을 제거하기 위해 약 70만 개에서 130만 개 사이의 격자수를 사용하여 격자의존성 테스트를 수행하였다. 격자의존성 테스트를 위해 설계 유량에서 단열 효율 및 전압력비를 비교하였으며 Fig. 2(a)와 같이 100만 개 이상의 격자수를 사용하였을 때 두 성능변수에 대해 공히 격자의존성이 사라짐을 알 수 있었다. Fig. 2(b)는 캐비티가 결합된 원심압축기에 대해 캐비티 내 격자의 격자의존성 테스트 결과를 임펠러 후단(trailing edge)의 스팬방향 압력분포에 대해 보여주고 있다. 격자테스트에서는 캐비티 내의 약 10만 개에서 60만 개 사이의 격자수를 시험하였고, 약 35만 개 이상에서 격자의존성이 사라졌으므로, 이 격자수를 캐비티 내에서 사용하여 계산을 수행하였다.

Fig. 2

Grid dependency test

3. 형상변수 및 성능함수

3.1 형상변수

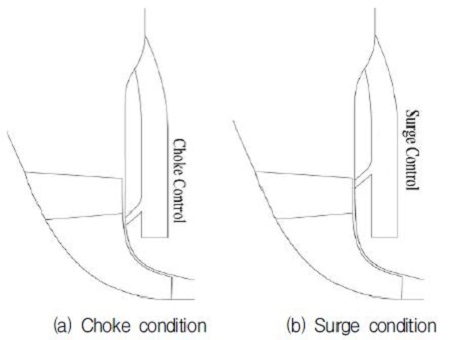
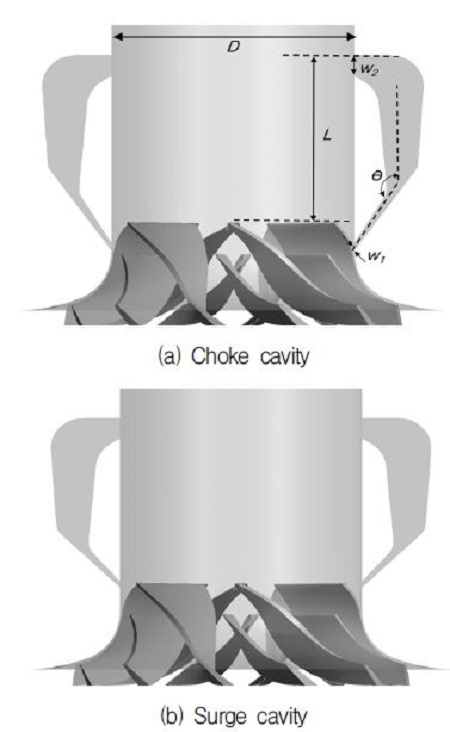
Fig. 3은 능동형 케이싱 트리트먼트의 개념 및 여기에 사용되는 캐비티의 단면을 보여주고 있다.⁽⁷⁾Fig. 3(a)와 같이 캐비티의 출구부, 즉 공기 분사구를 스플리터의 선단(leading edge)에 가깝게 위치시킨 형상을 초크 캐비티(choke cavity)라고 하고 Fig. 3(b)와 같이 캐비티의 출구부를 주날개의 선단에 위치시킨 형상을 서지 캐비티(surge cavity)로 명명하였다. 이와 같이 명명한 이유에 대해서는 뒤의 결과 검토 부분에서 설명할 것이다.

Fig. 3

Active casing treatment using cavity(7)

원심압축기의 초킹 및 서지 상태에 따른 캐비티의 기준 형상은 Fig. 4와 같이 캐비티 출구부의 각도를 다르게 하여 정의하였다. 캐비티의 형상변화가 원심압축기의 공력성능에 미치는 영향을 살펴보기 위하여 3개의 무차원화 된 형상변수를 선정하여 파라미터 연구를 수행하였다. 이에 따라, 캐비티 출구부의 폭(w₁/D), 입구부의 폭(w₂/D), 그리고 길이(L/D) 를 형상 변수로 선정하였으며(Fig. 4 참조), 파라미터 연구에 사용된 각 형상 변수들의 범위는 Table 2에 나타내었다.

Fig. 4

Location and geometric parameters of the cavity

Table 2

Ranges of geometric parameters

4. 결과 및 검토

4.1 능동형 케이싱 트리트먼트의 효과

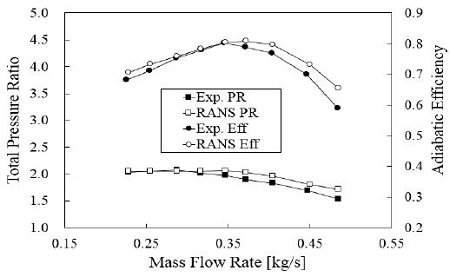
원심압축기에 대한 수치계산의 검증을 위해 기준 원심압축기의 RANS 해석결과와 실험결과⁽⁵⁾를 비교하여 Fig. 5에 나타내었다. 신뢰도 검증은 설계 유량을 포함한 9개의 유량점에서 단열 효율 및 전압력비의 비교를 통해 수행되었다. Fig. 5의 성능곡선에서 볼 수 있는 바와 같이 각 유량점에서 실험결과와 RANS 해석결과는 고유량 영역에서 다소의 차이를 보였고, 최대 오차는 약 2.8%로서 이는 유속이 증가함에 따라 임펠러 표면에서 발생하는 추가적인 손실을 사용된 난류모델이 잘 예측하지 못했기 때문으로 판단된다.

Fig. 5

Validation of numerical results with experimental data(5)

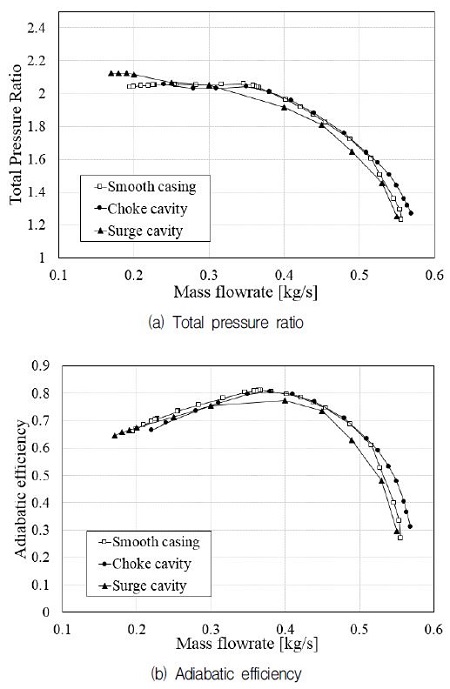
케이싱 트리트먼트가 적용되지 않은 원심압축기의 기준형상(smooth casing)과 초크 캐비티 및 서지 캐비티(Fig. 4 참조)를 적용한 원심압축기의 성능곡선들을 Fig. 6에 나타내었다. 설계 질량유량인 0.45 kg/s를 기준으로 성능곡선의 양 끝에 위치하는 초킹 유량과 서지 유량에서 초크 캐비티와 서지 캐비티는 서로 다른 특성을 나타내는 것을 확인할 수 있다. 우측의 초킹 유량 근처에서 초크 캐비티는 상대적으로 기준 원심압축기 보다 증가한 전압력비와 단열효율을 보여주고 있으나 서지 캐비티의 경우 이 성능변수들이 오히려 감소한 것을 알 수 있다. 반면에 좌측의 서지 유량 근처에서는 기준형상과 비교하여 서지 캐비티의 작동영역은 증가하고 초크 캐비티의 작동영역은 감소된 것을 확인할 수 있다. 초크 캐비티의 경우에는 전 유량영역에서 작동영역이 축소된 것을 제외하고는 기준형상과 비교하여 정압비와 효율에서 크게 떨어지지 않는 성능을 보였으나 서지 캐비티의 경우 두 성능이 전 유동영역에서 기준형상에 비해 크게 떨어지는 것을 알 수 있다. 그러므로, 고유량 영역에서는 초크 캐비티를 사용하고, 저유량 영역에서는 서지 캐비티를 사용하는 능동제어용 케이싱 트리트먼트 방식을 원심압축기에 적용하면 단열 효율 및 전압력비의 손실 없이 작동영역을 증가시킬 수 있다.

Fig. 6

Performance curves

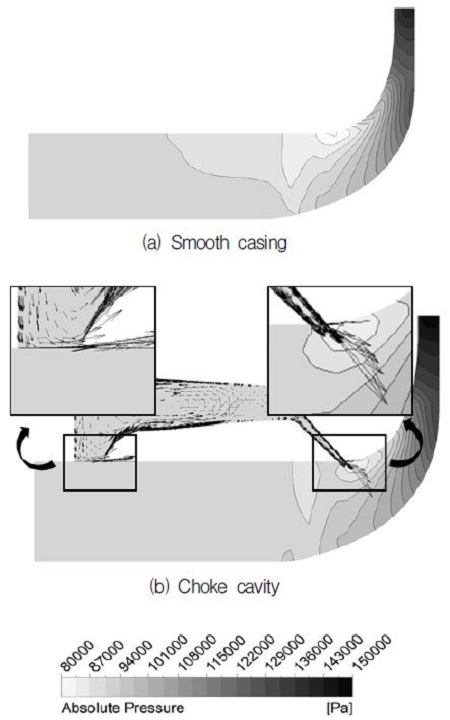
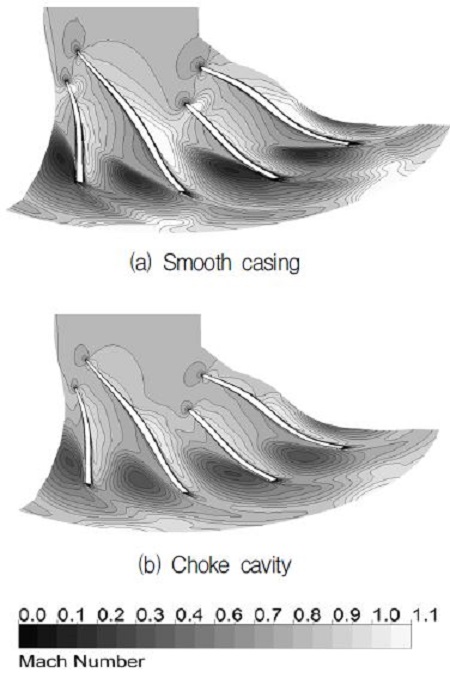
초킹 유량에서 기준 원심압축기와 초크 캐비티가 결합된 원심압축기 자오면의 정압 및 상대 마하수 분포를 각각 Fig. 7과 8에 나타내었다. 본 연구에서 사용된 원심압축기에서는 초킹 유량 근처에서 스플리터 선단 근처에 충격파가 발생하며 Fig. 7에서와 같이 저압 영역이 생성된다. 스플리터 선단 근처에 캐비티 출구부가 결합된 초크 캐비티의 경우 스플리터 선단의 저압 영역으로 고압의 공기 분사가 이루어지므로(Fig. 7(b)) 이 영역에서 정압이 회복되어 충격파의 영향이 줄어들고, 주날개와 스플리터 후단부에 생성된 저속영역의 감소로 인해 유로차폐 효과가 감소하게 된다(Fig. 8).

Fig. 7

Static pressure distribution with velocity vectors in the cavity at meridional plane

Fig. 8

Mach number distribution at 80% span

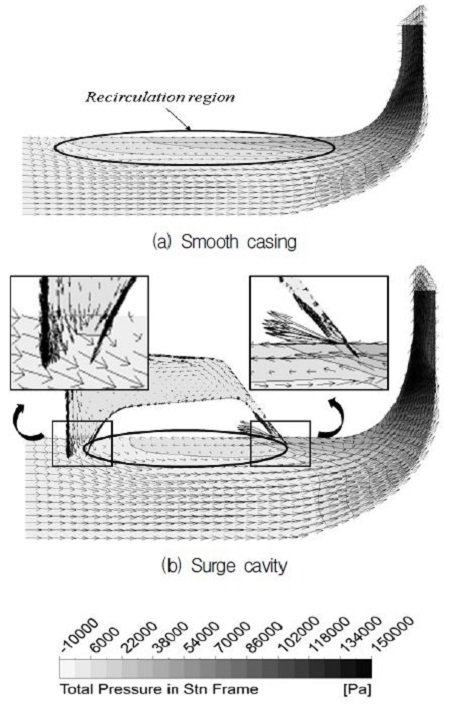
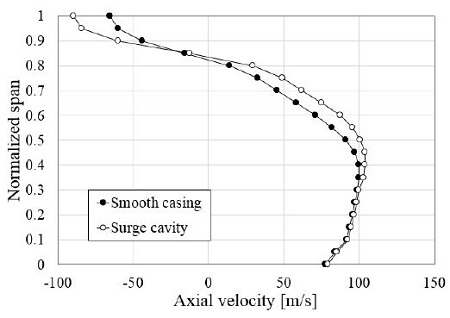
Fig. 9는 기준 원심압축기의 서지 유량에서 서지 캐비티가 결합된 원심압축기 자오면에서의 전압력 분포 및 속도벡터 분포를 나타내고 있다. 서지 캐비티가 결합된 원심압축기는 Fig. 9(b)와 같이 상대적으로 고압 영역인 주날개 선단부와 캐비티 출구부의 압력차로 인해 캐비티 내부로 주유동이 유입되는 것을 확인할 수 있으며, 이로 인해 Fig. 10에서 보는 바와 같이 케이싱 근처에서 유속이 감소하고, 캐비티 입구부에서 나오는 유동이 주유동과 혼합하여 50~80% 스팬에서의 유량을 증가시켜 쉬라우드 근처에 형성되는 재순환 영역(recirculation region)이 감소한 것을 확인할 수 있다.

Fig. 9

Total pressure distribution with velocity vectors at meridional plane

Fig. 10

Axial velocity distribution at impeller leading edge

4.2 파라미터 연구

앞서 기술한 바와 같이 원심압축기는 운전 상태에 따라 매우 다른 유동특성을 보이므로, 원심압축기의 작동안정성 및 공력성능의 향상을 위해 각 유동특성에 맞게 출구부의 위치를 조정한 캐비티의 형상을 사용하는 것이 필요하다. 본 연구에서는 파라미터 연구를 수행하여 캐비티의 형상 변수가 성능에 미치는 영향을 살펴 보았다.

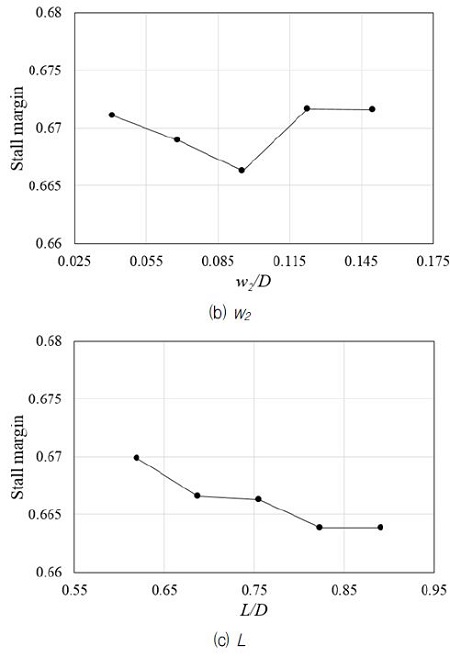
초크 캐비티의 경우 파라미터 연구 결과 3.1절에서 언급한 세 가지 형상 변수들이 단열효율에 미치는 영향이 모두 무시할 정도로 작았으므로 여기에서는 서지 캐비티의 경우에 대해서만 형상변수가 스톨마진에 미치는 영향을 Fig. 11에 나타내었다. 이 그림에서 모든 변수들이 스톨 마진에 민감하게 영향을 미치는 것을 알 수 있다. 특히 출구폭(w₁)의 영향이 상대적으로 큰 것으로 확인된다. 이는 원심압축기 작동 안정성에 큰 영향을 미치는 주날개의 선단부^(12-13)에 위치하고 있기 때문에 그 영향이 가장 큰 것으로 생각된다. 캐비티의 길이(L)는 0.619<L/D<0.891 범위 내에서 길이가 감소할수록 스톨 마진이 증가하는 경향을 보였고, 캐비티 내부 손실이 감소함으로 인해 재순환 유동의 속도가 증가하여 주유동과 혼합이 원활하게 이루어져 작동 안정성이 향상된 것으로 판단된다. 캐비티 입구폭(w₂)은 0.041<w₂/D<0.15 범위 내 0.122 이상의 값에서 스톨 마진이 거의 일정한 최대치를 보였다.

Fig. 11

Variations of stall margin with geometric variables of surge cavity

4.3 출구부 위치의 영향

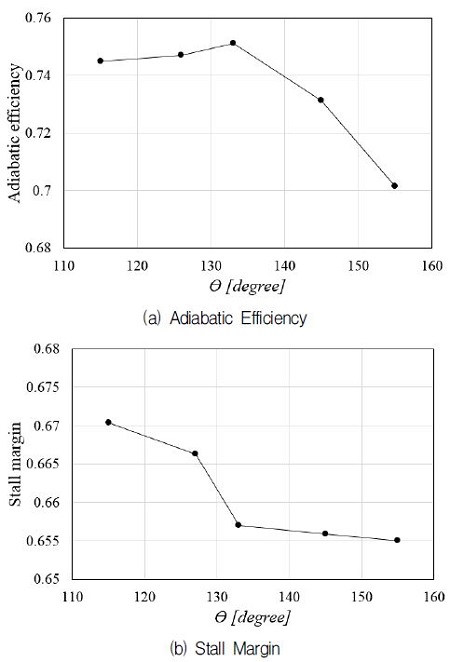
초크 캐비티와 서지 캐비티의 기본형상은 Fig. 4에서와 같이 캐비티 출구부가 각각 스플리터의 선단(θ=133°)과 주날개의 선단(θ=127°)에 위치하고 있다. 여기서는 이 출구부의 위치를 고정하지 않고 변화시킴으로써 출구부의 위치가 성능에 미치는 영향을 Fig. 12와 같이 살펴보았다. Fig. 12(a)에서 출구부의 각도가 설계점에서의 단열효율에 미치는 영향을 보여주는데 각도가 초크 캐비티의 기준치(θ=133°)보다 작은 경우, 즉 출구부가 스플리터의 상류에 위치하는 경우에는 효율이 감소하였으나 그 변화가 크지 않고, 이 기준치 보다 큰 각도의 경우 각도가 커짐에 따라 효율이 급격히 감소하는 것을 알 수 있다. 스톨마진은 Fig. 12(b)에 나타난 바와 같이 출구부 각도가 서지 캐비티의 기준치(θ=127°)보다 작은 경우, 스톨마진이 증가하였으나 기준치보다 큰 값을 갖는 경우 스톨마진이 감소하는 것을 알 수 있다.

Fig. 12

Variations of adiabatic efficiency and stall margin with θ of choke cavity

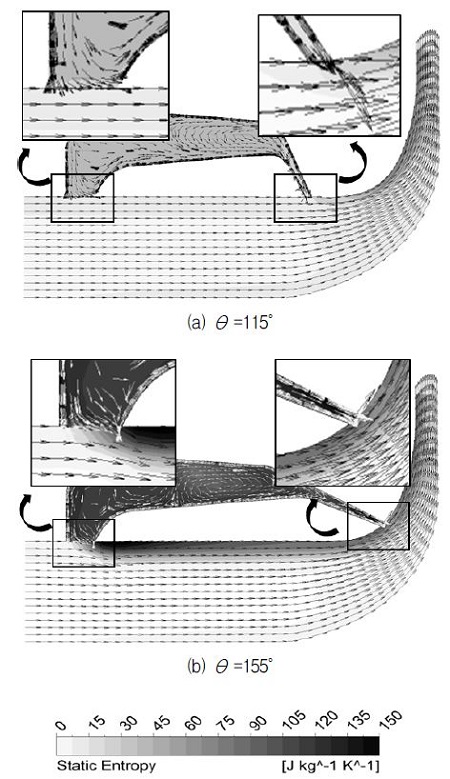
캐비티 출구부 각도가 115°와 155°를 갖는 두가지 형상에 대해 자오면에서 엔트로피와 속도 벡터 분포를 Fig. 13에 나타내었다. 각도가 115° 경우인 Fig. 13(a)에서는 주날개 상류에 공기가 분사되는 반면, 155° 경우인 Fig. 13(b)에서는 공기분사 위치가 상대적으로 고압 영역인 주날개 중심부에 있는데, 이 경우 공기분사가 원활하지 못해 캐비티 내에 재순환유동이 크게 형성되어 엔트로피와 손실이 증가하고 있음을 알 수 있다. 이는 Fig. 12(a)에 나타난 결과와 일치한다. 그러므로 분사구는 어떤 경우에도 압력이 낮은 스플리터 상류에 위치해야 하고 압력이 높은 주날개 중심부를 피해야 함을 알 수 있다.

Fig. 13

Static entropy distribution with velocity vector at meridional plane

5. 결 론

본 연구에서는 원심압축기의 운전 상태에 따라 캐비티의 출구부(공기분사구) 위치를 달리 적용하는 능동형 케이싱 트리트먼트 방식이 적용된 원심압축기에 대해 공력성능 분석과 캐비티의 형상변수들이 단열 효율 및 작동 안정성에 미치는 영향을 확인하기 위해 삼차원 RANS해석을 수행하였다. 계산결과의 타당성 검토에서 압력비와 단열효율에 대해 계산치는 고유량 영역에서 다소의 차이를 보이고 있으나 전반적으로 실험치와 잘 일치하였다. 능동형 케이싱 트리트먼트 방식을 적용할 경우 원심압축기는 설계점에서의 단열효율 및 전압력비의 손실 없이 초킹 조건에서는 향상된 효율과 압력비를 확보함과 동시에 서지영역에서 운전영역을 확장할 수 있음을 확인할 수 있었다. 캐비티의 세 가지 형상 변수들이 단열효율에 미치는 영향은 무시할 수 있었으나 스톨마진에는 민감한 영향을 미쳤으며 특히 출구부 폭(w₁)의 영향이 가장 크게 나타났다. 캐비티 출구부의 위치가 성능에 미치는 영향도 살펴보았는데 캐비티의 출구부가 스플리터의 상류에 위치하는 경우에는 출구부 각도의 감소에 따라 설계점의 효율은 감소하였으나 그 폭은 크지 않은 반면, 스플리터 선단의 하류에 위치하는 경우에는 각도가 커짐에 따라 효율이 급격히 감소하였는데 이는 공기분사가 압력이 높은 주날개 내부에서 이루어짐에 따라 분사가 원활하지 않아 캐비티 내의 손실이 증가하기 때문임을 알 수 있었다. 스톨마진은 출구부의 각도가 증가할수록 즉, 출구부가 주날개 선단부에서 중심부로 향할수록 스톨마진이 급격하게 감소하는 경향을 보였다.

References

• Filipi, Z., Wang, Y., and Assanis, D., (2001), “Effect of Variable Geometry Turbine (VGT) on Disel Engine and Vehicle System Transient Response”, SAE Technical paper 2001-01-1247.
• Shim, B. J., Park, K. S., Lee, C. H., and Kim, I. T., (2009), “Experimental Study to reduce Turbocharcer Surge during abrupt Decelearation on HSDI Diesel Engine”, KSAE 2009 Annual Conference, p587-592.
• Park, I. H., Park, M. S., Ahn, H. J., Kim, J. H., and Han, D. C., (2005), “Performance Enhancement of a Turbocharger Using a Variable Geometric Compressor”, KSAE 2005 Autumn Conference, p143-147.
• Halawa, T., Gadala, M. S., Alqaradawi, M., and Badr, O., (2015), “Optimization of the Efficiency of Stall Control Using Air Injection for Centrifugal Compressors”, Journal of Engineering for Gas Turbines and Power, Vol. 137(No. 7), paper 072604 (1-10). [https://doi.org/10.1115/1.4029169]
• Kim, J. H., Choi, J. H., and Kim, K. Y., (2009), “Design Optimization of a Centrifugal Compressor Impeller Considering the Meridional Plane”, The KSFM Journal of Fluid Machinery, Vol. 12(No. 3), p7-12.
• Park, C. Y., Choi, Y. S., Lee, K. Y., and Yoon, J. Y., (2011), “Numerical Investigation of Ring Groove Effect in a Centrifugal Compressr”, The KSFM Journal of Fluid Machinery, Vol. 14(No. 2), p11-16. [https://doi.org/10.5293/KFMA.2011.14.2.011]
• Sun, H., Hanna, D., Hu, L., Curtis, E., Yi, J., and Tjong, J., (2014), “Steady State Engine Test Demonstration of Performance Improvement with an Advanced Turbocharger”, Journal of Engineering for Gas Turbines and Power, Vol. 136(Iss. 7), paper 072601 (1-7). [https://doi.org/10.1115/1.4026611]
• ANSYS CFX-15.0, (2013), Ansys inc.
• Bardina, J. E., Huang, P. G., and Coakley, T., (1997), “Turbulence Modeling Validation”, AIAA 28th Fluid Dynamics Conference, p1997-2121.
• Heo, W. S., (2015), “A Numerical Study on Aerodynamic Performance by the Blade Mach Number of the Centrifugal Compressor”, Master of science thesis, Seoul National University.
• Choi, J. H., (2008), “A Study on Centrifugal Compressor Design Optimization for Increasing Surge Margin”, The KSFM Journal of Fluid Machinery, Vol. 11(No. 2), p38-45. [https://doi.org/10.5293/KFMA.2008.11.2.038]
• Schller, M., and Abhari, R. S., (2008), “Clearance Effects on the Evolution of the Flow in the Vaneless Diffuser of a Centrifugal Compressor at Part Load Condition”, ASME Journal of Turbomachinery, Vol. 130(No. 3), Paper 031009 (1-9).
• Zhou, S., Wang, J., Wang, C., and Li, Y., (2014), “Numerical Simulation Analysis of Tip Clearance Flow in a Centrifugal Compressor”, International Journal of Fluid Machinery and Systems, Vol. 7(No. 1), p28-33. [https://doi.org/10.5293/IJFMS.2014.7.1.028]