운전안정성 향상을 위한 원심 압축기의 유입부 형상변화에 관한 연구

1. 서 론

터보형 압축기의 한 종류인 원심압축기는 가스터빈,터보냉동기 그리고 터보차져 등에 주로 사용되는 장치로서, 산업적으로 없어서는 안 될 중요한 유체기계이다. 원심압축기는 대부분 운전점이 성능 곡선 상 높은 압력을 얻을 수 있는 곳에 위치하고 있다. 이런 특성을 갖는 원심압축기는 예상치 못한 상황이 발생할 경우 임계점(critical point) 또는 서지라인(surge line)근처에서 작동될 수 있기 때문에 원심압축기 전체시스템의 정상운전에 악영향이 미칠 수 있다. 원심압축기의 응용분야가 넓어짐에 따라 그에 따른 작동영역의 범위가 달라지고 있으므로 다양한 응용분야에서 안정적인 운전이 가능하도록 하기 위해서는 스톨마진 (stall margin)을 확대하여 운전안정성을 제고하는 것이 매우 중요하다. 이에 따라 입구부나 케이싱의 형상변경을 포함한 다양한 방법들이 원심압축기의 운전안정성을 제고하기 위해 연구되고 있다.

Pinarbasi 와 Johnson⁽¹⁾은 열선풍속계를 이용하여 원심압축기의 내부 유동특성을 조사하였으며, Filipenco 등⁽²⁾은 원심압축기 성능에 대한 원심압축기 디퓨져의 입구 마하 수, 유동 각도, 그리고 비균일 유동의 영향을 평가하기 위해 실험적 연구를 수행하였다. 그리고, Kang 과 Kang⁽³⁾은 터보압축기의 제어와 안정성에 대한 이해를 높이고자 스톨 발단에 대한 연구를 수행하였다. Galindo 등⁽⁴⁾은 터보차져용 내연기관에 사용되는 원심압축기의 서지 현상을 이해하기 위하여 실험 및 수치해석을 통한 연구를 수행하였다. 이들은 압축기 덕트의 길이 변화에 따른 압축기의 서지 특성을 조사하였다.

원심압축기의 성능을 향상시키기 위해 형상 최적화에 관한 연구들도 다수 수행되었다. Kim 등⁽⁵⁾은 Radial Basis Nueral Network(RBNN) 대리모델을 사용하여 원심압축기의 압력비를 향상시키기 위한 연구를 수행하였고, 이를 통해 원심압축기의 압력비를 약 2.46% 향상시킨 결과를 얻었다. 그리고, Bonaiuti 등⁽⁶⁾은 천음속 원심압축기 효율과 압력비을 향상시키기 위해 임펠러 형상에 대한 최적설계를 실험계획법을 사용하여 수행하였다. 또한, Wang 등⁽⁷⁾은 Kriging모델을 사용하여 임펠러에 대한 최적설계를 수행하였고, 이를 통해 원심압축기의 등엔트로피 효율을 약 2.49% 만큼 향상시키는 결과를 도출하였다.

이상과 같이 원심압축기의 작동특성을 이해하고 성능을 향상시키기 위한 많은 연구들이 수행되고 있다. 고압 원심압축기는 일반적으로 압력비가 증가할수록 운전안정성이 나빠지는 경향을 나타낸다. 최근 원심압축기의 응용분야와 시스템 요구사양이 달라짐에 따라 압축기의 효율이 저하되더라도 운전 안정성을 증대하기 위해 큰 스톨마진을 확보하기 위한 연구들이 다수 수행되고 있다. 압축기의 운전 안정성 확보를 위한 방안으로 최근에는 케이싱 트리트먼트(Casing treatment)와 입구 가이드 베인(Inlet guide vane) 등이 도입되고 있으며, 이들에 대한 선행 연구들이 수행되고 있다.

Tong 등⁽⁸⁾은 고압력 원심압축기의 스톨마진 증가를 위하여 새로운 방법인 자기조절이 가능한 케이싱트리트먼트 방법을 제안하였다. 이 방법은 쉬라우드(shroud) 케이싱에 홀을 설치하여 임펠러가 회전할 때 발생되는 누설 유동이 홀을 통하여 자동적으로 컨트롤 될 수 있게 해주는 방법으로서 원심압축기의 작동 안정성 향상에 기여한다는 것이 알려졌다. Chen 등⁽⁹⁾은 케이싱 트리트먼트를 통하여 원심압축기의 안정성이 향상된다는 것을 확인하였다. Wei 등⁽¹⁰⁾은 쉬라우드 케이싱에 설치된 홀의 직경을 변화시켜 홀 직경이 커질수록 원심압축기의 작동 안정성이 향상된다는 것을 확인하였다. Tetu⁽¹¹⁾은 원심압축기 성능 특성을 조사하기 위해 입구 가이드 베인을 적용한 압축기에 대해 실험적 분석을 수행하였고, Cui⁽¹²⁾는 원심압축기에 입구 가이드 베인을 적용하여 발생하는 유동의 불안정성을 수치해석적으로 평가하였다. 이와 같이 입구 가이드베인을 적용하여 원심압축기의 작동안정성을 향상시키는 연구들이 많이 수행되었다. 그러나, 입구 가이드베인의 적용은 압축기의 안정성을 높일 수는 있으나 압축기의 임계유량점에 나쁜 영향을 미칠 수 있다. 이러한 이유로 Yang 등⁽¹³⁾은 원심압축기의 운전안정성 확보를 위한 새로운 개념의 입구덕트 트리트먼트(Inlet Duct Treatment) 기법을 개발하였다. 이 기법은 입구 덕트에 원주 방향으로 여러 개의 홀들을 설치하는 것으로서, 케이싱트리트먼트의 장점인 pre-swirl를 발생시키는 역할을 하고 입구 가이드베인의 단점인 스로틀 효과(throttle effect)를 보완할 수 있다.

본 연구에서는 입구부에 원주 방향으로 여러 개의 홀을 설치하는 입구덕트 트리트먼트 기법이 적용된 원심압축기에 대해 삼차원 Reynolds-averaged Navier- Stokes(RANS) 해석을 수행하여 그 성능을 평가하였다. 매개변수 분석을 통해 원심압축기의 입구부에 원주방향으로 설치한 홀들의 직경, 길이, 기울기 각도, 그리고 홀과 임펠러 사이 거리 등의 형상변수들의 변화가 원심압축기의 효율 및 운전안정성에 미치는 영향을 분석하였다.

2. 대상모델

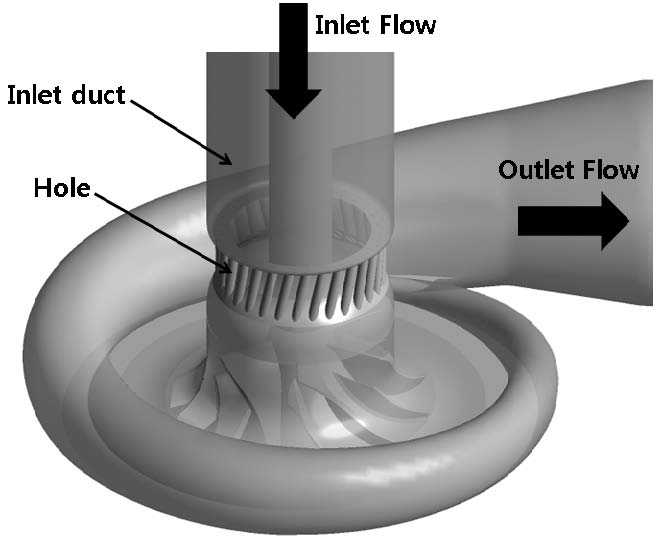
본 연구에서는 Kim 등⁽⁵⁾의 선행연구에서 대상으로 한 원심압축기 형상에 Fig. 1과 같이 Yang 등⁽¹³⁾이 제안한 입구덕트 트리트먼트 기법을 적용하였다. 입구부에 원주 방향으로 30개의 홀을 적용시킨 원심압축기를 본 연구에서는 기본형상으로 선정하였다. 임펠러 날개 및 스플리터는 각각 6개로 구성되어 있다. 설계사양으로 유량과 압력비는 각각 0.30 kg/s, 1.96이며, 임펠러 회전속도는 65,550 rpm이다. 구체적인 설계사양은 Table 1에 나타내었다.

Fig. 1

Geometry of the reference centrifugal compressor

Table 1

Design specifications of the centrifugal compressor (Kim et al.(5))

3. 유동해석방법

본 연구에서는 입구부에 원주방향으로 홀들이 설치된 원심압축기의 유동특성을 조사하기 위해 삼차원 압축성 RANS해석을 수행하였으며, 해석을 위해 상용코드인 ANSYS CFX 14.5⁽¹⁴⁾를 사용하였다.

작동유체는 이상상태의 공기로 가정하였으며, 계산을 위한 경계조건으로는 입구에는 전압력 및 전온도 조건을 적용하고 출구에는 유량조건을 부여했다. 정지영역과 회전영역 사이 경계면에는 고정회전자 기법(frozen-rotor method)을 사용하여 회전하는 원심압축기 블레이드의 구현을 용이하게 하였으며, 모든 벽면에는 점착조건을 적용하였다. 난류해석을 위해서는 SST(Shear Stress Transport) k-ω 난류모델을 사용하였다. 일반적으로 SST k-ω 난류모델은 역압력 구배로 인한 유동박리의 예측에 매우 효과적으로 예측 정확성이 뛰어나다고 알려져 있다.⁽¹⁵⁾ SST 모델은 k-ω 모델과 k-ε 모델의 장점만을 취한 모델로서 벽 근처 영역에는 k-ω 모델을 사용하고, k-ε 모델은 벽 근처를 제외한 영역에서 사용된다.

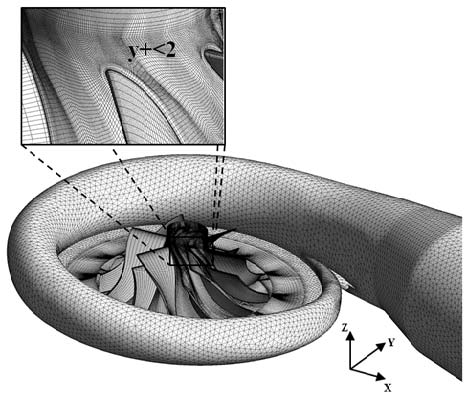
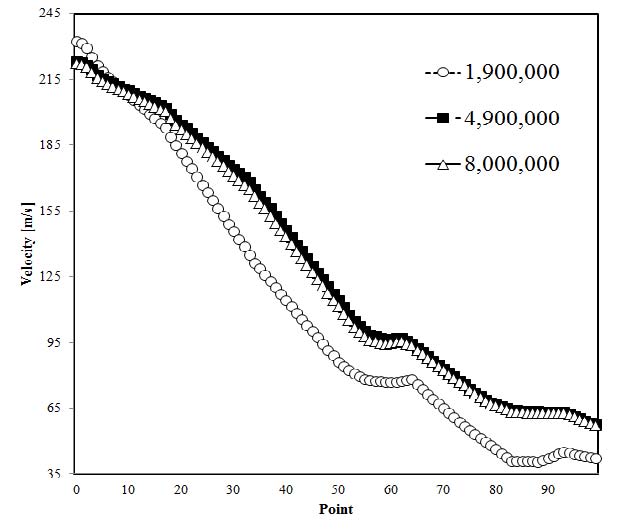
임펠러 날개 주위에는 O형 격자계, 그 외의 유동영역에는 H/J/C/L형 격자계를 사용하였다. Fig. 2에서 보는 것과 같이 계산영역은 육면체 격자를 사용하여 격자계를 구성하였고, 벽면 첫 번째 격자점에서의 y+값이 2 이하로 유지되도록 하였다. 계산격자에 대한 의존성시험을 Fig. 3과 같이 수행하였다. 격자 수 1,900,000-8,000,000 범위에서 격자의존성시험을 수행하여 약 4,900,000개의 격자 수를 계산의 경제성을 고려한 최적의 격자수로 결정하였다.

Fig. 2

Structure of the grid system

Fig. 3

Results of grid-dependency test

모든 해석에 있어 운동량보존과 질량보존에 대한 RMS (root mean square) 잉여값이 10^-6 이하로 설정하였을 때 만족스러운 수렴 값을 도출할 수 있었다. 지배방정식의 이산화를 위해 수치스킴으로 고해상도 수치도식(high resolution scheme)을 사용하였으며, 단일 계산에 Intel Core I7 CPU를 사용하여 수렴 값을 도출하기까지 약 10-12시간이 소요되었다.

4. 형상변수 및 성능함수

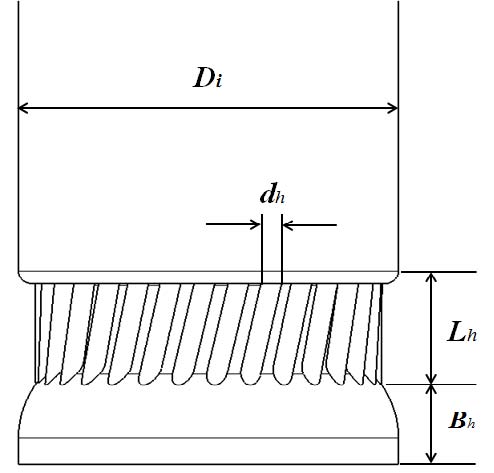
본 연구에서는 원심압축기 유입부에 원주방향으로 설치된 홀이 원심압축기에 공력학적 특성에 미치는 영향성을 조사하기 위한 연구를 수행하였다. 이를 위하여 Fig. 4에 표시된 홀의 직경(d_h), 홀의 길이(L_h), 홀과 임펠러 사이의 거리(B_h), 그리고 홀의 개수(N)를 형상변수로 선정하여 원심압축기의 공력학적성능에 대한 이들의 영향을 평가하였다. 이 값들의 기준치는 각각 d_h/D_i=0.054, L_h/D_i=0.28, B_h/D_i=0.22, 그리고 N=30이다.

Fig. 4

Definition of geometric parameters

유입부에 설치된 홀의 형상 변화에 따른 원심압축기의 성능에 대한 영향을 분석하기 위해 다음과 같이 정의된 원심압축기의 단열효율(adiabatic efficiency, η)과 스톨마진(SM)을 성능함수로서 고려하였다.

여기서, k, P_t 그리고 T_t 는 각각 비열비, 전압력, 그리고 전온도를 나타내며, m과 PR은 질량과 압력비를 의미한다. 또한, 하첨자 peak와 stall은 각각 단열 효율의 최대점과 실속점을 나타낸다.

5. 결과 및 검토

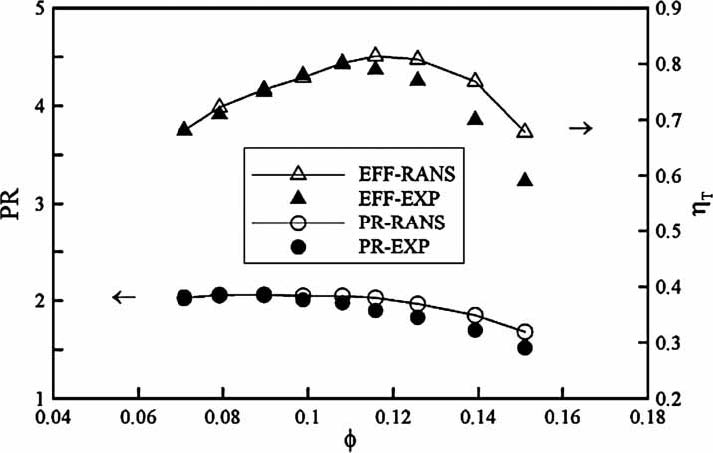
입구부 홀이 없는 압축기에 대한 본 수치해석 결과의 타당성 검증은 Kim 등⁽⁵⁾의 선행 연구에서 수행된 바(Fig. 5)와 동일하다. Fig 5에서와 같이 유량이 증가할수록 수치해석의 결과가 시험결과 보다 다소 낮게 나타나고 있지만, 전체적인 경향을 살펴보았을 때 성능시험 결과와 수치해석의 결과의 경향이 효율과 압력비에 대해 대체적으로 잘 일치하는 것을 확인할 수 있다.

Fig. 5

Validation of numerical results with experimental data (Kim et al(5))

Table 2는 삼차원 RANS 해석을 통해 계산된 원심압축기 입구부에 원주방향으로 홀들이 설치된 경우와 설치되지 않은 경우의 공력학적 성능들을 비교한 결과를 나타내고 있다. 입구부에 원주방향 홀들을 적용할 경우 효율은 3.8% 낮아지지만 원심압축기의 스톨마진은 15.3% 만큼이나 크게 증가하는 것을 확인할 수 있다.

Table 2

Performance parameters of the centrifugal compressor

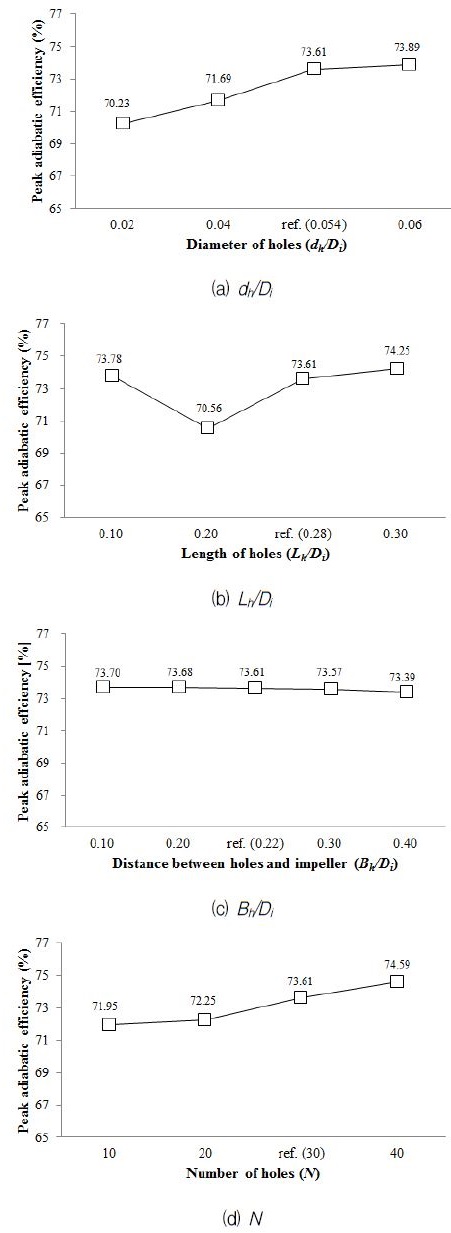
Fig. 6은 형상변수들의 변화에 따른 원심압축기의 최대 단열효율값의 변화를 나타낸다. Fig. 6(a)는 홀의 직경 변화에 따른 최대단열효율 변화를 보여주고 있다. 유입부에 원주방향으로 설치된 홀들의 직경이 증가할수록 최대단열효율이 증가하는 것을 확인할 수 있다. 시험된 범위에서 홀의 직경 변화에 따른 효율의 최대변화폭은 3.7% 정도이다. Fig. 6(b)는 홀의 길이 변화에 따른 최대단열효율의 변화를 나타낸다. L_h/D_i=0.2인 경우, 최대단열효율이 최소치를 갖는 것을 확인할 수 있다. 이 경우의 효율의 최대 변화폭도 홀의 직경의 경우와 동일하다. Fig. 6(c)는 홀과 임펠러 사이 거리 변화에 따른 원심압축기 최대단열효율 변화를 보여준다. 이 그림에서 보는 것과 같이 홀과 임펠러 사이 거리 변화는 원심압축기 최대단열효율에 대해 영향을 거의 주지 않는 것으로 확인된다. 원심압축기 유입부에 설치한 홀들의 개수에 따른 최대단열효율의 변화는 Fig. 6(d)에 나타나있다. 홀의 개수를 증가시킴에 따라 최대단열효율 값은 증가하는 경향을 보이고 그 변화폭은 2.6% 정도이다. 4가지 변수 변화에서 관찰되는 가장 큰 최대단열효율은 홀의 수 40에서의 74.6% 이다.

Fig. 6

Variations of peak adiabatic efficiency with the geometry variables

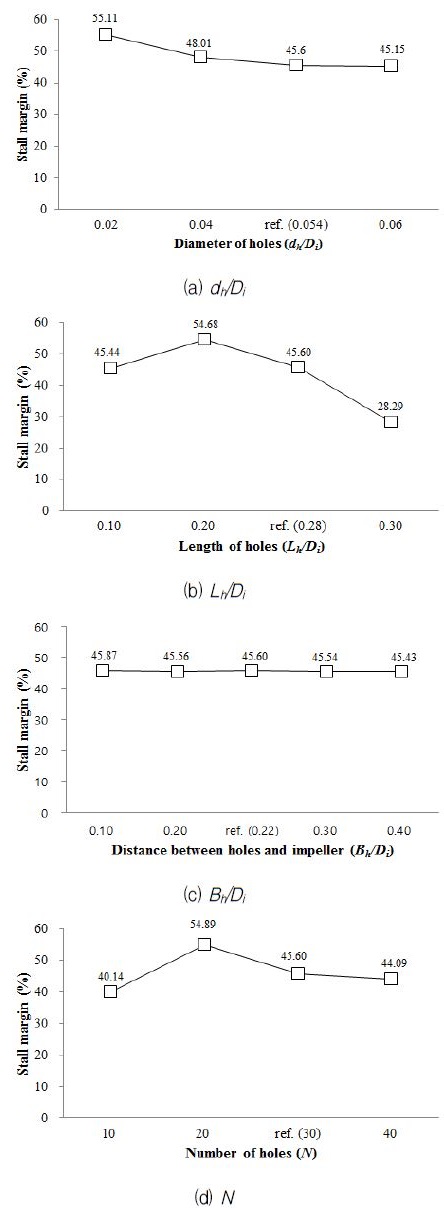
형상변수들의 변화에 따른 원심압축기의 스톨마진 변화는 Fig. 7에 나타난 바와 같다. Fig. 7(a)에서와 같이 홀의 직경이 커짐에 따라 스톨마진은 작아지는데 초기에 급속히 감소하다가 직경이 증가할수록 감소폭이 작아지고, 최대 감소 폭은 10.0%에 달한다. Fig. 7(b)는 홀의 길이 변화에 따른 원심압축기의 스톨마진 변화결과를 나타내고 있다. L_h/D_i= 0.20에서 최대 스톨마진 54.7%이 나타나고, L_h/D_i가 0.30 에서는 스톨마진이 28.3%까지 감소함을 보인다. 홀과 임펠러 사이 거리의 변화는 효율에 대해서와 마찬가지로 스톨마진에 대해서도 거의 영향이 없는 것으로 Fig. 7(c)에 나타난다. 입구부에 설치한 홀들의 개수를 변화시킬 경우, Fig. 7(d)에서 보는 것과 같이 N=20일 경우에 가장 큰 스톨마진을 보였으며 스톨마진의 최대변화폭은 14.8%에 달한다. Fig. 7에서 관찰되는 최대 스톨마진은 직경비 d_h/D_i=0.02에서 발생하는 55.1%이다. 홀의 직경과 홀의 길이가 변화하는 경우에 효율이 개선될 때 스톨마진은 오히려 나빠지는 상반된 경향이 나타남을 알 수 있다.

Fig. 7

Variations of stall margin with the geometry variables

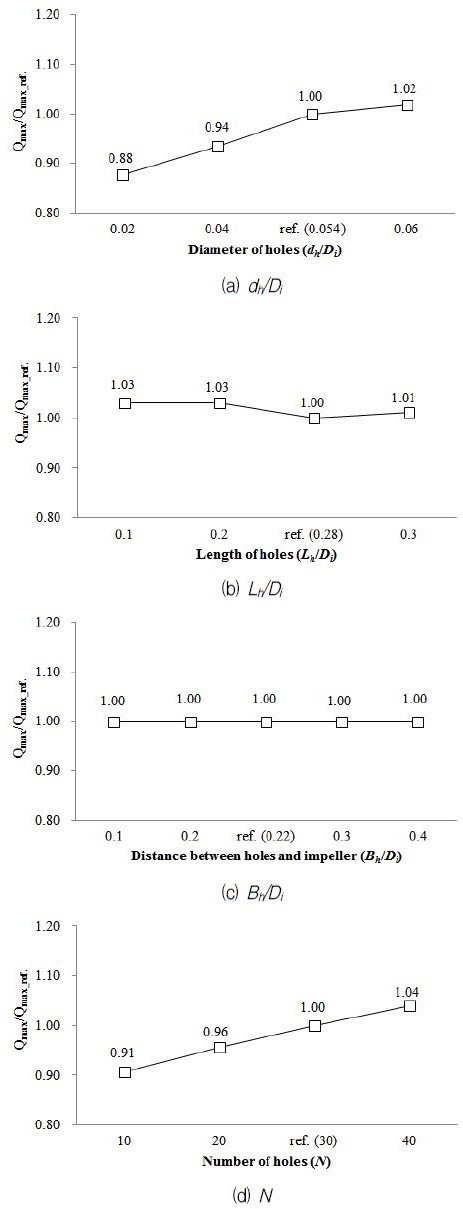
Fig. 8은 각 형상변수의 변화에 따른 최대유량의 변화를 보여주고 있다. 여기서 최대유량은 기준형상의 최대유량으로 무차원화 되었다. 홀의 직경 비의 변화에 따른 최대유량 값의 변화가 Fig. 8(a)에 나타나 있다. 직경 비가 증가할수록 최대유량 값이 증가하는 것을 확인할 수 있다. 아울러, Fig. 8(d)에서 확인할 수 있는 것과 같이 홀의 개수가 증가함에 따라 최대유량 값이 증가하는 경향을 보인다. 그러나 홀의 길이(L_h/D_i)와 홀과 임펠러 사이의 거리(B_h/D_i)의 변화는 최대유량 값의 변화에 거의 영향을 주지 않는 것을 Fig. 8(b)와 (c)를 통해 확인할 수 있다.

Fig. 8

Variations of maximum mass flow rate with geometric variables

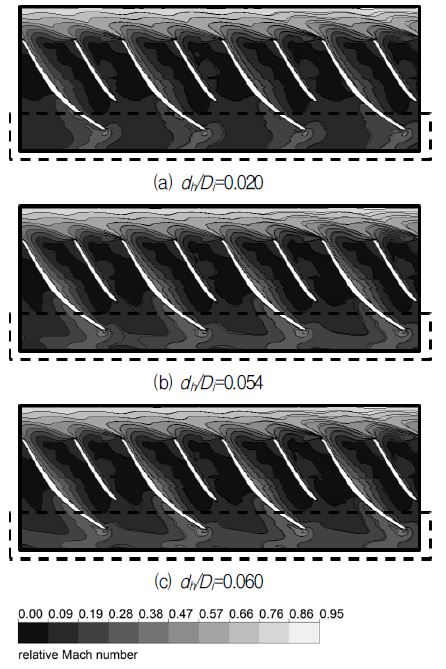
Fig. 9은 원심압축기 입구부에 원주방향으로 설치한 홀들의 직경 변화에 따른 임펠러의 90% 스팬(span)에서의 마하수 분포를 보여주고 있다. 홀의 직경이 증가할수록 임펠러 입구부의 마하수가 증가하고, 블레이드의 압력면(pressure side)에서의 속도가 증가하는 것을 확인할 수 있다.

Fig. 9

Relative Mach number distributions at 90% span in impeller with different diameter of holes

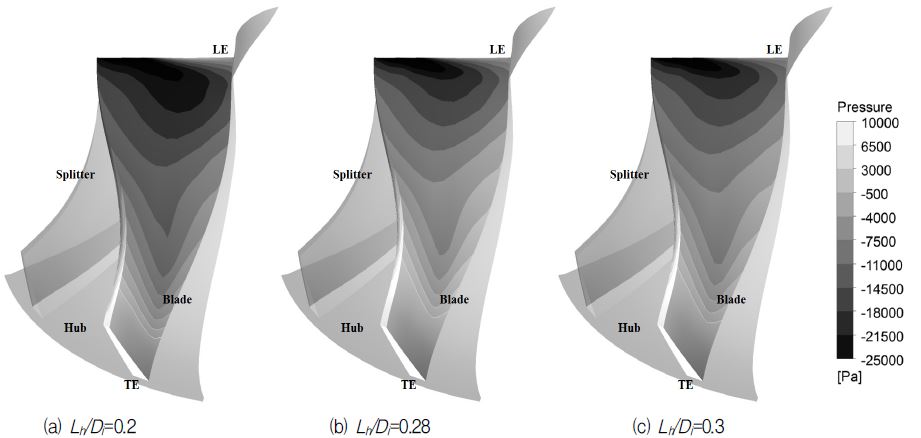
홀의 길이 변화에 따른 원심압축기 날개 흡입면에서의 정압분포 변화는 Fig. 10에 나타내었다. Fig. 6(b)에서 최소 효율을 보이는 L_h/D_i=0.20일 경우, 전익(leading edge)부근에 낮은 압력 영역이 넓게 분포하고 있는데, 이 영역은 홀의 길이를 증가할수록 축소되는 것을 확인할 수 있다.

Fig. 10

Static pressure contours on the suction surface of the blade

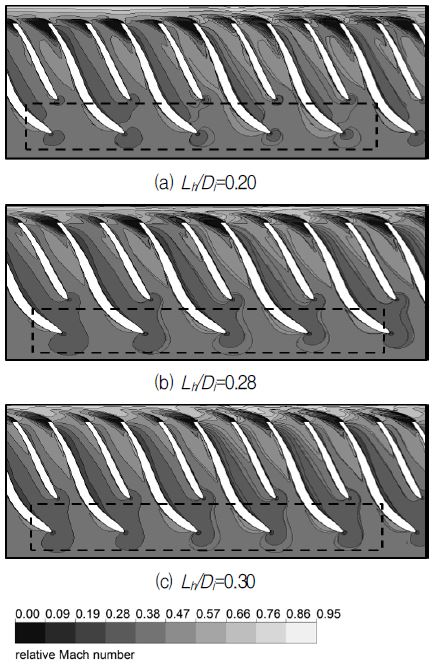
Fig. 11은 홀의 길이 변화에 따른 스톨 점 부근에서의 마하수 분포를 보여주고 있다. L_h/D_i=0.28과 0.30의 경우, 임펠러 입구에 상대적으로 낮은 마하수 영역이 넓게 분포하고 있으며, 이 낮은 마하수 영역은 스톨마진이 최대치를 보이는 L_h/D_i=0.20에서 상대적으로 줄어든 것을 확인할 수 있었다.

Fig. 11

Relative Mach number distributions the length of hole at the near-stall point (10% span)

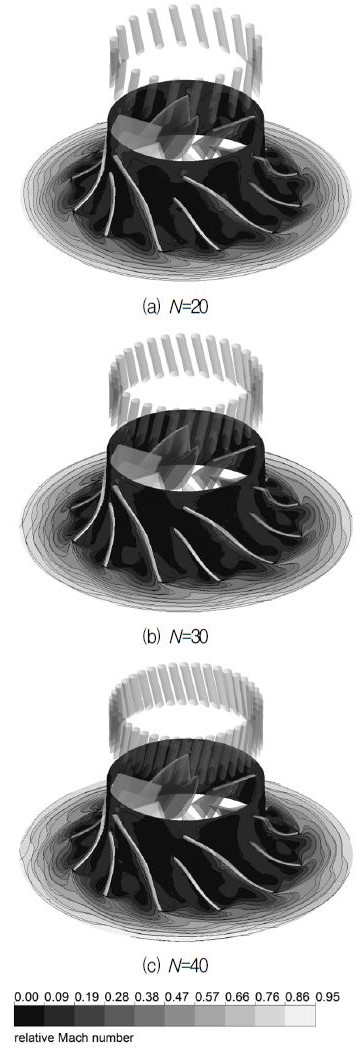
Fig. 12은 원심압축기 입구부의 홀 개수 변화에 따른 스톨점 부근에서의 마하수 분포를 50% span에서 나타내었다. N=30과 40의 경우, 임펠러 입구부에 낮은 마하 수 영역이 넓게 분포하는 것을 확인할 수 있으며, 이 낮은 마하수 영역은 N=20의 경우, 현저히 줄어들었다. 이 영향으로 인해 Fig. 7(d)에 나타난 바와 같이 원심압축기의 스톨마진이 증가한 것으로 사료된다.

Fig. 12

Relative Mach number distributions the number of hole at the near-stall point (50% span)

6. 결 론

본 연구에서는 유입부에 원주방향으로 홀들을 설치한 원심압축기를 대상으로 삼차원 RANS해석을 수행하였다. 유입부에 설치한 홀들의 직경, 길이, 개수, 그리고 홀과 임펠러 사이 거리를 형상변수로 선택하여, 원심압축기의 단열효율 및 스톨마진에 대한 이 형상변수들의 영향을 평가하였다. 매개변수 분석을 통해 홀의 직경과 개수를 각각 증가시킬수록 원심압축기의 최대단열효율이 증가하는 것을 알 수 있었다. 홀의 길이의 경우 시험된 범위의 중간값인 L_h/D_i=0.20에서 최대단열효율의 최소치와 스톨마진의 최소치가 발생하였고, L_h/D_i=0.30에서는 스톨마진이 급격히 감소하여 28.3%를 나타내었다. 홀과 임펠러 사이 거리의 변화는 효율과 스톨마진에 대해서 공통적으로 그 영향이 무시할 정도였다. 홀의 직경과 홀의 길이 변화에 대해서는 효율이 개선될 때 스톨마진은 오히려 나빠지는 상반된 경향이 나타남을 알 수 있다. 홀의 수 20에서 스톨마진은 최대치를 보였다. 4가지 변수 변화에서 관찰되는 가장 큰 최대단열효율은 홀의 수 40에서의 74.6%이고, 가장 큰 스톨마진은 직경비 d_h/D_i=0.02에서 발생하는 55.1%이다. 본 연구의 결과를 바탕으로 향후 연구에서는 최적설계기법을 적용하여 원심압축기의 성능을 향상시킬 수 있는 연구를 수행할 수 있을 것으로 기대한다.

References

• Pinarbasi, A., and Johnson, M. W., (1994), “Detailed Flow Measurements in a Centrifugal Compressor Vaneless Diffuser”, The American Society of Mechanical Engineers Journal of Turbomachinery, Vol. 116(No. 3), p453-460. [https://doi.org/10.1115/1.2929432]
• Filipenco, V. G., Deniz, S., Johnston, J. M., Greitzer, E. M., and Cumpsty, N. A., (2000), “Effects of Inlet Flow Field Conditions on the Performance of Centrifugal Compressor Diffusers: Part 1-Descrete-Passage Diffuser”, The American Society of Mechanical Engineers Journal of Turbomachinery, Vol. 122(No. 1), p1-10. [https://doi.org/10.1115/1.555418]
• Kang, J. S., and Kang, S. H., (2003), “Review of Stall Inception in Turbocompressors”, Journal of Fluid Machinery(in Korean), Vol. 6, p58-65.
• Galindo, J., Serrano, J. R., Climent, H., and Tiseira, A., (2008), “Experiments and Modelling of Surge in Small Centrifugal Compressor for Automotive Engines”, Experimental Thermal and Fluid Science, Vol. 32(No. 3), p818-826. [https://doi.org/10.1016/j.expthermflusci.2007.10.001]
• Kim, J. H., Choi, J. H., and Kim, K. Y., (2010), “Surrogate Modeling for Optimization of a Centrifugal Compressor Impeller”, International Journal of Fluid Machinery and Systems, Vol. 3(No. 1), p29-38. [https://doi.org/10.5293/IJFMS.2010.3.1.029]
• Bonaiuti, D., Arnone, A., Ermini, M., and Baldassarre, L., (2006), “Analysis and Optimization of Transonic Centrifugal Compressor Impellers Using the Design of Experiments Technique”, Journal of Turbomachinery, Vol. 128(No. 4), p786-797. [https://doi.org/10.1115/1.1579507]
• Wang, X. F., Xi, G., and Wang, Z. H., (2006), “Aerodynamic Optimization Design of Centrifugal Compressor’s Impeller with Kriging Model”, Proceedings of the Institution of Mechanical Engineers, Part A, Journal of Power and Energy, Vol. 220(No. 6), p589-597.
• Tong, W. X., Chuangang, G., and Jun, X., (2010), “A new Type of Self-Adaptive Casing Treatment for a Centrifugal Compressor”, Proceedings of American Society of Mechanical Engineers Turbo Expo, Glasgow, UK, GT2010-23457.
• Chen, H., and Lei, V. M., (2013), “Casing Tratment and Inlet Swirl of Centrifugal Compressors”, The American Society of Mechanical Engineers Journal of Turbomachinery, Vol. 135(No. 4), p041010, (8 Pages).
• Xu, W., Wang, T., Gu, C., and Ding, L., (2012), “Numerical Investigation of a Centrifugal Compressor With Holed Casing Treatment”, The American Society of Mechanical Engineers Journal of Engineering for Gas Turbines and Power, Vol. 134(No. 4), p044502, (4 Pages). [https://doi.org/10.1115/1.4004444]
• Tetu, L. G., (2004), “Improving Centrifugal Compressor Perfomrmance By Optimizing Diffuser Surge Control (Variable Diffuser Geometry) and Flow Control (Inlet Guide Vane) Device Settings”, International Compressor Engineering Conference at Purdue, C136, p1-9.
• Cui, M. M., (2004), “Unsteady Flow Around Suction Elbow and Inlet Guid Vanes in a Centrifugal Compressor”, Proceedings of American Society of Mechanical Engineers Turbo Expo, Vienna, Austria, GT2004-53273.
• Yang, M., Martinez-Botas, R., and Zhang, Y., (2013), “Inlet Duct Treatment for Stability Improvement on a High Pressure Ratio Centrifugal Compressor”, Proceedings of American Society of Mechanical Engineers Turbo Expo, San Antonio, Texas, USA, GT2013-95189.
• ANSYS CFX-14.5 Theory Guide of ANSYS CFX 14.5, (2012), ANSYS Inc.
• Bardina, J. E., Huang, P. G., and Coakley, T., (1997), “Turbulence Modeling Validation, testing, and development”, NASA TM 110446.