[ Original Paper ]

The KSFM Journal of Fluid Machinery - Vol. 19, No. 5, pp.20-27

ISSN: 2287-9706 (Print)

Print publication date Oct 2016

Received 24 Sep 2015 Revised 23 Mar 2016 Accepted 08 Apr 2016

DOI: https://doi.org/10.5293/kfma.2016.19.5.020

A Study on CFD Analysis Methods using Francis-99 Workshop Model

Vu Le^* ; Zhenmu Chen^* ; Young-Do Choi^**^{, †}

*Graduate School, Department of Mechanical Engineering, Mokpo National University, Mokpo
*Department of Mechanical Engineering, Institute of New and Renewable Energy Technology Research, Mokpo National University, Mokpo

Correspondence to: ^†E-mail : ydchoi@mokpo.ac.kr

Abstract

The Francis-99 is a workshop initiated by the Norwegian University of Science and Technology (NTNU), Norway, and Lulea University of Technology (LTU), Sweden, in order to further validate the capabilities of the CFD technologies. The goal of the first workshop is to determine the state of the art of numerical predictions for steady operating conditions. When performing the CFD analysis, some geometry details are often neglected. In case of Francis Turbine, labyrinth seals are usually not include in the simulation domain, this may lead to inaccurate prediction of turbine efficiency. In this study, the CFD analysis for Francis-99 Workshop model has been performed for full domain of machine including top and bottom labyrinth seals. The efficiency value and distribution of velocity and pressure have been investigated and compared to the experimental data obtained from NTNU. By comparing the results, it was found that: With the top and bottom labyrinth seals in the domain, the CFD result was significantly improved in prediction of efficiency at all the operating point, especially at part load.

Keywords:

CFD Analysis, Francis-99 Workshop, Losses Analysis, Performance, Pressure Distribution, Velocity Distribution

키워드:

CFD해석, 프란시스-99 워크샵, 손실해석, 성능, 압력분포, 속도분포

1. Introduction

Computational fluid dynamics (CFD) is an established tool in industry for the design of Francis and other type of turbines. The principle task of the CFD tools is to predict the hydraulic efficiency and pressure distribution as accurately as possible and capture flow phenomena of importance.⁽¹⁾ When performing the CFD analysis, the numerical model needs to cover all geometries of physical model. However, for reducing of computation time, some geometry details are often neglected. In case of Francis Turbine, labyrinth seals are usually not included in the simulation domain, this may lead to inaccurate prediction of turbine efficiency. In other studies of the Francis-99 workshop model, without labyrinth seals in domain, the difference between experimental and numerical efficiency at part load operating point is significant (14%).⁽²⁾

In this study, the efficiency prediction is not only focused on, but also the velocity distribution and pressure distribution are investigated, and compared to experimental data obtained from NTNU.

2. Francis-99 workshop model and Numerical Model:

2.1 Francis-99 workshop model

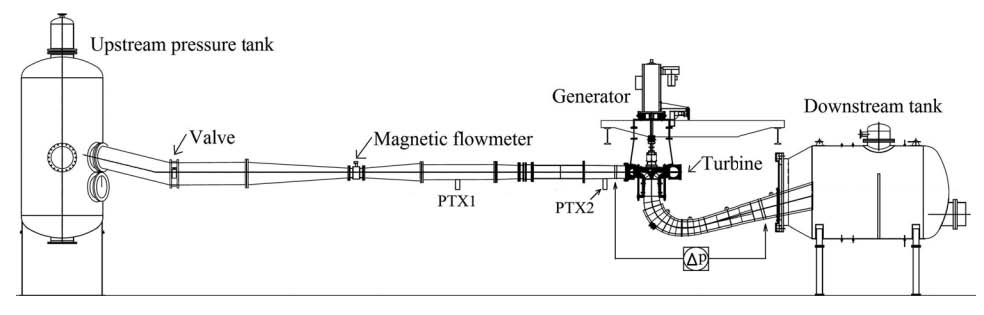
The experimental data is obtained from the test rig at the Waterpower laboratory, (NTNU, Norway). The test rig model turbine is shown in Fig. 1. Experimental measurements were carried out using the open loop water circuit to get realistic conditions. Water from the basement was pumped to the overhead tank and flowed down to the upstream pressure tank connected to the turbine inlet pipeline. A uniform level of the water/head was maintained in the overhead tank at all operating points.⁽²⁾ The model consists of 14 stay vanes conjoined inside the spiral casing, 28 guide vanes, a runner with 15 full length and 15 splitter blades.

Fig. 1

Francis-99 workshop turbine test rig at the Waterpower laboratory, NTNU(2)

2.2 Numerical model and mesh

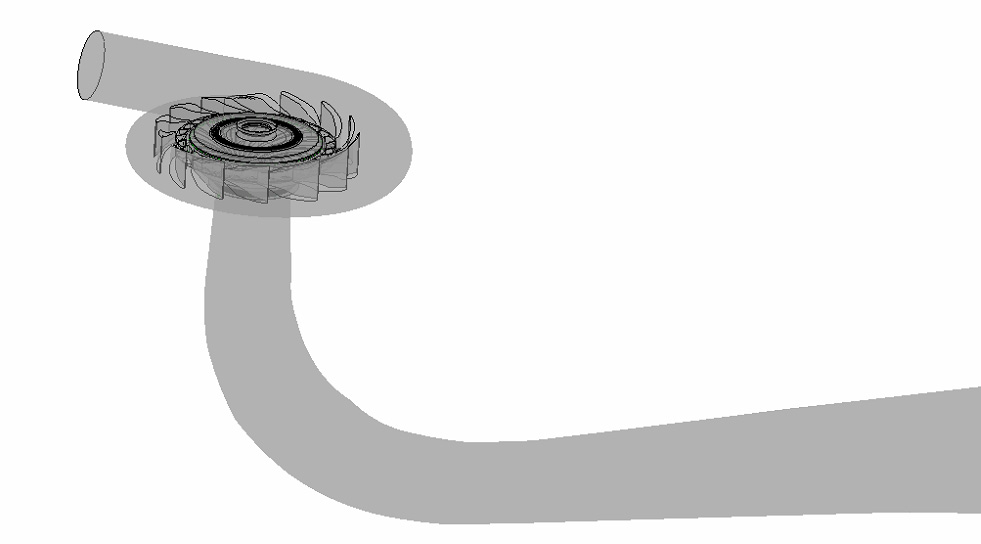
The computation domain consists of the spiral casing with stay vanes and guide vanes, runner, draft tube and also includes top and bottom labyrinth seals. Simulation were performed on 2 types of mesh. First, the computation mesh was provided by organizers,⁽³⁾ which is denoted as NTNU mesh, second mesh was prepared by the present study, which is denoted as MNU mesh. Both NTNU and MNU mesh were performed by ICEM CFD 15.0⁽⁴⁾ on the model size of turbine with block structured hexahedral mesh for all domain. Structured hexahedral mesh is preferred over tetrahedral mesh because it gives faster convergence, better quality and better results with less cells required. In MNU mesh, the O-grid blocks were created for runner blades for better capturing of the flow phenomena at the regions close to wall boundary. Fig. 2 shows the full simulation domain for Francis-99 workshop turbine model for CFD analysis.

Fig. 2

Francis-99 workshop turbine numerical model

A great care for labyrinth seal mesh is required. The mesh needs to cover all the detail of labyrinth seals and also the number of mesh should be as small as possible to reduce the computational cost. Table 1 shows the mesh number of simulation domains. In MNU mesh, the average values of y+ in distributor is equal to 20.9, the values in runner and draft tube are equal to 19.4 and 11.0, respectively. With a great care for labyrinth seals, the average y+ in top labyrinth seal is equal to 16.2 and in the bottom labyrinth seal is equal to 18.8. The computation mesh of runner and labyrinth seals in detail is shown in Fig. 3.

Table 1

Mesh number of simulation domains

Fig. 3

Computation mesh of runner and labyrinth seals in detail

Table 2 summarizes the operating conditions of the turbine and efficiency at each operating point by experiment. Mass flow rate and average pressure were prescribed at the inlet and outlet of simulation domain, using the normal method of other research results.^(5-9) The interaction between guide vanes-runner and runner-draft tube were set as frozen-rotor interaction. All the simulation both with NTNU mesh and MNU mesh were performed with SST turbulence model and steady state analysis. The advanced option of Curvature Corrrection (CC)⁽¹⁰⁾ are known to be very useful in tackling problems in high swirling flows. One case with the CC advance option was included in simulation cases and the result of efficiency prediction was compared with the normal SST turbulence model. Table 3 shows 4 cases of simulation condition, which were performed at each operating points to investigate the influence of labyrinth seals for efficiency prediction and comparison of mesh and turbulence model.

Table 2

Operating conditions of the turbine by experiment

Table 3

List of simulation conditions

3. Results and Discussion

3.1 Volumetric losses and torque losses

The losses in labyrinth mainly consists of volumetric loss and torque loss. The volumetric loss at all operating points is very small due to no balance hole in runner.

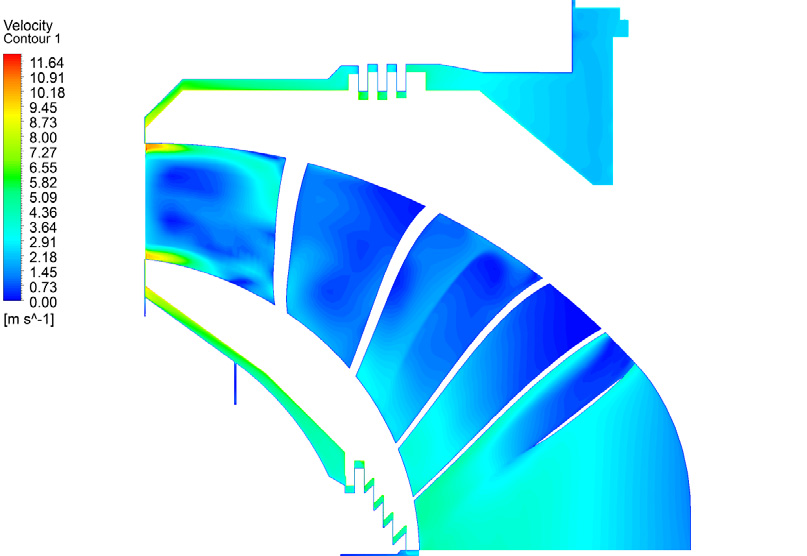
Table 4 shows the result of volumetric loss in labyrinth seals. The largest of proportion of volumetric loss is 0.61% at Part load, while at BEP and High load the proportions are 0.21%. Velocity distribution in runner and labyrinth seals is shown in Fig. 4.

Table 4

Volumetric loss in labyrinth seals

Fig. 4

Velocity distribution in runner and labyrinth seals

Table 5 shows the results of torque loss in labyrinth seals at several operating points. At part load, the largest loss in top labyrinth and bottom labyrinth seals was found.

Table 5

Torque loss in labyrinth seals

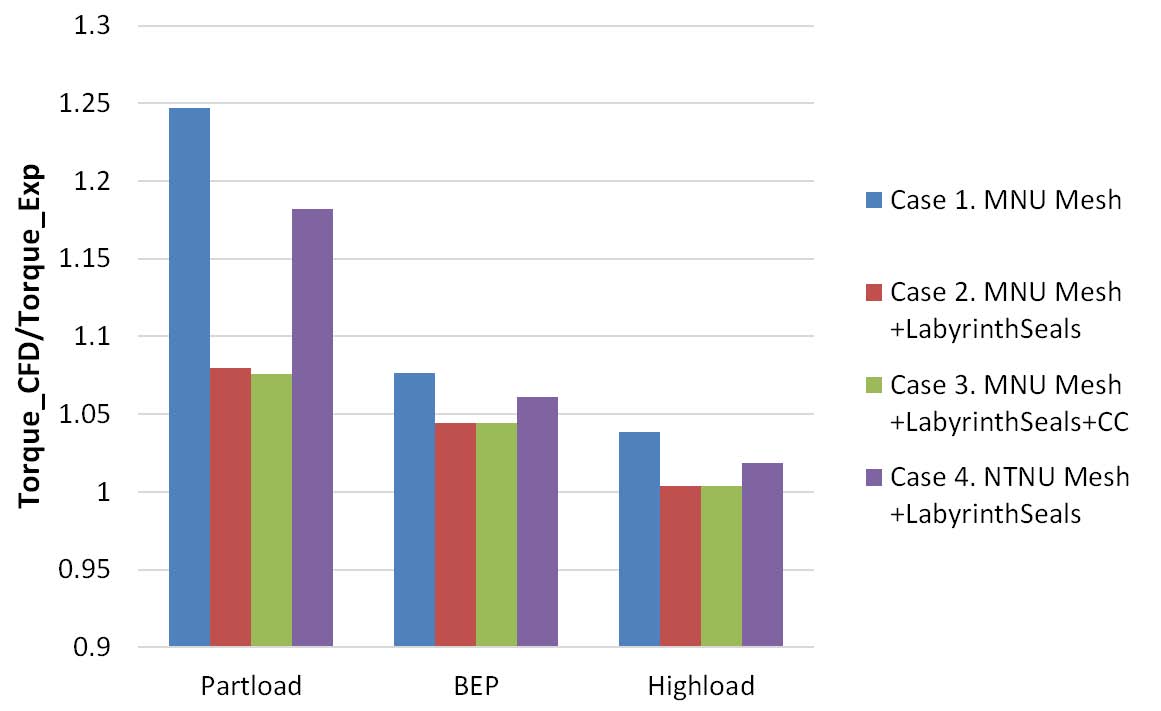
The difference between NTNU mesh and MNU mesh is that MNU mesh were better refined at runner blades. Table 6 shows the comparison of torque on the shaft in two cases of mesh. It is clear that torques on the shaft predicted by NTNU mesh are larger than by MNU mesh (Case 2). The coarse mesh at runner blades in NTNU mesh (Case 4) leads to overestimates torque on runner shaft. The influence of CC turbulence option also was investigated. At all operating points, the CC turbulence option shows reduced prediction torque on the shaft of runner, which makes the prediction torque is closer to measurement torque. Fig. 5 presents the comparison of numerical torque to the experimental torque with several simulation conditions. With including the top and bottom labyrinth seals in simulation domains (Cases 2 and 3), the torque prediction is significantly improved.

Table 6

Comparison of torque on the shaft with labyrinth seals

Fig. 5

Comparison of numerical torque to the experimental torque

3.2 Efficiency prediction

The efficiency of Francis hydro turbine is calculated by the equation:

η = Tω ρgHQ

Where, η is the efficiency of turbine; T is the torque on the shaft of runner; ω is runner angular speed; ρ is density of water; g is gravitational acceleration; Q is flow rate; H is effective head of turbine.

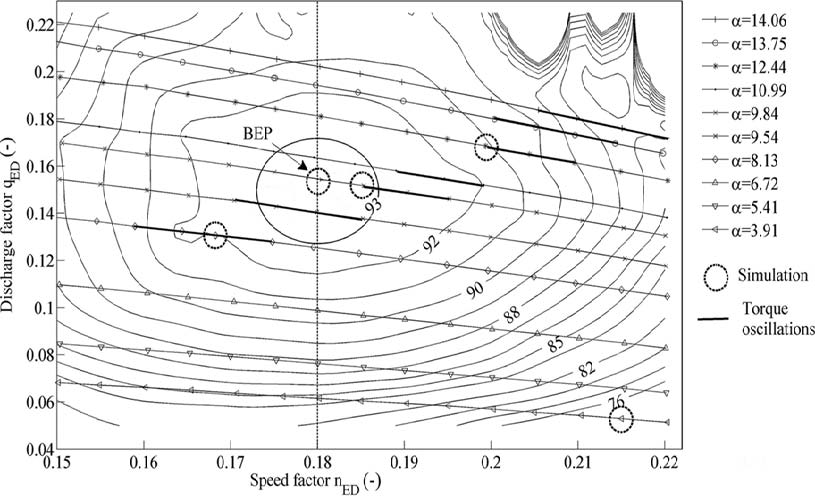
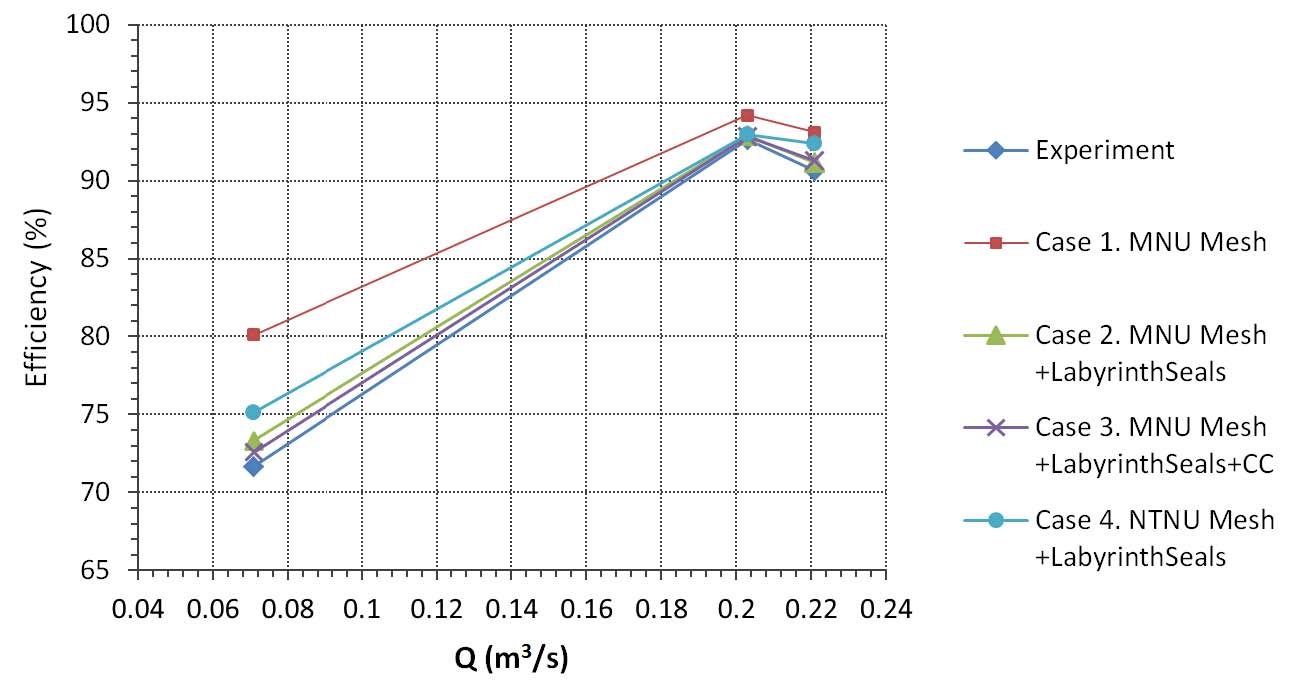
Fig. 6 shows the hill chart of the experiment. Table 7 and Fig. 7 shows the results of efficiency prediction with several simulation conditions at each operating point. From the results it is clear that the efficiency prediction is strongly influenced of labyrinth seals. With the top and bottom labyrinth seals in simulation domain, the efficiency difference becomes lower down from 8.4% to 1.6% at part load, at BEP and high load the differences are 0.3% and 0.5%, respectively. The results at part load and high load were more improved with CC advance turbulence option (Case 3), while at high load the difference slightly increased. By comparing the results between Cases 2 and 4, the refinement at runner blades significantly improved the efficiency prediction by correcting the torque of runner shaft.

Fig. 6

Hill chart of the experiment

Table 7

Results of efficiency prediction

Fig. 7

Comparison of numerical and experimental efficiency

3.3 Velocity distribution validation:

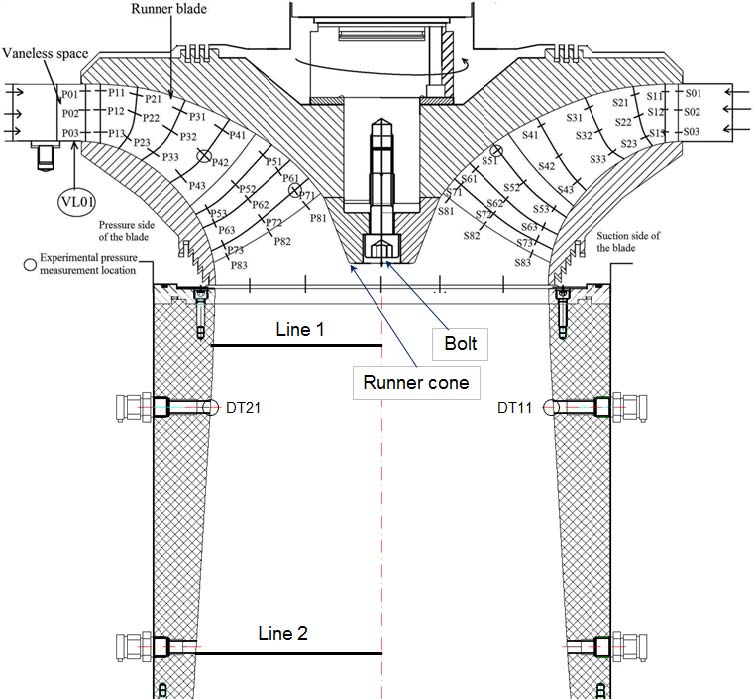
The Francis-99 workshop provided velocity data by experiment to validate the velocity distribution of numerical results. Velocity measurements (axial and tangential) were performed with a laser Doppler anemometer (LDA) along two horizontal lines in the draft tube. The two lines are located 64mm and 382mm below the draft tube inlet, respectively. The locations of velocity sensors were shown in Fig. 8 and Table 8. The validation of velocity distribution were performed for Case 2 (MNU mesh with top and bottom labyrinth seals).

Fig. 8

Sensor locations

Table 8

Velocity sensor locations

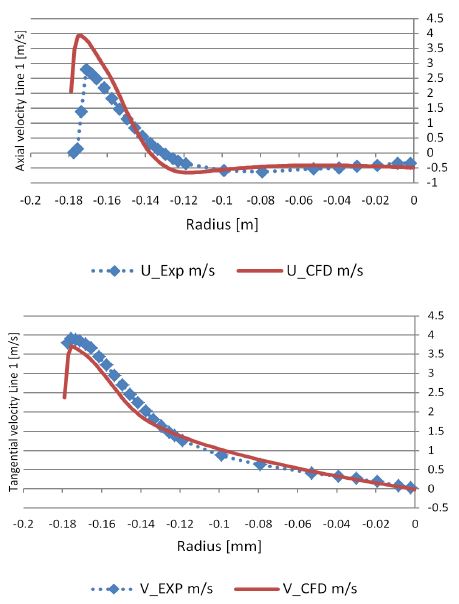
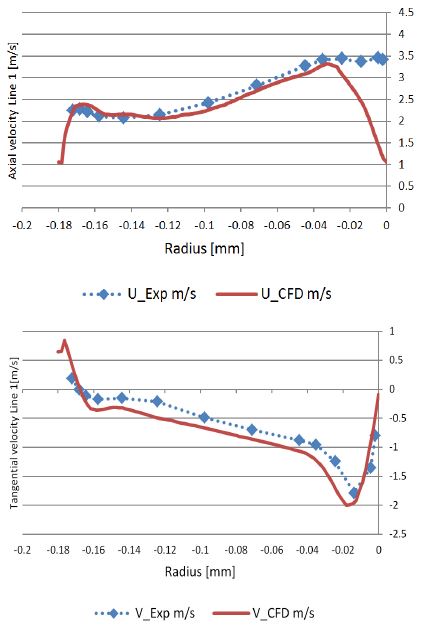
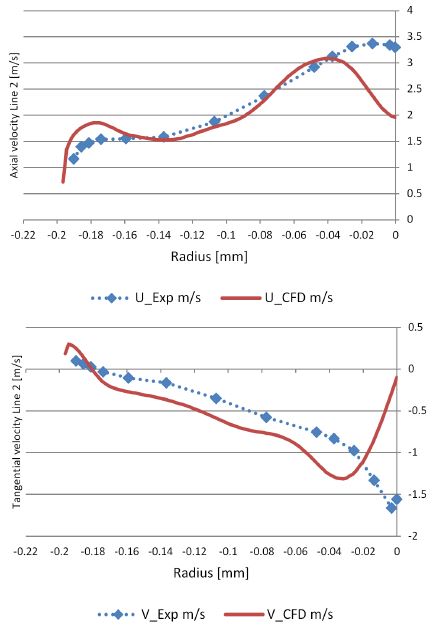
Figs. 9 and 10 show the velocity distribution along Line 1 and Line 2 at part load. The results of CFD analysis predicted similar results for the axial and tangential velocity along the radius. At Line 2, the axial velocity slightly overestimated and the tangential velocity slightly underestimated compared to the measurement data.

Fig. 9

Part load: Velocity distribution at Line 1

Fig. 10

Part load: Velocity distribution at Line 2

Fig. 11

BEP: Velocity distribution at Line 1

Fig. 12

BEP: Velocity distribution at Line 2

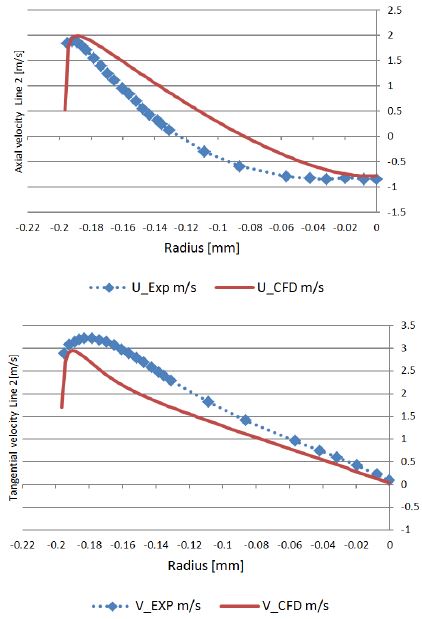
The velocity results at design point are shows in Figs. 11 and 12. The CFD analysis results is fairly close to the experimental results of the axial velocity. However, the results of CFD analysis clearly overestimate the tangential velocity close to the center.

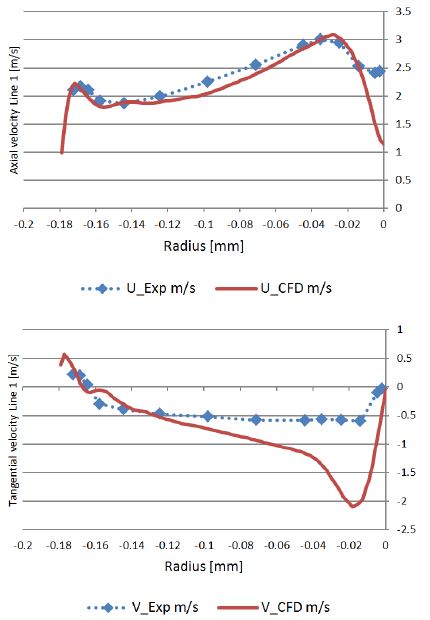
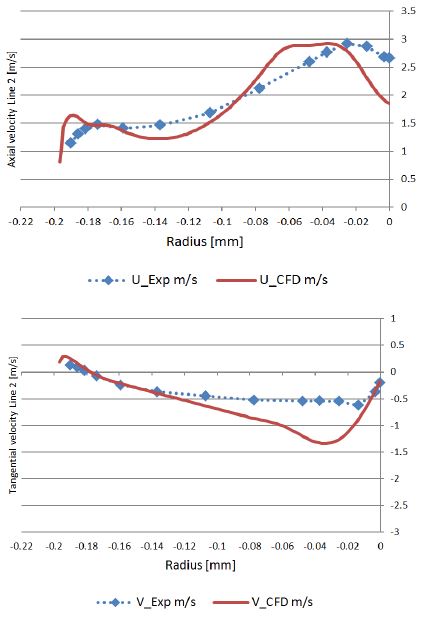
At high load, the results of CFD analysis underestimate the axial velocity at both two Lines and overestimates the tangential velocity at Line 2 at the area close to the center, as shown in Figs. 13 and 14.

Fig. 13

High load: Velocity distribution at Line 1

Fig. 14

High load: Velocity distribution at Line 2

The CFD analysis overestimates the velocity close to the center of the runner. It can be conjectured that the runner cone and bolt give effect on the flow velocity as shown in Fig. 8, because the runner cone and the bolt was not considered in the CFD analysis domain. Therefore, the CFD results over estimate the velocity at this part.

3.4 Pressure distribution validation

Pressure measurement were obtained at 6 locations at each operating point. The exact position of the pressure sensors are presented in Fig. 8 and Table 9. The numerical results obtained with Case 2 (MNU mesh with top and bottom labyrinth seals) were compared with measurement data.

Table 9

Pressure sensor locations

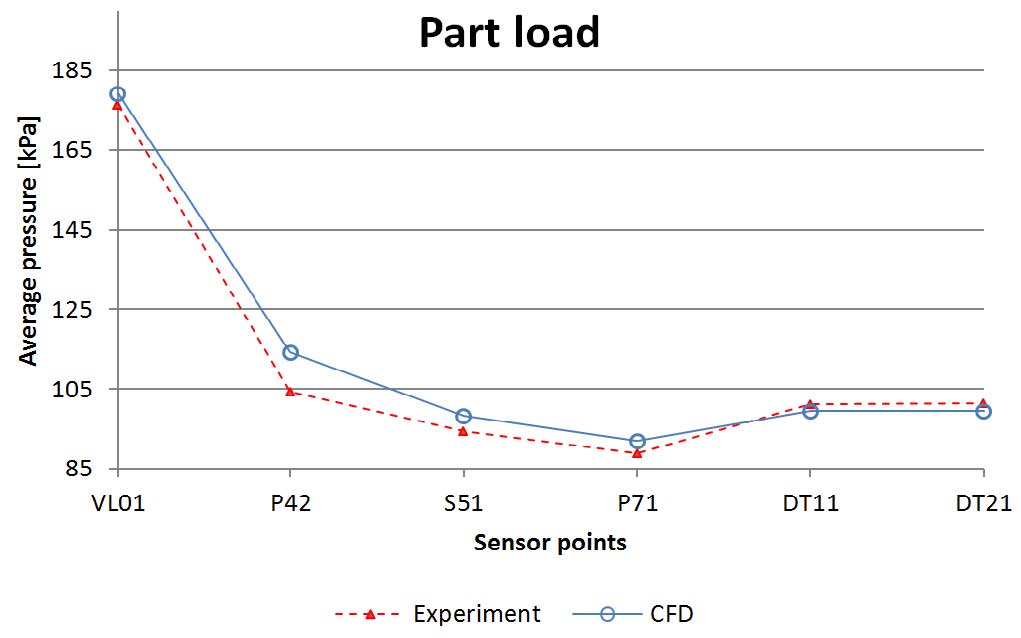
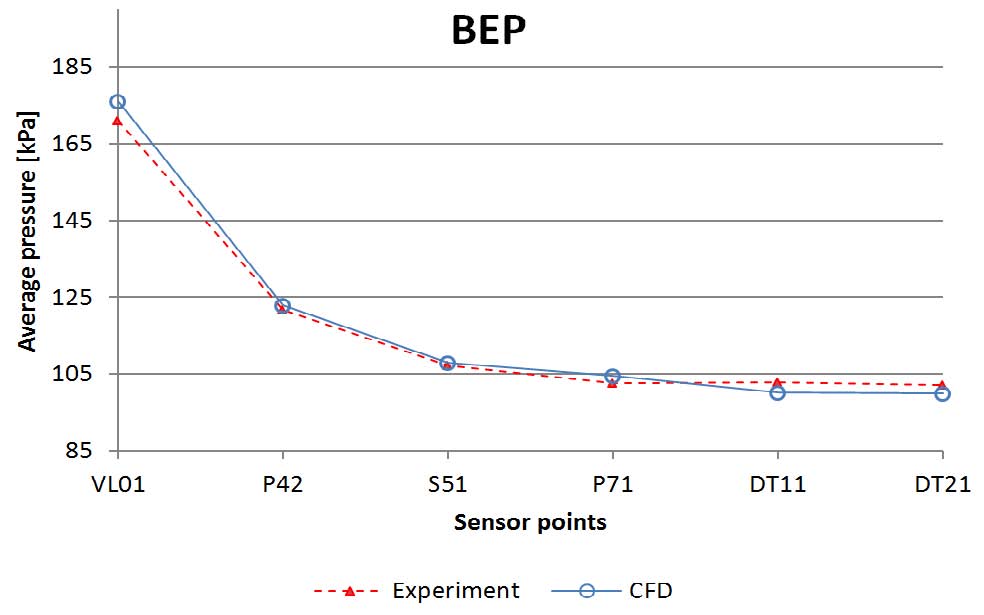
Fig. 15 presents pressure distribution at part load operating point. The results at VL01, DT11 and DT21 are very close to the experiment data, while the maximum difference observed in pressure side of a blade (P42, 9.56%). In case of BEP, the better agreement between numerical and experimental values was obtained as shown in Fig. 16. At all pressure sensors the differences are lower than 2.96%.

Fig. 15

Pressure distribution at part load

Fig. 16

Pressure distribution at BEP

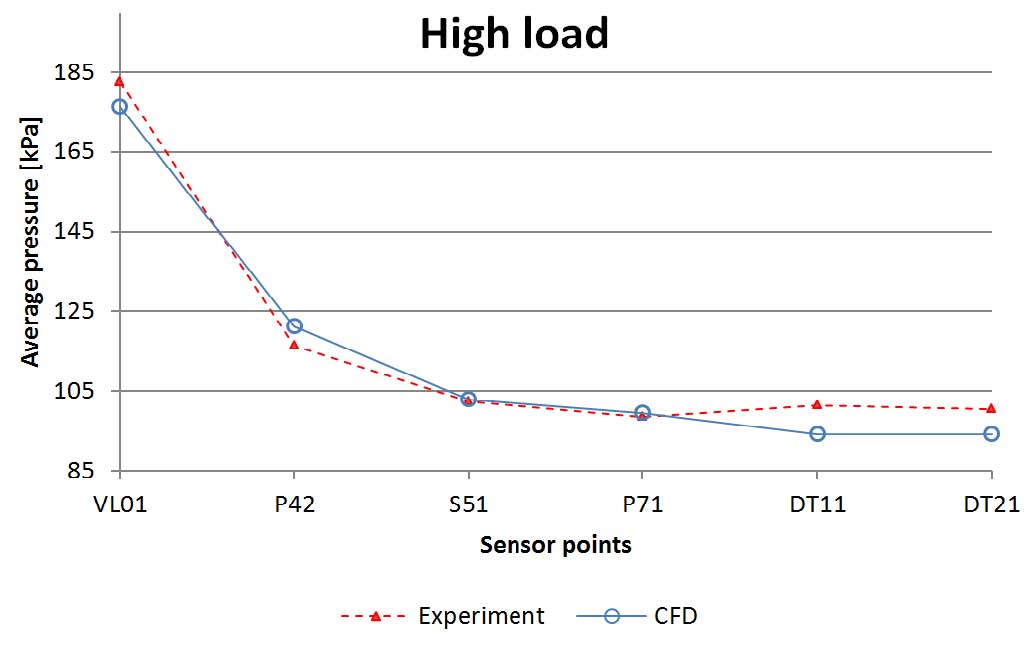
At high load, the average pressure difference in the location of VL01 is 3.46% and the numerical pressure is lower than the measured pressure. In draft tube, the differences between the numerical and measured values at DT11 and DT21 are 7.02% and 6.21%, respectively. The best agreement of pressure between experiment and simulation is obtained in suction side of a runner blade (S51).

Fig. 17

Pressure distribution at high load

4. Conclusion

In present study, the CFD analysis for Francis-99 workshop turbine has been performed for full domain including top and bottom labyrinth seals. The efficiency values and distribution of velocity and pressure have been investigated and compared to the experimental data obtained from NTNU. Including the labyrinth seals, the efficiency prediction were significantly improved. A very good agreement of efficiency between numerical and experimental efficiency were obtained at all operating point, the maximum difference is 1.61% at part load and the minimum difference at BEP is 0.29%.

The efficiency prediction at part load was more improved by including CC advance turbulence option. The difference between numerical and experimental efficiency at part load become lower down from 1.61% to 0.89%. The influence of refinement mesh at runner blades is significant. The coarse mesh in runner of NTNU mesh leads to overestimation of the torque in runner shaft and the efficiency, which are higher than those of experiment.

The distributions of velocity and pressure also were investigated in this study. The CFD analysis can predict accurate results for the axial and tangential velocities along the radius. However, the results of CFD analysis often overestimate or underestimate the axial and tangential velocities at the region close to the center. From the results of pressure distribution, numerically predicted pressures at six locations were compared to the measured results and showed the correct prediction, especially at BEP.

Acknowledgments

This work was supported by the New and Renewable Energy of the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government Ministry of Trade, Industry and Energy (No. 2013T100200079).

References

Wallimann, H., and Neubauer, R., (2015), “Numerical Study of a High Head Francis Turbine with Measurements from the Francis-99 Project”, In Journal of Physics, Vol. 579(No. 1), p012003. [https://doi.org/10.1088/1742-6596/579/1/012003]
Trivedi, C., Cervantes, M. J., Gandhi, B. K., and Dahlhaug, O. G., (2013), “Experimental and Numerical Studies for a High Head Francis Turbine at Several Operating Points”, The American Society of Mechanical Engineers Journal of Fluid Engineering, Vol. 135(No. 11), p111102. [https://doi.org/10.1115/1.4024805]
NTNU and LTU Francis-99 test case http://www.ltu.se/research/subjects/Stromningslara/Konferenser/Francis-99/Test-Case-1.111520?l=en, .
ANSYS Inc, (2013), “ANSYS CFX Documentation”, Ver. 15, http://www.ansys.com.
Wu, J., Shimmei, K., Tani, K., Niikura, K., and Sato, J., (2007), “CFD Based Design Optimization for Hydro Turbines”, The American Society of Mechanical Engineers Journal of Fluids Engineering, Vol. 129(No. 2), p159-168. [https://doi.org/10.1115/1.2409363]
Wu, Y., Liu, S., Wu, X., Dou, H., Zhang, L., and Tao, X., (2010), “Turbulent Flow Computation Through a Model Francis Turbine and Its Performance Prediction”, Earth and Environmental Science, Vol. 12(No. 1), p012004. [https://doi.org/10.1088/1755-1315/12/1/012004]
Cervantes, M. J., Andersson, U., and Lovgren, H. M., (2010), “Turbine-99 Unsteady Simulations-Validations”, Earth and Environmental Science, Vol. 12, p012014. [https://doi.org/10.1088/1755-1315/12/1/012014]
Zhang, L. X., Wang, W. Q., and Guo, Y., (2007), “Intrinsic Features of Turbulent Flow in Strongly 3-D Skew Blade Passage of a Francis Turbine”, Journal of Hydrodynamics, Vol. 19(No. 1), p92-99. [https://doi.org/10.1016/S1001-6058(07)60033-X]
Buntić, O. I., Dietze, S., and Ruprecht, A., (2005), “Numerical Simulation of the Flow in Turbine-99 Draft Tube”, In Proceedings of the Third IAHR/ERCOFTAC Workshop on Draft Tube Flow, Porjus, Sweden, p8-9.
Smirnov, P. E., and Menter, F., (2009), “Sensitization of the SST Turbulence Model to Rotation and Curvature by Applying the Spalart-Shur Correction Term”, Journal of Turbomachinery, Vol. 131(No. 4), p041010. [https://doi.org/10.1115/1.3070573]