Pre-swirl system의 유량계수 향상을 위한 Pre-swirl nozzle의 형상 최적화 전산해석 연구
Abstract
Optimization process of pre-swirl nozzle geometry was conducted to improve the discharge coefficient of pre-swirl system by using CFD. The optimization of pre-swirl nozzle shape covered the converging angle and the location of the converging nozzle. Optimization process included Optimal Latin Hyper-cube Design method to get the experimental points and the Kriging method to create the response surface which gives candidate points. The process was finished when the difference between the predicted value and CFD value of candidate point was less than 0.1%. This paper compared the Reference model, Initial model which is the first model of optimization and Optimized model to study flow characteristics. Finally, the discharge coefficient of Optimized model is improved about 17 % to the Reference model.
Keywords:
Computational Fluid Dynamics, Cooling System, Discharge Coefficient, Gas Turbine, Optimization Process, Pre-swirler, Swirl Ratio키워드:
전산유체역학, 냉각 시스템, 유량계수, 가스 터빈, 최적화 과정, 프리스월러, 스월비1. 서 론
가스터빈의 효율은 온도와 압력의 영향을 크게 받는다. 터빈으로 유입되는 온도가 상승할수록 가스터빈의 효율은 좋아지는데, 터빈으로 유입되는 온도가 어느 수준 이상으로 올라가게 되면 입구 안내익과 1단 로터 블레이드에서 구조적인 문제가 발생하게 된다. 이를 해결하기 위해 압축기를 지난 기체 일부를 빼내어 입구 안내익 및 1단 로터 블레이드의 냉각기체로써 사용한다. 압축기에서 빼낸 냉각기체는 연소기를 지나지 않고 2차 유로를 통과한다. 냉각기체는 비회전 영역과 회전영역을 지나는데, 이 때 많은 손실이 일어난다. Pre-swirler는 이러한 손실을 줄이기 위해 냉각유체가 회전영역에 진입하기 전에 미리 회전성분을 부여하는 장치를 일컫는다. 냉각유체의 유동손실이 줄어들수록 블레이드 냉각 성능이 향상되며, 이에 따라 블레이드의 수명이 증가할 뿐만 아니라 가스터빈의 전체적인 효율상승을 가능하게 한다. 이에 따라 최근 수년간 블레이드의 구조적 수명 연장 및 가스터빈의 효율상승의 일환으로 Pre-swirler 연구가 활발히 진행되고 있다.
Pre-swirler는 크게 Vane type과 Hole type으로 나뉘는데, Vane type은 유동의 손실이 적지만 가공이 힘들고, Hole type은 유동의 손실이 비교적 크지만 가공성이 뛰어난 특징을 가지고 있다. 이러한 특징 때문에 가스터빈마다 사용하는 Type이 다르며, Hole type의 유동손실을 줄이기 위해 Hole 의 형상을 변형하는 연구가 많이 이루어져왔다.
M. Dittmann 등(1)은 Pre-swirl system에서 발생하는 유량손실을 연구하였다. 이상적인 유량과 손실을 동반한 유량의 비인 유량계수를 사용하였으며, 압력비를 변화시키며 실험하였다. Pre-swirl nozzle의 유량계수는 회전영역의 회전수가 커짐에 따라 점차 작아짐을 보였다. Receiver hole의 유량계수는 Receiver hole로 유입되는 유동의 회전성분 속도의 영향과 Receiver hole의 개수의 영향을 많이 받는다는 결과를 보였다. 유량계수는 전체적으로 0.7–0.8 사이의 결과가 나왔다.
Javiya 등(2)은 Pre-swirl nozzle의 세 가지 형상을 연구하였다. 단순한 Hole과 공기역학적인 Hole, Vane type 형상의 유량계수와 온도변화를 관찰하였다. 유량계수는 회전을 고려하지 않는 노즐 유량계수를 사용하였다. 유량계수는 Vane type이 가장 높게 나왔으며, 그 다음으로는 공기역학적인 Hole이 높았고, 단순한 Hole 형상이 가장 낮은 결과를 보였다. 온도의 변화 역시 위와 같은 순서를 보였지만, 유량계수와 온도변화에서 Vane type과 공기역학적인 Hole type의 차이는 단순한 Hole 형상과 비교하였을 때 미비한 차이를 보였다. 유량계수는 Vane type, 공기역학적인 Hole type, 단순한 Hole type 순으로 약 0.9, 0.87, 0.7 의 결과를 보였다.
Lewis 등(3)은 Pre-swirl nozzle의 Radial location에 따른 유량계수와 Receiver hole의 Swirl ratio를 연구하였다. Nozzle의 위치변화에 따라 Receiver hole의 Swirl ratio는 큰 변화를 보였지만, 유량계수는 미비한 차이를 보였다. Swirl ratio가 1일 때, Receiver hole에서의 유량계수는 약 0.7이 나왔다.
Bricaud 등(4)은 다양한 Pre-swirl system design에 따른 유량계수와 온도 및 속도분포를 연구하였다. Pre-swirler의 형상과 Cavity 크기에 따라 유량계수가 크게 차이가 났으며, 온도와 속도분포는 Receiver hole에서 차이를 보였다. Pre-swirl 형상은 두 종류로 실험하였는데, 단순한 Hole type에 비해 공기역학적인 모양의 Hole type이 유량계수가 더욱 크게 측정되었다. 노즐 유량계수는 형상에 따라 최소 0.66, 최대 0.9의 결과를 보였다.
Chew 등(5)은 두 가지 Pre-swirl system을 실험 및 전산해석을 통해 연구하였다. 형상이 다른 두 개의 Hole type Pre-swirler를 유량계수와 속도계수 및 온도변화로 관찰하였다. 회전영역을 제외한 노즐에서의 유량계수만을 측정하였으며, 0.85–0.9 사이의 결과를 보였다.
Ciampoli 등(6)은 Pre-swirl nozzle의 직경을 입구부분과 출구부분으로 나누어 형상최적화를 진행하였다. 최적화 기법은 Direct Hill Climbing 및 Response Surface Model을 사용하여 두 기법을 비교하였다. 회전영역을 고려하지 않고 노즐의 유량계수만을 관찰하였으며, 최종적으로 0.83의 결과를 보였다.
Lewis 등(7)은 Pre-swirl system의 경계조건을 바꿔가며 Swirl ratio와 유량계수를 실험 및 전산해석 하였다. Swirl ratio가 약 1.0인 부근에서 유량계수가 가장 높은 실험값을 가졌다. 그 때 Receiver hole의 유량계수는 약 0.65의 결과를 보였다.
본 연구에서는 가공성이 뛰어난 Hole type의 Pre-swirler 형상을 실험계획법을 적용 후 최적화하여 Pre-swirl system의 유량계수를 최대화 하였다. 실제 가스터빈을 고려하여 유량계수는 회전하는 영역을 포함한 전체 System의 값을 관찰하였다. Dittmann 등(1)과 Yan 등(8)의 Pre-swirl system을 이용하였고, 기존 형상의 유량계수와 최적화된 형상의 유량계수를 비교하였다. 또한 Pre-swirl nozzle 출구부분에서 Swirl ratio를 구하여 유량계수와의 관계를 확인하였다. 최종적으로 Pre-swirl system 전체의 유량계수가 0.75 이상의 값을 갖도록 목표를 설정하였다.
2. 본 론
2.1 전산해석 모델
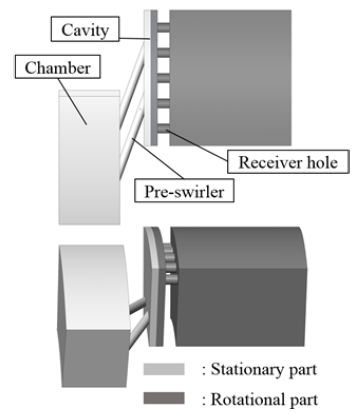
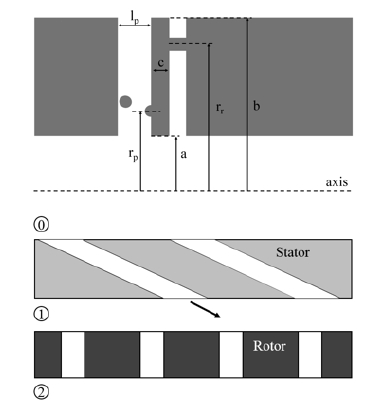
본 연구에서는 Dittmann 등(1)과 Yan 등(8)이 연구한 Pre-swirl 모델을 이용하여 전산해석을 하였다. 이 모델은 Pre-swirl 모델 중에서도 유량계수뿐만 아니라 Swirl ratio, 열전달 특성 등의 연구가 세계적으로 많이 진행되고 있기에 이 모델을 선정하였다. 위 연구의 전산해석 및 실험결과로부터 본 연구의 전산해석 기법을 검증하였으며, 그에 따라 형상 최적화 연구를 진행하였다.(13) Dittmann 등(1)의 Pre-swirler type(Reference model)은 단순한 Hole type인데, Nozzle 직경은 7.1 mm이며, Pre-swirl chamber와 Cavity 사이의 간격은 20 mm로 일정하다. Pre-swirl system의 Nozzle 개수는 24개이고, Receiver hole의 개수는 60개이다. Pitch ratio를 1로 맞추어 전산해석은 Nozzle 2개, Receiver hole 5개로 진행하였다. Pre-swirler 모델의 계산영역을 Fig. 1에 나타내었고, Pre-swirler 형상 정보를 Fig. 2와 Table 1에 나타내었다.
본 연구에서는 Hole type의 Pre-swirl nozzle 형상 최적화를 위해 Nozzle의 입구부분 직경과 출구부분 직경을 다르게 설정하였다(Initial model). 출구부분의 직경은 7.1 mm로 유지하여 기본 형상과의 유량계수 측정 단면적을 일치시켰고,(14) 입구부분의 직경은 Lewis 등(7)의 Pre-swirl nozzle 최적화 결과로부터 10.2 mm로 정하였다.(7) Fig. 3에 형상이 변형 된 Hole type(Initial model)의 Pre-swirl domain을 나타내었다.
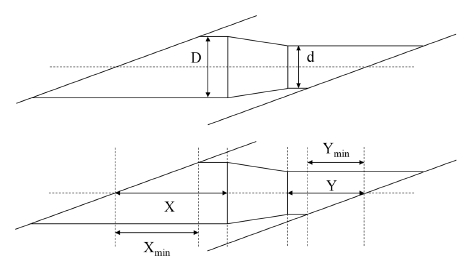
Initial model의 Pre-swirler는 Nozzle의 입구부분 길이와 출구부분 길이로 형상이 정의된다. 입구부분과 출구부분은 변수 크기에 따라 높이가 결정되는 원기둥을 형성하며, 그 사이의 부분은 Converging 영역으로 원뿔받침대 형상이 만들어지게 된다. Nozzle의 입구부분 높이 형상변수를 X, 출구부분은 Y로 정하였다. Nozzle의 직경과 형상변수는 Fig. 4에 나타내었고, 형상변수의 범위는 Table 2에 나타내었다.
2.2 Discharge Coefficient and Swirl Ratio
Pre-swirl system의 성능을 나타내는 지표로써 유량계수가 사용된다. 유량계수는 실제유량과 이상적인 유량의 비를 의미하고, 식 (1)에 나타내었다. 유량계수는 System의 단면적, 압력 및 온도 등으로 나타내어지며, Nozzle 벽면에서의 Viscous effect와 회전의 영향을 많이 받을수록 그 값은 감소한다. 유체가 이상적으로 흐를 수 없기 때문에 유량계수는 1을 넘을 수 없다.
| (1) |
여기서 AN은 Nozzle의 단면적이고, P0와 PS는 각각 전압과 정압, 그리고 Tt는 전온도이다. γ는 비열비이다.
Pre-swirl의 유동 특성을 나타내는 식으로 Swirl ratio가 있다. 이는 주로 Pre-swirl nozzle의 출구 또는 Receiver hole의 입구에서 측정한다. Swirl ratio는 측정하는 위치에서의 접선방향 속도성분과 터빈의 회전속도의 비로 정의되고, 식 (2)에 나타내었다. 유동의 접선방향 속도성분이 터빈의 회전속도와 일치할 경우 Swirl ratio는 1이고, 이 때 유동과 Receiver hole의 회전방향 상대속도는 0이 되어 Nozzle을 빠져나온 유동이 Receiver hole로 적은 손실로 유입된다. 하지만 Cavity 영역에서 유동의 손실이 많이 일어나기 때문에 Pre-swirl nozzle에서의 Swirl ratio를 1보다 큰 값으로 설계를 하여야 Receiver hole 입구에서 유동의 접선방향 속도가 회전속도와 일치할 수 있다.
| (2) |
여기서 r은 중심축으로부터의 거리, Ω는 터빈의 회전속도, vΦ은 Nozzle에서 분사된 유동의 접선방향 성분이다.
2.3 전산해석 기법
본 연구에서는 Pre-swirl system의 유량계수를 향상시키고자 전산해석을 수행하였고, ANSYS CFX Ver. 16.2를 사용하였다.
Pre-swirl nozzle에서 냉각유체의 거동과 회전에 의한 영향을 관찰하기 위하여 3차원 Reynolds Averaged Navier-Stokes(RANS) 모델을 사용하였다. RANS 모델은 유체의 거동을 정의하는 Navier-Stokes 방정식을 시간 평균한 모델이다. RANS 모델은 유동 특성과 난류 전단 응력간의 선형함수 관계를 가정한 Boussinesq 가정에 기반을 두고 있는데, 이는 단순하면서도 실제 유동을 성공적으로 예측하기 때문에 형상이 복잡하고 회전하는 Pre-swirl system의 전산해석에 적합하다. Pre-swirl system은 벽면에서의 Viscous effect와 유동이 회전하는 Cavity 영역의 해석이 중요하기 때문에 난류모델로써 Shear-Stress Transport k-ω model(SST k-ω model)을 사용하였다. SST k-ω model은 벽면에서는 k-ω 모델을 사용하고, 벽면과 떨어진 유동영역에서 k-ε 모델을 사용하여 각 모델의 장점을 취한 모델이다.
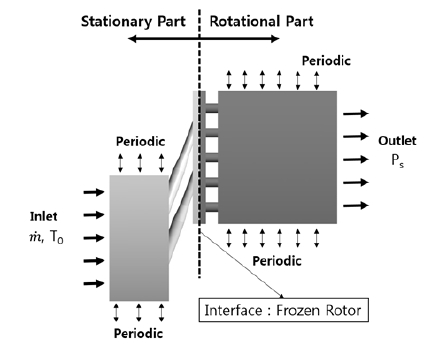
전산해석 영역은 두 개의 영역으로 구성되어 있다. Table 3에 경계조건을 나타내었고, Fig. 5에 Pre-swirl system의 유동 영역을 나타내었다.
Chamber부터 Pre-swirl nozzle영역은 회전하지 않는 고정된 영역이며, Receiver hole은 회전하는 영역이다. Cavity 영역은 고정 영역과 회전 영역이 공존하는 영역인데, Cavity의 중앙에 Mixing Plane 기법을 적용하였다.(7,15) Mixing Plane 기법은 Frozen Rotor 기법을 사용하였다. Frozen Rotor 기법은 회전하는 영역의 상대적인 위치에 따라 해석 결과가 조금씩 다르지만, 전산해석 결과가 Stage 기법에 비해 비교적 잘 맞는다. 그 이유는 Stage 기법은 원주방향의 유동을 평균하여 동일하게 회전영역으로 유입시키기 때문에 Nozzle에서 강하게 나오는 유동과 그렇지 않은 부분을 표현하기에는 적합하지 않다.
본 연구의 해석 시간을 단축시키기 위하여 Nozzle 2개, Receiver hole 5개를 해석하였다. Chamber로 유입되는 입구조건은 유량조건으로 0.006464 kg/s과 전온도 327.5 K를 주었다. 출구조건으로는 정압 102,320 Pa을 주었고, 회전하는 영역은 4,500 rpm으로 주었다.(7) 모든 벽면은 No slip condition을 주었다.
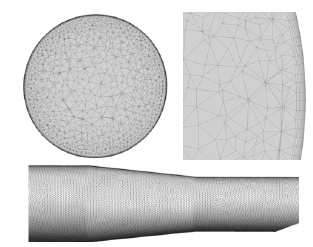
Pre-swirler 전산해석 모델의 격자 형성은 k-ω based SST 난류모델에 적합하도록 Prism 격자와 Tetrahedral 격자로 구성하였다. 벽면에 의한 유동의 변화는 Discharge Coefficient(CD)와 밀접한 관련이 있기 때문에 벽면 Prism 격자를 구성하였다. y+는 1 이하를 만족하였다. 그 결과 고정영역에서 약 480만 개, 회전영역에서 약 330만 개로 총 810만 개의 격자를 형성하였다. Fig. 6은 Pre-swirl nozzle의 격자를 나타내었다.
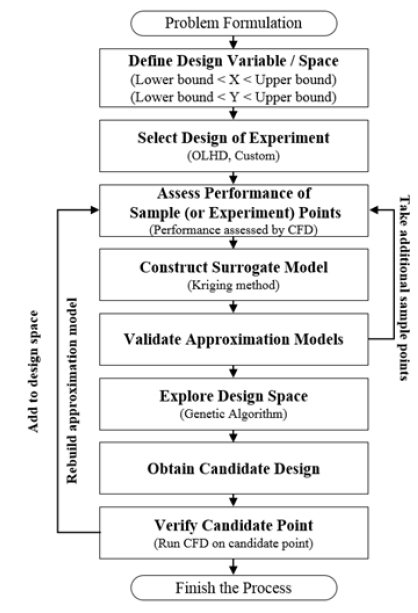
최적화 진행 과정을 Fig. 7에 나타내었다. 본 연구에서는 Pre-swirl nozzle의 형상변수 X와 Y를 변화시켜가며 유량 계수를 관찰하였다. 실험계획법(Design of Experiments)은 최소의 계산으로 많은 정보를 얻을 수 있다는 장점이 있다. 형상변수 X와 Y를 실험계획법의 변수로 적용하였으며, X와 Y의 하한선은 Pre-swirl nozzle의 형상이 만들어질 수 있는 최소값을 사용했고, 상한선은 각각의 변수가 Chamber와 Cavity의 중간 지점을 지나지 않도록 하는 값을 사용했다. 변수의 초기값은 각각 범위의 중앙값을 사용했다.
실험계획법 기법은 Optimal Latin Hypercube Design (OLHD)을 사용하였다. OLHD는 Latin Hypercube Design(LHD) 기법에서 후처리 작업을 한 것이다. LHD는 Design space를 일정하게 등분하여 Sample point를 무작위로 배치하는 기법으로 무작위도에 강점을 지니고 있다. OLHD는 LHD로부터 얻은 Sample point들 사이의 거리를 최대화한 기법이다. 그렇기 때문에 LHD의 단점인 Sample point의 치우침을 개선하여 보다 적은 Sample point를 통해 효율적으로 실험계획법을 수행할 수 있다.
실험계획법을 수행한 결과를 이용해 반응면을 형성하였다. 반응면은 Kriging type을 사용하였다. Kriging type은 Sample point들이 반응면 위에 존재하여 수치적으로 비교적 정확한 반응면을 형성할 수 있으며, 수치적 실험에 적합한 모델이다.(9-12)
본 연구에서는 Reference model의 Pre-swirl nozzle에서 유량계수를 향상시키는 것을 목표로 정하였다. 설계변수는 Nozzle의 형상을 결정하는 변수 X와 Y로 하였고, 목적함수는 유량계수로 설정하여 목적함수의 최대화를 목표로 하였다. 그 후에 Sampling method를 통해 DOE 실험점을 형성하였는데, 변수의 개수가 2개이기 때문에 6개의 실험점을 얻었다.(12) 실험점 모두 CFD를 거쳐 반응면을 만들었다. 반응 면형성 결과를 토대로 최적점을 예측하여 다시 계산을 수행하였다. 위 과정을 반복하여 최적점의 Discharge coefficient 예측 값과 계산의 결과 값이 0.1% 이하를 만족하였을 때 최적화 과정을 종료하였다.
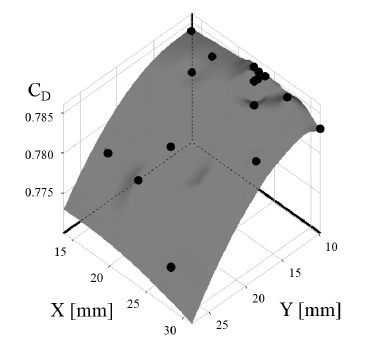
Fig. 8에 최적화 결과 형성된 반응면을 나타내었다. 각 축은 형상변수인 X와 Y, 목적함수인 CD를 의미한다. 최적점을 찾기 위해 총 5번의 Refinement를 거쳤으며, 총 19개의 실험점을 전산해석하였다.
형상변수 X는 형상변수 Y에 비해 유량계수에 미치는 영향은 적었지만, X의 값이 약 24 mm일 때 유량계수의 값이 가장 큰 결과를 보였다. 형상변수 Y는 작은 값을 가질수록 높은 유량계수를 나타냈지만, Y가 하한값일 때는 유량계수가 하락하였다.
2.4 결 과
Reference model, Initial model 그리고 Optimized model의 형상을 Fig. 9에 나타내었고, 형상변수를 Table 4에 나타내었다. Initial model과 Optimized model의 Nozzle 입구 부분이 Reference model에 비해 직경이 큰 것을 확인할 수 있다. Optimized model의 X값은 23.93 mm, Y는 10.72 mm가 되었다. Nozzle의 입구부분의 길이는 Initial model과 Optimized model 사이의 변화량이 1.72% 로 큰 차이는 없었으나, Optimized model은 출구부분의 길이가 Initial model 대비 약 54.5% 짧아진 형상을 보였다. Optimized model의 출구 부분의 길이가 짧아짐에 따라 Converging nozzle 부분의 길이가 길어져 비교적 완만한 Converging nozzle 형상을 만들었다. Converging nozzle의 길이는 약 23.8 mm, Converging angle의 크기는 약 3.8 degree가 되었다.
Swirl ratio는 Nozzle 출구에서의 값을 구하였는데, 유량계수가 상승했음에도 불구하고 Swirl ratio는 거의 동일한 값을 보였다. 이는 세 형상의 Nozzle 출구 속도의 접선성분이 일치함을 뜻한다. Pre-swirler의 출구 면적을 일치시켰기 때문에 동일한 유량이 흐를 때 Nozzle을 통해 나오는 유속은 동일한 결과를 보였다. 입구 경계조건으로서 유량을 주어 모든 전산해석에서 유량은 일치시켰고, 이에 따라 유량계수의 증가는 노즐에서의 압력강하 해소로 인해 증가하였다. Pre-swirl system의 설계는 Swirl ratio의 값을 1 부근으로 정한 후 시작하기 때문에 본 연구에서 Swirl ratio를 일치시키고 유량계수를 증가시켰다는 것은 의미가 있다.
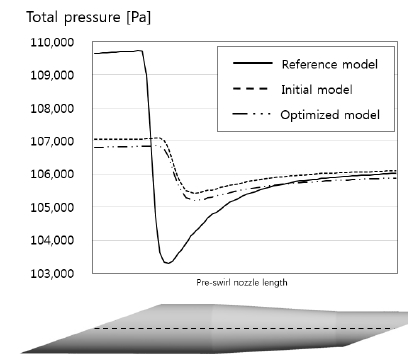
Nozzle 내부의 전압력 분포를 Fig. 10에 나타내었다. Reference model의 입구 압력이 Initial model과 Optimized model에 비해 높은 결과를 보였다. Nozzle의 출구부분의 압력은 세 형상 모두 비슷함을 확인할 수 있었다. 유랑계수는 식의 분모에 Pressure drop term이 있어 이 값이 작을수록 유량계수가 높은 값을 갖는다. 그렇기 때문에 형상을 개선한 두 형상의 유량계수가 상승했음을 알 수 있다. 또한 Optimized model이 Initial model보다 더욱 낮은 전압력 분포 결과를 보였는데, 이는 Initial model의 Converging angle이 크기 때문에 Blockage effect가 발생한 것이다. Reference model은 입구면적이 작아 전압력이 상대적으로 높았다.
세 형상 모두 노즐의 입구에서 전압력이 크게 강하를 했으며, 입구에서 생긴 불균일한 유동이 점차 회복을 하면서 완만한 전압력 상승을 보였다.
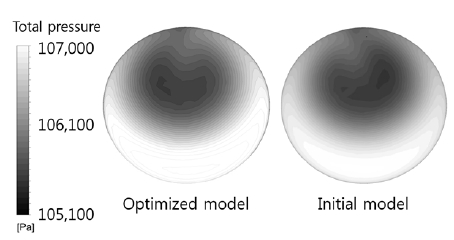
Fig. 11에 Initial model과 Optimized model의 Converging nozzle 시작 부분에서의 전압력분포를 나타내었다. 큰 차이는 아니지만 전체적인 압력이 Initial model이 높았고, 평균압력은 각각 106,176 Pa, 106,427 Pa로 약 250 Pa의 차이를 보였다. 특히 벽면 주위에서 높은 압력을 확인할 수 있었는데, 이에 따라 Optimized model이 Converging nozzle의 길이가 길어진 이유는 Blockage effect를 줄이기 위함임을 알 수 있었다.
Pre-swirl nozzle 표면에서의 정압력 분포를 Fig. 12에 나타내었다. 앞의 Fig. 10와 마찬가지로 출구부분의 정압력 분포는 세 형상 모두 비슷하지만, Reference model의 입구부분에서 국부적으로 높은 압력과 낮은 압력을 확인하였다. 낮은 압력을 보이는 부분에서는 다른 부분에 비해 유동이 잘 흐르지 못하고, 높은 압력을 보이는 부분에서는 유동이 빠르게 흐르기 때문에 이상적인 유동특성을 갖지 못한다. Initial model과 Optimized model은 입구의 직경이 10.2 mm로 Reference model에 비해 더 크기 때문에 동일한 유량이 흐를 때 Nozzle 입구에서 더 낮은 정압력을 보였으며, 국부적으로 높거나 낮은 분포를 보이지 않았다. Initial model과 Optimized model 모두 Converging nozzle의 시작 부분에서 압력이 상승하였으나, Optimized model에 비해 Initial model에서 더 크게 상승하였다.
본 연구에서 CFD를 수행한 형상에 따라 유량계수는 Reference model이 0.6523, Initial model이 0.7793, Optimized model이 0.7860이 되어 Optimized model이 Reference model에 비해 약 17 % 증가하였다. 동일한 유량조건을 주었기 때문에 유량계수의 증가는 Pre-swirl system에서의 압력강하 해소를 의미한다.
Optimized model의 유량계수 증가는 Reference model의 Nozzle 입구부분이 나머지 두 형상에 비해 작아 Chamber에서 냉각유체가 유입되는 과정에서 손실이 발생하였기 때문이다. Fig. 12에서 볼 수 있듯이 Reference model의 Nozzle 입구 부분에서 국부적으로 높고 낮은 압력분포를 보이기 때문에 유량이 고르게 흐르지 못해 유동의 손실을 야기하였다. Initial model과 Optimized model은 유량계수가 약 1 %의 차이를 보였다. Initial model의 Converging angle이 더욱 크기 때문에 Optimized model에 비해 큰 손실이 있었지만, 이는 Reference model의 입구 부분에서 발생한 손실에 비하면 무시할 수준이었다.
3. 결 론
본 연구에서는 Pre-swirl system 의 유량계수를 향상시키기 위해 참고문헌의 형상을 이용하여 Pre-swirl nozzle의 형상을 최적화 하였다. OLHD와 Kriging 기법을 사용하였으며, Candidate point의 예상값과 계산값의 차가 0.1 % 이내로 들어왔을 때 최적화 과정을 종료하였다. 유량계수 및 유동특성의 변화를 비교하기 위하여 Reference model, Initial model, Optimized model을 관찰하였다. 최종적으로 Optimized model의 형상은 Converging nozzle의 부분의 길이가 길고, 출구부분의 길이가 짧은 형상을 보였다.
출구 면적과 유량이 동일한 Pre-swirl nozzle이라도 유량계수는 형상에 따라 다르게 나타났다. Nozzle의 입구 면적을 넓힌 후, Converging nozzle로 형상을 바꾸면 유량계수는 증가하였다. 하지만 Converging angle이 커지면 Blockage effect가 발생하여 유량계수의 감소를 야기하였다. 또한 Nozzle의 입구 면적이 증가하면 입구 부분에서 발생하던 손실을 확연히 감소시킬 수 있음을 확인하였다.
Nozzle의 출구 면적과 각도, 유량이 동일하다면 Swirl ratio는 Nozzle형상에 큰 영향을 받지 않았다. Swirl ratio는 Nozzle출구에서의 접선 방향 유속의 영향을 받는데, 이 속도성분은 Nozzle의 출구면적과 Swirl angle의 영향을 받기 때문에 Nozzle의 형상을 변형하더라도 Nozzle의 출구 면적과 각도만 일치시킨다면 Swirl ratio는 동일한 결과를 갖는다.
가스터빈의 냉각시스템은 블레이드의 수명과 직결되는 연구 분야이다. 본 연구의 Pre-swirler를 활용하여 기존하는 Hole type의 Pre-swirl system 유량계수를 개선하면 가스터빈의 수명을 연장할 수 있을 것으로 보인다.
Pre-swirl system은 Nozzle의 형상이 전체 System의 유량계수에 큰 영향을 미친다. 하지만 Cavity 영역에서 발생하는 손실은 Nozzle의 형상으로 해결이 어렵기 때문에 Nozzle을 반경방향으로 이동하거나 Nozzle 출구 각도를 변경하여 Receiver hole로 유량이 더욱 잘 유입될 수 있도록 하는 연구가 필요하며, 추후에 위 연구를 진행할 예정이다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No.2013101010170A)
References
- Dittmann, M., Geis, T., Schramm, V., Kim, S., and Wittig, S., (2002), “Discharge Coefficients of a Preswirl System in Secondary Air Systems,”, ASME Journal of Turbomachinery, 124, p119-124.
-
Javiya, U., Chew, J., and Hills, N., (2011), “A Comparative Study of Cascade Vanes and Drilled Nozzle Designs for Pre-Swirl,”, ASME Turbo Expo, Vancouver, British Columbia, Canada, GT-2011-4006.
[https://doi.org/10.1115/GT2011-46006]

-
Lewis, P., Wilson, M., Lock, G., and Owen, J. M., (2008), “Effect of Radial Location of Nozzles on Performance of Pre-Swirl Systems,”, ASME Turbo Expo, Berlin, Germany, GT-2008-50295.
[https://doi.org/10.1115/GT2008-50295]

-
Bricaud, C., Geis, T., Dullenkopf, K., and Bauer, H. J., (2007), “Measurement and Analysis of Aerodynamic and Thermodynamic Losses in Pre-Swirl System Arrangements,”, ASME Turbo Expo, Montreal, Canada, GT-2007-27191.
[https://doi.org/10.1115/GT2007-27191]

-
Chew, J. W., Ciampoli, F., Hills, N. J., and Scanlon, T., (2005), “Pre-Swirled Cooling Air Delivery System Performance,”, ASME Turbo Expo, Reno-Tahoe, Nevada, USA, GT-2005-68323.
[https://doi.org/10.1115/GT2005-68323]

-
Ciampoli, F., Chew, F. W., Shahpar, S., and Willocq, E., (2006), “Automatic Optimisation of Pre-Swirl Nozzle Design,”, ASME Turbo Expo, Barcelona, Spain, GT-2006-90249.
[https://doi.org/10.1115/GT2006-90249]

- Lewis, P., (2008), “Pre-swirl rotor-stator systems: Flow and heat transfer,”, PH. D. Thesis, Department of Mechanical Engineering, University of Bath.
- Yan, Y., Gord, M. F., Lock, G. D., Wilson, M., and Owen, F. M., (2003), “Fluid Dynamics of a Pre-Swirl Rotor-Stator System,”, ASME Journal of Turbomachinery, 125, p641-647.
- Simpson, T., Mauery, T. M., Korte, J. J., and Mistree, F., (2001), “Kriging Models for Global Approximation in Simulation-based Multidisciplinary Design Optimization,”, AIAA Journal, 39(12), p2233-2241.
- Seong, S., Murayama, M., and Yamamoto, K., (2005), “Efficient optimization design method using Kriging model,”, Journal of Aircraft, 42(2), p413-420.
- Ahmed, M. Y. M., and Qin, N., (2009), “Comparison of Response Surface and Kriging Surrogates in Aerodynamic Design Optimization of Hypersonic Spiked Blunt Bodies,”, ASAT-13.
- Myers, R. H., and Montgomery, D. C., (2001), “Response Surface Methodology,”, Wiley Interscience Publication.
- Cagan, M., Benim, A. C., and Gunes, D., (2009), “Computational Analysis of Gas Turbine Preswirl System Operation Characteristics,”, WSEAS TRANSACTIONS on FLUID MECHANICS, (4), 4p117-126.
- Feng, Z., Xinjun, W., Gaoliang, L., and Jun, L., (2015), “Computational fluid dynamics analysis for effect of length to diameter ratio of nozzles on performance of pre-swirl systems,”, Journal of POWER AND ENERGY, 229(4), p381-392.
- Benim, A. C., Cagan, M., Bonhoff, B., and Brillert, D., (2005), “Simulation of flow in Gas Turbine Pre-Swirl Systems with Emphasis on Rotor-Stator Interface Treatment,” WSEAS int. Conf. on FLUID DYNAMICS & AERODYNAMICS, Corfu, Greece, p206-211, August 20-22.