수치해석을 이용한 부유식 파력발전의 계류 시스템 특성에 관한 연구
Abstract
The aim of this study is to find and select a suitable mooring system to apply on to a floating wave energy system (WEC) by studying the characteristics of its motion and response using a numerical analysis. The wave energy device converts the ocean wave motion into electrical energy. The waves influence the device's movement and in turn the device’s motion influences the incoming waves. The behaviour of the device’s motion is mainly affected by the type of mooring system that is attached to it. Therefore, as the mooring system has major influence on the output of the wave energy device, it is of high importance to study the response of the device with different mooring systems. In an actual sea, the currents and wind will affect the wave energy device. Therefore, there is a need for the device to have a multiple point mooring system to avoid unnecessary yawing on the surface of the ocean. It was expected that adding more mooring points the system, the RAO (Response Amplitude Operators) values would decrease. However, from the results of the multiple point mooring analysis, the RAO values obtained were similar to the single point mooring results. Therefore, it can be seen from these results of the numerical model that multiple point mooring do not interfere greatly with the motion of the wave energy device. In addition, when installing additional mooring lines or selecting the most suitable mooring system for wave energy devices, the results obtained in this study is needed for the selection process.
Keywords:
Mooring System, Ocean Energy, Wave Energy Converter키워드:
계류시스템, 해양에너지, 파력발전 장치1. 서 론
해양에너지는 지구 표면의 70%를 차지하는 풍부한 부존량과 영구적이고 친환경적이라는 장점을 지니고 있어 에너지 분야에서 각광을 받고 있다. 다양한 해양에너지 중 파랑을 이용한 파력발전은 전 세계적으로 상용화에 접근한 신재생에너지 자원이라 할 수 있다. 파력발전은 해수면의 상하운동으로 인하여 발생하는 에너지를 에너지 변환장치의 기계적인 운동에너지로 변환한 후, 전기 에너지로 변환하여 전기를 생산하는 시스템이다.
본 장치는 실스케일 모델의 내부에 U-Tube형 챔버를 가지는 이중 선체 구조를 가지며, 현재 연구되어지고 있는 다양한 파력발전장치 중 해수면에서 한 가지 혹은 그 이상의 자유도를 가지고 진동하여 발전하는 방식을 취하는 point absorber형 파력발전장치이다. 이 형태의 파력발전장치는 파랑의 상하 병진운동의 주기에 따른 고유진동수가 파력발전장치의 효율에 많은 영향을 미치며, 이를 맞추어 주어야 높은 효율의 발전을 기대할 수 있다.
부유식 파력발전시스템은 파력발전장치를 포함하는 선체와 그 부체를 일정 위치에 유지시키는 계류시스템으로 구성된다.(1) 이로 인해 부유식 파력발전시스템은 발전장치를 포함하는 부체를 계류시스템과 쉽게 분리할 수 있으며, 따라서 유지 보수에 유리하다는 장점이 있다. 하지만 계류시스템이 조류와 파랑에 의해 지속적으로 거동하게 되고, 계류시스템의 거동은 파력발전 장치의 효율에 직접적인 영향을 미칠 수 있다. 따라서 계류시스템의 거동이 부체의 거동에 최소로 영향을 미치도록 설계되어야 한다. 계류시스템에 의한 부체의 6-자유도 운동은 계류시스템의 방식에 따라 매우 다른 특성을 보인다. 계류 시스템의 방식에 따라 파력발전장치를 포함한 부체의 거동에 관여하게 되고, 이로 인해 파력발전장치의 효율에 직접적인 영향을 미치게 되는 것이다. 나아가 실제 해양의 상태는 굉장히 넓은 범위의 파고 특성을 가지고 있기 때문에 이에 대한 부체의 안정성 및 생존성의 대비가 필수적이다. 이를 적절한 계류시스템의 선정을 통하여 보완 할 수 있다. 이처럼 파력발전시스템의 연구에서 계류시스템의 중요성이 높은 비중을 차지하는 바 본 연구는 전산유체해석을 통하여 계류시스템이 파력발전장치에 미치는 영향에 초점을 두고 연구를 수행하였다.
2. 부유식 파력발전 장치 설계
2.1 개념 모델 및 구동원리
파력발전 장치의 설치를 위해 파랑의 특성을 이해하는 것은 매우 중요하다. 그중 수리모형 실험에서 주로 사용되는 규칙파의 경우, 이론적 계산이 가능하고 실험적 데이터 및 계산값이 큰 오차를 가지지 않기에 이론을 확인하는 과정이 필요하다. 파도 특성 연구는 특정지점의 파도에서 사용할 수 있는 에너지양을 평가하고 최적의 성능을 얻을 수 있는 적절한 WEC(Wave Energy Converter)를 설계하는데 필수적이다.
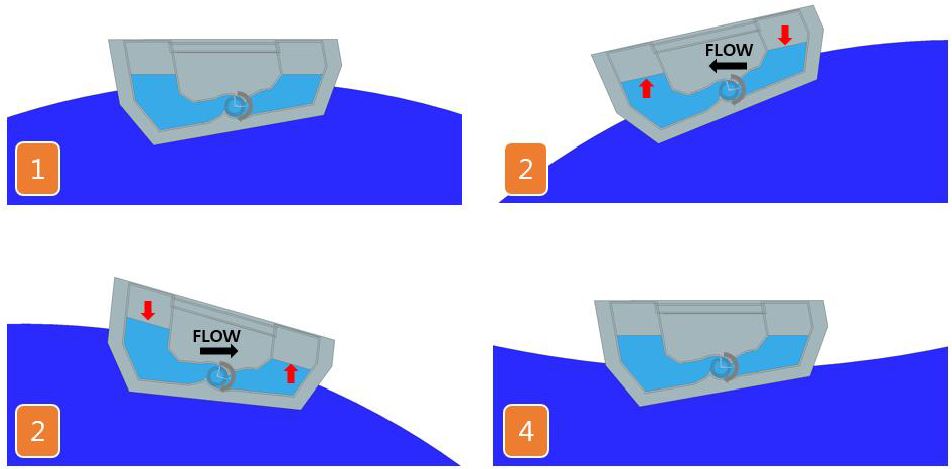
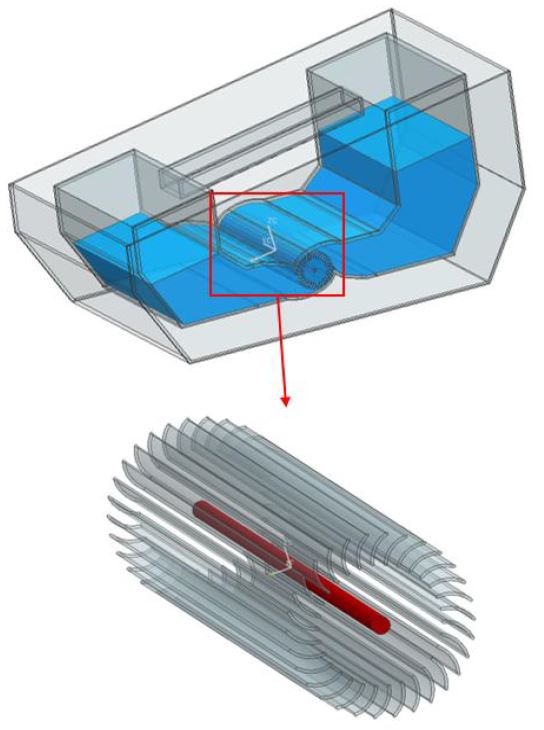
Fig. 1과 Fig. 2는 연구에서 진행한 부유식 파력발전장치의 구동원리와 형상을 나타낸다.(2) 파랑의 자유표면의 운동에너지와 위치에너지를 에너지원으로 이용하며 이는 본 장치의 Pitch 및 Heave 등의 운동을 일으킨다. 이러한 장치의 Pitch 및 Heave 운동에 의해 내부 선체의 작동 유체가 양단의 형상에서 진동수주 운동을 하게 되고 선체 내부의 작동유체인 물이 양방향의 흐름을 만든다. 이 양방향의 흐름을 축동력으로 변환시키는 Cross-flow터빈은 양방향의 흐름을 이용하여 축을 단일 방향으로 회전할 수 있게 설계되었다.
2.2 설계 파라미터 지정
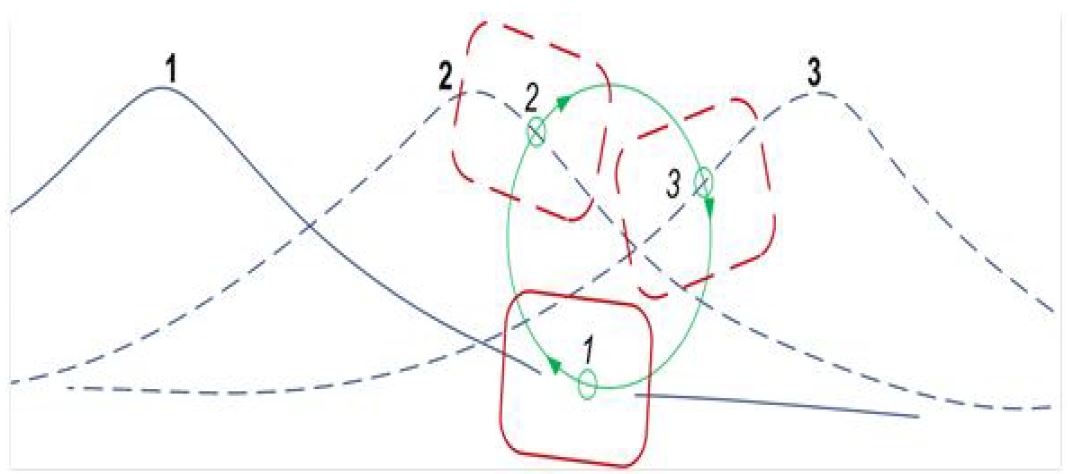
장치의 길이(L )를 선정하기 위하여 선형파 이론을 이용하여 자유표면의 파를 계산하여 설계 기준에 맞는 파고와 파장을 계산하였고, 이에 따른 파도의 경사면의 각도를 도식화화여 Fig. 3(2)에 나타내었다. 파력발전장치의 길이가 x보다 길경우와 x/2 인 경우를 볼 수 있다. 파력발전장치를 안정성을 위해 매우 중요한 요소인데, 작은 파장과 Pitching각이 장치의 길이보다 크거나 x와 동일한 경우 장치에 큰 손상을 줄 수 있다. 장치가 파장에 비하여 크게 되면 안정성뿐만 아니라 출력에도 영향을 미치게 되지만 작은 장치의 경우 거의 모든 조건에서 작동이 가능하게 된다. 또한 Fig. 4(2)는 부유체의 궤도운동을 나타내었으며, 파도가 가지고 있는 물 입자 궤도운동을 따라 부유체도 궤도운동을 하게 되며 Pitching 운동을 하게 된다. 이 움직임은 계류시스템에 영향을 미치며, 계류시스템 또한 Point absorber의 에너지 흡수에 영향을 줄 수 있다.
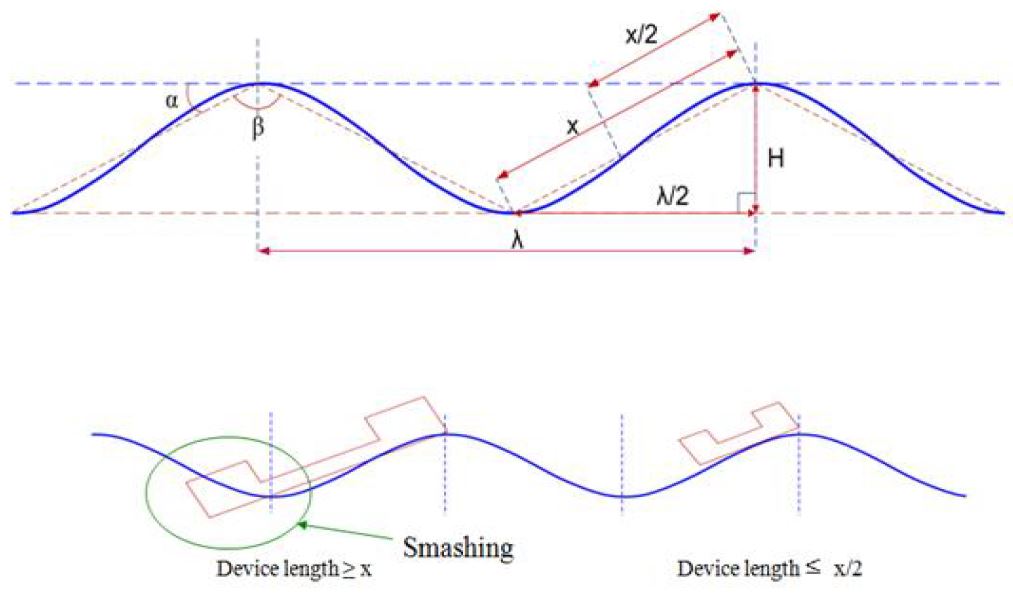
Schematic of a floating WEC with length greater than x and another with dimensions smaller than or equal to x/2
부유식 파력발전장치의 설계 파라미터를 선정할 때 가장 중요한 요인은 설치 해역의 파랑 조사이다. 이는 장치 거동의 직접적인 변수이기 때문에 이를 고려하여서 파라미터를 설정하는 것이 필수적이다. 다음의 Table 1에 실 스케일 장치의 실제 설치 지역인 한국해양대학교 인근 해역의 주된 수심과 파도 주기를 나타내었다.
파도의 파장은 주기와 수심에 의해 결정되는데 그 식(1)(3)은 아래와 같다.
| (1) |
여기서 g는 중력, T 는 파도 주기, Hw 는 수심을 나타낸다. 선행 연구(4)에서 사용된 실험장치의 길이는 1 m이며, 이 장치의 최적 파장은 2.6 m이다. 상사법칙을 활용하여 길이의 변화를 반영하여 각 수심 및 파도 주기로부터 장치의 길이를 도출해 낼 수 있다. Table 2(5)는 이를 반영하기 위해 나타내었으며, 수심 8 m, 파도 주기 5s의 해상 환경을 예로 들자면 이때 최적 장치의 크기는 13.4 m이며, 수심 7 m 파도주기 3s의 환경에서는 최적 장치의 크기 5.4 m이다.
본 연구의 장치 파라미터를 다음 Table 3에 나열하였다. 파력발전기의 성능을 평가하는데 사용하는 파라미터는 파력발전장치의 폭이다. 해당 장치의 폭과 동일한 입사파의 파면의 폭으로 효율을 평가한다. 하지만 해양에너지는 실제 측정하는 측정치와 다를 수 있으며, 장치 주변의 반사파로 인하여 결과에 차이를 반영하게 될 수 있다. Point absorber는 장치의 폭에 따라 에너지를 흡수하고 또한 진동과 증폭을 거치며 흡수율을 증가시킬 수 있는 특성을 가지고 있어 이를 통하여 성능을 향상시킬 수 있다. 장치의 폭을 결정하기 위해서는 설계 파상에서의 파랑의 에너지를 구하게 된다. 이는 파랑에너지 자체가 W/m 단위로서 단위 길이당의 에너지로 결정이 되게 되며, 단위 미터의 장치로 효율을 우선 선정하게 된다. 이렇게 계산되어졌을 때 단위 미터당의 장치의 출력을 계산할 수 있으며, 원하는 출력에 따른 장치의 폭을 선정하게 된다. 하지만 전체 스케일에 따른 장치의 길이도 함께 고려되어야 하며, 장치의 폭이 너무 좁거나 길 경우, 부유체의 안정성에 영향을 미치게 된다.
2.3 수치해석 기법
본 연구에서는 범용 상용 코드인 ANSYS CFX ver14(6)와 Star CCM+[7]를 사용하였다. 일반적으로 범용의 상용코드들은 SIMPLE 또는 SIMPLEC, Rhie and Chow(8) 방법과 같은 압력에 기초한 방정식으로부터 만들어져 있다. 이들 압력에 기초한 코드들은 일반적으로 다양한 물리적 모델들과 경계조건을 제공하고 다른 CAE 도구들과 연동을 포함하는 복잡한 Multi-physics 문제 등에 적용될 수 있다.
일반적인 유동에서 다루는 운동방정식은 질량, 운동량, 에너지 방정식이며, 식 (2), 식 (3), 식 (4)와 같이 표현된다.
| (2) |
| (3) |
여기서 응력텐서 :
| (4) |
여기서 전엔탈피 :
여기서, ρ=밀도[kg/m3 ], u=속도[m/s], P=압력[Pa], τ=응력텐서, μ=점성계수[kg/ms], δ=크로네커델타(정수 값을 가지는 두 개의 변수에 대해서 정의된 함수), htot =전엔탈피[J/kg], T=온도[K], λ=열전도율[W/mK], h=정적엔탈피[J/kg]를 나타낸다.
상태방정식 ρ = ρ(P,T), 점성계수와 변형률의 함수로서 응력텐서의 응력-변형률 관계, 그리고 h = h(P,T)가 이들 방정식에 추가된다. 난류유동은 와점성(eddy viscosity)이 추가되고 방정식은 레이놀즈 평균 물리량에 대해 푼다. 방정식의 일반적인 형태는 동일하다.
3. 계류시스템 특성 수치해석
3.1 수치해석 목적
계류선을 적용할 때 고려해야 할 사항으로 먼저 부유체의 수평이동 한계이다. 부유체의 수평이동 한계를 계류선 설계에 있어서 매우 중요한 인자 중 하나이다. 다음으로 계류선 길이의 선정이다. 계류선의 길이는 계류선의 안정성에 영향을 미치는 중요한 변수 중 하나이다. 계류선의 길이가 증가할수록 안정성은 증가하지만 경제적 비용이 증가하며 해상에서 점유하는 면적이 넓어지면 해역 활용도 측면에서 비효율적이다. 본 파력발전장치에서는 직접적으로 바닥의 앵커까지 연결하는 방식이 아니라 파력발전장치에서 부이를 거쳐 앵커까지 연결하는 방식이다. 이는 보통의 직접적인 계류선 연결에 적용되는 수심의 5∼15배로 설계하는 계류선의 길이 선정 방식과는 차이를 가지게 된다. 본 해석에는 파력발전장치에서 부이까지 6.7 m, 부이에서 바닥까지 6.9 m를 적용하여 수치해석을 수행하였다.
파력발전장치의 상용화를 위해서는 파력발전용 부유체를 효율적으로 설계하고 전체 시스템 제작 및 설치비용을 최소화하여 경제성을 높여야한다. 그리고 계류시스템에 의한 부체의 자유도 운동은 계류시스템의 방식에 따라 매우 다른 특성을 보인다. 계류시스템의 방식에 따라 파력발전장치를 포함한 부체의 거동에 관여하게 되고, 이로 인해 파력발전장치의 효율에 직접적인 영향을 미치게 되는 것이다. 이에 본 장에서는 계류시스템을 적용한 부유식 파력발전시스템의 거동에 관한 초기 수치해석을 수행하였다.
3.2 단일 및 다점 계류시스템을 적용한 수치해석
파력발전장치의 거동에 가장 큰 거동 요인인 장치의 길이는 5.37 m로 실 스케일의 장치의 길이와 같게 설정되었고 또한 실 스케일 장치와 같이 10°의 각도로 비대칭의 형상을 적용하였다. 계류선은 체인으로 적용하였으며, 형상과 파라미터는 Fig. 3을 적용한 Fig. 5와 Fig. 6에서 확인할 수 있다.
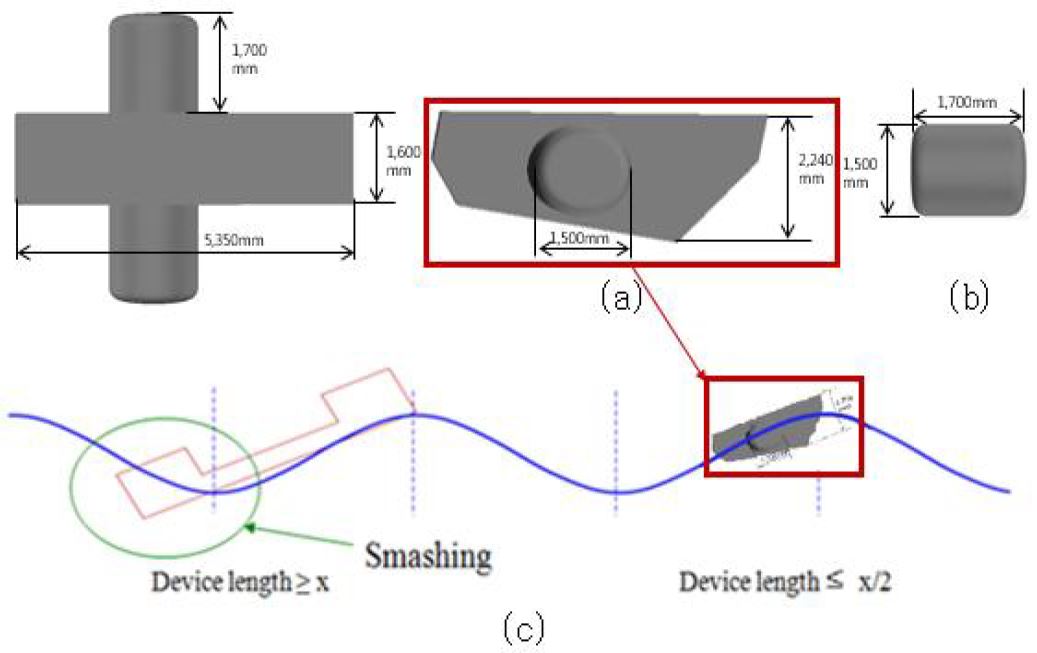
(a) Parameters of main WECs device (b) Parameters of buoy device (c) Application in schematic of a floating WEC with dimensions smaller than or equal to x/2
실제 파력발전장치의 거동에 있어 내부영역의 유동에 의해 터빈이 구동된다. 본 해석에서는 내부의 청수는 고정 조건으로 해석을 수행하였고, 파력발전장치의 외부 Casing만을 고려하여 장치의 거동 특성을 분석하였다. 1점과 2점 계류를 적용한 수치해석 모델은 Symmetry 조건으로, 3점과 4점 계류를 적용한 수치해석 모델에는 Full modeling 조건으로 해석을 수행하였다. 해석 case는 파장과 장치 길이의 비가 2∼4배일 때로 선정하여 총 5 case를 수행하였다. 자세한 경계조건 및 계산조건은 Table 4와 Table 5에서 확인 할 수 있다.
3.3 유동 해석 결과
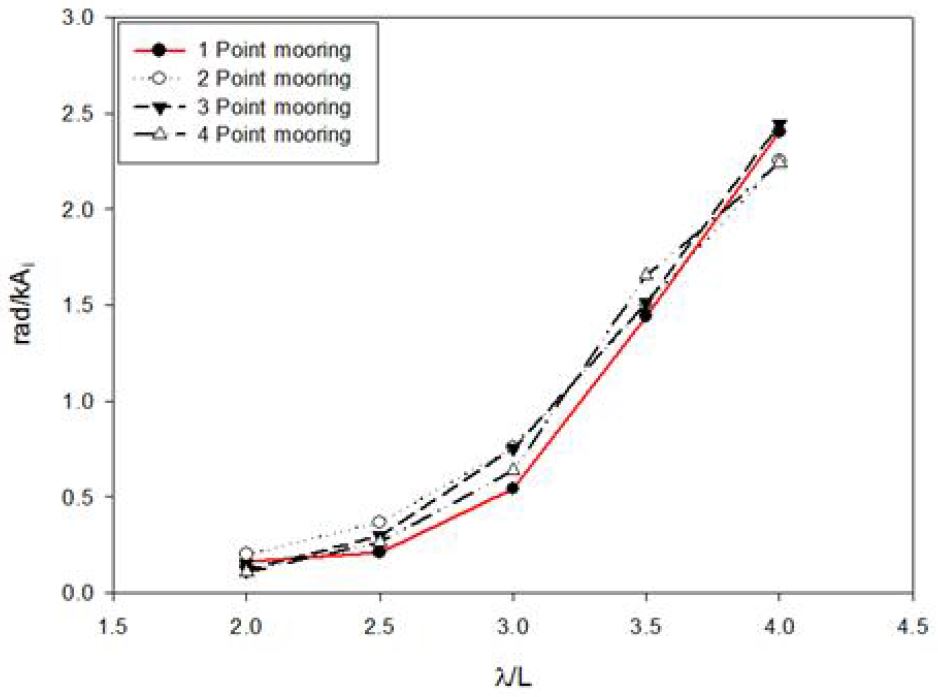
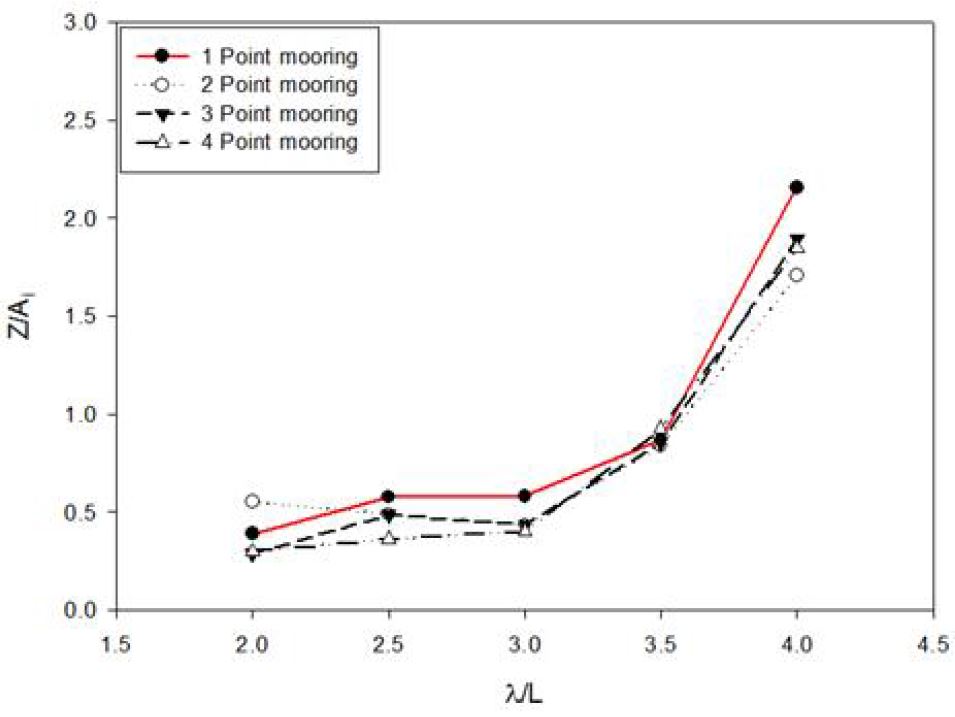
단일 계류시스템을 적용하였을 때의 파력발전장치의 거동이 다점 계류시스템을 적용하였을 때의 거동과 비교하여 어떠한 영향이 발생하는지를 알아보기 위하여 해석을 수행하였다. 일반적으로 예상할 수 있지만 계류선의 수가 증가 할수록 계류시스템이 장치의 거동을 더 방해할 것으로 예측하고 해석을 수행하였다. 장치의 거동은 부유체의 거동 특성을 나타내는 진폭응답함수 RAO(Response Amplitude Operators)를 사용하여 각각 Pitch RAO와 Heave RAO로 나타내었다. 결과를 살펴보면 먼저, 모든 계류방식에서 λ/L 4.0의 case 5일 때 가장 좋은 결과값을 얻었다. 이는 파장과 파력발전장치 길이의 비가 커질수록 진폭응답함수가 커짐을 나타낸다. Fig. 7과 Fig. 8을 보면 λ/L 4.0의 case 5에서 계류 시스템 각각의 Pitch RAO는 1점에서 4점 계류 시스템까지 2.241, 2.249, 2.443, 2.240의 값을 도출하였고, Heave RAO는 각각 1점에서 4점 계류 시스템까지 2.154, 1.705, 1.895, 1.843의 값을 도출하였다. Fig. 9는 장치가 구동하는 회전축을 방향의 angle을 의미하는 Pitch angle을 나타내는데 그 값은 각각 20.123°, 18.848°, 20.473°, 18.769°를 나타내었다. Fig. 7∼9에서와 같이 계류선이 증가함 따라 파력발전장치의 거동이 작아질 것으로 예상한 것과 달리 근소한 차이는 나타나지만 다점계류를 적용 시 단일계류 적용의 거동과 큰 차이를 보이지 않는 것을 알 수 있다.
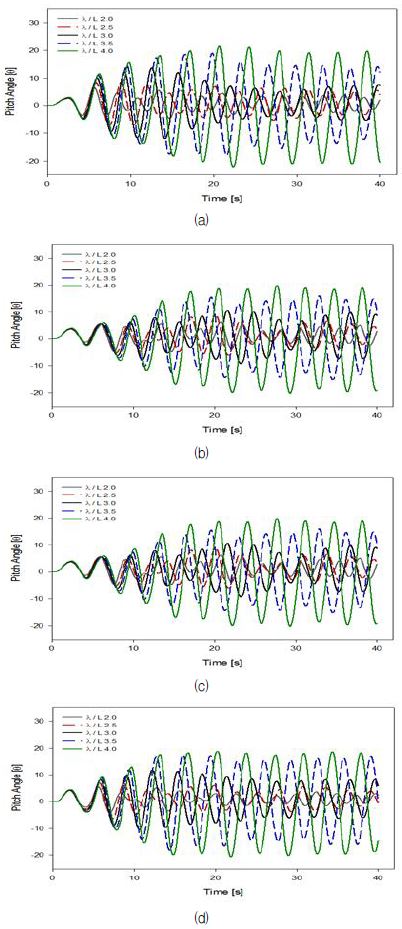
(a) Pitch angle at 1 Point mooring WECs, (b) Pitch angle at 2 Point mooring WECs, (c) Pitch angle at 3 Point mooring WECs, (d) Pitch angle at 4 Point mooring WECs
여기서
4. 결 론
부유식 파력발전장치에 새롭게 적용할 계류시스템의 영향을 알아보기 위하여 전산유체해석을 수행하였다. 먼저, 실제 파력발전장치에 적용된 단일 계류 시스템에 관하여 해석을 수행하였고 나아가 단일 계류시스템의 문제점을 보완하기 위한 방안으로 다점 계류시스템의 적용에 대하여 전산유체해석을 수행하였다. 이를 적용하였을 때 파력발전장치의 거동이 단일 계류시스템을 적용하였을 때의 거동과 비교하여 어떠한 영향이 발생하는지를 알아보기 위함이다. 이는 계류 시스템을 적용한 부유식 파력발전장치의 기초 자료 확보 및 거동 특성 예측 기법의 확립에 관한 연구이며, 다음과 같이 요약 정리할 수 있다.
단일 및 다점 계류 시스템을 적용하여 수행한 전산유체해석의 결과로 파장과 파력발전장치 길이의 비가 커질수록 진폭응답함수가 커짐을 알 수 있었다. 모든 계류시스템 전산유체해석 결과로 λ/L 4.0의 case5에서 가장 큰 Pitch Angle을 보였으며, 단일 계류시스템의 경우 최대 ±20.1°의 Pitch angle을 보이며 장치가 거동함을 확인 할 수 있다. 이는 선행연구에서 실제 설치된 파력발전장치와 비교하였을 때 육안으로 확인 할 수 있는 Pitch angle 값과 흡사한 값이라고 확인된다. 단일 계류시스템의 해석 결과값를 다점 계류시스템 해석 결과를 비교해 보면 계류선이 증가함 따라 파력발전장치의 거동이 작아질 것으로 예상한 것과 달리 파력발전장치의 거동의 방해요소로 작용하지 않고 단일 계류를 적용시의 파력발전장치의 해석값이 큰 차이를 보이지 않는 것을 알 수 있었다. 이를 추가의 계류선을 필요로 하는 기존의 계류시스템에 접목하여 본다면, 추후 파력발전장치의 계류시스템의 선정 시 필수적으로 반영되어야 하는 결과라고 할 수 있다.
References
-
Jung, D. H., Shin, S. H., Kim, H. J., and Lee, H. S., (2011), “A Preliminary Design of Mooring System for Floating Wave Energy Converter”, Journal of the Korean Society for Marine Environmental Engineering, 14(5), p184-191.
[https://doi.org/10.7846/jkosmee.2011.14.3.184]

- Kim, B. H., (2014), “A Study on Noble Floating Wave Energy Converter with Cross-flow Turbine”, Master's Degree Thesis, Department of Mechanical Engineering, Graduate School, Korea Maritime and Ocean University, Pusan, Korea.
- (2003), “Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-section Conduits Running Full-Part 2: Orifice plates”, European Committee for Standardization, ISO 5167-2, p5-8.
- Kim, S. Y., Kim, B. H., Jeong, H. S., and Lee, Y. H., (2015), “Performance Study of Floating Wave Energy Converter with a Cross-flow Turbine by Hydraulic Model Test and CFD Code”, The KSFM Journal of Fluid Machinery, Jeju, Korea, p270-271.
- Kim, S. Y., (2016), “A Study in Performance Improvement of a Floating Cross-flow Turbine Wave Energy Converter by an Orifice U Tube Concept”, Master’s Degree Thesis, Department of Mechanical Engineering, Graduate School, Korea Maritime and Ocean University, Pusan, Korea.
- ANSYS-CFX ver. 14 Manual, ANSYS, (2010).
- Star CCM+ ver.11.02 Manual, CD-Adapco, Siemens, (2016).
-
Rhie, C. M., and Chow, W. L., (1982), “A Numerical Study of the Turbulent Flow Past an Isolated Airfoil with Trailing Edge Separation”, AIAA 82-0998.
[https://doi.org/10.2514/6.1982-998]