Initial Hydraulic Design and Performance Analysis of 300 MW-Class Pump-turbine Model

1. Introduction

In developed countries with expanding economies, there is increasing demand for energy that calls for new and efficient power plants. Pumped storage plants are one of the most reliable systems for equalizing the power supply and demand. It provides balancing power for grid stability and can provide fast response within seconds to regulate the electrical grid during periods of rapidly changing demand.⁽¹⁾

The Yangyang Pumped Storage Power Station uses the Namdae-Chun River to operate a 1,000 MW pumped storage hydroelectric power system, about 10 km west of Yangyang in Gangwon Province, Korea. Construction on the power plant began in 1996 and it was completed and dedicated on September 13, 2006. The power plant contains four 250 MW reversible Francis turbine generators for an installed capacity of 1,000 MW.⁽²⁾ Table 1 shows the finished construction pumped storage plants in Korea. The capacity range of the plant is between 400 to 1000 MW.

Table 1

Pumped storage plants in Korea

In Korea, the performance of some pumped storage plant, which were constructed in 1980s, is unsatisfactory after long periods of operation. Redesign of the pump-turbine impeller for these plants have become necessary. Currently, the design technology of pumpturbine is monopolized by foreign companies and there’s lack of development of independent design ability in Korea. This study is an attempt to design a pump-turbine impeller that will contribute to the development of pump-turbines in Korea. There are two methods discussed in this paper. Each method has an important factor that affects the overall performance of the pump-turbine. These factors have been highlighted in this study.

2. Pump-turbine Impeller Design

The study has focused on two types of hydraulic designs. However, these are not complete designs so there are many assumptions that have been made to complete the design process. Additionally, actual dimensions of the pump-turbines are not publicly available. Therefore, by using a head of H_P=350 m and flow rate of Q=100 m³/s from P=300 MW-class pumpturbines, the impeller design was investigated. The turbine mode design head is H_T=340 m and flow rate is Q=115 m³/s. The corresponding specific speeds for pump and turbine modes are n_sp=37 m-m³/s and n_st=110 m-kW respectively. The first design considers the discharge speed constant derived by Stepanoff’s centrifugal pump design⁽³⁾ and the second design considers the gradient of discharge variation to head variation derived from pump-turbine design by Kubota.⁽⁴⁾

Most modern pump-turbines are developed using the pump design method. However, the design procedure does not completely follow the pump design method and is modified to accommodate the turbine mode. The blade number is reduced and blade length is increased. The blade exit width is also increased to cater for the added guide and stay vanes. For the past century, developed countries like America, Europe and Japan have devised pump-turbine designs by conducting several experiments and developed their own theories and relevant factors important to the pump-turbine design.^(4-7) It is used as a reference and certain techniques can be applied to the pump-turbine impeller design for the current study. The rotational speed is one of the most important parameters that are selected first. Most large pump-turbines greater than P=300 MW-class capacity have a rotational speed of n=300 min^-1.^(1,5) This study will also use this rotational speed. Both of the pump and turbine modes are operated at the same rotational speed because a synchronous motor generator is utilized in modern pump-turbines.

2.1 Pump Design by Discharge Speed Constant ‘Ku’

By referring to the basic hydraulic design of centrifugal pump, some initial dimensions for the meridional shape can be developed.⁽³⁾ The following method is adapted from reference (3). There is a relationship between the pump and turbine specific speeds. The turbine specific speed is approximately three times the pump specific speed. Using the specific speed, several important speed constants and inlet to outlet diameter ratios can be determined for the initial design. However, it should be noted that the pumpturbine needs a larger impeller exit width, which cannot be accurately determined from Fig. 1 and several trials have to be conducted to find near design point. The purpose of studying this method is to determine the correct impeller exit width B_g for a pump-turbine system by using the existing pump design method.

Fig. 1

Impeller constants(3)

The specific speed of the pump and turbine can be calculated by equations (1) and (2) respectively:

$\[ n_{sp}=\frac{n\sqrt{Q}}{H_P^{0.75}} \]$

(1)

$\[ n_{st}=\frac{n\sqrt{P}}{H_T^{1.25}} \]$

(2)

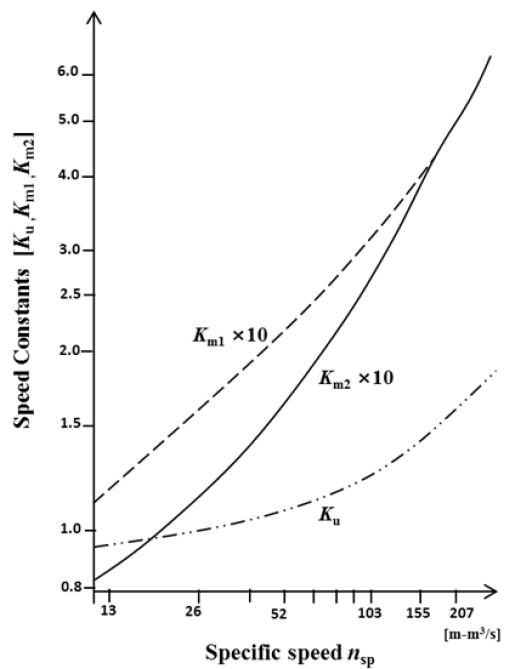
Another important factor in the design is the speed constant that gives the relation between the pump total head and the impeller peripheral velocity. Fig. 1 displays the relationship of several impeller constants to the specific speed. The most widely used speed constant K_u is defined in equation (3):

$\[ K_u=\frac{u_2}{\sqrt{2g{H}_P}} \]$

(3)

Where u₂ is the peripheral velocity at impeller exit. From Fig. 1, the values for K_u and K_m2 (speed constant at exit of meridional line) were estimated as 1.04 and 13.5 respectively. Equations (4) and (6) were utilized to calculate the initial impeller dimensions:

$\[ u_2=\frac{D_2}{2}\omega \]$

(4)

Where ω is the angular velocity. From equation (4) the impeller blade diameter, D₂ is calculated.

$\[ K_{m2}=\frac{c_{m1P}}{\sqrt{2gH}} \]$

(5)

Using the speed constant K_m2, the meridional velocity, c_m1P is obtained from equation (5). Using the meridional velocity the B_g is calculated by equation (6):

$\[ c_{m1P}=\frac{Q}{A}=\frac{Q}{\left(D_2\pi \right)B_g} \]$

(6)

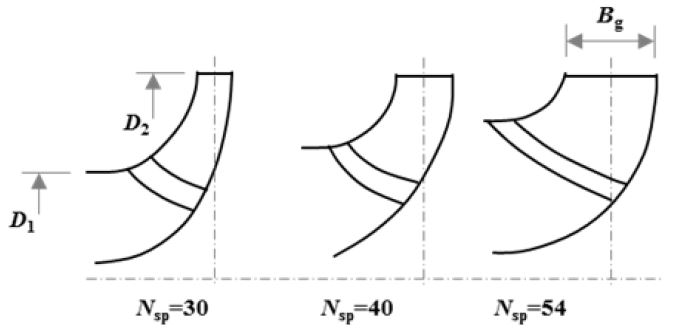
The value of B_g obtained from here is too small and cannot be used for the pump-turbine so it needs to be modified because of the addition of guide vanes and stay vanes. Other meridional shapes for pumpturbines at the design specific speed were also referred to estimate the initial meridional shape as shown in Fig. 2.^(6,7) It was noted from comparing other pumpturbine meridional shapes that a pump-turbine of similar size has almost twice the B_g of a normal centrifugal pump. Thereby, the calculated B_g was increased by a factor of 2.00, 2.03, 2.13 and 2.19 for further investigation. The initial design parameters are presented in Table 2, where four cases of blade exit width also known as guide vane height were investigated.

Fig. 2

General meridional shape for pump-turbine according to pump specific speed (6,7)

Table 2

Design parameter comparison for pump turbine design by Ku and gQ/H

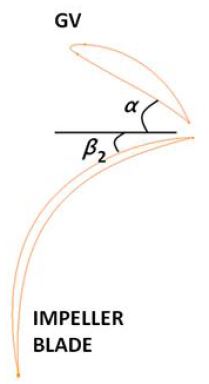
The impeller vane discharge angle β₂ is one of the most important single design elements. An average value of 22.5° is commonly used for all specific speeds. The upper limit of β₂ may be raised to 27.5° without affecting the efficiency appreciably. The lower limit of β₂ consistent with good design is about 17.5°.⁽³⁾ Fig. 3 shows the blade angles at the impeller blade and guide vane. The guide vane angle α is assumed to be 25° for the initial design and using the velocity triangle the β₂ can be calculated for both pump and turbine mode and checked with the range explained earlier. The initial β₂ is calculated as 21.7° using the pump flow rate and 26.9° using the turbine flow rate. The values are within the range of normal centrifugal pump designs. The blade angles has been kept constant for both design methods.

Fig. 3

Blade angles at impeller exit

2.2 Pump-turbine Design by Gradient of Discharge Variation to Head Variation ‘g_Q/H’

A fundamental procedure for hydraulic design of major dimensions of a Francis pump-turbine can be obtained from the method described by T. Kubota.⁽⁴⁾ However, detailed designs on the blade loadings are not discussed. For this method, dimensions are obtained through the relationship of several constants to the specific speed of the pump mode. The method is suitable for n_sp=30~60 m-m³/s and corresponding heads of 50~500 m.

Using the specific speed of the pump the corresponding constants can be obtained from Fig. 4 and estimation of the impeller meridional shape can be obtained from equations (7) to (10). The gradient of discharge variation to head variation g_Q/H is the most important factor that affects the overall size of the pump-turbine. The purpose of studying this method is to determine an appropriate factor of the gradient of discharge variation to the head variation g_Q/H.

Fig. 4

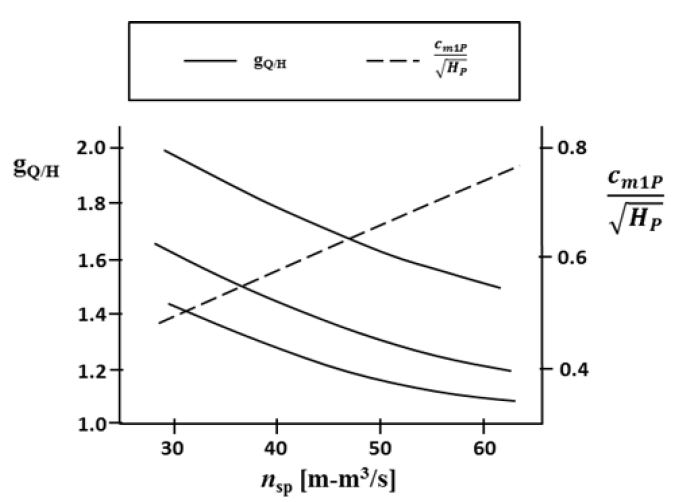
Gradient of discharge variation to head variation of pumping performance versus specific speed; meridional velocity at the impeller exit of a Francis pump-turbine(4)

The peripheral speed u₂ at the impeller exit at best efficiency point can be expressed by the following equation:

$\[ \frac{u_2}{\sqrt{H_P}}={\left(\frac{1+\frac{1}{g_{Q/H}}}{0.0765}\right)}^{0.5} \]$

(7)

From Fig. 4, three possibilities of g_Q/H (1.8, 1.5 and 1.3) can be selected at n_sp=37 m-m³/s from the three curves shown. After obtaining the peripheral speed the diameter at the impeller exit, D₂ can then be found by equation (8), which also gives three possibilities of D₂:

$\[ D_2=\frac{60}{\pi }\cdot \frac{u_2}{n} \]$

(8)

For the purpose of a rough estimation, the relation of c_m1P/H_P^0.5 versus n_sp is shown in Fig. 4. From this, the width B_g can be found by the following equation:

$\[ B_g=\frac{Q}{\pi D_2{c}_{m1P}} \]$

(9)

From equation (9) we get three values for width according to the three diameters calculated earlier B_g as 0.54, 0.57 and 0.59 m. Finally, a rough estimation of the impeller entrance diameter D₁ can be determined by:

$\[ D_1={\left(\frac{4Q}{\pi c_{m1P}}\right)}^{0.5} \]$

(10)

The initial design parameters are presented in Table 2, where three possible cases for initial design are presented as PT-D5765, PT-D5600 and PT-D5410. Considering the minimum and maximum size of the pump-turbine, two cases are conducted in this study to see which one performs best near the design condition. PT-D5765 and PT-D5410 are selected for further analysis. It is assumed that PT-D5600 would perform in between the two ranges.

3. Numerical Method

The fluid domain of the pump-turbine geometry was modelled in 3D and numerical mesh was generated. The analysis calculation was conducted using a commercial software ANSYS CFX.⁽⁸⁾ Previously available shape for guide vanes, stay vanes, draft tube and casing for a Francis pump-turbine was used for the full domain analysis. It consists of spiral casing, 20 stay vanes, 20 guide vanes and impeller with 6 blades.^(9-11)

The general connection between the rotational interface and fixed interfaces was set as frozen rotor for a steady state calculation. The shear stress tran_sport turbulence model has been adopted in this study because of its superiority to estimate both separation and vortex occurrence on the wall of complex blade shapes. The total pressure boundary condition was applied at the inlet and static pressure was set for the outlet in the turbine mode (TM). With this boundary condition the head can be fixed while the flow rate is determined by calculation according to guide vane opening. For the pump mode (PM) the static pressure boundary condition was applied at the inlet and mass flow rate was set for the outlet. The boundary conditions for the numerical analysis are summarized in Table 3.

Table 3

Boundary conditions

The numerical mesh for all components except the casing was constructed using hexahedral mesh. The casings complex geometry makes it difficult to generate hexahedral meshing in a short period of time, therefore tetrahedral meshing has been adopted only for the spiral casing. The full domain calculation model is shown in Fig. 5 and refined hexahedral mesh on a single impeller is shown in Fig. 6.

Fig. 5

Full domain calculation model

Fig. 6

Fine numerical meshing of a single impeller

4. Results and Discussion

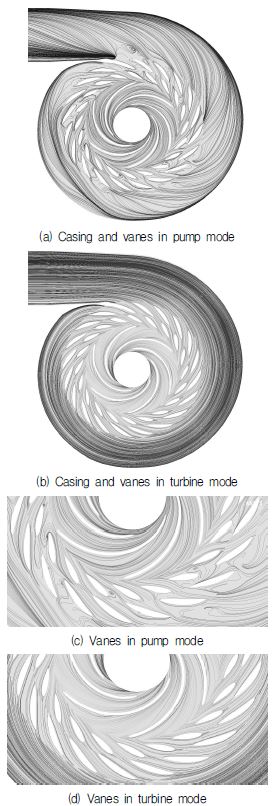
The results include the characteristics of flow rate, head, power and hydraulic efficiency to give an estimated performance of the pump-turbine. Fig. 7 and 8 compares the streamlines in cross-sections of the casing, stay vanes and guide vanes for the best results of the two methods: the first method by discharge speed constant K_u and the second method by gradient of discharge variation to head variation g_Q/H. It can be observed that in the pump mode for both methods, recirculation flows continuously occur starting from the guide vanes. This is a common characteristic in pump mode because of the inclusion of vanes. However, the turbine mode for both methods show very smooth streamlines evenly distributed along the casing, stay vanes and guide vanes. The performance results for the two methods will be compared to the design conditions at best efficiency point. The design conditions are shown in Table 4.

Fig. 7

Streamlines in pump and turbine mode by Ku

Fig. 8

Streamlines in pump and turbine mode by gQ/H

Table 4

Design conditions at best efficiency point

4.1 Performance Characteristics by ‘K_u’

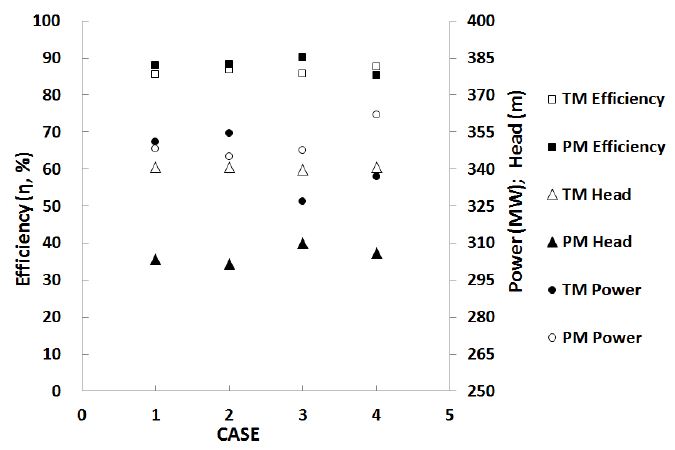
The first method by discharge speed constant K_u, produced four initial designs with different B_g dimensions. Among the four designs it can be seen that Case 3 with B_g of 0.68 m showed the best performance in the pump and turbine modes considering the nearest comparison to the design conditions. The results indicate that the design head was not achieved in pump mode for all the cases. This could be because of large recirculation flows in the guide vanes, stay vanes and casing as seen in Fig. 7, which would increase losses in these components. Another reason for a lower head could be due to the friction losses in the pipe. The turbine mode in contrast to pump mode shows relatively good comparison to the design conditions, but the efficiency is relatively lower. A summary of the results are shown in Fig. 9 and Table 5.

Fig. 9

Performance results by discharge speed constant Ku

Table 5

Performance results by Bg

4.2 Performance Characteristics by ‘g_Q/H’

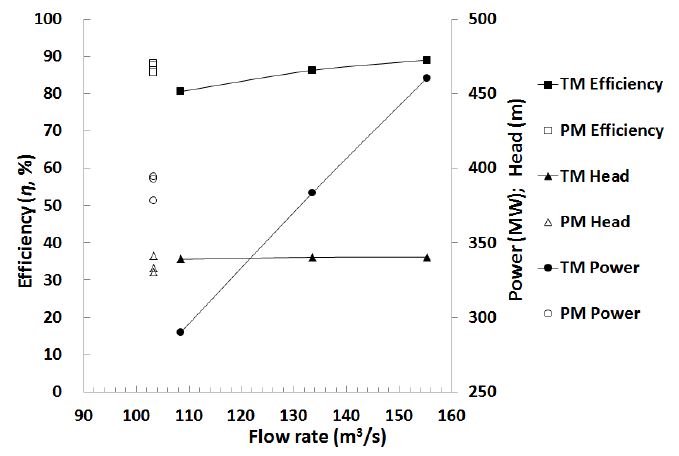
Table 6 and Fig. 10 summarizes the performance characteristics by the different cases of g_Q/H. This method by Kubota was studied in more detail in contrast to the previous method (Stepanoff) because it showed good comparison to the design conditions. Among the two designs PT-D5410 and PT-D5765 where g_Q/H=1.3 and 1.8 respectively, it was observed that PT-D5765 showed a better performance in comparison to the design conditions at full guide vane opening. Therefore, PT-D5765 was investigated for other guide vane openings and it was found that the pump mode produced better performance at a smaller guide vane opening in contrast to the turbine mode.

Fig. 10

Performance results by gradient of discharge variation to head variation gQ/H for PT-D5765

Table 6

Performance results by gQ/H

4.3 Relationship of B_g and g_Q/H

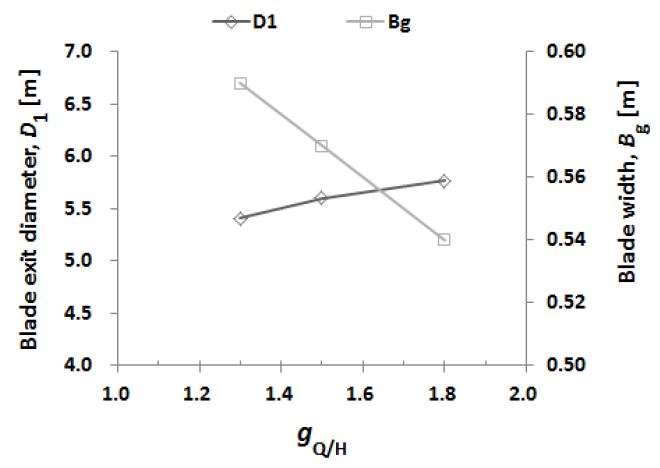
From the study it can be deduced that a higher value of g_Q/H gives considerably better results on performance. Another factor that is affected by the selection of g_Q/H is the B_g. The relationship of gradient of discharge variation to head variation g_Q/H, blade width B_g and diameter D₁ is plotted in Fig. 11. The g_Q/H and B_g are inversely proportional to each other. A higher selection of g_Q/H will result in a smaller B_g, where as a lower selection will result in a larger B_g. Additionally, it was observed that a lower g_Q/H results in a smaller head in pump mode and a lower efficiency in turbine mode.

Fig. 11

Relationship of gQ/H, Bg and D1

Comparing the size of B_g from the two methods, a large difference is observed. Initially, by the first method an increasing factor was applied on the calculated B_g size. However, this factor seems to be not well selected when comparing it to the second method. The best performance by the method of K_u shows that a B_g of 0.68 m is better, whereas the best performance from the method of g_Q/H was found at a much lower B_g. This could mean that the size of B_g has a significant effect on the performance of the pump-turbine. However, the impeller diameters for the two methods do not show very large difference as seen in Table 2.

Moreover, the current methods discussed in this study is only for obtaining the initial design of the impeller blade. To improve the overall performance, the design of guide vane, stay vane and casing shapes must also be improved. However, the latter is not part of the scope of this study.

5. Conclusion

The study has presented two techniques in designing a pump-turbine system from provided information of head, flow rate and rotational speed. Comparing the two methods of discharge speed constant K_u, and gradient of discharge variation to head variation g_Q/H, the second method of g_Q/H is a good suggestion for initial design dimensions of the pump-turbine impeller blade. From the study of B_g it can be concluded that it gives significant effect to the overall performance. Additionally, the first method of K_u did not show much improvement to the efficiency in turbine mode. However, the study of g_Q/H presented improved results in efficiency for both modes and also significant improvement of the head in pump mode. The inversely proportional relationship of g_Q/H and B_g was also observed from the second method of g_Q/H, which is an important contribution providing a better understanding to the designer when selecting a range for the size of the impeller blade. For future studies, further optimizations and much deeper study of the impeller blade loading and improvement to other componentssuch as guide vanes, stay vanes and casing-can see additional improvement in efficiency of both modes.

Acknowledgments

This work was supported by the New and Renewable Energy of the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government Ministry of Trade, Industry and Energy (No. 20163010060350).

References

• Nowicki, P., Sallaberger, M., and Bachmann, P., (2009), “Modern Design of Pump-turbines”, IEEE: Electrical Power & Energy Conference (EPEC), Montreal, October, p1-7. [https://doi.org/10.1109/epec.2009.5420368]
• Pumped-Storage Plants in Korea, (2011), Korea Hydro and Nuclear Power Co., Ltd., accessed June 2014, available online: http://cms.khnp.co.kr/eng/pumped-storagepower- status/.
• Stepanoff, A. J., (1948), “Centrifugal and Axial Flow Pumps”, 2nd Edition, John Wiley & Sons, Inc, New York, USA, p69-89. [https://doi.org/10.1016/0016-0032(48)90328-7]
• Krishna, H. R., (1997), “Hydraulic Design of Hydraulic Machinery”, Ashgate Publishing Limited, England, p465-484.
• Stelzer, R. S., and Walters, R. N., (1977), “Estimating Reversible Pump-turbine Characteristics”, U.S. Government Printing Office, Washington, Engineering Monograph No. 39.
• Kovalev, N. N., (1965), “Hydroturbines: Design and Construction”, S. Monson Binding, & K. Wiener Jerusalem.
• Wang, X., Zhu, B., Fan, H., Tan, L., Chen, Y., and Wang, H., (2014), “3D Inverse Design and Performance Investigation of Pump-turbine Runner”, Transactions of the Chinese Society for Agricultural Machinery, 45(12), p93-98, (in Chinese).
• ANSYS Inc., ANSYS CFX, Ver. 15, (2016).
• Chen, C., Zhu, B., Singh, P. M., & Choi, Y. D., (2015), “Design of a Pump-turbine Based on the 3D Inverse Design Method”, The KSFM Journal of Fluid Machinery, 18(1), p20-28. [https://doi.org/10.5293/kfma.2015.18.1.020]
• Singh, P. M., Chen, C., Chen, Z., and Choi, Y. D., (2015), “Investigation Into the Internal Flow Characteristics of a Pump-turbine Model”, The KSFM Journal of Fluid Machinery, 18(4), p36-42. [https://doi.org/10.5293/kfma.2015.18.4.036]
• Singh, P. M., Chen, C., Chen, Z., and Choi, Y. D., (2015), “Cavitation Characteristics of a Pump-turbine Model by CFD Analysis”, The KSFM Journal of Fluid Machinery, 18(4), p49-55. [https://doi.org/10.5293/kfma.2015.18.4.049]