비속도에 따른 원심펌프의 내부유동 특성 연구
Abstract
In this paper, a numerical investigation of a centrifugal pump for different specific speeds has been performed to study the flow characteristics inside the passage of an impeller. Three-dimensional steady Reynolds-averaged Navier-Stokes equations were solved by a finite volume-based solver, and the shear stress transport model was adopted as a turbulence closure. Numerical results for the performance parameters showed good agreements with experimental data. Jet-wake flow, secondary flow, three-dimensional streamlines, and total pressure loss distributions in the centrifugal pumps, were investigated to find a correlation between the flow characteristics and specific speed. It was observed that flow structure in the centrifugal pump varied remarkably with the specific speed of the pump. Also, it is noted that understanding of the jet-wake and secondary flow inside the passage of the impeller, is highly important to grasp the mechanisms of total pressure losses of the centrifugal pump.
Keywords:
Centrifugal Pump, Jet-wake Flow, Reynolds-averaged Navier-Stokes Analysis, Secondary Flow, Specific Speed키워드:
원심펌프, 제트-후류 유동, 레이놀즈평균 나비어-스톡스 해석, 이차 유동, 비속도1. 서 론
비속도는 터보기계의 설계 단계에서 요구되는 양정, 유량 및 회전수로 결정되는 무차원화 된 값으로, 기기의 운전성능 특성과 유로의 배열에 따른 기기의 유형(예를 들어 축류형, 원심형 등)이 이 비속도 값에 따라 결정된다. 특히, 일반 가정과 산업체에서 유체의 이송에 주로 이용되고 있는 펌프에 대해서는 비속도에 따른 성능 특성과 설계에 대한 가이드라인이 오랜 기간의 실험이나 실무에서의 통계적인 경험을 바탕으로 제시되고 있다.(1-4)
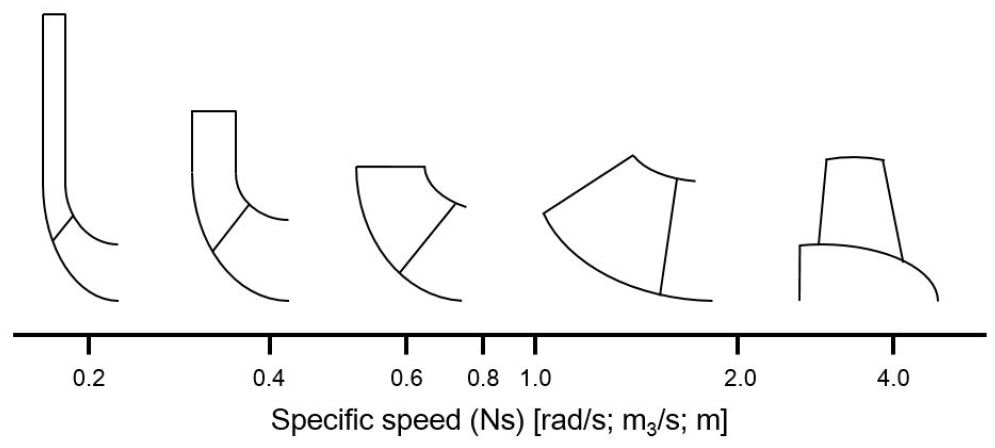
Fig. 1은 비속도에 따라 최대 효율을 가지는 펌프 형상들을 나타낸 것으로, 비속도가 작은 펌프의 경우 유동이 축방향으로 유입되어 반경방향으로 토출되는 원심형의 특성을 보이며, 비속도가 큰 펌프는 축방향으로 유입되어 그대로 축방향으로 토출되는 축류형의 특성을 보인다. 그러므로 설계자는 비속도에 따라 변하는 유로 형상으로 인해 유발되는 복잡한 난류유동과 손실 특성을 고려하여 임펠러(impeller) 형상 설계를 하여야 하는데, 유동특성을 정확하게 파악하여 설계에 반영하기에는 어려움이 있다.
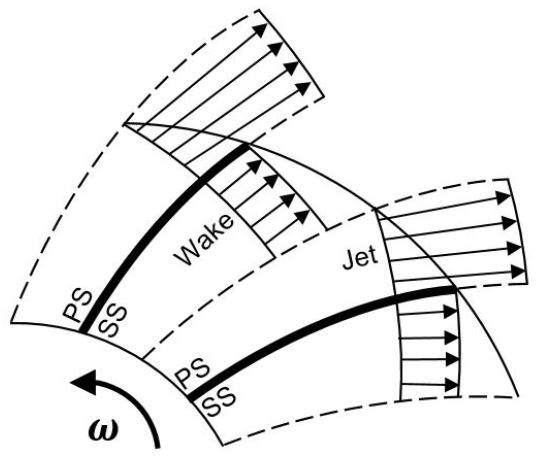
펌프 임펠러 내의 유동 특성과 구조를 파악하기 위해 초기에는 이론과 실험을 통해 많은 연구가 수행되었다. 이론식을 활용하여 곡률이 있는 유로에서 비점성 유동의 유동 구조의 예측에 대한 연구는 Johnson(5)에 의해 수행된 바 있다. 원심 압축기 임펠러의 유동구조 분석을 위한 실험적인 연구는 Eckardt(6)와 Johnson과 Moore(7)에 의해 수행되었다. 그들은 Eckardt 임펠러 모델을 대상으로 내부유동 구조를 관찰하기 위해 Laser-2-Focus (L2F) Velocimeter를 사용하여 유로 내부단면을 분석하였고, 공통적으로 Fig. 2와 같이 쉬라우드 흡입면 부근에서 유동박리로 인한 제트-후류(Jetwake) 유동 구조가 형성됨을 보고하였다. Hathaway 등(8)은 NASA 저속 압축기 임펠러를 대상으로 5공 프로브, 열선유속계(hot-wire anemometer) 및 ammonia-ozalid 유동 가시화 기법으로 측정된 유동 특성을 비교하여 기법에 따른 예측 정밀도에 대해 평가하고자 하였다. Visser(9) 등은 낮은 비속도 원심펌프에 대해 포텐셜유동 속도 성분을 예측하고 이를 레이저도플러 속도계(Laser Doppler Velocimeter)를 활용한 실제 실험 데이터와 비교하였다. Hong과 Kang(10)은 낮은 비속도 원심펌프의 출구 유동특성 연구를 통해 원심펌프의 유동에서는 원심 압축기 유동과는 달리 출구에서 넓은 유동박리 현상이 발생함을 보고하였다.
최근에는 실험으로 인해 소요되는 시간적, 경제적 비용을 줄이고 유로 내부의 정밀한 유동 분석을 위해 전산유체역학(CFD)을 활용한 원심형과 사류형 임펠러 유동 구조에 관한 연구가 많이 수행되고 있다. Choi와 Kang(11)은 Eckardt 임펠러를 대상으로 3차원 점성 내부유동을 해석하여 유로 내부의 이차유동(secondary flow)의 생성과 발달 과정을 고찰하였으며, Byskov 등(12)과 Westra 등(13)은 원심펌프 임펠러를 대상으로 각각 대와류모사(large eddy simulation)와 레이놀즈평균 나비어-스톡스(Reynolds-averaged Navier-Stokes (RANS))해석을 통해 설계유량과 탈 설계유량에서의 내부 유동을 예측하고 이를 실험값과 비교하였다. 아울러, 원심펌프 임펠러 내부유동의 박리현상을 개선하기 위해 Zangeneh 등(14)과 Kim과 Kim(15)은 CFD를 활용해 각각 역설계 기법과 최적설계 기법을 기반으로 임펠러와 디퓨저(diffuser) 형상을 개선하여 성능을 향상시키는 결과를 얻었다.
앞서 언급한 바와 같이 원심형 임펠러의 유동구조와 성능 특성을 분석하기 위한 연구는 많이 수행된 바 있으나, 다른 비속도를 가진 원심펌프들이 유동구조에 있어 어떠한 차이를 보이는지에 대한 연구는 아직 수행되지 않았다. 따라서 본 연구에서는 비속도가 다른 원심펌프들에 대해 유동특성과 유동구조에 대한 분석을 3차원 RANS 해석을 사용해 수행하였다. 수치해석의 타당성을 검증하기 위해 실험 데이터와 유동해석 결과를 비교하였고, 네 종류의 서로 다른 비속도를 가진 원심펌프들의 제트-후류 유동, 이차유동, 그리고 3차원 유동 등의 유동구조와 전압 손실을 비교하여 그 특성을 상세히 분석하였다.
2. 원심펌프 모델
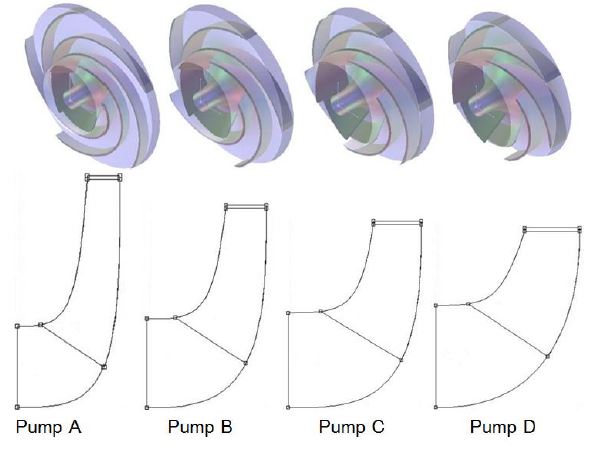
본 연구는 비속도에 따른 원심펌프의 내부유동 특성을 확인하기 위해 Fig. 3에 도시된 바와 같이 다양한 형상을 가지는 총 4종의 단단 벌류트(volute) 형태의 밀폐형 임펠러를 가진 원심펌프를 선정하였으며, 각 원심펌프의 설계유량에서의 유량계수 Φ, 양정계수 Ψ, 그리고 동력계수 τ의 정의식은 다음과 같이 표현된다.
| (1) |
| (2) |
| (3) |
이 때, H, Q, 그리고 P는 양정, 유량, 그리고 동력을 의미하며, g, ω, r2, 그리고 b2는 각각 중력가속도, 각속도, 임펠러 출구 반지름, 그리고 임펠러 출구 높이를 나타낸다.
선정된 원심펌프들의 성능 사양을 바탕으로 각 원심펌프의 비속도를 구할 수 있는데, 펌프 A-D에 대해 설계유량에서의 비속도는 각각 0.372, 0.558, 0.731, 그리고 0.899(rad/s, m3/s, m)이다. 이들은 Fig. 1에 도시된 바와 같이 일반적으로 사용되는 원심펌프의 비속도 범위를 대표하는 값들에 해당된다. 본 연구에 사용된 원심펌프 형상은 현재 진행 중인 산업통상자원부 주관 ‘비속도 150-1200급 원심 및 사류펌프 설계기술 개발’ 과제(16)의 결과물 중 일부를 채택한 것으로, 선정된 원심펌프들의 주요 사양은 Table 1과 참고문헌 16에 자세히 기술되어 있다.
3. 수치해석 방법
삼차원 비압축성 정상상태 유동의 해석을 위해 상용소프트웨어인 ANSYS CFX-15.0(17)을 사용하였으며, 3차원 RANS 방정식을 지배방정식으로 채택하였다. 해당 방정식은 유한체적법(finite volume method)을 통해 이산화되었고, 대류항(advection term)의 수치도식에는 2차의 정확도를 가지는 고해상도 도식을 사용하였다. 난류모델로는 터보기계의 유동예측에 정확도가 높은 것으로 입증된(18)k-ω 계열의 SST (shear stress transport) 모델을 사용하였다(19).
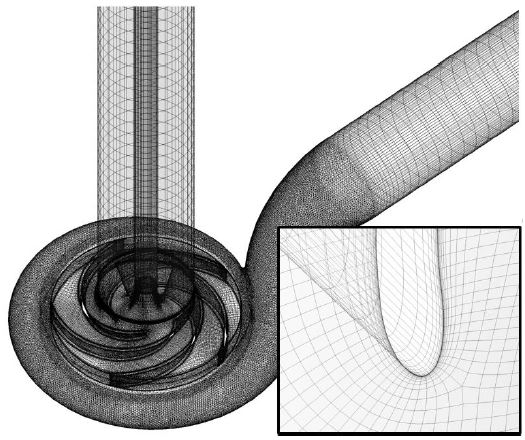
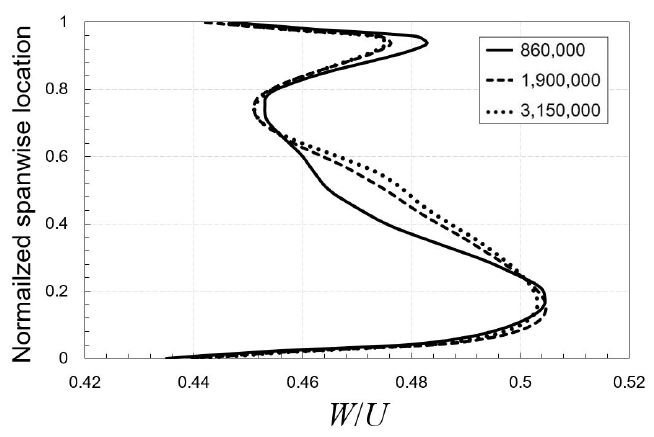
Fig. 4는 계산 격자계의 예를 나타낸 것으로, 벌류트 내부는 사면체 격자를 사용하여 비정렬 격자계로 구성하였으며, 임펠러, 입구배관과 출구배관은 육면체 격자로 구성하였다. 이 때, 고체 경계면 부근에는 조밀한 격자를 위치시켜 속도 구배가 큰 경계층 유동의 효과적인 해석이 가능하도록 하였다. 계산에 사용할 최종 격자계는 격자의존성 테스트를 통해 수치해에 영향을 미치지 않는 최소의 격자수로 결정함으로써 계산의 경제성을 꾀하였다. Fig. 5는 Pump B의 임펠러 출구에서의 상대속도 분포를 나타낸 것으로, 86~315만개 사이의 세 가지 격자수를 테스트하여 그림에 나타난 결과를 바탕으로 최적 격자수로 약 190만개가 선정되었다.
유동해석의 계산영역은 회전영역(임펠러)과 고정영역(벌류트, 입구배관, 출구배관)으로 구성하였으며, 주기조건 없이 전체 유동영역을 계산영역으로 구성하였다. 작동유체로는 단상(single phase)인 20℃의 물을 사용하였고, 입구와 출구 경계조건으로는 각각 대기압 상태의 전압력과 설계유량에 해당하는 질량유량을 부여하였으며, 고체 면에는 점착조건(no-slip condition)의 벽 조건을 부여하였다. 또한, 고정자 간의 경계면(벌류트와 출구배관)에서는 GGI (general grid interface) 기법을 사용하였으며, 상대운동이 있는 임펠러(회전자)와 벌류트 또는 입구배관(고정자) 사이의 경계면에서는 계산 값을 그대로 정지좌표계에 입력하는 방식인 Frozen-rotor기법을 적용하였다.
Fig. 6은 임펠러와 벌류트의 상대위치에 따른 수력성능의 변화를 나타낸다. 임펠러의 상대위치를 정의하기 위해 Fig. 6(a)와 같이 도식화하였으며, 이 때 φ는 벌류트 혀와 블레이드 뒷전 사이의 각도를 나타내고 φ0는 블레이드 1 주기의 각도를 의미한다. 블레이드 1 주기를 9등분하여 회전시켜 얻은 상대위치에 따른 펌프 B의 설계유량에서의 양정계수, 동력계수, 그리고 수력효율의 변화를 Fig. 6(b)에 나타내었다. 이 때, 하첨자 avg와 stage는 각각 frozen-rotor 기법으로 얻은 값들의 평균과 stage 기법으로 얻은 값을 의미한다. 양정계수와 동력계수의 경우 임펠러의 상대위치에 따라 포물선 형태를 나타내며 성능곡선이 변화하나, 수력효율은 위치에 따라 양정과 동력이 같은 비율로 증감하기 때문에 큰 변화가 없음을 알 수 있다. 한편, stage 기법으로 얻은 값과 frozenrotor 기법으로 얻은 값들의 평균값을 비교한 결과, stage 기법으로 얻은 양정계수와 동력계수가 frozen-rotor 기법으로 얻은 값보다 각각 4.78%, 4.73% 높고, 수력효율은 큰 차이가 없음을 확인할 수 있다.
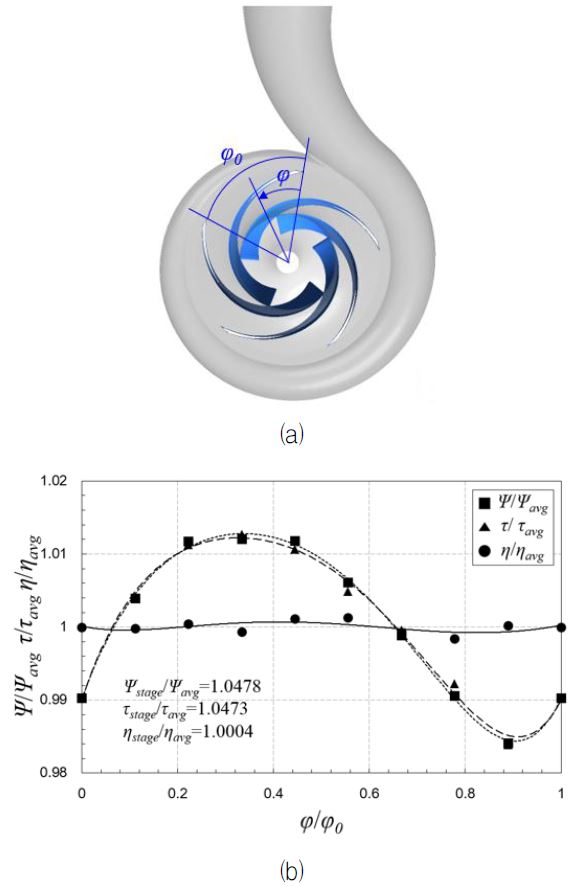
Effect of rotor position on hydraulic performance at design flow rate: (a) definition of φ and φ0, (b) variation of hydraulic performance for different rotor positions
수치해석의 수렴조건으로는 모든 방정식들의 잔차(residual)가 10-4 이하가 됨과 동시에 일정 해석 반복횟수 당 각 성능함수(수력효율, 양정, 동력)의 변화가 0.3% 이하가 되어야 한다는 조건을 사용하였다. 한번 해석에 소요되는 반복계산 횟수는 약 1000회이며, Intel i7 2.67 GHz CPU가 구비된 PC를 사용하여 병렬계산을 수행하여 약 10시간이 소요되었다.
4. 결과 및 검토
4.1 수치해석의 타당성 검증
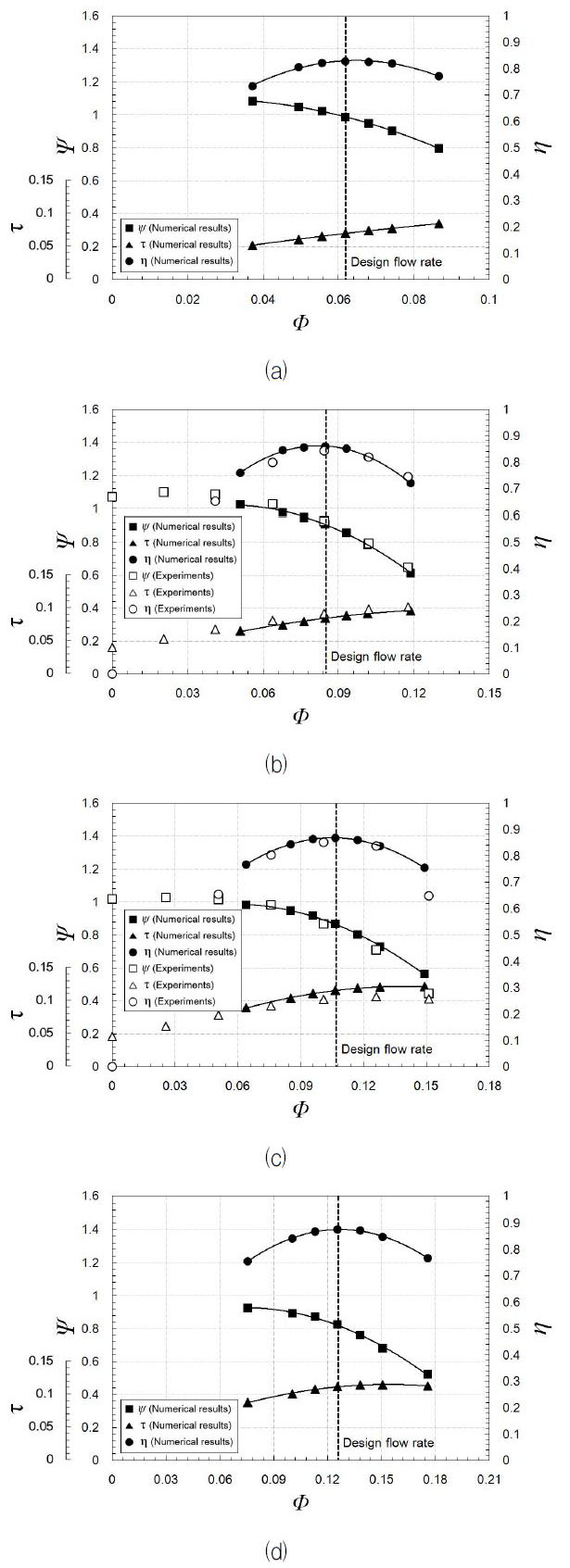
Fig. 7은 유동해석으로 도출된 각 원심펌프의 설계유량과 탈 설계유량에서의 성능곡선을 나타낸 것으로, 수치해석의 타당성을 검증하기 위해 이 중 펌프 B와 C의 유동해석 결과를 실험치와 비교하였다. 펌프 C의 경우 고 유량 영역에서 수력효율, 양정, 그리고 동력에 대해 실험치에 비해 미세하게 높은 예측을 하고 있으나, 성능곡선의 전반적인 경향은 두형상에 대해 잘 일치하고 있다. 유동해석과 실험 결과가 모두 설계유량에서 최고 효율을 가지는 것은 본 연구의 설계유량에서의 특정 비속도를 가진 원심펌프에 대한 유동해석이 신뢰성 있는 결과를 나타냄을 의미한다.
펌프 A와 D를 모두 고려하여 비속도에 따른 성능곡선의 경향을 보았을 때, 비속도가 커질수록 설계유량에서의 효율과 동력은 증가하였으며, 양정은 감소하였다. 아울러, 비속도가 증가함에 따라 탈 설계유량에서의 성능변화가 급격히 이루어지는 것을 확인할 수 있는데, 이는 기존에 널리 알려진 비속도에 따른 일반적인 성능곡선 특성(저(低) 비속도: 저유량, 고양정, 효율과 동력의 완만한 변화, 고(高) 비속도: 고유량, 저양정, 효율과 동력의 급격한 변화)과 잘 일치한다.
4.2 임펠러 내부 유동분포
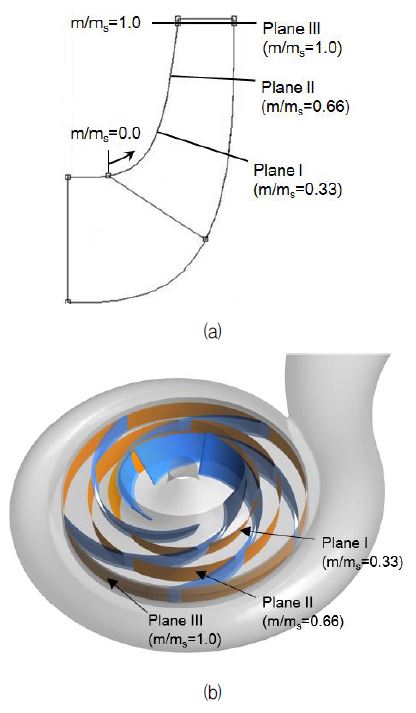
Fig. 8은 원심펌프의 자오면과 삼차원 형상을 나타낸 것으로, 본 그림에서 표기한 바와 같이 쉬라우드(shroud) 측에서 블레이드 앞전(leading edge)을 기점으로 뒷전(trailing edge)에 이르기까지 자오선을 총 3등분하여 각 지점에 대해 원주방향으로 곡면을 생성하였고, 각 유로에 대한 자오선 방향 속도분포를 평균하여 Fig. 9에 나타내었다. Fig. 9(a)의 Plane I은 유동의 진행방향이 축방향에서 반경방향으로 전환되는 지점으로, 모든 형상에 대해 흡입면 부근에서는 높은 유동속도를, 그리고 압력면 부근에서는 낮은 유동속도를 가진다. 압력면에서 흡입면으로 진행함에 따라 선형적으로 증가하는 속도분포를 가지며, 비속도가 커질수록 속도분포의 기울기는 증가한다. 이는 Visser 등(9)의 연구에서 밝혀진 바와 같이 곡률이 있는 유로의 회전하는 유동의 포텐셜 유동과 비슷한 양상을 보인다.
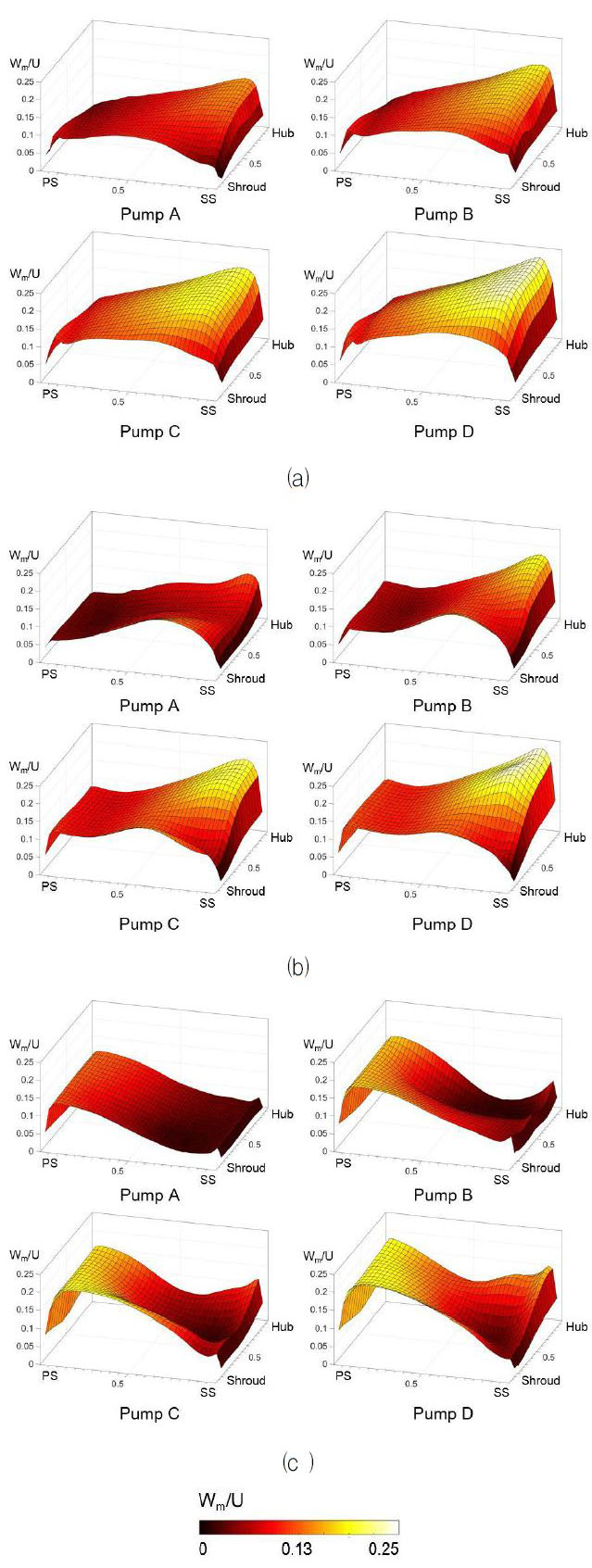
Meridional velocity distributions at three planes in Fig. 7: (a) Plane I, (b) Plane II, and (c) Plane III
Fig. 9(b)의 Plane II는 반경방향으로 진행된 유동이 발달되는 지점으로, Plane I에 비해 공통적으로 압력면에서 유로 중간에 이르기까지의 영역에서 낮은 속도 분포를 보인다. 또한, 흡입면의 쉬라우드 부근에서도 낮은 속도 분포를 나타내며, 비속도가 커질수록 유동 손실의 정도가 큰 것을 확인할 수 있다.
Fig. 9(c)의 Plane III은 임펠러를 지나는 유동이 완전 발달되는 구간으로, Plane II에서 발달되었던 압력면 부근에서의 저 운동량 영역은 흡입면 부근으로 이동하고, 압력면 부근의 유동속도는 증가한다. 이는 앞서 언급하였던 바와 같이 원심형 임펠러의 출구 유동에서 발견되는 전형적인 특징인 제트-후류 유동이다. 비속도가 증가함에 따라 압력면 부근에서의 유동속도는 증가하고, 흡입면 부근에서의 저 운동량 영역의 면적은 감소한다. 주목할 점은 비속도가 낮은 펌프 A에서는 흡입면 전 영역에 걸쳐 넓은 유동손실 구간이 관찰되고, 펌프 B는 허브 근처에서, 펌프 C는 중간 스팬(span)에서, 그리고 펌프 D는 쉬라우드 부근에 집중된 저 운동량 영역을 보이며 비속도가 변함에 따라 저 운동량 영역이 점차 이동하는 것인데, 이는 Eckardt(6)나 Hathaway 등(8)의 연구에서 보였던 유동구조와는 다른 양상이며, Hong과 Kang(10)의 결과와 비슷한 양상을 보인다. 이들은 이러한 결과가 원심펌프와 원심압축기의 임펠러 형상의 차이에 기인하는 것으로 기술하였다.
4.3 임펠러 내부유동 특성
Fig. 10은 임펠러 출구에서의 상대속도의 편향각(deviation angle) 분포를 나타낸 것으로, 가로 축은 임펠러 단일 유로 내에서 압력면에서 흡입면에 이르기까지의 원주방향 거리를 무차원화한 값, 세로 축은 편향각을 각 펌프의 블레이드 출구 각도 β2b로 무차원화한 값으로 각각 나타내었다. Fig. 10(a)는 10% 스팬에서의 편향각 분포로, 펌프 A의 경우, 흡입면 부근에 집중적으로 유동이 편향되었으며, 비속도가 커질수록 최대 편향각의 분포가 유로 중간으로 이동하는 것을 확인할 수 있다. 이 때, 펌프 B가 다른 형상들에 비해 가장 큰 편향각을 보이며, 나머지 형상들은 비슷한 편향 정도를 보인다. 중간스팬에서의 편향은 형상에 관계없이 흡입면 부근을 최대점으로 하여 일정한 크기와 경향으로 분포되어 있는 것을 Fig. 10(b)에서 확인할 수 있다. Fig. 10(c)는 90% 스팬에서의 유동의 편향각을 나타내고 있다. 펌프 A의 경우, 압력면에서 80% 떨어진 지점을 극대점으로 하여 유로 전 영역에 넓게 유동의 편향이 나타나며, 비속도가 커질수록 유동의 편향 정도는 줄어든다. 펌프 D의 경우, 압력면에서 90% 떨어진 지점에서 국부적으로 큰 유동 편향을 보이며, 압력면으로 갈수록 편향 정도는 급격히 줄어든다. 임펠러 출구의 편향각 분포는 앞서 언급한 자오선 방향 속도분포와 밀접한 관련이 있는 것을 확인할 수 있는데, 낮은 자오선 방향 속도 분포를 보이는 영역에서 유동의 편향각이 상대적으로 큰 것을 Fig. 9(c)에서 확인할 수 있다.
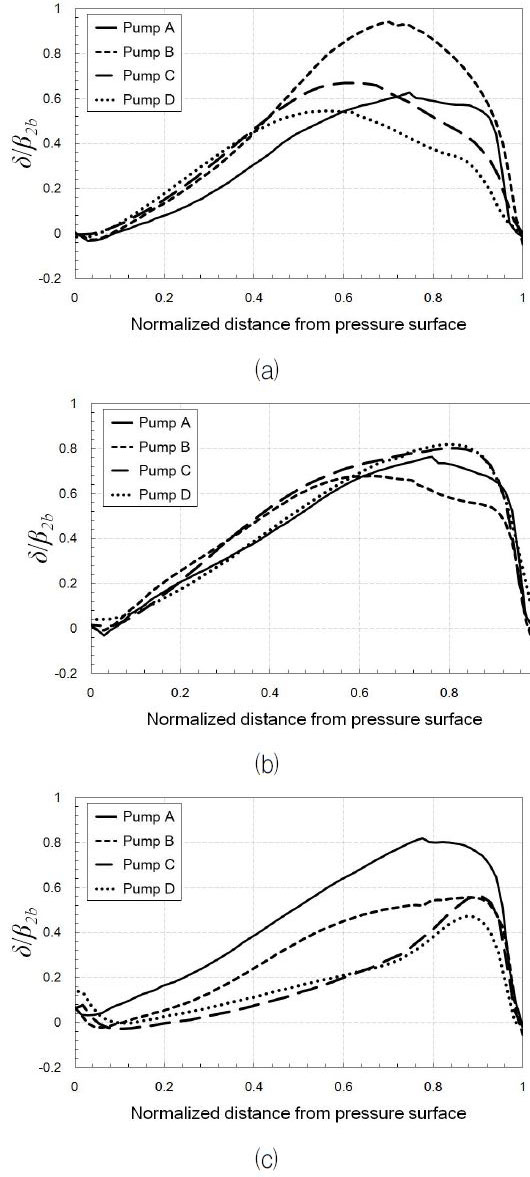
Distributions of dimensionless deviation angle at plane III: (a) 10% span, (b) 50% span, and (c) 90% span
Fig. 11은 앞서 설명된 Plane III에서의 자오선 속도 분포와 상대속도 유동각 분포를 기반으로 제트유동, 후류 그리고 면적 평균된 유동에 대해 각 형상별로 속도삼각형을 나타낸 것으로, 속도 성분은 각 형상의 임펠러 끝단 속도 U로 무차원화 하였다. 그림에서 확인할 수 있듯이 비속도가 증가함에 따라 제트유동의 상대속도는 증가하며, 이로 인해 제트유동의 운동량은 증가한다. 그러나 이러한 제트 유동의 운동량 증가에 비해 후류에서의 운동량은 비속도가 변함에 따라 큰 차이를 보이지 않고, 비속도가 커질수록 제트영역과 후류영역에서의 운동량의 편차가 커지는데, 이는 후류영역에서의 유동손실이 상대적으로 크다는 것을 의미한다.
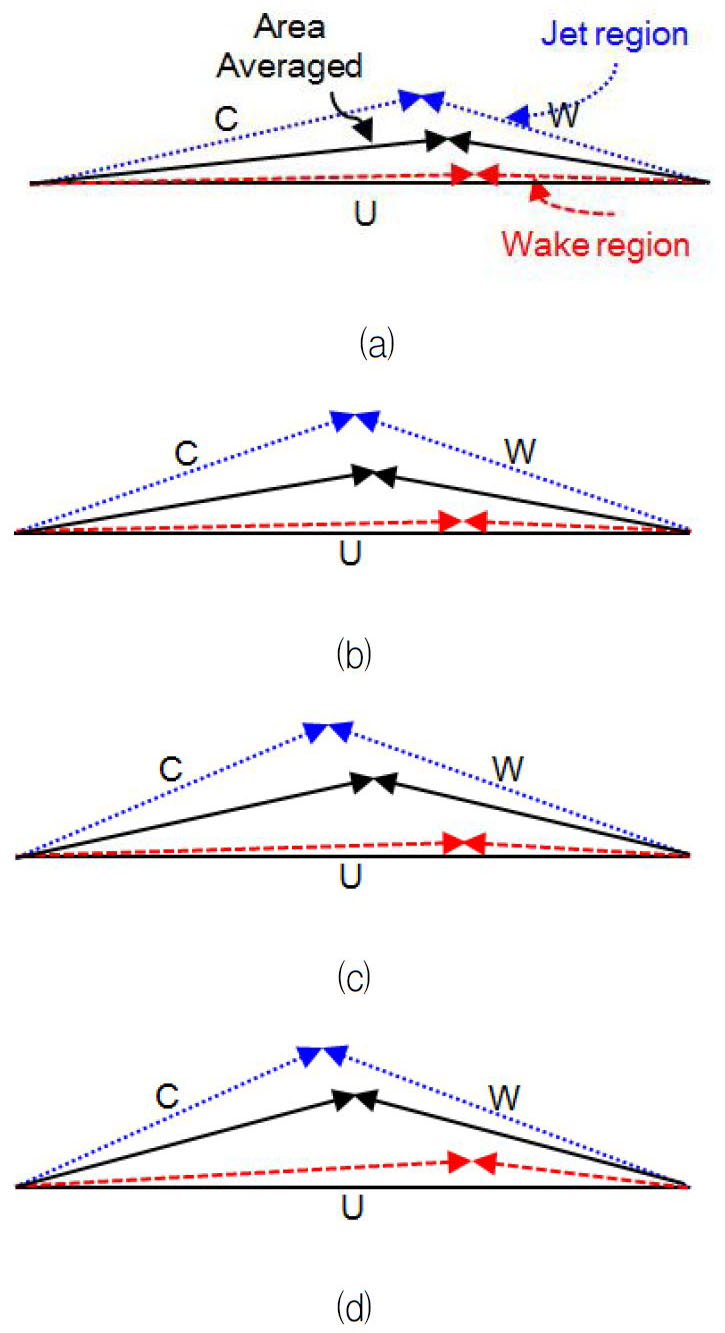
Normalized velocity triangles for jet-wake flow region at plane III: : (a) Pump A, (b) Pump B, (c) Pump C, and (d) Pump D
유로 내에서 유동 진행방향으로의 유동 특성을 확인하기위해 아래와 같이 정의된 무차원화 된 회전 총압(dimensionless rotary stagnation pressure), P*의 분포를 나타내었다.
| (5) |
| (6) |
여기서, p*는 회전총압을 나타내며, W는 임펠러 유동의 상대속도를 의미한다. p*max은 회전총압의 최대값으로 임펠러 입구에서의 회전총압을 의미하며, p*min은 계산영역 내에서의 회전총압의 최소값을 의미한다.(11) Zangeneh 등(12)의 연구에서는 회전총압의 구배(gradient)가 유로 내에서의 이차유동 형성에 기인하는 것으로 보고하였다.
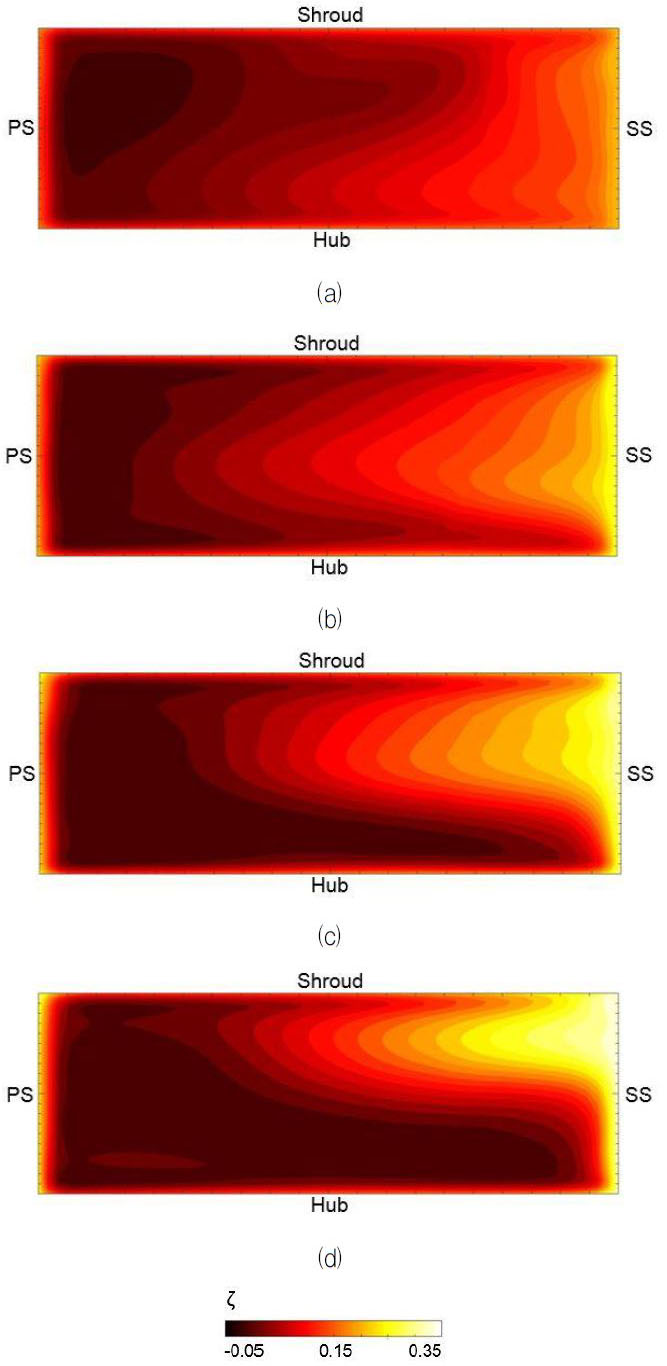
Fig. 12는 쉬라우드 부근에서의 회전총압 분포를 나타낸 것이다. 모든 형상에 대해 공통적으로 압력면 부근의 유로 중후반에 이르기까지 높은 회전총압이 분포하며, 압력면에서 흡입면으로 가까워질수록 급격히 감소하는데 이때 얼마나 회전총압이 급격히 변하느냐에 따라 회전총압의 구배가 결정된다. 펌프 A의 경우, 회전총압이 급격히 변화하는 영역이 앞전에서부터 뒷전에 이르기까지 유로 전체에 크게 형성되어 있다. 이러한 회전총압이 급격히 변화하는 영역은 비속도가 증가함에 따라 감소함과 동시에 유로 후방으로 이동한다. 특히 펌프 D에서는 회전총압이 급격히 변화하는 영역이 유로 후방에 주로 집중되어 있어 다른 형상들에 비해 전체 유로에 대한 이차유동의 영향이 상대적으로 작을 것으로 판단된다.
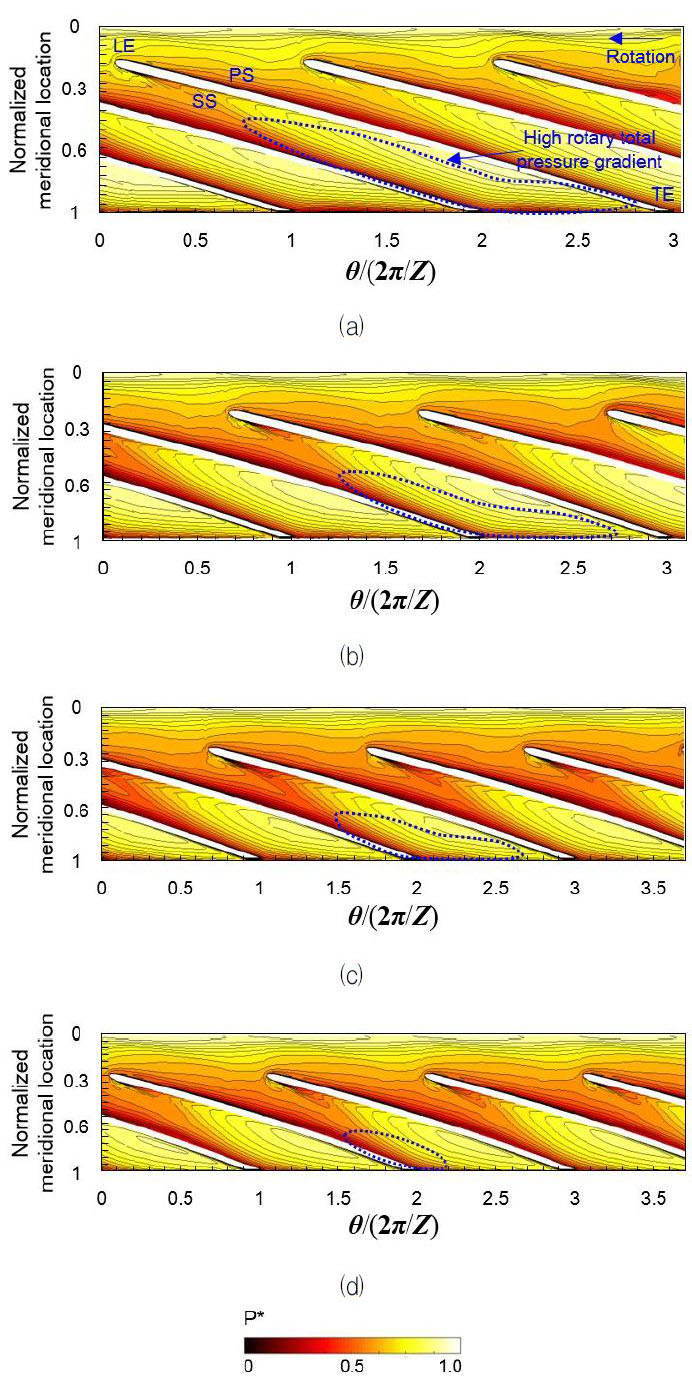
Contours of dimensionless rotary stagnation pressure and velocity vectors near shroud surface: (a) Pump A, (b) Pump B, (c) Pump C, and (d) Pump D
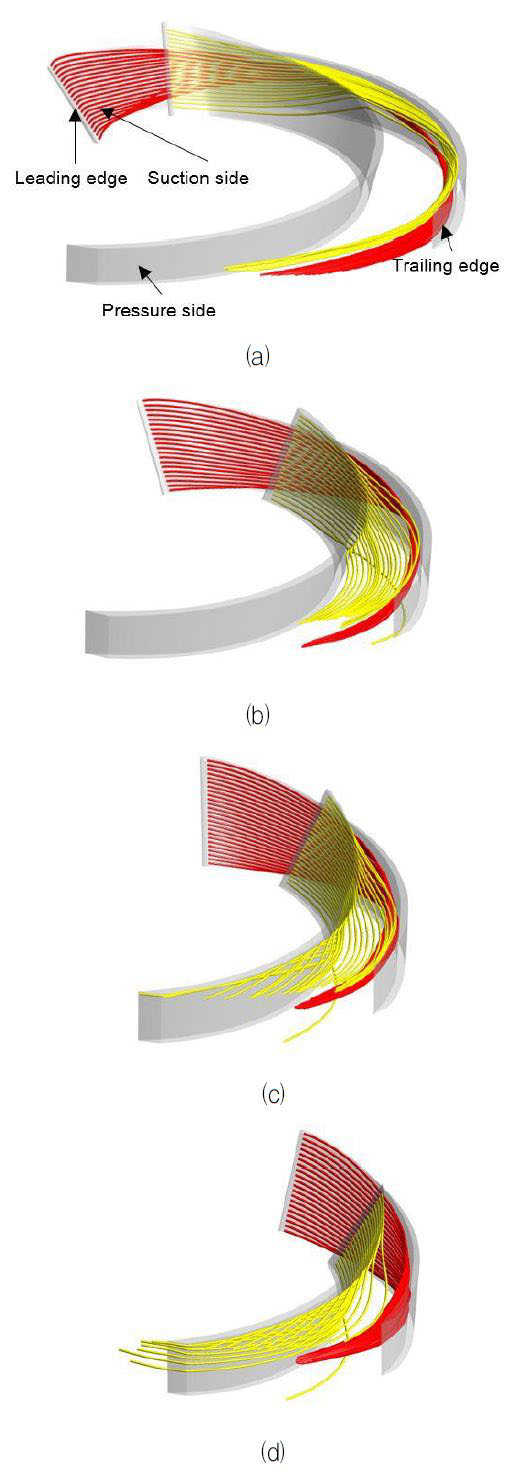
Fig. 13에서는 각 펌프에 대해 단일유로 내부의 3차원 유선의 궤적을 나타낸 것으로, 이 때 붉은 선과 노란 선은 각각 흡입면 앞전과 압력면 앞전으로부터 시작되는 유선을 나타낸 것이다. 전체 형상에 대해 흡입면 앞전으로부터 시작된 유선은 흡입면을 따라 이동하다 중간지점부터 유선이 모여 유로가 끝나는 지점까지 이동하며, 압력면 앞전으로부터 시작된 유선은 압력면을 따라 이동하다 곡률로 인한 유동의 박리로 인해 중간지점부터 쉬라우드 면을 따라 넓게 분포하는 것을 확인할 수 있다. Fig. 13(a)의 펌프 A의 경우 흡입면으로부터 시작된 유선은 중간에 모여 점차 허브 측으로 유선이 이동하는 경향을 보이며, 압력면으로부터 시작된 유선은 임펠러의 큰 곡률로 인해 이른 시점에서 박리가 시작되어 쉬라우드 면을 따라 이동하다 흡입면 중간지점에서 모여 흡입면의 유선과 함께 흡입면의 뒷전 부근에서 허브에서 쉬라우드에 이르기까지 넓은 분포를 보인다. 이러한 경향은 비속도가 증가함에 따라 점차 변하여, Fig. 13(d)의 펌프 D의 경우 임펠러의 작은 곡률로 인해 흡입면으로부터 시작된 유선은 흡입면의 뒷전 쉬라우드 부근에서 집중적으로 모이는 궤적을 보이고, 압력면으로부터 시작된 유선은 다소 박리가 발생하긴 하나, 주로 압력면을 따라 넓게 분포하여 이동하는 양상을 보인다.
4.4 임펠러 출구 전압 손실 분포
임펠러 출구에서의 전압손실 분포를 확인하기 위해 아래와 같이 정의된 전압손실계수(total pressure loss coefficient)의 분포를 Fig. 14에 나타내었다.
| (7) |
이 때, Po1과 Po2는 각각 임펠러 입구와 해당 지점에서의 전압을 나타낸다. 공통적으로 임펠러의 흡입면을 기점으로 하여 상대적으로 높은 전압손실을 보이며 압력면으로 갈수록 손실이 점차 감소하는 경향을 보인다. 펌프 A의 경우 전압손실의 강도는 미소하나, 전반적으로 넓은 영역에 걸쳐 전압 손실이 발생한다. 그리고 비속도가 증가함에 따라 전압손실 발생영역의 면적은 줄어드나 강도는 증가하며, 주 손실영역은 흡입면의 허브에서 쉬라우드 부근으로 이동한다. 이러한 전압손실 영역의 위치는 앞선 4.3절에서 설명하였던 바와 같이 자오선 방향 속도분포와 편향각 분포로 정의된 유동손실 영역과 일치하는 경향을 보이며, 전압손실의 크기 변화는 Fig. 11에서 설명하였던 바와 같이 제트-후류 유동의 운동량의 상대적인 편차와 경향이 일치하여 밀접한 관련이 있을 것으로 사료된다. 또한, Fig. 13와 비교하였을 때, 비속도에 따라 흡입면으로부터 시작된 유선이 뒷전 흡입면 부근에서 모이는 영역(비속도가 증가함에 따라 허브 측에서 쉬라우드 측으로 이동)과 Fig. 14에서의 주 전압 손실 영역이 이동하는 궤적이 유사함을 보인다.
5. 결 론
본 연구에서는 비속도가 다른 네 가지 원심펌프 형상에 대해 삼차원 RANS 유동해석을 수행하여 비속도가 설계유량에서의 원심펌프 임펠러 내부유동과 손실 특성에 미치는 영향을 파악하고자 하였으며, 내부유동 특성을 고찰하여 얻은 본 연구의 결론은 다음과 같다.
- 1) 임펠러 내부 유동의 자오선 방향 속도의 분포를 파악하여 출구 유동에서의 제트-후류 유동을 확인하였고, 흡입면 부근에 형성된 낮은 운동량 영역은 비속도가 증가함에 따라 허브에서 쉬라우드 방향으로 이동한다.
- 2) 비속도가 증가함에 따라 임펠러 출구에서의 유동손실영역의 면적은 감소하지만, 제트유동과 후류의 운동량의 상대적인 편차는 커진다.
- 3) 낮은 비속도를 가지는 펌프의 쉬라우드 측 유로에서는 회전총압의 급격히 변화하는 영역이 흡입면 부근에 넓게 형성되어 유로 내에서 이차유동을 유발하나, 비속도가 증가함에 따라 이러한 영역은 줄어듦과 동시에 주로 유로 후방에 분포한다.
- 4) 임펠러 유로에서 전압손실의 크기와 분포는 자오선 방향 속도성분과 편향각 분포, 그리고 제트-후류 운동량의 상대적인 편차와 밀접한 관계를 가진다.
본 연구를 통해 비속도에 따른 원심펌프의 설계유량에서의 내부 유동 특성 및 손실 발생 메커니즘을 이해할 수 있었다. 이에 따라 본 연구의 결과물은 추후 비속도에 따른 원심펌프의 유동 손실 저감 및 수력성능 최적화를 위한 전략 수립에 있어 큰 기여를 할 것으로 사료된다.
Acknowledgments
본 연구는 산업통상자원부 산업핵심기술개발사업의 연구비 지원에 의해 수행되었음을 밝힌다(No. 10044860).
References
- Gülich, J. F., (2008), “Centrifugal Pumps”, Springer, New York, USA.
- Stepanoff, A. J., (1957), “Centrifugal and Axial Flow Pumps, Wiley”, New York, USA.
- Pfleiderer, C., (1949), “Centrifugal Pump for Liquids and Gases”, Springer, Berlin, Germany.
-
Brennen, C. E., (2008), “Hydrodynamics of Pumps”, Cambridge University Press, New York, USA.
[https://doi.org/10.1017/cbo9780511976728]

-
Johnson, M. W., (1978), “Secondary Flow in Rotating Bends”, ASME Journal of Engineering for Power, 100, p553-560.
[https://doi.org/10.1115/1.3446393]

-
Eckardt, D., (1976), “Detailed Flow Investigations Within a High-Speed Centrifugal Compressor Impeller”, ASME Journal of Fluids Engineering, 98(3), p390-399.
[https://doi.org/10.1115/1.3448334]

- Joshnson, M. W., and Moore, J., (1980), “The Development of Wake Flow in a Centrifugal Impeller”, ASME Journal of Engineering for Power, 102, p382-389.
-
Hathaway, M. D, Chriss, R. M., Wood, J. R., and Strazisar, A. J., (1993), “Experimental and Computational Investigation of the NASA Low-speed Centrifugal Compressor Flow Field”, NASA Technical Memorandum 4481.
[https://doi.org/10.1115/1.2929285]

-
Visser, F. C., Brouwers, J. J. H., and Jonker, J. B., (1999), “Fluid ow in a Rotating Low-specific-speed Centrifugal Impeller Passage”, Fluid Dynamic. Research, 24, p275-292.
[https://doi.org/10.1016/s0169-5983(98)00033-1]

- Hong, S. S., and Kang, S. H., (2000), “Flow characteristics at the Impeller Exit of a Centrifugal Pump”, Proceedings of the KFMA Annual Meeting, Busan, Korea, p36-44.
- Choi, Y. S., and Kang, S. H., (1996), “Secondary Flows through an Impeller of Centrifugal Compressor at Design and Off-Design Conditions”, Transaction of Korean Society Mechanical Engineering B, 20(11), p3573-3588.
-
Byskov, R. K., Jacobsen, C. B., and Pedersen, N., (2003), “Flow in a Centrifugal Pump Impeller at Design and Off-Design Conditions—Part II: Large Eddy Simulations”, ASME Journal of Fluids Engineering, 125(1), p73-83.
[https://doi.org/10.1115/1.1524586]

-
Westra, R. W., Broersma, L., van Andel, K., and Kruyt, N. P., (2010), “PIV Measurements and CFD Computations of Secondary Flow in a Centrifugal Pump Impeller”, ASME Journal of Fluids Engineering, 132(6), p061104, (8 Pages).
[https://doi.org/10.1115/1.4001803]

-
Zangeneh, M., Goto, A., and Harada, H., (1998), “On the Design Criteria for Suppression of Secondary Flows in Centrifugal and Mixed Flow Impellers”, ASME Journal of Turbomachinery, 120, p723-735.
[https://doi.org/10.1115/1.2841783]

-
Kim, J. H., and Kim, K. Y., (2012), “Analysis and Optimization of a Vaned Diffuser in a Mixed Flow Pump to Improve Hydrodynamic Performance”, ASME Journal of Fluids Engineering, 134(7), p071104, (12 Pages).
[https://doi.org/10.1115/1.4006820]

- Korea Ministry of Trade, Industry and Energy, (2014), Development of Design Program for Centrifugal and Mixed-flow Pump (Ns 150-1200), Report No. 10044860.
- Ansys Inc., (2014), CFX-15.0 Solver Theory, Canonsburg, PA.
-
Lee, Y. G., Shin, J. H., Park, I. H., Kim, S., Lee, K. Y., and Choi, Y. S., (2015), “Mixed-Flow Pump Impeller- Diffuser Optimization Method by Using CFX and HEEDS”, Transaction of Korean Society Mechanical Engineering B, 39(10), p831-842.
[https://doi.org/10.3795/ksme-b.2015.39.10.831]

-
Menter, F. R., (1994), “Two-Equation Eddy-Viscosity Turbulence Model for Engineering Applications”, AIAA Journal, 32(8), p1598-1606.
[https://doi.org/10.2514/3.12149]