블레이드 형상 변화에 따른 초음속 분리기의 열유동 특성 연구

1. 서 론

최근 친환경성에 부합한 천연가스 이용이 증가하면서 천연 가스의 정제 및 수송 과정에 관심이 높아지고 있다. 더욱이 제대로 된 정제과정을 통해 천연 가스에 포함된 수분이나 황화수소, 이산화탄소 또는 탄수함량이 높은 탄화수소를 제거하지 못하면 배관에서 응축되고 축적되어 수송 효율을 떨어뜨리거나 부식시키는 등 여러 가지 문제를 야기할 수 있기 때문에 다양한 정제 기술이 등장하고 있다. 초음속 분리기는 이러한 기술 중 하나로 정익을 통과하며 선회하는 유동을 축소-확대 노즐로 유입시켜 팽창을 유도하고 상대적으로 무거운 불순물을 액화시켜 천연가스로부터 제거하는 기술이다. 초음속 분리기는 기존의 Joule-Thomson 밸브나 터보 팽창기에 비해 소형화가 가능하며 기기 내 회전부가 존재하지 않아 유지 및 보수비용이 적게 든다는 장점이 있어 초음속 분리기의 효율을 향상시키고자 다양한 연구가 수행된 바 있다. Wen 등⁽¹⁾은 사이클론 형상과 노즐 형상의 관계를 파악하고자 액체 입자를 구형 입자로 간주하고 기체를 연속체로 보는 이산입자법(Discrete Particle Method, DPM)을 통해 수치해석을 수행하였으며 실험으로 이를 검증하였다. 그 결과, 사이클론 부의 길이가 노즐 목(throat)의 10배일 때 분리 효율이 95% 이상이 되는 것을 확인하였다. Malyshkina⁽²⁾은 오일러 모델을 통해 속도 성분이나 압력 그리고 그 외 요인들을 유동 반경의 함수로 표현하는 수학적 모델을 개발하였다. Shooshtari 와 Shahsavand⁽³⁾는 두 가지 이상의 물질이 혼합된 혼합물을 초음속 분리기로 유입하여 황화수소와 물 등의 물질이 액화하여 분리되는 비율을 수치적으로 계산하는 해석 기법을 제시하여 불순물이 효과적으로 분리되는 것을 확인하였고 이를 알려진 실험 자료와 비교하여 검증하였다. 초음속 분리기에서 선회 유동은 큰 영향을 끼치기 때문에 선회유동을 효과적으로 형성하기 위한 연구도 활발히 진행되었다. Wen 등^(4,5)은 선회 유동의 각운동량을 보존하기 위해 central body를 삽입하여 선회 유동을 유지하려 하였으며 충격파(shock wave) 의 위치에 따른 효과도 분석하였다. 또한 세 가지 종류의 초음속 분리기 디퓨저를 비교하여 분석하였다. Yang 등⁽⁶⁾은 초음속 분리기에서 선회 유동을 만들기 위해 일반적으로 사용되는 정익을 대신하여 항공기익형으로 이용되는 delta wing을 삽입하여 선회 유동장을 형성하도록 전산모사 하였다. 그 결과, 회전 강도는 충분하지만 유체 거동이 불균일하고 압력 손실이 크다는 연구 결과를 도출하였다. 본 연구에서는 초음속 분리기의 선회 유동을 형성하는 정익의 블레이드 형상이 분리 효율에 미치는 영향을 고찰하기 위해 다양한 블레이드 형상을 적용하여 온도 강하, 회전 강도 그리고 압력 손실을 계산하여 비교하였다. 이를 통해 가장 적합한 정익 형상을 결정하였다.

2. 수치 해석

2.1 3차원 형상 설계

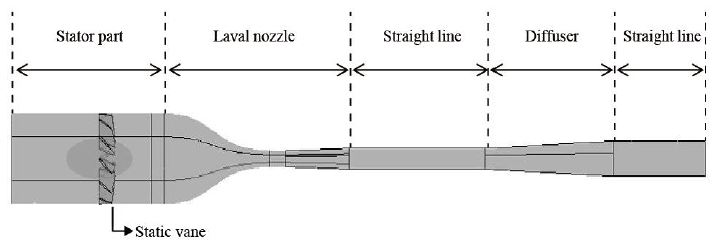
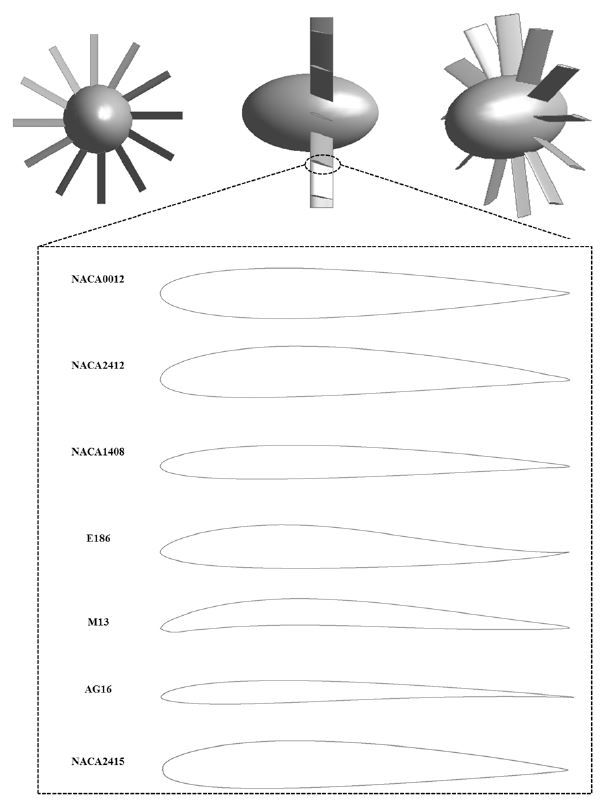
Fig. 1은 수치해석에 사용된 초음속 분리기의 개략도를 나타내고 있다. 초음속 분리기는 크게 회전 영역, 노즐 영역, 디퓨저 영역의 세 부분으로 나누어져 있다. 먼저 회전 영역에 정익은 장축과 단축이 2:1 비율인 난형체(oval body)를 중심으로 총 12개의 블레이드로 구성되어 있다. 본 연구에서는 NASA에서 개발한 서로 다른 7가지 익형을 사용하여 익형이 초음속 분리기 성능에 미치는 영향을 파악하고자 하였으며 이를 Fig. 2에 도시하였다. 익형 형상의 영향만을 파악하기위해, 블레이드는 모두 타원의 중심으로부터 40˚로 회전시켜 고정하였고 익형 형상 이외의 변수 또한 모두 같도록 하였다. 축소-확대 노즐의 경우, 축소부는 아래 공식을 이용하여 3차원 곡선으로 형성하였으며 확대부는 목에서부터 4˚로 확대되도록 설계하였다.⁽⁴⁾:

$\[ \frac{D-D_t}{D_i-D_t}=1-\frac{1}{X_m^2}{\left(\frac{x}{L}\right)}^3 \text{for} \left(\frac{x}{L}\right)\le X_m \]$

(1)

Fig. 1

Schematic of the supersonic separator

Fig. 2

Geometrical configurations of the stator in a supersonic separator

$\[ \frac{D-D_t}{D_i-D_t}=1-\frac{1}{{\left(1-X_m\right)}^2}{\left(1-\frac{x}{L}\right)}^3 \text{for} \left(\frac{x}{L}\right)\succ X_m \]$

(2)

$\[ X_m=0.3-0.7L \]$

(3)

여기서 D_i,와 D_t 그리고 L은 각각 유입구와 노즐 목의 직경, 그리고 수렴노즐의 길이를 나타낸다. 다음으로 디퓨저는 가장 성능이 좋은 것으로 알려진 원추형(conical)을 선택하였으며 이는 다음 공식에 따라 설계하였다.⁽⁵⁾:

$\[ \begin{array}{cc}q\left(Ma\right)\hfill & =\frac{\rho \upsilon }{{\rho }_t{\upsilon }_t}=\frac{A_t}{A}\hfill \\ & =\frac{Ma}{{\left[\left(\frac{2}{k+1}\right)\left(1+\frac{k-1}{2}M{a}^2\right)\right]}^{\frac{k+1}{2\left(k-1\right)}}}\hfill \end{array} \]$

(4)

$\[ L_d=\frac{r_2-r_1}{\text{tan}\alpha } \]$

(5)

여기서 q와 ρ 그리고 k는 각각 기체 유량과 밀도 그리고 단열 지수를 나타내며 L_d는 디퓨저 길이, r₁과 r₂는 디퓨저 유입구와 유출구 반경, 그리고 α는 발산각을 나타낸다.

2.2 격자계 구성

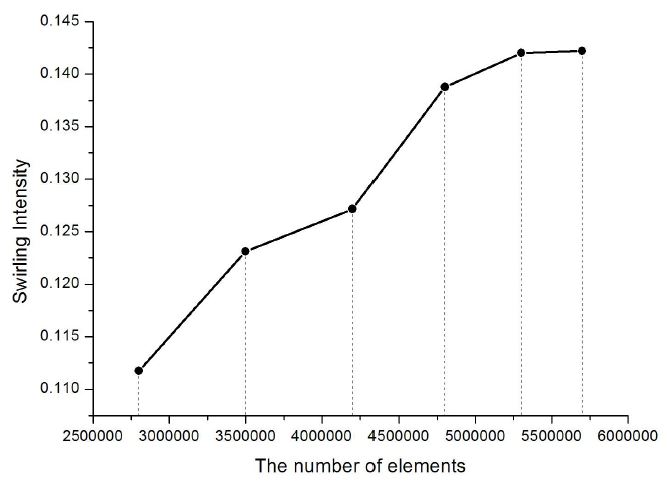
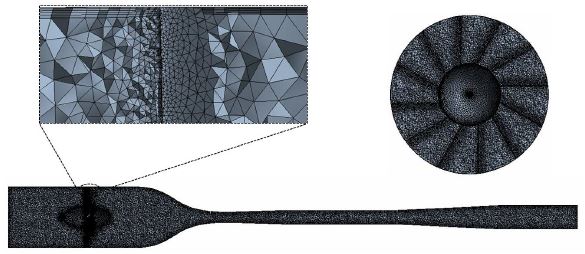
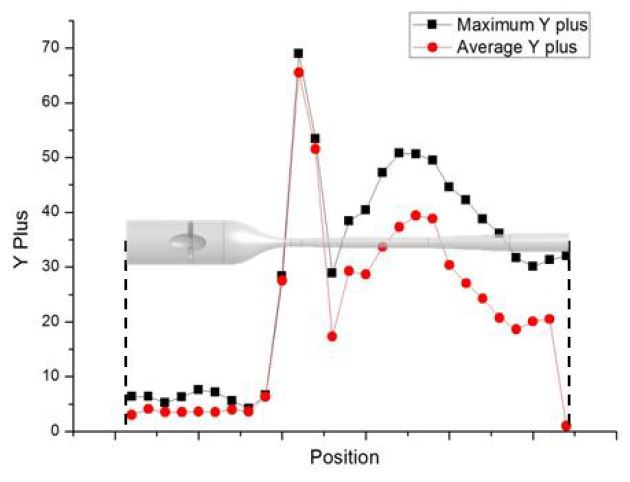
격자는 주로 사면체(tetrahedron)로 구성하였으며 벽과 블레이드 주변의 경우, 해석의 정확도를 높이기 위해 5겹의 오면체(pentahedron) 층을 구성하였다. 또한 수치해석에 사용된 격자 의존성(grid dependency)을 판단하기 위하여 내부 유동 영역의 벽면에서 거리가 있는 부피 격자를 변화시켜가며 초음속 분리기 성능 평가 지표 중 하나인 노즐 목에서의 회전 강도 변화를 관찰하여 이를 Fig. 3에 나타내었다. 이를 통해 격자수가 약 530만개를 넘으면서 격자에 대한 의존도가 급격하게 줄어드는 것을 확인하였다. 이에 격자계를 약 530만개의 요소로 구성하였으며 이를 Fig. 4에 나타내었다. 또한 벽 근처에서의 난류 유동에 대한 성공적인 예측을 위해 국부적인 Re수인 Y+값을 계산하여 Fig. 5에 나타내었다. 이를 보면 Y+값은 면적이 좁은 노즐 부분에서 가장 크지만 최대값이 70을 넘지 않도록 구성되어 있음을 알 수 있다.

Fig. 3

Grid dependency test

Fig. 4

Grid systems for the numerical analysis

Fig. 5

Y+ value distribution of the reference model

3. 결과 및 고찰

3.1 수치해석 결과

블레이드 익형 변화에 따른 초음속 분리기의 성능 특성을 고찰하기 위해 총 7가지 서로 다른 익형에 대해 수치해석을 수행하였다. Table 1은 그 결과를 나타낸 것으로 익형별 회전강도와 압력강하 그리고 가장 좋은 성능을 보인 case 3와의 상대적이 차이를 백분율로 나타내었다. 온도는 모든 경우에 대해서 물의 끓는점 보다는 높지만 메탄의 끓는점인 111.55 K에는 못 미치게 계산되어 천연가스에서 수분을 분리하고 수송하는데 적절하였다. 압력 손실은 대부분의 경우 커다란 차이가 없이 28% 만큼의 손실이 발생하였다. 이를 통해 블레이드 형상이 회전 강도에는 큰 영향을 미치지만 압력손실에는 거의 영향을 미치지 못하는 것으로 판단할 수 있다. 회전 강도의 경우 대체로 14% 이상의 회전 강도를 보였으며 특히 case 3의 경우, 회전 강도(S)가 0.19367로 다른 익형에 비해 높은 것으로 나타났다. 이는 해당 형상에서 가장 후류를 복잡하게 만들어 후류로 인한 저압 영역으로 인해 더 많은 접선 방향의 유동을 생성하기 때문인 것으로 판단된다. Fig. 6는 가장 회전 강도가 강한 case 3와 가장 약한 case 4를 비교한 것으로 case 3의 경우 블레이드 후류 영역이 더 넓은 것을 확인할 수 있다. 회전 강도가 강해지면 그만큼 더 큰 원심력을 생성하여 분리를 효과적으로 할 수 있다는 의미임으로 초음속 분리기의 최종 익형으로는 case 3의 NACA1408이 적합하다고 판단하였다.

Table 1

Results of the numerical analysis

Fig. 6

Flow fields around stator

3.2 선정된 초음속 분리기의 내부 열-유동 특성

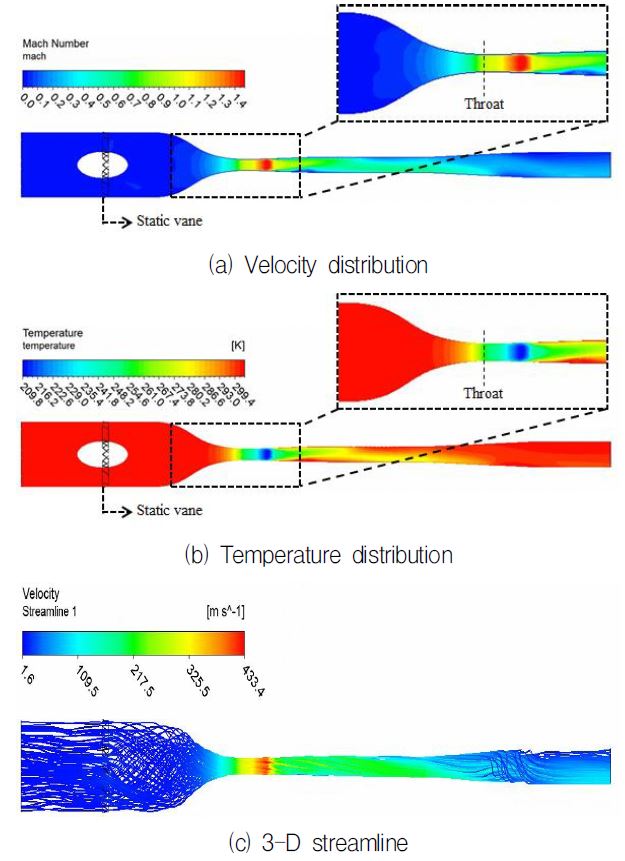
Fig. 7는 앞서 선정된 case 3의 NACA1408을 이용하여 설계된 초음속 분리기의 속도 분포와 온도 분포 그리고 3차원 유선을 나타낸 것이다. 속도 분포를 보면 목(throat)을 지나면서 초음속에 도달하고 점점 가속되어 마하 1.4까지 가속하였다가 충격파를 통과하면서 속도가 급감하는 것을 볼 수 있다. 온도 분포의 경우, 속도 증가로 인해 온도가 감소하여 최대 209.77 K까지 낮아지는 것을 알 수 있다. 이는 물의 끓는점 보다는 높지만 메탄의 끓는점인 111.15 K에는 못 미치므로 천연가스에서 수분을 분리하고 수송하는데 적절하다고 볼 수 있다.

Fig. 7

Y+ value distribution of the reference model

4. 결 론

본 연구에서는 초음속 분리기에서 선회유동을 형성하는 정익 형상을 설계하기 위해 총 7가지 블레이드에 대해 수치해석을 수행하였다. 회전 강도와 압력 손실 계수를 계산하여 각 익형을 평가하였고 이를 기반으로 블레이드에 적합한 익형을 선정하였다. 그 결과, 압력손실의 경우 차이가 뚜렷하지 않았으며 회전 강도의 경우 일반적인 초음속 분리기 목에서의 회전 강도인 10∼20%의 값⁽⁷⁾을 모든 경우에서 나타내었다. 특히 본 연구에서 고려한 여러 모델 중 case 3의 NACA1408 모델은 가장 높은 회전 강도인 0.19367를 보여 동일 조건 하에서 가장 큰 원심력을 생성할 수 있으므로 이를 최종 익형으로 선정하였다.

Acknowledgments

본 연구는 국토교통부 국토교통과학기술진흥원 플랜트연구개발사업의 연구비지원(16IFIP-B089065-03)에 의해 수행되었습니다.

References

• Wen, C., Cao, X., Yang, Y., and Zhang, J., (2012), “Evaluation of Natural Gas Dehydration in Supersonic Swirling Separators Applying the Discrete Particle Method”, Advanced Powder Technology, 23(2), p228-233. [https://doi.org/10.1016/j.apt.2011.02.012]
• Malyshkina, M. M., (2008), “The Structure of Gasdynamic Flow in a Supersonic Separator Ofnatural Gas”, High Temperature, 46(1), p69-76. [https://doi.org/10.1134/s10740-008-1010-5]
• Rajaee Shooshtari, S. H., and Shahsavand, A., (2013), “Numerical simulation of natural gas flows in diffusers for supersonic separators”, Separation and Purification Technology, 116(15), p458-470.
• Wen, C., Cao, X., and Yang, Y., (2011), “Swirling Flow of Natural Gas in Supersonic Separators”, Chemical Engineering and Processing, 50(7), p644-649. [https://doi.org/10.1016/j.cep.2011.03.008]
• Wen, C., Cao, X., Yang, Y., and Li, W., (2012), “Numerical Simulation of Natural Gas Flows in Diffusers for Supersonic Separators”, Energy, 37(1), p195-200. [https://doi.org/10.1016/j.energy.2011.11.047]
• Yang, Y., Wen, C., Wang, S., Feng, Y., and Witt, P., (2014), “The Swirling Flow Structure in Supersonic Separators for Natural Gas Dehydration”, RSC Adv., 4, p52967-52972. [https://doi.org/10.1039/c4ra08141b]
• Vaziri, B. M., and Shahsavand, A., (2015), “Optimal Selection of Supersonic Separators Inlet Velocity Components Via Maximization of Swirl Strength and Centrifugal Acceleration”, Separation Sci. and Tech., 50, p752-759. [https://doi.org/10.1080/01496395.2014.958782]