수렴형 입구형상의 막냉각홀에 대한 막냉각 성능 해석
Abstract
This work evaluated film-cooling performance of film-cooling holes with converged inlet shape. This novel geometry called converged shaped hole is composed of converged shaped inlet and cylindrical outlet of the hole. Numerical analyses were carried out using three-dimensional Reynolds-averaged Navier-Stokes equations and the turbulence was modeled using SST model. Numerical results for a cylindrical hole showed good agreements with experimental data. Film-cooling performance of the holes with the converged shape was compared with that of the cylindrical holes. The results showed that the converged inlet shape improved the film-cooling effectiveness by reducing the jetting effect. A parametric study was also performed to investigate the influence of geometry parameters of the converged inlet shape of the hole on film-cooling performance.
Keywords:
Converged Inlet Shape, Film-cooling, Film-cooling Effectiveness, Numerical Analysis, Reynolds-averaged Navier-Stokes Equation키워드:
수렴형 입구부, 막냉각, 막냉각효율, 수치해석, RANS 방정식1. 서 론
가스터빈은 높은 열효율을 위해 터빈부(turbine stage)에 대해 고온과 고압의 입구조건이 요구되며, 최근에는 요구되는 수준이 점점 증가되고 있는 추세이다. 그러나 이러한 고온의 환경은 블레이드에 가해지는 열적 하중을 증가시키고 이에 따른 부품의 파손을 유발하기 때문에 고효율 가스터빈 개발을 위해서는 보다 효과적인 냉각기술의 개발이 요구된다. 터빈 블레이드(blade) 냉각에 사용되는 기술은 크게 냉각유로를 이용한 내부냉각(internal cooling)과 블레이드 표면을 보호하는 외부냉각으로 나뉠 수 있다. 막냉각(filmcooling)(1) 기술은 대표적인 외부냉각기술로서 터빈 블레이드 표면에 일정한 각도를 가지는 미세한 홀을 배치하여 이를 통해 냉각유체를 분사시켜 고온의 가스에 노출되는 블레이드 표면에 냉각막을 형성하는 방법이다.
현 가스터빈 산업에서 가장 보편적으로 사용되고 있는 막냉각 홀은 원통형 막냉각홀(cylindrical film-cooling hole)이며 이 원통형 막냉각 홀의 막냉각 성능에 대해서는 많은 연구가 수행된 바 있다. Walters와 Leylek(2)은 원통형 막냉각 홀에 대해 유동의 구조와 특성을 실험과 수치해석을 통해 분석하였으며 냉각유체가 냉각표면에 접촉하는 것을 방해하는 콩팥 와류(kidney vortex)를 가시화 하였다. Hale 등(3)은 막냉각 홀의 직경대비 홀 길이의 비와 분사각이 길이가 짧은 원통형 홀에 미치는 영향에 대해 보고하였다. Lutum과 Johnson(4)은 홀 직경 대비 홀 길이 비의 변화에 의한 막냉각효율 변화를 살펴본 결과, 홀 직경 대비 홀 길이의 비가 5미만일 때는 길이가 증가함에 따라 막냉각효율이 증가하지만 5 이상일 때는 큰 변화가 없다고 보고하였다. Yuen과 Martinez-Botas(5)와 Rhee 등(6)은 분사율과 분사각도에 따른 원통형 막냉각 홀의 막냉각 성능을 실험을 통해 분석하였다. Lee와 Kim(7)은 원통형 막냉각 홀의 직경 대비 홀 길이의 비와 분사각을 설계변수로 하여 다양한 대리모델을 통한 수치최적 설계를 수행하였다. 최적화된 형상 중 크리깅(Kriging) 모델을 사용해 구한 최적 형상이 가장 높은 막냉각 성능을 보였으며 기준 형상 대비 약 3.6% 향상된 막냉각효율을 나타내었다.
원통형 막냉각 홀의 경우 제작의 용이성 및 경제성이 뛰어나지만 그 형상의 단순함으로 인해 높은 막냉각 성능을 이끌어 내기에는 한계가 있다. 이 때문에 많은 연구자들이 다양한 막냉각 홀 형상에 대해 연구해왔다. Saumweber와 Schulz(8)는 홴 형상 홀(fan-shaped hole)의 확장각, 분사각 그리고 입구부 원통형 홀의 길이 등이 막냉각효율 및 열전달 계수에 미치는 영향에 대해 보고하였다. Gritsch 등(9) 은 실험을 통해 홀의 주기, 측면 분사각도, 측면 확장각, 홀의 길이, 그리고 홀 입구 면적 대 출구 면적의 비가 막냉각 성능에 미치는 영향에 대해 분석하였으며 홀 사이의 주기를 제외한 나머지 형상 변수들은 막냉각효율에 비교적 큰 영향을 미치지 못하는 반면, 홀의 주기가 변화하는 경우 주기가 감소함에 따라 전체 영역에서 냉각 유체의 유량이 증가하기 때문에 큰 영향을 미친다고 보고하였다. Lee와 Kim(10)은 홴 형상 막냉각 홀에 대해 분사각, 측면방향 확장각 그리고 홀 직경 대비 홀 길이의 비를 설계변수로 선정하여 대리모델을 활용한 수치최적설계를 수행하였으며 최적화된 형상은 기준 형상 대비 약 28% 향상된 막냉각효율을 보였다. Lu 등(11)은 깊이와 너비가 다른 6가지의 트렌치(trench)가 존재하는 막냉각홀에 대한 막냉각 성능을 분석하였으며, 원통형 홀의 경우 분사율이 증가할수록 막냉각효율이 감소하는 반면 트렌치가 있는 형상은 분사율이 증가하여도 큰 변화를 보이지 않고 오히려 분사율 M=0.5에서 1.0으로 증가할 때 홀 출구 근처에서의 막냉각효율이 증가하는 경향을 보였다. 이에 더해 Lu 등(12)은 실험과 수치해석을 통해 세 가지의 타원형 크레이터(crater)가 있는 막냉각 홀의 막냉각 성능을 원통형, 확장형 및 트렌치가 있는 홀의 경우와 비교 분석하였다. 크레이터가 있는 막냉각 홀은 원통형 홀 대비 약 50% 증가된 막냉각효율을 보였으며 낮은 분사율에서 트렌치가 있는 홀보다 높은 막냉각효율을 보였다. Sargison 등(13)은 콘솔(convergingslot)홀이라는 새로운 형상의 막냉각 홀을 제시하였으며, 휀형상의 홀에 비해 비슷하거나 향상된 막냉각 성능을 보이면서 공력손실이 휀형상 보다 낮다고 보고하였다. Zhang과 Hassan(14)은 새로운 막냉각 형상인 루버(louver)홀을 제시하였으며, 원통형 홀, 콘솔 홀, 홴 형상 홀 등과 비교분석하였다. 루버 홀은 원통형 홀, 홴 형상 홀 등에 비해 월등히 향상된 막냉각 성능을 보이고, 콘솔 홀과 비슷한 막냉각 성능을 보였으며 분사율이 증가함에도 막냉각효율이 감소하지 않고 오히려 증가하는 경향을 보였다. Lu 등(15)은 크레센트(crescent) 홀이라는 막냉각 홀 형상에 대해 막냉각 성능을 분석하였으며 슬럿 및 원통형 홀에 비해 향상된 막냉각효율을 보였다. 덤벨(dumbbell) 홀과 빈(bean) 홀이라는 막냉각홀이 Liu 등(16)에 의해 개발되었으며 홴 형상 홀 대비 최대 약 33%의 향상된 막냉각효율을 보이고 동일한 경계조건에서 크레센트, 루버, 원통형 홀 보다 뛰어만 막냉각 성능을 나타낸다고 보고하였다. Lee와 Kim(17)은 나뭇잎 형상의 막냉각 홀을 개발하였으며 분사율 M=0.5일 경우 홴 형상 홀과 비슷한 막냉각 성능을 보였지만 분사율이 증가할수록 새로운 형상이 월등히 향상된 막냉각 성능을 나타내었다. Kusterer 등(18)은 이중분사 막냉각 홀(double-jet film cooling hole)을 기반으로 두 개의 홀을 결합시켜 만든 네코미미(nekomimi) 홀을 개발하였다. 고양이의 귀 같은 한쌍의 돌출된 형상이 반 콩팥 와류(anti-kidney vortex)를 발생시켜 냉각 유체를 더욱더 냉각면에 밀착시키는 효과를 보인다고 보고하였으며 M=1.5에서 원통형, 이중분사, 트렌치 홀에 비하여 높은 막냉각효율을 보이는 것을 확인하였다.
위에서 살펴본 바와 같이 앞서 개발되었던 막냉각 홀 형상의 경우 막냉각홀의 출구부 형상에 대한 연구만이 활발하게 진행되어 왔을 뿐 내부 냉각유로에 접한 막냉각 홀의 입구부 형상변화가 막냉각 성능 및 가스터빈 블레이드 구조에 미치는 영향에 대한 연구는 거의 진행되지 않았다. Hay 등(19)이 라운드된 입구(rounded entry)를 가지는 원형 막냉각 홀에 대하여 연구를 수행하였지만, 이는 단순히 원형홀의 입구 모서리에 라운드를 적용하였을 뿐 앞서 언급하였던 홴 형상홀 등과 같이 막냉각홀의 전체적인 형상을 변화시키지 않았다. 막냉각의 경우, 막냉각 홀 출구에서의 유동구조에 따라 막냉각 성능이 결정된다고 볼 수 있는데 입구부의 형상 변화로 인한 막냉각홀 내부 유동구조의 변화가 홀 출구에서의 유동구조에 상당한 영향을 미칠 것으로 판단된다. 이에 따라 본 연구에서는 확장된 입구부를 가지는 수렴형 막냉각 홀을 제시하고 수렴형 막냉각홀 입구부의 형상 변화가 유동구조 및 냉각 성능에 미치는 영향을 삼차원 Reynolds-averaged Navier-Stokes (RANS) 방정식을 사용한 수치해석을 통해 분석하였다.
2. 수치 해석 방법
본 연구에서는 수렴형 막냉각홀의 입구 형상이 막냉각 성능에 미치는 영향을 살펴보기 위해 삼차원 RANS 방정식과 shear stress transport (SST) 난류모델을 사용하여 수치해석을 수행하였으며, 이를 위해 상용 전산유체역학 코드인 ANSYS 15.0(20)을 사용하였다. SST 난류모델은 k-ε 난류모델과 k-ω 난류모델의 장점을 취해 혼합한 모델로, 벽에서 가까운 영역에서는 k-ω 난류모델을 적용하고 그 외 벽에서 떨어진 영역에서는 k-ε 난류모델이 적용된다. Bardina 등(21) 은 SST 난류모델이 다른 난류모델에 비해 역압력구배로 인한 유동박리를 효과적으로 예측하고 난류열전달 해석에도 뛰어난 정확성을 나타낸다고 보고하였다. 이와 더불어, 많은 막냉각 관련 연구(22)에서 SST 모델이 사용되었으며 수치해석결과는 실험결과와 비교해 좋은 일치성을 보였다.
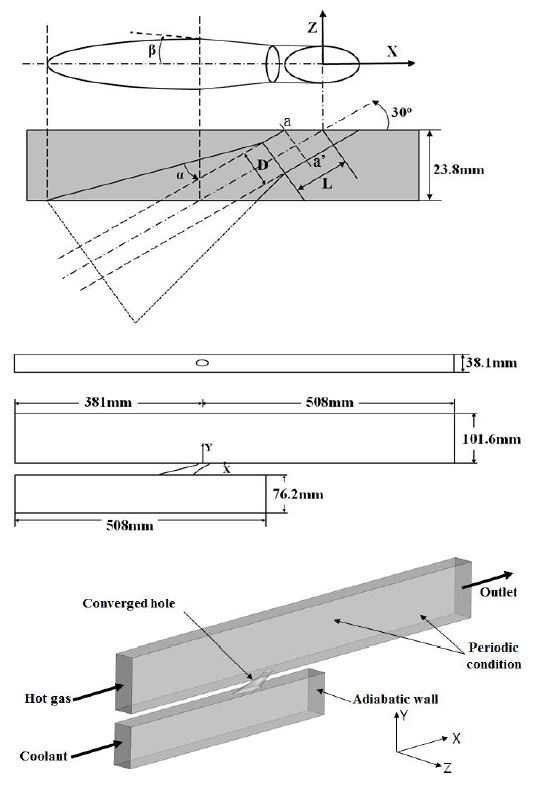
해석을 위해 사용된 계산영역을 Fig. 1에 나타내었다. 계산영역은 주유로, 냉각유로, 그리고 막냉각홀로 구성되어 있다. 본 연구에서 제시한 수렴형 막냉각 홀은 원통형 출구부와 출구부로 갈수록 좁아지는 원추형의 입구부로 구성되어 있으며 냉각홀 중심축에 수직한 입구부 단면은 타원형이다. 홀의 직경(D)은 12.7 mm 이고 z-방향 유로의 폭은 3D이다. 본 연구에서는 Lu 등(12)이 수행한 원통형 막냉각홀에 대한 실험과 동일한 경계조건을 사용하여 수치해석을 수행하였다. 작동유체는 공기이고, 주유로의 입구에는 13.8 m/s의 균일유속조건을 주었으며 고온가스의 온도는 321K이다. 우측 끝이 막혀 있는 냉각 유로의 입구에는 분사율 M=0.5에 해당하는 균일유속조건을 주었으며 냉각유체의 온도는 296K이다. 주유로의 출구에는 대기압의 정압조건을 부여하였으며 벽면에는 단열조건과 점착(no-slip) 조건을 적용하고 계산영역의 양 측면에는 주기(periodic) 조건을 부여하였다.
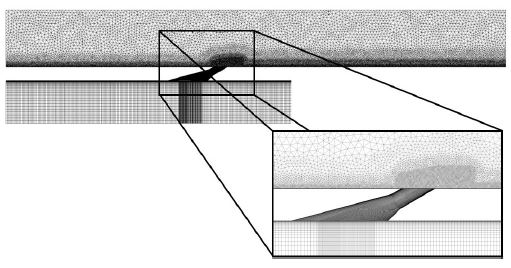
수치해석에 사용된 격자계를 Fig. 2에 나타내었다. 격자계는 비정렬 사면체 격자와 정렬 육면체 격자의 혼합 격자로 구성하였으며, 사면체 격자를 사용한 주유로 벽 근처 영역에서는 속도구배와 온도구배 해석의 정확성을 향상시키기 위해 프리즘 격자를 사용하였다. 벽 함수(wall function)를 사용하지 않고 층류저층(laminar sublayer) 영역을 포함한 벽근처 영역의 난류를 직접 해석하기 위해 벽면에서의 첫 번째 격자점의 y+값이 1.0 이하가 되도록 하였으며 주유동과 분사된 냉각유동이 충돌하여 복잡한 유동이 발생하는 홀 출구영역과 수렴형 막냉각홀 내부에는 격자를 상대적으로 조밀하게 구성하였다.
계산에 사용된 컴퓨터는 Intel i7 3.41GHz PC이며 한 형상을 계산하는데 평균적으로 1500번의 반복계산을 수행하여 약 48시간의 계산시간이 소요되었다. 수렴여부를 판별하기 위하여 RMS 잉여값(root-mean-squared residual)이 1.0×10-6보다 작을 때 수렴하였다고 판단하였다.
3. 형상 변수 및 성능 함수
수렴형 막냉각 홀의 입구부 형상변화가 막냉각 성능에 미치는 영향을 살펴보기 위해 입구부의 유동방향 확장각(α), 측면방향 확장각(β), 그리고 출구부 원통형 홀의 길이와 홀직경의 비(L/D) 등 세가지 변수(Fig. 1 참고)를 사용한 매개변수 연구를 수행하였다. 유동방향과 측면방향 확장각의 변화에 따라 입구부 타원형 수직 단면의 장축과 단축이 변화한다. Table 1에 각 변수의 기준값과 범위를 나타내었다.
각 형상 변수들의 변화에 따른 막냉각 성능을 평가하기 위해 열전달 면에서의 면적평균 막냉각효율(spatially averaged film-cooling effectiveness)을 성능함수로 사용하였다. 막냉각효율은 막냉각 성능을 평가하기 위해 많은 연구자들이 사용하고 있으며 그 정의는 아래와 같다:
| (1) |
| (2) |
여기서 ηs와 η는 각각 면적 평균 막냉각효율과 국부 막냉각 효율이고, Taw 는 단열벽면온도이며 Th 와 Tc는 각각 주유동과 냉각유체유동의 유로입구면 온도를 나타낸다.
4. 결과 및 분석
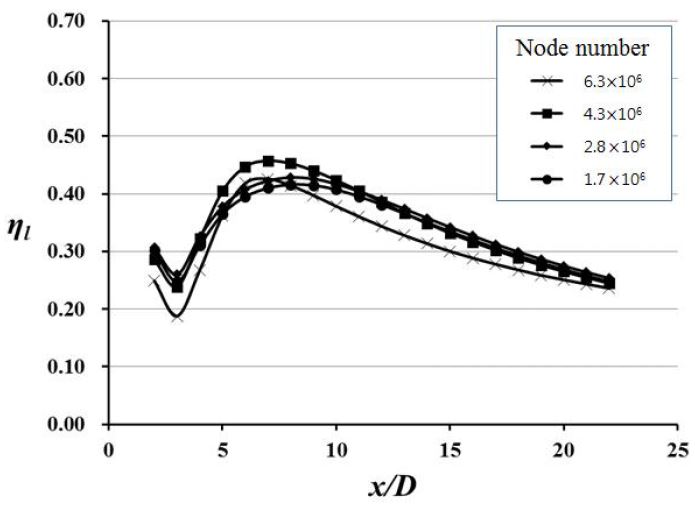
연구 수행에 앞서 계산결과의 격자의존성 테스트를 수행하였다. Fig. 3는 냉각면(y=0)에서의 측면평균 막냉각효율을 나타낸다. 그림에 나타난 바와 같이 약 170만개에서 630만개까지 4가지 격자수를 이용해 격자의존성 테스트를 수행하였으며 이 때 홀 내부의 격자수는 각각 약 29, 37, 51, 그리고 80 만개이다. 그 결과 최적격자수는 약 430만개로 결정되었다. 수렴형 막냉각 홀의 형상변화에 따라 격자수는 다소 달라지지만 홀 출구 영역과 홀 내부의 격자 밀도 및 크기는 균일하게 유지하며 격자계를 구성하였다.
수치해석의 타당성을 입증하기 위해 Lu 등(12)이 수행한 실험과 동일한 경계조건에서 원통형 막냉각홀의 실험결과와 수치해를 비교하였다. Fig. 4는 분사율 M=0.5에서 원통형 막냉각홀의 측면 평균 막냉각효율(ηl) 분포를 나타내고 있다. 그림에서 볼 수 있듯이 본 연구의 계산치와 실험치는 막냉각홀 인근 하류를 제외하고는 정성적인 경향과 크기에 있어 전반적으로 좋은 일치성을 보여주는 것을 확인할 수 있다.
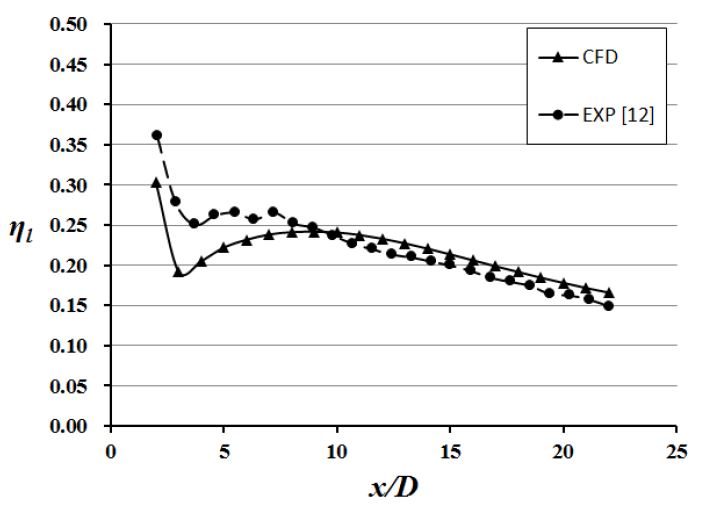
Validation of numerical results for laterally-averaged film-cooling effectiveness with experimental data
Fig. 5는 z/D=0인 x-y 평면에서 원통형 홀과 수렴형 막냉각 홀의 기준형상에 대한 속도 벡터와 등속도선 분포를 나타내고 있다. Fig. 1에 나타낸 a-a’선을 기준으로 a 방향의 영역을 홀의 상부, a’ 방향의 영역을 홀의 하부라 할 때, 원통형 홀의 경우 홀의 상부에 매우 높은 속도가 분포하고 하부에 낮은 속도가 분포하는 제트 효과(jetting effect)(8)가 관찰된다. 제트 효과에 의한 속도분포의 불균일성으로 인해 홀의 출구에서 냉각유체는 국부적으로 높은 운동량을 가지게 된다. 이로 인하여 냉각 유체가 주유동에 침투하려는 성향이 강화되어 결과적으로 냉각유체가 냉각면에 원활하게 분포하지 못하게 된다. 이와 반면에 수렴형 막냉각 홀의 경우, 홀의 상부와 하부의 속도차이가 크지 않아 속도분포가 상대적으로 균일한 것을 확인할 수 있다.
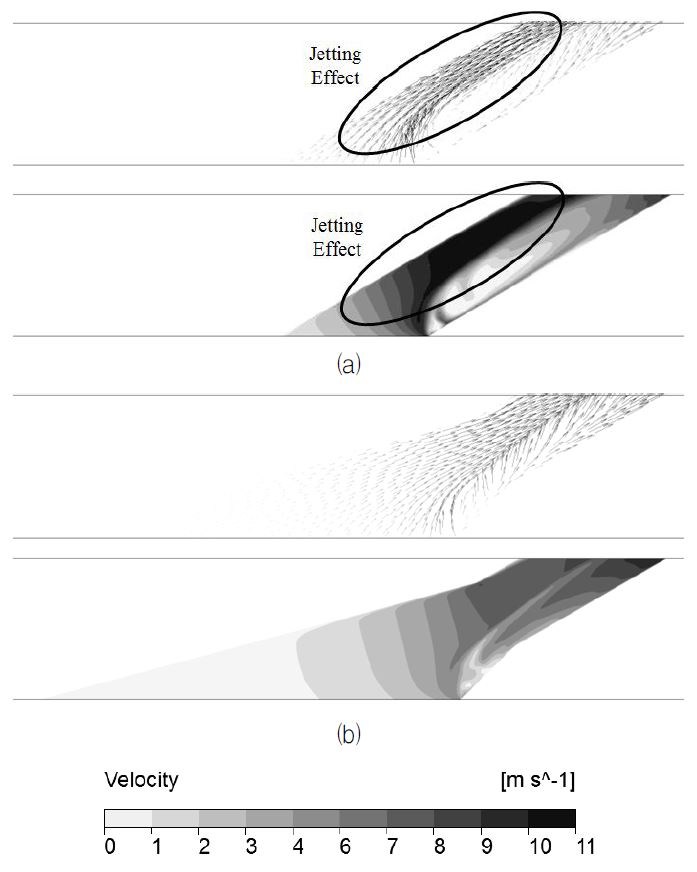
Velocity vectors and contours on the x–y plane at z/D=0 : (a) cylindrical hole and (b) converged hole (reference shape)
Fig. 6는 원통형 홀과 수렴형 막냉각홀의 기준형상에 대한 냉각면에서의 막냉각효율 분포를 나타낸다. 원통형 홀의 경우 앞서 언급한 제트 효과로 인해 냉각유체가 냉각 면에 원활하게 밀착하지 못하여 비교적 낮은 막냉각효율 분포를 나타내고 있다. 이와는 다르게 수렴형 막냉각 홀의 경우 약해진 제트효과로 인하여 원통형 홀에 비해 높은 막냉각효율 분포를 나타내는 것을 확인할 수 있다.
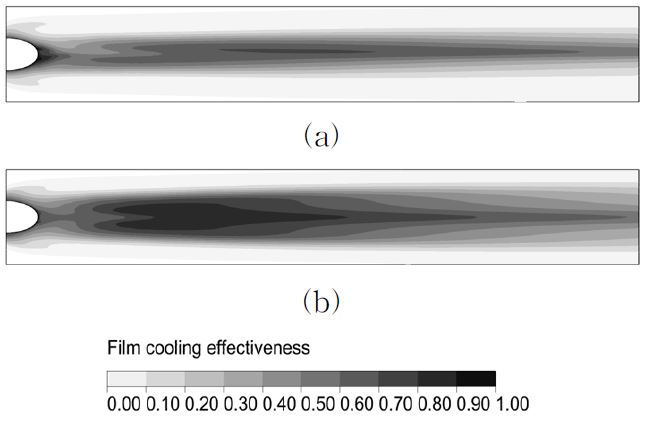
Distributions of local film-cooling effectiveness (η) on the cooling surface : (a) cylindrical hole and (b) converged hole (reference shape)
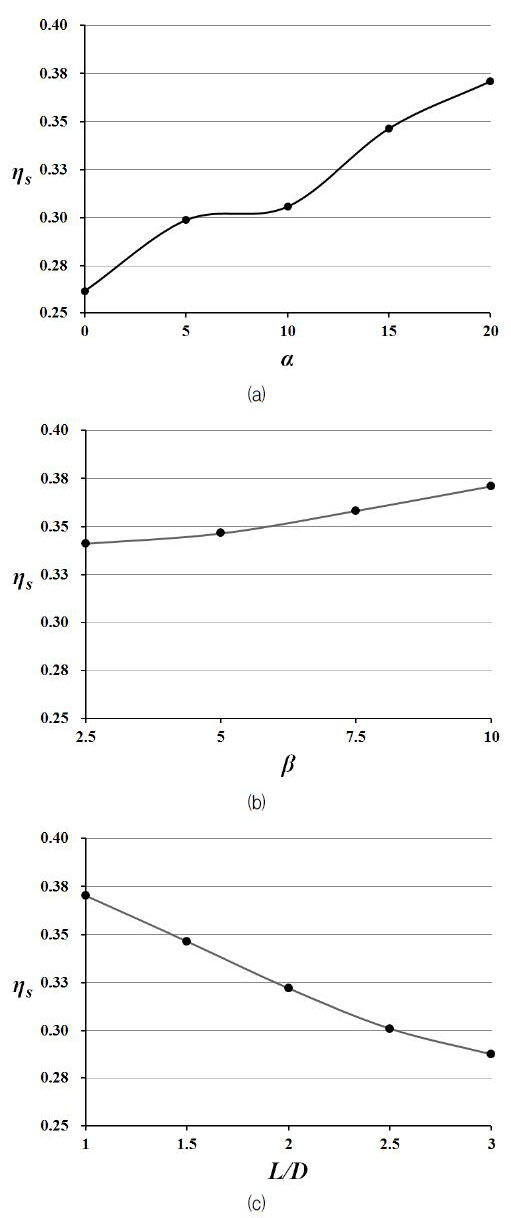
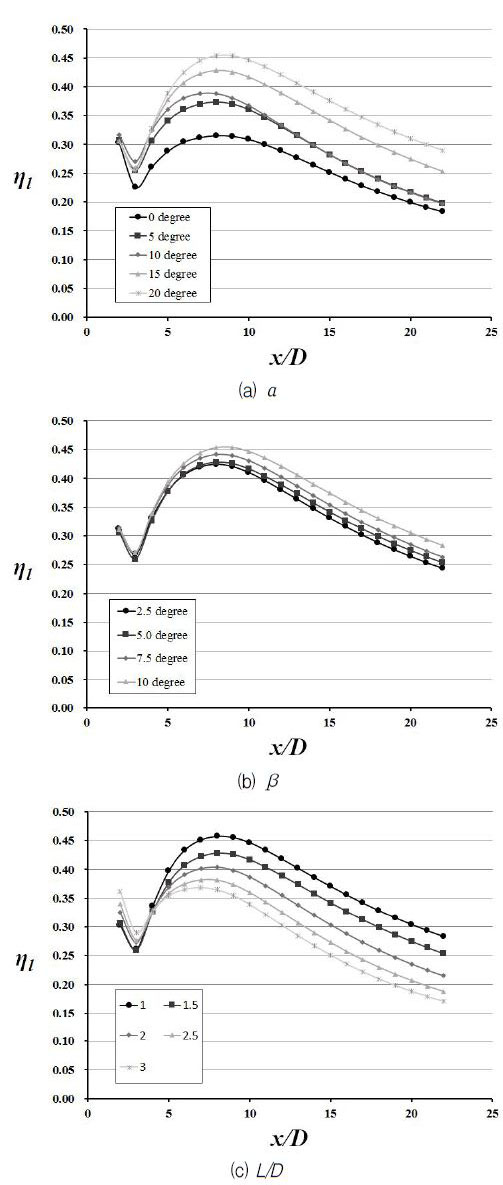
세 가지 형상변수의 변화에 따른 면적평균 막냉각효율(ηs)과 측면 평균 막냉각효율 분포의 변화를 Fig. 7과 8에 각각 나타내었다. 한 변수가 변화할 때 다른 변수들은 Table 1의 기준값으로 고정된다. 수렴형 막냉각홀 입구부의 유동방향과 측면방향 확장각이 증가할수록 면적평균 막냉각효율이 증가하는 경향을 나타내고 있으며, 출구부 원통형 홀의 길이는 증가할수록 면적평균 막냉각효율이 감소하는 것을 확인할 수 있다. 이 중 유동방향 확장각이 민감도 면에서 면적평균 막냉각효율에 가장 큰 영향을 미친다. α=20°의 경우 α=0°인 경우에 비하여 약 32.1%의 면적평균 막냉각효율 증가를 나타냈으며 β=2.5°일 때보다 β=10°일 때 면적평균 막냉각효율이 약 9.8% 증가하였다. L/D=1.0 과 L/D=3.0의 면적평균 막냉각효율의 차이는 약 10%로 나타났다. Fig. 8에서 볼 수 있듯이, 세 가지 형상변수의 변화에 따른 막냉각효율 분포의 변화는 상류에서 비교적 큰 차이를 보이지 않지만 후류로 갈수록 그 차이가 급격하게 증가하는 것을 확인할 수 있다. Fig. 9는 해석 형상 중 최저 막냉각효율을 보인 α=0°의 경우와 최고 막냉각효율을 보인 α=20°의 막냉각 면에서의 막냉각효율 분포를 나타내고 있다. 앞서 Fig. 8을 통해 확인하였듯이 홀 출구 근처에서의 막냉각효율 분포는 비슷한 형태를 나타내고 있으나 후류로 갈수록 α=20°의 경우가 0.8 이상의 높은 막냉각효율을 나타내는 부분이 더 넓게 분포하는 것을 확인할 수 있다.
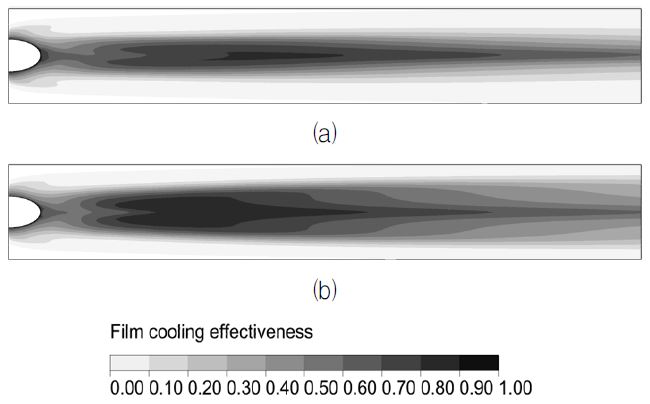
Distributions of local film-cooling effectiveness (η) on the cooling surface for converged hole : (a) α=0° (b) α=20°
Fig. 10-12는 Fig. 1에 나타낸 a-a’ 평면에서의 속도 벡터와 속도크기(속력) 분포를 나타내고 있다. Fig. 10에서 유동방향 확장각이 α=0°에서 20°로 증가하는 경우, 막 냉각 홀내부에서 생성되는 와류의 크기가 작아지는 것을 확인할 수 있다. 그리고 α=0°일 때 고속의 영역이 홀 상부(a 방향)에 위치하며 최고와 최저 속력의 차이가 비교적 큰 반면에, α=20°인 경우 고속의 영역이 홀 하부(a’ 방향)에 위치하며 속력분포가 α=0°인 경우에 비해 비교적 균일한 것을 확인 할 수 있다. Fig. 11은 측면 방향 확장각이 β=2.5°에서 β=10°로 증가하는 경우 와류의 크기가 작아지는 것을 나타내고 있으며 높은 운동량을 나타내는 고속의 영역이 감소하고 속력 분포가 균일해 지는 것을 확인 할 수 있다. Fig. 12에서 볼 수 있듯이, L/D가 증가할수록 홀 내부에서 생성되는 와류의 위치가 홀 하부에서 홀 중심으로 이동하는 것을 확인할 수 있다. 속력 분포 또한, L/D가 가장 낮은 경우(L/D=1.0)인 경우에 고속의 영역이 작아지고 속도분포가 균일해져 국부적으로 높은 운동량을 나타내는 영역이 감소하는 것을 확인할 수 있다.
Fig. 10-12에서 나타나는 홀 내부에서 생성된 와류와 동일한 방향으로 막냉각홀 하류의 냉각면 위에서 생성되는 와류를 콩팥와류라 하는데 이 와류는 냉각유체를 상승시켜 냉각면에 원활히 밀착하지 못하게 하고 냉각유체와 고온가스의 혼합을 일으켜 막냉각 효율을 저하시키는 요인이 된다. Fig. 10-12에서 알 수 있듯이 홀 입구부의 유동방향과 측면방향 확장각이 증가하거나 출구부 원통형 홀의 길이가 감소할수록, 홀 내부에서의 와류의 크기가 감소되어 콩팥와류의 발달을 억제하고, 국부적으로 높은 운동량을 나타내는 영역을 홀 상부가 아닌 냉각면에 밀접한 홀 하부에 위치되도록 하여 냉각유체가 냉각면에 원활히 밀착하는데 영향을 주는 것으로 판단된다.
5. 결 론
본 연구에서는 가스터빈의 터빈 블레이드 냉각을 위해 확장된 입구부를 가지는 수렴형 막냉각 홀을 제시하였다. 막냉각효율에 대한 막냉각홀 형상변수의 영향에 대해 알아보기 위해 삼차원 RANS 방정식을 사용하여 수렴형 막냉각 홀에 대한 매개변수 연구를 수행하였으며, 여기에 세 가지 형상변수, 즉 입구부의 유동방향 확장각, 측면방향 확장각 및 출구부 원통형 홀의 길이와 홀 직경의 비가 사용되었다. 막냉각 홀의 막냉각효율에 대한 계산결과는 실험치와 좋은 일치성을 나타낸 것이 확인되었다. 원통형 막냉각 홀과 수렴형 막냉각 홀을 비교 분석해본 결과, 본 연구에서 제안하는 수렴형 막냉각 홀의 경우 막냉각 성능에 부정적인 영향을 끼치는 제트 효과가 감소하여 막냉각 성능이 향상됨을 알 수 있었다. 세 가지 형상 변수 모두 막냉각효율에 민감한 영향을 주는 것으로 나타났으며, 입구부의 유동방향과 측면방향 확장각이 증가할수록 홀 내부에서 생성되는 와류의 크기가 감소하는 것을 확인하였다. 그리고 출구부 원통형 홀의 길이가 감소할수록 홀 내부에서 생성되는 와류의 위치가 홀 중심에서 열전달 면에 가까운 홀 하부로 이동하는 것을 확인하였다.본 연구에서 얻어진 결과를 토대로 향후 추가 연구를 통해 수렴형 막냉각 홀의 냉각성능을 극대화할 수 있는 최적형상을 도출 할 예정이다.
기호설명
| D : | 홀의 지름 |
| α : | 수렴형 막냉각 홀 입구부의 유동방향 확장각 |
| β : | 수렴형 막냉각 홀 입구부의 측면방향 확장각 |
| L : | 출구부 원통형 홀의 길이 |
| Tc : | 냉각 유로의 입구 온도 |
| Th : | 고온 가스 온도 |
| Taw : | 단열 벽면 온도 |
| M : | 분사율, |
| ρc : | 냉각유체의 밀도 |
| ρh : | 주유동의 밀도 |
| υc : | 홀 출구에서 냉각유체의 속도 |
| υh : | 주유동의 속도 |
| η : | 막냉각효율 |
| ηl : | 측면평균 막냉각효율 |
| ηs : | 면적평균 막냉각효율 |
| x, y, z : | 직교 좌표들 |
References
- Goldstein, R. J., (1971), “Film Cooling”, Adv. Heat Transfer, p321-379.
- Walters, D. K., and Leylek, J. H., (2000), “A Detailed Analysis of Film-Cooling Physics: Part I—Streamwise Injection WithCylindrical Holes”, Journal of Turbomachinery, 112, p102-112.
-
Hale, C. A., Plesniak, M. W., and Ramadhyani, S., (2000), “Film Cooling Effectiveness for Shore Film Cooling Holes Fed by a Narrow Plenum”, Journal of Turbomachinery, 122, p553-557.
[https://doi.org/10.1115/1.1303705]

-
Lutum, E., and Johnson, B. V., (1999), “Influence of the Hole Length-to-Diameter Ratio on Film Cooling With Cylindrical Holes”, Journal of Turbomachinery, 121, p209-216.
[https://doi.org/10.1115/1.2841303]

-
Yuen, C. H. N., and Martinez-Botas, R. F., (2003), “Film Cooling Characteristics of a Single Round Hole at Various Streamwise Angles in a Crossflow: Part 1 Effectiveness”, International Journal of Heat and Mass Transfer, 46, p221-235.
[https://doi.org/10.1016/s0017-9310(02)00274-0]

- Rhee, D. H., Kim, B. G., and Cho, H. H., (1998), “Characteristics of Heat/Mass Transfer and Film Cooling Effectiveness Around a Single Film Cooling Hole with Compound Injection Angles”, Trans. of KSME (B), 22(10), p1433-1444.
-
Lee, K. D., and Kim, K. Y., (2009), “Optimization of a Cylindrical Film Cooling Hole Using Surrogate Modeling”, Numer. Heat Transfer, Part A, 55(4), p362-380.
[https://doi.org/10.1080/10407780902720858]

-
Saumweber, C., Schulz, A., and Wittig, S., (2003), “Free-Stream Turbulence Effects on Film Cooling With Shaped Holes”, Journal of Turbomachinery, 125, p65-73.
[https://doi.org/10.1115/1.1515336]

-
Gritsch, M., Colban, W., Schär, H., and Döbbeling, K., (2005), “Effect of Hole Geometry on the Thermal Performance of Fan-Shaped Film Cooling Holes”, Journal of Turbomachinery, 127, p718-725.
[https://doi.org/10.1115/1.2019315]

-
Lee, K. D., and Kim, K. Y., (2010), “Shape Optimization of a Fan-shaped Hole to Enhance Film-cooling Effectiveness,", International Journal of Heat and Mass Transfer, 53, p2996-3005.
[https://doi.org/10.1016/j.ijheatmasstransfer.2010.03.032]

-
Lu, Y., Dhungel, A., Ekkad, S. V., and Bunker, R. S., (2009), “Effect of Trench Width and Depth on Film Cooling from Cylindrical Holes Embedded in Trenches”, ASME Journal of Turbomachinery, 131, p011003.
[https://doi.org/10.1115/1.2950057]

-
Lu, Y., Dhungel, A., Ekkad, S. V., and Bunker, R. S., (2009), “Film Cooling Measurements for Cratered Cylindrical Inclined Holes”, ASME Journal of Turbomachinery, 131, p011005.
[https://doi.org/10.1115/1.2950055]

-
Sargison, J. E., Guo, S. M., Oldfield, M. L. G., Lock, G. D., and Rawlinson, A. J., (2002), “A Converging Slot-Hole Film-Cooling Geometry - Part 1: Low-Speed Flat-Plate Heat Transfer and Loss”, Journal of Turbomachinery-Transactions of the ASME, 124(3), p453-460.
[https://doi.org/10.1115/1.1459735]

- Zhang, X. Z., and Hassan, I., (2006), “Film Cooling Effectiveness of an Advanced-Louver Cooling Scheme for Gas Turbines”, Journal of Thermophysics and Heat Transfer, 20(4), p754-763.
- Lu, Y., (2007), “Effect of Hole Configurations on Film Cooling from Cylindrical Inclined Holes for the Application to Gas Turbine Blades”, Ph. D Thesis, Louisiana State University.
-
Liu, J. S., Malak, M. F., Tapia, L. A., Crites, D. C., Ramachadran, D., Srinivasan, B., Muthiah, G., and Venkaramanan, J., (2010), “Enhanced Film Cooling Effectiveness with New Shaped Holes”, Proceedings of ASME Turbo Expo 2010, pGT2010-22774.
[https://doi.org/10.1115/gt2010-22774]

-
Lee, K. D., and Kim, K. Y., (2012), “Performance Evaluation of a Novel Film-Cooling Hole”, Journal of Heat Transfer, 134, p101702.
[https://doi.org/10.1115/1.4006752]

-
Kusterer, K., Elyas, A., Bohn, D., Sugimoto, T., Tanaka, R., and Kazari, M., (2011), “The NEKOMIMI Cooling Technology: Cooling Holes With Ears for High-Efficient Film Cooling”, ASME Turbo Expo, Canada, GT2011-45525, p303-313.
[https://doi.org/10.1115/gt2011-45524]

-
Hay, N., Lampard, D., and Khaldi, A., (1994), “The Coefficient of Discharge of 30° Inclined Film Cooling Holes With Rounded Entries or Exits”, ASME 1994 International Gas Turbine and Aeroengine Congress and Exposition, 94-GT-180.
[https://doi.org/10.1115/94-gt-180]

- CFX-11.0 Solver Theory, Ansysinc, (2006).
-
Bardina, J. E., Huang, P. G., and Coakley, T., (1997), “Turbulence Modeling Validation”, Fluid Dynamics Conference 28th, AIAA Paper, p1997-2121.
[https://doi.org/10.2514/6.1997-2121]

- Lee, K. D., and Kim, K. Y., (2011), “Surrogate Based Optimization of a Laidback Fan-shaped Hole for Film-cooling”, International Journal of Heat and Fluid Flow, p226-238.