정방향분사와 역방향분사에 따른 가스터빈 막냉각 유동 및 냉각 특성연구

1. 서 론

가스터빈의 출력을 향상시키기 위해서는 터빈 입구 온도는 지난 반세기 동안 꾸준히 상승되어왔다. 현재 터빈 입구 온도는 초내열합금의 녹는점을 상회하고 있어 연소가스로부터 고온부품을 보호하기 위해 열차폐코팅 및 다양한 냉각기법들이 사용되고 있다. 그 중 막냉각은 가스터빈 고온부품에 적용되고 있는 다양한 냉각기법 중 하나로 고온부품 표면에 온도가 낮은 냉각유체로 막을 형성시켜 높은 온도의 연소가스로부터 고온부품을 직접적으로 보호하는 기술이다.

Bogard⁽¹⁾는 막냉각 효율에 영향을 미치는 변수로 분사비(blowing ratio), 분사각(blowing angle), 홀의 형상 및 배열 등을 제시하였으며 이러한 변수에 따라 막냉각 효율 변화를 모식적으로 나타내었다.

Salcudean 등⁽²⁾은 냉각유체의 밀도가 막냉각 효율에 미치는 영향을 연구하였고 주유동의 밀도보다 높은 냉각유체는 표면으로부터 이격을 줄여 높은 막냉각 효율을 나타냄을 증명하였다. 더불어, 공기보다 높은 밀도를 지닌 CO₂를 냉각유체로 사용함으로써 막냉각 효율을 증대시킴을 Kim 등⁽³⁾은 설명하였다.

주유동을 에어포일 표면으로 유입시키는 한 쌍의 신장와류(kidney voltex)는 막냉각 효율을 크게 감소시키는 주요 원인으로 손꼽히고 있다. Leylek⁽⁴⁾은 원형 홀(cylinderical hole)을 이용한 막냉각에서 신장와류의 생성 원인을 규명하였으며, Walters⁽⁵⁾는 신장와류로 인해 주유동이 에어포일 표면으로 유입되는 현상에 대해 설명하였다.

엇갈린 형태의 복합 분사각을 가지는 이중 분사 홀(double jet hole)은 신장와류를 소멸시켜 효율을 증대시키는 반 신장와류(anti-kidney voltex)를 생성시켜 기존 막냉각 홀에 비해 냉각효율이 향상된 기법임을 Kusterer⁽⁶⁾는 설명하였다. Cho⁽⁷⁾는 이중 분사 홀 면적비와 분사각 변화에 따른 연구를 수행하였다. 연구결과를 바탕으로 이중 분사 홀의 최적면적 비 및 분사각을 제시하였다. 하지만, 이중 분사 홀은 냉각유체 유량증가에 따른 압축공기의 추가적인 손실을 발생시킬 뿐만 아니라 구조적으로 취약하여 실제모델에서는 제한적으로 활용되고 있다.

냉각유체의 분사비가 증가 할 경우, 냉각유체 운동량 증가로 인해 에어포일 표면에서 냉각유체의 이격현상(lift off)이 발생하여 막냉각 효율이 떨어지게 된다. 막냉각 효율을 향상시키는 방안으로 냉각유체의 운동량을 감소시키기 위한 디퓨져(diffuser) 형상의 막냉각 홀 등이 제안 연구되고 있다.^(8-11) 하지만, 디퓨져 형상의 막냉각 홀은 실제 에어포일 표면에 제작하기 까다로울 뿐만 아니라 생산비용이 증가되는 단점을 가지고 있다.

원형 막냉각 홀에서의 낮은 막냉각 효율을 개선하기 위해서 최근에 들어서는 냉각유체 분사 방향을 주유동과 반대되는 방향으로 분사하는 역방향분사(backward injection)에 대한 연구가 이루어져 왔다.^(12-15) Li⁽¹⁶⁾는 역방향분사가 정방향으로 분사(forward injection) 했을 때보다 횡방향 측면에서 막냉각 효율이 향상되는 것을 확인하였다. 하지만, 역방향분사는 정방향분사에 비해 유동형태가 복잡하고 주유동이 막냉각 홀 유로 내부로 유입되는 우려점 등을 가지고 있어 이에 대한 추가적인 연구가 더 필요하다.

국내에서 운영되는 가스터빈 베인 및 블레이드를 포함한 대부분의 고온부품은 수입에 의존하는 상황이다. 특히, 열응력 등에 의한 막냉각 홀 주변에서 파손이 빈번히 발생하여 가스터빈 유지보수 비용이 과도하게 발생하고 있다. 이와 같은 문제점을 해결하기 위해서 제작 및 정비단가가 저렴한 원형 막냉각 홀의 취약점을 보완하고 막냉각 효율을 증대시키는 연구가 필요한 실정이다.

본 연구에서는 원형 막냉각 홀의 단점 개선 및 냉각효율을 상승시키기 위해서 역방향분사에 대한 연구를 수행하였다. 역방향분사 시 국소적 유동특성을 분석하여 막냉각 효율을 극대화 시킬 수 있는 방안을 도출하고자 한다. 이를 위해 분사비 및 막냉각 홀 유로길이를 변경하여 막냉각 효율을 비교하였다. 본 연구를 통해 독자적인 막냉각 홀 설계 기술에 대한 데이터베이스를 확보하여 고온부품 설계 및 제작 기술 확보에 기여하고자 한다.

2. 수치해석방법

2.2 해석모델

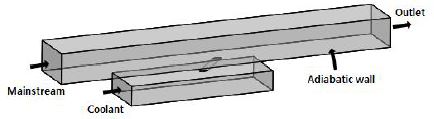
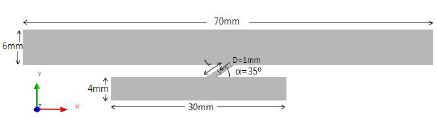
원형 홀에서 냉각유체의 유동특성을 고찰하기 위해 Fig. 1과 같이 형상화 하였으며 유체영역은 주유동 공급유로, 냉각유체 공급유로, 막냉각 홀을 포함하였다. 주유로 공급유로 70 mm, 냉각유체 공급유로 30 mm, 홀의 지름 1 mm, 분사각은 35°로 설정하여 Fig. 2에 도시하였다. 본 연구에서는 냉각유체의 발달을 고찰하기 위해 막냉각 홀 유로길이 L/D=1.75, 3.5로 설정하여 비교 분석하였다.

Fig. 1

Schematic of the modeled geometry

Fig. 2

Size of the schematically modeled geometry

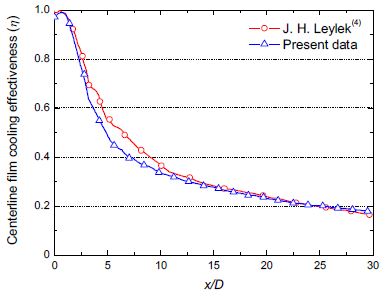
CFD결과 값의 정확도는 격자설정에 밀접하게 연관되어있으며 Leylek⁽⁴⁾의 해석 값과 본 저자의 결과 값은 Fig. 3에서 보이는 바와 같이 분석하여 최적화 된 격자를 생성하였다.

Fig. 3

Centerline film cooling effectiveness comparison present data to Leylek model

Fig. 4

Flow cross section and hole exit velocity contours of the forward injection

막냉각 효율은 에어포일 표면에서의 냉각성능에 관한 식으로, 다음과 같이 정의할 수 있다.

$\[ \eta =\frac{T_{\infty }-T_{aw}}{T_{\infty }-T_c} \]$

(2)

여기에서 T_∞는 주유동 온도, T_aw는 단열된 표면 온도, T_c는 냉각유체 온도이다.

2.3 경계조건

본 연구에서는 높은 레이놀즈 수, 벽면의 점성력이 지배적일 경우에 적합한 k-ϵ모델을 사용하였으며 모든 벽면에서 점착조건, 단열조건을 적용하였다. 해석 시 경계조건은 Leylek⁽⁴⁾의 실험결과와 동일하게 하기 위해 운전기압 1 atm, 주유동 온도 및 속도는 각각 330 K, 11 m/s로 입력하였다. 냉각유체의 온도는 300 K이며, 분사비에 따라 냉각유체 공급유로 입구에서 질량유량이 변경되었으며 상세조건은 Table 1에 명시하였다.

Table 1

Boundary condition

막냉각 기법에 있어서 분사비는 유체의 밀도와 속도에 의해 지배되며 다음과 같은 식으로 나타내어진다.

$\[ M=\frac{{\rho }_c{U}_c}{{\rho }_{\infty }{U}_{\infty }} \]$

(3)

여기에서 ρ_c는 홀 출구에서의 냉각유체 밀도, U_c는 홀 출구에서 냉각유체 속도, ρ_∞는 주유동 밀도, U_∞는 주유동 속도이다. 본 연구에서는 냉각유체의 운동량이 냉각유동 특성에 미치는 영향에 대해 설명하고자 분사비를 1, 2로 설정하였다.

3. 결과 및 고찰

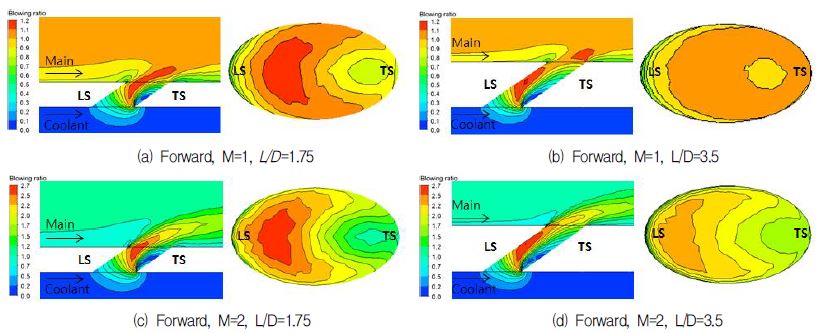
Fig. 4는 정방향분사 시 분사비와 막냉각 홀 유로길이 변화에 따른 유동단면과 홀 출구에서의 속도분포를 나타낸 것이다. 정방향분사 시 냉각유체가 유로에 유입되면서 유체의 관성에 의해 Fig. 4(a)~(d)와 같이 막냉각 홀 유로 내 전연면(leading side) 부근으로 유동이 집중적으로 분포하게 된다. 반면 막냉각 홀 입구 후연면(trailing side)에서는 냉각유체의 정체점이 발생하고, 냉각유체는 막냉각 홀 유로 내 후연면을 따라 흐르면서 경계층이 발달하게 된다.

막냉각 홀 유로 내 냉각유체의 불균일한 속도분포는 홀 출구 속도분포에 큰 영향을 미치게 된다. 유난히, Fig. 4(a), (c)는 짧은 유동발달 길이로 인해 홀 출구에서 불균일한 속도분포가 뚜렷이 나타나는 것을 확인할 수 있다. 특히, 분사비가 증가할 경우 냉각유체의 높은 운동량으로 인해 냉각 홀 출구에서 속도구배 현상이 매우 크게 발생하는 것을 Fig. 4(c)에서 확인할 수 있다. 이와 대조적으로 Fig. 4(b), (d)는 막냉각 홀 유로길이가 증가하여 냉각유체가 충분히 발달 할 수 있어 상대적으로 홀 출구에서 균일한 속도장이 보이게 된다.

정뱡향으로 분사된 냉각유체는 분사비가 낮을 경우 홀 출구에서 주유동에 의해 외부표면에 재부착 및 정체점이 발생하게 되며, 이에따라 경계층이 발달하게 된다.하지만 분사비가 증가 할 경우 냉각유체의 이격현상이 발생하여 외부표면에서 냉각유체의 경계층을 확인할 수 없다.

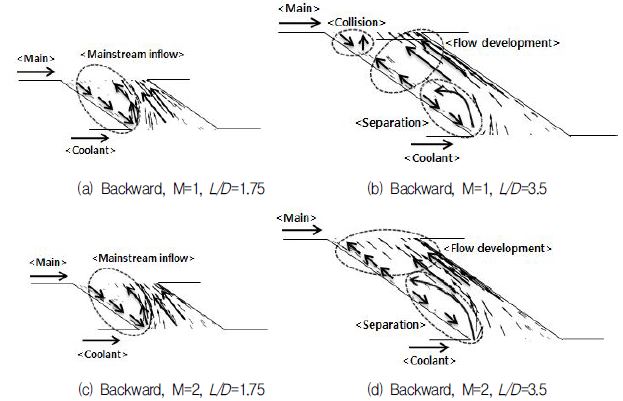
Fig. 5는 역방향분사 시 분사비와 막냉각 홀 유로길이 변화에 따른 유동단면과 홀 출구에서의 속도분포도를 나타낸 것이다. 냉각유체가 막냉각 홀 유로로 유입될 때 유체의 관성에 의해 막냉각 홀 유로 내 후연면 쪽으로 쏠리게 된다. 특히, L/D=1.75일 경우 막냉각 홀 유로 내의 후연면 부근으로 냉각유체의 쏠림 현상을 확인할 수 있다. 그 결과, 막냉각 홀 유로 내 전연면 영역에 냉각유체의 공급이 원활하지 않으며, 막냉각 홀 출구 전연면에서 주유동이 유입되는 역류현상이 발생한다.

Fig. 5

Flow cross section and hole exit velocity contours of the Backward injection

하지만, L/D=3.5인 경우 냉각유체가 막냉각 홀 유로 내 전연면 쪽 벽면에 재부착이 발생되는 것을 확인할 수 있다. 냉각유체의 재부착에 의해 주유동이 막냉각 홀 유로 내부로 역류하는 현상을 차단하게 된다. 특히 냉각유체의 분사비가 증가한 경우 주유동 역류차단 효과는 더욱 뚜렷이 나타난다.

Fig. 6는 막냉각 홀 유로 내 단면에서의 유동 벡터장으로써, 주유동의 역류 및 냉각유체의 재부착 등의 특성을 뚜렷하게 확인이 가능하다.

Fig. 6

Flow cross section velocity vector of the backward injection

L/D=1.75의 경우 주유동이 유입되는 흐름이 벡터장에서 뚜렷이 보인다. 외부 주유동은 냉각 유로 내 전연면 쪽 벽면을 따라 막냉각 홀 입구 영역까지 유입되는 것을 확인할 수 있다. 반면, M=1, L/D=3.5일 때 막냉각 홀 유로 내에서 냉각유체 재부착이 L/D=1.95지점에서 발생한다. 재부착 후 냉각유체가 전연면 쪽 벽면을 따라 흐르게 되지만 적은 운동량으로 인해 소량의 주유동 유입되어 L/D=3.12지점에서 주유동과 냉각유체의 충돌이 발생함을 확인할 수 있다. 하지만 냉각유체의 분사비가 증가할 경우 재부착 지점이 L/D=2.64으로 늦춰질 뿐만 아니라 냉각유체의 운동량이 증가하여 주유동의 역류를 차단하게 된다.

막냉각 홀 유로길이가 증가하면 냉각유체의 발달로 인해 정방향분사, 역방향분사 모두 홀 출구에서 속도구배가 저감되지만, 냉각유체와 막냉각 홀 유로와의 마찰로 인해 냉각유동의 압력강하가 발생하게 된다.

동일한 분사비, 막냉각 홀 유로길이일 경우 역방향분사가정방향분사보다 높은 압력강하 값을 Table 2에서 확인할 수 있다. 냉각유체가 막냉각 홀 입구로 유입되는 과정에서 역방향분사는 정방향분사와 달리 방향 전환이 발생하게 됨에 따라 더욱 복잡한 유동형태를 보이게 된다. 이러한 이유로, 역방향분사는 정방향분사보다 높은 압력강하 값을 가지게 된다.

Table 2

Total pressure difference of hole entrance and exit

정방향분사 시 동일한 분사비에서 막냉각 홀 유로길이가 증가하게 되면 압력강하 값이 증가하지만, 역방향분사는 오히려 압력강하 값이 감소하게 된다. L/D=1.75일 때 역방향분사 시 주유동의 역류로 인해 막냉각 홀 출구에서 냉각유체의 분사면적을 제한시키게 된다. 하지만, L/D=3.5일 경우에는 주유동의 역류가 차단되면서 상대적으로 냉각유체의 분사면적이 증가하게 되어 감소한 압력강하 값을 가지게 된다.

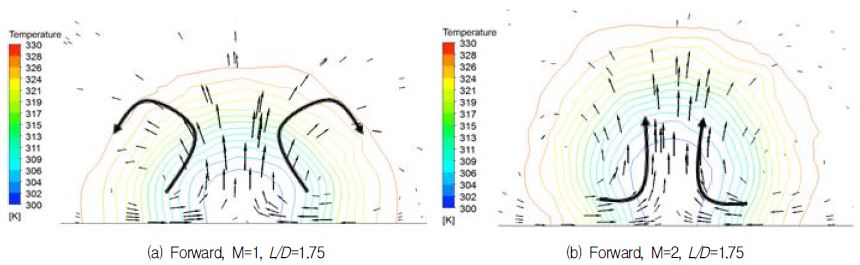
Fig. 7은 정방향분사 시 외부표면에서 유동의 속도벡터 및 온도분포이다. 막냉각 홀 출구에서 발생되는 불균일한 속도분포에 의해 신장와류가 Fig. 7(a), (b)와 같이 외부표면에서 형성된다. 서로 반대방향으로 회전하는 한 쌍의 신장와류는 고온의 주유동을 외부표면으로 유입시켜 막냉각 효율을 저감시키는 주요 원인이다. 이러한 신장와류는 분사비가 증가할 경우 더욱 발달하여 주유동이 외부표면으로 빠르게 유입되는 것을 확인할 수 있다. 더불어, 높은 분사비로 인해 일부 냉각유체가 홀 출구 후연면에서 재부착 되지 않고 주유동으로 관통하는 것을 속도벡터장을 통해 확인이 가능하다.

Fig. 7

Temperature contours and velocity vector at x/D=1 of the forward injection

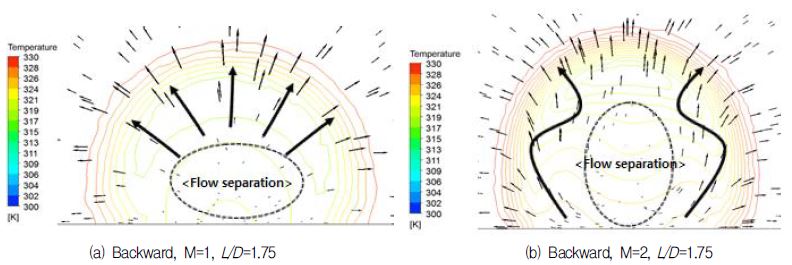
역방향분사 시 정방향분사와 대조적인 유동형태의 속도벡터 및 온도분포를 Fig. 8을 통해 확인할 수 있다. 역방향으로 분사되는 냉각유체는 주유동에 의해 방향이 전환되면서 정방향분사와 다른 속도벡터 형태를 보인다. 막냉각 홀 출구 후단에서 신장와류가 발달하지 않고, 냉각유체의 방향 전환에 따른 유동박리 영역이 x/D=1지점에서 발생하는 것을 Fig. 8(a),(b)에서 확인할 수 있다. 분사비가 1일 때 z축 방향으로 넓게 유동박리 영역이 위치하고 있지만, 분사비가 증가할 경우 유동박리 영역이 y축 방향으로 넓게 분포한다.이러한 이유는, 분사비 증가로 인한 냉각유체의 운동량 증가로 인한 현상이다.

Fig. 8

Temperature contours and velocity vector at x/D=1 of the backward injection

정방향분사 시 냉각유체는 주유동에 의해 외부표면에 낮게 깔리게 되어 외부표면 근처에서 낮은 온도분포를 보인다. 반면 역방향분사일 경우 냉각유체는 주유동과 상호작용으로 인해 넓게 퍼지게 됨에 따라 막냉각 홀 출구 외부표면에 상대적으로 높은 온도의 유동이 위치하게 된다. 그 결과 x/D=1지점에서 외부표면 근처에서의 온도가 주유동 온도에 근접한 것을 확인할 수 있다.

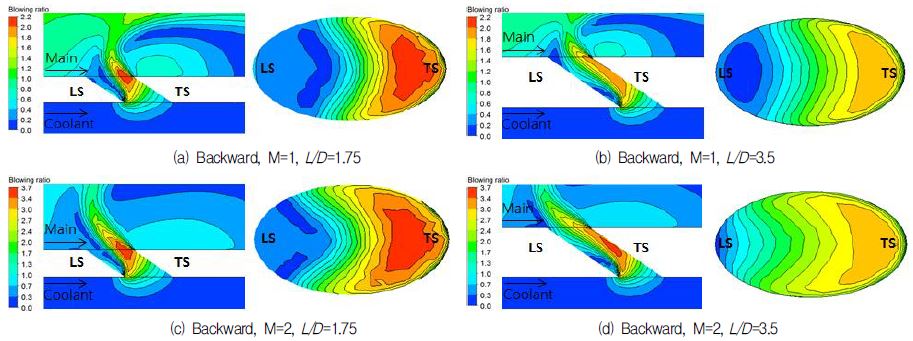
이러한 냉각유체의 유동 특성은 Fig. 9에서 보이고 있는 막냉각 효율 분포를 통해 확인이 가능하다. 외부표면에서의 막냉각 효율은 앞서 설명한 바와 같이 냉각유체의 분사방향에 따라 크게 변하는 것을 확인할 수 있다.

Fig. 9

Film cooling effectiveness contours on the external plane of the forward injection

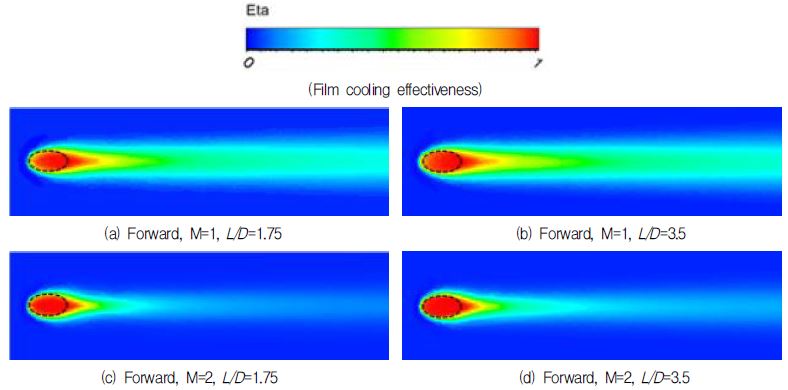
정방향분사 시 막냉각 효율은 홀 부근과 홀 중심을 따라 높게 나타난다. 앞서 유동장에서 설명한 바와 같이 정방향분사 시 냉각유체는 주유동에 의해 분사 후 표면에 낮게 깔려 흐르므로 높은 막냉각 효율을 보이게 된다. 하지만 후류로 갈수록 신장와류가 발달에 따른 외부 주유동의 유입으로 냉각되는 영역이 점점 좁아지면서 막냉각 효율이 낮아지게 된다.

막냉각 홀 유로길이가 증가할 경우 홀 출구에서 냉각유체의 속도구배가 균일해지는 것을 확인하였다. 홀 출구에서 균일한 냉각유체의 속도분포는 외부표면에서 막냉각 효율을 상승시키는 것을 L/D=3.5의 경우에서 확인 할 수 있다. 균일한 속도로 막냉각 홀에서 냉각유체가 분사될 경우 상대적으로 신장와류의 발달이 원활치 않아 막냉각 효율이 증가하게 되는 것이다. 하지만 분사비가 증가할 경우 냉각유체가 주유동 쪽으로 관통하여 흐르게 되어, 외부 표면에 부착되지 않을 뿐만 아니라 홀 출구에서 속도구배가 커지게 됨에 따라 막냉각 효율이 낮아지는 것을 Fig. 9(c),(d)에서 확인할 수 있다.

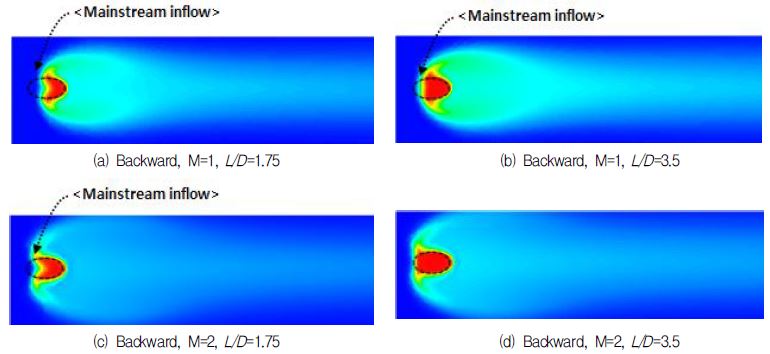
역방향분사 막냉각 홀의 경우가 정방향분사 막냉각 홀의 경우와 달리 홀 부근에서 낮지만 균일한 막냉각 효율을 보이고 있다. 또한 홀 출구의 전연면 부근으로 주유동이 유입함에 따라 막냉각 홀 영역임에도 불구하고 막냉각 효율이 낮은 것을 Fig. 10(a)~(c)에서 확인할 수 있다. 이러한 주유동의 막냉각 홀 내부로의 유입은 막냉각 홀 전연면 영역에 국소적 열부하를 급격히 상승시켜 막냉각 홀 의 파손을 야기시킬 수 있으며, 더 나아가 막냉각 홀의 역할을 원활히 하는데 방해하여 냉각성능을 떨어뜨릴 수 있다. 이러한 주유동의 막냉각 홀 유로 내부로 유입은 막냉각 홀 유로길이가 길거나, 분사비가 높을수록 줄어드는 것을 확인할 수 있다. Fig. 10(d)에서 보이는 바와 같이 주유동의 역류현상을 차단하여 막냉각 홀 부근에서 타원형상의 높은 막냉각 효율을 보이고 있다.

Fig. 10

Film cooling effectiveness contours on the external plane of the backward injection

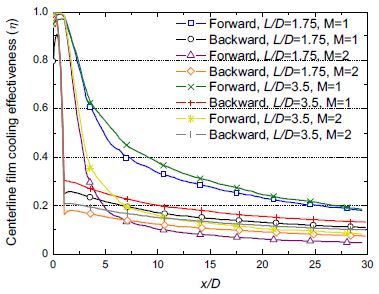
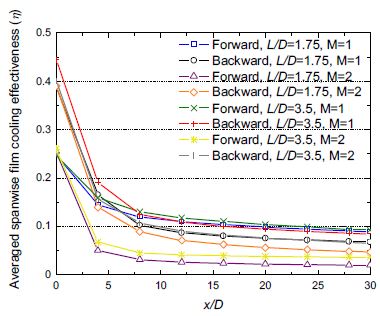
앞서 막냉각 유동 특성에서 확인한 바와 같이 정방향분사 홀의 경우 홀 후단에 냉각유체가 집중적으로 흘러 막냉각 효율을 높이는 것을 확인할 수 있다. 하지만 역방향분사 홀의 경우 냉각유체가 주유동에 의해 유체 흐름 방향이 전환하는 과정에서 횡방향으로 냉각유체가 퍼져나가 넓은 영역을 냉각하는 특성을 보인다. 이러한 냉각유체 분사 방향에 따른 막냉각 효율 특성 변화는 Fig. 11과 12에서 보이는 바와 같이 종방향 막냉각 효율과 평균된 횡방향 막냉각 효율 분포에서 정확히 보여주고 있다.

Fig. 11

Centerline film cooling effectiveness

Fig. 12

Averaged spanwise film cooling effectiveness

분사비가 낮고 정방향분사 홀의 경우 종방향을 따라 높은 막냉각 효율을 보이는 것을 확인할 수 있다. 이와 대조적으로, 역방향분사 홀의 경우 분사 직후 막냉각 효율이 0.2~0.3 정도로 크게 낮아지는 것을 확인할 수 있다. 하지만 분사비가 증가할 경우 x/D>7인 지점에서 정방향분사 시 막냉각 효율 보다 역방향분사 시 막냉각 효율이 높아지는 역전현상이 발생한다. 이는 신장와류에 의해 정방향분사 홀의 막냉각 효율이 급격히 낮아져 발생하게 되는 현상이다.

반면 횡방향 막냉각 효율은 역방향분사 홀의 경우가 정방향분사 홀의 경우보다 높게 나타나는 것을 볼 수 있다. 이는 전반적으로 역방향분사 홀의 경우 넓은 영역에서 표면 냉각을 담당하고 있기 때문이다. 더불어 역방향분사 홀의 경우 국소적인 냉각성능의 향상이 아닌 넓은 영역에서 균일한 냉각효율을 보임으로써 국소적 온도차에 의한 냉각홀 파괴를 예방할 수 있을 것으로 예상된다.

전반적으로 종방향 막냉각 효율과 횡방향 막냉각 효율 모두 막냉각 홀 유로길이가 증가하면 냉각효율이 상승되는 것을 확인할 수 있다. 이는 홀 출구에서의 냉각유체의 속도분포가 균일해져서 발생되는 현상이다. 균일한 속도분포의 냉각유체는 외부의 주유동과 혼합되는 과정에서 새로운 이차와류의 발생을 방지함으로써 냉각유체가 외부표면에 원활하게 재부착이 이루어질 수 있다.

분사비가 증가할 경우 홀의 분사 방향에 관계없이 냉각유체의 이격현상으로 냉각효율이 낮아지는 것을 볼 수 있다. 특히 정방향분사 홀의 경우가 분사비에 따른 막냉각 효율 변화가 크게 발생하여 향후 막냉각 운전조건 설정 시 세심한 조정이 필요할 것으로 보인다.

4. 결 론

본 연구에서는 막냉각 기법에 있어서 주요변수인 분사비와 막냉각 홀 유로길이를 변화시켜가며 정방향분사와 역방향분사의 유동 및 냉각 특성을 고찰하였다. 수치해석을 근거로 하여 다음과 같은 결론에 도달하였다.

• 정방향분사 홀의 경우 막냉각 홀 유로 내 전연면 부근으로 냉각유체가 집중된다. 홀 입구의 후연면에서는 정체점이 발생되며 막냉각 홀 유로 내 후연면을 따라서 새로운 경계층이 발달한다.
• 역방향분사 시 L/D=1.75인 경우 대부분의 냉각유체가 막냉각 홀 유로 내 후연면을 따라 흐르게 된다. 그 결과 홀 출구 전연면 쪽으로 주유동이 막냉각 홀 유로 내부로 역류하여 유입된다. 하지만, L/D=3.5인 경우 냉각유체가 막냉각 유로 내에서 균일하게 발달하여 주유동의 역류를 차단한다.
• 정방향분사 홀의 경우 막냉각 홀 출구에서 불균일한 속도장에 형성되는 신장와류가 외부표면에서 형성된다. 하지만, 역방향분사 홀의 경우 냉각유체의 방향 전환에 의한 유동박리 영역이 홀 뒷단에서 발생한다.
• 정방향분사 홀의 경우 막냉각 효율이 홀 근처 및 종방향을 따라 높게 나타난다. 반면 역방향분사 홀의 경우 횡방향으로 막냉각 효율이 넓게 나타난다.
• 분사비가 증가할 경우 냉각유체 분사방향에 무관하게 막냉각 효율이 낮아진다. 반면 막냉각 홀 유로길이가 증가할 경우 막냉각 효율이 상승하게 된다.
• 역방향분사 홀은 정방향분사 홀에 비해 넓은 영역에서 우수한 냉각성능을 보인다. 전체적으로 균일한 냉각성능을 보여 막냉각 홀의 국소적 파손현상이 적게 나타날 것으로 판단된다. 더불어 분사비에 따른 냉각성능 변화가 정방향분사 홀에 비해 적어 넓은 막냉각 홀 운전범위에서 설치 및 활용이 가능할 것으로 보인다.

Acknowledgments

본 연구는 한국전력공사의 2016년 선정 기초연구개발과제연구비에 의해 지원되었음 (과제번호 : R17XA05-5)

References

• Bogard, D. G., (2006), “Cooling design analysis”, Ch. 4.2.2.1, The Gas Turbine Handbook, U.S DOE-National Energy Technology Laboratory (NETL).
• Salcudean, M., Gartshore, I., Zhang, K., and Barnea, Y., (1994), “Leading Edge Film Cooling of a Turbine Blade Model Through Single and Double Row Injection: Effects of Coolant Density”, ASME, No. 94-GT-002. [https://doi.org/10.1115/94-gt-002]
• Kim, S. G., Lee, J. C., and Kim, Y. J., (2012), “A Numerical Study on the Film-Cooling Characteristics of Gas Turbine Blade using CO₂”, Journal of Fluid Machinery, Vol. 15(No. 2), p41-44. [https://doi.org/10.5293/kfma.2012.15.2.041]
• Leylek, J. H., and Zerkle, R. D., (1993), “Discrete-Jet Film Cooling: A Comparison of Computational Results With Experiments”, ASME, No. 93-GT-207. [https://doi.org/10.1115/93-gt-207]
• Walters, D. K., and Leylek, J. H., (1997), “A Detailed Analysis of Film-Cooling Physics: Part I-Streamwise Injection with Cylindrical Holes”, Journal of Turbomachinery, Vol. 112(No. 1), p102-112.
• Kusterer, K., Bohn, D., Sugimoto, T., and Tanaka, R., (2006), “Double-Jet Ejection of Cooling Air for Improved Film Cooling”, Journal of Turbomachinery, Vol. 129(No. 4), p809-815. [https://doi.org/10.1115/1.2720508]
• Cho, M. Y., Lee, J. C., and Kim, Y. J., (2014), “A Study on the Film-cooling Characteristics of Gas Turbine Blade with Various Area Ratios and Ejection Angles of the Double Jet Holes”, KSFM, Vol. 17(No. 3), p59-64. [https://doi.org/10.5293/kfma.2014.17.3.059]
• Gritsch, M., Colban, W., and Dobbeling, K., (2005), “Effect of Hole Geometry on the Thermal Performance of Fan-Shaped Film Cooling Holes”, ASME, Vol. 127(No. 4), p718-725. [https://doi.org/10.1115/1.2019315]
• Lee, K. D., and Kim, K. Y., (2010), “Shape Optimization of a Laidback Fan-Shaped Film-Cooling Hole to Enhance Cooling Performance”, ASME, No. GT2010-22398, p1447-1458. [https://doi.org/10.1115/gt2010-22398]
• Cho, H. H., Rhee, D. H., and Kim, B. G., (2002), “Enhancement of Film Cooling Performance Using a Shaped Film Cooling Hole with Compound Angle Injection”, JSME, Vol. 44(No. 1), p99-110. [https://doi.org/10.1299/jsmeb.44.99]
• Kim, S. M., Lee, K. D., and Kim, K. Y., (2011), “Numerical Study on Film Cooling Effectiveness for Various Film Cooling Hole Schemes”, KSOFE, Vol. 16(No. 4), p92-99. [https://doi.org/10.6112/kscfe.2011.16.4.092]
• Li, X., (2010), “Numerical Simulation on Fluid Flow and Heat Transfer of Film Cooling with Backward Injection”, ASME, Vol. 5, p257-265.
• Chen, A. F., Li, S. J., and Han, J. C., (2014), “Film Cooling With Forward and Backward Injection for Cylindrical and Fan-Shaped Holes Using PSP Measurement Technique”, ASME, No. GT2014-26232. [https://doi.org/10.1115/gt2014-26232]
• Park, S. J., Jung, E. Y., Kim, S. H., Sohn, H. S., and Cho, H. H., (2015), “Enhancement of Film Cooling Effectiveness Using Backward Injection Holes”, ASME, Vol. 5, No. GT2015-43853. [https://doi.org/10.1115/gt2015-43853]
• Park, S. J., Jung, E. Y., Seo, W. J., Kim, J. S., and Cho, H. H., (2015), “Effect of Blowing Ratio on Film Cooling Effectiveness of Backward Injetion”, KSME, Vol. 6, p8-9.
• Li, X. C., Subbuswamy, G., and Zhoum, J., (2013), “Performance of Gas Turbine Film Cooling with Backward Injection”, Energy and Power Engineering, Vol. 5(No. 4B), p132-137. [https://doi.org/10.4236/epe.2013.54b025]