회전유동의 스티워슨경계층을 이용한 미소버블 발생에 대한 실험적 연구
Abstract
An experimental study on small-bubble generation has been performed by using newly proposed coaxial rotating split disk system, in which it generates Stewartson shear layer parallel to rotating axis. A split disk system for small-bubble generation is proposed to solve the problem of scale-up in conventional spinning disk reactor. Parametric studies on tank pressure, disk angular velocity and gas injection type were conducted and a comprehensive explanation was given to dynamics of bubble stretching and break-up. It is confirmed that the proposed system could be very efficient tool to be a breakthrough of the bottleneck of conventional SDR.
Keywords:
Small-bubble, Rotating Flow, Spinning Disk Reactor, Stewartson Layer키워드:
미소버블, 회전유동, 회전판 반응기, 스티워슨 경계층1. 서 론
1995년 이후 최근 20년 동안 플랜트기술의 주된 이슈가 플랜트시스템 공정설계에서 흔히 PI로 불리어지는 프로세스 강화(process intensification)를 통한 단위공정 혁신연구이다.(1) 단위공정 혁신연구 중에서 가장 중요한 것은 거의 모든 플랜트에서 사용되는 공통장비인 반응로(reactor)와 분리기(separator) 같은 핵심장비에 대한 연구들이다.(2) 현재 진행되고 있는 반응로 연구에서 가장 주목받고 있는 기술이 SDR(Spinning Disk Reactor)로 불리어 지는 회전판반응기이다.
첫 번째 이유는 다른 방식에 비해 탁월한 성능을 가지고 있다는 것이다. 기존의 교반식 반응기의 에너지 소산율이 0.1∼100 W/kg인데 비해 SDR은 2000∼6000 W/kg으로 기존 대비 수십배 이상의 효율을 보여주고 있다. 이것은 SDR이 과거 수백 년 동안 플랜트 공정에서 사용되어오고 있는 대용량 반응로인 교반식 반응로를 대체할 수 있는 가장 중요한 기술임을 의미한다.
두 번째 이유는 영국 Newcastle 대학의 Ramshaw 연구팀(5)에서 의해 시작된 SDR에 대한 연구가 Eindhoven 연구팀(6)에 의해 계승 발전되어, 현재는 산업화 직전단계에 이르러 아직은 소형이지만 상업용 SDR이 판매되고 있는 시점에 이르렀다는 사실이다. 특히 Eindhoven 대학과 공동개발한 SPINID사 제품의 경우는 1일 처리용량이 300 ml, 10 ton/day으로 용량면에서 대규모 산업화 전 단계의 제품이다.
상기에 언급한 것처럼 기존에 개발된 SDR은 많은 장점을 가지고 있음에도 불구하고 아직은 대용량화(scale-up)에 대한 다음과 같은 문제점을 가지고 있다.
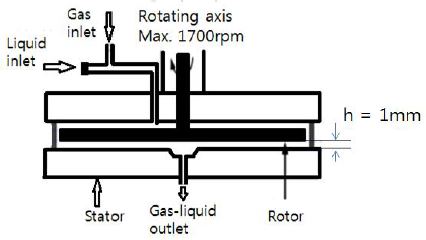
Fig. 1은 Eindhoven 대학에서 개발한 SDR의 전형적인 구조도이다.(6) SDR의 작동원리를 Meeusee 연구(6)의 경우에 대해 설명하면 다음과 같다. 1700 rpm으로 빠르게 회전하는 반경 6.6 cm 크기의 rotor를 아래, 위 한 쌍의 stator와 측벽 하우징이 둘러싸고 있다. 그리고 위로부터 반응액 과 반응기체가 동시에 유입되고 아래로 유출되는 형태로 작업이 이루어진다.
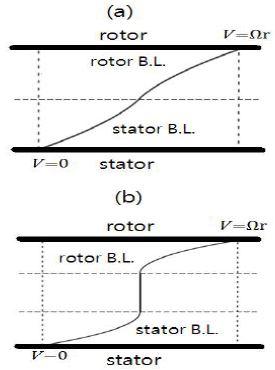
SDR은 이 과정에서 rotor와 stator의 속도차에 의해 액체유동 전단층이 반경방향으로 만들어지고 이때 발생한 전단력이 기체를 미소버블화로 작게 만들어 기액접촉면적을 극대화하는 방식으로 기체-액체 반응효율을 높이는 장치이다. 따라서 SDR [Fig. 1]이 제대로 작동하기 위해서는 rotor-stator 사이의 유동이 다음 조건을 만족할 필요가 있다 : (i) 높은 전단유동, 즉, dv/dz 값이 큰 유동, 여기서 z는 회전축방향 좌표이고 v는 회전속도성분이다; (ii) 전 유동영역에서 고른 전단력이 발생하는 유동, 즉, Couette 유동형태의 유동(Fig. 2(a)).
그러나 전단력을 극대화하기 위해, 즉, 조건 (i)을 충족시키기 위해 회전속도를 높이거나 rotor 반경을 크게 하면 유동은 rotor와 stator 부근에서 에크만 유동 형태의 경계층을 갖는 유동[Fig. 2(b)]으로 바뀌어 내부 영역에서 전단력을 발생시키기가 쉽지 않아 주입 가스를 미소버블로 깨뜨리기 힘든 문제를 야기한다.(7)
유동이 Fig. 2(a)처럼 되기 위해서는 전 유동영역에서 점성력이 지배하는 유동이 일어나야 하고, 이 조건을 Navier-Stokes 방정식으로부터 유추하면 rotator-stator 사이의 거리(h)가 경계층의 두께 ((v/Ω)1/2(h/RD))와 같거나 작아져야 한다는 것을 쉽게 확인할 수 있다. 즉, RD≤(v/Ω)1/2의 조건을 만족해야 한다. 여기서 RD는 rotor 반경, v는 반응액의 동점성계수, Ω는 rotor 각속도 이다.
결과적으로 rotor 반경(RD)과 회전각속도(Ω)를 동시에 높여 보다 효과적인 전단력 증가를 이루기 힘든 모순적 상황에 처해 기존 SDR 기술방식은 장비 대용량화(scale-up)에 대한 근본적인 애로를 안고 있다. 이것은 회전속도증가 혹은 rotor 반경(RD)의 증가가 레이놀즈수를 증가시켜 경계층의 두께를 얇게 하는 물리현상 때문에 발생하는 문제이다.
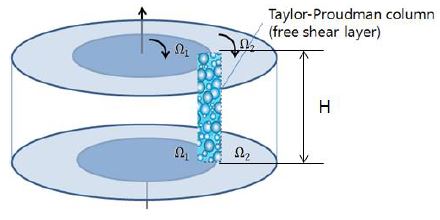
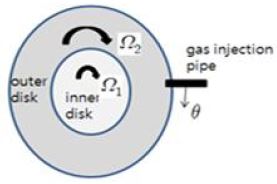
본 연구에서는 앞서 언급한 기존 SDR의 단점을 해결하는 방안으로 Fig. 3과 같은 회전축에 평행한 방향으로 발생하는 스티워슨 전단층(Stewartson shear layer)을 이용하는 방법을 고려하고자 한다. 유체가 회전하면 회전축방향으로 일정한 회전속도를 가지고 운동하려는 유동특성을 가지는데 이것을 Taylor-Proudman column 이라 하고, 회전축에 평행한 방향으로 발생하는 경계층을 스티워슨 전단층이라고 부른다. 스티워슨 전단층은 Fig. 3에서와 같이 회전속도가 서로 다른 아래, 위 한쌍의 내측 디스크(회전속도 Ω1)과 외측 디스크(회전속도 Ω2)를 통해 만들 수 있다는 사실이 단상유동(single phase flow)에 대해서는 이미 잘 알려져 있다.(7) 이 장치를 동축회전하는 분리디스크 시스템 (coaxial split disk system)이라 부른다. 본 연구에서는 이 장치를 이용하면 기존 SDR보다 훨씬 효과적으로 회전축에 평행한 방향으로 원하는 크기의 (기존 대비 30배 큰) 전단층을 만들 수 있고 이를 이용한 미소버블을 발생시키는 기술이 가능하다는 것을 보이고자 한다.
본 연구를 통해 기존 SDR 연구에서 구현한 rotor-stator 간격 h=1mm 보다 30배 큰 디스크 간격 H=30mm의 경우에 대해 실험적으로 미소버블을 효과적으로 발생시키는 것이 가능하다는 것을 보이고 결과적으로 본 연구에서 제시한 방식으로 기존 방식 SDR의 기술적 한계를 극복할 수 있는 가능성이 있다는 것을 확인하고자 한다.
2. 실 험
2.1 실험장치
Fig. 3에서 제시한 스티워슨 전단층을 이용한 미소버블발생 효과를 살험적으로 검증하기 위해 Fig. 4(a)와 같이 실험장치를 구성했다. 실험을 위해 먼저 투명한 아크릴을 이용하여 1 m×1m×0.5 m의 수조를 만들고 내부에 작동액체로 물을 채우고 수조 상부와 하부 면에 각각 2개의 BLDC 모터를 장착하여 Fig. 7과 같이 내측디스크(직경10 cm)와 외측디스크(직경20 cm)를 회전속도 100~3500 rpm 범위에서 독립적으로 제어할 수 있게 만들었다 (Fig. 4(b) & (c) 참조).
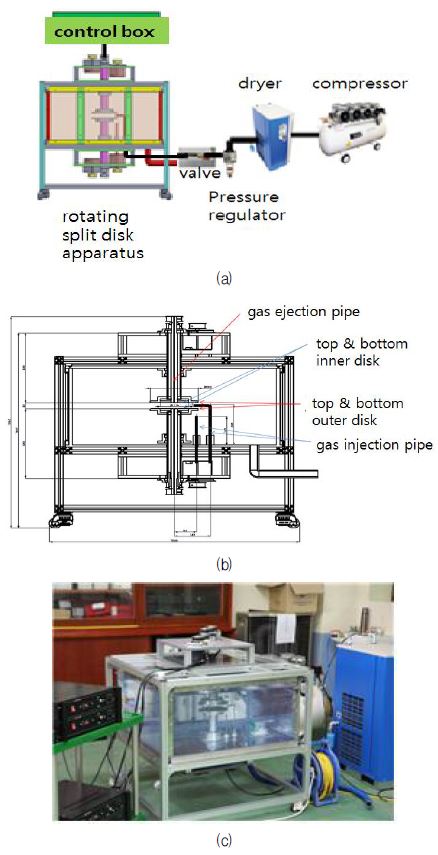
Schematics of (a) experimental system and (b) rotating split disk apparatus, and (c) Photography of the experimental stystem
외부에서 연속적으로 공기를 주입 배출할 수 있게 하기위해 Fig.4(b) 에서처럼 외경 9.95 cm의 상부 내측디스크 회전축을 따라 수직으로 5 mm의 가스유출구멍(gas ejection hole)을 뚫었다. 가스주입은 Fig. 4(a)에서처럼 탱크압을 최대 6기압까지 조절할 수 있는 압축기에서 압축공기가 습기제거용 건조기와 개도각을 5°로 고정시킨 밸브를 통해 수조에 연결된 공기주입파이프를 통해 연속적으로 공급되도록 설계했다. 공기주입파이프는 두 가지 방식, 즉, 아래에서 자연유입방식과 “ㄱ”자형의 파이프를 통해 외부디스크 안쪽 1 cm (원주방향에 직각인 경우), 아래디스크에서 위로 1 cm에서 유입하는 방식으로 실험을 수행했다(Fig. 5 참조). 특히 “ㄱ”자 형 유입은 유입방향을 자유롭게 조절할 수 있게 설계하여 여러 유입각에 대해 실험할 수 있게 했다. 실험은 유동안정성을 고려하여 외측디스크 회전속도(Ω2)가 내측디스크 회전속도(Ω1) 보다 크고, 위에서 아래로 바라볼 때 시계방향으로 회전하는 경우에 한정하여 수행했다. 기타 상세한 실험장치의 스펙은 Table 1, 2에 있다.
상기와 같이 설계된 실험장치(Fig. 4(c))에 물과 공기를 이용하여 실험장치의 설계변수에 대한 full matrix 실험을 수행하여 정성적인 측면에서 다음 2.2절에서 설명한 것과 같은 대표적인 결과를 얻었다.
2.2 실험결과 및 해석
앞서 언급한 실험장치를 이용하여, 탱크압을 1~5기압, 디스크회전수를 100~3600 rpm, 공기주입방식을 아래로부터 자연주입방식 혹은 “ㄱ”형 강제주입방식을 이용하여 공기주입각을 원주방향에 대해 0~90°로 변화시키면서 다양한 실험변수에 대해 파라미터 실험을 수행한 결과 정성적인 측면에서 다음 2.2.1과 2.2.2에서와 같은 결과를 얻었다.
비록 2.2.1과 2.2.2에서 제시한 결과가 상온 1기압 실험실 환경에서 작동유체를 물과 공기, 탱크압을 3기압, 공기주입은 “ㄱ”형 공기주입방식을 이용하여 주입각을 90°그리고 내, 외측 디스크의 회전속도비를 Ω1/Ω2=0.8로 고정한 경우에 대한 것이지만 본 실험장치의 실험변수 범위에서는 이 결과가 정성적인 대표성을 가진다는 것을 실험을 통해 확인했다. 여기서 대표성을 갖는다는 의미는 0<Ω1/Ω2<1.0의 범위에서 생성되는 전단류가 버블발생에 미치는 정성적인 영향에 대한 것으로, 0<Ω1/Ω2<1.0범위에서 실험을 통해 정성적으로 거의 동일하다는 것을 확인했다는 의미이다.
가시화 영상은 좌우 한쌍의 250 W 할로겐조명과 캐논 EOS5D Mark-III 카메라를 이용하여 조건 1/7000초의 셔터스피드, ISO감도 25600에서 촬영한 것이다. 동영상과 정지영상을 모두 이용한 해석을 수행했지만 본 논문에서는 정지화상에 대한 논의에 국한한다.
앞서 설명한 것처럼 실험장치에 작동액체가 물로 채워진 경우의 유동을 고려하면 내측디스크 영역에서는 유체가 내측디스크와 동일한 회전 속도로, 외측디스크 영역에서는 외측디스크와 동일한 회전속도로 운동하려는 경향성을 보인다. 따라서 내측 디스크와 외측디스크가 만나는 내측디스크 외경 부근에서는 수직방향으로 원통형 전단층이 만들어지게 된다. 이것이 스티워슨 경계층(Stewartson layer)이다.
그리고 외측디스크 외경(r=L)에서는 측벽(하우징)을 설치하지 않았기 때문에 이 영역에서도 전단층이 발생한다. 외측 디스크 외부(r>L)에서 상대적으로 느리게 회전하는 자유와류(free vortex) 형태의 운동이 일어나고, 내부(r<L)에서는 강제와류(forced vortex) 형태의 운동이 일어나는 것을 고려하면 이 사실을 유추할 수 있다.
이제 주입된 압축공기가 더 작은 버블로 쪼개지는 거동에서 가장 중요한 영향을 미치는 변수인 디스크회전속도의 영향을 설명하고자 한다. 내, 외측 디스크의 회전속도비를 Ω1/Ω2=0.8로 고정시킨 경우 전체 시스템의 평균회전속도(=(Ω1+Ω2)/2)는 =0.9Ω2이 된다.
이때 공기버블이 받게 되는 부력의 방향은 수직방향 중력가속도(g)와 반경방향 구심가속도()의 비(B=/g)에 의해 결정된다. 여기서 r은 버블운동의 회전반경이다. 그리고 쪼개진 공기버블의 크기는 액체유동이 공기버블에 가하는 전단력의 크기가 클(작을)수록 작아(커)진다. 따라서 디스크의 회전속도()가 낮은(높은) 경우 공기버블의 크기가 커(작아)진다.
공기주입 파이프를 통해 회전하는 액체 속으로 연속적으로 주입된 공기는 두 가지 프로세스를 통해 더 작은 버블로 쪼개지게 된다는 것이 Luo & Svendsen(8)의 연구에 의해 밝혀져 있다. 첫째는 액체유동에 의해 발생한 전단력이 버블의 형태를 전단력 방향으로 늘이는 과정을 만들고, 일정량 이상 늘어난 버블이 더 작은 버블로 쪼개지는 과정을 반복한다. 표면장력이 전단력을 이길 수 있을 정도로 버블의 크기가 충분히 작아지면 버블이 더 작은 버블로 쪼개지는 과정을 멈추고 평형상태에 도달한다. 둘째 과정은 액체유동의 난류요동에 의해 국지적으로 버블이 더 작은 버블로 쪼개지는 과정이다. SDR에서는 시스템 스케일 크기의 버블이 작은 버블로 쪼개져야 하므로 첫째 프로세스가 더 중요하다. 물론 미소버블이 형성된 최종 단계에서는 난류요동이 버블의 붕괴 및 합체 그리고 버블의 확산에 영향을 미친다.
본 실험결과는 Fig. 6(a), (b)에서 볼 수 있듯이, 상대적으로 느리게 회전하는 Ω2=1000rpm인 경우에서는 전단층의 강도가 약하기 때문에, 상대적으로 쪼개진 버블의 크기가 Ω2=2500rpm인 경우보다 크다. 결과적으로 Ω2=1000rpm일 때는 부력효과가 커서 버블운동이 주로 부력에 지배되고 버블운동은 부력방향(중력과 구심력의 합력의 방향)을 따라 회전축 방향(반경 안쪽방향)으로 이동하면서 수직방향으로 상승해서 상부 내측디스크의 회전중심에 있는 가스유출구를 통해 수직으로 배출된다(Fig. 6(a)). 반면 Ω2=2500rpm 경우는 액체유동에 의한 전단력 효과가 매우 커서 주입된 기체가 주입구 근처에서부터 작은 미소버블로 빠르게 쪼개지게 된다는 것을 Fig. 6(b)에서 관찰할 수 있다. 이것은 외측 디스크의 외경에 하우징이 없기 때문에 이 근처에서 전단층이 발생한다는 앞서의 설명을 확인시켜준다. 사실 Fig. 6(b)에서 관찰되는 작은 버블분포로부터 내측디스크의 외경부터 외측디스크의 외경 사이의 전 영역에서 전단층이 발생한다는 것을 알 수 있다. 그리고 이 경우 버블은 크기가 매우 작아 부력효과보다는 인접한 액체운동에 의한 전단력이 버블운동을 지배해서 버블이 수평면 위에서 거의 원운동을 하는 것이 관찰된다.

Patterns of bubble generation when Ω1/Ω2 = 0.8 and (a) Ω2 = 1000 rpm, (b) Ω2 = 2500 rpm in a front view of 180°≤θ≤360°. For θ, see Fig. 7.
구형버블을 생각할 때 부력은 버블반경의 3승에 비례하고 점성력은 버블반경의 2승에 비례한다는 것을 고려하면(부력은 체적력이기 때문에 부피에 비례하고 전단력은 표면력이기 때문에 표면적이 비례한다) Fig. 6(a), (b)의 결과 및 해석은 타당하다.
Fig. 6(a), (b)의 결과에 대해서 한 가지 언급해야 할 사실은 두 경우 버블 궤적이 서로 다르다는 사실이다. 저속(Ω2=1000rpm)의 경우(Fig. 6(a)), 주입된 기체 모두가 반경안쪽으로 이동하여 내측디스크 회전 중심축에 설치된 가스 배출구를 통해 배출된다(Fig. 6(a)). 한편 고속회전(Ω2=2500rpm)인 경우, 미소버블로 쪼개진 작은 버블이 액체운동을 따라 원운동을 하면서 확산에 의해 주변으로 퍼져나가 외측디스크 반경근처, 즉, 외측 디스크의 원주영역에서 난류요동에 의해 조금씩 외부로 이동하여 부력효과에 의해 서서히 위로 떠오르는 현상을 볼 수 있다(Fig. 6(b)).
고속회전(Ω2=2500rpm)하는 경우에는 회전할 때 발생하는 액체의 원심력효과가 회전축부근에 저압영역을 발생시켜 장치에 설치된 회전축의 가스유출구를 오히려 가스유입구(gas intake)로 작동하게 만들어 회전축 부근이 공기층으로 채워지게 만드는 것을 볼 수 있다. 그리고 포물형 자유표면이 상하회전 디스크 각각에 접촉점(contact point)을 만드는 현상을 볼 수 있다.
실험장치의 여러 설계변수 들의 작동범위 -100rpm≤ Ω1,Ω2≤3600rpm, 탱크압<6기압, 2 종류의 공기주입파이프 - 에 대한 파리미터 실험을 통해서 내측디스크와 외측디스크의 회전속도비(Ω1/Ω2) 보다는 외측 디스크의 회전속도 Ω2와 내측디스크의 회전속도 Ω1의 차이, 즉, ∆Ω=Ω2-Ω1이 더 중요한 변수라는 것이 밝혀졌다. 이것은 회전속도비 보다 회전속도차가 전단력 증가에 더 큰 영향을 미치는 인자이고 이것이 버블발생에 절대적인 영향을 미치는 것으로 파악됐다.
무차원수 관점에서 이것을 정리하면 버블이 쪼개지는 다이나믹스에 가장 중요한 역할을 하는 변수가 기준회전수(Ω1) 대비 두 디스크의 회전수 차의 비, 즉 R=(Ω2-Ω1)/Ω1 보다는 두 디스크의 회전속도차로부터 발생하는 전단력을 나타내는 Re=∆ΩH2/v이라는 것이다. 여기서 R은 회전유동에서 로스비수로 불리어지는 무차원수이고 Re는 레이놀즈수이다. H는 상, 하 디스크 간격이고 v는 액체의 동점성계수이다. 다시 말하면 유동의 비선형성의 척도인 로스비수보다는 유동이 발생시키는 전단력 척도인 레이놀즈수가 버블이 쪼개지는 프로세스에 직접적인 영항을 미치는 변수라는 것을 의미한다.
따라서 이 후 설명에서 회전속도비를 Ω1/Ω2=0.8로 고정(로스비수를 0.25로 고정)시키고 Ω2를 1000 rpm에서 2500 rpm 로 증가(레이놀즈수를 증가)시키면서 특성변화를 설명하고자 한다. 비록 이후에 제시된 실험결과가 한정된 경우에 대한 것이지만 실험장비 설계변수에 대한 파라미터 연구를 통해 이 결과는 분리 회전디스크 시스템에서 발생하는 미소버블 발생 프로세스에 대한 일반적 특성이라고 할 수 있다.
Fig. 8, 9에는 Ω1/Ω2=0.8일인 경우 Ω2를 (a) 1000 rpm,(b)1500 rpm, (c) 2000 rpm, (d) 2500 rpm로 변화시키며 실험한 버블붕괴에 대한 순간모습이다. Fig. 8은 전면(0≤θ≤180°)에 대한 사진이고, Fig. 9는 후면(180°≤θ≤360°)에 대한 사진이다. 각 θ에 대한 정의는 Fig.7에 있다. 가스주입구로 연속적으로 들어간 공기가 전단력에 의해 늘어짐(stretching)을 겪다가 작은 버블로 붕괴되는 과정은 시간에 따라 일정하지 않고 임의적이다. 따라서 동일시간에 대한 전면과 후면 사진이 아닌 점을 고려하면 버블의 위치가 두 경우(Fig. 8, 9)에 일치하지는 않는 것은 당연하다.

Front view of snap shots of bubble dynamics at Ω1/Ω2 = 0.8: (a) Ω2 = 1000 rpm, (b) Ω2 = 1500 rpm, (c) Ω2 = 2000 rpm, (d) Ω2 = 2500 rpm. (0≤θ≤180°)

Rear view of snap shots of bubble dynamics at Ω1/Ω2 = 0.8: (a) Ω2 = 1000 rpm, (b) Ω2 = 1500 rpm, (c) Ω2 = 2000 rpm, (d) Ω2 = 2500 rpm. (180≤θ≤360°)
Ω2=1000rpm에 대한 결과가 Fig. 8(a)와 Fig. 9(a)있다. 이 경우는 액체유동이 발생시키는 전단력의 크기가 상대적으로 작고, 중력 대비 구심력의 크기도 작은 경우이다. 따라서 가스주입구에서 액체 속으로 주입된 가스버블이 큰 덩어리로 쪼개져 부력방향을 따라 움직이는 것을 관찰 할 수 있다. 따라서 가스주입구 근처에서 반경방향으로 주입된 공기가 큰 버블덩어리 형태로 빠르게 수직방향으로 이동하여 회전중심축에 도달하기 이전에 위 디스크표면에 도착하는 것을 볼 수 있다. 이 후 이 버블은 상부 디스크 표면을 따라 구심력 효과에 의해 중심축방향으로 이동하여 중심축에 설치된 수직방향의 가스유출구를 통해 배출된다.
Ω2의 값을 1500, 2000, 2500 rpm으로 증가시키면, Fig. 8, 9의 (b), (c), (d)에서 볼 수 있는 것처럼 가스주입구를 통해 주입된 공기가 더 큰 전단력에 의해 찢어지기 때문에 버블의 크기가 점점 작아지는 것을 볼 수 있다. 이 때 액체유동이 버블에 가하는 전단력을 버블에서 발생하는 표면장력이 버틸 수 있을 때까지 버블의 크기가 작아진다. 그리고 Ω2의 값이 커짐에 따라 버블이 받는 (중력에 의한) 수직방향의 부력은 점점 작아지고, 회전속도 증가에 의한 (구심력이 일으키는) 반경방향 부력이 커져 버블운동은 점차적으로 구심력의 지배를 받기 시작한다. 때문에 버블의 궤적이 Fig. 8 & 9에 볼 수 있듯이 (a)->(b)-> (c)->(d)로 감에 따라 점점 수평방향으로 변해 감을 알 수 있다.
Fig. 8 & 9에 나타난 버블의 공간적인 분포를 살펴보면 다음과 같은 흥미로운 사실을 알 수 있다 (쪼개진 버블의 공간적 분포는 θ=180°영역에서 보다 잘 관찰할 수 있다).
상대적으로 저속인 Ω2=1000rpm(Fig. 8(a), Fig. 9(a)) 와 Ω2=1500rpm(Fig. 8(b), Fig. 9(b)인 두 경우에는 발생한 버블의 크기가 크고 버블의 위치는 상, 하 디스크사이 공간 윗부분에 주로 치우쳐 있는 것을 볼 수 있다. 이것은 저속인 경우 발생하는 상대적으로 큰 버블이 수직방향 부력효과에 의해 위로 움직였기 때문에 나타난 현상이다. 그리고 버블 사이즈가 큰 이 경우에 발생하는 버블의 형태를 살펴보면 버블의 형태는 비구형 모양으로 크기가 일정하지 않고, 공간적 분포도 임의적으로 발생함을 알 수 있다. 이 현상은 상대적으로 큰 버블이 액체유동의 전단력에 의한 늘어짐 효과를 더 많이 받고, 나아가 버블운동이 액체유동 자체를 변화시키는 기체-액체 운동의 복잡한 상호작용을 유발시키는 이유 때문으로 설명할 수 있다.
한편 고속인 Ω2=2000rpm((Fig. 8(c), Fig. 9(c))의 경우를 살펴보면 버블의 크기는 더욱 작아지고, 형태는 구형에 가깝게 균일해지면서 버블분포는 아래쪽에 많이 치우쳐 있음을 알 수 있다. 이것은 액체유동의 강한 회전이 발생시킨 전단력 증가가 버블을 더욱 작은 크기로 쪼개어 수직방향 부력효과는 감소하고 반경방향 구심력효과는 증가해서 부력의 방향이 반경방향으로 변한 결과이다. 버블이 아래로 치우쳐 분포하는 현상은 공기주입구의 위치가 상, 하 디스크의 중간보다 약간 아래쪽임을 기억하자(Fig. 5). 이와 함께 이 경우 버블의 크기가 작아지면서 이 체적력인 부력의 크기는 작아지고 상대적으로 표면력인 액체유동에 의해 발생하는 원주방향의 전단력(점성력)이 커져 버블은 동일높이에서 원운동에 가까운 나선운동을 하면서 서서히 회전축방향으로 끌려들어가는 운동을 하는 현상이 나타난다.
마지막으로 회전속도를 Ω2=2500rpm((Fig. 8(d), Fig. 9(d))로 더욱 높이면, 버블의 크기는 mm 척도 이하로 더욱 작아져 미소 버블화하고 버블의 형태는 구형으로 상, 하 디스크 사이영역에서 균일하게 분포하는 것을 볼 수 있다. Ω2=2000rpm(Fig. 8(c), Fig. 9(c))의 경우와 Ω2=2500rpm(Fig. 8(d), Fig. 9(d)) 경우에 버블의 공간적 분포가 차이를 보이는 이유를 물리적으로 설명하면 다음과 같다. 외측디스크 회전속도(Ω2)가 증가하면 전단력이 커지고 이것이 버블을 더욱 작게 만들고, 이것이 다시 부력효과를 감소시켜 버블운동이 액체유동에 의해 완전히 지배받게 된다. 결과적으로 이 때 발생한 미소 버블은 액체와 같이 운동하게 된다. 따라서 회전속도 Ω2=2500rpm(Fig. 8(d), Fig. 9(d))인 경우는 난류강도가 상대적으로 높은 레이놀즈수 영역에서의 유동이기 때문에 난류확산에 의해 효과적으로 버블이 유동공간 전체로 퍼져나가 균일한 분포를 보이게 된다. 상기의 논의는 Fig. 9의 흰색 원 안쪽을 비교해 보면 더욱 분명히 확인할 수 있다.
마지막으로 한 가지 언급해야 할 사실은 본 연구에서 기존 SDR 구조와 비슷한 크기와 회전속도 범위에서 디스크 간격을 30배로 키운 실험이 수행되었고, mm 척도 이하의 균일한 공간적 분포를 갖는 미소버블을 만들 수 있다는 것을 보였다는 것이다. 이 결과는 본 연구에서 제시한 방법이 기존 SDR의 반응부피를 효과적으로 30배 혹은 그 이상 키울 수 있는 가능성을 제공한다.
3. 결 론
본 연구를 통해 아래, 위 한 쌍의 직경 10 cm 크기의 내측 디스크와 직경 20 cm 크기의 외측 디스크로 구성된 동축회전하는 디스크 시스템을 이용하는 미소버블 발생 장치를 제안하고 이것에 대한 파라미터 실험을 미소버블 생성에 대한 체계적인 해석을 수행했다.
기존 SDR이 회전축에 수직한 방향의 Couette 유동 형태의 전단층을 만들어 이용하는데 반해 본 연구에서 제안한 시스템은 회전유동 특성을 이용해 회전축에 평행한 방향으로 보다 효과적으로 긴 구조의 전단층을 만들고 이 때 생기는 전단력을 이용해 버블을 쪼개는 구조이다.
본 연구에서 수행한 실험장치의 크기는 기존 SDR(디스크 사이간격 1 mm) 과 비교할 때 30배 더 큰(디스크 간격 30 mm) 크기를 갖는다. 이 장치를 이용해서 설계변수 -탱크압, 디스크회전수, 공기주입방식-에 대한 파라미터 실험을 수행하고 버블발생 및 운동특성에 대한 체계적인 해석을 했다.
실험을 통해 새롭게 제안한 미소버블 발생 시스템이 SDR의 스케일엎에 매우 효과적인 기술이 될 수 있다는 것을 확인했다. 디스크 간격이 30배라는 것은 기존 SDR 대비 반응부피를 30배 키울 수 있는 기술이라는 의미이기 때문에 이 방식을 이용한 신개념 SDR 개발은 기존 SDR의 치명적인 단점인 스케일엎 문제를 해결하는데 매우 효과적일 것으로 기대된다.
References
- Stankiewc, A. I., and Moulijn, J. A., (2000), “Process Intensification: Transforming Chemical Engineering”, Chemical Engineering Progress, January, p22-34.
-
Visscher, F., van der Schaaf, J., Nijhuis, T. A., and Schouten, J. C., (2013), “Rotating Reactors - A Review”, Chemical Engineering Research & Design, Vol. 91, p1923-1940.
[https://doi.org/10.1016/j.cherd.2013.07.021]

-
Dudukovic, M. P., (2010), “Reaction Engineering: Status and Future Challenges”, Chemical Engineering Science, Vol. 65, p3-11.
[https://doi.org/10.1016/j.ces.2009.09.018]

-
Boodhoo, K., and Harvey, A., (2013), “Process Intensification: An Overview of Principles and Practice”, Process Intensification for Green Chemistry: Engineering Solutions for Sustainable Chemical Processing, First Edition, 2013 John Wiley & Sons, Ltd.
[https://doi.org/10.1002/9781118498521.ch1]

-
Aoune, A., and Ramshaw, C., (1999), “Process Intensification: Heat and Mass Transfer Characteristics of Liquid Films on Rotating Discs”, Int. J. Heat & Mass Transfer, Vol. 42, p2543-2556.
[https://doi.org/10.1016/s0017-9310(98)00336-6]

-
Meeuwse, M., van der Schaaf, J., Kuster, B. F. M., and Schouten, J. C., (2010), “Gas-liquid Mass Transfer in a Rotor-stator spinning disk reactor”, Chemical Engineering Science, Vol. 65, p466-471.
[https://doi.org/10.1016/j.ces.2009.06.006]

-
Greenspan, H. P., (1968), The Theory of Rotating Fluids, Cambridge Univ. Press.
[https://doi.org/10.1088/0031-9112/19/12/015]

-
Luo, H., and Svendsen, H. F., “Theoretical Model for Drop and Bubble Breakup in Turbulent Dispersions”, AIChE J, Vol. 42(No. 5), p1225-1233.
[https://doi.org/10.1002/aic.690420505]