초임계 CO₂ 발전용 구동 터빈 설계

1. 서 론

환경 오염에 대한 심각성이 부각되고 있는 가운데, 신(新) 기후체제(Post-2020)와 같은 환경 보호와 관련된 협약들이 전 세계적으로 제정되고 있다. 우리나라는 2024년까지 발전량의 10%를 신재생에너지를 이용하여 발전하는 신재생에너지 연료혼합의무화 제도를 발표하였다. 이와 관련하여 주위에서 쉽게 얻을 수 있지만 활용이 잘 되지 않는 산업폐열, 태양열, 지열, 해수 에너지 등과 같은 미활용 에너지원을 이용한 발전에 많은 연구가 수행되고 있다. 예를 들어, 유기 냉매를 이용하여 100~300℃정도의 열원으로 발전을 하는 유기 랭킨 사이클(Organic ranine cycle) 시스템과 표층수와 심층수의 해수 온도차를 이용하는 해수 온도차 발전(Ocean thermal energy conversion) 시스템이 그러하다. 이러한 발전 시스템은 미활용 에너지를 활용하여 발전을 하기 때문에 발전에 있어 기존의 발전 설비 대비 경제적이며, 친환경 적인 특징이 있다. 가용 열원의 온도에 따라 최적으로 적용될 수 있는 시스템이 연구 되고 있다.

초임계 CO₂ 발전은 이산화탄소를 랭킨 싸이클(Rankine cycle)이나 브레이튼 싸이클(Brayton cycle)을 이용하여 임계점 이상의 온도(30.9℃)와 압력(73.6 bar)에서 작동 시켜 발전을 하는 방식이며, 초임계 조건의 CO₂ 특성으로 인해 기존의 신재생에너지발전 시스템보다 다음과 같은 장점이 있다. 첫 번째는 초임계 CO₂ 발전 시스템에서 복열기(리큐퍼레이터)를 이용할 경우 기존 폐열 회수 시스템 보다 높은 발전 효율을 얻을 수 있다. 발전 시스템이 적용할 수 있는 열원의 온도 대역이 다르기는 하지만 ORC 발전시스템(η∼10%)과 비교해 본다면, 2배 이상의 사이클 효율(η∼20%, source temperature 260℃시 약 24% [1])을 얻을 수 있다. 두 번째는 터보기계의 크기가 다른 작동 유체를 사용하는 발전 시스템의 터보기계보다 작다. 이는 초임계 CO₂의 높은 밀도 때문인데, 공간이 협소한 곳에 설치하여 작동 시킬 수 있다는 장점이 있다.

이러한 초임계 CO₂ 발전에 관하여 국내/외에서 많은 관심을 가지고 연구가 활발히 진행되고 있다. 하지만 고온, 고압에서 작동된다는 특징으로 씰, 베어링과 같은 요소 부품에서 발생하는 문제, 축 추력이나 회전체 밸런싱과 관련된 로터 다이나믹 안정 문제 등 해결해야 할 문제가 많다. 이것은 아직 전 세계적으로도 상용화 제품을 출시한 경우가 드문 이유이다.

한국기계연구원에서는 초임계 CO₂ 발전 시스템 개발을 위한 연구가 수행되었다. 본 논문은 초임계 CO₂ 발전 시스템의 구성 요소 중 구동 터빈 개발에 관한 사항이다. 운전 조건을 만족시키기 위한 터빈의 일차원 설계 과정을 설명하여 차기 대용량 초임계 CO₂ 터빈 설계에 참고가 될 수 있도록 하였다. 뿐만 아니라 본 논문에서는일차원 설계 결과를 바탕으로 터빈 로터에서 발생 할 수 있는 손실을 발생 원인에 따라 종류별로 구분하였고, 운전점에 대한 크기와 경향을 분석하였다. 초임계 CO₂용 터빈 로터를 대상으로 발생할 수 있는 손실량을 예측함으로써 터빈 설계에 활용 될 수 있도록 하였다.

2. 초임계 CO₂용 발전 사이클

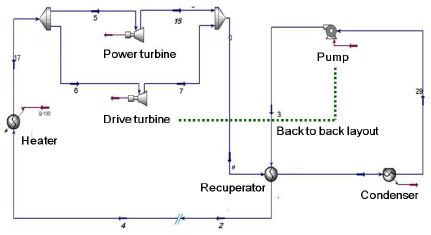
본 연구에서는 문헌에 소개되고 있는 논문, 특허, 미디어 매체 등의 자료를 통해 실제 구성이 가능할 수 있는 초임계 CO₂ 발전 사이클을 구성하였다. Fig. 1은 펌프, 히터, 터빈, 응축기, 복열기(리큐퍼레이터)로 구성된 초임계 CO₂ 발전 사이클이다. 구성 요소 중 터빈은 펌프를 구동시키기 위한 구동터빈(Drive turbine)과 파워터빈(Power turbine)으로 구분하였다. 구동 터빈에서 펌프 임펠러와 구동 터빈 로터는 축 추력을 고려하여 동일 축으로 back to back으로 연결된다. 초임계 CO₂ 발전 시스템의 효율을 높이기 위해 복열기(리큐퍼레이터)를 적용하였다. Fig. 1에서는 실제 구동에 필요한 시동펌프(start pump), 탱크, 각종 밸브 등의 표현은 생략되었다. 구동 터빈의 출력은 2 MW급이며, 회전수는 36,000rpm으로 상세 운전 조건은 Table 1에 도시하였다. 터빈 입구 온도 등 터빈의 운전 조건은 초임계 CO₂ 관련 논문과 학술 발표 자료^(1,11)를 참고하여 선정하였다. 선정된 운전 조건은 초임계 CO₂ 조건에서 작동되는 터빈의 성능 특성을 파악하는데 적절하다고 판단된다.

Fig. 1

Schematic of SCO2 cycle

Table 1

Design Conditions of Drive Turbine

3. 초임계 CO₂용 터빈 설계

3.1 터빈 비속도, 비직경 분석

설계된 사이클 조건을 바탕으로 구동 터빈에 대한 비속도,비직경 분석을 하였다. 비속도, 비직경 분석을 통해 기본적인 터빈의 크기, 회전속도, 효율 등의 크기를 알 수 있고, 터빈 설계 영역을 선정할 수 있다. 본 연구에서는 회전 속도, 효율, 출력을 고려하여 비속도를 선정하였다. 비속도(Ns)와 비직경(Ds)은 각각 다음과 같이 정의된다. 여기서 ω는 회전속도(rad/s), Q₅는 터빈 출구 유량, Δh_os는 터빈 입/출구 등엔트로피(Isentropy) 조건의 엔탈피(Enthalpy) 차이이다.

$\[ Ns=\frac{\omega \sqrt{Q_5}}{∆h_{os}^{0.75}} \]$

(1)

$\[ Ds=\frac{d_2∆h_{os}^{0.25}}{\sqrt{Q_5}} \]$

(2)

Table 2는 터빈 설계를 위해 수행된 비속도, 비직경 분석 결과를 도시한 것이다. 일반적으로 터빈의 효율은 비속도 0.5~0.6에서 가장 높다. 하지만 이 비속도 구간에서 설계된 초임계 CO₂용 구동 터빈의 RPM이 고속이기 때문에 회전체 안정화 측면에서 부담이 크다는 단점이 있다. 그리고 구동 터빈과 펌프가 동일 축에 연결되었기 때문에 펌프의 성능 또한 고려해야 한다. 본 연구에서는 구동 터빈과 펌프의 성능을 모두 고려하여 회전수를 36,000 rpm으로 선정 하였으며, 이때의 터빈 비속도는 0.259이다. 선정된 비속도에서 예상되는 로터 팁 직경은 214 mm이며, 출력은 1.916 MW이다.

Table 2

Sizing for SCO2 Turbine Design

3.2 터빈 자오면 설계

앞에서 소개된 비속도, 비직경 분석 결과를 바탕으로 터빈 자오면 설계를 수행하였다. 본 연구에서는 Concepts NREC社의 RITAL 프로그램을 사용하여 일차원 설계를 하였다. 초임계 CO₂용 터보기계를 설계하는 데에는 정확한 물성치의 적용이 중요하다. 사용된 RITAL 프로그램은 NIST의 REFPROP과 연동되어 초임계 CO₂의 물성치를 활용한다.

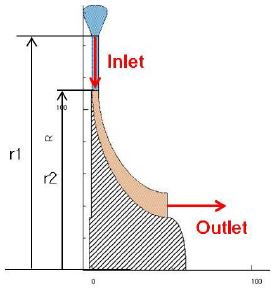
Fig. 2는 설계된 구동 터빈의 자오면 형상을 도시한 것이다. 설계 비속도가 낮은 관계로 날개의 높이가 일반적인 경우보다 낮은 형상적 특징이 있다. Table 3은 구동 터빈의 일차원 설계 결과를 나타낸다. 로터 입구 유동과 날개각 사이에서 박리의 발생을 방지하기 위해 로터 입사각을 설정하였다. 일반적으로 로터 입사각은 -20°에서 많게는 -40°로 설계하며, 본 연구에서는 보수적으로 로터 입사각을 선정하였다. 설계된 드라이브 터빈은 볼류트, 노즐, 로터로 구성된다. 디퓨저에서의 동압 회복이 전체적으로 보았을 때 그 비중이 작을 것이라 예상하여 디퓨저는 생략하였다.

Fig. 2

Meridional view

Table 3

Specification of Drive Turbine

계산된 로터의 반경을 볼 때, 앞 절에서 소개한 비직경 분석 결과와 상당히 유사한 값을 얻을 수 있었다. 설계 결과 초임계 CO₂ 사이클에서 요구하는 조건을 만족시킬 수 있었다. 참고로, RITAL 프로그램에서 적용된 노즐과 로터의 손실모델은 각각 Rodgers loss model과 NASA passage loss model이 적용되었다.

3.3 터빈 1차원 성능 해석

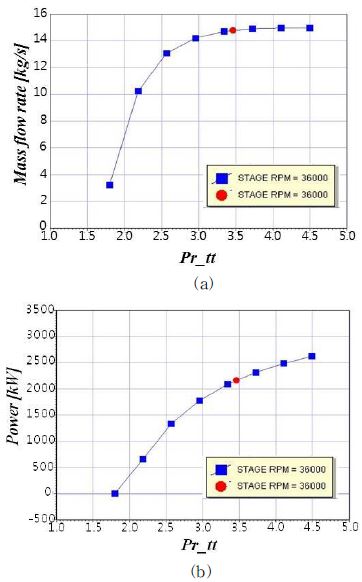
본 연구에서는 자오면 설계 결과를 통해 선정된 형상에 대해 탈 설계점 성능 해석을 수행하였다. Fig. 3, Fig. 4는 설계 회전수인 36,000 rpm에서 설계점과 탈 설계점에서의 성능을 도시한 것이다. 적색 점은 설계점을 나타내며, 청색 점은 동일 회전 속도인 36,000 rpm에서 탈 설계점 성능을 나타낸다. 청색 점을 이은 선은 36,000 rpm에서의 터빈 성능 곡선이다.

Fig. 3

Design and off design performance point estimation : (a) Pr vs Mass flow rate, (b) Pr vs Power

Fig. 4

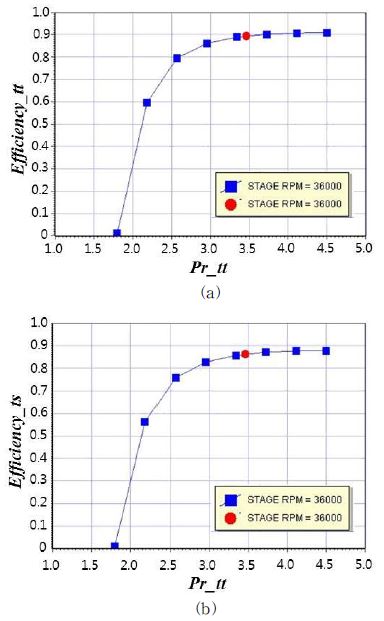
Design and off design performance point estimation : (a) Pr vs total to total efficiency, (b) Pr vs total to static efficiency

Fig. 3, Fig. 4의 X 축(Pr_tt)은 터빈 입구와 출구의 전압력비를 나타낸다. Fig. 3(a)는 팽창비와 유량의 관계를 나타낸 것인데, 정해진 조건에서 최대 출력을 얻기 위해 초킹(Choking)현상이 발생 할 수 있는 영역에 운전점이 형성될 수 있도록 하였다.

Fig. 3(b)는 Pr_tt에 따른 터빈 출력을 도시하였다. 설계점 이후 질량 유량이 초킹으로 인해 늘어나지 않지만, 팽창비 증가 즉, 터빈 입구와 출구의 엔탈피 차이의 증가로 Pr_tt에 따른 터빈 출력이 증가하였다.

Fig. 4(a)는 Pr_tt에 따른 전효율을 나타낸 것이다. 설계점에서 팽창비 4.5까지 전효율 값을 유지하는 것을 확인할 수 있었다. 이것은 팽창비가 설계점에서 4.5까지 늘어남에도 실제 엔탈피 차이와 등엔탈피 차이의 비율이 유지됨을 의미한다.

Fig. 4(b)는 Pr_tt에 따른 정효율의 관계를 도시한 것이다. 앞의 Fig. 4(a)와 비교한다면, 설계점에서 약 3%의 효율 차이가 발생하였는데, 이는 정효율에서는 터빈 내부 손실 뿐만아니라 출구 에너지 손실도 포함되었기 때문이다. 만약 디퓨져를 설치한다면 이러한 손실을 회복시킬 수 있을 것이다.

4. 터빈 손실 분석

4.1 터빈 손실 모델

본 연구에서는 터빈 로터에서 발생할 수 있는 손실을 구분하고 그 크기가 어느 정도 될 것인지를 기존의 선행 연구 자료에서 소개된 모델을 이용하여 분석하였다(Hany Moustapha et al⁽²⁾, Zicheng Wei⁽³⁾). 터빈 설계에 활용된 프로그램에도 주요 위치의 손실값을 얻을 수 있지만, 문헌에 소개된 관계식을 이용하여 손실량을 직접 구함으로써 손실을 보다 세부적으로 분석할 수 있었다.

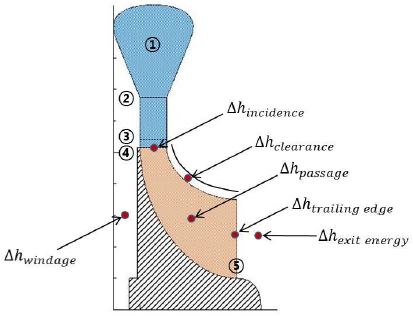
Fig. 5는 로터에서 발생할 수 있는 손실을 위치에 따라 표기한 것이다. 일반적으로 손실을 엔탈피 차이로 나타낼 수 있다. 식 (3)은 터빈의 효율을 엔탈피로 나타낸 식이다. 분자는 터빈 입/출구에서의 엔탈피 차이를 나타내며, 분모에는 분자의 엔탈피 차이와 식 (4)와 같이 손실로 인한 엔탈피 차이의 합으로 정의 되었다. 손실은 Table 4에 도시된 바와 같이 6가지로 구분 하였다. 즉, 노즐 출구에서의 유동이 로터 날개 입구와 이루는 각도에 의한 입구 입사각 손실(incidence losses,식 5), 로터 내부 유로 마찰에 의한 유로 손실(passage losses, 식 6), 로터 팁과 쉬라우드 사이의 간극에서 발생한 손실(tip clearance losses, 식 7), 로터 뒷면에서 디스크와 케이싱 사이의 유체 마찰에 의한 윈디지 손실(windage losses, 식 8), 로터 유로의 목에서 로터 출구까지의 팽창에의한 로터 후단 손실(trailing edge losses, 식 9), 로터 출구에서의 속도 성분이 가지고 있는 출구 에너지 손실(exit energy losses, 식 10)이다.

$\[ {\eta }_{ts}=\frac{\Delta h_0}{\Delta h_0+\sum \Delta h_{loss}} \]$

(3)

$\[ \sum \Delta h_{loss}=\Delta h_{incidence}+\Delta h_{passage}+\Delta h_{trailing edge}+\Delta h_{clearance}+\Delta h_{windage}+\Delta h_{exitenergy} \]$

(4)

$\[ \Delta h_{incidence}=\frac{1}{2}{W}_2^2{\sin }^2\left({\beta }_2-{\beta }_{2,opt}\right) \]$

(5)

$\[ \Delta h_{passage}=m_f\bullet 0.11\bullet \left[\left(\frac{L_h}{D_h}\right)+0.68\cdot \left(1-{\left(\frac{r_t}{r_2}\right)}^2\right)\cdot \frac{\text{cos}\left({\beta }_t\right)}{\left(\frac{b_t}{c}\right)}\right]\cdot \frac{W_2+W_t^2}{2} \]$

(6)

$\[ \Delta h_{clearance}=\frac{U_4^3{N}_R}{8\pi }\left(K_a{ϵ}_a{C}_a+K_r{ϵ}_r{C}_r+K_{ar}\sqrt{{ϵ}_a{ϵ}_r{C}_a{C}_r}\right) \]$

(7)

$\[ \Delta h_{windage}=K_f\frac{\overline{\rho }{U}_2^3{r}_2^2}{2m{W}_3^2} \]$

(8)

$\[ \Delta h_{trailing edge}=\frac{2}{\gamma M_{3re.l}^2}\frac{\mathrm{\Delta }{P}_{0re.l}}{P_3{\left(1+\frac{W_3^2}{2T_3{C}_p}\right)}^{\left(\frac{\gamma }{\gamma -1}\right)}} \]$

(9)

$\[ \Delta h_{exitencrgy}=\frac{C_3^2}{2} \]$

(10)

Fig. 5

Location of defined loss

Table 4

Specification of Drive Turbine

앞 절에서 소개한 1차원 터빈 설계를 통해서 도출된 터빈 형상 치수, 유동 속도, 유동 각도 정보를 이용하여 6개 손실 요소의 크기를 계산하고 그 특성을 분석하였다.

4.2 터빈 손실 분석 결과

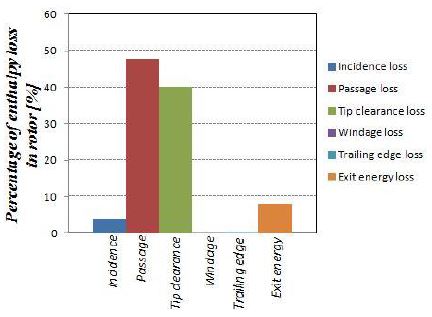
터빈 로터에서 예상되는 손실의 비율을 위치별로 비교한 것이 Fig. 6에 도시되었다. 그림과 같이 passage loss와 tip clearance loss가 터빈 로터에서 발생하는 손실의 대부분을 차지하였다. 그밖에 incidence loss와 exit energy loss가 그 다음이었으며, windage loss와 trailing edge loss는 미약하였다.

Fig. 6

Comparison of loss in drive turbine rotor

가장 큰 손실을 보인 passage loss는 식 (6)과 같이 로터 블레이드 표면에서 발생하는 friction loss와 유로 형상에 의해 형성된 2ndary flow loss가 합쳐진 값으로써 전체 손실량의 약 47%를 차지하였다. 여기서 friction loss는 로터 블레이드의 형상과 날개 개수에 영향을 받는다. Friction loss를 줄이기 위해서는 로터 형상 설계에 대한 최적화가 필요하다는 것을 알 수 있다. Tip clearance loss는 쉬라우드와 로터 팁 사이의 간극에서 발생하는 손실로써 축방향 간극과 원주방향 간극 크기의 영향을 받는다. 일반적으로 원주방향 간극이 축방향 간극보다 큰 경향이 있다고 알려져 있지만 터보기계 운전 및 설계 조건에 따라 차이가 있다.

Exit energy loss는 rotor 출구에서 나가는 속도에너지를 활용하지 못해서 발생하는 손실로써 로터 후단에 디퓨져(diffuser)를 설치한다면 개선할 수 있을 것이다. 본 연구에서는 구조상 디퓨져를 고려하지 않았다.

Incidence loss는 최적화된 유입각과 설계점에서의 유입각과의 차이에서 발생한다. 본 연구에서는 입구에서의 유동 박리(separation)가 발생하는 것을 방지하기 위해 마이너스 입사각(incidence angle)을 충분한 크기로 설정하였다. Incidenceloss를 줄이는 것이 중요한 경우이라면 노즐 각의 조정을 통해 로터 유입각을 조정할 필요가 있을 것이다.

로터 디스크 뒷면과 케이싱 사이에서의 마찰에 의한 windageloss는 생각보다 작게 예측이 되었는데, 이 부분은 추후 3차원 수치해석을 통해 확인할 필요가 있다. 그리고 trailing edge loss는 다른 손실량보다 작게 예측되었는데 그 이유는 로터 throat에서 로터 끝단까지의 압력 변화량이 미약했기 때문인 것으로 판단된다. Hany M. et al.⁽²⁾, Zicheng W.⁽³⁾에서도 일반적인 터보기계에서 본 연구의 결과와 같이 Passage loss와 tip clearance loss가 지배적인 것을 알 수 있다.

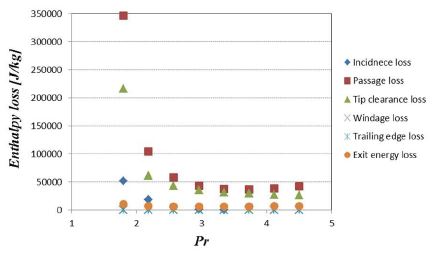
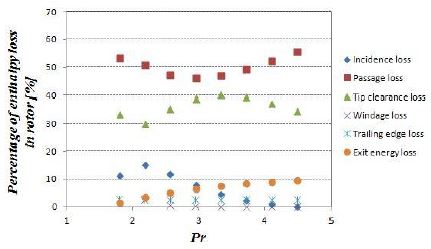
Fig. 7은 설계점 및 탈 설계점에서의 손실량을 구한 것이다. 설계점 및 탈 설계점에서 손실의 대부분을 차지하는 성분은 passage loss와 tip clearance loss였으며, 전체적으로 낮은 팽창비 구간에서의 손실량이 높은 팽창비 구간에서 보다 높게 나타났다. 팽창비 3 이상의 구간에서는 손실량이 유사함을 확인할 수 있었다. 이는 팽창비 3 이상에서 유량이 초킹 유량 근처이기 때문에 속도 성분에 있어서도 팽창비가 증가함에 따라 큰 변화가 없었기 때문인 것으로 판단된다. Fig. 8은 팽창비에 따른 로터에서의 각 요소별 손실량을 비율로 나타낸 것이다. 팽창비가 높아질수록 exit energy loss를 제외한 다른 손실 요소에서는 경향성이 뚜렷하지는 않았지만, Fig. 6, Fig. 7을 통해 예상되는 바와 같이 passage loss와 tip clearance loss가 지배적임을 알 수 있다. 특히 passage loss는 전체 로터 손실의 약 50%를 차지하였다. Incidence loss는 낮은 팽창률에서는 높았지만 설계점을 포함한 높은 팽창률 구간에서는 손실량이 감소하는 것을 알 수 있다.

Fig. 7

Loss deviation in rotor about design and off design point

Fig. 8

Percentage of enthalpy loss in rotor about design and off design point

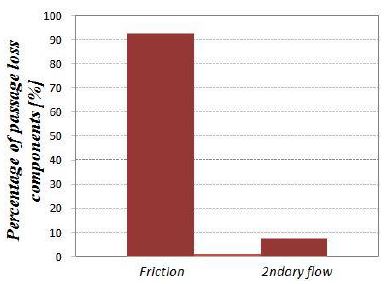
이와 같이 구동 터빈에 대한 1차원 설계를 통해 터빈 로터에서의 손실을 6가지로 구분하여 분석하였다. 이 결과에 의하면, 터빈 효율을 개선시키는데 passage loss와 tip clearance손실의 양을 줄이는 것이 중요하다는 것을 알 수 있었다. Passage loss는 식 (6)과 같이 유로에서의 마찰 손실과 이차 유동 손실로 구분 할 수 있다. Fig. 9에 도시된 바와 같이 마찰 손실이 passage loss의 92%를 차지하였다. 이를 줄이기 위해 유로 형상 설계가 중요함을 확인할 수 있었다.

Fig. 9

Comparison of passage loss components

5. 결 론

본 연구의 결과를 요약하면 다음과 같다.

• 1) 초임계 CO₂ 발전 시스템 개발을 위해 사이클 해석이 수행되었다. 본 연구에서는 구동 터빈과 발전 터빈으로 구성된 랭킨 사이클을 구성하였으며, 본 논문에는 구동 터빈에 대한 1차원 설계 결과를 설명하였다.
• 2) 사이클 해석 결과를 바탕으로 비속도, 비직경 분석을 수행하였다. 구동 터빈은 펌프 임펠러와 back to back으로 연결되었기 때문에 펌프 성능도 고려하여 36,000 rpm이란 운전 회전수와 비속도를 결정하였다.
• 3) 자오면 해석을 수행하였으며, 이 결과를 이용하여 설계점 및 탈 설계점에서의 성능을 예측하였다. 성능 예측 결과, 사이클에서 요구하는 기본 조건을 만족시켰다.
• 4) 1차원 해석 결과를 기존 문헌에 소개된 손실 모델에 적용하여 로터에서 발생될 수 있는 손실량을 구하였다. 손실을 6개로 구분하였으며, 각각의 손실량이 어느 정도인지 정량적으로 구하였다.
• 5) Passage loss와 tip clearance loss가 주요 손실의 원인으로 해석 되었다. 설계점 뿐만 아니라 탈 설계점에서도 손실의 특성을 분석하였다. 경향은 설계점인 경우와 동일하게 앞의 두 손실이 주요 손실 요인으로 해석 되었다. 특히 낮은 팽창비에서는 손실의 양이 크게 나타났다.
• 6) 초임계 CO₂ 터빈에서 가장 큰 손실을 발생시키는passage loss에 대해 분석하였으며, passage loss를 구성하는 마찰 손실과 이차 유로 손실 중 마찰 손실이 지배적임을 알 수 있었다.

Acknowledgments

본 연구는 한국기계연구원의 주요사업(SC1230)을 통해 수행되었으며, 지원에 감사드립니다.

References

• Grant, O. Musgrove, Aaron, M. Rimpel, Jason C. Wilkes, (2012), “Fundamentals of Supercritical CO₂”, Proceedings of ASME Turbo Expo 2012, Copenhagen, Denmark, GT2012-70181.
• Hany Moustapha, Mark F. Zelesky, Nicholas C. Baines, and David Japikse, (2003), “Axial and Radial Turbines”, Concepts NREC.
• Wei, Z., (2014), “Meanline Analysis of Radial Inflow Turbines at Design and Off-design Conditions”, MS Thesis, Department of Mechanical & Aerospace Engineering, Carleton University.
• Daily, J. W., and Nece, R. E., (1960), “Chamber Dimension Effects on Induced Flow and Frictional Resistance of Enclosed Rotating Disks”, Journal of Basic Engineering, Vol. 82(No. 1), p217-230. [https://doi.org/10.1115/1.3662532]
• Glassman, A. J., (1995), “Enhanced Analysis and user Manual for Radial-inflow Turbine Conceptual Design Code RTD”, NASA Contractor Report 195454.
• David, Macmanus, et al, (2014), “Axial Turbine Design and Performance”, Cranfield University Lecture Notes.
• Aungier, R. H., (2005), “Turbine Aerodynamics: Axialflow and Radial-inflow Turbine Design and Analysis”, The American Society of Mechanical Engineers Press, New York.
• Ventura, C. A. M., Jacobs, P. A., Rowlands, A. S., Petrie-Repar, P., and Sauret, E., (2012), “Preliminary Design and Performance Estimation of Radial Inflow Turbines: An Automated Approach”, ASME Journal of Fluids Engineering, Vol. 134(No. 3), p031102. [https://doi.org/10.1115/1.4006174]
• Wasserbauer, C. A., and Glassman, A. J., (1975), “Fortran Program for Predicting the Off-design Performance of Radial Inflow Turbines”, NASA TN-8063.
• Dixon, S. L., (1998), “Fluid Mechanics and Thermodynamics of Turbomachinery”, Fourth Edition, Butterworth Heinemann Press.
• Lee, J. I., Ahn, Y. H., and Cha, J. E., (2014), “Introduction to Supercritical CO₂ Power Conversion System and its Development Status”, The KSFM Journal of Fluid Machienry, Vol. 17(No. 6), p95-103.
• Ghosh, S. K., Sahoo, R. K., and Sarangi, S. K., (2011), “Mathematical Analysis for Off-design Performance of Cryogenic Turboexpander”, Journal of Fluids Engineering, March 2011, Vol. 133. [https://doi.org/10.1115/1.4003661]
• Suhrmann, J. F., Peitsch, D., Gugau, M., Heuer, T., and Tomm, U., (2010), “Validation and Development of Loss Models for Small Size Radial Turbines”, Proceedings of ASME Turbo Expo 2010, Glasgow, UK, GT2010-22666. [https://doi.org/10.1115/gt2010-22666]