USC 보일러 입구 온도 분포 변화에 따른 내부 열교환기 표면 온도 및 스팀 온도 분포 예측

1. 서 론

석탄화력 발전 효율을 상승시키기 위해서 보일러 내 증기 압력 및 온도는 지속적으로 상승되어 왔다. 최근에는 보일러 내 증기의 온도가 700℃이상인 Ultra-supercritical (USC) 보일러의 개발로 최대 45% 이상의 고효율의 석탄화력 발전설비 운영이 가능해졌다.

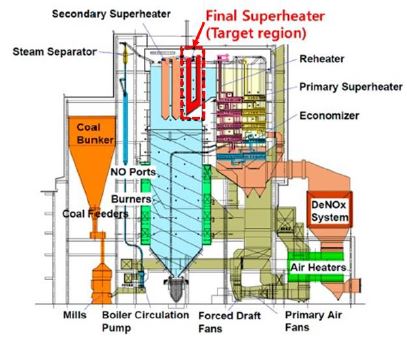
Fig. 1에서 보이는 바와 같이 USC 보일러 내부에는 외부의 연소가스와 증기 간의 열교환을 위한 다수의 봉다발이 설치되어 있다. 열교환기의 안정성 및 효율을 향상시키기 위해서 봉다발 파손 및 열교환에 대한 연구들이 수행되었다.^(1,2) 이와 더불어, USC 보일러의 운전조건인 700℃이상 35기압 이상의 고압고온의 환경에서 안정적인 봉다발 재료에 대한 연구가 수행되었다.^(3~5)봉다발 재료의 경우 연소가스에서 발생되는 재(Soot) 및 높은 온도 등에 견디기 위해서는 내산화성 및 내식성이 뛰어난 재료가 사용되어야 하며 최근에는 SUS 및 니켈 합금을 봉다발의 주재료로 이용되고 있다.

Fig. 1

Schematic of ultra-supercritical boiler(1)

USC 보일러에서 발생하는 열교환량을 예측하기 위해서는 봉다발 외/내부표면에서의 대류 열전달 예측이 매우 중요한 요소이다. 단순히 원형 실린더 하나가 설치되어 있는 것이 아니라 다수의 원형 실린더가 배열된 봉다발 형태의 열교환기이므로, 각 열 실린더에서의 대류열전달 계수를 확보하는 것이 중요하다. Metzger⁽⁶⁾, Armstrong⁽⁷⁾, Goldstein⁽⁸⁾ 및 Chyu⁽⁹⁾ 등에 의해 봉다발 주변에서의 유동장 및 열전달 특성이 규명되었다. 봉다발 유동장 내에서 유동 및 열전달에 영향을 주는 주요 인자로는 튜브 배열이 1순위롤 손꼽힌다. 봉다발이 일렬로 배열된 경우보다 엇갈린 배열일 경우 약 1.5 ~2.0배 높은 열전달 계수가 나타나는 것을 선행 연구를 통해 확인할 수 있다. 이 외에도 다양한 형상 및 배열의 봉다발에서의 열전달 특성연구가 수행되어 왔으며, 이를 통해 USC 보일러 내 열교환기 성능이 지속적으로 상승되어 왔다.^(10~13)

기존의 연구들은 연소가스가 이상적인 상태로 들어왔을 때만 가정하였을 뿐만 아니라 직관 형태의 봉다발 열교환기만을 가정하여 연구가 이루어졌다. 실제 USC 보일러 내 열교환기의 경우 연소가스의 온도 및 유동조건이 불균일할 뿐만 아니라 증기 회수를 위해 U자형 튜브로 봉다발로 이루어져 있다. 이러한, 봉다발의 경우 극단적인 종횡비를 가지고 있어 복합 열전달 해석을 통한 성능예측하기 위해서는 많은 양의 컴퓨터 계산 용량을 요구하여 다양한 설계점에서 해석적인 연구가 원활히 이루어지지 않고 있다.

본 연구에서는 보일러에서 공급되는 연소가스의 온도 및 유속 분포 변화에 따른 봉다발 파이프 외부표면의 최고온도 및 회수 증기 온도를 적은 컴퓨터 계산 용량을 이용하여 예측하고자 한다. 이를 위해 외부 연소장 해석 및 실험식을 활용하였으며, 최종적으로 1-D 열전달 계산을 통해 본 연구에서 구하고자하는 봉다발 파이프 외부표면 및 회수 증기 온도를 계산한 수 있었다. 이를 바탕으로 USC 보일러 내 봉다발 형태의 열교환기의 운전성능을 예측할 뿐만 아니라 정상운전 범위를 벗어난 환경에서의 안정성을 검토하는데 활용하고자 한다.

2. 연구방법

2.1 연구대상 모델

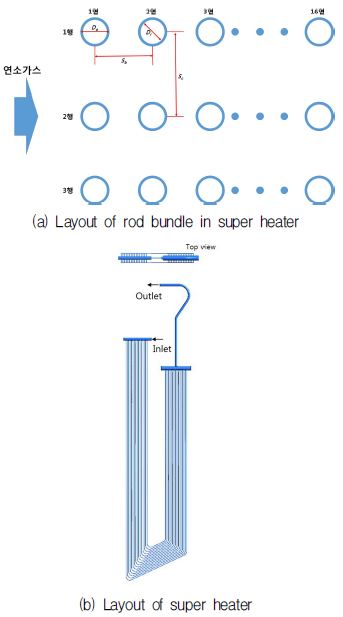
본 연구에서는 1,000 MW급 USC 보일러 내 Final superheater 의 봉다발 형 열교환기를 대상으로 수행되었다. USC 보일러 내 봉다발 열교환기는 Fig. 2에서 보이는 바와 같이 한 열에 16개씩 3행으로 구성되어 총 48개의 관으로 구성 되어있다. 열교환기 내에는 이와 같은 봉다발 튜브 다발이 총 131개를 설치되어 증기를 가열시키는 히터 역할을 하게 된다. 단일 봉다발 내 파이프는 일렬형태로 배치되어있으며, 각 관의 외경(Do)은 42.2 mm, 내경(Di)은 34.7 mm 이다. 외측 관의 길이의 경우 25.55 m이며, 내측 관의 길이는 20.21 m이다. 행 간 거리(Sc)는 230 mm 이며, 열 간 거리(Sb)는 84 mm이다. 더불어, 열교환 파이프의 운전 온도가 500~600도 내외로 상대적으로 낮음에도 불구하고 니켈비중이 높은 SUS316을 파이프의 재료로 사용되었다.

Fig. 2

Schematic of rod bundle for super heater

봉다발 외부에 흐르는 연소가스의 평균 속도는 약 11.2 m/s이며, 평균온도는 913℃이다. 하지만, 연소가스의 온도 및 속도의 불균일성이 매우 심해 본 연구에서는 균일 온도/속도 장일 때와 극한 조건 시나리오를 3개를 구성하여 해석에 활용하였다.

관 내 입구에서 증기의 압력은 27.06 MPa이며, 입구온도는 561℃이다. 각 관 별 평균 입구 질량유량은 0.39 kg/s이다. 이 때 증기의 Pr 수는 0.915이며, 입구 기준 관 내 증기의 Re 수는 약 460,000이다.

2.2 전산해석 방법

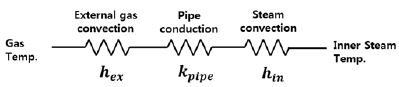
Fig. 3에서 보이는 바와 같이 전체적인 봉다발에서의 열전달 회로는 봉다발 파이프 외/내부 표면의 대류 열저항과 파이프 전도 열저항으로 구성되어 있다. 파이프의 전도 열저항은 파이프 소재가 SUS316이므로 온도에 의한 함수로 표현이 가능하나, 대류 열저항의 경우는 외/내부 모두 열교환기 운전조건에 따라 달라지는 부분이다. 대류 열저항 값을 계산하기 위해서는 각 영역에서의 대류 열전달 계수 분포 정보가 필요하다. 이와 같은 열저항 정보를 획득하기 위해서 해석 대상 봉다발 전체를 복합 열전달 해석을 수행할 경우, 해석 모델의 큰 종횡비로 인해 격자 생성의 어려움 및 많은 양의 컴퓨팅 용량이 요구되어 실질적으로 매우 어려운 작업이다. 그래서 본 연구 에서는 봉다발 파이프 외부 표면에서의 온도분포 및 회수 증기의 온도를 예측하기 위해 외부 유동만 전산해석을 수행하였고, 전도 열전달 관련해서는 1D 열전달 계산을 통해 결과를 도출하였다

Fig. 3

Heat transfer circuit in rod bundle

2.2.1 외부 유동 전산해석

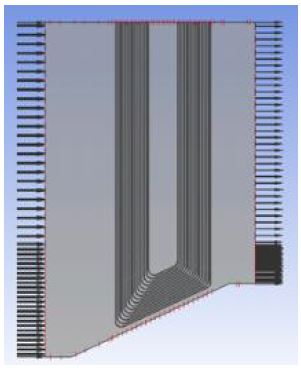
보일러 내 봉다발 열교환기 외부의 연소장 해석을 위하여 Fig. 4과 같이 외부 유동장 모델링 및 격자를 구성하였다. 격자 민감도 테스트 결과를 바탕으로 총 800만개의 격자로 해석 모델을 구성하였다. 표면에서 y+<1 이하로 격자를 구성하기 위해 10층의 inflation 영역을 설정하였다. 해석에는 Ansys CFX v.15을 이용하여 수행하였으며, 봉다발 파이프 표면에서의 유동 및 열전달을 정확하게 예측하기 위해서는 유동의 박리 및 천이 현상 계산이 가능한 난류모델을 선택하여야한다. 본 연구에서는 이를 위해 천이 모델을 포함한 SST 난류모델을 이용하여 해석을 수행하였다. 연소가스의 물성치는 이상기체 방정식 및 참고문헌⁽¹⁴⁾ 통해 온도에 관한 함수로 설정하여 계산하였다.

Fig. 4

Numerical analysis model for external flow

해석 시 경계조건으로는 봉다발 파이프 외부표면은 일정 온도조건으로 설정하였으며, 이때 표면 온도는 증기의 평균온도와 동일한 600도로 설정하였다. 연소 유동장의 입구조건은 균일한 온도/속도 분포 및 실제 운전 조건의 온도/속도 분포로 나누어서 해석을 수행하였다. 균일한 온도/속도 분포는 설계 시 연소장의 온도 및 속도의 최댓값(1,005℃), 최솟값(776℃)및 평균값(913℃)을 사용하였다. 봉다발 파이프 외부 표면에서의 대류 열전달 계수는 아래식을 통해 계산을 하였다.

$\[ h=\frac{\dot{s}}{T_{\infty }-T_s} \]$

Eq. (1)

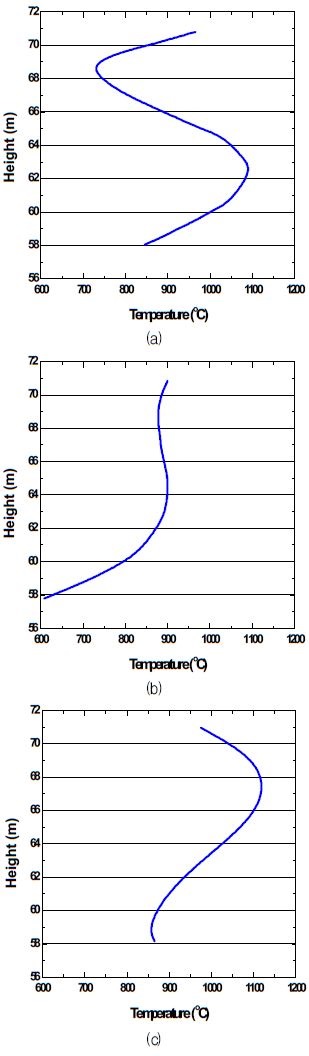
Fig. 5에서 보이는 바와 같이 연소 유동장 입구에서 평균값, 최댓값 및 최소값의 온도 프로파일을 설정하여 실제 운전 조건을 반영한 해석의 입구 경계조건으로 활용하였다.

Fig. 5

Inlet temperature profile; (a) Average temperature profile, (b) Minimum temperature profile, (c) Maximum temperature profile

2.2.2 내부 열전달 계수 및 온도 분포 예측

열교환기 내 봉다발 파이프 외부표면 온도 및 회수 증기 온도를 예측하기 위해서는 내부 증기에 의한 내부 표면의 대류 열전달 계수가 필요하다. 봉다발 파이프 내부는 원형 튜브 형태이며 Re 수가 약 460,000이므로, Dittus-Boelter 식 (Eq. (2))을 통해 내부 표면의 대류 열전달 계수를 계산하면 약 1,645 W/m²K 이다. 본 연구에서는 증기 질량유량을 설계 값 대비 90%, 100%, 110%로 변화시키 연구를 수행하였다.

$\[ Nu=0.023{Re}^{0.8}{Pr}^{0.3} \]$

Eq. (2)

앞서 진행된 연소장 해석을 통해 확보한 외부 표면 대류열전달 계수와 실험식을 통해 계산된 내부 표면 대류열전달 계수를 Eq. 3 ~5에 대입하여 1D 열전달 계산을 수행하였다. 파이프 입구 초기 조건은 초기스팀온도로 정의하였으며, 외부 가스 온도는 외부 유동 전산해석 결과를 활용하였다. 0.1 m 간격으로 스팀출구온도 및 파이프 외부표면 온도를 계산하였으며, 계산 결과는 다음 계산점의 초기조건으로 활용하여 계산하였다. 그 결과 국소 봉다발 파이프 표면의 온도 및 회수 증기의 온도를 획득할 수 있다. Table 1에서 본 논문에서 수행한 해석 경우를 정리하였다.

$\[ \dot{m_s}Cp\left(T_{ce}-T_{ci}\right)={\int }_A^{}{h}_{ex}\left(T_g-T_m\right)dA=h_i{P}_c\left(T_m-T_c\right)d{L}_C \]$

Eq. (3)

$\[ {\eta }_c=\frac{T_{ce}-T_{ci}}{T_m-T_{ci}}1-\text{exp}\left[-h_i{P}_c{L}_c/{\dot{m}}_c{C}_p\right] \]$

Eq. (4)

$\[ \frac{T_g-T_m}{T_m-T_{ci}}={\eta }_c\frac{{\dot{m}}_c{C}_p}{\overline{h_{ex}}A} \]$

Eq. (5)

Table 1

Spec. of Super Heater

3. 연구결과

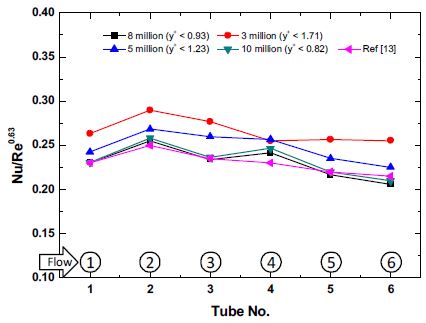
외부 연소가스에 의한 파이프 외부표면에서의 열전달 계산의 정확도를 확인하기 위해서 Fig. 6에서 보이는 바와 같이 평균 연소가스 조건 시 파이프 중앙에서의 평균 Nu/Re 0.63 값을 계산하여 기존 연구^(13,15)결과와 비교하였다. 이때 지수 0.63은 봉다발 주변에서의 주유동의 Re 수가 10³~10⁵일 때의 상관식의 지수 값이다. 격자개수가 증가할수록 최대 y+값이 감소하도록 격자를 구성하였다. 비교 결과 격자 개수가 증가할수록 실험값과 일치하는 경향을 보이며, 격자가 800만개 이상으로 구성할 경우 계산 결과값 간의 차이는 크게 발생하지 않았다. 이를 바탕으로 외부 유동장 해석 시 격자를 800만개로 구성하여 계산을 수행하였다.

Fig. 6

Averaged Nu/Re0.63 on the external surface of pipe at Re=5,000

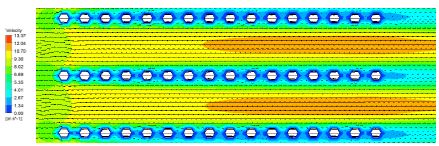
외부 연소가스 유동의 흐름은 Fig. 7에서 확인이 가능하다. 입구에서 들어온 유동은 봉다발을 만나 파이프 주변으로 갈라져 흐르게 된다. 그 결과 파이프와 파이프 사이에는 유동의 공급이 원활하지 않아 정체되는 유동 특성을 보이게 된다. 정체영역의 영향으로 봉다발 주변에서 낮은 속도 분포를 보이게 되며 후류로 갈수록 정체영역의 영향력이 커지게 되는 것을 확인할 수 있다. 이러한 유동특성의 발달은 5~6번째 파이프에서 완전 발달이 이루어지는 것을 확인이 가능하다.

Fig. 7

Flow around tube bundles

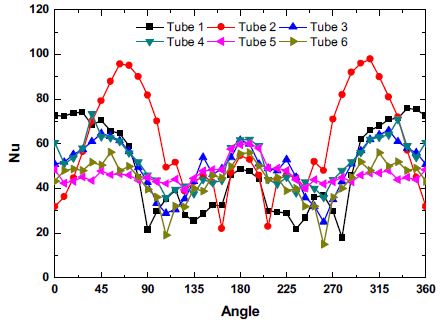
유동 특성에 의한 봉다발 파이프 표면에서의 대류 열전달 계수 특징은 Fig. 8에서 확인이 가능하다. 전체적인 외부 연소가스 유동의 Re 수는 파이프 직경 기준 시 5,000 이하로 낮은 편이다. 그 결과 파이프 외부표면 대류 Nu 수 분포는 Fig. 8에서 보이는 바와 같이 약 50~100 내 외의 값을 보이고 있다. 첫 열 파이프의 정체점에서는 100 이상의 값을 보이나 파이프 후단의 유동 박리 영역에서는 매우 낮은 열전달 계수 값을 보이게 된다.

Fig. 8

Nusselt number distribution on the external surface of pipe at Re=5,000

반면 두 번째 열 파이프 표면에서는 첫번째 파이프에서 박리된 유동이 두 번째 파이프의 약 60o 지점에 충돌하게 됨에 따라 높은 열전달 계수 분포를 보이는 것을 확인할 수 있다.

하지만 이러한 파이프 둘레 방향의 열전달 계수 분포의 변화는 3열 이후부터는 점점 줄어들게 되며, 5열 이후부터는 파이프 둘레 방향으로 거의 일정한 값의 대류 열전달 계수 분포를 보이게 된다.

이와 같이 계산된 파이프 외부표면 대류 열전달 계수와 실험식을 통해 도출된 내부표면 대류 열전달 계수를 이용하여 1번부터 16번 파이프 외부 표면의 둘레 방향 평균 온도를 증기가 흐르는 방향으로 모두 계산하였다.

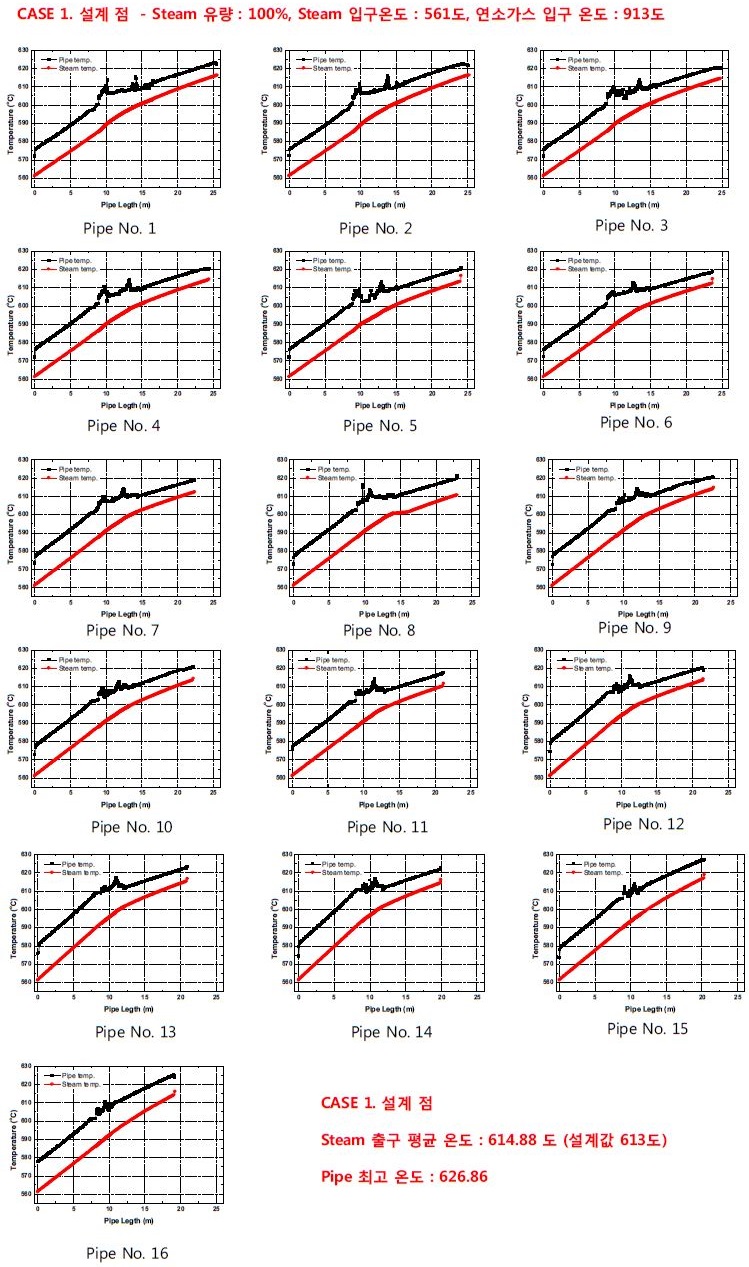
Fig. 9는 평균온도의 연소가스가 균일하게 입구 부에서 공급 될 시 1번부터 16번 파이프 외부표면 및 증기의 온도 변화를 보이고 있다. 파이프 외부표면 온도 및 증기의 온도는 증기가 흐르는 방향으로 지속적으로 상승되는 결과를 보이고 있다. 파이프 중앙의 곡관부의 시작 및 끝 지점에서 파이프 외부표면 온도가 높게 나타나나, 파이프 외부 대류 열전달 계수가 낮아 스팀의 온도 상승 기울기가 감소하는 것을 확인 할 수 있다. 곡관부 이후 회수부 영역에서도 지속적으로 파이프 외부표면 및 증기 온도가 상승하여 출구 지점에서는 증기의 온도 614.88℃로 설계값 613℃와 거의 일치하는 것을 확인할 수 있다. 봉다발 내 파이프 외부표면 및 스팀 온도변화 특성은 파이프의 위치가 봉다발 내에서 변화되어도 큰 차이가 없는 것을 확인하였다.

Fig. 9

Temperature of External surface and steam in the pipe at design point condition

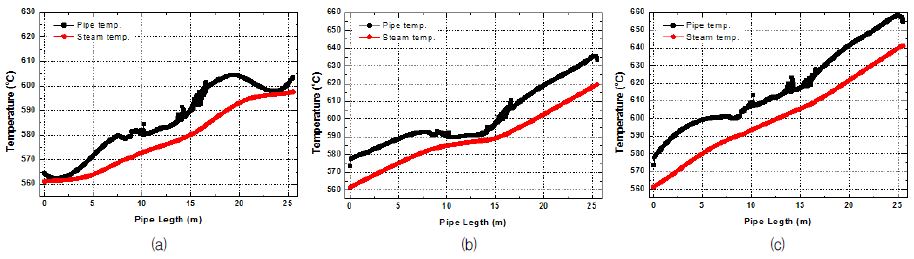
Fig. 9는 실제 온도 프로파일(Fig. 5)을 연소 가스 입구 조건으로 부과하였을 때 파이프 외부표면 및 증기의 온도 변화이다. 평균온도 기준의 온도 프로파일은 (Fig. 5(a)) 파이프 하부에서는 연소가스의 온도가 높고 상부에서는 연소가스의 온도가 낮은 입구 연소 가스 온도 분포 특성이 파이프 외부표면 온도 분포에 뚜렷이 나타난다. 파이프 외부표면의 온도는 최하단 곡관부를 전후로 해서 급격히 상승하나, 파이프 배관의 상부에서는 증기의 온도가 상승함에도 불구하고 파이프 외부표면의 온도가 낮아지는 것을 볼 수 있다. 이와 같이 연소가스 온도분포 변화에 따라 파이프 외부표면 및 증기의 온도 분포가 상이한 것을 확인할 수 있다.

반면 최소온도 기준 온도 프로파일 (Fig. 5(b))와 최고온도 기준 온도 프로파일(Fig. 5(c))은 파이프 하부에서 온도가 낮고, 상부에서 온도가 높은 형태를 띠고 있다. 그 결과 두 경우 파이프 외부 표면 및 스팀의 온도 변화 형태가 비슷한 것을 확인할 수 있다. 온도가 낮은 파이프 곡관부에서 파이프 외부 및 스팀의 온도 변화율이 낮으며, 상부에서는 빠르게 온도가 증가한다.

이와 같이 연소가스 온도 프로파일에 의해 봉다발 파이프 외부표면 및 스팀의 온도변화 형태가 크게 영향을 받는 것을 확인할 수 있다. 특히 파이프 표면 온도 변화는 파이프 금속 열용량이 스팀 열용량보다 작을 뿐만 아니라 외부 연소가스에 직접 노출되어 있어 스팀의 온도 변화보다 외부연소가스 온도 변화에 민감하게 반응한다. 그러므로 스팀의 온도를 상승시키기 위해서 외부 연소가스 온도를 상승시킬 경우 봉다발 파이프의 외부 표면온도가 급격히 상승하여 파이프에 열적 내구성 저하가 야기할 것으로 보인다.

그 외의 연소가스 입구 온도프로파일, 평균온도 변화 및 증기 질량유량 변화에 따른 증기 및 파이프 외부표면에서의 최고 온도를 Table 2에서 정리하였다. 입구 온도 및 속도 프로파일이 매우 복잡한 형태이더라도 최종 회수 되는 증기의 출구온도는 공급된 총 열량에 의해 결정됨에 따라, 증기의 질량 유량 및 평균 연소가스 온도 분포 값에 의해 결정되는 것을 확인할 수 있다. 증기 유량이 증가할 경우 증기 및 파이프 외부표면의 최고 온도가 낮아지는 것을 확인할 수 있다. 이는 연소가스에 의해 공급되는 총 열량이 고정된 상태에서 증기 유량이 증가함에 따른 결과이다.

Table 2

Maximum Temperature of Steam and Pipe in Rod Bundle

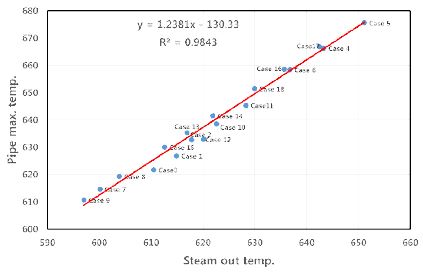
각 계산 결과를 Fig. 10과 같이 파이프 외부표면 온도 및 증기 출구 온도 결과로 나타내면 선형적인 결과를 보이는 것을 확인 할 수 있다. 이는 회수된 증기의 온도를 알면 파이프 외부표면 최고 온도 값을 예측할 수 있는 것이다. 더불어 각 계산 결과 경우들을 분석하면 연소가스의 평균 입구 온도와 증기 회수 온도가 선형적 비례 관계를 가지는 것을 확인할 수 있다. 이와 같이 파이프의 과열현상에 대한 예측 및 증기 열회수량을 계산 및 예측을 할 수 있는 데이터 베이스를 확보하였으며, 향후 USC 보일러의 봉다발을 설계할 때 유용하게 활용할 수 있을 것으로 기대된다.

Fig. 10

Temperature of External surface and steam in the pipe at real condition; ; (a) Average temperature profile, (b) Minimum temperature profile, (C) Maximum temperature profile

4. 결 론

본 연구는 USC 보일러 내 봉다발 내에서의 파이프 외부표면 온도 및 회수 증기의 온도를 예측하기 위한 일련의 연구과정을 수행하였다. 이를 위해 외부 연소가스 열/유동장 해석 및 1-D 열전달 계산을 수행하였다. 그 결과 연소가스 입구 유동 조건에 따라 국소적으로 열교환량의 변화가 있어 파이프 외부표면 및 증기의 온도 변화의 변곡은 존재하는 것을 확인하였다.그럼에도 불구하고 전체 열교환 열량에 의해 파이프 외부표면 최고 온도 및 회수 증기 온도가 선형적으로 변화되는 것을 확인하였다. 최종적으로 회수 증기 온도에 따른 파이프 외부표면 최고 온도 간의 관계를 도출함에 따라 향후 USC 보일러 봉다발 설계 시 과열 구간 예방 설계를 위한 기초 자료로 활용 될 것으로 기대한다.

Fig. 11

Pipe maximum temperature vs steam outlet temperature

Acknowledgments

이 논문은 2016년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2016R1D1 A1B03935374).

References

• Ultra Super Critical Pressure Coal Fired Boiler—State of the Art Technology Applications. Available online: https://www.yumpu.com/en/document/view/40407524/ultra-supercritical-pressurecoal-fired-boiler/1, .
• Fan, Z., Goidich, S., Robertson, A., and Wu, S., “Ultra-Supercritical Pressure CFB Boiler Conceptual Design Study”, Foster Wheel, 83, (Dev 2006).
• Viswanathan, R., Coleman, K., and Rao, U., (2006), “Materials for Ultra-supercritical Coal-fired Power Plant Boilers”, International Journal of Pressure Vessels and Piping, Vol. 83(No. 11), p778-783. [https://doi.org/10.1016/j.ijpvp.2006.08.006]
• Viswanathan, R., Henry, J. F., Tanzosh, J., Stanko, G., Shingledecker, J., Vitalis, B., and Purgert, R., (2005), “US Program on Materials Technology for Ultra-Supercritical Coal Power Plants”, Journal of Materials Engineering and Performance, Vol. 14(No. 3), p281-292.
• Castello, P., Guttmann, V., Farr, N., and Smith, G., (2000), “Laboratory-simulated Fuel-ash Corrosion of Superheater Tubes in Coal-fired Ultra-supercritical-boilers”, Materials and Corrosion, Vol. 51(No. 11), p786-790. [https://doi.org/10.1002/1521-4176(200011)51:11<786::aid-maco786>3.0.co;2-m]
• Metzger, D. E., Berry, R. A., and Bronson, J. P., (1982), “Developing Heat Transfer in Rectangular Ducts with Staggered Arrays of Short Tube Fins”, Journal Heat Transf, Vol. 104(No. 4), p700-706.
• Armstrong, J., and Winstanley, D. A., (1988), “Review of Staggered Array Tube Fin Heat Transfer for Turbine Cooling Applications”, Journal Turbomach, Vol. 110, p94-103.
• Goldstein, R. J., Chyu, M. K., and Hain, R. C., (1985), “Measurement of Local Mass Transfer on a Surface in the Region of the Base of a Protruding Cylinder with a Computer-controlled Data Acquisition System”, International Journal of Heat and Mass Transfer, Vol. 28(No. 5), p977-985. [https://doi.org/10.1016/0017-9310(85)90279-0]
• Chyu, M. K., Hsing, Y. C., Shih, T. P., and Natarajan, V., (1999), “Heat Transfer Contributions of Tubes and Endwall in Tube-fin Arrays: Effects of Thermal Boundary Condition Modeling”, Journal of Turbomach, Vol. 121, p257-263.
• Zhang, L. Z., Ouyang, Y. W., Zhang, Z. G., and Wang, S. F., (2015), “Oblique Fluid Flow and Convective heat Transfer Across a Tube Bank under Uniform Wall Heat Flux Boundary Conditions”, International Journal of Heat and Mass Transfer, Vol. 91, p1259-1272. [https://doi.org/10.1016/j.ijheatmasstransfer.2015.08.062]
• Shen, S., Liu, H., Gong, L., Yang, Y., and Liu, R., (2015), “Thermal Analysis of Heat Transfer Performance in a Horizontal Tube Bundle”, Desalination and Water Treatment, Vol. 54(No. 7), p1809-1818. [https://doi.org/10.1080/19443994.2014.895780]
• Pis’mennyi, E. N., Terekh, A. M., Polupan, G. P., Carvajal-Mariscal, I., and Sanchez-Silva, F., (2014), “Universal Relations for Calculation of the Drag of Transversely Finned Tube Bundles”, International Journal of Heat and Mass Transfer, Vol. 73, p293-302.
• Choi, S. M., Park, J. S., Sohn, H. S., Kim, S. H., and Cho, H. H., (2016), “Thermal Characteristics of Tube Bundles in Ultra-Supercritical Boilers”, Energies, Vol. 9(No. 10), p779-792. [https://doi.org/10.3390/en9100779]
• Kadoya, K., Matsunage, N., and Nagashima, A., (1985), “Viscosity and Thermal Conductivity of Dry Air in the Gaseous Phase”, Journal of Physical and Chemical Reference Data, Vol. 14(No. 4), p947-970. [https://doi.org/10.1063/1.555744]
• Žkauskas, A., (1972), “Heat Transfer from Tubes in Crossflow”, Advances in Heat Transfer, Vol. 8, p93-160.