10 MW급 초임계 CO2 발전용 축류 터빈의 구성 설계 및 회전체 동역학 해석
Abstract
This paper presents component design and rotordynamic analysis results of axial turbine applied to a 10 MW super-critical CO2 cycle. The axial turbine consists of 3 stage turbine blades and a shaft supported by two fluid film bearings. To prevent the leakage, we installed two seals near the turbine inlet and exit side. We adopts a tilting pad bearing for the stable operation of the rotor. The tilting pad bearing consists of 5 pads and leading edge grooves are installed for the effective thermal management. Based on the rotor layout, we conduct a rotordynamic analysis. The dynamic coefficients of the tilting pad bearings were calculated based on the thin film lubrication theory. Turbine blades, thrust collar and seals were modeled as equivalent inertia. The predicted Campbell diagram showed that there are three critical speeds, namely the conical and the first , second and third bending critical speeds under the rated speed and it is predicted that the rotor have 20% separation margin for the fourth bending critical speed. In addition, unstable modes are not presented under the rated speed and the unbalance response prediction showed that vibration levels are controlled within 0.02 mm for all speed ranges owing to the high damping ratio of the modes.
Keywords:
Axial Turbine, Super Critical CO2, Leading Edge Groove Bearing키워드:
축류 터빈, 초임계 CO2, 선단 홈 베어링1. 서 론
초임계 이산화탄소(CO2) 발전 시스템은 비교적 낮은 온도와 압력에서도 초임계 상태에 도달이 가능한 CO2를 작동유체로 사용한다. 초임계 CO2 발전 시스템은 사이클의 효율이 높고, 작동 유체의 높은 밀도로 인하여 동급의 다른 발전 시스템에 비해 작은 부피로 구성이 가능하며, 비교적 넓은 온도 범위의 열원에 대하여 적용이 가능한 장점을 가지고 있다. 이러한 장점들 때문에 초임계 CO2 발전 시스템은 현재 미 활용되거나 버려지는 에너지 활용을 위한 대체 발전 수단으로 많은 주목을 받고 있으며, 선진국을 중심으로 태양열, 화석연료, 지열 등의 다양한 열원에 적용하기 위한 연구들이 진행 되고 있다.
초임계 CO2 발전 시스템과 관련된 연구로는 기존의 스팀 사이클을 초임계 CO2 발전 사이클로 대체하였을 때의 효율 향상을 계산하거나, 주어진 열원에 대하여 초임계 CO2사이클 적용하였을 경우, 전체 시스템의 효율을 예측하는 연구들이 있었다.(1,2) 또한, 기존의 가스 터빈 복합 발전 플랜트의 효율 향상을 위해 초임계 CO2 사이클을 하부 사이클로 적용하기 위한 연구들이 수행되었다.(3,4) 이렇게 초임계 CO2 발전 시스템의 설계 및 효율 해석에 관한 연구와 함께 초임계 CO2 사이클에 적용하기 위한 압축기나 터빈과 같은 유체 기계에 대한 연구 또한 현재 활발히 진행되고 있다.(5~7)
초임계 CO2 발전 시스템에 사용되는 터보 기계는 주로 고온, 고압, 고속 환경에서 운전되기 때문에 이와 관련된 베어링과 씰에 대한 요소 기술 확보가 선행 되어야 하며, 높은 부하 조건에서 동작을 하기 때문에 설계 단계에서 구조 해석 및 열응력 해석을 통한 구조 안정성에 대한 검토가 필수적이다. 또한, 고속으로 회전하는 터보 기계의 특성상 설계 시 회전체 동역학 해석을 통해 설계 건전성에 대한 검토가 필수적으로 이루어져야 한다.
본 연구에서는 현재 한국기계연구원에서 개발 중인 10 MW급 초임계 CO2 발전용 축류 터빈에 대하여 설계 단계에서 수행한 구성 설계와 회전체 동역학 해석 결과에 대해 기술하였다.
2. 연구 방법
2.1 축류 터빈 구성
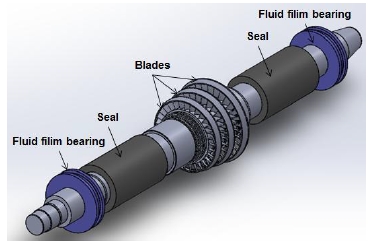
Fig. 1은 본 논문의 연구 대상인 축류 터빈을 나타낸다. 터빈의 출력은 10 MW이며, 정격 회전 속도는 30,000 rpm이다. 블레이드는 3단으로 설계 되었으며 Shroud 형식으로 구성하였다. 작동 유체의 터빈 입구 온도와 압력은 각각 550 ℃, 200 bar이다. 회전축은 2개의 유체 베어링으로 반경 방향 하중이 지지되며, 터빈 입구와 출구 근처에 작동유체의 누설을 방지하기 위한 고압용 씰이 장착되어 있다.
축류 터빈에 장착되는 유체 베어링은 터빈이 30,000 rpm의 고속에서 운전되므로 고속 안정성이 우수한 틸팅 패드 베어링을 사용하였다. 틸팅 패드 베어링은 5개의 패드로 구성되며, 패드 사이로 하중이 작용하는 ‘Load Between Pads’형식의 베어링을 선택하였다.
2.2 회전체 동역학 해석
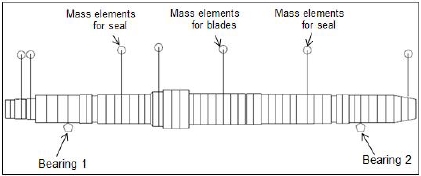
Fig. 2는 Fig. 1의 축류 터빈에 대한 회전체 동역학 해석 모델을 나타낸다. 운동 방정식은 식(1)과 같은 형태를 가지며, 유한 요소법을 통해 계산된 질량(M), 자이로스코픽(J), 강성(K), 감쇠(C)행렬로 구성된다.
| (1) |
회전축은 굽힘 강성을 가지는 강성 요소로 모델링 되며, 회전축에 조립되는 스러스트 칼라, 씰 등의 부품과, 블레이드는 Fig. 2와 같이 질량과 관성을 가지는 집중 질량 요소로 모델링 하였다. 베어링은 별도의 해석 프로그램을 통해 계산된 강성 감쇠 요소로 모델링하였다. 회전체 동역학 해석은 상용 프로그램인 DYROBES를 통해 수행하였으며,(8) 해석에 사용된 로터와 베어링의 주요 정보는 Table 1과 같다.
2.3 베어링 열 윤활 해석
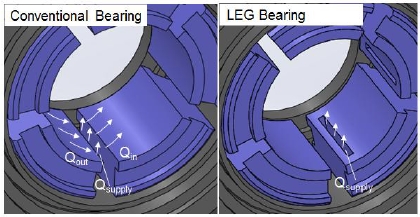
본 논문의 연구 대상인 축류 터빈은 터빈 입구 온도가 550℃의 고온 환경에서 운전 되며, 정격 회전 속도가 30,000 rpm인 고속으로 회전하기 때문에 시스템의 안정적인 운영을 위해서는 베어링에서 점성 마찰에 의해 발생되는 열의 효과적 배출이 필수적이다. 이러한 베어링의 Thermal management 특성은 베어링의 여러 가지 설계 변수에 의해서 결정이 되지만, 중요한 변수 중의 한 가지가 베어링으로의 윤활유 공급 방식이다. 일반적으로 틸팅 패드 베어링의 윤활유는 외부 공급 라인을 통해 Fig. 3의 왼쪽 그림과 같이 패드와 패드 사이의 Groove를 통해 공급이 된다. 패드와 패드 사이의 Groove에는 Fig. 3을 통해 볼 수 있듯이 일반적으로 이전 패드에서 점성 마찰에 의해 온도가 상승된 윤활유와 외부에서 공급되는 낮은 온도의 윤활유가 섞인 후 다음 패드로 유입 되게 된다. 이러한 경우 패드 선단의 오일 온도는 일반적으로 아래와 같은 식으로 계산이 된다.
| (2) |
상기의 식에 Qout, Qin은 각각 이전 패드에서 배출되는 윤활유 유량과 현재 패드로 유입되는 윤활유 유량을 나타내며, Tout, Tsupply는 각각 이전 패드에서 배출되는 윤활유의 온도와 외부에서 공급되는 윤활유 온도를 나타낸다. 식(2)를 통해서 볼 때 패드 입구에서의 윤활유 온도를 낮추려면 이전 패드에서 점성 마찰에 의해 온도가 상승된 오일은 외부로 배출 시키고 외부에서 공급되는 낮은 온도의 오일의 많은 양이 패드 선단으로 유입되도록 해야 한다. 이러한 기능을 위해 Fig. 3의 오른쪽 그림과 같이 패드 선단에 가공된 Groove를 통해 윤활유를 내부로 직접 공급되는 LEG (Leading Edge Groove) 베어링이 제안되었고, 온도 특성에 대한 효과가 여러 연구들을 통해 입증 되었다.(9) LEG 형식의 베어링의 경우 패드 선단에서의 윤활유 온도는 일반적으로 아래 식과 같이 외부에서 공급되는 윤활유의 온도와 동일하다고 하여 해석을 수행한다.
| (3) |
본 연구에서는 축류 터빈에 사용되는 베어링의 온도 특성 예측을 위해 Fig. 3에 나타난 일반적인 틸팅 패드 베어링과 LEG 형식의 틸팅 패드 베어링에 대해 열 윤활 해석을 수행하였다. 해석 수행 시 패드 선단 온도는 각각의 경우 식(2)와 (3)을 사용하였으며, 다른 조건은 동일하게 하였다. 회전축의 온도는 전체 윤활 막의 평균온도와 같다고 가정하였고, 패드 측면과 아래 면은 자연 대류 조건으로 가정하였다. 열 윤활 해석은 상용 프로그램은 XLRotor를 사용하여 수행하였으며, 해석과 관련된 이론은 참고문헌(10)에 기술 되어 있다.
3. 연구 결과
3.1 임계속도(Critical speed)해석 결과
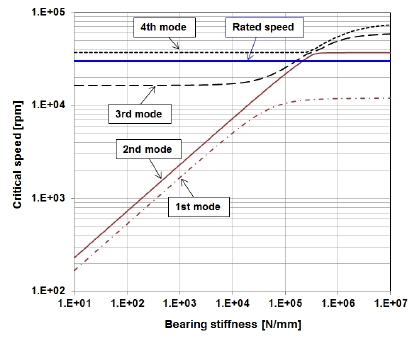
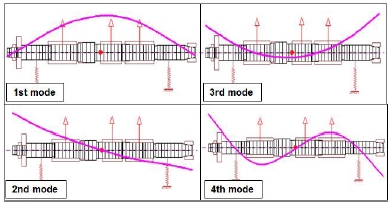
축류 터빈에서 사용될 베어링의 적절한 강성 값을 산출하기 위해 베어링 강성에 따른 임계속도해석을 수행하였으며, Fig. 4는 해석 결과를 나타낸다. 그림을 통해 볼 수 있듯이 정격 회전속도인 30,000 rpm 이하와 정격 회전속도 근처에서 모두 4가지 임계속도가 계산되었으며, 각각의 모드 형상은 Fig. 5에 표기 하였다. Fig. 5를 통해 볼 수 있듯이 1, 3, 4차 모드는 축의 굽힘과 관련된 모드 이며, 2차 모드는 코니컬 운동이 지배적인 모드로 나타났다. 1차와 2차 모드는 베어링의 강성에 따라 임계속도가 크게 변화하는 것을 볼 수가 있으며, 3차와 4차 모드는 베어링 강성에 따른 임계속도변화가 상대적으로 적게 나타났다. 3차 모드는 베어링 강성이 2×105 N/mm 이하의 영역에서는 정격 속도 아래에서 임계속도가 나타났으며, 4차 모드는 정격 속도보다 높은 37,000 rpm 부근에서 임계속도가 나타났다. 상기의 결과에 따라 축류 터빈은 1, 2, 3차 임계속도를 지나서 운전되어야 할 것으로 생각되었으며, 4차 임계속도와 충분한 분리 여유가 있어야 할 것으로 판단되었다. 또한, 베어링 강성은 정격 회전속도와 인접한 3, 4차 임계속도와 20% 이상의 분리 여유를 위해 1☓104~8☓104 N/mm의 범위에서 설계하는 것이 적당할 것으로 생각되었다.
3.2 베어링 열 윤활 해석 및 동특성 해석 결과
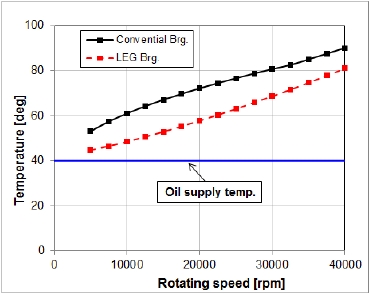
틸팅 패드 베어링의 윤활유 공급 방식 및 온도 특성을 예측하기 위해 앞장에서 기술한 일반적인 형식의 틸팅패드 베어링과 LEG 형식의 베어링에 대하여 열 윤활 해석을 수행하였다. Fig. 6은 해석을 통해 계산된 회전속도별 패드 표면의 최대 온도를 나타낸다. 그림을 통해 볼 수 있듯이 회전 속도 증가에 따라 베어링 내에서 발생하는 점성 마찰 증가로 패드 표면 온도가 상승하는 것을 볼 수가 있으며, 모든 회전 속도에 대하여 LEG 형식의 베어링이 일반적인 베어링 보다 패드 온도가 낮은 것으로 예측 되었다. 정격 회전속도인 30,000 rpm에서 LEG 형식의 베어링은 일반 틸팅 패드 베어링에 비해 패드 표면 온도를 10℃ 이상 낮추는데 효과가 있을 것으로 예측 되었다. 이상의 결과를 통해 축류 터빈의 안정적인 운전을 위해서 온도 해석 결과 설계 여유가 더 큰LEG 형식의 베어링을 사용하는 것이 적합할 것으로 판단하였다. 각 회전속도별 LEG 형식의 베어링과 일반 틸팅패드 베어링의 패드 표면 온도 변화에 대한 고찰은 향후 베어링의 열윤활 해석 연구를 통해 수행할 예정이다.
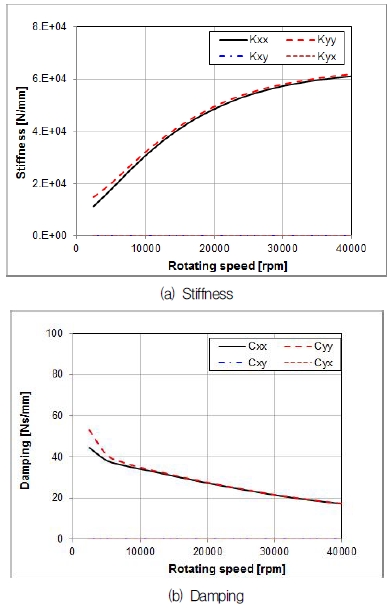
베어링의 열 윤활 해석을 통해 선정된 LEG 형식의 틸팅 패드 베어링에 대해 동특성 해석을 수행하였으며, Fig. 7은 해석을 통해 계산된 터빈 입구 측에 위치한 베어링 1의 강성, 감쇠 계수를 나타낸다. Fig. 7-(a)에서 볼 수 있듯이 모든회전 속도에 대하여 베어링의 수평 방향과 수직방향 강성이 유사하게 나타났으며, 회전 속도 증가에 따라 강성은 증가하는 경향을 보였다. 또한, 강성의 연성 항은 모든 회전 속도에서 나타나지 않았다. 정격 회전 속도인 30,000 rpm에서의 베어링의 수평 방향과 수직 방향 강성은 모두 6☓104 N/mm로 나타났으며, 임계속도해석을 통해 선정된 베어링의 강성 범위 내에 위치하는 것으로 나타났다. 베어링의 감쇠는 Fig. 7-(b)에서 볼 수 있듯이 수직 방향과 수평 방향이 유사하게 나타났으며, 연성 항 또한 나타나지 않았다. 그러나 감쇠의 경우 강성과 달리 회전 속도 증가에 따라 감소하는 경향을 보였다.
3.3 감쇠 고유 진동수 해석 결과
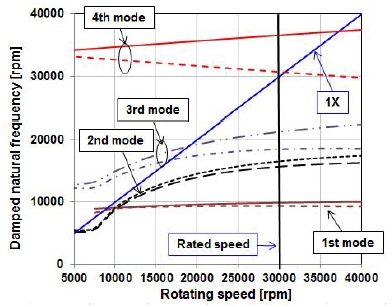
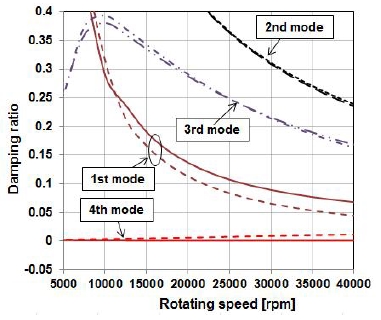
3.2절에서 계산된 베어링 동특성 계수를 이용하여 회전 속도별 감쇠 고유 진동수 해석을 수행하였다. Fig. 8, 9는 해석 결과를 나타내며, 각각 회전속도별 감쇠 고유진동수인 Campbell 선도와 모드 감쇠 비를 나타낸다. 각각의 고유 진동 모드는 Fig. 8에서 볼 수 있듯이 Forward와 Backward 모드가 함께 나타났다. Fig. 8의 결과를 볼 때, 축류터빈의 정격 회전속도가 30,000 rpm이므로 주어진 설계에서는 1, 2, 3차 임계속도를 지나서 운전이 될 것으로 예상 되었다. 또한, Fig. 9에 나타난 각 모드들에 대한 감쇠 비를 보면 1, 2, 3차 모드는 상대적으로 모드 감쇠가 큰 것으로 나타났지만, 4차 모드의 감쇠는 아주 작게 나타났다. 이렇게 4차 모드의 감쇠가 작은 이유는 Fig. 5에서 볼 수 있듯이, 4차 모드의 형상이 유체 베어링이 위치한 노드에서 변위가 거의 없기 때문에 유체 베어링의 감쇠력이 모드 감쇠에 기여를 못 하기 때문으로 판단된다. 따라서, 축류 터빈의 안정적인 운전을 위해서는 4차 모드와 관련된 임계속도와 충분한 분리 여유를 가져야 할 것으로 판단되었다. 해석을 통해 예측된 4차 모드와 관련된 임계속도는 약 37,000 rpm으로 정격 회전 속도인 30,000 rpm에서 20% 이상의 분리 여유를 가지는 것으로 예측되었다.
3.4 잔류 불균형 응답 해석
회전축에 존재하는 잔류 불균형에 의한 회전축 진동을 파악하기 위해 잔류 불균형 응답 해석을 수행하였다. 잔류 불균형은 로터에 가장 큰 질량이 조립되는 부분인 씰과 블레이드가 장착되는 노드에 부여하였으며, 불균형 질량의 크기는 총 잔류 불균형 질량이 ISO 2.5등급에 해당하도록 부여하였다. 잔류 불균형이 부여되는 씰과 블레이드가 장착되는 노드 위치는 Fig. 2에 표기하였다. 터빈 입구측 씰과 블레이드 위치의 불균형 질량은 동위상이며, 터빈 입구측 씰과 출구측 씰 노드에 위치한 불균형 질량은 180o의 위상차를 가진다.
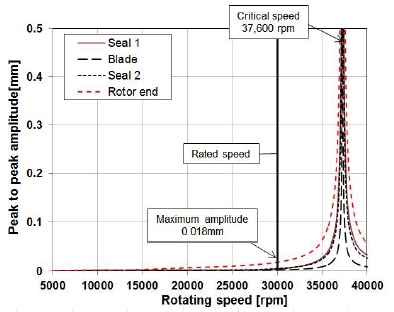
Fig. 10은 잔류 불균형 응답 해석 결과를 나타낸다. 그림의 결과들은 로터에서 잔류 불균형이 부여된 씰과 블레이드에 해당하는 노드점들과 터빈 출구측 끝단에서의 진동들을 나타낸다. 해석 결과 모든 회전 속도에서 로터 터빈 출구 쪽 끝단에서 가장 큰 진동이 나타났으며, 정격 속도인 30,000 rpm에서 0.018 mm의 진동이 나타날 것으로 예측되었다. 또한, 정격 속도인 30,000 rpm 이하의 속도에서는 뚜렷한 공진 형상이 관찰되지 않았는데, 이것은 Fig. 9에서 나타났듯이 정격 속도 이하에 존재하는 1, 2, 3차 모드들의 모드 감쇠가 크기 때문인 것으로 판단된다. 또한, 4차 모드와 관련된 임계속도는 Fig. 8의 Campbell 선도에서 예측되었듯이 37,000 rpm 근방에서 나타나는 것 또한 확인할 수 있었다.
4. 결 론
본 연구에서는 현재 한국기계연구원에서 개발 중인 10 MW급 초임계 이산화탄소 발전용 축류 터빈에 대하여 회전체 동역학 해석 모델을 수립하고, 이에 대한 해석을 수행하였다. 적절한 베어링 강성 선정을 위해 베어링 강성에 따른 임계속도해석을 수행하였고, 이를 통해 정격 회전속도 이하와 근처에서 모두 4개의 임계속도가 존재하는 것을 파악하였다. 또한, 해석 결과를 바탕으로 정격 회전속도와 임계속도가 충분한 분리 여유를 가지도록 베어링 강성을 선정하였다. 적절한 윤활유 공급방식 선정을 위해 베어링에 대한 열윤활 해석을 수행하였고, 이를 통해 축류터빈의 운전 조건에서 LEG 형식의 베어링이 일반적인 베어링보다 패드 표면 온도를 10℃ 정도 낮추는 효과가 있는 것으로 예측 되었다. 또한, 선정된 베어링의 동특성 계수를 바탕으로 수행한 감쇠 고유진동 해석을 통해 정격 회전속도 보다 높은 주파수를 가지는 4차 모드의 감쇠가 매우 작은 것을 확인할 수 있었다. 그러나, 정격회전속도 아래 존재하는 1,2,3차 모드의 감쇠는 상대적으로 크기 때문에 잔류 불균형응답 해석에서 정격회전속도 이하에서는 뚜렷한 공진현상이 나타나지 않는 것으로 예측되었다.
Acknowledgments
본 연구는 한국에너지기술평가원(KETEP)의 “고효율 석탄 화력용 초임계 CO2발전 원천기술 개발 및 시험” 및 국가과학기술연구회 “초임계 CO2 발전시스템용 핵심기계 기술 기반 구축” 과제의 지원을 받아 수행되었습니다.
References
- Dostal, V., (2004), “A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors”, Ph. D. Thesis, Massachusetts Institute of Technology, USA..
-
Turchi, C. S., Ma, Z., Neises, T. W., and Wagner, M. J., (2013), “Thermodynamic Study of Advanced Supercritical Carbon Dioxide Power Cycles for Concentrating Solar Power Systems”, Solar Energy Engineering, 135(4), p041007.
[https://doi.org/10.1115/1.4024030]

-
Cho, S. K., Kim, M., Baik, S., Ahn, Y., and Lee, J. I., (2015), “Investigation of the Bottoming Cycle for High Efficiency Combined Cycle Gas Turbine System with Supercritical Carbon Dioxide Power Cycle”, In ASME Turbo Expo 2015: Turbine Technical Conference and Exposition (pp. V009T36A011-V009T36A011). American Society of Mechanical Engineers.
[https://doi.org/10.1115/gt2015-43077]

- Huck, P., Freund, S., Lehar, M., and Peter, M., (2016), “Performance Comparison of Supercritical CO2 Versus Steam Bottoming Cycles for Gas Turbine Combined Cycle Applications”, In 5th International Supercritical CO2 Power Cycle Symposium.
-
Kus, B., and Nekså, P., (2013), “Development of Onedimensional Model for Initial Design and Evaluation of Oil-free CO2 Turbo-compressor”, Intertional Journal of Refrigeration, 36(8), p2079-2090.
[https://doi.org/10.1016/j.ijrefrig.2013.05.009]

-
Pecnik, R., Rinaldi, E., and Colonna, P., (2012), “Computational Fluid Dynamics of a Radial Compressor Operating with Supercritical CO2”, Journal of Engineering for Gas Turbines and Power, 134(12), p122301.
[https://doi.org/10.1115/1.4007196]

-
Lee, D., and Kim, B., (2016), “Bearing and Rotordynamic Performance Analysis of a 250 kW Reduction Gear System”, Journal of Korean Society Tribology and Lubrication Engieering, 32(4), p107-112.
[https://doi.org/10.9725/kstle.2016.32.4.107]

- Chen, W. J., (2007), Introduction to Dynamics of Rotor Bearing Systems, Chap. 6, Eigen Technologies, USA.
-
Dmochowski, W. K. S. A., Brockwell, K., Decamillo, S., and Mikula, A., (1993), “A Study of the Thermal Characteristics of the Leading Edge Groove and Conventional Tilting Pad Journal Bearings”, Journal of Tribology, 115(2), p219-226.
[https://doi.org/10.1115/1.2920995]

- Branagan, L. A., (1988), “Thermal analysis of Fixed and Tilting Pad Journal Bearings Including Cross-Film Viscosity Variations and Deformations”, Ph. D. Thesis, Department of Mechanical Engineering, University of Virginia, USA.