팬 형상 막냉각 홀이 위치한 평판 막냉각 유동에 대한 대와류 모사해석
Abstract
Large eddy simulations (LES) on a flat plate film cooling flow have been performed to investigate detailed flow fields around a 7-7-7 fan-shaped film cooling hole. In addition, RANS simulations were performed to compare with the LES results. The adiabatic film cooling effectiveness from the LES results showed similar distribution compared to that from the measured data. However, the RANS results over-predicted adiabatic film cooling effectiveness compared to the LES results. Injected flow from the inclined cooling hole was developed to the vortical structure and it covered the wall close to the cooling hole to form a high film cooling effectiveness region. The vortical structure then broke down and was dissipated to mix with the main flow. Part of the dissipated vortex still covered the wall to extend film cooling effect downstream. The LES results revealed that large eddy shedding from the cooling hole which is truncated in the RANS simulations has a dominant role in elucidating the flow structure near the film cooling hole and the corresponding film cooling effectiveness distributions.
Keywords:
Film Cooling, Turbulence Model, Large Eddy Simulation, CFD키워드:
막냉각, 난류모델, 대와류 모사해석, 전산유체역학1. 서 론
가스터빈의 출력 및 효율을 높이기 위하여 가스터빈의 터빈입구 온도는 지속적으로 증가하는 추세이며, 이에 일반적으로 터빈입구 온도가 소재의 내열온도를 초과하여 운용되기 때문에 적절한 냉각기법이 적용되어야 한다. 막냉각 기법은 터빈유로를 흐르는 작동유체보다 낮은 온도의 냉각유체를 분사하여 터빈 날개 표면에 얇은 막을 형성하여 작동유체가 직접 날개에 접촉하는 것을 억제하여 날개를 고온의 작동유체로부터 보호하는 외부 냉각기법이다.
막냉각 홀의 냉각성능을 수치해석 기법으로 평가하기 위해서 평판 막냉각 홀 주변 혹은 실제 터빈에 적용된 막냉각 홀에 대해 주로 RANS(Reynolds Averaged Navier-Stokes) 해석기법이 이용되었다. 하지만 많은 경우에 있어 RANS 해석결과는 실험에 의해 측정된 막냉각 효율 분포와 차이를 나타낸다. 이는 일반적으로 RANS해석의 난류모델에서 모델링으로 처리되는 와류의 영향이 존재하기 때문으로 여겨진다. 한편 최근 들어 컴퓨터 성능의 향상에 힘입어 LES(Large Eddy Simulation), Detached Eddy Simulation(DES), Scale Adaptive Simulation(SAS) 등과 같이 대와류(Large Eddy)를 직접 해석하는 수치해석 기법이 막냉각 유동장 예측에 활용되기 시작되었다.
프랑스의 CERFACS에서는 막냉각 유동에 대한 LES의 가용성에 대해 지속적인 연구를 진행 중이며, 이에 대한 일환으로 Simiriotis(1)는 LES 기법을 이용해 펜실바니아 주립대학에서 제안한 7‐7‐7 팬 형상 막냉각 홀(2)의 막냉각 성능을 예측하였고 이를 Schroeder 등(3)이 시험을 통해 측정한 시험결과와 비교 하였다. 지배방정식에 적용되는 대류항 차분기법에 따라 해의 정확도가 달라지는 것을 확인하였으며, Taylor Galekin기법에 기반한 차분 방법이 가장 실험값과 유사한 결과를 도출하는 것을 확인하였다. 또한 막냉각 홀 주변의 유동장 및 막냉각 로부터 분사되는 Rolling Vortex으로부터 Hairpin Vortex로의 발달 이후 와류가 소산되는 과정 등을 확인하였다. Perry 등은 원통형 막냉각 홀에 대해 k-ω SST 모델 및 LES 해석결과를 실험결과와 비교하였고, LES 해석모델이 k-ω SST 모델에 비해 막냉각 홀 하류에서의 예측한 유동장이 실험결과와 유사한 것을 확인하였다.(4) Andrew 등은 NEK5000 해석 프로그램을 이용하여 원통형 막냉각 홀에 대해 블라인드 해석을 수행하여 막냉각 유동에 대한 LES의 가용성을 확인하고자 하였다.(5) Shuo Li 등은 주 유동에 대해 수직으로 분사되도록 설계된 막냉각 홀에 대해 k-ε, k-ω SST모델을 적용한 RANS해석과 LES해석 결과를 비교하였고 LES해석에서는 RANS 해석에서는 나타나지 않은 와류 구조를 확인하였다.(6)
국내에서도 막냉각 유동장에 대한 수치해석 연구가 꾸준히 발표되어 왔다. 나상권은 원통형 막냉각 홀에 대해 3가지 난류모델을 적용하여 막냉각 유동장을 해석하였으며, 난류모델에 따라 결과가 상당히 상이함을 확인하였다.(7) 김선민 등은 원통형, 크레센트, 덤벨, 루버 형태의 막냉각 홀이 적용되었을 때, SST난류모델이 적용된 RANS 해석 기법을 이용하여 막냉각 홀 형태에 따른 막냉각효율 분포 및 홀 주변 유동장을 살펴보는 연구를 수행하였다.(8) 조문영 등은 2개의 원통형 막냉각 홀의 상대적 위치에 따른 막냉각 효율 및 홀 주변 유동장을 RANS 해석기법을 통해 수행하였다.(9) 서현재 등은 CFD 기법을 이용하여 팬 형상의 막냉각 홀을 대상으로 막냉각 효율이 극대화되도록 최적설계를 수행하였다.(10) 이처럼 국내에서도 많은 막냉각 홀 문제에 대해 수치해석 연구를 수행하였으나, 대부분 RANS 해석방법을 이용하였다.
선행연구들의 사례를 살펴보면 막냉각 유동 해석에 있어 LES 해석방법은 RANS 해석의 견고성 및 DNS(Direct Numerical Simulation) 해석의 정확성을 적절히 조화시키는 매력적인 해석수단으로 점차 인식되고 있으며, 학계를 넘어 산업계에서도 설계 및 성능평가까지 그 활용폭을 넓혀가고 있다. 한국항공우주연구원에서도 팬 형상 막냉각 홀 최적화 연구의 일환으로 LES 해석기법을 막냉각 유동장 해석에 적용하고자 하였다. 본 연구에서는 다수의 선행연구에서 연구대상으로 선정되었던, 주 유동에 대해 30°의 각도로 분사되는 7‐7‐7 팬 형상의 막냉각 홀에 대한 LES 해석을 수행하였다. 이를 선행연구에서 측정된 막냉각 효율분포와 비교함으로써 평판 막냉각 유동장에 대한 LES 해석기법의 가용성을 확인하고자 한다. 또한 난류모델에 따른 RANS 해석결과와 비교하고 LES 해석결과에서 나타난 막냉각 홀 주변의 유동장 특성을 파악함으로써, 막냉각 홀 주변의 유동장 및 이에 따른 막냉각 효율 분포 매커니즘을 설명하고, 막냉각 유동장에 대한 RANS 해석기법의 한계를 평가하고자 한다.
2. 수치해석 기법
2.1 막냉각 홀 형상 및 수치해석 영역 정의
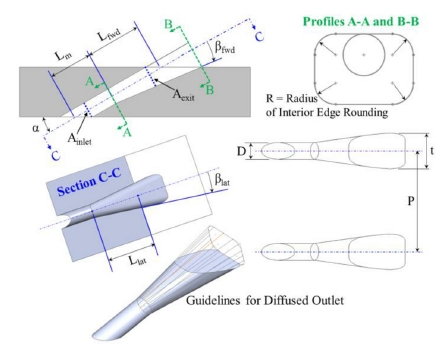
동일한 조건의 막냉각 유체가 공급되더라도 막냉각 홀의 형상에 따라 표면 막냉각 효율의 크게 달라진다. 팬 형상의 막냉각 홀의 경우 원통형 막냉각 홀에 비해 가공의 난이도가 높지만 일반적으로 원통형 막냉각 홀에 비해 막냉각 효율이 우수한 것으로 알려져 있다. 본 연구에서 활용한 막냉각 홀 형상은 Schroeder 등이 시험을 수행한 대상인 주 유동에 대해 30° 각도로 분사되는 7‐7‐7 팬 형상의 막냉각 홀이다.(2) 막냉각 홀의 형상 및 정보는 Fig. 1과 Table 1에 제시되어 있다.
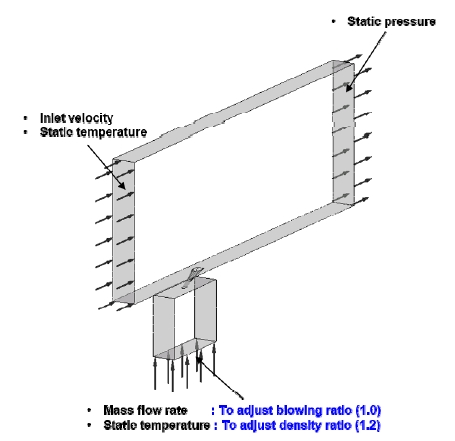
Fig. 2는 수치해석 영역을 나타낸다. 막냉각 홀 직경(D)을 기준으로 상/하류로 각각 35D/70D만큼 확장시켜 해석영역을 정의하였다. 수치해석을 위한 격자계는 Ansys Mesh를 이용하여 구성하였다. LES 해석에서는 격자의 등방성이 매우 중요하기 때문에 모든 영역에서 기본적으로 사면체 격자계를 사용하고, 경계층에서는 종횡비를 모니터링하면서 경계층 영역 격자 수 및 크기 등을 조정하여 최종적으로 모든 영역에서 y+의 값이 1전후의 값을 가지도록 조정하였다. 수치해석에는 냉각유동과 주 유동을 흐르는 유체의 밀도비 및 분사비의 정의 및 값은 식 (1), (2)와 같으며 해당 조건에서 냉각유체의 레이놀즈 수(Reynolds number)는 식 (3)과 같다.
| (1) |
| (2) |
| (3) |
본 연구에서는 수치해석 코드로 Ansys CFX 16.2를 사용하였다. CFX는 RANS 해석에서 다양한 난류모델을 지원하며, 해석하고자 하는 문제의 특성에 따라 난류모델을 적절히 선택하여 사용할 수 있다. 본 연구에서는 타 선행 연구 등에서 많이 활용된 다음과 같은 세 종류의 난류모델을 RANS 해석에 적용하였다.
- ・ Scalable k-ε model
- ・ k-ω SST model
- ・ 레이놀즈 응력(Reynolds stress) model
주 유동 입구 경계조건으로 속도 및 정온도 값이 주어졌으며, 주 유동의 입구 난류강도는 0.5%로 설정하여 동일한 난류조건에서 시험한 결과와 비교하고자 하였다. 주 유동 출구에서의 경계조건은 대기압이 주어졌다. 냉각유체의 입구조건으로는 질량유량과 정온도 값을 주었다. 전산해석 중 질량유량과 입구온도 값을 변경하면서 분사비와 밀도비를 각각 조절할 수 있었으며, 냉각유체의 입구온도가 242K에 도달하였을 때에 밀도비 요구조건을 만족시킬 수 있었다.
한편 LES 해석을 위해서는 아래와 같은 아격자(subgrid) 모델을 사용하였다.
- ・ WALE model
- ・ Smagorinsky model
RANS 해석에서는 CFX의 대류항 차분에 기본옵션인 고차 차분방법이 적용되나, LES 해석 시에는 중앙차분법을 적용하였다. LES 해석은 본질적으로 비정상 해석이므로, 물리적인 시간 간격(time step)이 주어져야 한다. LES 해석 시 수치해석의 안정성을 확보하기 위하여 평균 Courant 수가 0.75 이상이 되지 않도록 시간 간격을 설정하였으며, 이 경우 해석이 발산되지 않고 진행되는 것을 확인할 수 있었다. 또한 주 유동 및 냉각유체의 밀도가 다르기 때문에, 각 물리 시간 단계에서 내부 반복계산(internal loop)은 3회 반복하도록 설정하였다.
2.2 수치해석 결과
막냉각 홀 주변의 표면 막냉각 효율 분포의 정의는 식 (4)와 같다.
| (4) |
Fig. 3는 Schroeder 등(3)이 실험한 결과와 본 연구에서 수행한 RANS 및 LES 해석결과에서 도출한 막냉각 효율을 나타내고 있다. LES 해석결과는 시간 평균된 벽면 온도값을 사용하였다.

Distributions of film cooling effectiveness from CFD results with (a) k-ε model (b) SST model (c) RSM model (d) LES-WALE model (e) LES Smagorinsky model and (f) experimental data(3)
RANS 해석결과의 막냉각 효율 분포를 살펴보면 k-ε 모델을 사용하였을 경우, 가장 실험결과와 유사한 막냉각 효율 분포를 나타내고 있다. 이는 서현재 등(10)이 동일한 형태의 팬형상 막냉각 홀에 대해 수치해석을 수행한 결과와 유사하다. RANS 해석결과는 모두 막냉각 홀 출구 직후 좌우 끝단에서 막냉각 효율이 크게 나타난다. k-ε 모델의 경우 그러한 현상이 하류로 갈수록 사라지고 중앙선을 따라 가장 높은 막냉각 효율값이 형성된다. 반면 SST 모델과 레이놀즈 응력 모델을 사용하였을 경우 좌우 끝단에서 나타난 높은 막냉각 효율 영역이 하류까지 유지된다. RANS 해석결과 중 SST 모델이 적용된 결과가 가장 높은 막냉각 효율 분포를 나타냈으며, 레이놀즈 응력모델이 적용된 결과는 SST모델과 k-ε 모델의 중간정도의 분포를 보인다.
LES 해석결과는 좀 더 실험값과 유사한 결과를 나타낸다. Smagorinsky와 WALE 모델 모두 실험값과 정량적, 정성적 분포가 매우 유사하였다. 막냉각 효율이 0.6 이상인 코어영역의 길이와 형태가 실험결과와 유사하며 또한 막냉각 효율이 0.2~0.6인 구간의 범위 역시 실험값과 유사하다. Smagorinsky 모델에 비해 WALE 모델을 사용하였을 경우, 하류에서 막냉각 효율이 줄어드는 경향이 부드러우며 실험값과 더욱 유사한 형태를 보인다. 반면 막냉각 홀 측면에서 분사되어 주 유동 방향으로 흐르는 냉각유체로 인해, 막냉각 홀 상류에서는 실험값보다 높은 막냉각 효율값 분포를 보이고 있다. 실제 실험에서는 측면에서 냉각유체의 분사가 억제되거나 혹은 주 유동과 빨리 혼합되어 막냉각 홀 좌우에서의 막냉각 효율값이 높지 않은 반면, LES 해석결과에서는 냉각유체가 측면으로 분사되어 주 유동을 따라 흐르며 와류로 발달하면서 벽면을 따라 흐르기 때문으로 파악된다. LES 해석결과에 대한 상세 유동장 분석은 2.2.3절에서 자세히 다루도록 한다.
막냉각 효율값의 정량적인 비교를 위하여, Fig. 4와 같이 세 가지 위치 혹은 영역에서 막냉각 효율 분포를 실험결과와 비교하였다.
- ・ 0 < x/D < 30 에서의 횡방향으로 면적평균
- ・ x/D=5, 30에서 횡방향 막냉각 효율 분포
- ・ 3 < x/D < 35 평면에서 면적평균
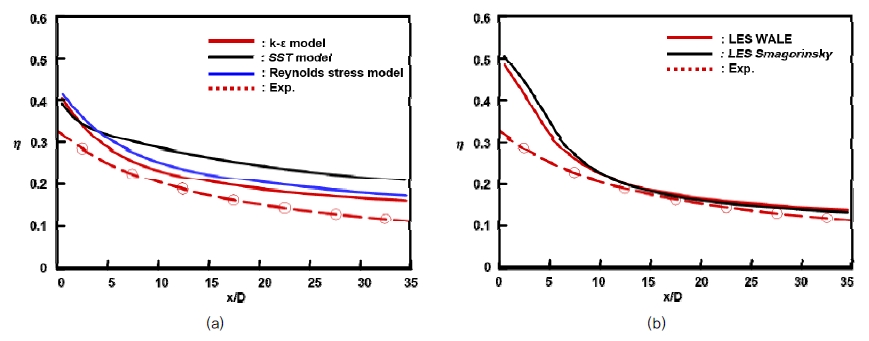
횡방향 면적평균된 막냉각 효율 분포의 경우, Fig. 5 (a)의 RANS 해석결과에서는 k-ε 모델의 해석결과가 실험결과와 가장 가까운 값을 나타낸다. 레이놀즈 응력모델의 경우 k-ε 모델 결과보다 전체적으로 0.02정도 높은 값을 나타내며, SST 모델의 경우 막냉각 홀 출구에서의 막냉각 효율값은 다른 두 개의 난류모델을 적용하였을 때와 유사한 값을 보이나 하류로 갈수록 막냉각 효율 값이 다른 난류모델을 적용하였을 때 보다 높은 값을 나타내며 x/D=35에서 실험값보다 약 0.1 정도 높은 값을 나타낸다.
Fig. 5 (b) 의 LES 해석의 경우 WALE, Smagorinsky 모델이 적용되었을 때 모두 막냉각 홀 출구직후에서 막냉각 효율 값이 매우 크게 나타난다. 이는 앞서 Fig. 3에서 설명한 것과 같이 막냉각 홀 측면으로 분사된 냉각유체의 영향으로 생각된다. 하류로 갈수록 급격히 막냉각 효율이 감소하기 시작하여 x/D가 10 이후부터는 실험에서 측정한 막냉각 효율값과 매우 유사한 분포를 나타낸다.
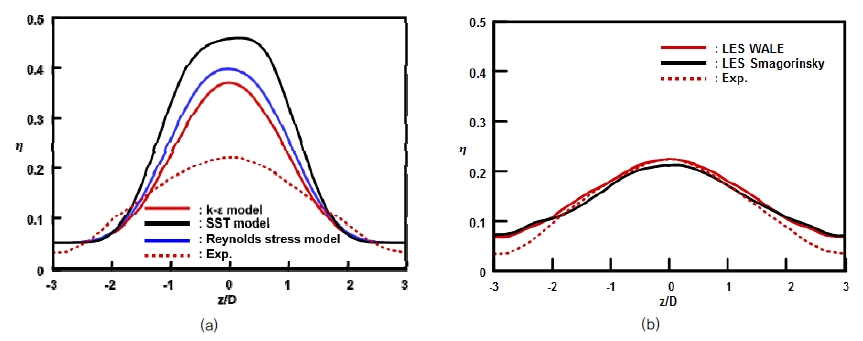
Fig. 6 (a)와 (b)는 각각 RANS 및 LES 해석결과에서 x/D=5 위치에서의 횡방향 막냉각 효율 분포를 나타낸다. Fig. 6 (a)의 RANS 해석결과에서는 막냉각 홀 중심에서는 전체적으로 수치해석의 결과가 실험값보다 높게 나타난다. k-ε 모델의 경우 ∩형태의 막냉각 효율 분포를 나타내지만, SST 모델 및 레이놀즈 응력모델의 경우 막냉각 홀 중심이 아닌 좌우에서 가장 높은 효율값을 나태내고 있다. 한편 LES 해석결과에서는 중심에서 막냉각 효율 분포가 실험값과 동일한 완만한 ∩형태를 나타내고 있으며, 막냉각 홀 중심에서의 막냉각 효율은 실험값과 큰 차이를 보이지 않으나, z/D의 값이 1 이상이 되면 실험값보다 높은 값을 나타낸다. 이는 앞서 설명한 것과 같이 막냉각 홀 측면에서 분사되어 주 유동을 따라 흐르는 냉각유체의 영향으로 생각된다. Fig. 7 (a)와 (b)에서는 훨씬 하류인 x/D=30 위치에서의 횡방향 막냉각 효율 분포를 나타낸다. RANS 해석결과에서는 실험값에 비해 매우 높은 막냉각 효율을 나타낸다. 난류모델에 따라 중심선에서 0.15~0.25이상 실험값보다 큰 값을 나타낸다. 반면에 LES 해석결과에서는 WALE 모델의 경우 실험값과 거의 차이를 보이지 않으며, Smagorinsky 모델의 경우에도 실험값보다 약간 작은 값을 나타내지만 RANS 해석모델에 비해 잘 일치한다고 볼 수 있다. 상류에서는 z/D값이 작을수록 LES 해석결과에서의 막냉각 효율이 크게 나타났으나, 하류에서는 그 차이가 줄어들어 전체적으로 LES 해석결과는 실험값과 잘 일치한다고 볼 수 있다.
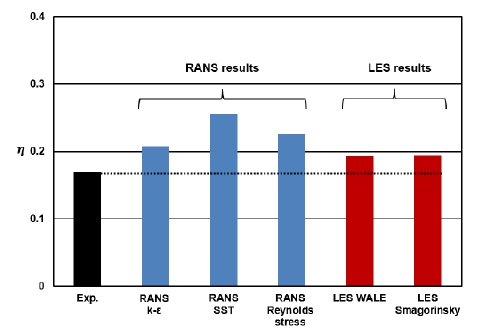
Fig. 8에서는 x/D가 3~35 사이의 평면에서 막냉각 효율을 면적 평균한 값을 비교하고 있다. 실험값은 약 0.17인데 반해 RANS 해석결과는 최소 0.21에서 최대 0.26까지 분포하며 이는 실험값 대비 약 20~50% 정도 큰 값이다. 반면에 LES 해석결과는 아격자 모델에 관계없이 약 0.19의 값을 나타내며 이는 실험값 대비 12% 정도 큰 값이다. LES해석결과는 측면에서 분사되는 냉각유체로 인하여 막냉각 홀 출구 직후에서의 막냉각 효율이 높게 예측된 것 때문으로 판단된다.
본 연구에서는 LES 해석모델 중 WALE 모델을 적용한 해석결과가 가장 실험값과 유사한 막냉각 효율 분포를 나타낸다고 판단하여 WALE 모델을 적용한 해석결과에 대해 내부 유동장 분석을 수행하였다.
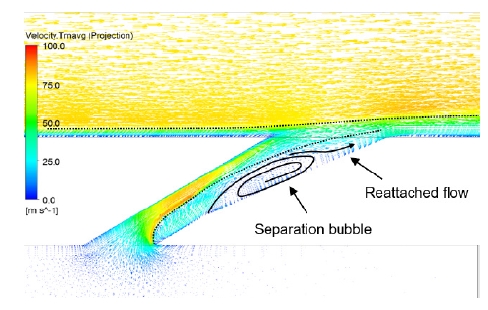
Fig. 9는 계산영역 중 중심선을 따라 자른 단면에서의 속도벡터 분포를 보여주고 있다. 팬형상 막냉각 홀의 경우 Fig. 1의 확장각(Laidback) 영역의 면적이 증가하면서 해당영역에서 역압력 구배 영역이 형성된다. 이에 막냉각 홀 입구에서 유동이 박리되어 속도가 크게 줄어들게 되고 확장각 영역에 이르러서는 역압력 구배를 극복하지 못하고 재순환 영역이 발생한다. 이후 막냉각 홀 출구 근처에서 유동이 재부착된다. 이에 대부분의 냉각유체는 해당영역을 회피하여 막냉각 홀 전연으로 치우쳐 분사가 된다. 분사되는 냉각유체는 해당 영역을 통과하면서 속도구배에 따른 와도(Vorticity)를 가지게 된다. 이에 해당 와도를 가지고 분사되는 냉각유체가 Fig. 10 (a)와 같이 와류(Vortex)로 발달하면서 분사된다. 막냉각 효율이 0.5인 지점까지는 해당 와류가 구조를 유지한 채 벽면을 따라 하류로 흐르면서 벽면을 보호하여 높은 막냉각 효율이 나타나는 영역을 형성한다. 이후 와류가 붕괴되고 소산됨에 따라 냉각유체의 상당량이 주 유동과 혼합하게 되고, 냉각유체의 일부는 평판을 따라 흐르며 하류까지 막냉각 효과를 유지시킨다. 이에 해당영역에서 막냉각 효율이 급격하게 감소하는 것으로 보인다. 즉 평판 막냉각 유동에 있어서 LES 해석방법을 통해 모사되는 대와류가 막냉각 홀 주변의 유동장 및 막냉가 효율분포를 설명하는데 매우 중요한 역할을 담당하는 것으로 보인다. 반면 RANS 해석의 경우 기본적으로 해당 와류들에 대한 난류 에너지 및 난류 점성 등의 정보로 평균된 유동장을 해석하기 때문에 막냉각 홀 주변의 유동장 및 이에 따른 막냉각 효율 분포를 정확히 예측하는데 어려움이 있다.
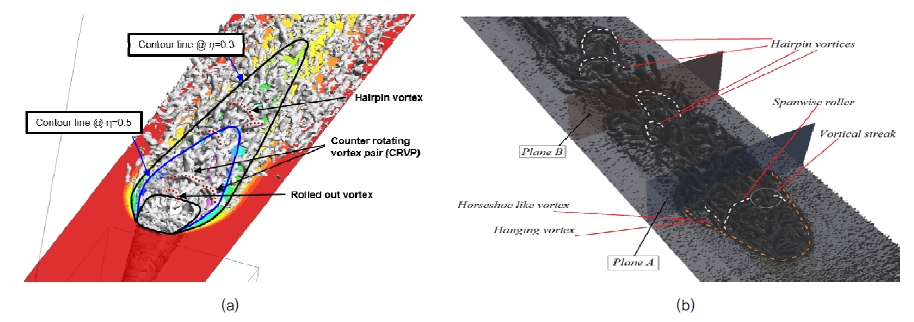
Vortex structure distributions from (a) CFD result with LES WALE and (b) CFD result by Simiriotis(1) (DR=1.48, BR=1.55)
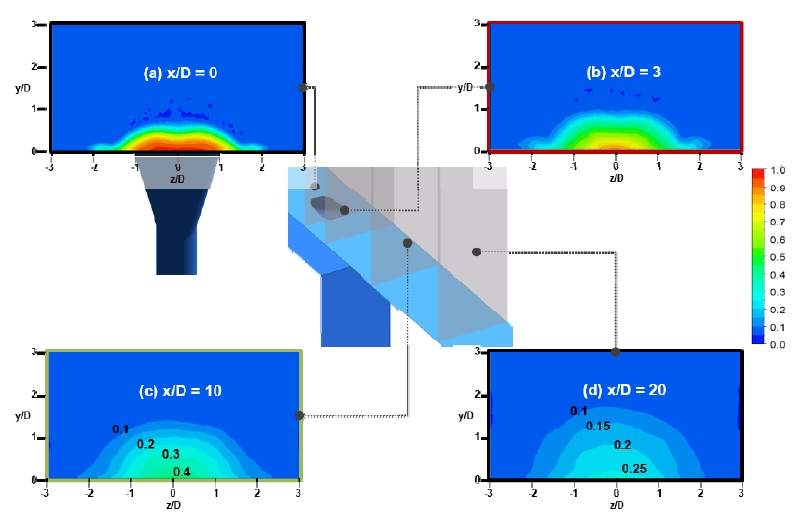
Fig. 11은 막냉각 홀 하류에서의 식 (5)와 같이 정의된 무차원 온도 분포를 나타낸다.
| (5) |
막냉각 홀 후연(x/D=0) 위치에서는 분사된 냉각유체가 와류로 발달하면서 중심선을 기준으로 좌우가 약간 볼록하며 냉각유체가 얇게 펴진 것을 확인할 수 있다. 하지만 하류로 이동할수록 와류의 소산 및 주 유동과의 혼합이 활발히 이루어짐에 따라 무차원 온도값이 크게 떨어져 x/D가 20에 이르면 주 유동과의 온도차가 크게 줄어들게 된다. 또한 분사비가 1.0으로 크지 않고 팬 형상 막냉각 홀로 분사되는 냉각유체의 특성으로 인해, 냉각유체가 벽면에서 이탈하지 않고 벽면에 따라 이동하는 것을 알 수 있다. 유사한 분사비 및 밀도비의 조건에서 운용되는 팬형상 막냉각 홀에 대해 Atul 등(11)이 시험을 통해 측정한 무차원 온도 분포에서도, Fig. 12와 같이 동일한 무차원 위치에서 본 LES 해석결과와 유사한 무차원 온도 분포를 나타내는 것을 확인할 수 있다.

Non-dimensional temperature distributions where (a) X/D=0 (b) x/D=3 and (c) x/D=10 from experimental data (BR=0.8, DR=1.6, Atul et al.(11))
이상의 결과로부터 막냉각 유동장에서 대와류의 발생 및 소산 등의 현상이 냉각유체의 거동 및 막냉각 효율을 예측하는데 지배적인 영향력을 행사하는 것을 확인할 수 있었다. 이러한 현상은 RANS 해석을 통해서는 예측이 불가능하며, 이러한 이유로 RANS 해석결과와 실험결과 사이에 차이가 발생하는 것으로 생각된다.
3. 결 론
본 연구에서는 주 유동 대비 30° 각도로 분사되는 7‐7‐7 팬 형상의 막냉각 홀에 대해, 난류모델에 따른 RANS 해석 및 LES 해석을 수행하여, 이를 선행연구에서 측정한 막냉각 효율 분포와 비교하여 아래와 같은 결론을 얻을 수 있었다.
- 1) RANS 해석결과에서는 k-ε 모델을 사용하였을 때에 가장 실험결과와 유사한 막냉각 효율 분포를 나타내었다. 이는 k-ε 모델이 SST 모델이나 레이놀즈 응력모델에 비해 주 유동과의 혼합되기 쉬운 모델 특성에 기인한다고 생각된다.
- 2) 하지만 전체적으로 RANS 해석결과는 실험값보다 높은 막냉각 효율 분포를 나타낸다. 이에 RANS 해석을 통해 막냉각 효율을 예측하기 위해서는, RANS 해석결과와 실험결과와의 차이에 대한 데이터를 충분히 확보하여 RANS 해석결과로부터 실제 막냉각 효율을 도출할 수 있어야 할 것이다.
- 3) LES 해석결과는 아격자 모델과 관계없이 실험결과와 막냉각 효율의 정성정 분포 및 위치별 정량적 분포가 매우 유사함을 확인하였다. 막냉각 홀 측면에서 분사되는 냉각유체로 인해 막냉각 홀 직후에서는 실험값에 비해 막냉각 효율이 높게 예측되었으나, 하류로 이동할수록 실험값과의 차이가 줄어드는 경향을 보였다.
- 4) 막냉각 홀 전연에서 속도구배에 따른 와도를 가진 냉각유체가 주 유로로 혼입되면서 와류로 발달하며, 해당 와류가 벽면을 따라 하류로 흐름에 따라 높은 막냉각 효율 영역을 형성한다. 해당 와류가 붕괴되어 소산과정을 거치며 일부는 주 유동과 혼합되고 일부는 벽면을 따라 흐르면서 하류까지 막냉각 효과를 유지시킨다. 이는 LES 해석에서 예측된 대와류가 냉각유체의 유동장 분포 및 이에 따른 막냉각 효율 분포에 지배적인 영향을 미치는 것을 의미한다.
기호설명
| BR : | 분사비 (Blowing ratio) |
| D : | 냉각홀 직경 (Cooling hole diameter) |
| DR : | 밀도비 (Density ratio) |
| Re : | 레이놀즈 수 (Reynolds number) |
| T : | 온도 (Temperature) |
| : | 시간평균 온도 (Time averaged temperature) |
| U : | 속도 (Velocity) |
| : | 무차원 온도 (Non-dimensional temperature) |
| η : | 막냉각 효율 (Film cooling effectiveness) |
| ρ : | 밀도 (Density) |
| μ : | 동점성 계수 (Dynamic viscosity) |
하첨자
| c : | 냉각유체 (Cooling flow) |
| aw : | 단열벽면 (Adiabatic wall) |
| ∞ : | 주 유동 (Main Flow) |
Acknowledgments
본 연구는 항공우주부품기술개발사업의 일환으로 수행 중인 ‘항공기용 가스터빈 블레이드 적용을 위한 고효율 fan shaped 막냉각 홀 기술 개발’ 과제(과제번호 : 10083654)의 지원을 받아 수행되었습니다.
References
- Simiriotis, Nikolaos, (2016), “Large Eddy Simulation of the Film Cooling Flow System of Turbine Blades: Public Shaped Holes”, Master Thesis, Institut Superieur de l’Aeronautique et de l’Espace.
- Schroeder, R. P., and Thole, K. A., (2013), “Shaped Hole Literature Review Database,” Penn State Experimental and Computational Convection Laboratory (ExCCL), Web, <http://www.mne.psu.edu/psuexccl/>.
- Robert P. Schroeder, and Karen A. Thole, (2014), “Adiabatic Effectiveness Measurements for a Baseline Shaped Film Cooling Hole,” ASME GT2014-25992.
- Perry L. Johnson, (2012), “Large Eddy Simulation of a Film Cooling Flow Injected From an Inclined Discrete Cylindrical Hole Into a Cross flow With Zero-Pressure Gradient Turbulent Boundary Layer,” NASA/TM 2012-217295.
- Andrew, Duggleby, Josh L. Camp, and Greg, Laskowski, (2013), “Evaluation of Massively-Parallel Spectral Elemenent Algorithm for LES of Film-Cooling,” ASME GT2013-94281.
-
Shuo Li, Jiemin Zhan, Yejun Gong, and Wenqing Hu, (2015), “Numerical investigation of film cooling using RANS and LES”, Procedia Engineering, 126(70), p1-705.
[https://doi.org/10.1016/j.proeng.2015.11.274]

- 나상권, (2008), “CFD를 이용한 막냉각 (Film-Cooling) 해석”, 유체기계저널, 11(6), p64-68.
-
Kim, S. M., Lee, K. D., and Kim, K. Y., (2011), “Numerical Study on Film-Cooling Effectiveness for Various Film Cooling Hole Schemes”, The KSFM Journal of Fluid Machinery, 16(4), p92-99.
[https://doi.org/10.6112/kscfe.2011.16.4.092]

-
Cho, M. Y., Lee, J. C., and Kim, Y. J., (2014), “A Study on the Film-cooling Characteristics of Gas Turbine Blade with Various Area Ratios and Ejection Angles of the Double Jet Holes”, The KSFM Journal of Fluid Machinery, 17(3), p59-64.
[https://doi.org/10.5293/kfma.2014.17.3.059]

- Seo, H. J., Park, S. H., Kang, Y. S., and Kwak, J. S., (2018), “Optimization of Fan Shaped Film Cooling Hole with Injection Angle of 30°”, Korean Society of Propulsion Engineers Spring Conference, TB4-1.
- Atul Kohil and David G. Bogard, “Effects of Hole Shape on Film Cooling with Larger Angle Injection”, ASME 99-GT-165.