SMART 원자로 자연대류 현상 모의 개별효과실험 및 해석
Abstract
The SMART is a small modular nuclear reactor that was developed at the Korea Atomic Energy Research Institute and is in the process of being evaluated using intense validation tests for future construction in Saudi Arabia. The system design was based on accidents that include station black out, in which the SMART can assure integrity of nuclear fuels by removing decay heat through natural circulation. Facility to Investigate Natural Circulation in SMART (FINCLS) was constructed to understand single- and two-phase natural circulation phenomena in SMART using a simplified loop. Two single-phase natural circulation tests were performed under two different pressures(i.e., 1.1 MPa and 2.5 MPa). When the heater power was increased, the circulation mass flow rate increased due to the higher density-driven force. The experimental results were compared with those from a force-balance equation and from a code calculation. For the code calculation, the MARS-KS code was employed by considering FINCLS geometry and the heat loss. The error in the flow rate from the force-balance equation improved from 6.2% (1.1 MPa) and 10.7% (2.5 MPa) to 2.7% (1.1 MPa) and 3.0% (2.5 MPa), respectively, when the core to steam generator elevation difference was defined based on the density distribution rather than the geometry. In the MARS-KS code calculation, the error was 1.1 % at 1.1 MPa, but the error increased to 5.5% at 2.5 MPa. At 2.5 MPa, the temperature profile inside the steam generator was not well reproduced, which led to higher driving force. Further analysis is required using a wider range of test data.
Keywords:
SMART, Integral reactor, Natural circulation, MARS, Force-balance equation키워드:
SMART 원자로, 일체형 원자로, 자연순환, 힘 평형 방정식1. 서 론
한국원자력연구원에서 개발한 일체형 원자로인 SMART (System-Integrated Modular Advanced Reactor)(1)는 330 MW의 열출력을 생산하며 전기 생산 및 해수 담수화를 목적으로 한 원자로이다. SMART는 가압기, 증기발생기, 원자로냉각재펌프, 원자로 노심이 하나의 압력용기에 담겨 있어 대형 배관의 파단을 가정하는 대형냉각재상실사고를 원천적으로 배제하고 있다.
또한 후쿠시마 원자력 발전소 사고 이후 안전성 향상을 위한 노력이 진행되어 SMART의 피동안전계통 비중이 강화되었다. 피동안전계통이란 펌프와 같이 외부 전원에 의해 작동하는 기기를 이용하지 않고, 자연 구동력만을 이용하여 사고 시에 노심의 건전성을 보장하는 계통을 가리킨다. SMART의 대표적인 피동안전계통으로는 중력에 의해 냉각수를 주입하는 피동안전주입계통이나 자연순환에 의해 노심의 잔열을 제거하는 피동잔열제거계통이 있다. 중력이나 자연순환은 펌프와 같은 기기에 비해 구동력이 작기 때문에 예측이 어렵고 실험에 의한 검증이 필요하다. 따라서 다양한 설계 기준 사고 상황에서 SMART의 피동안전계통 성능을 검증하기 위하여 SMART 종합시험장치(SMART-ITL, SMART Integral Test Loop)가 구축되었고 이를 이용한 다수의 시험이 수행되었다. 하지만 SMART-ITL은 대규모 종합효과 실험장치이므로 매 시험마다 많은 인력과 비용이 소모되며 장치의 변경이 어렵다. 따라서 다양한 사고 조건 및 유로형상에 따른 자연순환 경향을 확인하기 위하여 개별효과실험장치인 FINCLS (Facility to Investigate Natural Circulation in SMART)가 구축되었다. FINCLS는 SMART 설계안전사고 시 과도상황을 모의하며, 파단이 없는 경우(소내정전사고나 주급수파단 사고) 단상 자연대류 및 파단이 있는 경우(소형냉각재상실사고) 이상 자연대류 현상을 모두 다룬다.
본 논문에서는 FINCLS를 이용한 단상 자연순환 실험 및 분석 결과를 소개한다. 특히 자연순환 유량은 노심의 잔열제거에 중요한 변수이기에 정확한 예측이 필요하다. 따라서 FINCLS 실험에서 얻어진 정상상태 자연순환 유량에 대하여 힘평형 방정식의 적용 가능성 및 개선 가능성을 살피었고, 이후 1차원 열수력 해석코드인 MARS-KS 코드의 예측 능력을 확인하였다.
2. 실험 장치 및 실험 결과
2.1 실험 장치
FINCLS는 SMART의 단상 및 이상 자연순환 유동 특성을 연구하기 위해 구축된 실험시설이다. FINCLS는 SMART 설계보다는 실험 데이터가 있는 SMART-ITL을 기반으로 축소 설계되었으며, SMART-ITL과 비교하여 일차계통 자연순환 및 차압 특성을 다양한 조건에서 상세하게 계측할 수 있다는 장점이 있다. 척도법으로는 열수력 특성을 보존하기 위하여 체적 척도법(3)을 사용하였다. 실험시설의 높이는 SMART-ITL과 동일하며, 유동 면적과 노심 출력은 1/64로 축소되었다. FINCLS와 SMART-ITL의 척도 변수와 척도 비는 Table 1에 나타나있다. 본 시험 장치는 체적 척도법을 사용하였기 때문에 이론적으로 원형에 비해 압력강하가 증가한다. 그러나 계통을 단순화하였기 때문에 예비 계산 결과 시험장치의 구간별 압력강하 값은 설계 압력강하 값에 비해 작게 나타났다. 이러한 압력강하 값 차이를 보정하기 위해 유로 구간별 오리피스 플레이트를 설치하여 실험장치의 압력강하 값을 설계 값에 맞출 수 있도록 하였다.
Scale ratio of FINCLS
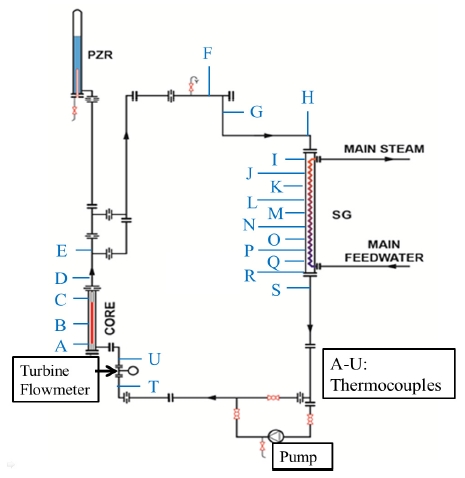
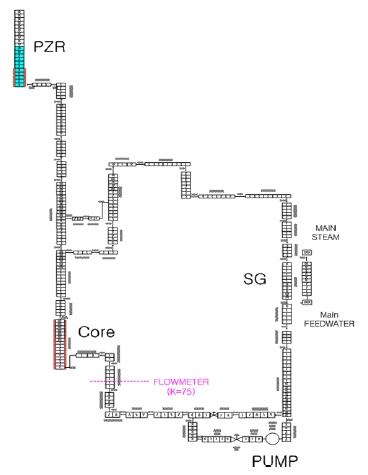
Fig. 1은 FINCLS의 개략도를 나타낸다. FINCLS는 일차계통과 이차계통으로 구성되어 있다.
Schematic of FINCLS
FINCLS의 일차계통은 노심, 가압기, 증기발생기, 원자로냉각재펌프로 구성되어 있으며 일차계통 설계 압력과 온도는 각각 17 MPa, 360 ℃이다. 노심 히터는 조립을 용이하게 하도록 가열구간 및 비가열구간을 포함한 봉으로 설계하였다. 노심 히터의 최대 출력은 50 kW이며, 이는 SMART의 정상운전 출력의 47.5%에 해당한다. 노심 히터는 SCR (Silicon-Controlled Rectifier)에 의해 조절되며 넓은 출력 범위에 대하여 다양한 자연순환 실험을 가능하게 한다. 가압기는 일차계통 상부에 위치하며 가압기 히터의 출력 제어를 통해 일차계통의 압력 조절에 활용된다. 가압기 상부에는 공기 제거와 압력 조절을 위한 분출라인과 제어밸브가 설치되어 있다. 증기발생기의 주요 설계 요소로는 열전달 면적, 유동 면적, 체적이 있으며, 열전달 요건을 충족하도록 증기발생기가 설계되었다. 증기발생기 내 열교환기의 설계 조건은 17 MPa, 360 ℃이며, 일차계통의 설계 조건과 일치한다. 또한 모든 배관에 계통의 열손실을 막기 위한 단열재가 설치되어 SMART 자연순환 모의의 왜곡을 최소화하였다.
일차계통의 온도, 압력, 및 유량을 측정하기 위하여 다양한 계측기들이 설치되었다. 열전대의 번호 및 위치는 자연순환 유로를 따라 Fig. 1에 알파벳으로 표기하였다. 계측기의 정밀도는 Table 2에 나타나있다.
Accuracy of instruments in FINCLS
일차계통의 가압 및 예열 과정 중에는 일차계통 하단부에 설치된 순환 펌프를 작동하여 노심 히터의 건전성을 보장하였고, 자연순환 시험 중에는 순환 펌프를 정지하고 펌프 전단과 후단의 밸브를 폐쇄하였다.
이차계통은 0.5 MPa보다 작은 압력에서 운전되며, 개방 루프(Open Loop) 형태를 가진다. 이차계통에는 급수를 저장하기 위한 재장전수조 및 수조 내 물의 온도를 유지하기 위한 히터가 설치되어 있다. 급수 유량을 조절하기 위하여 이차계통의 하단부에 펌프를 설치하였고 펌프의 회전속도로 이차계통의 유량을 제어하였다. 증기발생기 입구 및 출구의 온도와 압력을 측정하도록 계측기가 설치되어 있으며 증기발생기에서 방출된 물과 증기는 대기로 방출되었다.
2.2 실험 방법 및 결과
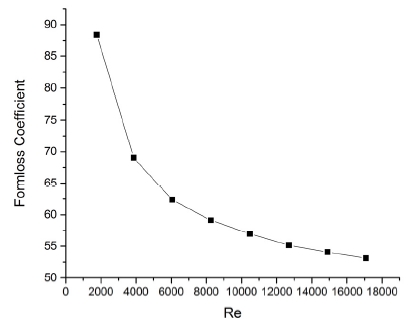
본 시험에 앞서 시험장치 특성시험을 수행하여 계통 내 압력강하특성을 확인하였다. 특별히 유량을 점차 증가시키며 압력강하가 많이 발생하는 노심 입구의 터빈 유량계 형상손실계수를 확인하였다. 이를 통해 Fig. 2에서 나타내는 것과 같이 유량계의 형상손실계수 값을 레이놀즈 수의 함수로 얻었다.
Form loss coefficients of turbine flowmeter at different Reynolds numbers
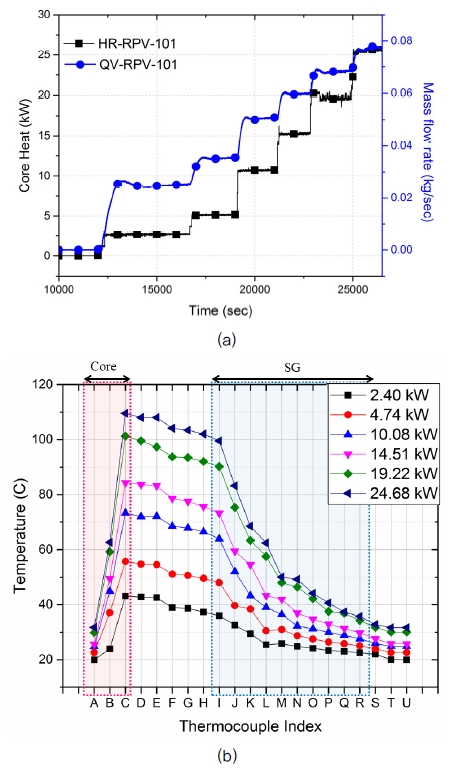
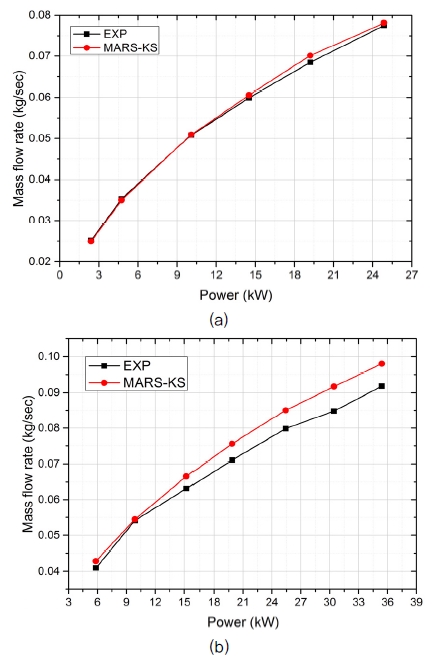
SMART에서 설계사고사고 시 노심출력정지 이후 일차계통 압력이 15 MPa에서 대기압까지 서서히 감소한다. 따라서 다양한 압력 조건에서의 자연대류 모의실험이 필요하다. 우선 1.1 MPa 과 2.5 MPa 조건에서의 일차계통 단상 자연순환 실험을 수행하며 노심출력에 따른 순환유량을 측정하였다. Table 3은 실험 조건 및 주요 결과를 나타낸다. 일차계통의 과냉도를 확보하기 위해 가압기 히터를 이용하여 계통 압력을 일정하게 유지시키고, 상온에서 천천히 노심출력을 인가하였다. 노심 출력 값은 최소 2.40 kW에서 최대 35.74 kW까지 변화시켰으며, 이 출력범위는 SMART 정상운전 출력 대비 최소 2.3%에서 최대 33.8%에 해당한다. 각각의 출력에서 이차계통의 유량을 조절하여 일차계통의 온도, 압력, 유량을 정상상태 조건으로 유지하였다. Fig. 3은 1.1 MPa 실험에서 각 노심 출력 별 일차계통 자연순환 유량 및 위치별 온도 분포를 나타낸다. 실험에서 증기발생기 출구와 노심 입구를 연결하는 배관(S-U)은 전체적으로 일정한 온도를 나타냈으나 노심 출구와 증기발생기 입구를 연결하는 배관(D-H)은 열손실로 인한 온도 감소를 나타냈다.
Experimental Conditions and Results
(a) Mass flow rate trend, and (b) steady-state temperature distribution for the 1.1 MPa test
3. 해석 방법
3.1 힘평형 방정식 해석
Vijayan은 열원과 열침원의 방향이 수직일 때와 수평일 때 단상 및 이상 자연순환 실험을 수행하였으며, 힘평형 방정식으로부터 자연순환 유량 상관식을 제시하였다(4-7). 이와 같은 힘평형 방정식을 사용할 때에 열수력 조건에 따른 유동 특성에 관한 통찰력을 얻을 수 있으며 해석코드를 사용하지 않아도 쉽게 자연순환 유량을 예측할 수 있다.
식 (1)은 중력과 마찰력의 평형을 나타낸 정상상태 힘평형 방정식이다.
| (1) |
식 (1)에서 g, ρ, z, N, fi, Li, Di, Ki, W, Ai는 각각 중력가속도, 밀도, 길이방향 거리, 구간 개수, 구간 i의 마찰손실 계수, 구간 i의 길이, 구간 i의 직경, 구간 i의 형상손실 계수, 자연순환유량, 구간 i의 면적을 나타낸다. FINCLS 장치 내 배관의 크기가 자주 바뀌기 때문에 총 구간을 12개로 나누었다.
식 (1)에서 열손실을 무시하여 노심 출구에서 증기발생기 입구까지의 온도가 일정하고, 증기발생기 출구에서 노심 입구까지의 온도가 일정하다고 가정하면 식 (1)은 다음과 같이 표현된다.
| (2) |
식 (2)에서 ρc와 ρh는 각각 노심 입구 및 출구의 밀도를 나타낸다. 노심 입구 온도를 알면 노심 출구의 온도는 다음 식을 통해 쉽게 계산할 수 있다.
| (3) |
이 때, h는 엔탈피를 가리키며, qh는 노심 히터 출력을 가리킨다.
식 (2)의 마찰손실 계수로는 Vijayan이 제시한 레이놀즈 수와 마찰 손실계수와의 관계를 사용하였다.
| (4) |
| (5) |
| (6) |
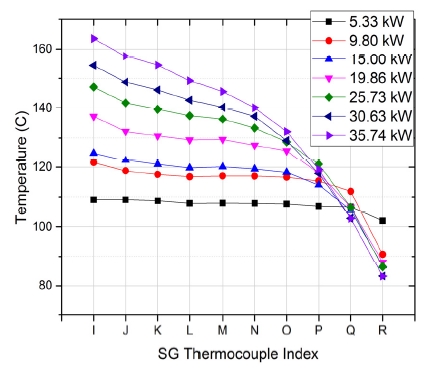
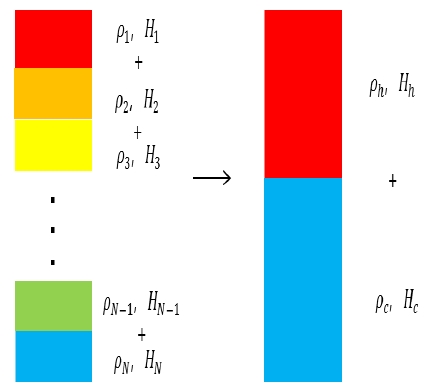
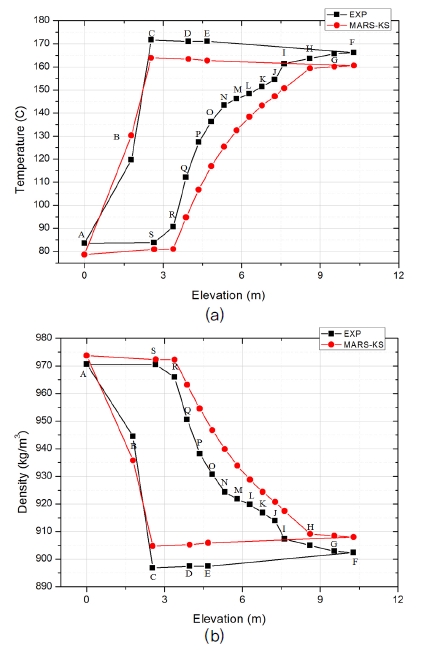
추가로 식 (2)의 좌변에서 노심과 증기발생기의 높이 차(H)를 계산해야 하는데, 가장 쉽게 계산하는 방법은 노심과 증기발생기의 설치 위치를 기반으로 기하학적 중심 높이 차를 계산하는 것이다. 이와 같이 계산하면 노심과 증기발생기의 높이 차는 4.07 m가 된다. 또 다른 높이 차 계산 방법은 노심과 증기 발생기 내 온도 변화를 반영하여 중심높이 차를 계산하는 것이다. Fig. 4의 (a)와 (b)는 1.1 MPa 실험과 2.5 MPa 실험의 증기 발생기 내부 온도 분포를 나타낸다. 1.1 MPa 실험의 경우 이차계통의 유량이 크기 때문에 증기발생기 전반에 걸쳐 이차계통 유체가 낮은 온도를 유지한다. 따라서 증기발생기 상부에서부터 일차계통 유체의 온도가 급격히 감소한다. 반면 2.5 MPa 시험의 경우, 이차계통의 유량이 낮기 때문에 증기발생기의 상부에 도달할 때 이차계통 유체가 높은 온도를 갖게 된다. 따라서 증기발생기의 상부에서는 열전달이 잘 되지 않으며 하부에서 열전달이 활발하게 일어난다.
Temperature profiles in the steam generator (SG) at (a) 1.1 MPa, (b) 2.5 MPa
노심이나 증기발생기 내부 온도 변화를 반영한 중심 높이 개념은 Fig. 5에 나타나있다. 예를 들어 증기발생기 내부 온도가 서서히 감소한다고 할 때, 이에 따라 내부 밀도는 서서히 증가한다. 증기발생기 중심 높이를 계산할 때, 중심 높이 이하는 노심 입구 온도의 차가운 물로 차있고 중심 높이 이상은 노심 출구 온도의 뜨거운 물로 가득 차 있다고 가정한다. 이 때, Fig. 5에서 왼쪽의 온도가 서서히 변한 물의 중력과 Fig. 5에서 오른쪽의 단순화된 물의 중력이 같아야 한다. 이를 수식으로 정리하면 다음과 같다.
Concept for average elevation difference calculation
| (7) |
식 (7)에서 NTC는 노심이나 증기발생기에 설치된 열전대 개수를 가리킨다. 노심 내 열전대 개수(NTC)는 3개이며, 증기발생기 내 열전대 개수(NTC)는 10개이다. Hi는 설치된 열전대의 각 높이를 나타내며, ρi는 열전대로 측정한 온도로부터 얻은 밀도를 나타낸다. ρc와 ρh는 각각 노심 입구와 출구 온도로부터 얻은 밀도를 가리킨다.
이 때, Hc와 Hh의 합은 노심이나 증기발생기의 길이(Ht)에 해당한다.
| (8) |
식 (8)을 식 (7)에 대입하여 중심 높이인 Hc에 대해 정리하면 다음과 같다.
| (9) |
노심과 증기 발생기에서 계산된 식 (9)의 Hc를 활용하여 최종적으로 노심과 증기발생기의 중심 높이 차를 계산한다.
| (10) |
Hc,SG와 Hc, Core는 노심과 증기발생기의 중심 높이이며, HSG는 증기발생기 바닥의 위치, HCore는 노심 바닥의 위치를 나타낸다. 식 (10)을 활용하여 출력 별 노심과 증기발생기의 높이 차이를 계산하였으며, Table 4는 그 결과를 나타낸다. 증기발생기와 노심의 기하학적 높이 차가 4.07 m임을 고려할 때, 1.1 MPa 시험의 경우 평균밀도를 이용한 높이 차가 약 1 m 가량 증가하였다. 이는 이차계통의 유량이 크기 때문에 증기발생기의 열전달이 상부에서 많이 이루어졌기 때문이다. 반면 2.5 MPa의 시험의 경우, 평균밀도를 이용한 중심 높이가 기하학적 중심 높이보다 80 cm 정도 낮게 계산되었다. 이는 이차계통의 유량이 낮기 때문에 열전달이 증기발생기 하부에서 많이 이루어졌기 때문이다.
SG-Core elevation difference at different core power levels. (Test 1: 1.1 MPa, Test 2: 2.5 MPa)
Table 4의 노심과 증기 발생기의 중심 높이 차이는 식 (2)에 적용되어 자연순환 유량을 계산하는데 활용되었다.
3.2 MARS-KS 코드 해석
MARS-KS (Multi-dimensional Analysis of Reactor Safety) 코드는 경수로의 과도현상을 해석하기 위한 열수력 안전해석 계통코드이다. MARS-KS 코드는 물과 증기의 이상유체에 대해 질량, 운동량, 에너지 보존방정식을 풀며, 다양한 유동양식 맵, 압력강하 및 열전달 모델들을 포함한다. 그 외에도 펌프나 밸브와 같은 기기들에 대한 모델도 포함한다.
Fig. 6은 FINCLS의 수치해석을 위한 격자 모습을 나타낸다. 격자를 만들 때 노심을 비롯한 기기들의 형상 및 높이를 실험 장치와 동일하게 설정하였다. 노드의 길이 대 직경 최소값은 22로 충분히 큰 값을 사용하였다. 노드 민감도 계산을 통해 수렴성을 확인하였으며, 수렴도에 따라 시간격자 크기를 조정하는 MARS 내 시간격자 계산방법을 이용하여 계산을 수행하였다. 노심 입구에 설치된 터빈 유량계의 형상손실계수 값으로 힘평형 방정식 계산 때와 동일하게 레이놀즈 수의 함수를 사용하였다. 또한 MARS-KS 모델 중 돌연 확대관 및 돌연 축소관 형상손실계수 모델을 이용하여 유로 면적 변화에 따른 압력강하를 반영하였다.
MARS-KS Nodalization for FINCLS
실험에서 열손실을 정확하게 측정하지 못하였기 때문에, 이 값은 임의로 설정하였다. 즉, 대기 중의 온도를 15 ℃로 설정하고 대기의 열 전달계수를 변화시키며 실험과의 온도 분포를 비교하여 적절한 값을 찾았다.
또한 계산 경계조건으로 실험과 동일한 노심 출력, 이차계통 급수 유량 및 온도를 설정하였다. 노심 출력은 열구조체를 통해 제공하였으며, 이차계통 급수 유량과 온도는 각각 Time-Dependent Junction/ Time-Dependent Volume을 이용하여 제공하였다. 일차계통의 압력을 유지하기 위해 가압기 히터의 출력을 압력 값에 따라 조절하였다. 일차계통의 노심 주입 온도는 증기발생기 내 열전달 및 배관 열손실에 의해 결정되는 것이기 때문에 따로 지정하지 않았다.
4. 실험 및 해석 결과 비교
4.1 힘평형 방정식 해석 결과
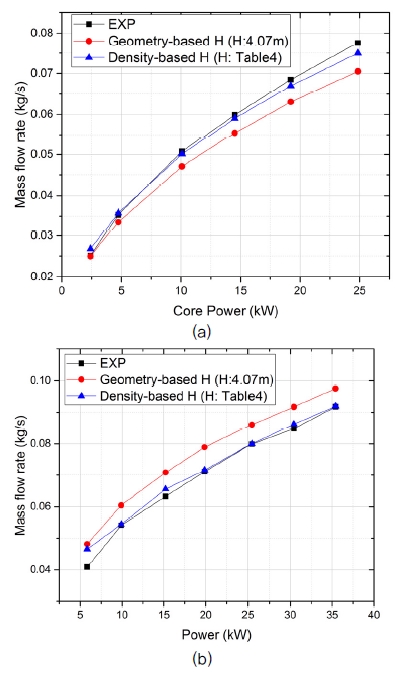
Fig. 7은 실험과 힘평형 방정식 (2)를 통해 얻은 자연순환 유량을 나타낸다. Fig. 7에서 가로축은 노심출력을 나타내며, 1.1 MPa 실험과 2.5 MPa 실험에서 각각 6단계 및 7단계로 노심 출력을 변화시켰다. 각 단계에서의 노심과 증기발생기의 높이 차로 Table 4에 나타나있는 밀도평균 높이차를 사용하였다. 출력의 상승에 따라 밀도차에 의한 구동력이 증가하여 유량이 점차적으로 증가하였다.
Mass flow rate from the experiment and heat-balance equation at (a) 1.1 MPa and (2) 2.5 MPa
특별히 증기발생기와 노심의 높이차 정의 방법에 따른 자연 순환 유량 예측의 정확도를 확인하였다. 기하학적 형상 높이차를 이용한 경우, 1.1 MPa 시험에서는 유량을 낮게 예측하였고, 2.5 MPa 시험에서는 유량을 높게 예측하였다. 평균 오차는 각각 6.2%, 10.7% 이었으며 최대 오차는 각각 9.1%, 17.8%이었다. 반면, 증기발생기와 노심의 내부 온도 변화를 고려하여 높이차를 계산한 경우 평균 오차가 1.1 MPa과 2.5 MPa 시험에서 각각 2.7%, 3.0% 이었으며 최대 오차는 6.5%, 13.9%로 예측능력이 상당히 향상되었다. 이는 밀도 차에 의한 자연대류 구동력을 계산할 때 온도 분포 혹은 밀도 분포를 적절히 반영하는 것이 중요함을 나타낸다. 마찬가지로 Vijayan 논문에서도 자연순환 상관식을 타 실험 데이터에 적용하였을 때 최대 오차가 54%에 이르렀으나 온도 변화에 따른 효과를 반영할 때 최대 오차가 12% 정도로 감소되었다.(5)
4.2 MARS-KS 코드 해석 결과
MARS-KS 코드는 힘평형 방정식 해석과는 다르게 노심, 증기발생기 및 배관 내부 온도 변화를 계산하기 때문에 노심과 증기발생기의 높이 차를 따로 입력해줄 필요가 없었고, 노심 입구 온도 또한 자동으로 계산되었다.
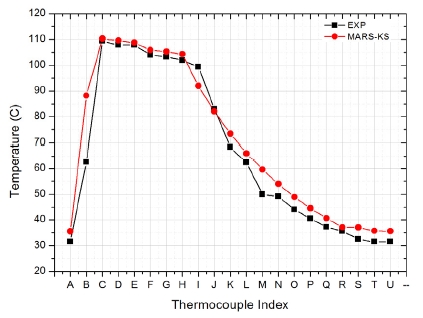
Fig. 8은 가압기 압력 1.1 MPa, 노심출력 24.68 kW 조건에서 실험과 MARS-KS 코드의 일차계통 온도분포를 나타낸다. Fig. 8의 가로축은 열전대 번호를 나타내며 각 열전대 위치는 Fig. 1에 나타나있다. 일차계통의 배관 열손실을 고려하기 위하여 대기로의 열전달계수 값을 설정하였다. 일반적으로 대기로의 열전달계수는 5-30 W/m2K 이기에 이 값을 변화시키며 실험결과와 비교하였다(8). 열손실을 고려할 때 노심출구에서 증기발생기 입구까지의 고온 영역 (D-H)의 온도경향 예측이 중요한데, 전반적으로 10 W/m2K에서 온도 감소 경향을 가장 잘 예측하였다. 따라서 본 논문에서는 대기 열전달계수 10 W/m2K의 계산 결과를 소개한다.
Temperature profile from the experiment and MARS-KS code at 24.68 kW and 1.1 MPa
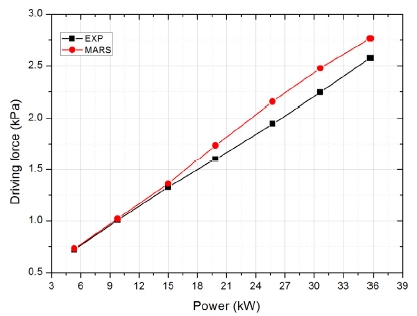
Fig. 9는 MARS-KS코드와 실험의 자연순환 유량 비교 결과를 나타낸다. 1.1 MPa 시험에서는 평균 오차 1.1% , 최대 오차 2.4%가 발생하였다. 2.5 MPa 시험에서는 평균 오차 5.5%, 최대 오차 8.1%로 최대 오차의 경우 차이가 발생하였다. 특히 출력이 높은 영역에서 오차가 더 커지는 문제가 발생하였다. 그 원인을 파악하기 위해 일차계통 유체 온도 및 밀도 분포를 확인하였다. Fig. 10은 가압기 압력 2.5 MPa, 노심출력 35.74 kW 조건에서 높이에 따른 온도 및 밀도 분포를 나타낸다. 특별히 증기발생기 영역에서 MARS-KS 코드가 온도를 낮게 예측하였기에 밀도를 높게 예측하였음을 볼 수 있다. 밀도를 높이에 대해 적분한 뒤 중력가속도를 곱하여 밀도차에 의한 구동력을 확인하였고, 그 결과는 Fig. 11에 나타나있다. MARS-KS 코드는 노심 출력이 높을 때 밀도차로 인한 구동력을 높게 예측하였다. MARS-KS 코드의 일차계통 단상 열전달 식으로 Zukauskas 식을 사용하였다. Zukauskas 식은 In-line 튜브가 수평하게 배열되었을 때를 기반으로 한 실험상관식이기에 나선형 열교환기가 설치된 FINCLS 증기발생기에 적용할 때 오차가 발생할 수 있다. 하지만 정확한 원인은 향후 추가 분석으로 확인할 필요가 있으며, 다른 압력 및 온도 조건에서 잘 예측하는지 확인하는 것이 필요하다.
Mass flow rate from the experiment and MARS-KS code at (a) 1.1 MPa and (2) 2.5 MPa
(a) Temperature and (b) density profile along elevation at 35.74 kW and 2.5 MPa
Gravity-driven force from the experiment and MARS-KS code at 2.5 MPa
5. 결 론
FINCLS는 SMART 일차계통에서 나타나는 단상 및 이상 자연순환 유동의 열수력 현상을 고찰하기 위해 구축된 개별효과 실험장치이다. 본 논문에서는 1.1 MPa과 2.5 MPa에서의 단상 자연순환 실험 결과를 제시하고, 힘평형 방정식과 MARS-KS 코드 계산 비교 결과를 제시하였다.
힘평형 방정식 계산에서는 노심과 증기발생기의 높이 차를 정의하는 방식이 중요하며, 형상정보를 기반으로 정의할 때, 자연순환 유량의 평균오차가 6.2% (1.1 MPa)와 10.7% (2.5 MPa)로 크게 나타났다. 반면 밀도 평균으로 높이 차를 정의할 때, 오차가 2.7% (1.1 MPa)와 3.0% (2.5 MPa)로 예측 능력이 상당히 향상되었다. MARS-KS 코드는 1.1 MPa의 순환유량은 평균 오차가 1.1%로 잘 예측하였으나 2.5 MPa의 순환유량은 평균 오차 5.5%로 상대적으로 잘 예측하지 못하였다. 밀도 분포 및 구동력 분석을 통해, 노심 출력이 높을 때 증기발생기 내부 온도 분포를 낮게 예측한 것이 과도한 구동력 증가로 이어짐을 확인하였다. 향후 다양한 온도 및 압력 조건에 대한 추가 분석을 수행할 예정이다.
Acknowledgments
이 논문은 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(SMART 고도화 공동개발사업, No. 2016M2C6A1004894)
References
- Kim, K. K., et al., (2014), “SMART: The First Licensed Advanced Integral Reactor”, Journal of Energy and Power Engineering, 8, p94-102.
- KAERI, (2009), “MARS code manual vol.1: Code structure, system models and solution methods.”.
- Bestion, D., D’Auria, F. Lien, P. and Nakamura, H., A State-of-the-art Report on Scaling in System Thermal-hydraulics Applications to Nuclear Reactor Safety and Design, NEA/CSNI/R(2016)14-3267.
-
Gartia, M. R., and Vijayan, P. K., and Pilkhwal, D. S., (2006), “A Generalized Flow Correlation for Two-phase Natural Circulation Loops”, Nuclear Engineering and Design, 236, p1800-1809.
[https://doi.org/10.1016/j.nucengdes.2006.02.004]
-
Swapnalee, B.T., and Vijayan, P. K., (2011), “A Generalized Flow Equation for Single Phase Natural Circulation Loops Obeying Multiple Friction Laws”, International Journal of Heat and Mass transfer Heat and Mass transfer, 54, p2618-2629.
[https://doi.org/10.1016/j.ijheatmasstransfer.2011.01.023]
-
Vijayan, P. K., (2002), “Experimental Observations on the General Trends of the Steady State and Stability Behaviour of Single-phase Natural Circulation Loop”, Nuclear Engineering and Design, 215, p139-152.
[https://doi.org/10.1016/s0029-5493(02)00047-x]
- Vijayan, P. K., Sharma, M., Pilkhwal, D. S., Saha, D., and Sinha, R. K., (2010), “A Comparative Study of Single-Phase, Two-Phase, and Supercritical Natural Circulation in a Rectangular Loop”, 132, p102913--1.
- Kakac, S., and Yener, Y., (1995), Convective Heat Transfer, CRC Press, p18.