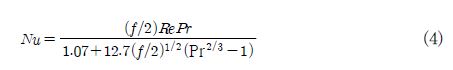Effect of the Configurations of Coolant Flow Passage on the Thermal-Flow Characteristics of Screw Compressor

1. 서 론

스크류 압축기는 원통형 밀폐용기 내에 로터가 서로 다른 반대방향으로 맞물려 회전하면서, 로터와 하우징 사이에 생기는 밀봉선(sealing line)에 의해 작동유체를 흡입, 압축, 토출시켜 압축공기를 만드는 장치이다. 스크류 압축기는 1934년 Lvsoholm에 의하여 발명된 이후, SRM(Svenska Rotor Maskiner)사를 주축으로 꾸준히 개발되어 왔고, 오늘날에는 많은 산업분야에서 사용되고 있는 중요한 에너지 전달체이다.

스크류 압축기 로터는 고압 상태의 공기를 얻기 위하여 하우징에서 고속으로 회전하게 된다. 이때 회전력과 체적변화에 따라 작동유체인 공기의 온도는 약 250℃까지 상승하게 되는데, 이러한 온도 분포가 지속적으로 유지되기 때문에 로터의 내구성을 확보하기 위하여 효과적인 냉각시스템 확보가 필요하다.

스크류 압축기 냉각 시스템은 복잡한 내부 냉각유로 구조를 가지고 있으며, 효과적인 냉각성능을 얻기 위하여 오래 전부터 터빈 블레이드 내부에 사용되었던 이중냉각유로를 적용하였다. 이중냉각유로는 기본적으로 두 개의 직관과 곡관이 연결되어 있으며, 곡관부로 작동유체가 유입되면서 발생하는 외벽과의 충돌, 회전에 의한 원심력, 그리고 이로 인한 유동박리(flow separation) 등으로 인하여 열전달 성능이 증가하게 된다. 또한, 곡관부에서 발생하는 압력강하는 전체 압력강하의 50∼60%를 차지할 정도로 곡관 내부 작동유체의 유동 특성에 큰 영향을 미친다. 따라서 보다 뛰어난 성능의 냉각유로 설계를 위하여 덕트 내부의 유동이 압력강하 및 열전달에 미치는 영향을 파악하는 것이 필수적이다.(1)

덕트 내부에서의 유동특성과 열전달 해석에 관한 실험과 이론적인 연구들이 많이 진행되어 왔다. 대부분의 연구들은 기하학적 변화와 Re 수 영향을 고찰하였으며, 상대적으로 큰 곡률 반경을 갖는 곡관을 따라 나타나는 현상에 대하여 초점을 두었다. 특히, 큰 곡률 반경을 따라 흐르는 작동유체는 급격한 회전력으로 인한 원심력에 의해 재순환 영역이 생성되기 때문에, 유동 성능과 열전달에 많은 영향을 미친다.(2)

관련된 선행 연구를 살펴보면 Prabhu와 Vedula(3)는 곡관 분리벽의 곡률 반경 변화에 따른 압력강하 특성에 대한 연구를 수행하였는데 분리벽의 곡률 반경이 증가할수록 내부에서 발생하는 유동박리 현상이 감소하여 압력강하가 감소한다고 밝혔다. Kim과 Cho(4)는 매끈한 덕트 내에서 나타나는 국소적인 압력강하 특성을 수치해석을 통해 고찰하였으며, 이를 통해 곡관부를 따라 흐르는 유동 방향이 하류로 급속히 전환되면서 압력차를 발생시켜 재순환 영역이 생성되는 것을 예측하였다. Su 등(5)은 이중냉각유로의 종횡비 변화에 따른 복잡한 내부 유동과 열전달 성능을 연구하였는데, 좁은 유로의 곡관부를 지나는 작동유체는 원심력과 회전력의 영향을 받아 하류에서 열전달이 잘 되는 것을 확인하였다.

냉각효율을 높이기 위해 냉각유로 형상 변화뿐만 아니라 난류 형성을 촉진하는 리브(rib)를 설치한 연구도 많은 연구자들에 의하여 수행되었다(6^∼9). 이들은 리브 설치를 통해 열전달 향상과 압력 강하 특성을 이론적으로 고찰하였으며, 딤플, 핀 등 유동간섭을 야기시키는 다양한 형상의 매개체를 설치하여 냉각 성능을 확보하는 방법에 대한 연구를 수행하였다.

본 연구에서는 선행 연구를 토대로 스크류 압축기 냉각유로의 최적 설계를 위해 이중냉각유로의 분리벽 길이비(L_s/D)와 두께비(t/D) 변화에 따른 압력강하 및 Nu 수 변화와 같은 열유동 특성을 고찰하였다.

2. 수치해석

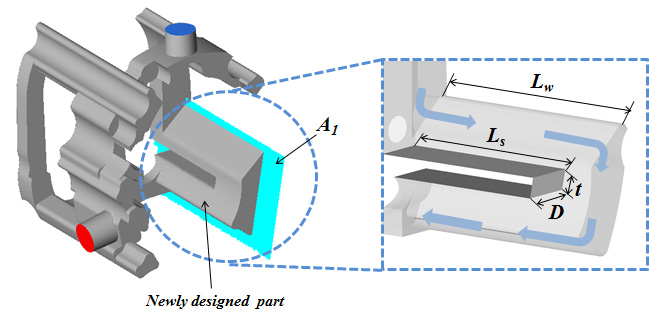
본 연구에서는 스크류 압축기 냉각유로의 수치해석을 위해 Fig. 1과 같이 스크류 압축기의 하우징(housing)과 냉각유로(water jacket) 영역으로 구성하였다. 선행 연구 결과를 토대로 기존 모델 보다 냉각 효율이 높은 냉각유로 설계를 위하여 이중냉각유로를 설계하였으며, Fig. 2에 새롭게 설계된 냉각유로를 나타내었다. 이중냉각유로의 길이비(L_w/D)와 분리벽의 길이비(L_s/D)에 대한 제원은 Table 1에 나타내었다.

Fig. 1

Geometry of the basic coolant passage model

Fig. 2

Geometry of the newly designed coolant passage model.

Table 1

Dimensions of the newly designed coolant passage model

이중냉각유로의 분리벽 형상 변화에 따른 열유동 특성 확인을 위해 지배방정식으로 연속방정식, 운동량 방정식, 에너지 방정식을 사용하였고, 해를 구하기 위해 범용 유한체적해석(Finite Volume Method, FVM) 소프트웨어인 ANSYS CFX를 활용하였다.

난류모델로는 경계층 및 유동 박리 모사에 우수한 SST (Shear Stress Transport) 모델을 사용하였다.

본 연구에 사용된 냉각유로의 운전 및 경계 조건은 Table 2에 표기하였다. 냉각유로는 고정된 입구압력 300kPa을 가지며, 작동유체로 20℃의 물을 사용하였다. 또한, 스크류 압축기 로터 회전구간에는 250℃의 단열조건을 설정하여 하우징 열전달 현상을 고찰하였다. 수치해석을 위한 격자계 형성은 ANSYS 자동 격자계를 사용하였으며, 대략 4,500,000개 격자로 구성하였다. Figure 3은 수치해석에 사용된 스크류 압축기 하우징과 냉각유로에 대한 격자계를 도시한 것이다.

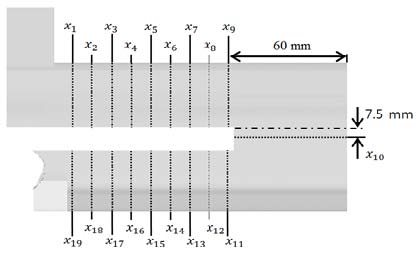
분리벽 형상 변화에 따라 나타나는 열유동 특성을 고찰하기 위하여 냉각유로 내부 작동유체의 압력강하와 Nu 수를 확인하는 것이 중요하다. 이에 따라 이중냉각유로의 각 구역에 계산영역을 지정하였으며, Fig. 4에 도시하였다. 이중냉각유로의 상류(1≤x_n≤9)와 하류(11≤x_n≤19)는 10mm 간격으로 열유동 계산 결과를 확보하였으며, 작동유체의 급격한 방향 전환에 따른 유동 특성을 확인하기 위하여 계산영역 x₁₀을 설정하였다.

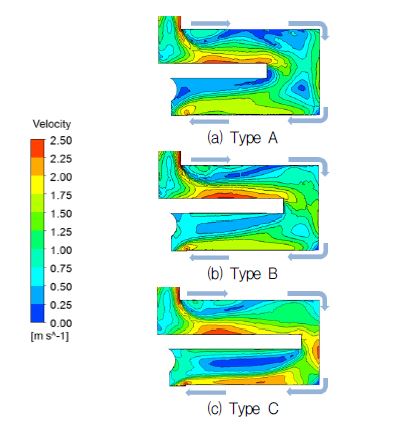
또한, 냉각유로의 성능을 확인하기 위하여 Fig. 2에 표시된 A₁영역에서의 유동 특성을 가시화하여, 기본 모델과 개선된 모델의 열유동 특성을 비교 분석하였다.

Table 2

Numerical methods and boundary conditions.

Fig. 3

Grid systems.

Fig. 4

Locations for measuring fields in the water jacket.

3. 결과 및 고찰

3.1 기존 냉각유로의 유동 고찰

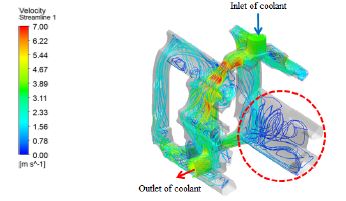
본 연구에서는 우선적으로 기존 냉각유로에 대한 수치해석을 수행하였다. Figure 5는 기존 냉각유로 내부에서의 유선 분포를 나타낸 것으로, 복잡한 냉각유로를 통해 유입된 작동유체는 우측 하부에서 낮은 유속분포를 나타내고 있다. 이는 곡관을 따라 이동하는 작동유체가 압력강하에 의해 유속이 감소하여 유동정체구간을 형성하는 것으로 판단된다.

Fig. 5

Streamline distributions in the water jacket.

Fig. 6

Velocity distributions of the basic model.

Fig. 7

Pressure drop profiles with three-different models.

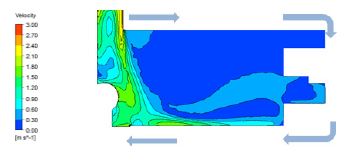
Figure 6에서는 계산영역 A₁에 대한 속도분포를 도시하였다. 냉각유로로 유입된 작동유체가 확장되는유로에서 확산 현상이 발생하므로 작동유체 속도 분포가 약 0.3m/s이하로 감소하는 것을 확인하였다. 이는 작동유체의 원활한 순환이 제대로 이루어지지 않아 압축기 하우징을 효과적으로 냉각시킬 수 없는 결과를 초래한다고 할 수 있다.

3.2 냉각유로 분리벽 길이비 변화

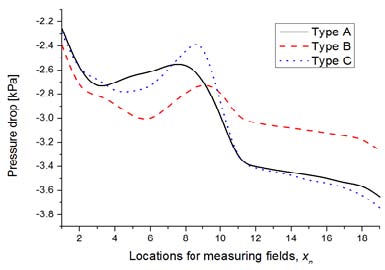
유동정체구간이 형성되는 기본 모델의 냉각 성능을 높이기 위해 분리벽이 설치된 이중냉각유로의 유동특성을 수치적으로 해석하였다. Figure 7은 냉각유로 내 각 계산영역(Fig. 4 참조)에서 도출된 압력 분포를 나타낸 것으로, 특히 주유동이 상류에서 하류로 선회하는 영역(9≤x_n≤11)에서는 높은 압력강하 분포를 확인할 수 있다. 이는 작동유체의 급격한 방향전환이 압력차를 유발시켜 유동박리 영역이 발달하기 때문이다.

Figure 8에서는 냉각유로 분리벽 길이비에 따른 내부 속도 분포를 나타내었다. 앞서 제시한 기존 모델 결과보다 이중냉각유로를 설치한 냉각유로는 곡관부를 지나면서 일정 속도 이상의 유속을 확보하였다. Type C와 같이 분리벽 길이비가 길어질수록 곡관부에서 노즐 효과로 인해 유속이 증가함을 확인할 수 있었으며, 기본 모델에 비해 더 효율적인 작동유체의 유동성능을 나타내었다. 또한, 원심력으로 인한 냉각유로 내 속도차를 유발시켜 이중냉각유로 하류에서 재순환 영역이 나타나게 된다. 재순환 영역이 발생하는 하류에서는 원활한 열전달 효과를 기대할 수 있어 기존 모델에 비하여 효과적인 방열성능을 확보할 수 있을 것으로 판단된다.

냉각유로 내 기하학적 형상변화에 따른 대류 열전달 정도를 고찰하기 위하여 Nu 수를 사용하였으며, 본 연구에서 사용한 식은 다음과 같다.(10)

여기서

위 식에서 Re는 Reynolds 수, f는 마찰 저항 계수, Pr은 Prantl 수, α는 열확산계수, a는 동점성계수, C_p는 정압비열, μ는 점성계수, 그리고 k는 열전도도를 각각 나타낸다.

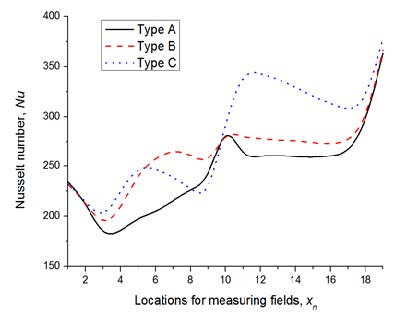
Figure 9는 이중냉각유로의 각 구간에서 Nu 수를 도시한 것이다. 이중냉각유로로 유입된 작동유체는 냉각유로 하류 영역(9≤x_n≤16)에서 높은 Nu 수를 나타내었다. 이는 냉각유로 하류에서 원심력과 유동박리 증가로 인해 재순환영역이 발달한 것으로 판단할 수 있다. 따라서 냉각유로 Type C는 Type A와 B보다 좁은 곡관을 형성하고 있어 재순환영역이 증가하고, Nu 수가 증가하는 것으로 나타났으며, 효과적인 방열성능을 확보할 수 있는 것으로 판단된다.

Fig. 8

Pressure and velocity distributions of three different models.

Fig. 9

Nusselt number profiles with three-different models.

3.3 냉각유로 분리벽 두께비 변화

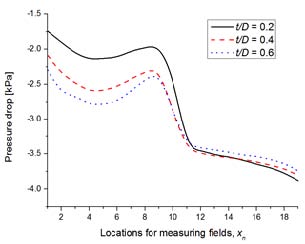
Type C의 분리벽 두께비 변화에 따른 열유동 특성을 확인하기 위하여 추가적으로 수치해석을 수행하였다. Figure 10에서는 Type C 분리벽 두께비에 따른 각 계산영역(Fig. 4 참조)의 압력 분포를 도시 하였다. 그 결과 분리벽 길이비 변화와 마찬가지로 주유동이 상류에서 하류로 선회하는 영역(9≤x_n≤11)에서는 높은 압력 강하 분포를 나타내고 있지만, 분리벽 두께비 변화에 따른 압력 분포는 비슷한 경향을 나타내었다.

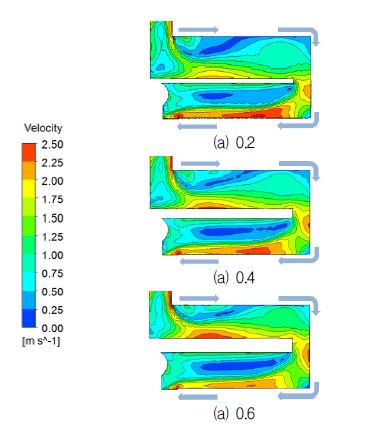
Figure 11에서는 냉각유로 Type C의 분리벽 두께비 변화에 따른 속도분포를 도시하였다. 분리벽 두께가 얇아질수록 작동유체가 곡관부를 지나면서 유속이 더 증가하는 것을 알 수 있다. 이는 분리벽 두께비가 얇아지면 냉각유로 상류(1≤x_n≤9)의 체적이 하류(11≤x_n≤19)의 체적보다 증가하기 때문에 곡관부에서 노즐 효과가 증가하는 것으로 판단된다.

Fig. 10

Pressure drop profiles for different numbers of thickness(t/D) of separation block at Type C.

Fig. 11

Effects of the thickness(t/D) of separation block of Type C on the velocity distribution.

Fig. 12

Nusselt number profiles for different numbers of thickness(t/D) of separation block at Type C.

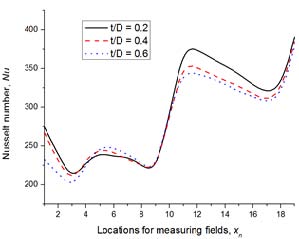
Figure 12는 분리벽 두께비 변화에 따른 Nu 수를 나타내었으며, 냉각유로 하류 영역(9≤x_n≤16)에서 높은 열전달 성능을 확인할 수 있었다. 이는 두께 비가 얇은 곡관부에서 유속의 증가는 원심력 증가와 비례하므로 재순환영역이 발달하기 때문이다.

4. 결 론

본 연구에서는 스크류 압축기 냉각유로 분리벽 형상 변화에 따른 열유동 특성 및 Nu 수를 해석하였으며, 다음과 같은 결론을 얻었다.

1) 기본 모델의 냉각유로는 유입구 형상으로 인해 넓은 유동정체구간이 형성되었으며, 원활한 유동이 이루어지지 않아 효율적인 냉각성능 확보가 어려움을 알 수 있었다.

2) 작동유체의 효과적인 유동을 확보하기 위하여 냉각유로 분리벽을 설치하였으며, 좁은 곡관 형상을 가지는 Type C에서 높은 열전달 성능이 나타났으며, 이러한 유로를 따라 이동하는 작동유체는 곡관 하류에서 유동박리 및 원심력으로 인한 재순환 영역을 생성하였다.

3) 열전달 성능이 우수한 Type C의 분리벽 두께비 형상 변화로 냉각유로 내부 열유동 특성을 해석하였다. 두께비가 얇을수록 냉각유로 상류에서 하류로 작용하는 노즐 효과 증가로 인해 재순환영역이 증가하기 때문에 열전달 성능이 우수한 것으로 나타났다.

이상에서 살펴본 바와 같이 냉각유로 분리벽 형상 변화를 통하여 열전달 성능을 증가시킬 수 있음을 확인하였다. 향후최적 냉각 성능 확보를 위하여 로터의 압축과정에서 발생하는 열전달 현상을 반영한 추가적인 연구 및 실험적인 고찰이 필요하다.

Acknowledgments

본 연구는 교육부의 재원으로 지원을 받아 수행된 산학협력 선도대학(LINC) 육성사업의 연구결과입니다.

References

• M.-A. Moon, K.-Y. Kim, “Shape Optimization of a Rotating Two-Pass Duct with a Guide Vane in the Turning Region”, Journal of Fluid Machinery, (2011), 14(1), p66-76. [https://doi.org/10.5293/KFMA.2011.14.1.066]
• S. V. Ekkad, J.-C. Han, “Detailed Heat Transfer Distributions in Two-Pass Square Channels with Rib Turbulators”, Int. J. Heat Mass Transfer, (1997), 40(11), p2525-2537. [https://doi.org/10.1016/S0017-9310(96)00318-3]
• S. V. Prabhu, R. P. Vedula, “Pressure Drop Characteristics in a Rotating Smooth Square Channel with a Sharp 180〫 bend”, Experimental Thermal and Fluid Science, (2000), 21, p198-205. [https://doi.org/10.1016/S0894-1777(00)00003-0]
• K.-M. Kim, H.-H. Cho, “Pressure Drop Characteristics in a Coolant Passage with Turning Region and Rotation”, Journal of Fluid Machinery, (2007), 10(2), p32-40.
• G. Su, H.-C. Chen, J.-C. Han, J.-D. Heidmann, Computation of Flow and Heat Transfer in Rotating Two-Pass Rectangular Channels(AR=1:1, 1:2 and 1:4) with Smooth Walls by a Reynolds Stress Turbulence Model”, Int. J. of Heat Mass Transfer, (2004), 47, p5665-5683. [https://doi.org/10.1016/j.ijheatmasstransfer.2004.07.019]
• J. S. Park, J. C. Han, Y. Huang, S. Ou, “Heat Transfer Performance Comparisons of Five Different Rectangular Channels with Parallel Angled Ribs”, Int. J. Heat Mass Transfer, (1992), 35(11), p2891-2903. [https://doi.org/10.1016/0017-9310(92)90309-G]
• J. C. Han, Y. M. Zhang, “High Performance Heat Transfer Ducts with Parallel Broken and V-Shaped Broken Ribs”, Int. J. Heat Mass Transfer, (1992), 35(2), p513-523. [https://doi.org/10.1016/0017-9310(92)90286-2]
• R. T. Kukreja, S. C. Lau, R. D. Mcmillin, “Local Heat/Mass Transfer Distribution in a Square Channel with Full and V-Shaped Ribs”, Int. J. Heat Mass Transfer, (1993), 36(8), p2013-2020.
• K.-M. Kim, S.-I. Kim, D.-H. Rhee, H.-H. Cho, “Experimental Study of Heat/Mass Transfer in Rotating Cooling Passages with Discrete Ribs”, Trans. Korean Soc. Mech. B, (2005), 29(5), p590-598. [https://doi.org/10.3795/KSME-B.2005.29.5.590]
• S. Kakac, H. Liu, Heat exchangers: selection, rating, and thermal design, New York, USA, (2004).