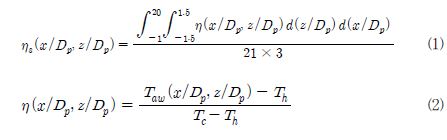Effects of Geometry of Anti-Vortex Holes on Film-Cooling Effectiveness

기호설명

α : 홀의 분사각도

D_p : 주 홀의 지름

D_a : 보조 홀의 지름

D_a,ref : 기준형상의 보조 홀의 지름

: 질량 유량

β : 보조 홀의 측면 분사 각도

l₁ : 주 홀과 보조 홀 사이의 측면방향 길이

l_1,ref : 기준형상의 주 홀과 보조 홀 사이의 측면방향 길이

T_c : 냉각 유로의 입구 온도

T_h : 고온 가스 온도

T_aw : 단열 벽면 온도

P_c : 냉각유체의 밀도

P_h : 주유동의 밀도

ν_c : 홀 출구에서 냉각유체의 속도

ν_h : 주유동의 속도

η : 막냉각 효율

η_l : 측면방향 길이 평균된 막냉각 효율

η_s : 면적 평균된 막냉각 효율

x, y, z : 직교 좌표들

1. 서 론

가스터빈은 높은 열효율을 성취하기 위해서 고온의 터빈 입구 조건이 요구된다. 그러나, 고온의 기체 온도가 블레이드의 허용 온도를 초과함에 따라 터빈 블레이드의 성능과 수명을 유지시키기 위해 블래이드 냉각기술이 반드시 필요하게 되었다. 이에 따라 다양한 냉각 기술들이 터빈 블레이드에 적용되어 왔으며, 특히 막냉각 기술은 높은 온도를 가지는 블레이드 표면에 냉각유체의 막을 형성함으로써 블레이드의 표면 온도를 낮추는 대표적인 냉각 기술로 알려져 있다. 이러한 막냉각의 중요성이 높아짐으로서 이에 대한 많은 연구들이 지난 10-15년간 진행되어 왔다.

초기 막냉각 기술에 대한 연구에서는 원통형 홀의 형상 변수의 변화에 따른 막냉각 성능에 대한 다양한 연구가 수행되었다. 막냉각 효율(film-cooling effectiveness)은 막냉각의 성능을 평가하기 위한 척도로 많은 연구자들에 의해 사용되어 왔다. 홀의 길이, 분사율(blowing ratio), 분사 각도(injection angle) 및 측면 분사각(diffuser angle)등이 막냉각 효율에 영향을 미치는 주 형상 변수로서 간주되었다. Nasir 등(1) 은 원통형 홀의 측면 각도와 분사각도가 막냉각 성능에 미치는 영향을 연구하였다. 그 결과 측면 분사각을 가진 형상이 더 좋은 막냉각 성능을 나타낸다고 보고하였다. Walters와 Leylek (2)는 수치해석과 실험을 병행하여 원통형 홀에 대한 유동장 분석을 수행하였고, 또한 주유동의 콩팥 와류(kidney vortex)를 가시화하였다. 이 연구 결과에 따르면 콩팥 와류는 냉각유체와 냉각표면의 접촉을 저하시키는 것으로 보고되었다.

원통형 홀의 경우 간단한 홀의 형상 때문에 비용 및 제작 측면에서는 긍정적이지만 막냉각 성능을 향상시키기에는 한계가 있다. 따라서 더 높은 막냉각 성능을 위해서 홴 형상 홀(fan-shaped hole)에 대한 연구가 수행되었다. 많은 연구자들은 막냉각 성능을 향상시키 위한 방법으로써 냉각 유체의 측면분사 길이를 증가시키는 것에 관심을 가졌다. Yen 등 (3)은 원통형 홀과 홴 형상 홀의 분사 각도와 측면분사 각도가 막냉각 성능에 끼치는 영향에 대하여 실험연구를 수행하였다. 연구결과에 따르면 홀 출구에서 냉각유체의 수직 방향 운동량이 감소됨에 따라 홴 형상 홀이 원통형 홀 보다 훨씬 향상된 막냉각 성능을 나타내는 것으로 보고되었다. Gritsch 등(4)은 홀의 길이, 홀 면적의 입구 대 출구 비, 홀의 주기, 측면분사 각도와 측면 확장각이 막냉각 효율에 미치는 영향에 대한 실험결과를 제시하였다. 홀의 주기가 감소할수록 전체 영역에서의 질량유량이 증가하기 때문에 막냉각 효율에 큰 영향을 미치는 반면, 나머지 형상 변수들은 막냉각 효율에 비교적 작은 영향을 미치는 것으로 보고하였다. Baheri 등(5)은 홴 형상 홀과 트렌치가 있는 원통형 홀에 대한 수치해석을 수행하였는데 트렌치가 있는 원통형 홀이 높은 막냉각 성능을 보인다고 보고하였다. Brauckmann 과 Wolfersdorf (6)은 측면 분사각 및 분사율이 열전달 계수와 막냉각 효율에 미치는 영향에 대한 실험을 수행하였다. 이들의 실험결과에서 측면분사 각도의 변화는 막냉각 효율에 거의 영향을 주지 않는다고 보고하였다.

홴 형상 홀의 경우 높은 막냉각 성능을 나타내는 반면, 복잡한 형상 때문에 실질적인 적용이 어려운 단점이 있다. 따라서 쉬운 제작과 높은 막냉각 성능을 만족시키기 위해 다양한 막냉각 홀 형상들이 개발되었다. 이런 연구 중 하나가 이중 분사 막냉각(double-jet film-cooling)에 대한 연구 (7)이다. 이중 분사 막냉각 홀은 두 개의 엇갈린 원통형 홀로 구성되어 있어 쉬운 제작과 반콩팥 와류(anti-kidney vortex)의 형성으로 인해 기존의 콩팥 와류에 의한 막냉각 성능의 저하 방지를 꾀하고 높은 막냉각 성능을 나타내는 장점이 있다. 이중 분사 막냉각과 관련해서는 이미 많은 연구들이 수행되었다(8-13). Heidmann (14)에 의해 처음 제안된 반와류(anti-vortex) 형상은 쉬운 제작과 높은 막냉각 성능의 두 가지 조건을 만족시킨다. 반와류 형상은 원통형 모양의 주 홀과 두 개의 원통형 모양의 보조 홀로 구성된다. 주 홀을 기준으로 보조 홀들이 좌우 대칭으로 배열되어, 막냉각 효율을 감소시키는 콩팥와류의 영향을 줄이기 위해 디자인 되었다(Fig. 1). 그는 adjacent anti-vortex 홀 형상은 원통형 홀 및 upstream anti-vortex 홀 보다 높은 막냉각 성능을 나타낸다고 보고하였다. 반와류 홀의 실험연구 또한 Dhungel 등 (15)에 의해 수행되었다. 이 연구에서 행해진 여섯 개의 서로 다른 반와류 홀 형상 중에 가장 기본적인 형상인 주 홀과 보조 홀의 위치가 동일 선상에 있는 반 와류 홀이 본 연구의 기준형상으로 선정되었다.

반 와류 형상에 관한 실험 및 수치해석적 연구가 다수 진행 되었으나, 주 홀에 대한 보조 홀의 위치와 크기 변화가 막냉각 효율에 얼마만큼 영향을 미치는 지에 대한 상세한 연구는 아직 수행 되지 않았다. 따라서 본 연구에서는 반와류 홀의 두 개의 형상 변수, 즉 주 홀과 보조 홀 사이의 측면 거리 및 보조 홀의 지름 변화가 막냉각 성능에 미치는 영향을 수치해석을 통해 분석하였다.

2. 수치해석방법

본 연구에서 삼차원 유동 및 열전달 해석을 위해 상용 전산유체역학 코드인 ANSYS CFX 11.0 (16)이 사용되었다. 반와류 홀의 형상 변수들이 막냉각 효율에 미치는 영향을 알아보기 위해 정상상태 압축성 RANS(Reynolds-averaged Navier-Stokes) 방정식을 사용하였다. 난류 모델로는 SST (shear stress transport) 모델을 사용하였다. SST 모델은 벽 근처에서는 k-ω 모델이 사용되고, 그 밖의 영역에서는 k-ε 모델이 사용된다. Bardina 등 (17)과 Lee 등 (18)에 의해 SST 모델의 우수한 예측결과가 제시되었다. 그들이 제시한 결과에 의하면 SST 모델은 다른 난류 모델보다 유동 박리와 같은 벽 근처의 난류 유동을 더 정확하게 예측하는 것으로 나타났다. 또한 Lee (18) 등은 SST 모델을 사용하여 홴 형상 홀과 원통형 홀에 대한 수치해석치를 제시하였으며, 이 연구의 수치해석치가 실험결과와 매우 좋은 일치성을 보였다고 보고하였다.

Fig. 1

Computational domain

Fig. 2

Computational grids

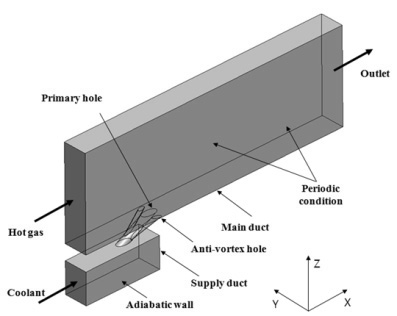
Fig. 1은 본 연구의 계산 영역 및 경계조건을 나타낸다. 계산 영역은 고온 가스와 냉각유체가 흘러가는 두 개의 덕트(duct)와 이를 연결해주는 하나의 원통형 주 홀과 두 개의 원통형 보조 홀들로 구성되어 있다. 보조 홀들은 주 홀을 기준으로 좌우대칭으로 배열되어 있으며, 냉각유체는 주 홀과 보조 홀들을 통해 주 유로로 유입된다. 본 연구에서는 경계 조건으로 Dhungel 등(15)이 실험에 사용한 경계 조건을 동일하게 적용하였다. 작동유체는 이상기체로 간주되었고, 벽면에는 단열 조건과 점착 조건(no-slip condition)이 부여되었다. 주 유로의 입구에 13.8m/s의 속도 조건을 주었고 출구에는 1 atm의 정압조건을 부여하였다. 막냉각 효율에 대한 분사율의 영향을 알아보기 위해서 M=0.5 와 M=1.0 의 조건에 대하여 해석을 수행하였으며, 이에 따라 냉각 유로의 속도조건은 형상 및 분사율의 변화에 따라 다르게 설정하였다. 냉각 유체와 고온 가스의 온도는 각각 290K과 320K으로 주어졌고, 주 유로의 측면 벽면에는 주기 조건이 부여되었다. 주 유로에서의 난류강도는 2%값을 주었다.

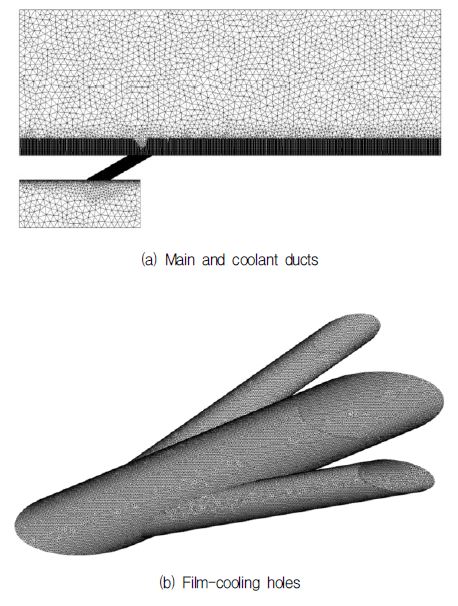
계산에 사용된 격자계를 Fig. 2에 나타내었다. 본 연구에서는 비정렬 사면체 격자계가 사용되었으며 벽 근처에서의 해석의 정확성을 향상시키기 위해 프리즘 격자가 사용되었다. 벽면으로부터의 첫 번째 격자에서의 y⁺값은 30이상으로 사용되었으며 자동변환 벽함수 (automatic wall function)가 적용되었다(16). Lee 등(19)과 Baheri 등(20)도 동일한 y⁺ 조건으로 이중분사 막냉각 홀에 대하여 수치해석을 수행하였으며, 수치해석치와 실험값이 좋은 일치성을 보여주었다고 보고하였다. 복잡한 유동현상이 일어나는 홀 내부와 냉각유체의 유동과 주 유동이 혼합되어 복잡한 유동이 발생하는 주 유동 채널의 바닥 근처에는 자세한 해석을 위하여 많은 수의 격자를 밀집시켰으며 격자의 크기를 제한하는 기법을 사용하였다.

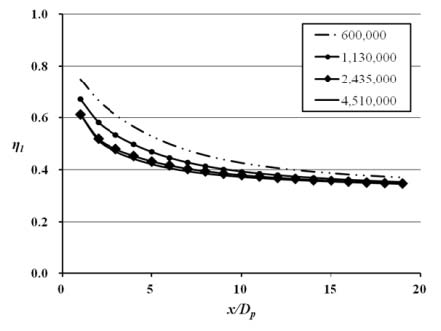
계산시간 단축과 효율적인 컴퓨터 메모리 사용을 위해 격자 의존성 테스트가 수행되었다. 격자 의존성 테스트는 기준 형상으로 수행되었으며, Fig. 3에서 나타낸 바와 같이 격자수의 범위, 600,000∼4,510,000개에서 격자를 시험한 결과 2,435,000개의 격자가 최적 격자수로 선정되었다. 격자수는 형상 변수의 변화에 따라 약간의 차이가 있었지만 모든 경우에서 벽근처 y⁺값은 비교적 일정하게 유지되었다.

Fig. 3

Grid dependency test

Fig. 4

Geometric variables and dimensions

Table 1

Dimensions of the reference geometry of the anti-vortex hole

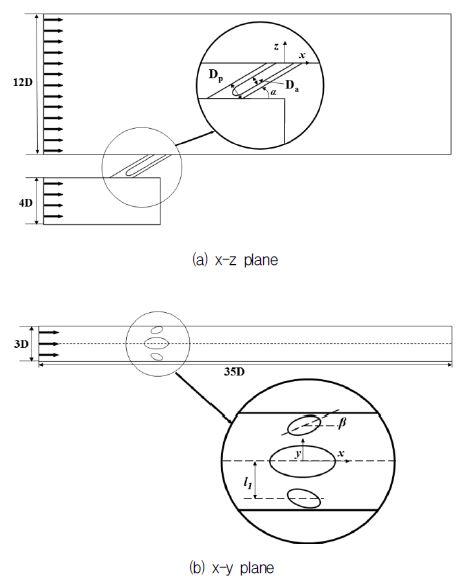
Fig. 4는 형상 변수 및 계산 영역의 크기를 나타낸다. 유동해석과 열전달해석을 위해서 두 가지의 형상 변수, 즉 보조 홀의 지름(D_a)과 주 홀과 보조 홀 사이의 측면방향 거리(l₁)가 선정되었다. α와 D_p는 각각 분사각과 주 홀의 지름을 의미한다. Fig. 4에 도시된 계산영역 및 기준형상의 크기정보를 Table 1 에 제시하였다.

수렴여부를 판정하기 위해서 RMS 잉여값(root-meansquared residual)이 1.0 E-6 보다 작을 때 수렴하였다고 판정하였다. 계산에 사용된 컴퓨터는 Intel i7 3.41 GHz PC며, 한 개의 형상을 계산하는데 평균적으로 900번의 반복계산과 약 15시간정도의 계산시간이 소요되었다.

Fig. 5

Validation of numerical results

3. 결과 및 검토

수치해의 신뢰성을 검증하기 위해서 반와류 홀의 수치해와 실험결과를 비교하는 수치해의 타당성 검증이 수행되었다. Fig. 5에는 Dhungel 등(15)이 제시한 반와류 홀의 측면평균 막냉각 효율과 막냉각 효율 분포에 대한 실험값과 수치해의 비교가 도시되었다. 두 가지 분사율에서 실험값과 수치해의 오차율은 각각 약12%, 약 4%로 나타났다. 수치해와 나타났지만 분사율 변화에 따른 막냉각 효율변화의 경향성은 수치해와 실험값이 대체적으로 좋은 일치성을 보였다. 막냉각 효율 분포의 경우 실험과 수치해석 결과가 차이가 나는 것으로 보이지만 실험의 경우 효율분포를 정확하게 표현하는 것이 어렵고, Fig. 5(a)에서 후류에서의 정량적인 결과가 거의 일치하므로 온도분포의 경향이 크게 차이나지 않는다고 판단된다. 그러므로, 본 연구에서 수행된 수치해는 타당성이 있는 것으로 판단되었다.

반 와류 홀의 막냉각 성능을 측정하기 위해서 면적 평균된 막냉각 효율(spatially-averaged film-cooling effectiveness), η_s가 사용되었다. 막냉각 효율(η)은 막냉각 성능을 측정하기 위해 널리 사용되고 있으며, 막냉각 효율 및 면적 평균된 막냉각 효율의 정의는 아래와 같다:

여기서 T_aw는 단열벽면온도를 나타내며, T_h와 T_c는 각각 주 유로와 냉각유로의 입구 온도를 의미한다. η_s는 -1.5 ≤ z / D_p ≤1.5 및 -1≤ x / D_p ≤ 20의 범위에서 면적평균되었다.

본 연구는 분사율 변화에 따른 반와류 홀의 막냉각 성능에 대한 연구를 수행하기 위해서 두 가지 분사율에 대해 해석을 수행하였다. 분사율(M)은 일반적으로 막냉각 효율에 큰 영향을 미치는 중요한 변수이며 다음과 같이 정의되었다:

여기서 P_c와 P_h와는 각각 냉각유체와 고온가스의 밀도를 의미한다. ν_c와 ν_h는 반 와류 홀과 주 홀 출구영역 전체에서의 평균 냉각유체속도와 주 유동 속도를 의미한다. 본 연구에서는 반 와류 홀 지름 변화에 따라 달라지는 분사율을 일치시키기 위해 냉각 유로의 속도조건을 형상 마다 다르게 부여하였다. 이에 따라, 홀 출구를 기준으로한 분사율은 일정해지지만 홀 입구를 기준으로 한 분사율은 달라지게 된다. 홀 출구 기준 분사율이 일정할 때의 홀 입구 기준 분사율을 Table 2에 나타내었다.

Table 2

Relatiomship between blowing ratios at the entrance hole with Da / Dp for exit hole blowing ratios, M = 0.5 and 1.0.

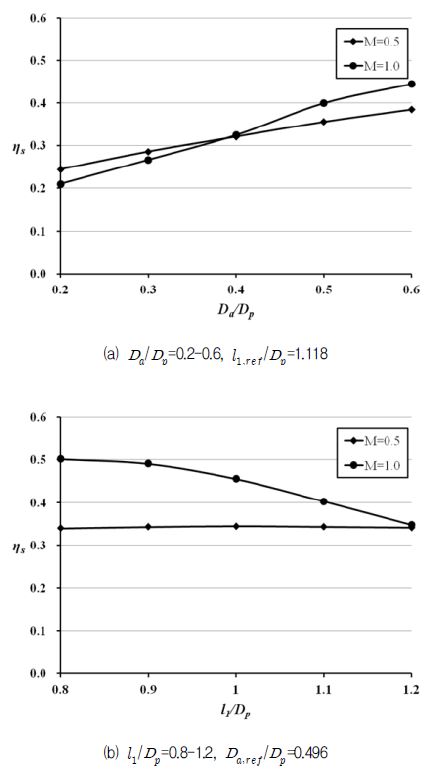
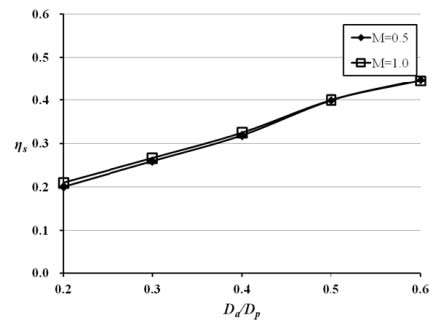
두 가지 분사율에서 형상 변수 D_a / D_p와 l₁ / D_p에 따른 면적평균된 막냉각 효율 값의 변화를 Fig. 6에 나타내었다. Fig. 6(a)의 경우, 두 가지 분사율 모두에서 D_a / D_p가 증가할수록 막냉각 효율이 증가하는 경향을 보여주고 있다. D_a / D_p가 0.4 보다 작으면 분사율이 낮을 때 막냉각 효율이 더 높은 경향을 볼 수 있으며, D_a / D_p가 0.4 보다 크면 분사율이 높을 때 막냉각 효율이 더 높은 경향을 볼 수 있다. Fig. 6(b)의 경우 분사율에 따른 막냉각 효율의 경향이 다르게 나타났다. M=1.0 일 때, 주 홀과 보조 홀의 거리가 가까울수록 막냉각 효율이 증가함을 보여준 반면에, M=0.5일 경우 주 홀과 보조 홀의 거리 변화에 따른 영향이 거의 없는 결과를 보여주었다.

Fig. 6

Effects of the geometric variables on the spatially-averaged film-cooling

분사율이 일정한 경우, D_a / D_p가 증가할수록 냉각유체의 유량은 증가한다. 따라서 Fig. 6(a)에 나타낸 막냉각 효율의향상이 D_a / D_p의 증가에 의한 것인지 냉각 유체의 유량의 증가에 의한 것인지를 명확히 하기 위하여 Fig. 7에 일정한 유량( 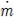= 1.888× 10^-3kg/s)에서의 D_a / D_p 변화에 따른 막냉각 효율의 변화를 Fig. 6(a)의 M=1.0의 경우와 비교하여 나타내었다. 일정한 냉각유체의 유량은 기준형상의 분사율이 1.0일 때의 냉각 유량을 사용하였으며 두 결과가 거의 차이가 나지 않는 것을 볼 수 있다. 이에 따라, D_a / D_p가 증가할수록 면적평균된 막냉각 효율이 증가하는 결과가 냉각유량 증가의 의한 효과가 아니라 형상변화에 따른 결과라는 것을 알 수 있다.

각 형상에 대한 주 유로 바닥면에서의 막냉각 효율 분포를 Fig. 8과 9를 통해 나타내었다. Fig. 8(a)에서 D_a / D_p=0.6의 형상이 D_a / D_p=0.2의 형상보다 더 넓은 면적에서 높은막냉각 효율 분포를 볼 수 있는데, 막냉각 효율 0.7 이상의 면적이 약 6.6배 정도 넓었다. Fig. 8(b)에서도 Fig. 8(a)에서와 비슷한 경향을 보여주었다. Fig. 9(a)에서 l₁ / D_p=0.8인 경우 전체적인 막냉각 효율 분포가 비교적 좁은 반면, 막냉각 효율이 0.7 이상인 부분이 l₁ / D_p=1.2 인 경우 보다 약 2.7배 넓은 것으로 나타났다. 기준형상과 비슷한 l₁ / D_p=1의 경우 다른 두 형상에 비해 막냉각 효율이 0.2 이상인 면적이 약 1.2배 정도 넓어 막냉각 효율이 비교적 넓게 분포하고 있다. l₁ / D_p=1.2의 경우 주 홀과 보조 홀 사이의 거리가 멀어 상호간에 영향이 적은 것을 알 수 있다. M=0.5인 Fig. 9(b)를 보면 각 경우에서 높은 막냉각 효율을 가지는 부분의 면적이 큰 차이가 없는 것을 볼 수 있다. l₁ / D_p=1의 경우가 다른 경우에 비해 비교적 균일한 막냉각 효율의 분포를 가지는 것을 보여주었다.

Fig. 7

Area-averaged film-cooling effectiveness with Da / Dp for the constant mass flow through the hole and the blowing ratio

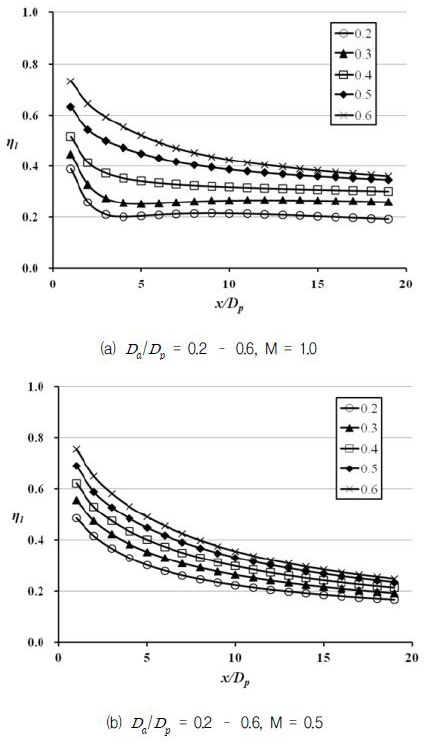
Fig. 8과 Fig. 9의 결과를 정량적으로 살펴보기 위하여 두 가지 분사율에서 형상 변수 D_a / D_p와 l₁ / D_p에 따른 측면방향으로 평균된 막냉각 효율 값의 변화를 Fig. 10과 Fig. 11에 나타내었다. Fig. 8의 결과와 같이 두 가지 분사율 모두에서 D_a / D_p가 증가 할수록 측면방향 평균된 막냉각 효율의 그래프가 증가하는 것을 Fig. 10을 통해 볼 수 있으며, Fig. 11에서도 M = 1.0일 때 l₁ / D_p가 증가할수록 측면방향 평균 막냉각 효율이 증가하는 것을 볼 수 있다. Fig. 9의 막냉각 효율 분포에서 보았듯이 M=0.5인 경우 형상변화에 따른 막냉각 효율분포의 차이가 크지 않았으며, Fig. 11(b)에서도 5가지 형상의 측면방향 평균 막냉각 효율의 그래프가 거의 일치하는 것을 볼 수 있다.

Fig. 8

Distributions of the local film-cooling effectiveness(η) on the cooling surface for different Da / Dp (l1,ref/Dp =1.118)

Fig. 9

Distributions of the local film-cooling effectiveness (η ) on the cooling surface for different l1 / Dp (Da,ref/Dp =0.496)

Fig. 10

variations in laterally-averaged film-cooling effectiveness with Da / Dpfor (a) M = 1.0 (b) M = 0.5

Fig. 11

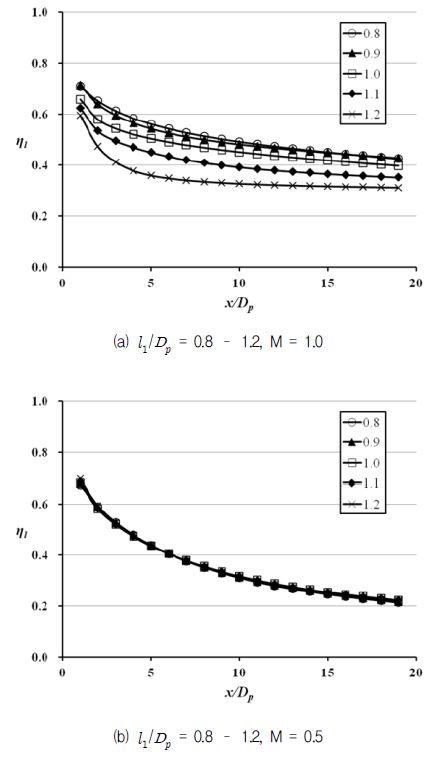
variations in laterally-averaged film-cooling effectiveness with l1 / Dp for (a) M = 1.0 (b) M = 0.5

Fig. 12

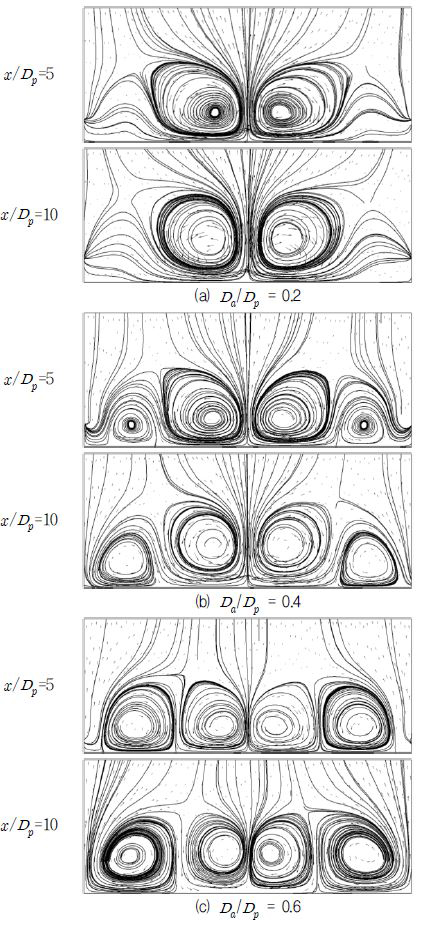
Streamlines and velocity vectors on z - y plane at x /Dp =5 and 10 for different Da / Dp (l1,ref/Dp=1.118, M=1.0)

Fig. 13

Streamlines and velocity vectors on z - y plane at x /Dp =5 and 10 for different Da / Dp (l1,ref/Dp=1.118, M=0.5)

M=0.5, 1.0에서 D_a / D_p의 변화에 따른 z - y평면에서의 유선과 속도벡터를 Fig. 12과 13에 나타내었다. 이 그림들에서 분사율은 서로 다르지만 D_a / D_p의 변화에 따라 대체적으로 비슷한 경향을 나타냈다. D_a / D_p=0.2인 Fig. 12(a)에서 주 홀에서 분사된 유동에 의한 와류의 강도와 크기가 매우 크고 보조 홀에서 분사된 유동에 의한 와류가 거의 존재하지 않는 것을 볼 수 있으며, 중앙와류의 x-축 와도의 최고치는 918.8 s^-1로 나타났다. 반면에, Fig. 12(b)와 12(c)에서 볼 수 있듯이 D_a의 크기가 커질수록 보조 홀에서 분사된 냉각유체의 강한 운동량 때문에 양쪽 끝에서의 와류의 강도가 커짐에 따라 주 홀의 와류의 크기가 감소하는 것을 볼 수 있으며, 중앙 와류의 x-축 와도의 최고치가 각각 515.5 s^-1(D_a / D_p=0.4)와 261.3 s^-1(D_a / D_p=0.6)로 D_a / D_p=0.2 일 때 보다 감소한 결과를 보여주었다.

Fig. 14

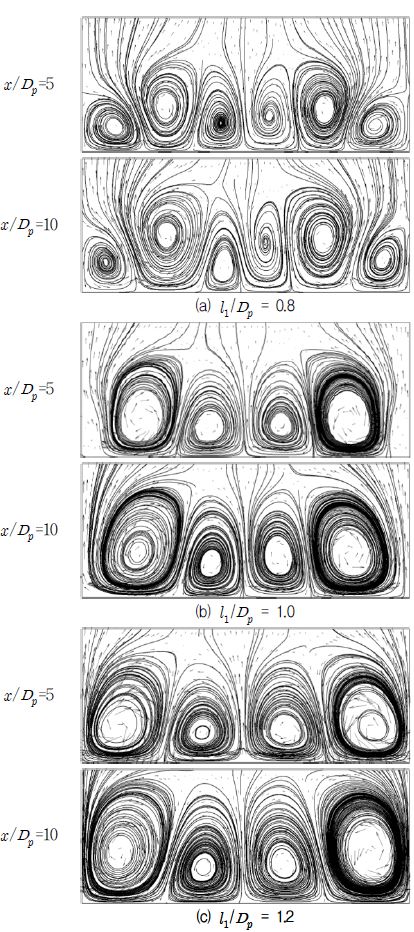
Streamlines and velocity vectors on z - y plane at x /Dp =5 and 10 for different l1 / Dp (Da,ref/Dp=0.496, M=1.0)

Fig. 15

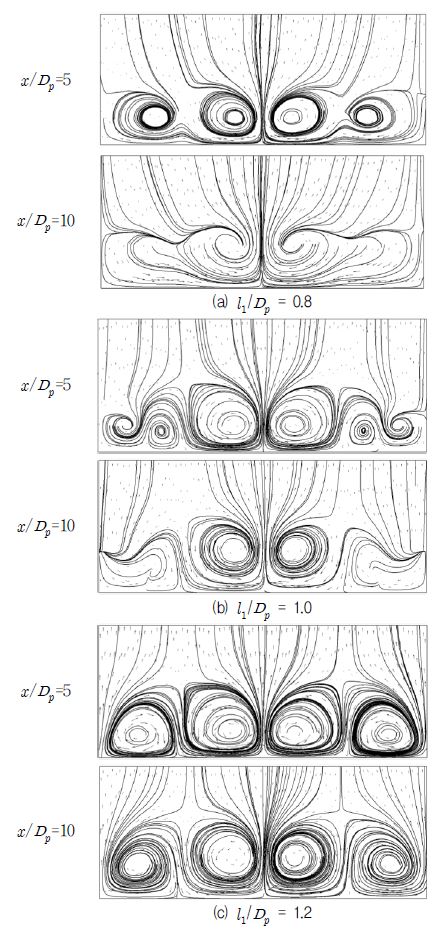
Streamlines and velocity vectors on z - y plane at x /Dp =5 and 10 for different l1 / Dp (Da,ref/Dp=0.496, M=0.5)

Fig. 14과 15는 각각 M=1.0와 0.5 조건에서 l₁ / D_p의 변화에 따른 z - y평면에서의 유선과 속도벡터를 보여준다. 이 그림들에서 볼 수 있는 바와 같이 분사율에 따라 다른 유동 구조를 나타내었다. Fig. 14을 보면 여러 형상들의 결과가 두 쌍의 와류를 가지는 반면, l₁ / D_p=0.8인 Fig. 14(a)의 경우 양쪽 끝에 한 쌍의 와류가 더 생성되어 총 세 쌍의 와류가 생성되는 것을 볼 수 있으며, Fig. 14(b), (c)의 결과에 비해주 홀에 의한 와류의 크기가 작게 나타나고 있다. 중앙 와류의 x-축 와도의 최고치도 l₁ / D_p=0.8일 때 127.9 s^-1로 나타나 모든 형상 중 가장 작은 값을 보여주었다. M=0.5에 대한 Fig. 15의 경우 M=1.0인 경우와 비슷하게 주 홀과 보조 홀 사이의 거리가 가까울수록 중앙와류의 크기가 감소하였지만 그 차이는 매우 작은 것을 볼 수 있으며, 중앙와류의 x-축 와도 최고치가 l₁ / D_p의 세가지 값에 대해 각각 187.2 s^-1, 171.4 s^-1, 및 137.4 s^-1로 큰 차이를 보이지 않았다. Fig. 15(b)를 보면 M=1.0인 경우 l₁ / D_p=0.8일 때 세 쌍의 와류가 생성되는 반면, M=0.5인 경우 l₁ / D_p=1.0을 가질 때 세쌍의 와류가 생기는 것을 확인할 수 있었다.

Fig. 16

Nondimensional temperature distributions(T / Th ) on z - y plane at x /Dp =5 and 10 for different Da / Dp (M=1.0)

Fig. 17

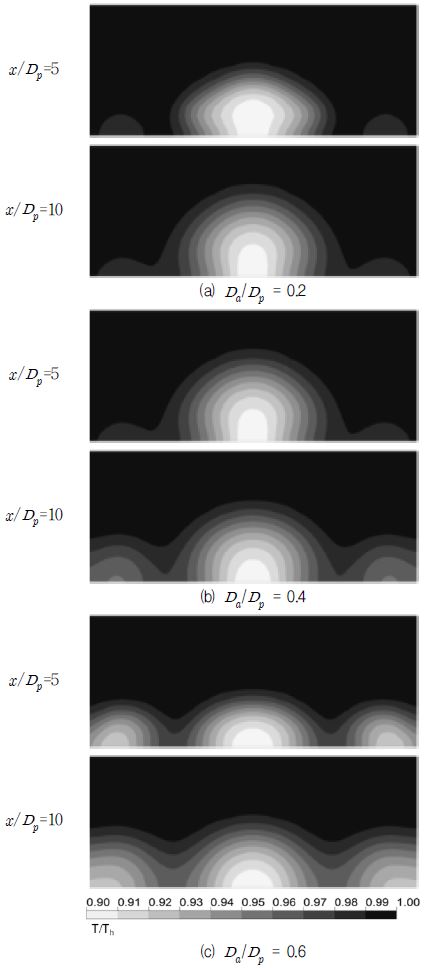
Nondimensional temperature distributions(T / Th ) on z - y plane at x /Dp =5 and 10 for different Da / Dp (M=0.5)

Fig. 16과 17에서는 분사율 M=0.5, 1.0에서 D_a / D_p의 변화에 따른 z - y평면에서의 온도분포를 나타내고 있다. 온도분포는 무차원 온도(T / T_h)로 나타내었다. 앞선 결과에서 보조 홀의 지름이 커질수록 냉각 평면 중앙의 와류가 감소하는 것을 볼 수 있었는데 이러한 이유 때문에 Fig. 16과 17에서 보여지는 것과 같이 보조홀의 지름이 커질수록 냉각유체가 냉각 평면에 더욱 더 원활히 밀착되는 것을 볼 수 있다.

Fig. 18

Nondimensional temperature distributions(T / Th ) on z - y plane at x /Dp =5 and 10 for different Da / Dp (M=1.0)

Fig. 19

Nondimensional temperature distributions(T / Th ) on z - y plane at x /Dp =5 and 10 for different Da / Dp (M=0.5)

Fig. 18와 19은 두 가지 분사율에서 l₁ / D_p변화에 따른 z - y평면에서의 온도분포를 보여준다. Fig. 16의 경우 역시 주 홀과 보조 홀의 거리가 가까울수록 냉각 평면 중앙에서의 와류가 감소하기 때문에 l₁ / D_p=0.8인 경우가 가장 원활하게 냉각유체가 냉각평면에 밀착하는 것을 볼 수 있다. 하지만 Fig. 17에선 각 경우의 와류 크기 차이가 크지 않아 냉각유체의 밀착정도 역시 큰 차이를 보이지 않았다.

4. 결 론

본 연구에서는 삼차원 RANS 방정식을 사용하여 반와류 홀에 대한 매개변수 연구가 수행되었다. 막냉각 효율에 대한형상 변수의 영향에 대해 알아보기 위해 두 개의 형상 변수, 즉 주 홀과 보조 홀의 지름비 및 주 홀과 보조 홀의 측면방향의 거리가 선정되었다. 반와류 홀의 수치해석치와 실험치가 좋은 일치성을 나타낸 것이 확인되었다. 두 가지 분사율. 0.5와 1.0에 대해 차이는 있었지만 두 개의 형상 변수 모두 막냉각 효율에 큰 영향을 주는 것으로 나타났다. 보조 홀의 지름이 커질수록, 주 홀과 보조 홀의 측면방향 거리가 가까울수록 냉각 표면 중앙에서 발달된 와류의 크기와 강도가 작아져 냉각유체가 냉각표면에 더 원활하게 밀착되어 막냉각 효율이 높아진다. 냉각홀의 지름비가 0.4 보다 작으면 분사율이 낮을 때 막냉각 효율이 더 높은 경향을 볼 수 있으며, 0.4 보다 크면 분사율이 높을 때 막냉각 효율이 더 높은 경향을 볼 수 있다. 그리고, 분사율 1.0 일 때, 주 홀과 보조 홀의 거리가 가까울수록 막냉각 효율이 증가하는 반면에, 분사율 0.5일 경우에는 주 홀과 보조 홀의 거리 변화가 막냉각 효율에 미치는 영향이 거의 나타나지 않는다.

Acknowledgments

이 논문은 2012년도 교육과학기술부의 재원으로 한국연구 재단의 지원을 받은 ‘다중현상 CFD연구센터(ERC)’의 과제로 수행된 연구임(No.2009-0083510).

References

• Nasir, H., Ekkad, S. V., Acharya, S., “Effect of Compound Angle Injection of Flat Surface Film Cooling with Large Streamwise Injection Angle”, Experimental Thermal and Fluid Science, (2001), 25(1-2), p23-29. [https://doi.org/10.1016/S0894-1777(01)00052-8]
• Walters, D. K., Leylek, J. H., “A Detailed Analysis of Film-Cooling Physics: Part I—Streamwise Injection With Cylindrical Holes”, Journal of Turbomachinery, (2001), 112(1), p102-112. [https://doi.org/10.1115/1.555433]
• Yuen, C. H. N., Martinez-Botas, R. F., Whitelaw, J. H., “Film Cooling Effectiveness Downstream of Compound and Fan-shaped Holes”, ASME Turbo Expo, New Orleans, Louisiana, (2001), 2001-GT-0131.
• Gritsch, M., Colban, W., Schär, H., Döbbeling, K., “Effect of Hole Geometry on the Thermal Performance of Fan-Shaped Film Cooling Holes”, Journal of Turbomachinery, (2005), 127, p718-725. [https://doi.org/10.1115/1.2019315]
• Baheri, S., Alavi Tabrizi, S. P., Jubran, B. A., “Film cooling effectiveness from trenched shaped and compound holes”, Heat Mass Transfer, (2008), 44(8), p989-999. [https://doi.org/10.1007/s00231-007-0341-9]
• Brauckmann, D., Wolfersdorf, J., “Influence of Compound Angle on Adiabatic Film Cooling Effectiveness and Heat Transfer Coefficient for a Row of Shaped Film Cooling Holes”, ASME Turbo Expo, Reno-Tahoe, Nevada, USA, GT2005-68036, (2005). [https://doi.org/10.1115/GT2005-68036]
• Japanese Patent Application, 332530.
• Kusterer, K., Bohn, D., Sugimoto, T., Tanaka, R., “Double-Jet Ejection of Cooling Air for Improved Film-Cooling”, ASME Turbo Expo 2006, Barcelona, Spain, (2006), GT2006-90854. [https://doi.org/10.1115/GT2006-90854]
• Kusterer, K., Bohn, D., Sugimoto, T., Tanaka, R., “Influence of Blowing Ratio on The Double-Jet Ejection of Cooling Air”, ASME Turbo Expo 2007, Montreal, Canada, (2007), GT2007-27301. [https://doi.org/10.1115/GT2007-27301]
• Kusterer, K., Elyas, A., Bohn, D., Sugimoto, T., Tanaka, R., “Double-Jet Film-Cooling for Highly Efficient Film-Cooling with Low Blowing Ratios”, ASME Turbo Expo 2008, Berlin, Germany, (2008), GT2008-50073. [https://doi.org/10.1115/GT2008-50073]
• Kusterer, K., Elyas, A., Bohn, D., Sugimoto, T., Tanaka, R., Kazari, M., “A Parametric Study on the Influence of the Lateral Ejection Angle of Double-Jet Holes on the Film Cooling Effectiveness for High Blowing Ratios”, ASME Turbo Expo 2009, Orlando, Florida, USA, (2009), GT2009-59321. [https://doi.org/10.1115/GT2009-59321]
• Kusterer, K., Elyas, A., Bohn, D., “Film Cooling Effectiveness Comparison Between Shaped and Double Jet Film Cooling Holes In A Row Arrangement”, ASME Turbo Expo 2010, Glasgow, UK, (2010), GT2010-22604. [https://doi.org/10.1115/GT2010-22604]
• Wang, Z., Liu, J. J., An, B. T., Zhang, C., “Effects of Axial Row-spacing For Double-jet Filmcooling On The Cooling Effectiveness”, ASME Turbo Expo 2011, Vancouver, Canada, (2011), GT2011-46055.
• Heidmann, J. D., “A Numerical Study of Antivortex Film Cooling Designs At High Blowing Ratio”, ASME Turbo Expo, Berlin, Germany, (2008), GT2008-50845.
• Dhungel, A., Lu, Y., Phillips, W., Ekkad, S. V., Heidmann, J., “Film Cooling From A Row of Holes Supplemented With Anti Vortex Holes”, ASME Turbo Expo, Montreal, Canada, (2007), GT2007-27419. [https://doi.org/10.1115/GT2007-27419]
• CFX-11.0 Solver Theory, Ansys inc, (2006).
• Bardina, J. E., Huang, P. G., Coakley, T. J., “Turbulence Modeling Validation”, AIAA 97-2121, (1997). [https://doi.org/10.2514/6.1997-2121]
• Lee, K. D., Kim, K. Y., “Surrogate based optimization of a laidback fan-shaped hole for filmcooling”, International Journal of Heat and Fluid Flow, (2011), 32(1), p226-238.
• Lee, K. D., Choi, D. W., Kim, K. Y., “Optimization of Ejection Angles of Double-jet Filmcooling Holes Using RBNN Model”, International Journal of Thermal Sciences, (2013), 73, p69-78.
• Baheri, S., Alavi Tabrizi, S. P., Jubran, B. A., “Film cooling effectiveness from trenched shaped and compound holes”, Heat Mass Transfer, (2008), 44, p989-998. [https://doi.org/10.1007/s00231-007-0341-9]