진공단열재를 적용한 컨테이너의 단열성능 평가에 대한 연구
Abstract
The thermal insulation performance of a container with a vacuum-insulated panel was numerically investigated herein. The heat loss caused by natural and mixed convection through the container was calculated for various indoor/outdoor air temperatures and outdoor air velocities. The outdoor velocities had a minor influence on the heat loss because of the extremely low thermal conductivity of the vacuum insulated panel. The amount of heat loss was mainly determined using the temperature difference between the indoor and outdoor air. The monthly variations of the total heat loss through the container were evaluate d using the monthly averaged climate data, including the maximum and minimum outdoor temperatures. The results revealed that the container with the vacuum insulated panel exhibited superior thermal insulation performance, as evidenced by the maximum heat loss value of 324.5 W.
Keywords:
Shipping container, Conjugate heat transfer, Thermal resistance, Thermal conductivity, Freight transport키워드:
선박용 컨테이너, 복합열전달, 열저항, 열전도도, 화물 수송1. 서 론
냉동 및 냉장 화물 수송용으로 사용되는 리퍼 컨테이너는 일반적으로 벽체에 50—70mm 두께의 폴리우레탄폼 (Polyurethane form, PUF)으로 단열층을 형성하고, 외부로부터 전력을 공급받아 작동되는 공조장치를 사용하여 강제적으로 내부 온도를 조절한다. 리퍼 컨테이너는 단열성능이 높을수록 공조장치의 적재용량이 작아질 수 있으며 그 반대의 경우도 성립되므로, 단열성과 공조장치 용량은 상호 보완적이라 할 수 있다. 한편, 리퍼 컨테이너는 내부 항온유지를 위해 상시전원에 연결 상태를 유지해야 한다는 단점이 있다. 이는 수송운임 등 물류비 증가, 상하역 작업 또는 인적오류에 의해 저온유통시스템(Cold-chain)이 단절되는 원인이 된다.
한국철도기술연구원에서는 신선식품 등 정온물류(Temperature controlled supply chain)의 수송효율 향상을 목표로 스마트 고단열 컨테이너를 개발 중에 있다. 1단계로 20ft 컨테이너 벽체에 30mm의 진공단열재(Vacuum insulated panel, VIP)와 PUF를 결합한 단열구조를 형성하여 단열성능을 강화한 컨테이너를 개발하였고, 이를 Passive type이라 하였다. Passive type의 스마트 고단열 컨테이너의 단열성능 평가를 위해 대형 챔버 내에 기존의 PUF로만 구성된 컨테이너와 개발된 Passive type의 스마트 고단열 컨테이너를 배치하고 챔버의 온도변화에 따른 각 컨테이너의 내부 온도를 시간에 따라 측정하였다. 컨테이너의 내부 온도가 외부의 챔버 온도에 도달하는 시간은 Passive type의 스마트 고단열 컨테이너의 경우가 기존 컨테이너의 경우보다 평균 1.91배 길며, 이는 개발된 스마트 고단열 컨테이너의 우수한 단열성능을 나타낸다. 2단계는 단열성능을 강화함에도 장기간 운송과정에서 발생하는 에너지(냉기/열기) 손실 보충을 위해 배터리 전력의 저에너지 고효율 하이브리드 공조장치 개발을 진행 중에 있다. 이를 Active type이라 하였다.
Kan 등(1)은 실험 및 수치해석을 통해 리퍼 컨테이너 내부 화물 적재방식에 따라 내부 온도분포가 결정된다고 하였으며, Budiyanto와 Shinoda(2)은 리퍼 컨테이너의 단면에 대한 2차원 수치해석을 통해 리퍼 컨테이너의 외벽과 내벽의 온도를 계산하여 필요한 냉동용량을 예측하였다. Getahun 등(3)은 리퍼 컨테이너 내부의 화물을 다공성 매질로 가정하여 수치해석을 진행하였으며 이를 통해 예측한 리퍼 컨테이너 내부 온도분포 및 내기의 속도분포를 실험 결과와 비교하여 수치해석의 타당성을 검증하였다. Ho와 Rahman(4)은 컨테이너가 적재된 냉동창고 내부의 열전달 및 공기 흐름을 수치해석을 통해 계산하였고, 이를 통해 냉동 효율을 높이고 온도분포가 균일하기 위한 방안을 제시하였다.
본 연구는 상용 수치해석 프로그램인 ANSYS FLUENT(5)를 사용하여 Passive type 컨테이너의 내기 자연대류, 외기 자연대류 및 강제대류, 컨테이너 자체의 열전도를 함께 고려한 복합열전달 해석을 수행하였다. 이를 통해 컨테이너의 열전달 특성을 파악하고 컨테이너 벽체를 통한 손실 열량을 계산하여, Active type 컨테이너에 장착될 하이브리드 공조장치의 적정 제원을 설계하기 위한 기초 데이터로 활용하고자 한다.
2. 수치해석 모델
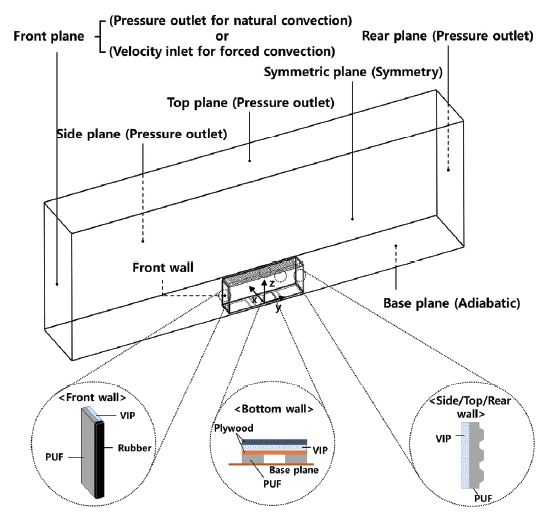
Fig. 1은 컨테이너와 내/외기를 포함하는 3차원 계산 영역(Computational domain)을 나타내며, 이를 통해 컨테이너 내/외기의 대류와 컨테이너의 전도를 함께 고려한 복합열전달 해석을 수행하였다. 수치해석의 계산시간을 단축하기 위해, yz-평면을 대칭면(Symmetric plane)으로 하여 전체 컨테이너와 외기의 1/2만 모델링하였다.
해석 결과의 격자 의존성 확인을 위해 400만, 800만, 1200만 개의 격자를 포함하는 계산 영역에 대한 수치해석을 진행하였다. 외기의 속도가 0m/s, 내/외기의 온도가 –20/40℃인 조건에서 각 격자 시스템에서 계산된 컨테이너의 열손실량은 각각 179.85, 180.25, 184.63W이고 열손실량 간의 최대 변화량은 2.43%로 격자에 대한 낮은 의존성을 보였으며, 본 연구의 모든 수치해석에 800만 개의 격자 시스템을 사용하였다. Fig. 2는 해석에 사용된 수치모델의 격자구조를 나타내며, 컨테이너 벽면에서 발달하는 경계층에 대한 정확한 해석을 위해 벽 근처에 격자를 조밀하게 생성하였고, 계산의 수렴성을 높이기 위해 벽체의 굴곡 부분을 제외한 대부분의 계산 영역을 정렬격자로 구성하였다.
내/외기의 유동은 정상상태 비압축성으로 가정하였으며, 질량, 운동량, 에너지 보존에 대한 지배방정식은 다음과 같다.
| (1) |
| (2) |
| (3) |
ρ, U, P, μ, μt, Cp, kf, T는 각각 밀도, 국부 속도, 국부 압력, 점성계수, 국부 난류 점성계수, 등압 비열, 유체의 열전도율, 국부 온도이다. 난류 점성계수를 해석하기 위해 Realizable k-ε 모델(6)을 사용하였으며, 난류 운동 에너지(k)와 난류 소산(ε)에 대한 수송 방정식은 다음과 같다.
| (4) |
| (5) |
식 (4)와 (5)에서 σk = 1.0, σε = 1.2, C2 = 1.9이며, 식 (4)의 Gk, Yk와 식 (5)의 C1은 다음과 같다.
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
식 (5)의 마지막 항은 ε에 대한 부력효과를 의미하며, C1ε = 1.44이고 C3ε과 Cb은 다음과 같다.
| (11) |
| (12) |
이 때, u와 v는 각각 중력방향에 대해 수직인 속도성분과 평행한 속도성분을 의미한다. Prt는 난류 프란틀수를 나타내며, Realizable k-ε 모델의 초기값 0.85를 사용하였다. 식 (2)의 Xi는 체적력으로, 본 연구에서는 –z방향으로 중력을 설정하여 컨테이너의 높이 방향으로만 존재한다. 온도에 따른 공기의 밀도 변화에 의한 자연대류 계산을 위해 Boussinesq 모델(7)을 사용하였으며, 체적력의 밀도는 다음과 같이 근사된다.
| (13) |
이 때, β와 ρ0는 각각 작동온도, T0, 에서의 체적 열팽창계수와 밀도이다. Boussinesq 모델에 대한 작동온도는 외기 온도와 같도록 설정하였으며, 내/외기 온도조건 범위에서 실제 밀도와 식 (13)로부터 계산된 밀도의 오차는 4% 이내로 Boussinesq 근사가 타당함을 확인하였다. 공기의 정압비열, 점성계수, 열전도율은 NIST (National Institute of Standards and Technology)의 REFPROP 9.1(8) 프로그램을 사용하여 얻었으며, 계산 시 온도에 따라 선형보간 되도록 설정하였다.
고체의 표면에서 점착 조건(No-slip condition)을 가정하였으며, Enhanced wall treatment(10)를 적용하였다. Fig. 1에서 바닥면(Base plane)과 대칭면에 대해 각각 단열과 대칭 조건을 적용하였다. 자연대류 해석 시에 외기의 앞면(Front plane), 옆면(Side plane), 윗면(Top plane) 및 뒷면(Rear plane)을 모두 Pressure outlet으로 설정한 반면, 강제대류 해석 시에는 앞면을 Velocity inlet으로 설정하고 옆면, 윗면, 및 뒷면을 Pressure outlet으로 설정하였다. 한편, 컨테이너 내부 공기의 일정 부피를 열원으로 설정하여 내부 공기에 대한 냉/난방을 모사하였으며, 내기의 온도가 목표한 온도로 유지되도록 하였다.
Table 1은 본 연구에서 해석하는 리퍼컨테이너에 사용된 재료의 물성을 정리한 것으로, Fig. 1에 나타난 것과 같이 바닥면은 합판, VIP 및 PUF으로 구성되며, 그 외의 벽체는 VIP와 PUF으로 이루어진다. 또한 외기의 앞면과 마주하는 컨테이너 벽체에는 개폐문(Container door)이 있어 그 주변을 고무로 실링(Sealing)하였다. Table 2는 본 연구의 외기 속도 조건 및 내/외기 온도 범위를 나타낸다. 부산의 월별 기후 통계 데이터(11)를 바탕으로 외기의 속도 및 온도 범위를 설정하였으며, 내기 온도는 리퍼 컨테이너의 냉동-보온 온도조절 가능 범위로 설정하였다.
이산화기법은 압력에 대해 Pressure staggering option (PRESTO!)(12), 운동량과 에너지에 대해 Second order upwind를 적용하였으며, Semi-implicit method for pressure linked equations-consistent (SIMPLEC)(13) 알고리즘을 사용하여 계산하였다. 각 조건에 대한 계산에서 모든 변수의 잔차(residual)가 5×10-3 이하가 되면 계산이 수렴했다고 판단하였다.
3. 수치해석 결과
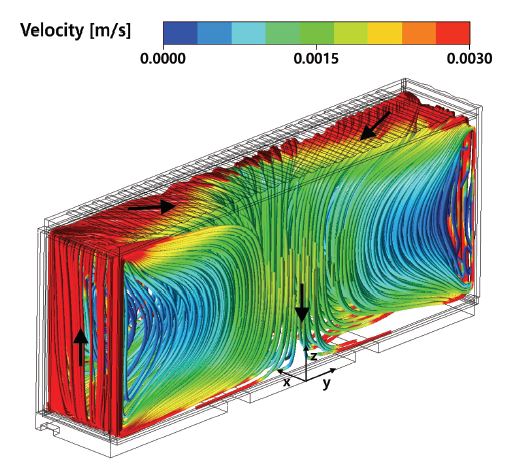
Fig. 3는 외기의 속도가 0m/s, 내/외기의 온도가 –20/40℃인 조건에서 내기의 유선을 나타낸 것이다. 벽체 부근의 내기의 온도가 외부에서 유입되는 열에 의해 가열됨에 따라 밀도가 감소하여 옆면을 따라 위로 상승하는 기류가 형성된다. 상승한 공기는 윗면의 중심부에서 만나 바닥면으로 하강하고, 이후 바닥면을 따라 옆면으로 이동하면서 순환하게 된다.
Fig. 4(a)-(d)는 각각 내/외기의 온도가 –20/40℃, -2/0℃, 2/0℃, 30/-20℃인 조건에서 해석된 속도벡터장을 대칭면에 대해 나타낸 것이며, Fig. 5(a)-(d)는 Fig. 4(a)-(d)의 각 온도조건에 대응하는 온도장을 대칭면에 대해 나타낸 것이다. Fig. 4과 Fig. 5의 속도와 온도 범위는 내/외기의 온도조건에 따라 달리하였다. Fig. 4(a)와 (b) 같이 내기 온도가 외기 온도보다 낮은 경우, 벽면 부근의 내기는 가열되어 밀도가 감소하면서 상승하는 반면, 벽면 부근의 외기는 냉각되어 밀도가 감소하면서 하강한다. 반대로 Fig. 4(c)와 (d) 같이 내기 온도가 외기 온도보다 높은 경우, 벽면 부근의 내기는 냉각되어 하강하는 기류가 나타나는 반면, 외기는 가열되어 상승하는 기류가 나타난다. Fig. 4(a)와 (b) 및 Fig. 4(c)와 (d) 사이의 비교를 통해 외기와 내기의 온도차가 클수록 상승 또는 하강하는 기류의 속도가 커짐을 확인할 수 있으며, 이는 밀도차에의한 부력이 온도차가 커짐에 따라 증가하기 때문이다. 한편, Fig. 5(a)와 (b) 및 Fig. 5(c)와 (d)의 비교를 통해 외기와 내기의 온도 차이가 클수록 컨테이너 주변의 온도 구배가 커짐을 알 수 있으며, 이는 온도차가 클수록 열손실량이 증가함을 나타낸다. 또한, 컨테이너 오른편의 온도경계층이 왼편의 온도 구배보다 작게 형성되는데, 이는 고무 실링을 포함하는 왼쪽 개폐문에 비해 단열재로만 구성된 오른편 벽면의 전도 열저항이 높아 열손실량이 작기 때문이다.
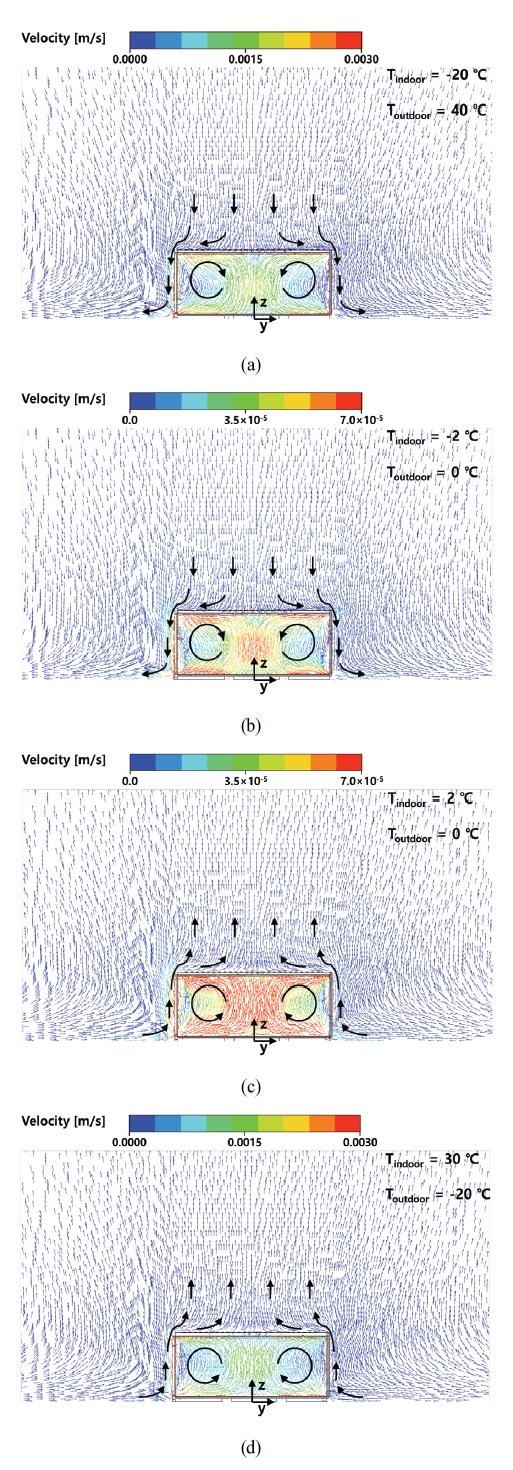
Velocity vectors at symmetric plane for Voutdoor = 0 m/s, (a) Tindoor = -20℃, Toutdoor = 40℃, (b) Tindoor = -2℃, Toutdoor = 0℃, (c) Tindoor = 2℃, Toutdoor = 0℃, (d) Tindoor = 30℃, Toutdoor = -20℃
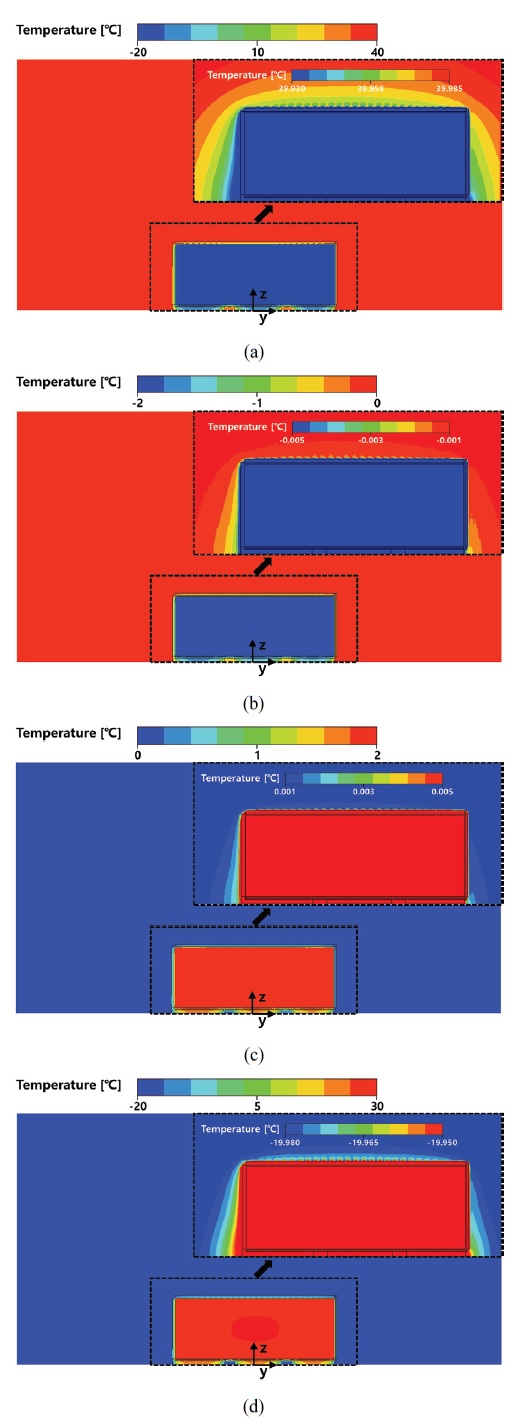
Temperature contours at symmetric plane for Voutdoor = 0m/s, (a) Tindoor = -20℃, Toutdoor = 40℃, (b) Tindoor = -2℃, Toutdoor = 0℃, (c) Tindoor = 2℃, Toutdoor = 0℃, (d) Tindoor = 30℃, Toutdoor = -20℃
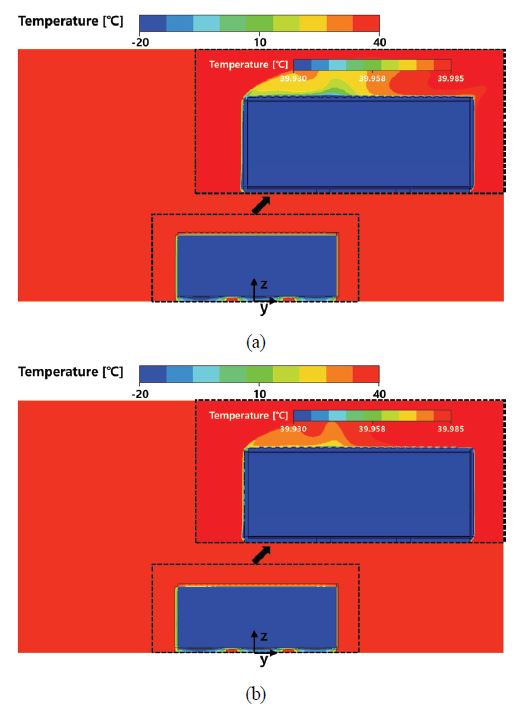
Fig. 6(a)와 (b)는 외기가 40℃이고 내기가 –20℃인 온도조건에서 외기의 속도가 각각 15와 25m/s인 경우에 해석된 속도벡터장을 대칭면에 대해 나타낸 것이며, Fig. 7(a)와 (b)는 각각 대응되는 온도 및 속도조건에서 해석된 온도장을 대칭면에 대해 나타낸 것이다. Fig. 6에서 컨테이너의 개폐문이 있는 면에 부딪힌 외기는 개폐문을 따라 그 속도경계층이 발달하다가 컨테이너의 개폐문과 윗면의 모서리에서 분리되었으며, 분리된 속도경계층의 내부에 재순환영역이 발생하였다. 외기의 하류지역으로 갈수록 분리된 속도경계층의 두께는 감소하며, 컨테이너의 후면에는 후류가 형성되는 것을 확인할 수 있다. Fig. 7에서 컨테이너 윗벽에 형성되는 외기의 온도경계층은 Fig. 4에서 컨테이너 윗벽에 형성된 외기의 온도경계층과는 확연히 다른 형상을 보인다. 이는 Fig. 7의 온도경계층이 Fig. 6의 속도 경계층 내부에 발생한 재순환영역과 상호작용하여 억제되거나 성장하기 때문인 것으로 보인다. 한편, Fig. 4(a)와 Fig. 7의 비교를 통해 외기의 속도가 클수록 개폐문 부근과 컨테이너 윗면의 온도경계층이 얇게 형성됨을 확인할 수 있으며, 이는 컨테이너 표면에서 상대적으로 큰 온도 구배가 형성되어 컨테이너 벽면을 통한 열손실량이 증가함을 의미한다.
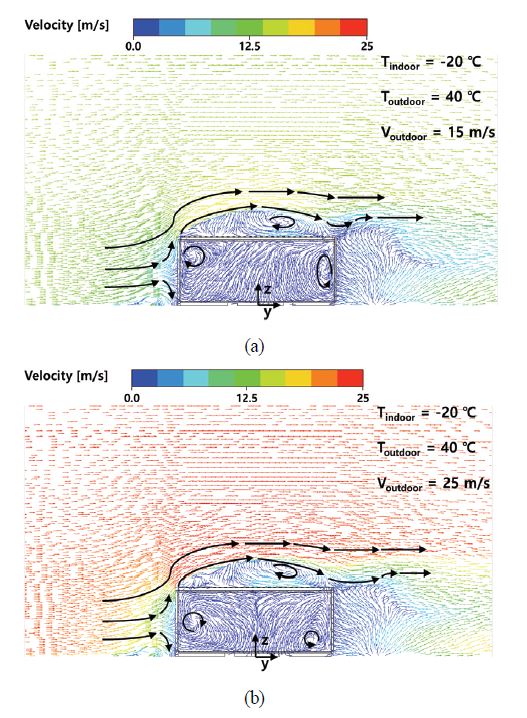
Velocity vectors at symmetric plane for Tindoor = -20℃, Toutdoor = 40℃, (a) Voutdoor = 15 m/s and (b) Voutdoor = 25 m/s
4. 내/외기 조건에 따른 열손실량
Fig. 8은 Table 2의 내/외기 온도 범위에 대해 외기의 속도가 0m/s인 자연대류와 외기의 속도가 각각 15와 25m/s인 강제대류 조건에서 예측된 컨테이너의 열손실량을 외기와 내기의 온도차에 따라 그래프로 나타낸 것이다. 각 외기 속도조건에서 컨테이너의 열손실량이 외기와 내기의 온도차에 선형적으로 비례하여 증가하는 것을 확인할 수 있으며, 그 관계는 다음과 같이 표현된다.
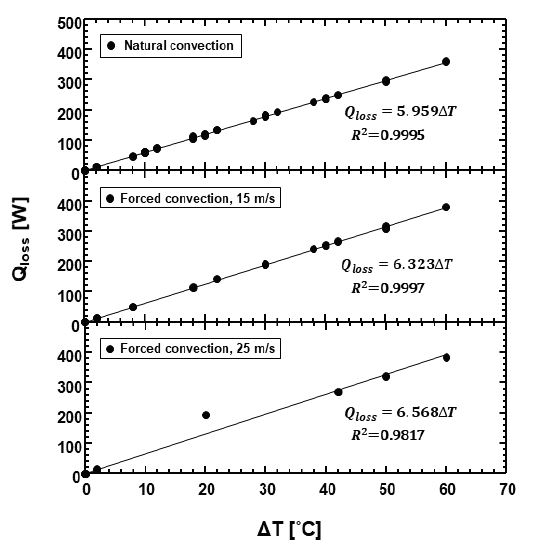
Relationship between total heat loss of container and indoor-outdoor temperature difference with respect to different outdoor velocities
| (14) |
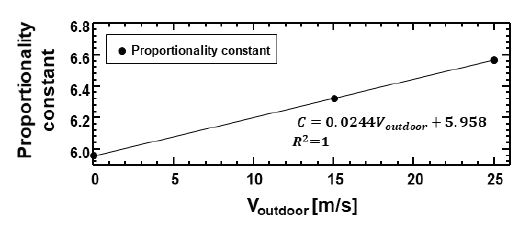
선형회귀분석을 통해 얻은 외기-내기 온도차(ΔT)와 컨테이너의 열손실량(Qloss) 간의 비례 상수(C)가 각각 5.959, 6.323, 6.568로 외기의 속도가 증가함에 따라 증가하는 경향을 보였으며, 이는 컨테이너의 열손실량이 외기의 속도와 비례하여 증가함을 의미한다. Fig. 9는 외기의 속도와 비례상수 간의 선형적인 관계를 나타내며, 선형회귀분석을 통해 그 관계를 다음과 같이 구하였다.
| (15) |
식 (14)와 (15)로부터 내/외기 온도 차이가 같을 경우, 외기 속도 증가에 따른 열손실량의 최대 증가율은 10.24%로 예측되며, 최대 외기 속도가 25m/s임을 고려할 때 외기 속도의 변화가 컨테이너 열손실량에 미치는 영향은 상대적으로 적음을 확인하였으며 이는 컨테이너 복합열전달의 총 열저항이 외기의 대류 열전달 계수보다 VIP의 매우 낮은 열전도도에 의해 지배적으로 결정되기 때문인 것으로 판단된다.
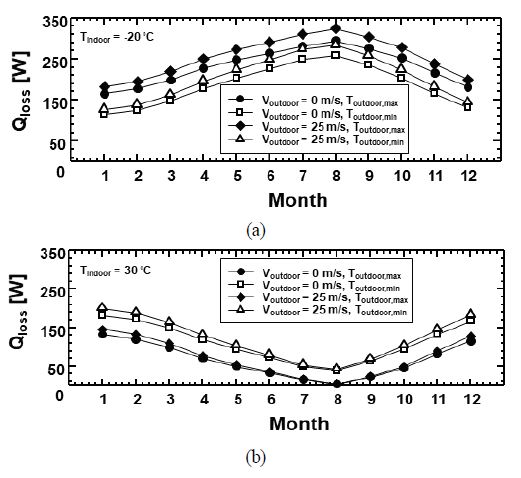
마지막으로, 국내 수출입 물류의 주요 수송요지인 부산항에서 가까운 일본 주요 무역항 간 스마트 고단열 컨테이너를 이용한 해운수송을 가정하고, 내/외기 온도차가 극단적 조건에서 컨테이너의 최대 열손실량을 추산하였다. Fig. 10은 부산 지역의 월별 평균 최고 및 최저 온도에 관한 기상청 데이터(11)를 바탕으로 내기의 온도가 각각 -20℃와 30℃로 유지되는 고단열 컨테이너의 열손실량을 식 (14)와 (15)를 통해 예측하여 외기가 자연대류인 경우와 외기의 속도가 25m/s인경우에 대해 월별로 나타낸 그래프이다. Fig. 10(a)에 나타난 바와 같이 내기 온도가 -20℃로 설정된 컨테이너는 연중 최고 기온이 나타나는 8월에 외기 속도가 25m/s일 때 324.5W의 가장 큰 열손실량을 보일 것으로 예측된다. 반면, Fig. 10(b)에 나타난 것과 같이, 내기 온도가 30℃로 설정된 컨테이너는 연중 최저기온이 나타나는 1월에 외기 속도가 25m/s인 경우에 대하여 201.0W의 가장 큰 열손실량이 발생할 것으로 예측된다. 이는 VIP로 구성된 고단열 컨테이너의 뛰어난 단열성능을 나타내며, 따라서 본 연구의 고단열 컨테이너는 냉동용량이 작은 공조장치로도 온도 민감화물의 수송을 가능케 하여 그 효율을 향상시킬 수 있을 것으로 판단된다.
5. 결 론
본 연구에서는 국내에서 개발이 진행 중인 스마트 고단열 컨테이너의 단열성능을 평가하기 위해 다양한 외기 온도와 속도, 그리고 컨테이너 내부 설정 온도조건을 상정하고 컨테이너의 열손실량을 복합열전달 수치해석을 통해 정량적으로 계산하였다. 이를 통해 외기와 내기의 온도 조건과 외기의 속도에 따른 대칭면의 속도벡터장 및 온도장을 확인하였다. 또한, 컨테이너의 열손실량이 내부와 외부의 온도차와 외기의 속도에 대해 선형적으로 증가함을 확인하였다. 그러나 증가된 외기 속도에 의한 열저항 감소 효과는 작게 나타났는데, 이는 컨테이너 복합열전달의 총 열저항이 진공단열재의 낮은 열전도도에 의해 지배적으로 결정되기 때문이다. 한일노선을 Test-bed로 하여 월별 평균 최고 및 최저 온도 데이터를 기반으로 실제 사용환경에서의 컨테이너 열손실량을 계산한 결과, 외기 속도가 25m/s일 때 내부 온도가 -20℃로 설정된 컨테이너가 8월 중 324.5W의 최대 열손실량을 보일 것으로 예측되었으며, 이는 최대 열손실량과 등가의 에너지를 공급한다면 컨테이너 내부의 장시간 항온유지가 가능함을 시사한다. 본 연구결과는 향후 Active type 스마트 고단열 컨테이너의 공조장치의 제원 설계를 위한 기초 자료로 활용될 것이다. 한편, 향후 실험을 통해 컨테이너 내/외벽의 대류에 대한 Re 수 및 Ra 수와 Nu 수의 상관관계를 분석하고, 본 연구의 내/외기 온도조건과 컨테이너의 굴곡진 외벽 조건에서 사용 가능한 열전달계수 예측상관식을 개발할 계획이다. 또한, 본 연구에서 실제 해운수송 환경에서 컨테이너의 선적 위치나 방향에 대한 일반화가 어려워 태양 복사에너지에 대한 분석은 제외되었으며, 이에 대한 보완연구가 수반되어야 할 것으로 판단된다.
Acknowledgments
본 연구는 한국철도기술연구원 주요사업의 연구비 지원으로 수행되었습니다.
References
-
Kan, A., Hu, J., Guo, Z., Meng, C., and Chao, C., 2017, “Impact of Cargo Stacking Modes on Temperature Distribution Inside Marine Reefer Containers.” International Journal of Air-Conditioning and Refrigeration, Vol. 25, No. 3, pp. 1750020.
[https://doi.org/10.1142/S2010132517500201]

-
Budiyanto, M. A., and Shinoda, T., 2017, “Study on the CFD simulation of refrigerated container.” In IOP Conference Series: Materials Science and Engineering, Vol. 257, No. 1, pp. 012042.
[https://doi.org/10.1088/1757-899X/257/1/012042]

-
Getahun, S., Ambaw, A., Delele, M., Meyer, C. J., and Opara, U. L., 2017, “Analysis of airflow and heat transfer inside fruit packed refrigerated shipping container: Part I-Model development and validation.” Journal of food engineering, Vol. 203, pp. 58-68.
[https://doi.org/10.1016/j.jfoodeng.2017.02.010]

-
Ho, S. H., Rosario, L., and Rahman, M. M., 2010, “Numerical simulation of temperature and velocity in a refrigerated warehouse.” International Journal of Refrigeration, Vol. 33, No. 5, pp. 1015-1025.
[https://doi.org/10.1016/j.ijrefrig.2010.02.010]

- ANSYS. Inc., 2017, “ANSYS FLUENT 18.0 in Workbench User's Guide”.
-
Shih, T. H., Liou, W. W., Shabbir, A., Yang, Z., and Zhu, J., 1995, “A new k-ε eddy viscosity model for high reynolds number turbulent flows.” Computers & Fluids, Vol. 24, No. 3, pp. 227-238.
[https://doi.org/10.1016/0045-7930(94)00032-T]

- Bergman, T. L., Incropera, F. P., DeWitt, D. P., and Lavine, A. S., 2011, Fundamentals of heat and mass transfer, John Wiley & Sons.
- Lemmon, E. W., Huber, M. L., and McLinden, M. O., 2013, “REFPROP 9.1,” NIST Standard Reference Database 23.
-
Kalnæs, S. E., and Jelle, B. P., 2014, “Vacuum insulation panel products: A state-of-the-art review and future research pathways.” Applied Energy, Vol. 116, pp. 355-375.
[https://doi.org/10.1016/j.apenergy.2013.11.032]

-
Kader, B., “Temperature and concentration profiles in fully turbulent boundary layers,” International journal of heat mass transfer, Vol. 24, No. 9, pp. 1541-1544.
[https://doi.org/10.1016/0017-9310(81)90220-9]

- 기상청(2018), “기상관측데이터”, http://www.kma.go.kr, .
- Patankar, S., 1980. Numerical heat transfer and fluid flow, CRC press.
-
Van Doormaal, J. P., and Raithby, G. D., 1984, “Enhancements of the SIMPLE method for predicting incompressible fluid flows,” Numerical heat transfer, Vol. 7, No. 2, pp. 147-163.
[https://doi.org/10.1080/01495728408961817]