유동-구조 연성해석 기법을 이용한 플라스틱 축류홴의 블레이드 진동특성 평가

1. 서 론

냉동 공조용 축류 홴은 대풍량 저압이 요구되는 운전 조건에서 주로 사용되며, 그 적용 예로는 냉동기 및 에어콘의 실외기용 홴들을 들 수 있다. 이러한 용도의 홴들은 대량 생산이 가능하여야 하며 생산 단가도 저렴하여야 하므로, 홴을 플라스틱 재질로 제작하는 경우가 일반적이다. 그러나 플라스틱 재질은 금속 재질에 비해 구조적 강도가 약하므로, 플라스틱 홴의 날개에 가해지는 압력이 상승하는 경우 홴 블레이드 표면의 심각한 변형 및 진동이 발생하여 이로 인해 추가적인 소음이 발생하기도 한다. 즉 날개의 강성 부족으로 인하여 회전 중 떨림이 발생하는 경우 유동이 불균일해져 심한 진동과 소음이 발생하게 되므로 홴의 내구성에 심각한영향을 주게 되고, 심한 경우 날개의 파손으로 이어지기도 한다⁽¹⁾.

이러한 이유로, 플라스틱 축류 홴의 설계 시 기존의 유동 및 성능 해석뿐만 아니라 유동-구조 연성 해석(flow-structure coupled analysis)을 통한 홴 블레이드의 구조 변형 및 진동 특성에 대한 검토가 필수적임을 알 수 있다. 그러나, 축류 홴의 유동-구조 연성 해석에 대한 필요성은 인식되고 있지만, 해석을 위해 많은 시간과 방대한 데이터가 필요하므로, 아직은 활발한 연구가 진행되지는 못하는 실정이다.

축류 홴의 유동해석에 관한 논문은 이미 많이 발표되었으나^(2,3), 축류 홴의 유동-구조 연성 해석에 대한 논문은 많이 미흡한 실정이다. 권순국등⁽⁴⁾은 자동차용 냉각홴 블레이드에 관한 유동-구조 연성 해석에 대하여 연구를 진행하였다. 장보연⁽⁵⁾은 저압용 축류홴에 관한 유동-구조 연성해석 연구를 진행하였다.

본 연구는, 축류 홴 유동-구조 연성 해석의 일환으로서, 냉동기용 플라스틱 축류 홴을 설계하였고, 설계된 홴에 대해 전산유체역학 방법을 이용하여 비정상 유동계산을 수행하였다. 비정상 유동계산 결과를 토대로, 플라스틱 홴 블레이드에 대한 정상상태 구조해석을 수행하였고, 이를 통해 블레이드 표면의 응력과 변형 분포를 계산하였으며 그 특성을 검토하였다. 더 나아가, 홴 블레이드에 대한 비정상 구조해석을 수행하여 블레이드 표면의 진동 특성도 규명하였다.

2. 플라스틱 축류 홴의 설계

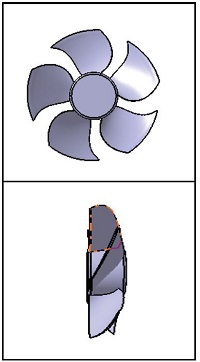
본 연구의 대상인 플라스틱 축류 홴은 냉동기에 사용되는 저압 홴으로 회전수가 1100 rpm이고, 5개의 블레이드로 구성되어 있으며, 블레이드의 주요 설계제원은 Table 1에 표시한 바와 같다. 이때 홴의 설계점 유량은 2520 m³/h, 압력은 73.5 Pa 이다. 앞서의 홴 설계제원들을 토대로, 홴의 3차원 블레이드 형상은 FANDAS 코드^(6,7)를 이용하여 설계하였고, 이때 홴 블레이드 각도 설계는 combined vortex 방법을 사용하였으며 설계된 블레이드의 형상 모델링은 CATIA 코드를 이용하였다. 본 방법에 의해 설계된 홴 블레이드 형상이 Table 1 에 나타나 있다. 블레이드 시위길이는 허브에서 끝단까지 60 mm 에서 180 mm 로 변화되고, 평균유선 반경에서의 시위길이(mean chord length)는 126.7 mm 로 나타나고 있다.

Table 1

Design specifications of the present fan model

Fig. 1

3D fan design

본 연구의 홴 모델은 폴리에틸렌 재질로 제작되었으며, 이때 폴리에틸렌 재질의 물성치는 Table 2 와 같고 이러한 물성치들은 본 연구의 홴 블레이드 구조/진동 해석 시 사용되었다.

Table 2

Material properties of polyethylene

3. 플라스틱 축류 홴의 유동-구조 연성해석 방법

본 연구의 유동-구조 연성 해석은 상용프로그램인 ANSYS사의 CFX 와 Transient Structure 코드⁽⁸⁾를 사용하였으며, 유동-구조 연성 해석 절차는 다음과 같다: CFX 코드를 이용하여 홴 내부 유동장에 대한 정상상태 계산을 수행하고, 정상상태 계산 결과를 초기값으로 가지고 비정상상태 유동 계산을 수행한다. 이렇게 얻어진 정상 및 비정상 유동 계산 결과들은 구조/진동 해석을 위한 Transient Structure 해석의 입력 데이터로 사용되며, 이때 홴 허브 부분의 고정 경계조건과 날개 표면에 작용하는 유체의 압력을 가진 조건으로 설정한다.

또한, 본 연구는 블레이드 변형이 홴 공력성능에 미치는 영향이 무시할 만큼 적다는 가정하에, 1방향 연계(one-way coupling) 해석을 수행하였다.

3.1 유동해석 방법

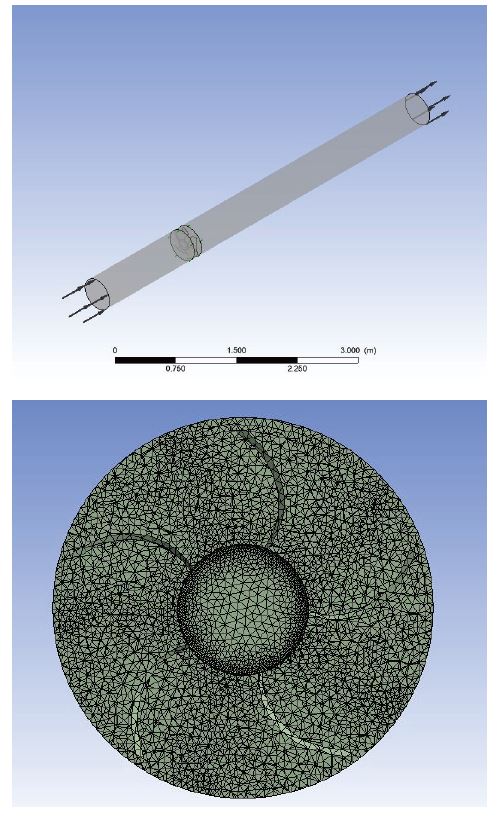
본 연구의 홴 내부 3차원 난류 유동장 해석을 위해서 ANSYS CFX 코드를 사용하였다. 전산해석을 위한 유동영역은 직경이 415 mm, 길이가 6 m 인 원통형 덕트로 구성하였고, 홴을 포함하고 있는 내부 회전영역과 외부 정지 영역으로 구분하였으며 이때 사용된 격자의 수는 총 4,066,430 개 이다(Fig. 2 참조).

Fig. 2

Computational domain and mesh system for steady-state and transient flow calculations

본 유동해석의 난류 모델로는 k-ω 기반의 Shear-stress Transport(SST k-ω) 모델을 사용하였다. 회전하는 블레이드 유동 영역과 정지 유동 영역의 경계면 조건은 정상상태 계산 시 Frozen rotor 조건을 사용하였으며, 구조/진동 해석을 위한 비정상상태 유동 계산 경우에는 Transient rotor-stator 조건으로 설정하였다.

3.2 구조 및 진동해석 방법

본 연구의 홴 블레이드 표면의 구조 및 진동 해석을 위해서 ANSYS Transient Structural 코드를 사용하였다. Fig. 3 은 구조 및 진동 해석에 사용된 홴 블레이드 표면의 격자계를 보여주고 있으며, 격자 의존성 테스트를 거쳐 최적화된 격자의 수는 30,000 이다.

Fig. 3

Mesh system for structural and vibration calculations

본 연구의 구조/진동 해석을 위한 Transient Structural 적용 시, 홴 허브 부분은 고정단(fixed end) 경계조건으로 설정하였고, 날개 표면에 작용하는 유체압력은 정상/비정상 상태 유동계산결과들로부터 얻어내어 블레이드 표면의 하중(loading)/가진(oscillation) 조건으로 설정하였다.

4. 유동-구조 연성해석 결과 및 고찰

4.1 유동해석 결과

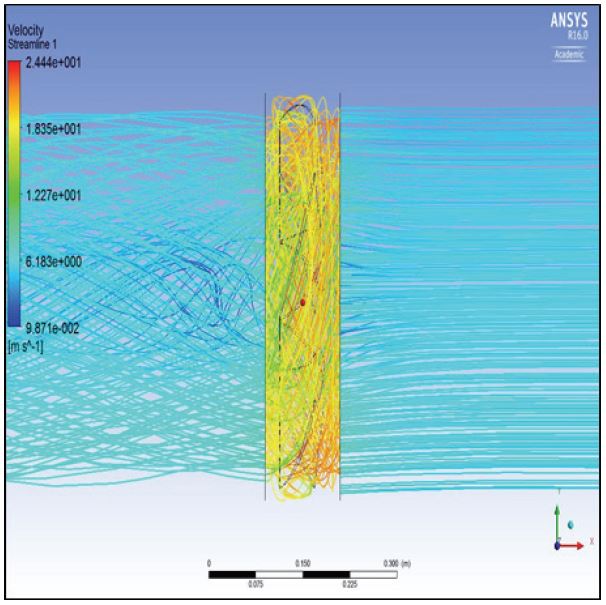
정상 상태의 홴을 통과하는 공기의 흐름은 Fig. 4와 같이 계산되었으며, 홴 입구에서 축방향으로 유입된 공기가 블레이드를 통과하며 선회유동을 보여주고 있다. 본 연구에서 사용된 모델 홴의 끝단 틈새(tip clearance)가 비교적 큰 이유로, 슈라우드와 케이싱간의 틈새로 인한 누설 유동(leakage flow)이 눈에 띄게 관찰되며, 이러한 누설 유동은 홴의 성능을 저하시키고 진동과 소음을 유발할 것으로 판단된다⁽⁹⁾.

Fig. 4

Flow pattern of air passing through fan blades

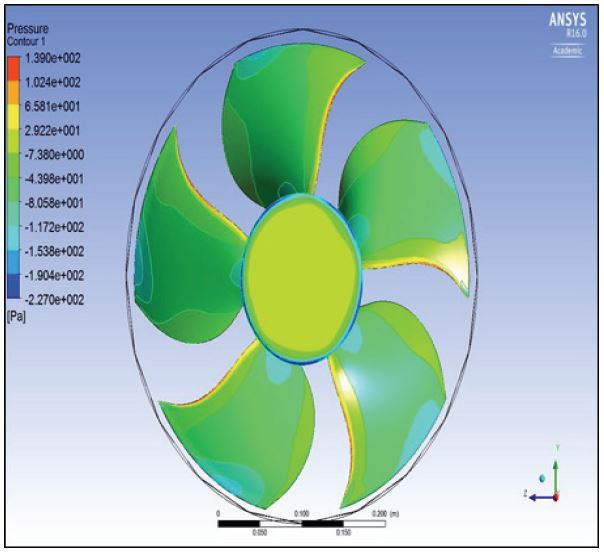
홴 블레이드 표면의 압력분포가 Fig. 5 에 나타나 있다. 홴 블레이드 끝단 근처에서 현저한 압력저하로 인한 저압 구간이 관찰되며, 이러한 저압 구간은 누설유동에 의한 압력손실에 의한 것으로 판단된다. 그리고 블레이드 전연(leading edge)에서 압력이 가장 크고, 후연(trailing edge)으로 갈수록 압력이 줄어드는 경향을 볼 수 있다. 이러한 압력변동의 폭은 최대 30 Pa 까지 나타나고 있다.

Fig. 5

Pressure distribution on fan blade surface

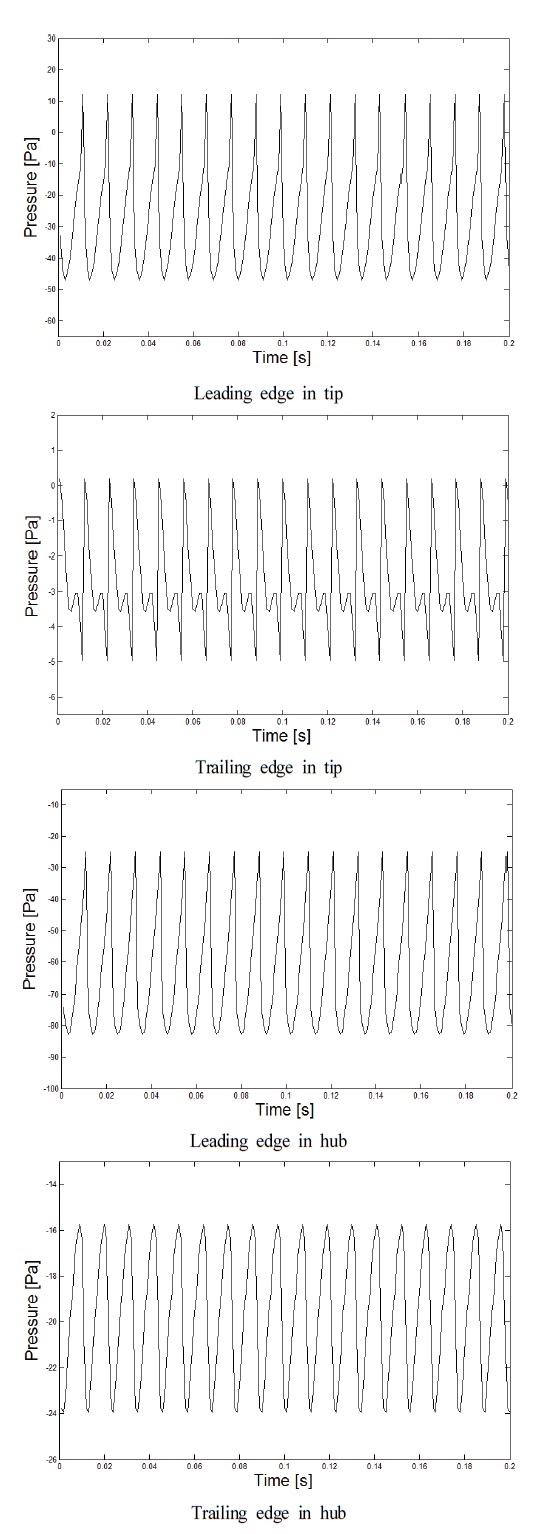
비정상 유동 계산을 통해 얻어진 시간에 따른 홴 내부의 압력 변동에 대한 결과가 Fig. 6 에 도시되어 있다. 블레이드 허브와 끝단에서 모두 주기적인 압력변동을 보여주고 있으며, 허브에서의 압력변동이 전형적인 정현파의 특징을 보이는 반면 끝단 후연에서의 압력 변동은 정현파에 작은 충격(impulse)이 가해져 2개의 정점을 가지는 주기적 형태로 나타나고 있다. 이러한 끝단에서의 압력변동 형태는 앞서 언급한 누설유동에 의한 영향으로 판단된다. 즉 블레이드 끝단에서 누설된 2차유동이 날개 끝단 후연쪽으로 흘러 나가며 블레이드 표면 압력에 영향을 미치는 것이다⁽¹⁰⁾. 그리고 블레이드 후연에서 보다 전연에서 시간에 따른 압력변동의 폭이 큼을 알 수 있으며, 이는 앞서의 정상상태 유동해석결과에서 전연의 압력이 후연에 비해 높은 것과 연관이 있다.

Fig. 6

Time variations of fan pressures

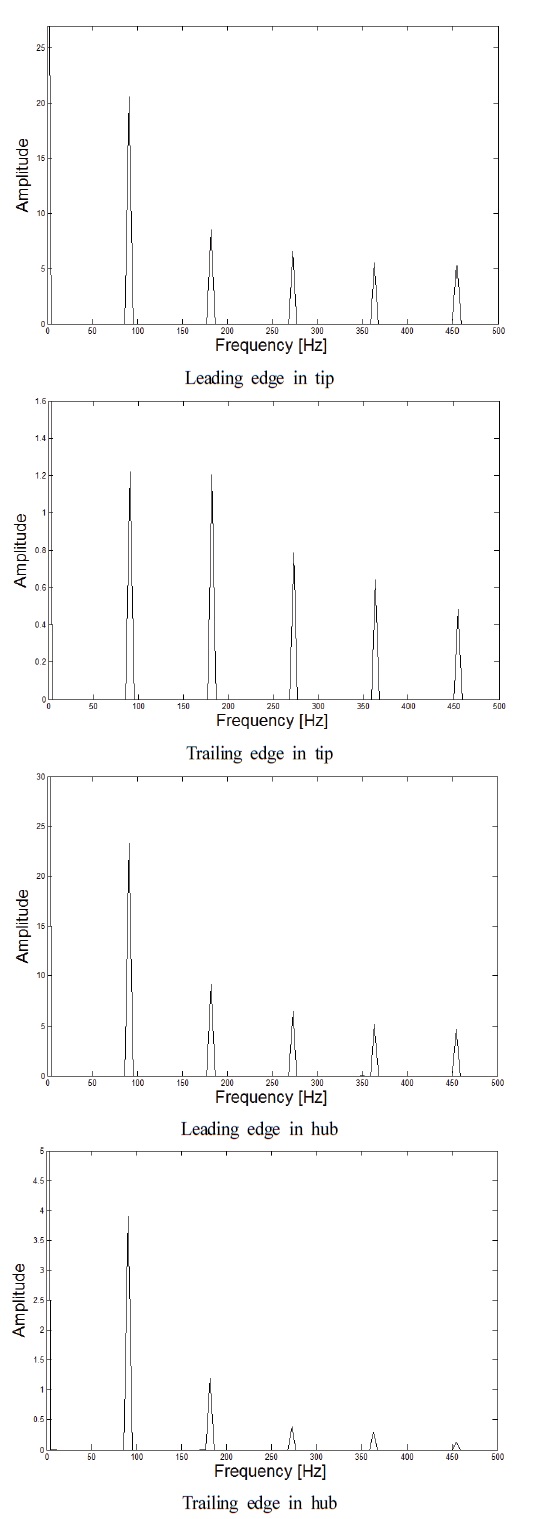
시간에 따른 압력변동 결과를 고속 푸리에변환(FFT:Fast Fourier Transform) 신호 처리한 결과가 Fig. 7 에 도시 되어있다. 홴 블레이드 표면의 모든 지점에서 압력 피크가 90, 180, 270, 360, 450 Hz 에서 발생하는 경향을 볼 수 있으며, 이러한 주파수들은 홴의 날개통과주파수(BPF:Blade Passing Frequency) 조화성분과 일치 한다. 즉 홴 블레이드 표면의 압력변동 및 블레이드 끝단에서의 누설유동에 의한 압력변동 모두 BPF 배수에서 발생하는 이산주파수(discrete frequency)의 주기적 현상임을 알 수 있다. 또한 블레이드 끝단 후연에서 2차 BPF 성분이 1차 BPF 성분에 비해 크게 줄어들지 않는 경향은, 앞서 Fig. 6의 압력변동 결과에서 알 수 있듯이, 끝단 근처의 누설유동에 의한 효과로 보여진다.

Fig. 7

FFT results of fan pressures

4.2 구조 및 진동해석 결과

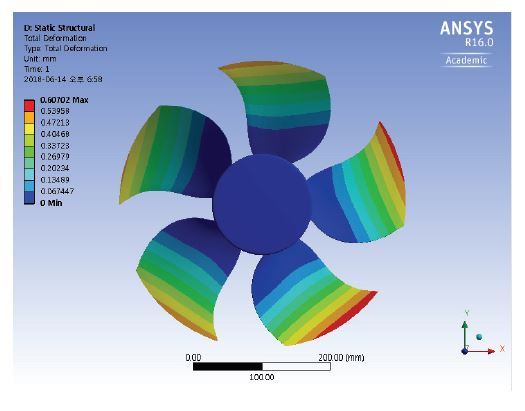
정상 상태의 홴 블레이드 표면의 변형분포에 대한 구조계산 결과가 Fig. 8 에 나타나 있다. 홴 블레이드 표면의 끝단 근처에서 변형이 가장 크며, 허브 쪽으로 갈수록 변형이 줄어드는 것을 볼 수 있다. 또한 블레이드 전연에서의 변형이 후연에 비해 더 큼을 알 수 있으며, 이러한 결과는 앞서의 유동해석의 압력계산 결과와 상관성을 가진다. 최대 변형은 끝단 근처에서 발생하며, 그때의 최대 변형량은 0.492 mm이고 홴의 회전축인 Z 방향으로의 변형이 가장 큰 0.370 mm이고 회전축과 수직인 X 방향과 Y 방향으로는 0.229 mm, 0.227 mm로 비슷하게 변형이 발생하고 있다.

Fig. 8

Deformation distribution on fan blade surface

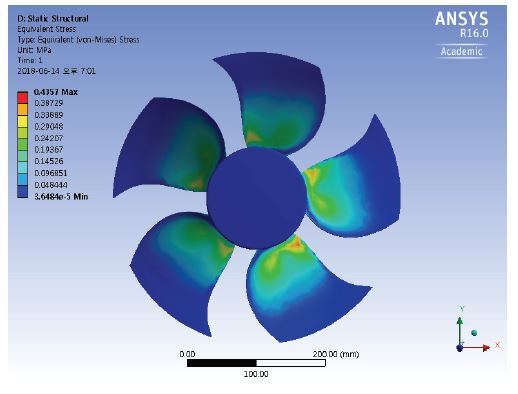
Fig. 9의 홴 블레이드 표면상의 응력분포를 보면, 홴의 허브 부근에서 최대 응력이 발생하는 것을 볼 수 있고, 끝단 근처로 갈수록 응력이 줄어드는 것을 볼 수 있다. 이러한 현상은, 일반적으로 블레이드 표면에 작용하는 응력은 블레이드 회전에 의한 원심력과 기체의 압력하중에 의한 것으로서, 그중에서도 원심력에 의한 응력은 정상상태 응력이고 허브에서 최대값을 가지며, 반면에 기체 하중에 의한 응력은 비정상 특성을 보이고 원심응력에 비해 그 크기가 상대적으로 작기 때문이다⁽¹¹⁾.

Fig. 9

Stress distribution on fan blade surface

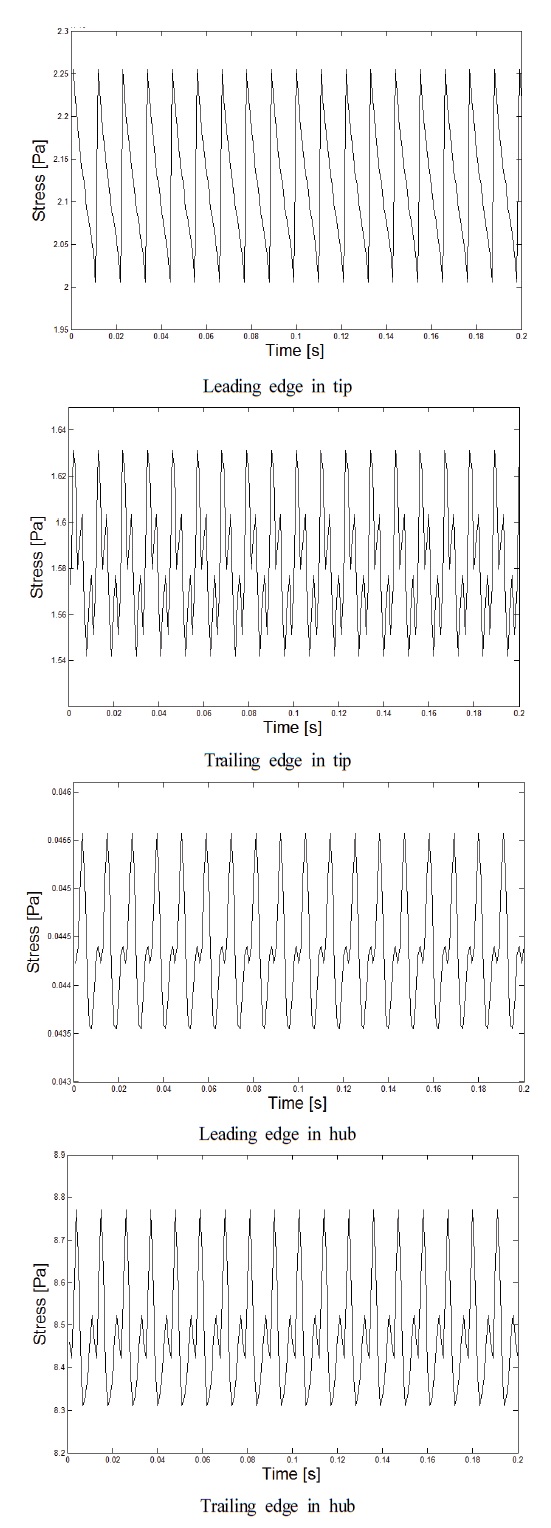
비정상 구조계산을 통해 얻어진 시간에 따른 홴 블레이드 표면의 응력변화가 Fig. 10 에 나타나 있다. 응력변동 곡선에서 보여지듯이, 블레이드 표면응력이 주기적으로 변화되며 진동을 유발함을 알 수 있다. 이러한 블레이드 표면응력 변동의 계산결과는 앞서의 공기압력 변동의 계산결과와 같은 주기(0.011 sec)를 가지고 동기화되어 있는 것으로 보이며, 이는 블레이드 표면의 진동이 공기압력의 변동에 의해 발생됨을 암시한다. 이때 진동의 최대 진폭은 250 kPa 에 이른다. 또한, 블레이드 끝단 후연에서의 응력변동 계산 결과로부터, 앞서 유동해석에서 관찰되었던 블레이드 끝단과 슈라우드 사이의 틈새에서 발생하는 누설 유동이 블레이드 진동에도 현저한 영향을 미치고 있음을 알 수 있다. 그리고 블레이드 허브 근처보다는 끝단 근처에서, 후연 보다는 전연에서 응력의 진폭이 더 큼을 확인할 수 있고, 이러한 결과들도 앞서의 공기압력 계산결과들과 밀접한 상관관계를 보여주고 있다.

Fig. 10

Time variations of stresses

그러나 블레이드 표면 응력의 변동 형태를 앞서 공기압력의 변동 형태와 비교하여 보면, 2가지 변동 형태들이 BPF 배수에서 동일하게 발생하고는 있으나 정점 발생 측면에서는 서로 다른 양상을 보이고 있다. 예를 들어, 블레이드 허브의 후연에서의 압력변동은 전형적인 정현파의 형태를 보이나 응력변동(또는 진동특성)은 2개의 정점을 가지는 주기적 형태를 보인다. 이러한 차이는, 비록 전체 블레이드 진동이 공기압력에 의해 야기되지만, 블레이드 진동 모드가 굽힙(bending)과 비틀림(twisting)에 의한 것으로 구분될 수 있고 이때 2가지 진동 모드가 위상차를 가지고 발생하는 것으로 설명될 수 있으며⁽¹²⁾, 이러한 진동 모드의 위상차는 향후 좀 더 상세한 연구 및 규명이 필요하다.

5. 결 론

본 연구에서는 축류 홴의 유동-구조 연성 해석 방법을 제안하였고, 이를 이용하여 냉동기용 플라스틱 축류 홴의 유동-구조 연성 해석을 수행하였다. 본 연구의 해석결과들로부터 얻어진 결론은 다음과 같다:

• 1) 홴 블레이드 끝단 틈새의 누설유동이 블레이드 표면의 공기 압력분포에 영향을 미치며, 이러한 유동현상은 블레이드 진동특성에도 현저한 영향을 미친다.
• 2) 홴 블레이드 표면의 압력가진 및 그에 따른 진동은 BPF 배수에서 발생하며, 블레이드 진동 특성은 블레이드 표면 공기압력 분포 및 변동 특성과 밀접한 연관관계를 가진다.
• 3) 홴 블레이드의 진동은 후연보다는 전연에서, 허브보다는 끝단 근처에서 크게 발생하며, 끝단 근처에서 진동특성은 끝단 틈새의 누설유동에 의해 큰 영향을 받는다.
• 4) 홴 블레이드 진동은 공기 압력의 시간변동 특성과 주기(또는 주파수) 측면에서 동기화 되어있으나, 진동주기 동안의 정점특성(peak-characteristics)은 압력특성과 다소간의 차이를 보인다.

Acknowledgments

본 연구는 2017 산업통상자원부 주관 에너지수요관리핵심기술개발의 일환으로 한국에너지기술평가원의 [정방향 운전 위주의 가역형 축류홴 개발] 지원으로 수행되었습니다.

References

• S. B. Ma, 2017, “Investigation on Aerodynamic Performance of a Highly-Loaded Axial Fan with Active/Passive Flow Control Using FSI Analysis”. Trans. of Korean Hydrogen and New Energy Society, Vol. 28, No. 1. [https://doi.org/10.7316/KHNES.2017.28.1.113]
• 김재우, 김진혁, 이찬, 김광용, 2010, “삼차원 수치해석을 통한 환기용 축류송풍기의 유동특성에 관한 연구,” 대한기계학회 유체공학부분 춘계학술대회 논문집, pp. 90-91.
• H. Hu, L. A. Jordan Jr., and J. D. Baeder, 2005, “Computational aimulation and analysis of double-swept blade in BVI noise reduction,” Advances in Engineering Software, Vol. 36, pp. 67-76. [https://doi.org/10.1016/j.advengsoft.2004.08.002]
• 권순국, 이영신, 배용채, 2010, “발전용 저압터빈 최종단 블레이드의 정적 유체-구조 연계해석,” 대한기계학회 논문집 A권 제34권 제8호, pp. 1067-1074.
• 장보연, 2016, 저압용 축류 홴에 관항 유체-구조 연성해석 연구, 석사학위논문, 수원대학교.
• 이찬, 길현권, 2010, “성능 및 소음특성을 고려한 축류 홴 설계의 전산체계,” 유체기계저널, 제13권 제2호, pp. 48-53. [https://doi.org/10.5293/KFMA.2010.13.2.048]
• Kyungwon Tech., 2017, FANDAS, Version 1.0.
• ANSYS, Inc., 2011, ANSYS Release 16.0.
• T. Zhu, M. Sturm, and T. H. Carolus, 2014, “Experimental and numerical investigation of tip clearance noise of an axial fan using a Lattice Boltzmana method,” 21st International Congress on Sound and Vibration Proceedings. [https://doi.org/10.1115/TBTS2013-2034]
• H. Hamakawa, M. Shiotsuki, T. Adachi, and E. Kurihara, 2012, "Correlation between aerodynamic noise and velocity fluctuation of tip leakage flow of axial flow fan," Open Journal of Fluid Dynamics, Vol.2, pp. 228-234. [https://doi.org/10.4236/ojfd.2012.24A026]
• H. Cohen, G.F.C. Rogers, and H.I.H. Saravanamuttoo, 1996, Gas Turbine Theory, 4th ed., Longman Group Limited.
• 김효상, 2018, 플라스틱 축류홴의 유동-구조 연성해석, 석사학위논문, 수원대학교.