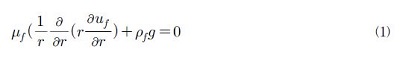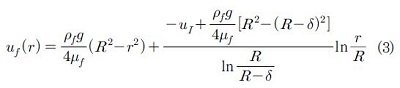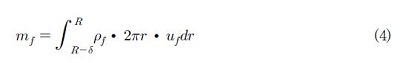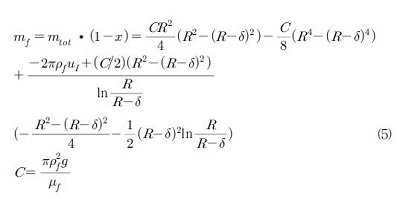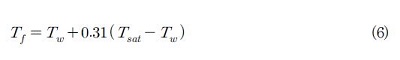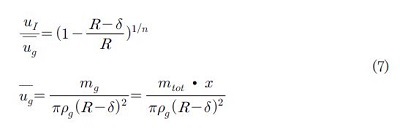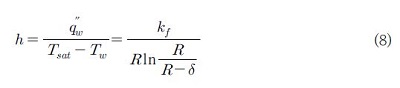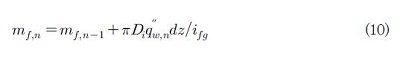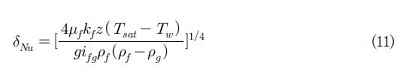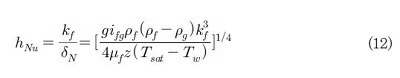Laminar Film Condensation Model of Pure Steam in a Vertical Tube

1. 서 론

수직관 내에서의 순수 증기의 응축은 원자력 발전소를 비롯한 다른 동력 및 전력생산 시스템에서 안전 및 사이클 효율 증진을 위한 핵심적인 메커니즘으로 활용되어 왔다. 이러한 증기 응축 현상은 크게, 고온의 증기가 저온의 표면에서 액적의 형태를 형성하면서 응축되는 적응축(Drop‐wise condensation) 및 액막을 형성하면서 응축되는 막응축(Film‐wise condensation)으로 구분할 수 있다. 그리고 발전 및 대부분의 산업 시스템에서 응용하는 응축과정은 막응축이며, 이러한 응축 시스템에서 막응축 현상은 열전달을 지배하는 주된 변수로 작용한다. 즉, 수직으로 배치된 응축기 튜브 내에서 응축수는 벽면에 특정 두께를 갖는 환형의 액체막(Liquid film)을 형성하고, 응축되지 않은 증기는 중심 영역에서 유동을 형성하게 된다. 이러한 환형의 액막은 응축과정에서 저온의 벽면과 고온의 증기 사이에서 주된 열저항(Thermal resistance)으로 작용하게 된다. 특히, 이러한 환형의 액막에서 액체의 유동이 층류일 때, 응축 열전달계수(Condensation heat transfer coefficient)는 액막의 열전도도 및 액막 두께의 함수로서 정의할 수 있게 된다. 또한, 중심 영역에 존재하는 증기 유동의 속도는 벽면 근처에 위치하는 액막의 속도보다 빠르기 때문에 증기‐액체 계면에 계면 전단응력을 발생시키게 되고, 이러한 증기 유동에 의한 전단 응력은 액막 내에서의 속도 분포를 변형시켜 액막 두께에 영향을 주게 된다.

Nusselt [1]는 저온의 수직 평판에 증기가 접촉하여 응축될 때 나타나는 층류 막응축 현상에 대한 이론적 모델을 최초로 제안하였다. 그의 연구에서 응축 액막은 층류로 가정하였고, 액막 내에서의 열, 물리적 물성치의 변화 및 과냉 효과는 무시하였다. 그리고 액체‐증기 사이에서 발생하는 계면 전단 응력 및 액막 내에서의 운동량 변화 또한 무시하였다. 이러한 가정들로 인하여 Nusselt [1]의 모델은 실제의 수직 액막 응축 현상을 정확하게 예측하는 데 있어 여러 가지 한계점을 가지고 있다. 그리하여 수직관 내 액막 응축 열전달에 관한 기존의 연구들은 Nusselt [1]의 모델에서 나타난 가정들을 실제 현상에 부합하도록 제거하고 개선된 모델을 도출하는 방식으로 수행되어 왔다. Rohsenow등 [2]은 액막 내에서의 과냉 효과 및 대류 에너지 전달을 반영할 수 있도록 Nusselt [1]의 모델에 나타나는 잠열 텀(latent heat term)을 수정하였다. 그리고 McAdams [3]는 액막 내에 존재하는 굴곡(waviness)으로 인한 열전달 면적의 증가를 고려하여, Nusselt의 상관식에 계수 1.2를 곱해야 올바른 열전달계수 값을 획득할 수 있다고 제안하였다. Dobran과 Thorsen [4]은 응축 열전달 과정을 지배하는 핵심 변수들을 도출하였고, 그러한 변수들의 변화에 따른 유동의 수력학적 특성 및 열전달 특성을 수치해석을 활용하여 연구하였다. Blanggetti와 Naushahi [5]는 액체‐증기 계면에서 계면 전단응력에 대한 응축 물질전달 기인 흡입 속도(suction velocity)의 효과를 이론적으로 연구하였다. Nakayama와 Koyama [6]는 이상 경계층 이론(two‐phase boundary layer theory)에 기초하여 층류 액막 응축 열전달에 관한 일반 적분 접근법을 제안하였다. 그리고 Chen과 Ke [7]는 수직 튜브 내 강제 대류 막응축에 관한 이론적인 연구를 수행하였다. 그들의 연구에서 튜브 중심영역에 형성되는 난류 증기 유동으로 인해 액막에 작용하는 계면 전단 응력을 고려할 수 있는 응축모델이 개발되었고, 이러한 모델은 Goodykoontz와 Dorsch [89]의 실험 데이터를 사용하여 검증되었다. Kuhn등 [10]은 수직관 응축실험을 통해 국부 응축 열전달에 관해 연구하였으며, 그들은 저감 인자 방법(degradation factor method), 확산층 이론(diffusion layer theory) 및 물질 전달 전도 모델(mass transfer conductance model)을 포함하는 3개의 상관식을 제안하였다. 최근에 Panday [11]는 액체 및 증기 상의 연계 경계층 방정식에 기초하여 수직관내에 액막 응축 열전달에 관한 수치적인 연구를 수행하였다. Oh와 Revankar [12]는 수직관 피동 응축기에서의 완전 응축에 관한 이론적 분석을 수행하여, 증기 계면 전단 응력 효과를 고려한 수정된 Nusselt모델을 제안하였고, 이를 위해 계면 전단 응력에 대한 물질 전달의 영향을 고려하였다. 또한 Lee [13]는 증기 전단 응력을 고려한 응축 열전달 상관식을 제안하였으며, 이 상관식에서 열전달계수는 Nusselt의 상관식 [1]에 무차원 증기 전단 응력 텀을 곱하는 방법으로 계산되었다.

층류 액막 응축상황에서 국부 열전달계수를 예측하기 위해서는 액막과 증기 영역에서의 수력학적 현상과 관련된 물리적 근거에 기초하여 국부 액막 두께가 결정되어야 한다. 수직관 응축에서 이러한 액막 두께는 중력, 액체 점성 및 중심 영역에서의 증기 유동에 현저한 영향을 받는다. 본 연구에서는 이러한 수직관 응축에서의 액막 두께 및 응축 열전달계수를 계산하기 위한 새로운 모델을 제안할 것이다. 그리고 제안된 모델로부터 획득된 결과를 기존의 수직관 증기 응축 실험 및 다른 연구자들의 응축 모델과 비교할 것이다.

2. 모델 개발

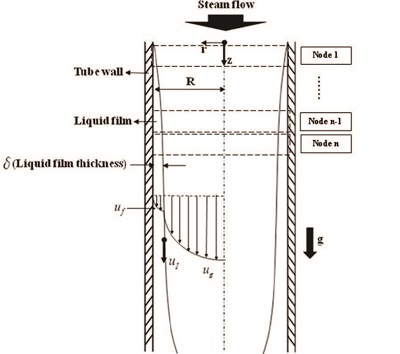
Fig. 1은 수직관 응축에서의 액막 및 증기 유동에 관한 간단한 모델 개념도를 나타낸다. 이 모델에서 증기 및 액체‐증기 계면의 온도는 포화온도로 가정하였으며, 액막 유동은 층류로 가정하여 액막에서의 열전달은 1차원 열전도 메커니즘으로 가정하였다. 그리고 액체 및 증기의 유동 방향은 수직 하향이다. 국부 관 내벽온도 및 입구 증기 질량 유량은 경계조건으로 주어진다. 그리고 액막 유동은 벽면 유체 점착조건(No‐slip condition) 및 액체‐증기 계면에서의 속도에 의해 유발되는 쿠에트 유동(Couette flow)으로 가정하였다.

Fig. 1

Simple model concept of the film condensation in a vertical tube

2.2. 액체‐증기 계면에서의 계면 속도

본 연구에서 제안하고자 하는 모델에서 액체‐증기 계면에서의 계면 속도는 핵심적인 변수이다. 이러한 계면 속도를 정확하게 결정하기 위해서는 관 중심 영역에서 형성되는 기체의 난류 유동과 액막의 층류 유동에 관한 지배 방정식을 풀어야 하고 계면에서의 물질 전달 및 운동량 전달에 관한 다수의 가정 및 경험적 상관식들을 사용해야 한다. 그러나 이것은 복잡한 계산 과정과 긴 계산시간이 요구된다. 그리하여 본 연구에서는 액체‐증기 계면 속도를 예측하기 위해 계면 속도 및 증기의 평균 속도의 관계를 관의 반경과 액막 두께에 대한 지수법칙으로 단순화할 수 있다는 가정하에 식 (7)의 경험적 지수법칙 속도 분포(empirical power‐law velocity profile) [15]를 도입하였다.

여기서 n은 양의 상수, 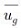는 증기 평균속도, m_g는 증기 질량 유량 그리고 ρ_g는 증기의 밀도이다.

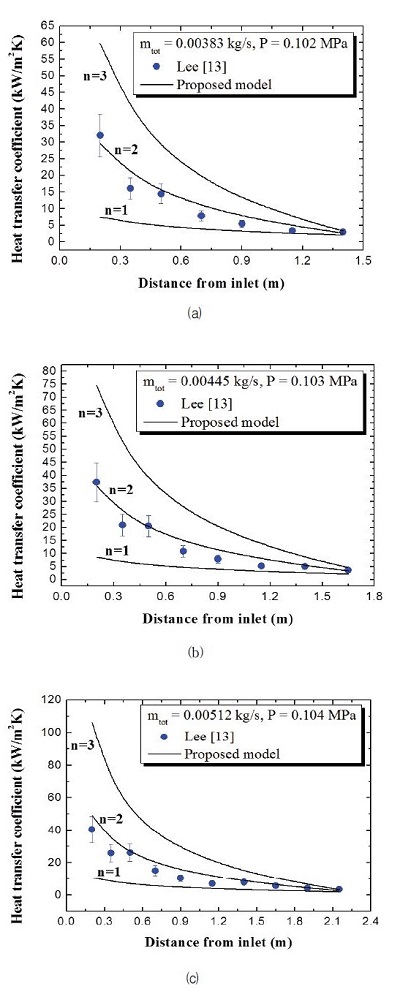
그러므로 본 연구에서 제안되는 모델의 예측 값은 식 (7)로부터 계산되는 계면 속도에 따라 크게 좌우될 것이다. 즉, 식 (7)의 n은 매우 중요한 변수이다. 층류 액막 응축에서 액막의 두께는 매우 얇고(수십∼수백 μm 오더), 이러한 액막 내에서는 점성력이 지배적으로 작용한다. 그러므로 벽면 근처에 위치하는 계면의 속도가 층류 속도 구배를 따른다는 것은 합리적인 가정이 될 수 있을 것이다. 이론적으로, 층류 유동에서 n의 값은 2이다. 또한 본 연구에서는 층류 액막 응축 실험 데이터와 모델의 비교를 통해 n=2는 실험 데이터를 적절하게 예측할 수 있는 값이라고 판단하였다(Fig. 2a, b 및 c). 이러한 3개의 그래프에서 보는 바와 같이, 본 연구에서 제안된 모델을 통해 예측한 응축 열전달 계수는 Lee [13]의 상압 조건에서의 유량에 따른 응축 열전달계수 실험 데이터를 n=1, 3 일 때에 비해 n= 2 일 때 정확하게 예측하는 것을 알 수 있다.

Fig. 2

Condensation heat transfer coefficients data (Lee [13])predicted from the proposed model by the variation of n value in Eq. 7: (a) mtot = 0.00383 kg/s, P = 0.102 MPa, (b) mtot = 0.00445 kg/s, P = 0.103 MPa, and (c) mtot = 0.00512 kg/s, P = 0.104 MPa

3. 모델해(Solution) 도출 절차

본 연구에서 제안되는 모델로부터 획득되는 최종 결과는 층류 액막의 두께 및 응축 열전달계수 이다. 수직관 내에 환형의 액막과 액막에서의 전도에 의한 열전달 메커니즘을 고려하면 Fig. 1에서와 같이 응축관을 수직 방향으로 n개의 구역으로 나누었을 때 n번째 위치에서의 열전달계수에 관한 식을 아래와 같이 획득할 수 있다.

여기서 q^″_w는 벽면 열유속 그리고 k_f는 액막의 열전도도 이다. 식 (8)로부터 n번째 위치에서의 국부 열유속은 다음과 같다.

그리하여 n번째 지점에서의 액막의 질량 유량은 다음과 같이 표현할 수 있다.

여기서 D_i는 관의 내경(국부 열유속을 관 내경 기준으로 산출하였으므로), dz는 국부 지점 사이의 축방향 거리, 그리고 i_fg는 증기 응축 잠열이다.

그리하여 국부 응축 액막 두께는 식 (5)와 식 (10)에서 각각 획득된 액막의 질량 유량의 차이가 최소가 되도록 반복 계산법(iteration)을 수행하여 구할 수 있다. 이러한 반복 계산절차는 식 (5)를 통해 계산된 액막의 질량 유량이 식 (10)에서 구한 액막의 질량 유량보다 작아질 때까지 반복 수행되었다. 모델해의 도출을 위해 축방향 격자 크기(dz)는 1 mm로 설정하였다. 본 연구에서 제안된 모델은 z=0지점에서 특이점(singularity)를 나타내기 때문에 모든 계산은 z=1 mm를 시작점으로 하여 수행되었다. 본 모델에서 액막은 층류 상태로 가정하였기 때문에 모델은 액막 레이놀즈 수, Re_f = 4m_f/(πD_iμ)가 2300보다 작은 영역에서 적용할 것을 추천한다.

다음 장에서는 본 연구에서 제안된 모델을 검증하기 위해 모델에서 획득된 액막 두께 및 응축 열전달 계수를 Goodykuntz와 Dorsch [8] 및 Lee [13]의 실험데이터와 비교할 것이다.

4. 결과 및 토론

본 연구에서는 제안된 모델을 검증하기 위해 Goodykuntz와 Dorsch [8] 및 Lee [13]의 증기 응축 실험데이터를 활용하였다. Goodykuntz와 Dorsch의 실험에서, 응축 튜브는 길이 2.4 m의 스테인레스 스틸 관이었으며, 내경은 15.9 mm 였다. 그리고 Lee의 실험에서 응축관은 3 m 길이의 304 스테인레스 스틸 관이었으며, 내경은 13 mm, 관 두께는 2.5 mm 이며, 열전달 유효 길이는 2.8 m 였다. 두 실험 모두 응축관의 냉각과 국부 열유속 측정을 위해 시험부 응축관의 외부에 냉각 재킷(cooling jacket)를 장착하여 냉각수 유동을 증기 유동과 반대 방향으로 평행하도록(counter‐current flow) 조성하였다. 또한 두 실험 모두 증기 유동의 방향은 수직 하향이었다. Table 1은 본 모델의 분석을 위해 활용된 실험데이터들의 실험 조건을 나타낸다. 또한 제안된 모델은 기존의 Nusselt모델 [1] 결과와도 비교되었다. Nusselt의 액막 응축 모델에서 액막 두께와 응축 열전달계수는 각각 식 (11) 과 식 (12)와 같다.

여기서 z는 증기가 유입되는 응축관 입구로부터의 축방향 거리이다.

Fig. 3a, b 및 c에서 볼 수 있는 것처럼 본 연구에서 제안된 모델로부터 획득된 응축 열전달계수 값은 Goddykuntz와 Dorsch [8]의 데이터를 비교적 정확하게 예측하였다. 그러나 Nusselt모델(식 (12))는 실험데이터를 현저히 낮게 예측하였다. 이것은 Nusselt모델에서 관 중심 영역에서의 증기 유동의 효과를 무시하였기 때문이다. 반면에 본 연구에서 제안된 모델은 증기 유동에 의한 액막 두께가 얇아지는 현상을 적절히 반영하고 있는 것으로 판단된다. 그리고 Fig. 4a, b 및 c에서 볼 수 있듯이 제안된 모델로부터 획득된 액막 두께는 입구 근처에서는 서서히 증가하며 수직 응축 튜브의 하단부에서 급격히 증가하는 결과를 나타냈다. 그리고 이러한 모델로부터 계산된 액막 두께는 출구 근처를 제외 한 대부분의 영역에서 Nusselt모델로부터 획득된 액막 두께(식 (8))보다 현저히 얇은 경향을 나타냈다.

Table 1.

Selected experimental conditions of previous researchers (Goodykuntz and Dorsch [8], and Lee [13])

Fig. 3

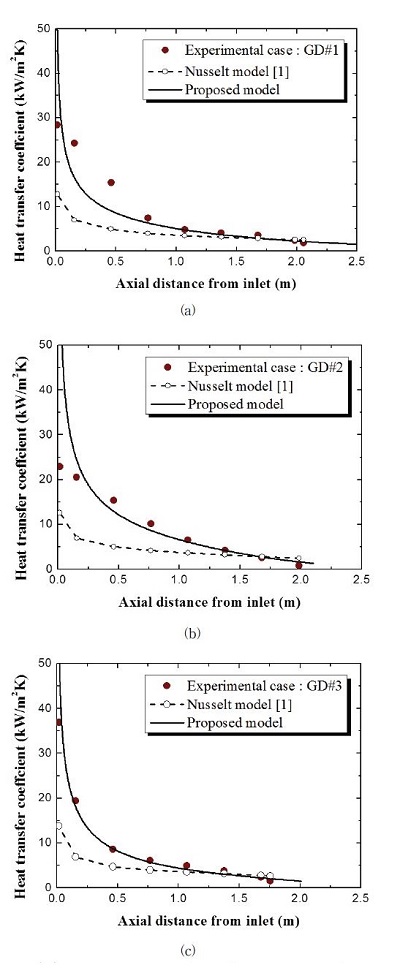
Condensation heat transfer coefficient distributions from the experiments (Goodykuntz and Dorsch [8]), the Nusselt model [1] and the proposed model at (a) Experimental case: GD#1, (b) Experimental case: GD#2, and (c) Experimental case: GD#3

Fig. 4

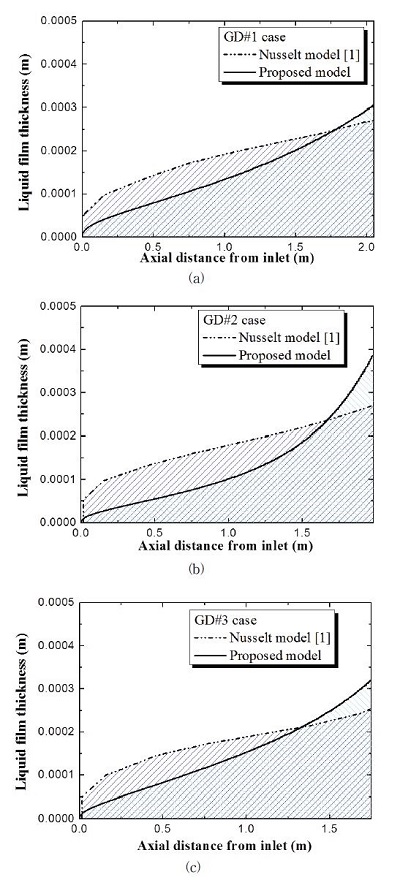
Liquid film thickness distributions from the proposed model and Nusselt model: (a) Experimental case: GD#1, (b) Experimental case: GD#2, and (c) Experimental case: GD#3

다음으로 제안된 모델로부터 계산된 계면 속도는 Fig. 5에서 볼 수 있는 것처럼 입구 근처의 영역에서 급격하게 증가하였다. 이것은 이 영역에서의 액막 두께가 매우 얇기(δ≪0.1mm) 때문인 것으로 판단된다. 그리고 응축 튜브의 하단부에서는 액막 두께가 증가함에 따라 계면 속도가 차츰 감소하였다. 또한 본 연구에서는 제안된 모델의 응축 열전달계수 예측결과를 Lee [13]의 실험데이터와도 비교하였다. Lee는 무차원 증기 전단 응력을 활용하여 식 (13)의 액막 응축 열전달에 관한 상 관식을 제안하였다.

Fig. 5

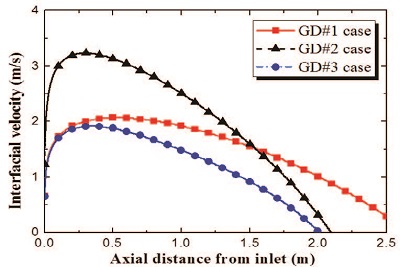
Interfacial velocity profile calculated from the proposed model in experimental case GD#1, GD#2 and GD#3

여기서 무차원 전단 응력 τ^*_g는 다음과 같이 정의되었다.

여기서 f는 증기 유동에서의 마찰 계수 이고, L 은 L = [μ²_f/(gρ²_f)]^1/3로 정의되는 특성 길이(characteristic length)이다.

Fig. 6a, b 및 c에서 볼 수 있는 것처럼, Nusselt모델은 Lee의 실험데이터를 현저히 낮게 예측하였다. 그리고 식 (13)의 Lee의 모델은 수직 응축관 하단부에서의 실험데이터는 잘 예측하였으나, 상단부에서의 열전달계수 데이터를 다소 낮게 예측하였다. 하지만 본 연구에서 제안된 모델의 경우 Lee [13]의 열전달계수에 대한 실험데이터를 대부분의 영역에서 잘 예측하였다. 그리고 본 연구에서는 제안된 모델의 신뢰성을 평가하기 위해 앞서 언급한 Goodykuntz와 Dorsch [8] 및 Lee [13]의 실험데이터를 모델 예측값과 비교하였다(Fig. 7). 그림에서 볼 수 있는 것처럼 본 모델의 예측값은 실험데이터를 ±30 % 오차범위 이내에서 비교적 정확하게 예측하였다.

Fig. 6

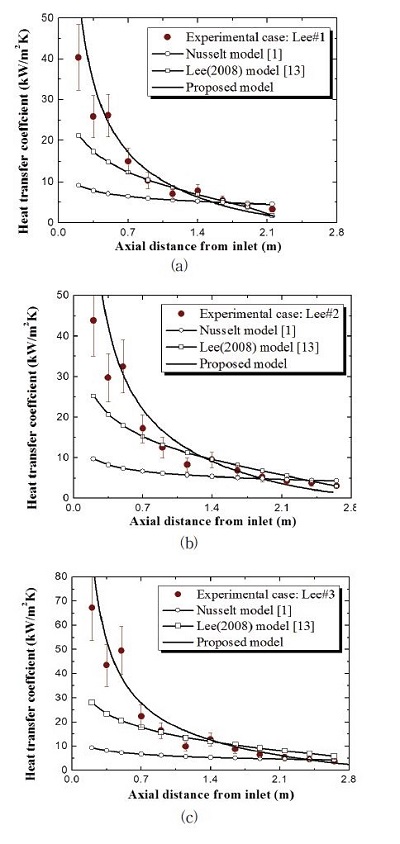
Condensation heat transfer coefficient distributions from the experiments (Lee [13]), the Nusselt model [1], Lee model and the proposed model at (a) Experimental case: Lee#1, (b) Experimental case: Lee#2, and (c) Experimental case: Lee#3.

Fig. 7

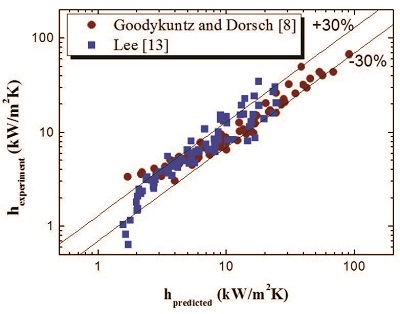
Comparison of the heat transfer coefficients from the present model (hpredicted) and from the experiments (hexperiment) of Goodykuntz and Dorsch [8] and Lee [13]

본 절에서는 수직관 내 층류 액막 응축열전달에 관한 새로운 모델이 제안되었고, 이러한 모델을 기존 연구자들의 실험 데이터 및 Nusselt모델 [1] 및 Lee모델 [13]과의 비교를 통해 분석하였다. 그러므로 본 연구에서 제안된 증기 응축 열전달 모델은 관 중심 영역에 형성되는 증기 유동에 의해 유발되는 증기 전단응력으로 인한 액막이 얇아지는 현상을 반영할 수 있고, 다른 연구들에서 수행된 실험으로부터 획득된 응축 열전달계수 데이터를 합리적으로 예측할 수 있는 것으로 판단된다.

5. 결 론

본 연구에서는 중력, 액체 점성 및 유동 중심부에서의 증기 유동을 고려하여 수직 응축관 내에서의 액막 두께 및 응축 열전달계수를 계산하기 위한 새로운 모델을 제안하였다. 액막 내에서의 속도 분포를 도출하기 위해 액막 유동은 액체‐증기 계면에서의 속도에 의해 유발되는 쿠에트 유동(Couette flow)으로 가정하였다. 또한 모델 개발을 위한 수치적 계산 과정을 단순화하기 위해 액체‐증기 계면 속도를 추정하는 데 있어, 경험적 지수법칙 속도분포(empirical power‐law velocity profile)를 도입하였다. 응축 액막의 두께는 모델 방정식으로부터 반복 계산법을 통해 계산하였으며, 모델 계산의 결과로부터 획득된 국부적인 응축 액막 두께 및 열전달계수 값은 Goodykuntz와 Dorsch [8] 및 Lee [13]의 실험데이터, 그리고 Nusselt모델 [1] 및 Lee모델 [13]과 비교되었다. 결론적으로, 본 연구에서 제안된 증기 응축 열전달 모델은 관 중심 영역에 형성되는 증기 유동에 의해 유발되는 증기 전단응력으로 인한 액막이 얇아지는 현상을 반영할 수 있고, 다른 연구들에서 수행된 실험으로부터 획득된 응축 열전달계수 데이터를 합리적으로 예측할 수 있는 것으로 나타났다.

References

• W. Nusselt, ‘Die ober achenkondensation des wasserdampfes– the surface condensation of water’, Zeitschrift Vereines Deutscher Ingenieure, (1916), 27, p541-546.
• W. M. Rohsenow, J. H. Webber, A. T. Ling, ‘Effect of vapour velocity on laminar and turbulent film condensation’, Trans. ASME, (1956), 78, p1637-1643.
• W. H. McAdams, “Heat transmission 3rd ed.”, McGraw-Hill, New York, (1954).
• F. Dobran, R. S. Thorsen, ‘Forced flow laminar filmwise condensation of a pure saturated vapor in a vertical tube’, Int. J. Heat Mass Transfer, (1980), 23, p161-177. [https://doi.org/10.1016/0017-9310(80)90194-5]
• F. Blangetti, M. K. Naushahi, ‘Influence of mass transfer on the momentum transfer in condensation and evaporation phenomena’, Int. J. Heat Mass Transfer, (1980), 23, p1694-1695. [https://doi.org/10.1016/0017-9310(80)90231-8]
• A. Nakayama, H. Koyama, ‘An integral procedure for a two-phase boundary layer in laminar film condensation’, Int. J. Multiphase Flow, (1986), 12, p135-144. [https://doi.org/10.1016/0301-9322(86)90009-1]
• S. L. Chen, M. T. Ke, ‘Forced convective film condensation inside vertical tubes’, Int. J. Multiphase Flow, (1993), 19, p1045-1060. [https://doi.org/10.1016/0301-9322(93)90077-8]
• J. H. Goodykoontz, R. G. Dorsch, ‘Local heat-transfer coefficients for condensation of steam in vertical down flow with 5/8 in. diameter tube’, Report NASA TN, D3326, (1966).
• J. H. Goodykoontz, R. G. Dorsch, ‘Local heat-transfer coefficients and static pressures for condensation of high velocity steam within a tube’, Report NASA TN, D3953, (1967).
• S. Z. Kuhn, V. E. Schrock, P. F. Peterson, ‘An investigation of condensation from steam-gas mixtures flowing downward inside a vertical tube’, Nuc. Eng. Des, (1997), 177, p53-69. [https://doi.org/10.1016/S0029-5493(97)00185-4]
• P. K. Panday, ‘Two-dimensional turbulent film condensation of vapours flowing inside a vertical tube and between parallel plates: a numerical approach’, Int. J. Refrigeration, (2003), 26, p492-503. [https://doi.org/10.1016/S0140-7007(02)00162-7]
• S. Oh, S. T. Revankar, ‘Analysis of the complete condensation in a vertical tube passive condenser’, Int. Comm. Heat Mass Transfer, (2005), 32, p716-727. [https://doi.org/10.1016/j.icheatmasstransfer.2004.10.013]
• K. Y. Lee, ‘The effects of noncondensable gas on steam condensation in a vertical tube of Passive Residual Heat Removal System’, Ph. D. Thesis., POSTECH, Korea, (2008).
• W. J. Minkowycz, E. M. Sparrow, ‘Condensation heat transfer in the presence of noncondensabls, interfacial resistance, superheating, variable properties and diffusion’, Int. J. Heat Mass Transfer, (1966), 9, p1125-1144.
• B. R. Munson, D. F. Young, T. H. Okiishi, “Fundamentals of fluid mechanics 4th ed.”, John Wiley & Sons, New York, (2002).